② 吉林大学地球探测科学与技术学院, 吉林长春 130026
② College of Geoexploration Science and Techno-logy, Jilin University, Changchun, Jilin 130026, China
铀矿是关系国家安全、国计民生的重要战略资源,对其的需求与日俱增。近年来,随着低成本、低污染的地浸采铀技术的成熟,砂岩型铀矿逐渐成为中国能源部门重要的找矿类型[1-4]。在勘探不断深入的同时,面临的地质问题也日趋复杂。为此,进入21世纪以来, 有关部门也开展了针对砂岩型铀矿的地震勘探工作,主要目的是查清含矿层的形态和构造特征。在地震反演方面,主要应用叠后波阻抗反演预测有效储层[5-9]。但是,有关铀矿体的预测技术的相关研究报道十分有限,其中一个主要原因是铀矿体的厚度普遍较小(一般小于10m), 常规确定性反演的纵向分辨率很难满足精度需要。
地质统计学反演的概念最早由Haas等[10]在1994年提出,到了1998年Dubrule等[11]将该技术用于三维地震数据体反演。地质统计学反演技术由地质随机建模与地震数据共同驱动,可以将各类地质信息和测井资料融入反演,突破了地震频带宽度的限制,可实现纵向高精度表征;同时利用地震资料横向信息丰富的优势,反演结果充分展示了储层等信息的横向变化及非均质性[12-16]。该技术广泛用于油气勘探、开发领域,预测结果与井上地质信息吻合更好,大幅提高了薄储层的表征精度[17-20]。在铀矿勘探领域,人们也尝试应用地质统计学反演预测铀矿体的展布[21],但是由于其预测结果的随机性较强,实际应用效果局限性较大。地质统计学反演的可靠性主要受控于变差函数等关键参数的选取[22-24],传统的求取变差函数横向变程方法的随机性较强。
为了降低地质统计学反演的随机性,提高有效性和反演精度,需要在求取横向变程时融入更多的先验信息并赋予变差函数更明确的地质含义。在油气储层反演领域,樊鹏军等[25]认为对变差函数赋予明确的地质含义可以大幅提高反演可靠性和精度。鉴于此,本文将该思想引入QJD大型典型砂岩型铀矿的矿体预测。该区在早期的石油勘探中采集了大量的三维地震资料,在多年的勘探过程中还积累了丰富的地质、钻井、测井以及含矿性等资料。因此,完全可以充分利用该地区勘探程度高、井数多、井网分布均匀等先验信息和三维地震资料丰富的横向信息预测铀矿体,尤其是在测井数据、矿体规模和含矿性等数据的充分控制下提出准确的变差函数求取方法,可降低地质统计学反演的随机性,进而更精确、有效地反演矿体形态。为此,首先阐述地质统计学反演的基本原理;其次,阐述变差函数的定义及地质意义;然后,提出新的变差函数求取方法;最后,分析反演结果的可靠性和实际应用效果并给出相关结论。
1 地质统计学反演的基本原理与实现流程面向目标参数估计的地质统计学反演问题实际上可以归结为一个贝叶斯参数估计问题,即:在一些观测信息的基础上,通过不断更新先验信息得到目标参数估计问题的条件最优解。在贝叶斯推论框架下,地震数据反演问题实际为测井数据约束下基于地震数据的目标参数反演问题,其表达式为
| $ P(R\left| {L, S) = } \right.P(R\left| {L)} \right.P(S\left| R \right.)/P(S) $ | (1) |
式中:R为待反演的目标参数分布;L为测井数据;S为地震数据。式(1)的含义为:在同时满足L和S条件下的R的后验概率P(R│L, S)为已知L的条件概率P(R│L)与S的似然函数P(S│R)/P(S)的乘积。由于概率分布的复杂性,式(1)无法求得解析解,但可以采用MCMC(Markov Chain & Monte Carlo)方法进行概率评价。面向砂岩型铀矿的地质统计学反演步骤如下(图 1)。

|
图 1 地质统计学反演方法的实现流程 |
(1) 基础数据分析,包括对地震、测井、矿体等数据的分析。地震数据分析包括资料面积分布、资料规则化、资料主频和频宽等分析,确定地震资料是否满足目标预测的需要,同时可以对成果数据进行提频、去噪等预处理;测井资料分析包括井的数量、空间分布、曲线完整性、标准化等分析,核心是分析测井属性的岩石物理敏感性,进而确定目标反演参数,其中面向砂岩型铀矿矿体的目标参数是自然伽马(GR)数据。
(2) 结合井震数据对反演目标实施精细井震标定、精细构造解释和构造地质建模。该地质模型构成整个反演的模型框架,并采用三维网格模型将其离散,构成模型参数的分布空间,进而获取反演的初始模型。
(3) 求取纵向、横向变差函数。统计、分析测井数据求取纵向变差函数,统计、分析已开发区矿体规模和含矿性信息求取横向变差函数,分别作为地质统计学的纵向和横向约束条件,构成了反演的核心参数。
(4) 利用MCMC算法获得统计意义下的储层参数随机样点分布。MCMC算法步骤为:①根据步骤(1)~步骤(3)确定初始模型和反演参数;②通过后验概率密度函数采样随机生成一个新的模型;③对新模型实施正演计算得到合成地震数据,并利用实测地震数据计算上述新模型的似然函数;④求取新模型的先验概率,再乘以步骤③得到的似然函数,得到新模型的后验概率;⑤对比新模型的后验概率与当前目标模型的后验概率,若前者大于后者则接受新生成的模型,并将Markov链移动到新模型位置,否则随机决定是否保留;⑥重复步骤②~步骤⑤,直到后验概率不再改变,循环结束,并输出计算结果。
2 变差函数的求取方法 2.1 变差函数的地质意义从上述的地质统计学的基本原理与反演实现过程发现,选择合适、有效且最能刻画目标参数的先验信息尤其重要,涉及求取纵向和横向变差函数。同时,在地质统计学反演中,变差函数具有重要的地质意义。在铀矿体预测方面,变差函数实际上反映了矿体在三维空间的变化特征,表征矿体的空间各向异性。其中,纵向变程反映矿体垂向厚度,其值决定反演的纵向分辨率;横向变程则反映矿体的横向发育规模,其不同方向取值反映储层的空间各向异性,长轴方向代表矿体长度,短轴方向代表矿体宽度。鉴于变差函数具有实际地质指导意义,因此其求取方法非常重要。准确求取变差函数是降低地质统计学反演随机性的重要途径,是反演结果有效性和精度的重要保证。
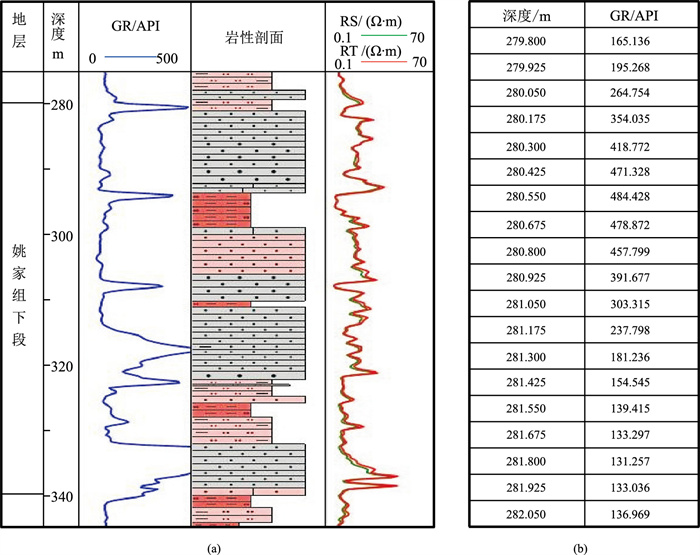
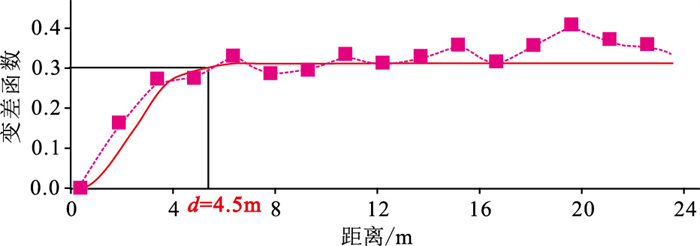
2.2 纵向变程的求取砂岩型铀矿体厚度较小且变化快,在预测矿体时过大的纵向变程会使反演结果不能精确地反映矿体厚度,而过小的纵向变程则会成倍增加计算时间并增大反演结果的随机性。为此,本文在求取纵向变程时,提出了一种结合测井资料与实际矿体形态的综合统计方法,分析工区内均匀分布的20口井的GR曲线样本点。目的层姚家组下段地层厚度普遍大于60m,测井数据采样间隔为0.125m,因此样本点个数远大于(一般要求的)50(图 2)。QJD矿区31个主要矿体的最大厚度为7.70m,最小厚度为2.25m,平均厚度为4.48m,综合测井数据和实际矿体厚度,确定研究区的纵向变程为4.5m。通过分析测井数值得到的变差函数(图 3)可以看出:数据点间相关性很明显,且当纵向变程大于4.5m时,变差函数曲线趋于平缓。上述计算纵向变程的方法以大量实测数据统计、分析结果作为反演的纵向约束,尽可能在已有先验井数据控制下得到符合地质意义的反演结果,进而最大限度地降低反演的随机性。
|
图 2 工区测井资料分析 (a)测井解释图(GR代表伽马测井,RT代表深双侧向电阻率测井,RS代表浅双侧向电阻率测井);(b)部分深度段测井数据 |
|
图 3 纵向变程分析图 块金值约等于0,基台值为0.3,因此空间相关度远小于25% |
利用常规方法求取横向变差函数时,由于井网密度很难达到横向采样要求,通常提取叠后稀疏脉冲反演平面属性求取一个大致的变差范围。本次研究首先对该方法进行测试,结果表明:在矿体横向预测方面,反演结果横向连续性较差,与实际矿体展布情况差别较大。说明该方法虽然弥补了井曲线横向样本不足的缺陷,但是其横向分辨率有限且没有充分结合变差函数的地质意义,所以很难解决地质统计学反演的横向不确定性问题。
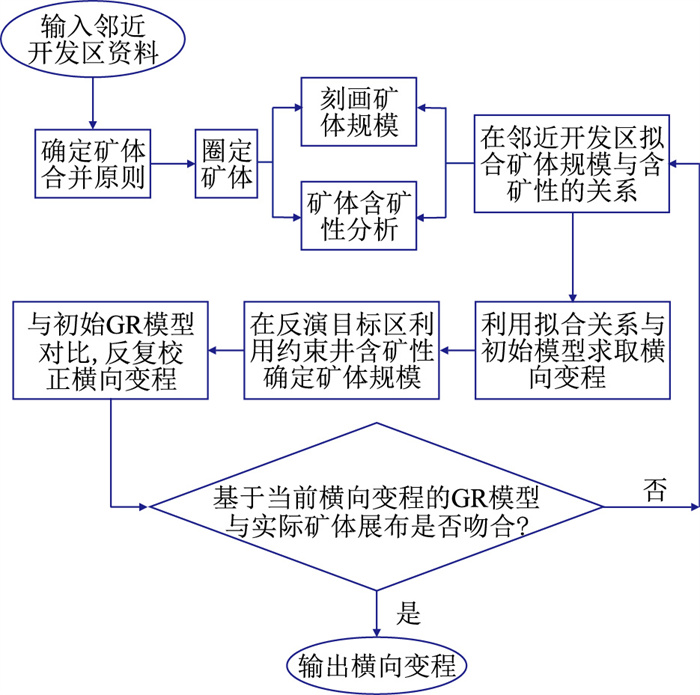
针对上述问题,基于QJD铀矿床勘探程度较高且对矿区的沉积模式、矿体规模和成矿规律等的较成熟认识,并结合变差函数的地质意义,提出一种在已开发区矿体成矿模式和矿体展布规律先验信息约束下的横向变程求取方法。该方法的核心思想是:首先在有大量开发井的邻近已开发区域建立矿体规模和单矿点最高平米铀量之间的拟合关系,然后在反演的目标区域利用该拟合关系和反演约束井的最高平米铀量,计算反演目标区矿体规模的横向变程作为反演的核心参数(图 4)。为了建立上述拟合关系,首先需要确定矿体合并原则并圈定矿体,然后统计、分析矿体规模与矿体含矿性关系,最终在反演目标区域求取横向变程,详述如下。
|
图 4 横向变程求取流程图 |
(1) 矿体合并原则
结合研究区储层和区域隔水层发育特征,将目的层姚家组划分为6套含矿层系,在各含矿层系内将可渗透砂岩中的异常层合并,将合并后平米铀量大于1kg/m2且品位大于0.1‰的矿体定为工业层,将平米铀量小于1kg/m2且品位大于0.1‰的矿体定为矿化层。本次研究以工业层为主要对象。
(2) 圈定矿体
在充分考虑控矿因素的基础上,参考相关行业规定,将各工业井的井点位置作为矿体中心位置的水平投影点,矿体的边界线由各邻井的外推点直接相连而成,连接时走向点与走向点相连、倾向点与倾向点相连。工业井与矿化井之间按勘查工程间距的1/2平推;工业井与无矿井之间则按勘查工程间距的1/4平推。
(3) 矿体规模与矿体含矿性的关系
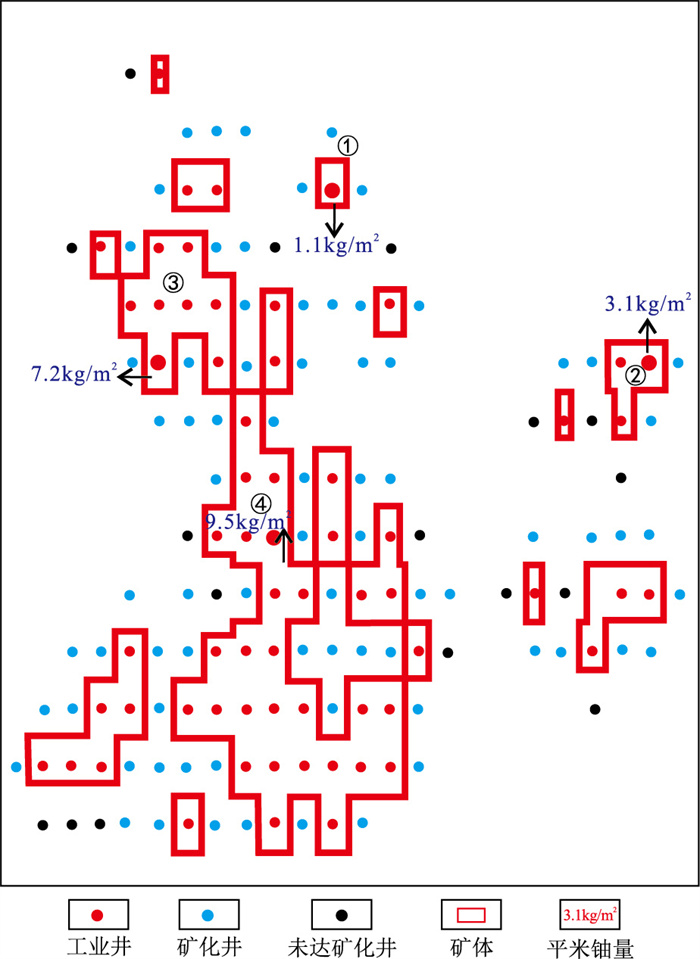
分析矿体规模与矿体含矿性的关系,首先圈定矿体的空间展布形态并确定矿体规模(长度和宽度),然后标注各矿体的含矿性(平均平米铀量),最后通过拟合两者的数值关系即可建立矿体规模与矿体含矿性的关系(图 5)。统计、分析QJD地区上百个矿体的规模与含矿性关系表明:在储层非均质性变化不大的情况下,矿体的规模(长度及宽度)与矿体的平米铀量呈明显的正相关,即矿体规模越大则含矿性越高。
|
图 5 矿体的平面分布 图中显示了一个局部区块圈定的矿体①~④及其含矿性 |
(4) 求取横向变程
在步骤(1)~步骤(3)的基础上,即可求取横向变程,具体为:
(a) 通过步骤(3)建立矿体规模与矿体最高平米铀量之间的拟合关系
| $ l = 169.9\ln x + 102.7 $ | (2) |
| $ b = 7.2x + 60 $ | (3) |
式中:l为矿体长度;b为矿体宽度;x为矿点的最高平米铀量。
(b) 在反演的目标区域,利用20口井资料,基于式(2)和式(3),在已知单矿点x的情况下,求取研究区各矿体的规模。
(c) 对比步骤(b)的结果与初始GR模型,反复修正横向变程。
(d) 判断基于当前变程的GR模型与矿体展布规律的吻合程度。若吻合程度达到要求,则输出横向变程;否则重复步骤(a)~步骤(d),直至吻合程度达到要求。
基于步骤(a)~步骤(d),最终确定表征研究区矿体长度和宽度的横向变程分别为700、300m。
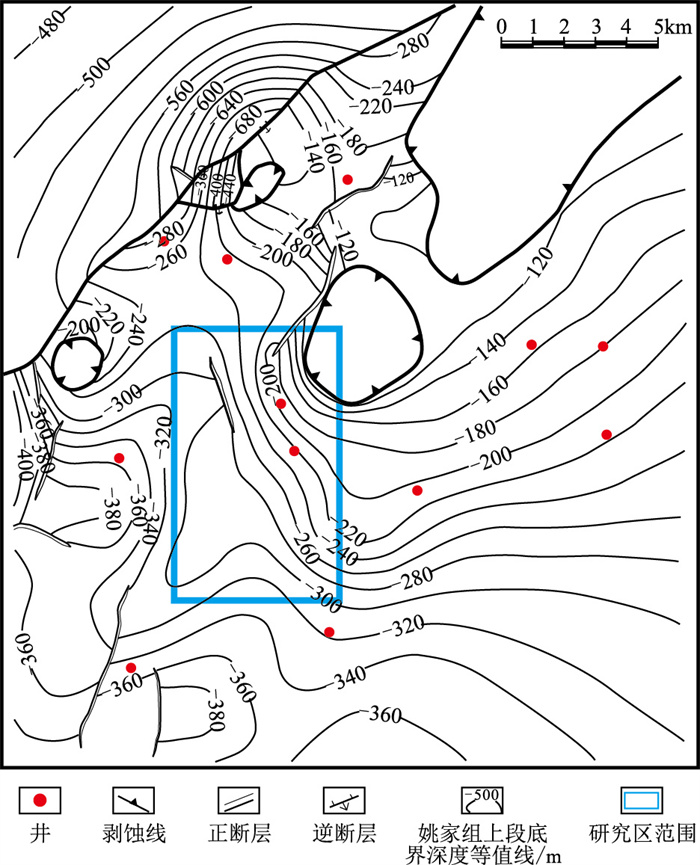
3 铀矿体预测精度分析及实际应用为了评估基于本文提出的变差函数求取方法的铀矿体反演精度及其实际应用效果,选取面积约为50km2的研究区展开试验。研究区位于中国QJD矿区(图 6),该区实际地震资料与井中合成地震记录吻合良好(图 7),其中矿区北部是近年QJD铀矿床勘探的重点区域。随着勘探程度的提高,矿体逐渐接近边界,勘探成功率呈下降趋势(近两年的成功率不足40%),迫切需要具有针对性的预测手段提高勘探效率,降低勘探成本。研究区构造北高南低,层间氧化带由南向北发育,目的层姚家组主要为辫状河三角洲平原相地层,砂体厚度大,储层物性变化较小,目前共完钻探井200余口,根据钻井资料可以较准确地刻画矿体的展布特征。
|
图 6 工区范围示意图 |

|
图 7 研究区合成地震记录(a)与实际地震资料(b) |
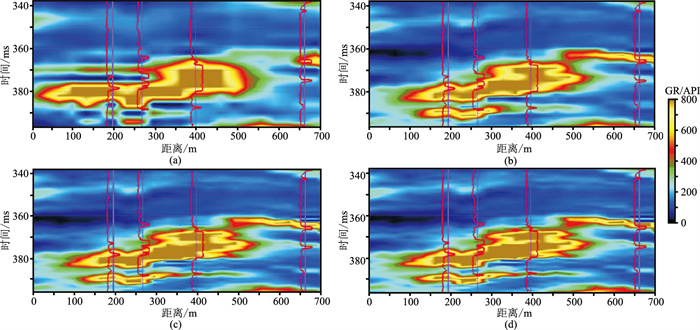
根据提出的纵向变程求取方法,求得该区的纵向变程为4.5m。为了验证所取纵向变程的合理性,对比、分析了不同纵向变程的反演结果(图 8),可见:①当纵向变程为15.0m时,反演结果分辨率很低,不能清晰地反映纵向的多个矿体,且矿体边界较圆滑,与尖灭的矿体形态不符(图 8a);②当纵向变程为10.0m时,反演结果纵向分辨率略有提高,矿体边界逐渐清晰,但对尖灭的矿体形态的刻画仍不够清晰(图 8b);③当纵向变程为4.5m时,反演结果的纵向分辨率较高,位于中间的主矿体形态清晰,且清晰地刻画了其上、下的两套小矿体,较真实地反映了矿体形态(图 8c);④当纵向变程为2.0m时,反演结果的纵向分辨率提高不明显。因此,纵向变程明显影响反演结果,基于本文方法求取纵向变程的反演结果很好地刻画了矿体(包括小矿体)形态。
|
图 8 不同纵向变程的反演结果 (a)15.0m;(b)10.0m;(c)4.5m;(d)2.0m |
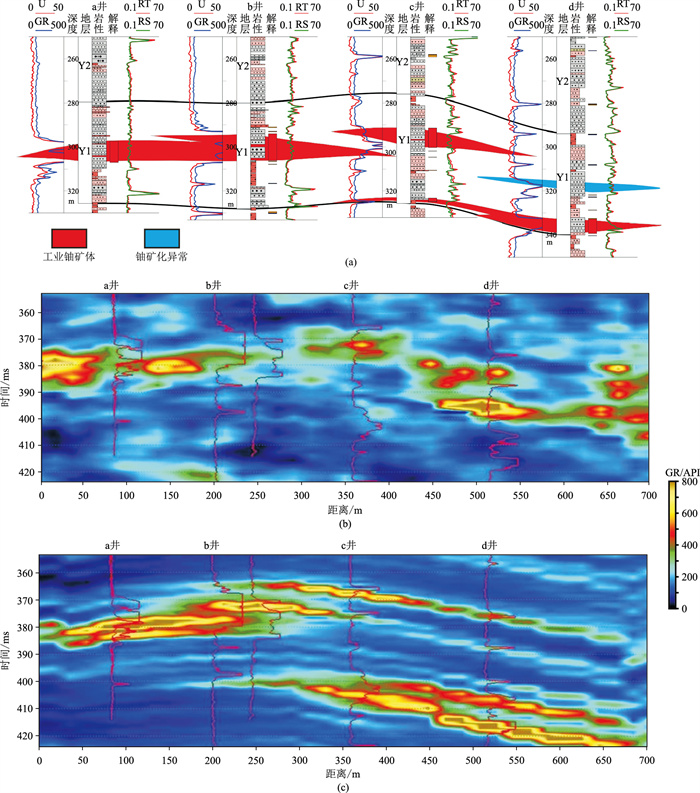
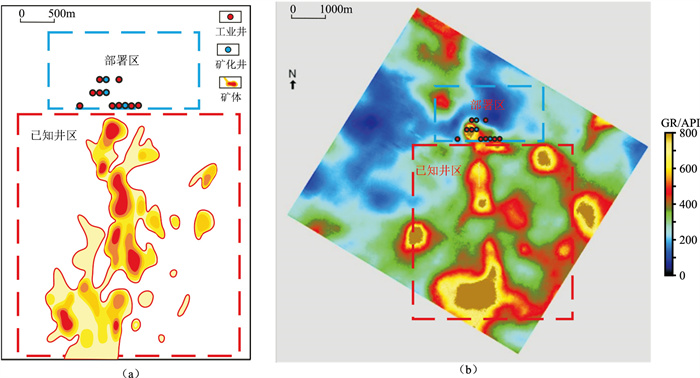
为了测试本文求取横向变程方法的效果,对比、分析了不同求取横向变程方法的反演结果(图 9),可见:①基于叠后稀疏脉冲反演平面属性进行横向约束方法(图 9b)、本文方法(图 9c)获得的反演结果均刻画了Y1旋回矿体,并且预测的矿体垂向厚度与矿体实际厚度(图 9a)基本吻合。②在横向上,图 9b将旋回顶部的一套完整矿体描述为多个独立小矿体,既不符合矿体合并原则也不符合矿体展布规律;图 9c将旋回顶部的矿体描述为同一套矿体,更好地反映了矿体的连续性,更符合矿体展布规律。图 10为实际矿体平面展布与本文求取横向变程方法反演结果的GR均方根属性平面图。由图可见:①两者均呈现南北向的展布特征;②在红色虚线圈定区域的反演结果中,不同规模矿体的主体空间位置、含矿性(图 10b)与已知井区的实际矿体空间位置、含矿性(图 10a)对应关系很好。综上所述,基于本文方法求取横向变程的反演结果具有很高的横向分辨率,能准确地刻画矿体形态。
|
图 9 不同求取横向变程方法的反演结果
(a)实际矿体剖面;(b)基于叠后稀疏脉冲反演平面属性进行横向约束;(c)本文方法 U(铀含量)、GR的量纲分别为0.001%、API,RT、RS的量纲均为Ω·m;Y1、Y2、Y3分别为姚一段、姚二段、姚三段。图11同 |
|
图 10 实际矿体平面展布(a)与本文求取横向变程方法反演结果的GR均方根属性平面图(b) |
前文分析了纵向、横向变程对反演结果的影响,分析结果证明了本文提出的变差函数的有效性。但在将反演结果用于实际勘探之前,必须由验证井验证反演结果。为了验证反演结果,本文采用去除已知井进行验证的方法。反演时选取e井、f井、g井、h井所在区域进行测试,测试过程仅采用e井、g井、h井数据进行约束反演得到反演结果(图 11a)。可见,预测矿体与实际矿体的对应关系较好,反演结果准确预测了发育于f井目的层底部的矿体,预测矿体与e井连通,在g井附近尖灭,与实际矿体剖面(图 11b)吻合良好,充分证明了本文反演方法的可靠性。

|
图 11 反演结果的验证 (a)仅应用e井、g井、h井数据约束得到的反演结果;(b)实际矿体连井剖面 |
前文的精度分析表明,基于本文方法的反演结果,无论在纵向还是横向都能准确刻画矿体的空间展布特征,对于矿体的实际勘探具有重要意义。为了验证本文方法的实际应用效果,通过综合分析反演结果与控矿因素(氧化带发育特征等)发现,在现有矿体北部的一个部署区域(图 10a蓝色虚线框)内还存在矿体发育区,2019年底在该区部署并实施了12口探井,其中9口为工业矿井,见矿率为75%,远高于QJD详查勘探工业见矿率的平均水平。实际勘探成果充分证实了本文方法反演结果的可靠性。
综上所述,当赋予变差函数明确的地质含义后,反演结果与矿体的实际展布特征吻合更好,准确刻画了铀矿体的展布形态,同时也可以根据反演结果在未知区预测矿体分布,指导勘探部署。
4 结论本文提出了在测井数据和地质意义控制下的变差函数求取方法,并用于QJD砂岩型铀矿体预测的地质统计学反演,取得如下结论:
(1) 地质统计学反演基于测井数据随机建模,相对于常规确定性反演,继承了地震资料横向分辨率高的特点,同时具有更高的纵向分辨率。因此对于厚度小、横向变化快的砂岩型铀矿体的预测效果较好,其中变差函数的求取是影响反演结果的重要因素。
(2) 基于本文提出的结合测井资料与实际矿体形态的综合统计方法求取纵向变程的反演方法,在已有先验井数据控制下得到了符合地质意义的反演结果,进而最大限度地降低了反演的随机性,反演结果很好地刻画了矿体(包括小矿体)的纵向形态。
(3) 变差函数反映了矿体的三维空间展布规律,通过统计、分析矿体规模和矿点含矿性,拟合了两者的关系,提出在已开发区矿体成矿模式和矿体展布规律等先验信息约束下的横向变程求取方法,获得的反演结果与实际矿体分布吻合更好。
(4) 利用本文方法得到的反演结果更准确地预测了矿体形态,参考反演结果部署的勘探井位显著提高了矿体预测的可靠性和钻探成功率。
| [1] |
陈戴生, 李胜祥, 蔡煜琦. 我国中新生代盆地砂岩型铀矿研究现状及发展方向的探讨[J]. 沉积学报, 2003, 21(1): 113-117. CHEN Daisheng, LI Shengxiang, CAI Yuqi. A dis-cussion on research situation and developmental direction of sandstone-type uranium deposit in the Meso-Cenozoic basins in China[J]. Acta Sedimentologica, 2003, 21(1): 113-117. |
| [2] |
陈祖伊. 亚洲砂岩型铀矿区域分布规律和中国砂岩型铀矿找矿对策[J]. 铀矿地质, 2002, 18(3): 129-137. CHEN Zuyi. Regional distribution regularity of sandstone uranium deposits in Asian continent and prospecting strategy for sandstone uranium deposits in China[J]. Uranium Geology, 2002, 18(3): 129-137. DOI:10.3969/j.issn.1000-0658.2002.03.001 |
| [3] |
夏毓亮, 林锦荣, 李子颖, 等. 松辽盆地钱家店凹陷砂岩型铀矿预测评价和铀成矿规律研究[R]. 中国核科技报告, 2003, 105-117. XIA Yuliang, LIN Jinrong, LI Ziying, et al. Perspective and Resource Evaluation and Metallogenic Studies on Sandstone-type Uranium Deposit in Qianjiadian Depression of Songliao Basin[R]. China Nuclear Science Progress Report, 2003, 105-117. |
| [4] |
马亮. 沉积盆地铀成矿规律研究——以内蒙古查干德勒苏地区为例[D]. 湖北武汉: 中国地质大学(武汉), 2008.
|
| [5] |
徐国苍, 张红建, 朱琳. 浅层地震勘探在砂岩型铀矿勘查中的应用研究[J]. 铀矿地质, 2013, 29(1): 37-46. XU Guocang, ZHANG Hongjian, ZHU Lin. Application of shallow seismic exploration method in the prospecting for in-situ leachable sandstone-type uranium deposits[J]. Uranium Geology, 2013, 29(1): 37-46. DOI:10.3969/j.issn.1000-0658.2013.01.006 |
| [6] |
吴曲波, 李子伟, 潘自强, 等. 砂岩型铀矿地震勘探中若干问题研究[J]. 地球物理学进展, 2017, 32(5): 2097-2106. WU Qubo, LI Ziwei, PAN Ziqiang, et al. Study on some problems in the seismic exploration of sandstone type uranium deposits[J]. Progress in Geophysics, 2017, 32(5): 2097-2106. |
| [7] |
李子伟, 陈敬国, 吴曲波, 等. 地震勘探方法在伊犁盆地南缘砂岩型铀矿勘查中的应用研究[J]. 铀矿地质, 2016, 32(4): 235-241, 250. LI Ziwei, CHEN Jingguo, WU Qubo, et al. Application of seismic method in the exploration of sandstone type uranium deposit in the southern margin of Yili Basin[J]. Uranium Geology, 2016, 32(4): 235-241, 250. |
| [8] |
马小雷. 鄂尔多斯盆地西南部地球物理场特征与砂岩型铀矿关系[D]. 陕西西安: 西安石油大学, 2016.
|
| [9] |
薛志恒. 浅层地震勘探在砂岩铀矿勘查中的应用[J]. 河南理工大学学报(自然科学版), 2010, 29(增刊): 170-171. |
| [10] |
Haas A, Dubrule O. Geostatistical inversion: A sequential method of stochastic reservoir modeling constrained by seismic data[J]. First Break, 1994, 12(11): 561-569. |
| [11] |
Dubrule O, Thibaut M, Lamy P, et al. Geostatistical reservoir characterization constrained by 3D seismic data[J]. Petroleum Gesocience, 1998, 4(2): 121-128. DOI:10.1144/petgeo.4.2.121 |
| [12] |
范廷恩, 马良涛, 胡光义, 等. 基于层序地层学的地质统计学反演[J]. 地球物理学进展, 2019, 34(1): 80-89. FAN Ting'en, MA Liangtao, HU Guangyi, et al. Geostatistical inversion based on sequence stratigraphy[J]. Progress in Geophysics, 2019, 34(1): 80-89. |
| [13] |
韩东, 胡向阳, 邬兴威, 等. 基于地质统计学反演的缝洞储集体物性定量评价[J]. 地球物理学进展, 2016, 31(2): 655-661. HAN Dong, HU Xiangyang, WU Xingwei, et al. Quantitative evaluation for porosity of the fracture-cavity reservoir based on geostatistical inversion[J]. Progress in Geophysics, 2016, 31(2): 655-661. |
| [14] |
尚建林, 李太辉, 霍新勇, 等. 地质统计学反演预测百口泉油田百34井区薄砂体[J]. 新疆石油地质, 2009, 30(6): 758-760. SHANG Jianlin, LI Taihui, HUO Xinyong, et al. App-lication of geostatistical inversion to prediction of thin sand body of Karamay formation in Bai-34 well area in Baikouquan oil field[J]. Xingjiang Petroleum Geology, 2009, 30(6): 758-760. |
| [15] |
宁松华, 曹淼, 刘雷颂, 等. 地质统计学反演在三道桥工区储层预测中的应用[J]. 石油天然气学报, 2014, 36(7): 52-54. NING Songhua, CAO Miao, LIU Leisong, et al. App-lication of geostatistical inversion method in reservior prediction of Sandaogiao area[J]. Journal of Oil and Gas Technology, 2014, 36(7): 52-54. |
| [16] |
王雅春, 王璐. 地质统计学反演在杏北西斜坡区储层预测中的应用[J]. 地球物理学进展, 2013, 28(5): 2554-2560. WANG Yachun, WANG Lu. Application of geostatistical inversion to reservoir prediction in the Western Slope of the northern Xingshugang oil field[J]. Progress in Geophysics, 2013, 28(5): 2554-2560. |
| [17] |
慎国强, 孟宪军, 王玉梅, 等. 随机地震反演方法及其在埕北35井区的应用[J]. 石油地球物理勘探, 2004, 39(1): 75-81. SHEN Guoqiang, MENG Xianjun, WANG Yumei, et al. Random seismic inversion and its application in Chengbei No.35 well-zone[J]. Oil Geophysical Prospecting, 2004, 39(1): 75-81. |
| [18] |
易平, 林桂康. 随机地震反演技术及在文昌13-1油田的应用[J]. 石油地球物理勘探, 2005, 40(1): 87-91. YI Ping, LIN Guikang. Seismic stochastic inversion and its application in Wenchang 13-1 oilfield[J]. Oil Geophysical Prospecting, 2005, 40(1): 87-91. |
| [19] |
孙思敏, 彭仕宓. 地质统计学反演方法及其在薄层砂体预测中的应用[J]. 西安石油大学学报(自然科学版), 2007, 22(1): 41-44, 48. SUN Simin, PENG Shibi. Geostatistical inversion method and its application in the prediction of thin reservoirs[J]. Journal of Xi'an Shiyou University(Na-tural Science Edition), 2007, 22(1): 41-44, 48. |
| [20] |
王晓平, 尚建林, 王林生, 等. 地质统计反演在准噶尔盆地玛北油田的应用[J]. 新疆石油地质, 2013, 34(3): 320-323. WANG Xiaoping, SHANG Jianlin, WANG Linsheng, et al. Application of geostatistic inversion technology to Mabei oilfield in Junggar Basin[J]. Xinjiang Petroleum Geology, 2013, 34(3): 320-323. |
| [21] |
罗林. 地质统计学反演在钱家店地区砂岩型铀矿勘探中的应用[J]. 铀矿冶, 2018, 37(1): 68-72. LUO Lin. Application of geostatistical inversion for exploration of sandstone type uranium ore in Qianjiadian area[J]. Uranium Mining and Metallurgy, 2018, 37(1): 68-72. |
| [22] |
董奇, 卢双舫, 张学娟, 等. 地质统计学反演参数选取及反演结果可靠性分析[J]. 物探与化探, 2013, 37(2): 328-332, 337. DONG Qi, LU Shuangfang, ZHANG Xuejuan, et al. Selection of parameters and reliability analysis of results in geostatistical inversion method[J]. Geophysical & Geochemical Exploration, 2013, 37(2): 328-332, 337. |
| [23] |
刘兴冬. 随机反演变差函数适用性研究[J]. 石油天然气学报, 2010, 32(2): 253-256. LIU Xingdong. Adaptability for variation function in random inversion[J]. Journal of Oil and Gas Techno-logy, 2010, 32(2): 253-256. |
| [24] |
秦月霜, 郭海晓, 陈友福. 变差函数对地震反演精度的影响[J]. 大庆石油学院学报, 2009, 33(5): 37-40. QIN Yueshuang, GUO Haixiao, CHEN Youfu. Effect of variogram on seismic inversion accuracy[J]. Journal of Daqing Petroleum Institute, 2009, 33(5): 37-40. |
| [25] |
樊鹏军, 马良涛, 王宗俊, 等. 地质统计学反演中变差函数地质含义及求取方法探讨[J]. 地球物理学进展, 2017, 32(6): 2444-2450. FAN Pengjun, MA Liangtao, WANG Zongjun, et al. Variogram geological implication and its calculating method discussing for geostatistical inversion[J]. Progress in Geophysics, 2017, 32(6): 2444-2450. |



 孙章庆, 吉林省长春市西民主大街938号吉林大学朝阳校区地探学院波动理论与程序技术实验室, 130026。Email:
孙章庆, 吉林省长春市西民主大街938号吉林大学朝阳校区地探学院波动理论与程序技术实验室, 130026。Email: 