② 中国石油大学(北京)油气资源与探测国家重点实验室, 北京 102249;
③ 西南交通大学地球科学与环境工程学院, 四川成都 611756;
④ 中海油研究总院有限责任公司, 北京 100028;
⑤ 中国石油勘探开发研究院西北分院, 甘肃兰州 730020
② State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum (Beijing), Beijing 102249, China;
③ Faculty of Geoscience and Environmental Engineering, Southwest Jiaotong University, Chengdu, Sichuan 611756, China;
④ CNOOC Research Institute Co. Ltd., Beijing 100028, China;
⑤ Northwest Branch, Research Institute of Petroleum Exploration & Development, Petrochina, Lanzhou, Gansu 730020, China
弹性参数反演、岩石物理反演和储层岩相识别是油藏表征和评价的有效手段[1-3]。测井资料可提供井位附近油藏参数的直接或间接测量结果,而地震数据提供了获取井间油藏参数的唯一指导信息。但由于地震频带、观测误差以及岩石物理建模误差等因素的影响,地震反问题的求解仍然面临较大挑战。传统方法通常利用井数据低频信息和单道地震数据通过多步骤反演策略依次得到储层弹性参数、储层物性参数和储层岩相等信息,忽略了井数据高频信息和地震数据横向信息以及各反演环节不确定性信息对反演结果的影响,降低了最终反演精度,增加了油藏评价和开发的风险。因此,如何充分利用现有资料获取客观、准确表征反演结果不确定性的信息,从而指导储层评价尤为重要。
对于油藏参数预测及其不确定性评价,前人做了大量的研究工作。基于概率方法的贝叶斯反演框架通过引入先验信息约束项,有效降低了地球物理反演的多解性,提高了反演精度,被广泛用于求解地球物理反问题。贝叶斯反演的最终解由后验概率分布定义,表示在给定观测数据条件下待求模型参数正确的可能性。Buland等[4]基于贝叶斯反演框架,结合线性AVO方程和高斯分布假设,推导了弹性参数后验概率分布解析表达式,在获得弹性参数的同时,定量表征了反演结果的不确定性。Grana等[5]在Buland等[4]的研究基础上,将贝叶斯线性反演的高斯假设推广到混合高斯假设,得到了弹性参数的解析解。为提高反演结果的横向连续性,Hamid等[6]基于贝叶斯反演框架,引入横向约束项开展多道叠后阻抗反演。张广智等[7]基于Fatti波阻抗近似式,利用蒙特卡洛—马尔科夫链(MCMC)算法预测了弹性三参数,并提供了相关的不确定性信息。Aleardi等[8]针对某一特定研究区,通过对比线性反演方法与非线性反演方法的结果,验证了前者求取储层参数及其不确定性的有效性。黄捍东等[9]利用非线性随机反演方法预测了陆相薄砂岩储层。Larsen等[10]阐述了地震反演不确定性对储层岩相识别的影响,引入马尔科夫链先验信息提高了岩相识别精度,并实现了岩相随机模拟。李军等[11]将马尔科夫链模型从二维形式推广到三维,获得了更准确的储层岩相模拟结果。刘兴业等[12]基于贝叶斯框架,引入核贝叶斯算法预测了物性参数、岩相及其不确定性信息。袁成等[13-14]系统介绍了由地震数据识别储层岩相各环节的不确定性评价方法。然而,上述方法均为多步骤反演,很难考虑各个环节的不确定性。Bosch等[15]以地震数据作为输入,利用MCMC方法同时预测波阻抗和孔隙度,并定量分析了反演结果的不确定性。de Figueiredo等[16]提出基于岩石物理的贝叶斯反演方法,同时估计了波阻抗、孔隙度和储层岩相及其不确定性信息。Grana[17]提出了一种基于模型参数为混合非参数分布统计假设的贝叶斯反演方法,定量表征了储层岩相和储层流体。李海山等[18]利用平面波分解技术提取地层信息,建立更可靠的波阻抗初始模型用于反演,获得了横向更连续的反演结果。曹丹平等[19]、周晓越等[20]尝试多属性联合反演。
基于前人的工作,本文提出基于构造约束联合概率反演的油藏参数表征方法。基于贝叶斯反演框架提出油藏参数同时反演策略,利用最小二乘井数据插值将地质构造信息和井信息整合到同时反演框架,经推导得到油藏参数后验概率分布解析表达式。最终,利用获得的后验概率分布信息定量评价和表征反演结果。所提方法通过同时反演策略客观表征各环节的不确定性,构造约束保证反演结果横向空间耦合性,最终反演结果为油藏表征和评价提供了更可靠的参考信息。实际资料应用和井测试验证了方法的有效性。
1 方法理论为了研究基于岩石物理分析统计的油藏参数关系,引入构造约束地质模型,构建油藏参数同时反演解析表达式,获取构造约束的油藏参数(包括波阻抗、孔隙度和储层岩相)联合概率分布信息,并开展定量评价。理论方法包括岩石物理建模及分析、构造约束和井信息融合以及油藏参数联合概率表征。
1.1 线性岩石物理建模及分析岩石物理模型(rock physics model,RPM)是连接储层物性参数和储层弹性参数的桥梁,是联合反演的基础,也是参数敏感性分析以及参数优选的重要工具。文中主要针对叠后数据,其RPM(即波阻抗和储层物性参数之间关系)为
| $ Z_{\mathrm{p}}=f_{\mathrm{RPM}}(R)+\varepsilon $ | (1) |
式中:fRPM(R)为线性或理论RPM,R为储层物性参数;Zp为声阻抗;ε为观测误差,代表建模结果与实际观测值之间的失配程度,通过分析井数据确定。
为得到油藏参数联合后验概率解析表达式,需建立储层物性参数与声阻抗自然对数线性RPM,即
| $ \ln Z_{\mathrm{p}}=a_{1}+a_{2} D+a_{3} \varphi+a_{4} S_{\mathrm{w}}+a_{5} V_{\mathrm{sh}} $ | (2) |
式中:D为深度;φ、Sw、Vsh分别为孔隙度、含水饱和度和泥质含量;a1~a5为利用井数据或者岩心数据得到的回归系数。
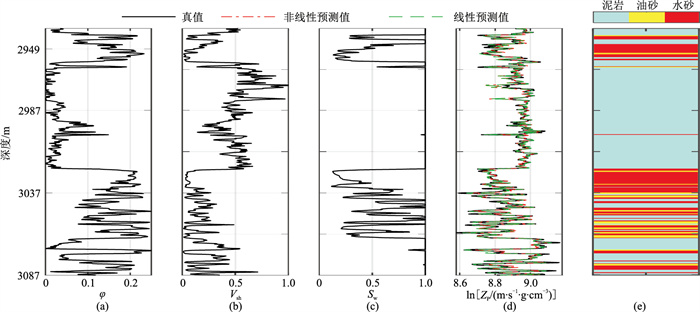
对M区井数据(图 1)利用多元线性回归方法得到a1~a5,则由式(2)得
|
图 1 M区井数据 (a)φ;(b)Vsh;(c)Sw;(d)lnZp;(e)岩相 |
| $ \begin{aligned} \ln Z_{\mathrm{p}}=& 9.0542+8 \times 10^{-5} D-2.4415 \varphi+\\ & 0.0092 S_{\mathrm{w}}-0.5464 V_{\mathrm{sh}} \end{aligned} $ | (3) |
式(3)表明:孔隙度在声阻抗预测中起决定作用,其次是泥质含量和含水饱和度;由于有限的深度范围,深度对阻抗预测的影响非常小。
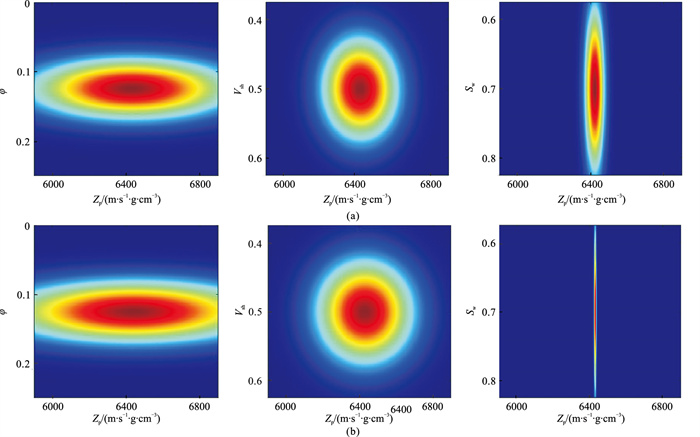
结合M区地质与地球物理特征以及测井阻抗和物性参数之间的响应关系,选取基于Hertz-Mindlin接触理论的RPM(表 1)建立阻抗与物性参数的关系(图 2),以证明线性RPM在M区的可行性[21]。Hertz-Mindlin模型已被证明可以较好地表征砂岩物性参数与弹性参数之间的关系。
|
|
表 1 Hertz-Mindlin理论RPM参数 |
|
图 2 Hertz-Mindlin理论RPM(a)与多元线性回归得到的线性RPM(b)的Zp与φ(左)、Vsh(中)、Sw(右)敏感性分析图 |
由图 1、图 2可见:两种RPM阻抗预测结果与实测阻抗吻合,证明了RPM的有效性(图 1);两种RPM参数敏感性分析结果一致,证明线性RPM可以很好表征阻抗与物性参数的关系,且敏感性分析结论与式(3)一致,即孔隙度对阻抗预测起决定性作用,另外两种物性参数对于阻抗预测作用较小(图 2)。因此,本文重点研究阻抗与孔隙度之间的关系。
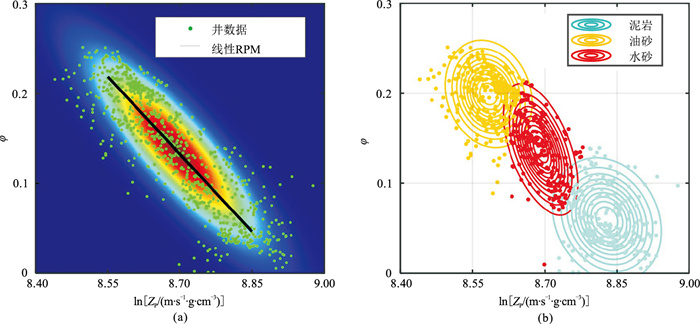
将井数据φ—lnZp联合向量记为m,则地下某一时间点(t时刻)的阻抗和孔隙度联合分布(图 3a的彩色底图,服从多元高斯分布)为
|
图 3 孔隙度与阻抗对数交会图 (a)lnZp和φ联合分布(彩色底图)、线性RPM(黑色曲线)及φ—lnZp交会图(绿色散点)叠合图;(b)不同岩相的φ—lnZp交会图(散点)及其先验分布 |
| $ p\left(m_{t}\right)=p\left[\ln \left(Z_{{\rm{p}} t}\right), \varphi_{t}\right] \sim N\left(m_{t} ; \boldsymbol{\mu}, \boldsymbol{\varSigma}\right) $ | (4) |
式中:下标t表示t时刻的相应变量(下同);N表示均值为μ、协方差为Σ的多元高斯分布
| $ \left\{\begin{array}{l} \boldsymbol{\mu}=\left(\begin{array}{cc} \mu_{\mathrm{p} t} \\ \mu_{Z{\varphi_{t}}} \end{array}\right) \\ \boldsymbol{\varSigma}=\left(\begin{array}{cc} \sum\limits_{Z_{\mathrm{p}t}} & \sum\limits_{Z_{\mathrm{p} t}, \varphi_{t}} \\ \sum\limits_{\varphi_{t}, Z_{\mathrm{p}t}} & \sum\limits_{\varphi_{t}} \end{array}\right) \end{array}\right. $ | (5) |
其中Σ对角线上的元素为各个随机变量的方差,非对角线上的元素为两两随机变量之间的协方差。
将式(4)扩展到整个地震道,同时引入垂向空间耦合信息,有
| $ p(\boldsymbol{m})=p\left[\ln \left(Z_{\mathrm{p}}\right), \varphi\right] \sim N\left(\boldsymbol{m} ; \boldsymbol{\mu_{m}}, \boldsymbol{\varSigma_{m}}\right) $ | (6) |
其中
| $ \left\{\begin{array}{l} \boldsymbol{\mu_{m}}=\left(\begin{array}{c} \mu_{Z_\mathrm{p}} \\ \mu_{\varphi} \end{array}\right) \\ \boldsymbol{\varSigma_{m}}=\left(\begin{array}{cc} \varSigma_{Z_{\mathrm{p}}} \boldsymbol{\varGamma} & \varSigma_{Z_{\mathrm{p}}, \boldsymbol{\varphi}} \boldsymbol{\varGamma} \\ \varSigma_{\varphi, Z_{\mathrm{p}}} \boldsymbol{\varGamma} & \varSigma_{\varphi} \boldsymbol{\varGamma} \end{array}\right) \end{array}\right. $ | (7) |
式中Γ代表垂直相关矩阵,可定义为[4]
| $ \boldsymbol{\varGamma}(\boldsymbol{\tau})=\exp \left[-\left(\frac{\boldsymbol{\tau}}{l}\right)^{2}\right] $ | (8) |
式中:τ为时间变量矩阵;l为垂直方向耦合系数,通过统计井数据获得,本研究中l=9。
1.2 构造约束和井信息融合横向连续性和分辨率是储层参数表征的重要要求,而地质构造信息和井数据可分别提供横向空间耦合关系和高频细节信息。为进一步提高反演结果的横向连续性和分辨率,建立储层参数m和构造约束井插值结果f的关系,即
| $ \mathit{\boldsymbol{f}} = \mathit{\boldsymbol{m}} + {\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{f}}} $ | (9) |
式中ef代表误差容忍参数,即m与f之间的相似性,可以利用距井距离的函数表示。
| $ \mathit{\boldsymbol{Mf}} = \mathit{\boldsymbol{w}} $ | (10) |
式中:M为采样算子;w为已知井数据。对式(10)利用最小二乘方法求解,有
| $ \hat{\boldsymbol{f}}=\arg \min \limits_{\boldsymbol{f}}\left\{\frac{1}{2}\|\boldsymbol{M} \boldsymbol{f}-\boldsymbol{w}\|_{2}^{2}+\frac{\lambda^{2}}{2}\|\boldsymbol{f}\|_{2}^{2}\right\} $ | (11) |
式中:
为了引入地质构造信息,用Sk代替f,其中S为利用平面波分解滤波技术得到的构造约束算子(即地层倾角),k为预条件算子。将Sk代入式(11),得到构造约束井插值结果
| $ \hat{\boldsymbol{f}}=\hat{\boldsymbol{S}}=\boldsymbol{S}\left(\boldsymbol{S}^{\mathrm{H}} \boldsymbol{M}^{\mathrm{H}} \boldsymbol{M} \boldsymbol{S}+\lambda^{2} \boldsymbol{S}^{\mathrm{H}} \boldsymbol{S}\right)^{-1} \boldsymbol{S}^{\mathrm{H}} \boldsymbol{M}^{\mathrm{H}} \boldsymbol{w} $ | (12) |
式中:上角H表示共轭转置;
高精度储层参数表征及其不确定性评价是储层表征的另一重要需求。与传统多步反演方法相比,同时反演方法可以更准确地表征储层参数并量化其不确定性。为实现同时反演,联合观测地震数据和构造约束井插值结果建立如下方程
| $ \left( {\begin{array}{*{20}{l}} \mathit{\boldsymbol{f}}\\ \mathit{\boldsymbol{d}} \end{array}} \right) = \left( {\begin{array}{*{20}{l}} 1&1&0\\ \mathit{\boldsymbol{G}}&0&1 \end{array}} \right)\left( {\begin{array}{*{20}{l}} \mathit{\boldsymbol{m}}\\ {{\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{f}}}}\\ {{\mathit{\boldsymbol{e}}_\mathit{\boldsymbol{d}}}} \end{array}} \right) $ | (13) |
式中:d为地震响应;ed为观测误差;G=[W D 0]为地震响应正演算子,其中W为子波矩阵,而
| $ \boldsymbol{D}=\left[\begin{array}{ccccc} -1 & 1 & 0 & \cdots & 0 \\ 0 & -1 & 1 & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & 0 & -1 & 1 \end{array}\right] $ |
为一阶差分矩阵。
通过构建W和D得到由阻抗到地震响应的正演算子。将
| $ p(\boldsymbol{m} \mid \boldsymbol{y}) \sim N\left(\boldsymbol{m} ; \boldsymbol{\mu}_{\boldsymbol{m} \mid \boldsymbol{y}}, \boldsymbol{\varSigma}_{\boldsymbol{m} \mid \boldsymbol{y}}\right) $ | (14) |
其中
| $ \boldsymbol{\mu}_{\boldsymbol{m} \mid \boldsymbol{y}}=\boldsymbol{\mu}_{\boldsymbol{m}}+\boldsymbol{\varSigma}_{\boldsymbol{m}, \boldsymbol{y}} \boldsymbol{\varSigma}_{\boldsymbol{y}}^{-1}\left(\boldsymbol{y}-\boldsymbol{\mu}_{\boldsymbol{y}}\right) $ | (15) |
| $ \boldsymbol{\varSigma}_{\boldsymbol{m} \mid \boldsymbol{y}}=\boldsymbol{\varSigma}_{\boldsymbol{m}}-\boldsymbol{\varSigma}_{\boldsymbol{m}, \boldsymbol{y}} \boldsymbol{\varSigma}_{\boldsymbol{y}}^{-1} \boldsymbol{\varSigma}_{\boldsymbol{y}, \boldsymbol{m}} $ | (16) |
而
| $ \left\{ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{y}} = \left( {\begin{array}{*{20}{l}} \mathit{\boldsymbol{f}}\\ \mathit{\boldsymbol{d}} \end{array}} \right)}\\ {{\mathit{\boldsymbol{\mu }}_\mathit{\boldsymbol{y}}} = \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\mu }}_\mathit{\boldsymbol{m}}}}\\ {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{\mu }}_\mathit{\boldsymbol{m}}}} \end{array}} \right)}\\ {{\mathit{\boldsymbol{\varSigma }}_{\mathit{\boldsymbol{y,m}}}} = \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\varSigma }}_\mathit{\boldsymbol{m}}}}\\ {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{\varSigma }}_\mathit{\boldsymbol{m}}}} \end{array}} \right)}\\ {{\mathit{\boldsymbol{\varSigma }}_{\mathit{\boldsymbol{m,y}}}} = \mathit{\boldsymbol{\varSigma }}_{\mathit{\boldsymbol{y,m}}}^{\rm{T}}} \end{array}} \right. $ | (17) |
| $ {\mathit{\boldsymbol{\varSigma }}_y} = \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\varSigma }}_\mathit{\boldsymbol{m}}} + {\mathit{\boldsymbol{\varSigma }}_\mathit{\boldsymbol{f}}}}&{{\mathit{\boldsymbol{\varSigma }}_\mathit{\boldsymbol{m}}}{\mathit{\boldsymbol{G}}^{\rm{T}}}}\\ {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{\varSigma }}_\mathit{\boldsymbol{m}}}}&{\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{\varSigma }}_\mathit{\boldsymbol{m}}}{\mathit{\boldsymbol{G}}^{\rm{T}}} + {\mathit{\boldsymbol{\varSigma }}_\mathit{\boldsymbol{d}}}} \end{array}} \right) $ | (18) |
在某一岩相(对应m)服从高斯分布(图 3b)假设条件下,有
| $ p\left(m_{t} \mid \kappa\right) \sim N\left(m_{t} ; \mu_{\kappa}, \varSigma_{\kappa}\right) $ | (19) |
式中μκ和Σκ分别为岩相κ对应的储层参数m的均值和协方差。
根据链式法则,得到
| $ p\left(\kappa_{t} \mid y_{t}\right)=\int p\left(\kappa_{t} \mid m_{t}\right) p\left(m_{t} \mid y_{t}\right) \mathrm{d} m_{t} $ | (20) |
其中
| $ p\left(\kappa_{t} \mid m_{t}\right) \propto p\left(m_{t} \mid \kappa_{t}\right) p\left(\kappa_{t}\right) $ | (21) |
p(mt|κt)、p(mt|yt) 均服从高斯分布,有p(mt|κt)~N(m; μ1, Σ1),p(mt|yt)~N(m; μ2, Σ2)。其中,μi、Σi(i=1, 2)分别表示高斯分布中的均值和协方差矩阵。结合式(20)和式(21),根据概率统计法则[24-25],岩相后验分布为(附录A)
| $ p\left({\kappa}_{t} \mid y_{t}\right) \propto p\left({\kappa}_{t}\right) c_{c} \int N\left(m_{t} ; \boldsymbol{\mu}_{c}, \boldsymbol{\varSigma}_{c}\right) \mathrm{d} m_{t} $ | (22) |
其中
| $ c_{c}=\exp \left(\sum\limits_{i=1}^{2} \xi_{i}+\xi_{c}\right) $ | (23) |
而
| $ \xi_{i}=-\frac{1}{2}\left[2 \ln (2 {\rm{ \mathsf{ π} }})+\ln \left|\boldsymbol{\varSigma}_{i}\right|+\boldsymbol{\mu}_{i}^{\mathrm{T}} \boldsymbol{\varSigma}_{i}^{-1} \boldsymbol{\mu}_{i}\right] $ | (24) |
| $ \xi_{c}=\frac{1}{2}\left[2 \ln (2 {\rm{ \mathsf{ π} }})+\ln \left|\boldsymbol{\varSigma}_{c}\right|+\boldsymbol{\mu}_{c}^{\mathrm{T}} \boldsymbol{\varSigma}_{c}^{-1} \boldsymbol{\mu}_{c}\right] $ | (25) |
式中:μc= (Σ1-1+ Σ2-1) -1(Σ1-1 μ1+ Σ2-1 μ2);Σc= (Σ1-1+ Σ2-1)-1。
假定式(22)积分项为1,同时引入马尔科夫链先验,则式(22)改写为
| $ p\left(\kappa_{t} \mid y_{t}\right) \propto \prod p\left(\kappa_{t} \mid \kappa_{t-1}\right) c_{c} $ | (26) |
其中p(κ1|κ0)=p(κ1)表示岩相先验分布,p(κt|κt-1) 可利用马尔科夫链转移概率矩阵(通过统计井数据获得)计算。
最后,可以得到油藏参数(阻抗、孔隙度、岩相)预测结果及其不确定性评价信息。
1.4 算法实现流程(1) 数据准备,包括井数据和地震数据;
(2) 利用平面波分解滤波技术由地震数据提取地层倾角信息;
(3) 结合提取的地层倾角信息和井数据建立构造约束与井融合的地下参数模型;
(4) 统计、分析井数据,获取岩相依赖阻抗和孔隙度联合先验分布、垂向耦合系数以及转移概率矩阵等相关信息;
(5) 最后,计算式(15)、式(16)、式(26),分别得到阻抗、孔隙度、岩相及其后验概率分布。
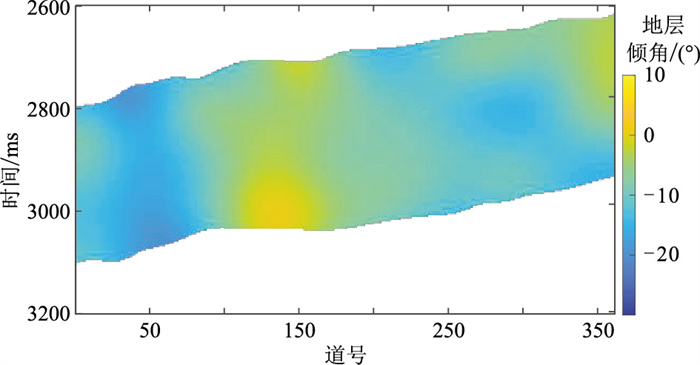
2 应用实例为了验证所提方法的有效性,利用M区资料进行试算。M区存在浊积砂岩油藏,在储层段有含油砂岩、含水砂岩和泥岩等三种岩相。图 4为叠后地震剖面。利用3口井(A、B、D)数据直接参与反演,而另1口井(C)作为盲井验证反演结果的可靠性。首先利用平面波分解滤波技术获取地层倾角数据(图 5),结合地层倾角信息和3口井数据,利用式(12)得到构造约束井插值结果(图 6)。

|
图 4 叠后地震剖面 黑色曲线之间代表主要油藏目的层;A,B,C,D为井位 |
|
图 5 地层倾角 |
|
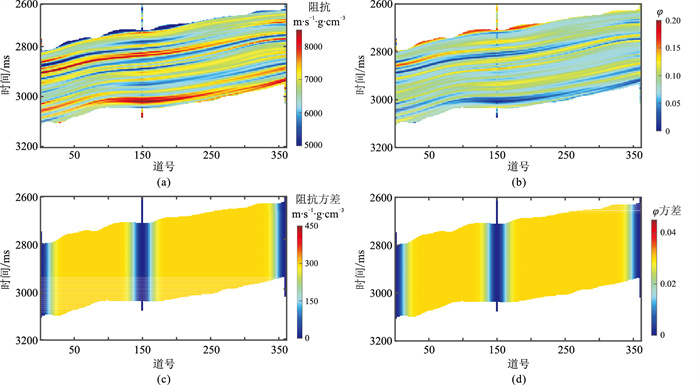
图 6 构造约束井插值结果
(a)阻抗;(b)孔隙度;(c)阻抗方差;(d)孔隙度方差 方差代表井数据对最终反演结果的影响,是距井的距离的函数,在井附近井约束权重较大,远离井约束权重逐渐减小 |
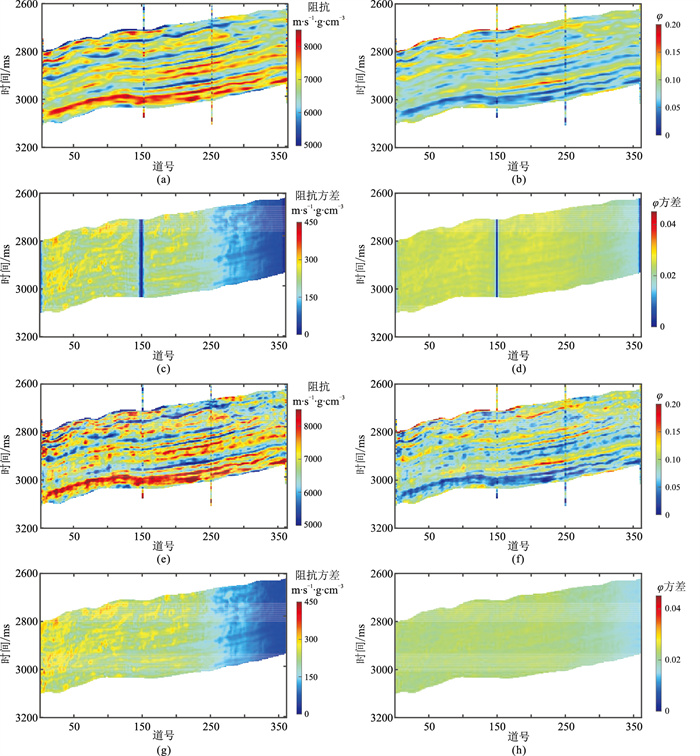
将观测地震数据和构造约束井插值结果代入式(13),利用式(15)和式(16)得到阻抗及孔隙度反演结果(图 7)。可见:①本文方法反演结果(图 7a、图 7b)的横向连续性较无约束反演结果(图 7e、图 7f)更好;②除约束井(A,B,D)附近以外,两种方法获得的阻抗方差(图 7c、图 7g)相近;③由于本文方法同时考虑了阻抗反演与孔隙度反演之间的耦合关系,除约束井附近以外,孔隙度方差(图 7d)大于无约束反演结果(图 7h),更好地反映了反演结果的不确定性;④井数据既能提供低频信息,又能提供高分辨率信息,本文方法同时引入井约束,在井附近可获得更高分辨率反演结果,对应概率在井位处的方差接近0,即反演结果与井数据一致(图 7c、图 7d)。
|
图 7 阻抗及孔隙度反演结果 (a)阻抗(本文方法);(b)孔隙度(本文方法);(c)阻抗方差(本文方法);(d)孔隙度方差(本文方法);(e)阻抗(无构造约束多步方法);(f)孔隙度(无构造约束多步方法);(g)阻抗方差(无构造约束多步方法);(h)孔隙度方差(无构造约束多步方法) |
将得到的岩相依赖孔隙度与阻抗联合高斯分布均值和方差(图 3b)、阻抗与孔隙度及其方差(图 7)代入式(26),可以得到M区储层岩相概率,其中转移概率矩阵T由统计已知测井数据得到
| $ \boldsymbol{T}=\left(\begin{array}{lll} 0.96 & 0.01 & 0.03 \\ 0.01 & 0.82 & 0.17 \\ 0.07 & 0.05 & 0.88 \end{array}\right) $ | (27) |
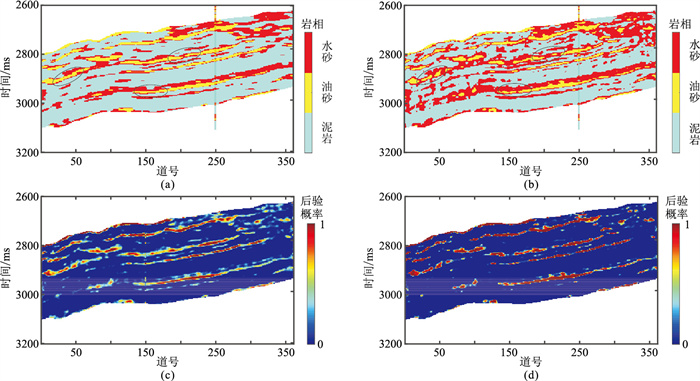
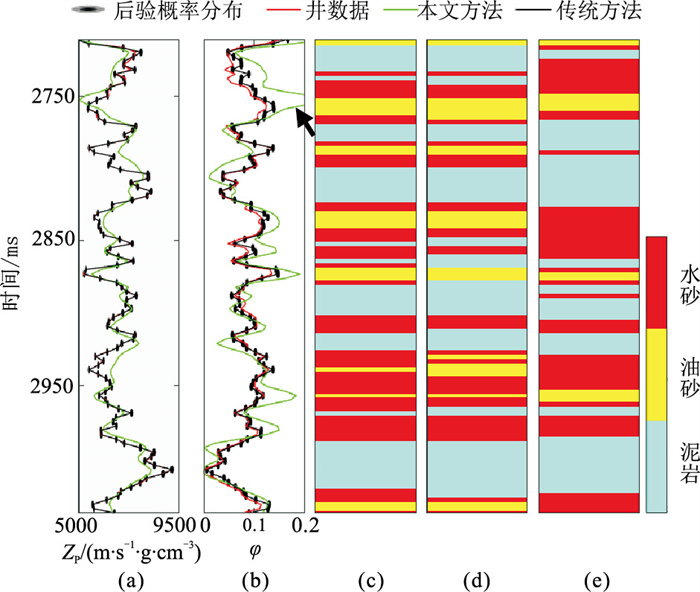
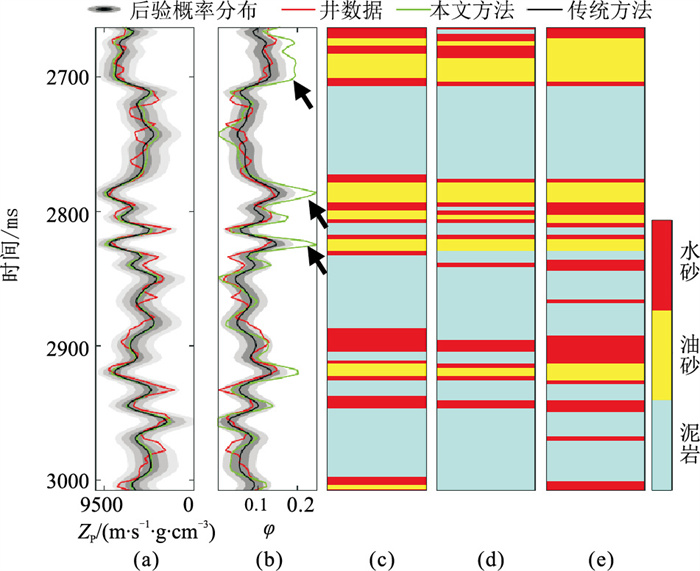
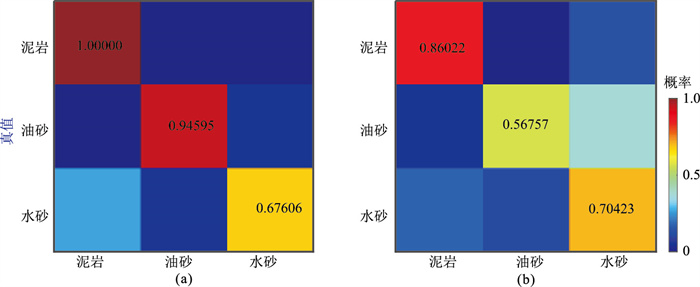
图 8为岩相预测结果及其不确定性。由图可见:本文方法识别的岩相(图 8a)较传统多步法(图 8b)更可靠,通过引入构造约束信息提高了岩相的连续性;本文方法考虑了不确定性在各环节的传递,得到的岩相后验概率(图 8c)较传统多步法(图 8d)更准确,客观表征了不确定性,为油藏表征、评价提供了重要参考依据。为进一步验证本文方法的有效性,图 9、图 10分别展示了条件井(B)、盲井(C)测试结果。由图可见:①在条件井井位处,本文方法考虑了已知井信息,阻抗以及孔隙度反演结果与实测井数据吻合很好,不确定性小(图 9a、图 9b);多步法由于未考虑已知井信息和不确定性传递,波阻抗反演结果的分辨率较低(图 9a),且孔隙度预测结果偏高(图 9b箭头处)。②储层岩相识别结果(图 9c~图 9e、图 10c~图 10e)也验证了本文方法的有效性。图 11为图 9的岩相识别归一化混淆矩阵,可见其对角线元素数值之和较大,定量验证了本文方法的有效性。由盲井测试结果(图 10、图 12)可见:①本文方法的波阻抗反演结果与多步法相似,且与实测曲线基本吻合(图 10a)。②由于多步法存在较大累积误差,孔隙度反演结果与实测井曲线偏差较大(图 10b);本文方法同时考虑了波阻抗反演与孔隙度反演之间的耦合关系,孔隙度反演结果与井数据匹配更好(图 10b)。③多步法的混淆矩阵油砂预测值(图 12b,0.8)高于本文方法(图 12a,0.71429),这是由于多步法在井顶端孔隙度预测值偏大(图 10)导致错误油砂预测结果所致,但本文方法的混淆矩阵对角线元素数值之和(图 12a,2.28756)大于多步法(图 12b,2.19781),因此本文方法的岩相预测精度高于多步法。由图 7~图 12可知,本文方法的油藏参数预测性能较传统方法更好,可以为油藏表征、评价提供客观、可靠的参考信息。
|
图 8 岩相预测结果及其不确定性 (a)岩相(本文方法);(b)岩相(多步法);(c)岩相后验概率(本文方法);(d)岩相后验概率(多步法) |
|
图 9 条件井(B)测试结果 (a)阻抗曲线与本文方法反演结果不确定性信息(底图)叠合图;(b)孔隙度曲线;(c)参考岩相;(d)本文方法预测岩相;(e)多步法预测岩相 |
|
图 10 盲井(C)测试结果 (a)阻抗曲线与本文方法反演结果不确定性信息(底图)叠合图;(b)孔隙度曲线;(c)参考岩相;(d)本文方法预测岩相;(e)多步法预测岩相 |
|
图 11 图 9的岩相识别归一化混淆矩阵 (a)本文方法;(b)多步法 |

|
图 12 图 10的岩相识别归一化混淆矩阵 (a)本文方法;(b)多步法 |
本文通过分析实际资料提出一种基于构造约束联合概率反演的油藏参数表征方法。新方法基于贝叶斯理论,利用阻抗和孔隙度的联合先验分布和岩相依赖先验分布,引入线性岩石物理模型,得到油藏参数(阻抗、孔隙度、岩相)后验概率分布解析表达式,客观、准确地表征了不确定性传递。同时,将地质构造信息和井信息集成到反演过程,提高了反演结果的横向连续性和分辨率。为验证新方法的有效性,对M区实际数据集通过条件井和盲井测试,对比、分析了无构造约束多步方法与新方法的反演结果,后者基于线性化模型且服从高斯分布假设,获得了较好的反演效果,为油藏表征、评价提供了有利依据。针对叠前地震资料,在油藏参数与地震响应之间满足线性关系假设时,新方法可以实现叠前同时反演油藏参数。
然而,在一些较复杂地区线性表达式常常会降低反演精度,因此新方法很难直接求解非线性反演问题。非线性反演方法可以在一定程度上避免线性反演方法的一些假设和限制,从而提高油藏参数预测精度。
目前求解非线性问题主要有以下策略:①将复杂问题进行线性化近似,然后直接应用本文方法求解,但线性化不可避免地会降低反演精度;②引入全局寻优算法求解非线性反问题,如MCMC采样算法,但该类算法计算效率较低,限制了实际应用;③在有足够井数据情况下,利用基于数据驱动类方法训练已知井数据,获得油藏参数与地震数据之间的匹配函数式,从而求解非线性反问题。
另外,新方法中模型参数服从高斯分布假设可以较容易地推广到混合高斯分布;针对一些更复杂的分布,可以利用上述求解非线性问题的策略②或③求解相应问题。
附录A 后验分布根据贝叶斯定理,岩相κt后验概率密度分布为
| $ p\left(\kappa_{t} \mid y_{t}\right) \propto p\left(\kappa_{t}\right) \int p\left(m_{t} \mid {\kappa}_{t}\right) p\left(m_{t} \mid y_{t}\right) \mathrm{d} m_{t} $ | (A-1) |
式中p(κt)为岩相先验概率密度分布,积分项内p(mt|κt)、p(mt|yt)均服从高斯分布。
如果参数m的高斯分布记为N(m; μ, Σ),即p(mt|κt)~N(m; μ1, Σ1),p(mt|yt)~N(m; μ2, Σ2),有
| $ N\left(m ; \boldsymbol{\mu}_{1}, \boldsymbol{\varSigma}_{1}\right) \times N\left(\boldsymbol{m} ; \boldsymbol{\mu}_{2}, \boldsymbol{\varSigma}_{2}\right)=c_{c} N\left(\boldsymbol{m} ; \boldsymbol{\mu}_{c}, \boldsymbol{\varSigma}_{c}\right) $ | (A-2) |
式(A-2)等式左边表示式(A-1)中积分项内高斯分布乘积,式(A-2)等式右边可表示为
| $ \begin{aligned} &c_{c} N\left(\boldsymbol{m} ; \boldsymbol{\mu}_{c}, \boldsymbol{\varSigma}_{c}\right)=\frac{1}{(2 {\rm{ \mathsf{ π} }})^{d / 2} \operatorname{det}\left(\boldsymbol{\varSigma}_{1}\right)^{1 / 2}} \times \\ &\quad \exp \left[-\frac{1}{2}\left(\boldsymbol{m}-\boldsymbol{\mu}_{1}\right)^{\mathrm{T}} \boldsymbol{\varSigma}_{1}^{-1}\left(\boldsymbol{m}-\boldsymbol{\mu}_{1}\right)\right] \times \\ &\quad(2 {\rm{ \mathsf{ π} }})^{d / 2} \operatorname{det}\left(\boldsymbol{\varSigma}_{2}\right)^{1 / 2} \times \\ &\quad \exp \left[-\frac{1}{2}\left(\boldsymbol{m}-\boldsymbol{\mu}_{2}\right)^{\mathrm{T}} \boldsymbol{\varSigma}_{2}^{-1}\left(\boldsymbol{m}-\boldsymbol{\mu}_{2}\right)\right] \end{aligned} $ | (A-3) |
式中d为数据采样长度。
将式(A-3)展开并进行整理,得
| $ \begin{aligned} &c_{c} N\left(\boldsymbol{m} ; \boldsymbol{\mu}_{c}, \boldsymbol{\varSigma}_{c}\right)= \\ &\quad \exp \left\{-\frac{1}{2}\left[d \ln (2 {\rm{ \mathsf{ π} }})+\ln \left|\boldsymbol{\varSigma}_{1}\right|+\boldsymbol{\mu}_{1}^{\mathrm{T}} \boldsymbol{\varSigma}_{1}^{-1} \boldsymbol{\mu}_{1}\right]\right\} \times \\ &\quad \exp \left\{-\frac{1}{2}\left[d \ln (2 {\rm{ \mathsf{ π} }})+\ln \left|\boldsymbol{\varSigma}_{2}\right|+\boldsymbol{\mu}_{2}^{\mathrm{T}} \boldsymbol{\varSigma}_{2}^{-1} \boldsymbol{\mu}_{2}\right]\right\} \times \\ &\quad \exp \left(-\frac{1}{2}\left\{\boldsymbol{m}^{\mathrm{T}}\left(\boldsymbol{\varSigma}_{1}^{-1}+\boldsymbol{\varSigma}_{2}^{-1}\right) \boldsymbol{m}-\boldsymbol{m}^{\mathrm{T}} \times\right.\right. \\ &\quad \left(\boldsymbol{\varSigma}_{1}^{-1}+\boldsymbol{\varSigma}_{2}^{-1}\right)\left(\boldsymbol{\varSigma}_{1}^{-1}+\boldsymbol{\varSigma}_{2}^{-1}\right)^{-1}\left(\boldsymbol{\varSigma}_{2}^{-1} \boldsymbol{\mu}_{1}+\boldsymbol{\varSigma}_{2}^{-1} \boldsymbol{\mu}_{2}\right)- \\ &\quad \left.\left.\left[\left(\boldsymbol{\varSigma}_{1}^{-1}+\boldsymbol{\varSigma}_{2}^{-1}\right)^{-1}\left(\boldsymbol{\varSigma}_{1}^{-1} \boldsymbol{\mu}_{1}+\boldsymbol{\varSigma}_{2}^{-1} \boldsymbol{\mu}_{2}\right)\right]^{\mathrm{T}}\left(\boldsymbol{\varSigma}_{1}^{-1}+\boldsymbol{\varSigma}_{2}^{-1}\right) \boldsymbol{m}\right\}\right) \end{aligned} $ | (A-4) |
将式(A-4)中的(Σ1-1+ Σ2-1)-1(Σ1-1 μ1+ Σ2-1 μ2)记为μc,(Σ1-1+ Σ2-1)-1记为Σc,则
| $ \begin{aligned} &c_{c} N\left(\boldsymbol{m} ; \boldsymbol{\mu}_{c}, \boldsymbol{\varSigma}_{c}\right)= \\ &\exp \left\{-\frac{1}{2}\left[d \ln (2 {\rm{ \mathsf{ π} }})+\ln \left|\boldsymbol{\varSigma}_{1}\right|+\boldsymbol{\mu}_{1}^{\mathrm{T}} \boldsymbol{\varSigma}_{1}^{-1} \boldsymbol{\mu}_{1}\right]\right\} \times \\ &\exp \left\{-\frac{1}{2}\left[d \ln (2 {\rm{ \mathsf{ π} }})+\ln \left|\boldsymbol{\varSigma}_{2}\right|+\boldsymbol{\mu}_{2}^{\mathrm{T}} \boldsymbol{\varSigma}_{2}^{-1} \boldsymbol{\mu}_{2}\right]\right\} \times \\ &\exp \left\{\frac{1}{2}\left[d \ln (2 {\rm{ \mathsf{ π} }})+\ln \left|\boldsymbol{\varSigma}_{c}\right|+\boldsymbol{\mu}_{c}^{\mathrm{T}} \boldsymbol{\varSigma}_{c}^{-1} \boldsymbol{\mu}_{c}\right]\right\} N\left(\boldsymbol{m} ; \boldsymbol{\mu}_{c}, \boldsymbol{\varSigma}_{c}\right) \end{aligned} $ | (A-5) |
其中
| $ \begin{aligned} &c_{c}=\exp \left\{-\frac{1}{2}\left[d \ln (2 {\rm{ \mathsf{ π} }})+\ln \left|\boldsymbol{\varSigma}_{1}\right|+\boldsymbol{\mu}_{1}^{\mathrm{T}} \boldsymbol{\varSigma}_{1}^{-1} \boldsymbol{\mu}_{1}\right]\right\} \times \\ &\quad \exp \left\{-\left[\frac{1}{2} d \ln (2 {\rm{ \mathsf{ π} }})+\ln \left|\boldsymbol{\varSigma}_{2}\right|+\boldsymbol{\mu}_{2}^{\mathrm{T}} \boldsymbol{\varSigma}_{2}^{-1} \boldsymbol{\mu}_{2}\right]\right\} \times \\ &\quad \exp \left\{\frac{1}{2}\left[d \ln (2 {\rm{ \mathsf{ π} }})+\ln \left|\boldsymbol{\varSigma}_{c}\right|+\boldsymbol{\mu}_{c}^{\mathrm{T}} \boldsymbol{\varSigma}_{c}^{-1} \boldsymbol{\mu}_{c}\right]\right\} \end{aligned} $ | (A-6) |
式(A-6)可简记为
| $ c_{c}=\exp \left(\sum\limits_{i=1}^{2} \xi_{i}+\xi_{c}\right) $ | (A-7) |
其中
| $ \xi_{i}=-\frac{1}{2}\left[d \ln (2 {\rm{ \mathsf{ π} }})+\ln \left|\boldsymbol{\varSigma}_{i}\right|+\boldsymbol{\mu}_{i}^{\mathrm{T}} \boldsymbol{\varSigma}_{i}^{-1} \boldsymbol{\mu}_{i}\right] $ | (A-8) |
| $ \xi_{c}=\frac{1}{2}\left[d \ln (2 {\rm{ \mathsf{ π} }})+\ln \left|\boldsymbol{\varSigma}_{c}\right|+\boldsymbol{\mu}_{c}^{\mathrm{T}} \boldsymbol{\varSigma}_{c}^{-1} \boldsymbol{\mu}_{c}\right] $ | (A-9) |
| [1] |
周爽爽, 印兴耀, 裴松, 等. 地震波形约束的蒙特卡洛-马尔科夫链随机反演方法[J]. 石油地球物理勘探, 2021, 56(3): 543-554, 592. ZHOU Shuangshuang, YIN Xingyao, PEI Song, et al. Monte Carlo-Markov Chain stochastic inversion constrained by seismic waveform[J]. Oil Geophysical Prospecting, 2021, 56(3): 543-554, 592. |
| [2] |
李坤, 印兴耀. 混合概率模型驱动的叠前地震反演方法[J]. 石油地球物理勘探, 2020, 55(4): 839-853. LI Kun, YIN Xingyao. Prestack seismic inversion driven by mixture probabilistic models[J]. Oil Geophysical Prospecting, 2020, 55(4): 839-853. |
| [3] |
王芳芳, 李景叶, 陈小宏. 基于马尔科夫链先验模型的贝叶斯岩相识别[J]. 石油地球物理勘探, 2014, 49(1): 183-189. WANG Fangfang, LI Jingye, CHEN Xiaohong. Baye-sian facies identification based on Markov-chain prior model[J]. Oil Geophysical Prospecting, 2014, 49(1): 183-189. |
| [4] |
Buland A, Omre H. Bayesian linearized AVO inversion[J]. Geophysics, 2003, 68(1): 185-198. DOI:10.1190/1.1543206 |
| [5] |
Grana D, Della R E. Probabilistic petrophysical-properties estimation integrating statistical rock physics with seismic inversion[J]. Geophysics, 2010, 75(3): O21-O37. DOI:10.1190/1.3386676 |
| [6] |
Hamid H, Pidlisecky A. Multitrace impedance inversion with lateral constraints[J]. Geophysics, 2015, 80(6): M101-M111. DOI:10.1190/geo2014-0546.1 |
| [7] |
张广智, 王丹阳, 印兴耀, 等. 基于MCMC的叠前地震反演方法研究[J]. 地球物理学报, 2011, 54(11): 2926-2932. ZHANG Guangzhi, WANG Danyang, YIN Xingyao, et al. Study on prestack seismic inversion using Markov Chain Monter Carlo[J]. Chinese Journal of Geophy-sics, 2011, 54(11): 2926-2932. DOI:10.3969/j.issn.0001-5733.2011.11.022 |
| [8] |
Aleardi M, Ciabarri F, Gukov T. A two-step inversion approach for seismic-reservoir characterization and a comparison with a single-loop Markov-chain Monte Carlo algorithm[J]. Geophysics, 2018, 83(3): R227-R244. DOI:10.1190/geo2017-0387.1 |
| [9] |
黄捍东, 张如伟, 魏世平. 地震非线性随机反演方法在陆相薄砂岩储层预测中的应用[J]. 石油学报, 2009, 30(3): 386-390. HUANG Handong, ZHANG Ruwei, WEI Shiping. Research on application of seismic nonlinear random inversion to reservoir prediction in the thin sandstone of continental deposits[J]. Acta Petrolei Sinica, 2009, 30(3): 386-390. DOI:10.3321/j.issn:0253-2697.2009.03.011 |
| [10] |
Larsen A L, Ulvmoen M, Omre H, et al. Bayesian lithology/fluid prediction and simulation on the basis of a Markov-chain prior model[J]. Geophysics, 2006, 71(5): R69-R78. DOI:10.1190/1.2245469 |
| [11] |
李军, 杨晓娟, 张晓龙, 等. 基于三维马尔可夫链模型的岩性随机模拟[J]. 石油学报, 2012, 33(5): 846-853. LI Jun, YANG Xiaojuan, ZHANG Xiaolong, et al. Lithologic stochastic simulation based on the three-dimensional Markov chain model[J]. Acta Petrolei Sinica, 2012, 33(5): 846-853. |
| [12] |
刘兴业, 陈小宏, 李景叶, 等. 基于核贝叶斯判别法的储层物性参数预测[J]. 石油学报, 2016, 37(7): 878-886. LIU Xingye, CHEN Xiaohong, LI Jingye, et al. Reservoir physical property predicteion based on kernel-Bayes discriminant method[J]. Acta Petrolei Sinica, 2016, 37(7): 878-886. |
| [13] |
袁成, 李景叶, 陈小宏. 基于概率统计的地震岩相识别不确定性定量评价方法[J]. 地球物理学报, 2015, 58(10): 3825-3836. YUAN Cheng, LI Jingye, CHEN Xiaohong. Quantitative evaluation of uncertainties in seismic facies idetification based on probabilistic statistics[J]. Chinese Journal of Geophysics, 2015, 58(10): 3825-3836. DOI:10.6038/cjg20151032 |
| [14] |
袁成, 李景叶, 陈小宏. 地震岩相识别概率表征方法[J]. 地球物理学报, 2016, 59(1): 287-298. YUAN Cheng, LI Jingye, CHEN Xiaohong. A probabilistic approch for seismic facies classification[J]. Chinese Journal of Geophysics, 2016, 59(1): 287-298. |
| [15] |
Bosch M, Cara L, Rodrigues J, et al. A Monte Carlo approach to the joint estimation of reservoir and elastic parameters from seismic amplitudes[J]. Geophy-sics, 2007, 72(6): O29-O39. |
| [16] |
de Figueiredo L P, Grana D, Santos M, et al. Bayesian seismic inversion based on rock-physics prior mode-ling for the joint estimation of acoustic impedance, porosity and lithofacies[J]. Journal of Computational Physics, 2017, 336(5): 128-142. |
| [17] |
Grana D. Joint facies and reservoir properties inversion[J]. Geophysics, 2018, 83(3): M15-M24. DOI:10.1190/geo2017-0670.1 |
| [18] |
李海山, 杨午阳, 雍学善. 基于平面波解构的初始波阻抗建模方法[J]. 石油地球物理勘探, 2018, 53(2): 388-394. LI Haishan, YANG Wuyang, YONG Xueshan. Initial wave impedance modeling based on plane-wave destruction[J]. Oil Geophysical Prospecting, 2018, 53(2): 388-394. |
| [19] |
曹丹平, 印兴耀, 张繁昌, 等. 多尺度地震资料联合反演方法研究[J]. 地球物理学报, 2009, 52(4): 1059-1067. CAO Danping, YIN Xingyao, ZHANG Fanchang, et al. A study on the method of joint invrsion of multiscale seismic data[J]. Chinese Journal of Geophysics, 2009, 52(4): 1059-1067. DOI:10.3969/j.issn.0001-5733.2009.04.023 |
| [20] |
周晓越, 甘利灯, 杨昊, 等. 利用叠前振幅和速度各向异性的联合反演方法[J]. 石油地球物理勘探, 2020, 55(5): 1084-1091. ZHOU Xiaoyue, GAN Lideng, YANG Hao, et al. A joint inversion method using amplitude and velocity anisotropy[J]. Oil Geophysical Prospecting, 2020, 55(5): 1084-1091. |
| [21] |
Mavko G, Mukerji T, Dvorkin J. The Rock Physics Handbook: Tools for Seismic Analysis of Porous Media[M]. Cambridge University Press, 2009, 1-524.
|
| [22] |
Chen Y K, Chen H M, Xiang K, et al. Geological structure guided well log interpolation for high-fide-lity full waveform inversion[J]. Geophysical Journal International, 2016, 207(2): 1313-1331. DOI:10.1093/gji/ggw343 |
| [23] |
Fomel S. Applications of plane-wave destruction filters[J]. Geophysics, 2002, 67(6): 1946-1960. DOI:10.1190/1.1527095 |
| [24] |
Petersen K B, Pedersen M S. The Matrix Cookbook[M]. Technical University of Denmark, 2008.
|
| [25] |
Sugiyama M. Introduction to Statistical Machine Learning[M]. Elsevier, 2016.
|



 李景叶, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院物探系, 102249。Email:
李景叶, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院物探系, 102249。Email: 