随着油气勘探开发需求的提高,尤其是在剩余油的挖潜方面,需要精细刻画多级次断裂、渗流屏障等不连续性特征。
近几年来,针对如何在地震数据中精确识别隐含的不连续性特征这一问题,地球物理学家开展了大量的研究工作。1999年,Gersztenkorn等[1]提出基于本征结构的C3算法,实现了在含噪数据中的不连续性特征识别,但这容易受地层倾角影响,并且计算量较大[2-3]。2000年,Randen等[4]提出三维纹理属性,如倾角、方位角和混沌纹理属性等,用于相干体难以识别的小断层、小构造。2003年,Pedersen等[5]开发蚂蚁追踪算法,实现了地震数据体中不连续信息的自动识别。2005年,Jacquemin等[6]应用双霍夫变换方法实现了断层自动提取。2018年,代荣获等[7]提出一种自适应的边缘保持平滑滤波(AEPS)方法,该方法兼顾了噪声压制和地质信息的有效保留。同年,梯度结构张量(GST)算法得到广泛应用,王研博[8]采用Sobel算子、Canny算子和GST算法在地震图像中提取地层边界及断层、褶皱等;周钰邦等[9]针对非常规油藏的裂缝精细识别和碳酸盐岩等复杂储层预测进行了GST算法研究;崔正伟等[10]结合构造导向滤波与GST相干技术,实现了储层裂缝的精细识别;刘宏杰等[11]利用GST算法改进拉普拉斯滤波的随机噪声压制方法,提高了地质体边缘特征细节和断层成像精度。2019年,刘艺璇等[12]提出多窗口最小峰态约束的多步中值滤波技术,在有效压制随机噪声的同时最大程度地保留了地震不连续性特征。2020年,张栋等[13]在地震属性分析中引入数学形态学方法,实现储层边界及其内部不连续性特征的骨架提取。另外,许辉群等[14]、苟量等[15]验证了边缘检测技术识别地质体边界的有效性。
目前存在的地震不连续性特征识别方法往往因为噪声而导致提取的边界出现模糊、过于破碎和细节信息丢失的现象。在油气藏开发过程中,不连续性特征提取的准确性和完整性尤为重要。张量投票方法是提高特征信息完整性和准确性的有效手段。该方法由南加利福尼亚大学Guy[16]在1997年根据格式塔“整体大于部分之和”原则提出的一种显著性结构特征推理,特点在于能从带有强噪声、离群点的点云信息中推理隐含的结构特征[17-20],将人类视觉看到的形态特征信息通过机器算法将其可视化。目前该方法已成功应用于图像处理、点云处理、计算机视觉等多个领域,如图像修复[21]、特征提取[22-24]、曲率估算[25]等。2004年,Tong等[26]应用张量投票方法实现了二维人脑MRI影像的边界结构推理,减少了离群点、噪声、方向不连续等因素的影响。2005年,左西年等[27]通过张量投票方法实现蚁蛉翅脉信息提取。2017年,Wu等[28]在三维断层面的基础上应用张量投票方法实现了断层的修复。
本文重点探索基于张量投票的地震不连续性特征增强方法。通过张量特征值与数据结构特征之间的关系,对地震数据的特征值进行投票叠加,进而得到数据形式为张量的投票结果;然后对其进行张量分解并加以分析,确定数据中各类特征的置信度[29-30],即能迅速引起观察者视觉注意的突出程度,从而实现对地震数据中结构特征的检测和增强,使之能有效识别断层等不连续性特征的边界信息并将其骨架化,这有利于识别地震数据中的裂缝、断层及地质体边界等。
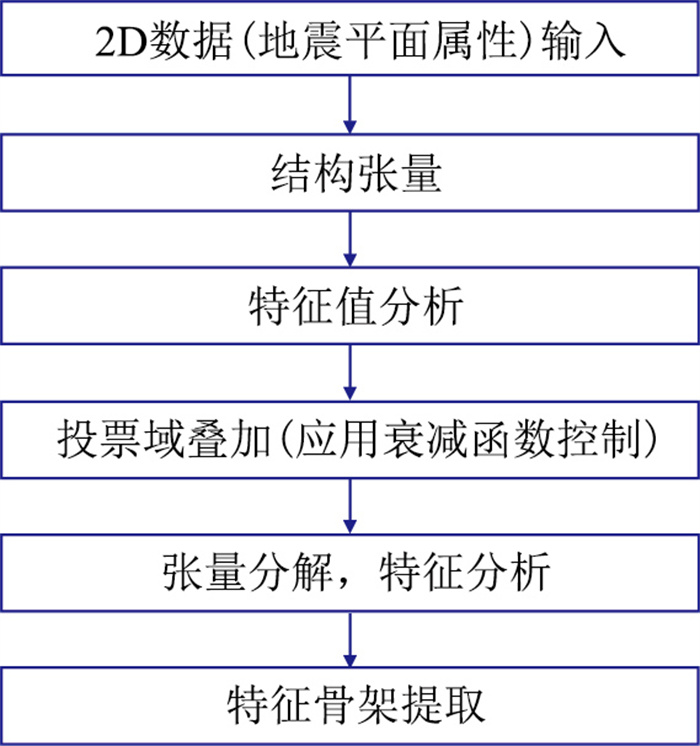
1 张量投票方法张量投票方法流程如图 1所示。首先,利用梯度向量构造张量矩阵的方法将地震属性数据编码为张量的形式;其次,通过分解张量矩阵得到含有目标信息的特征值,并对特征值进行投票叠加;最终得到地震不连续性特征的骨架结构,从而达到增强不连续性特征的目的。
|
图 1 张量投票方法流程 |
张量投票方法的第一步是将输入数据的像素点编码为二阶对称半正定张量的形式,它本质上表明了数据中结构特征的显著性及其优先的法线和切线方向。
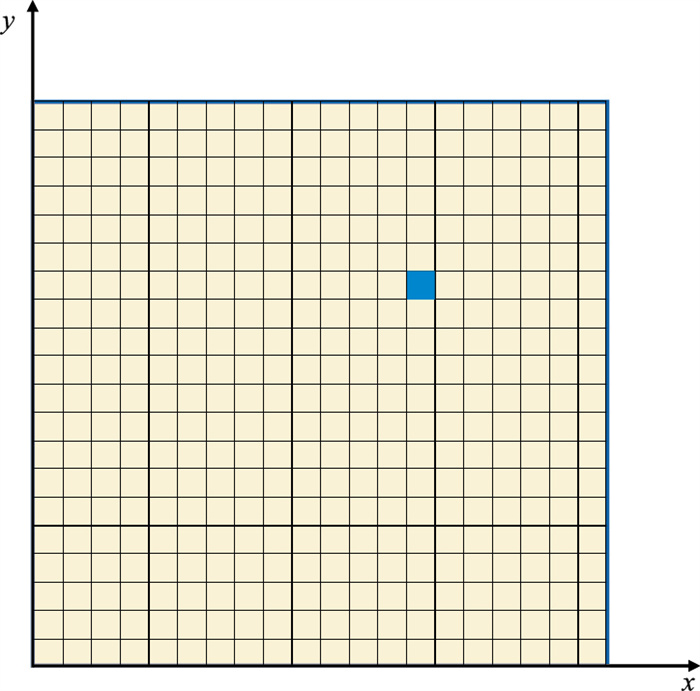
在二维地震数据中,以图像I (x, y)表示地震数据,如图 2所示,图像在计算机中是通过像素矩阵的结构形式存储。图中小正方形代表像素节点,x方向为主测线方向,y方向为联络测线方向,以主、联络测线表示图像像素的坐标。每个像素值用Ii(xi, yi)表示,其梯度向量为
|
图 2 图像结构说明 |
| $ \nabla \mathit{\boldsymbol{I}} = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial \mathit{\boldsymbol{I}}}}{{\partial x}}}\\ {\frac{{\partial \mathit{\boldsymbol{I}}}}{{\partial y}}} \end{array}} \right] $ | (1) |
利用梯度向量构造梯度平方张量,即
| $ \mathit{\boldsymbol{G}} = (\nabla \mathit{\boldsymbol{I}}){(\nabla \mathit{\boldsymbol{I}})^{\rm{T}}}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {{{(\frac{{\partial \mathit{\boldsymbol{I}}}}{{\partial x}})}^2}}&{\frac{{\partial \mathit{\boldsymbol{I}}}}{{\partial x}}\frac{{\partial \mathit{\boldsymbol{I}}}}{{\partial y}}}\\ {\frac{{\partial \mathit{\boldsymbol{I}}}}{{\partial y}}\frac{{\partial \mathit{\boldsymbol{I}}}}{{\partial x}}}&{{{(\frac{{\partial \mathit{\boldsymbol{I}}}}{{\partial y}})}^2}} \end{array}} \right] $ | (2) |
取平方使同一走向但方向相反的梯度矢量不至于相互抵消,反而可以相互增强。针对二阶矩阵G,任意二阶对称非负定张量可分解为
| $ \mathit{\boldsymbol{G}} = {\lambda _1}{\mathit{\boldsymbol{e}}_1}\mathit{\boldsymbol{e}}_1^{\rm{T}} + {\lambda _2}{\mathit{\boldsymbol{e}}_2}\mathit{\boldsymbol{e}}_2^{\rm{T}}\;\;\;{\lambda _1} \ge \;{\lambda _2} \ge 0 $ | (3) |
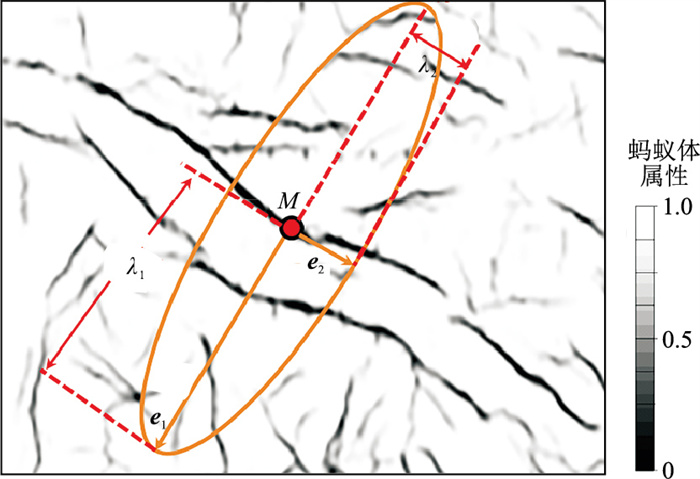
式中:λi(i=1, 2)表示特征值;ei(i=1, 2)表示特征向量。如图 3所示,以蚂蚁体切片为例,通过上述方法计算得到的二阶张量可图示为椭圆。在断裂带上的M点,特征向量e1正交于断裂的主结构方向,特征向量e2平行于断裂的主结构方向。当λ1>λ2>0时,表示M点处存在各向异性;当λ1-λ2≫λ2时,M点处各向异性较强,反映M点处为断裂, 将这种各向异性较强的点记为种子点。
|
图 3 张量分解示意图 |
将种子点通过投票域叠加的方式可以提高特征信息的连续性及完整性。根据格式塔原理[16],在投票过程中,衰减函数(DF)决定了以种子点为中心的投票强度变化。求取投票强度的表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{DF(}}s, k, \sigma {\rm{) = 0}}\;\;\;\;\;\theta {\rm{ > }}\frac{{\rm{ \mathit{ π} }}}{2}}\\ {{\rm{DF(}}s, k, \sigma {\rm{) = }}{{\rm{e}}^{ - (\frac{{{s^2} + \varepsilon {k^2}}}{{{\sigma ^2}}})}}\;\;\;\;0 \le \theta \le \frac{{\rm{ \mathit{ π} }}}{2}} \end{array}} \right.\; $ | (4) |
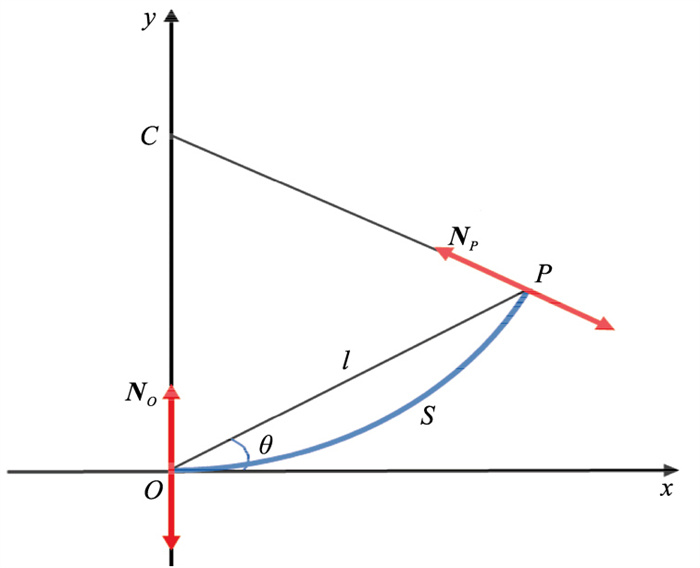
过程如图 4所示。式中:θ为种子点O的曲率圆切线与直线OP间的夹角(本文以种子点O的曲率圆切线作为直角坐标系的横轴,以种子点O的曲率圆法线作为直角坐标系的纵轴。NO和NP分别是O点和P点的法向量);
|
图 4 投票规则示意图
C表示圆心,种子点O表示投票者,种子点P表示接收者。双箭头表示法线方向。格式塔原理表示:O到P最有可能的平滑路径是保持恒定曲率的弧。当投票者O与接收者P相邻时,曲率圆退化为一条直线;当O到P不相邻时,O对P的影响随距离增大而减小。为避免衰减函数在种子点附近出现投票强度特性紊乱现象,人为设定0≤θ≤ |
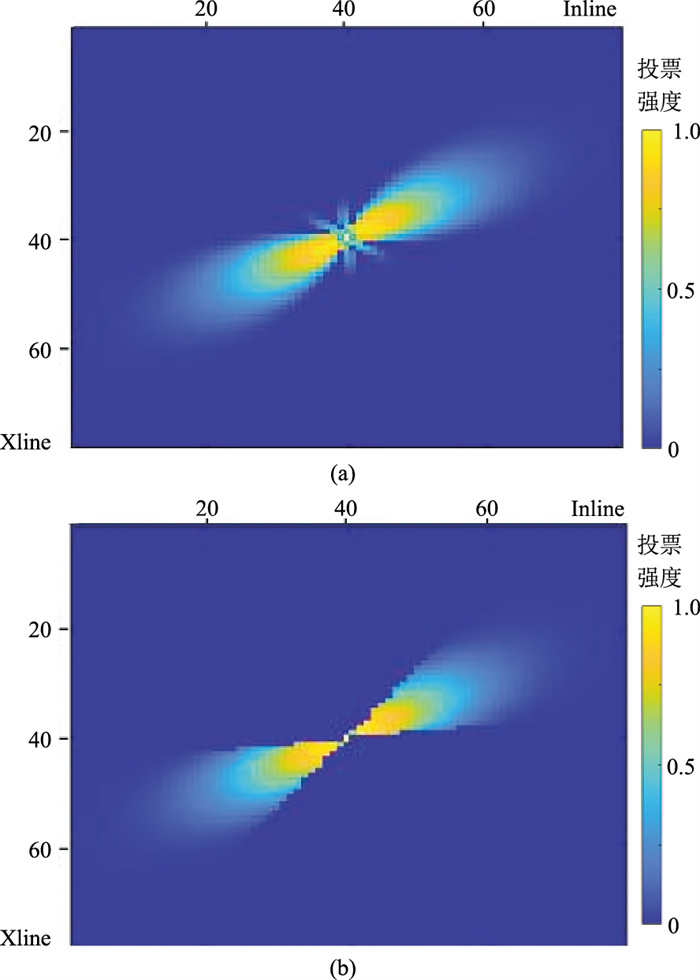
图 5所示为θ范围设定前后投票域的变化。由图可见,当未设置θ范围时,种子点位置出现紊乱现象,这会导致种子点附近出现毛刺等假性特征(图 5a);当设定0≤θ≤
|
图 5 投票域强度
(a)未设置θ范围(0≤θ≤2π);(b)设置θ范围(0≤θ≤ |
P点收到来自于O点的投票算子为
| $ {\mathit{\boldsymbol{V}}_P} = {\rm{DF(}}s, k, \sigma {\rm{)}} · {\mathit{\boldsymbol{N}}_P} · \mathit{\boldsymbol{N}}_P^{\rm{T}} $ | (5) |
其中
| $ {\mathit{\boldsymbol{N}}_P} = {\mathit{\boldsymbol{N}}_O}{[ - \sin 2\theta \;\;\;\;\cos 2\theta ]^{\rm{T}}} $ | (6) |
将每个以种子点为中心的投票域进行叠加,累计每个种子点的邻域投票,可得种子点投票的数量和大小。在每个种子点上形成一个新的张量
| $ \mathit{\boldsymbol{V}} = \sum\limits_{i = 1}^K {{\mathit{\boldsymbol{V}}_P}} $ | (7) |
式中:V表示累计投票;K表示投票域中心邻域像素点的个数。对投票后的张量可分解为
| $ \mathit{\boldsymbol{V}} = ({\lambda _1} - {\lambda _2}){\mathit{\boldsymbol{e}}_1}\mathit{\boldsymbol{e}}_1^{\rm{T}} + {\lambda _2}({\mathit{\boldsymbol{e}}_1}\mathit{\boldsymbol{e}}_1^{\rm{T}} + {\mathit{\boldsymbol{e}}_2}\mathit{\boldsymbol{e}}_2^{\rm{T}}) $ | (8) |
式中:e1e1T定义为棒张量;λ1-λ2表示棒形张量的显著性大小;e1e1T+ e2e2T定义为球张量;λ2表示圆形张量的显著性大小。如果λ1-λ2>λ2,说明主导张量是棒张量,种子点最有可能位于以e1为法线的特征曲线上;如果λ1≈λ2>0,说明种子点很有可能位于多条特征曲线的相交处,或者是该点位于一个区域内,所有方向都是近似的,无线性特征;当λ1和λ2都极小时,说明该点可能是离群值。
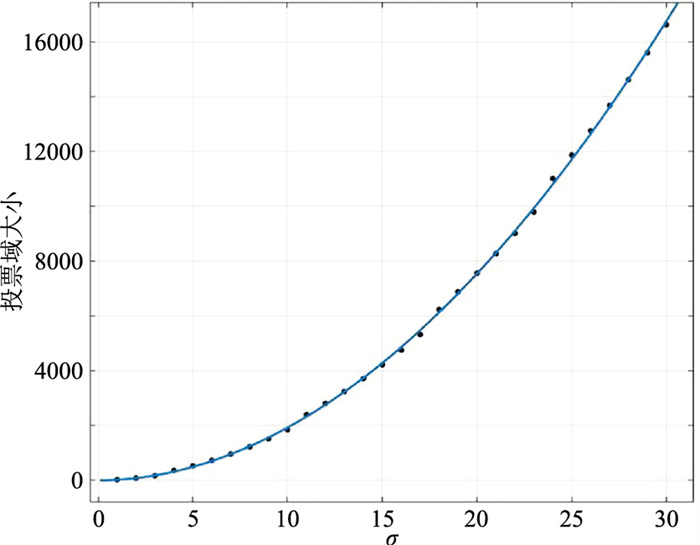
2 关键参数及方法验证 2.1 尺度参数对投票结果的影响张量投票方法中尺度参数σ是整个投票过程中唯一的交互参数,它的大小决定了投票算子控制的投票域范围。图 6显示了不同尺度下投票域的变化。假设连接A、B两点的直线为断层,A、B为种子点,通过遍历投票尺度参数(数值范围设定为0~30)进行测试。当σ为4时,投票域范围较小,张量投票算法的平滑能力较弱,突出A、B两点断层局部特征信息,连接性较差;随着σ逐渐增大,张量投票算法的平滑能力提高,两点之间存在一定的连接性,同时投票域范围呈现指数级增长(图 7)。在实际应用中,需要突出特征连续性时,建议σ选择范围大于7;需要突出细节信息时,建议σ选择范围小于7,但这需要结合实际情况进行测试。

|
图 6 以两点为例表示不同尺度投票域 (a)σ=4;(b)σ=7;(c)σ=10 |
|
图 7 投票尺度与投票域的关系 |
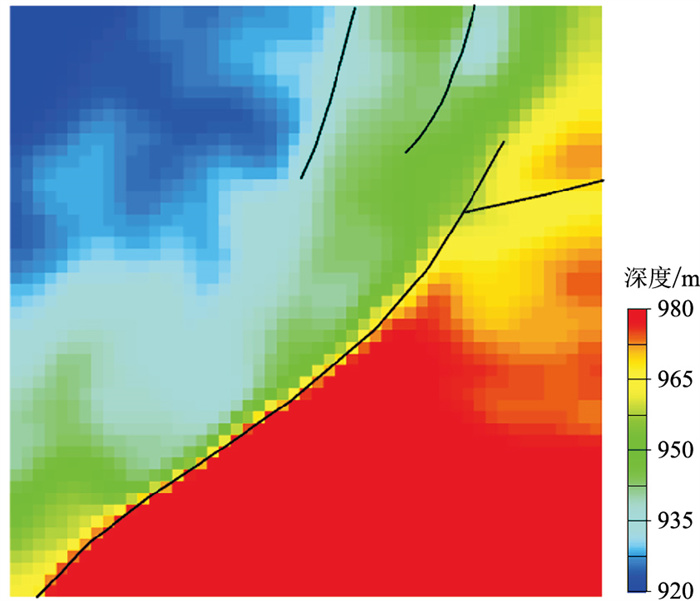
为了验证张量投票方法的有效性,建立一个三维断层模型,其地震数据体如图 8所示。H层位深度如图 9所示,图中黑色线段表示断层位置。

|
图 8 包含断层的三维理论模型 |
|
图 9 H层位深度图 |
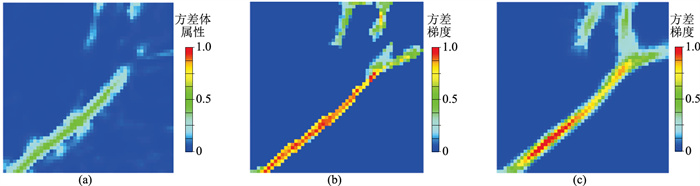
在地震数据体上提取反映构造不连续性的方差体属性切片(图 10a)。可以看出,方差体不能有效识别主断层的次级断层。在方差体属性切片基础上,应用不同尺度的张量投票方法进行处理。投票结果数值越大,表明构造不连续性的特征越强。小尺度投票结果(图 10b) 在有效压制边缘噪声的同时,清楚地刻画了断层的走向及连接方式,与断层解释结果(图 9)一致。尺度较大的张量投票结果(图 10c)重点在于刻画较完整的断层轮廓,不利于刻画细节信息。模型试算结果表明,张量投票方法在增强构造不连续性特征信息的同时,又兼顾了特征骨架提取的完整性。
|
图 10 不同投票尺度对方差体属性切片的不连续性特征增强处理结果 (a)方差体属性切片;(b)小尺度张量投票;(c)大尺度张量投票 |
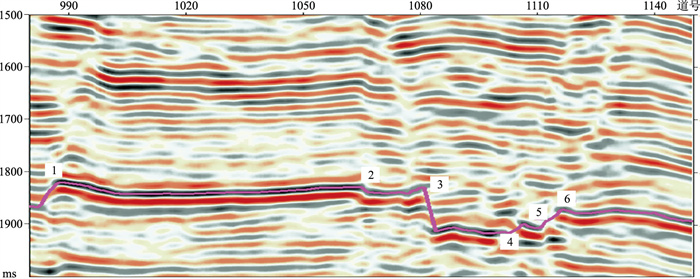
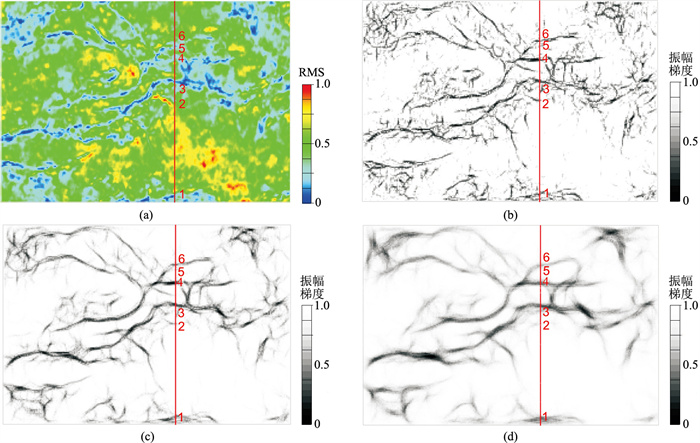
为了验证本文方法对实际数据中不连续性特征骨架的检测效果,选取R区实际地震数据进行分析对比。图 11所示为第1627线地震剖面,紫线为地震反射层位,数字对应地震剖面同相轴挠曲或错断的位置,即不连续性特征的位置。断层受NE向走滑应力场控制,根据安德森模式[31],除NE向走滑主断层外,还派生NWW-SEE向正断层、NE-SW向同向走滑断层和NW-SE向反向走滑断层。沿层提取均方根振幅属性切片(图 12a),通过不同尺度的张量投票处理挖掘并提取均方根振幅属性中不连续性特征骨架,图 12b~图 12d分别是投票尺度为3、5、8的均方根振幅属性张量投票结果,可见投票结果与该区内三组断层一致。当σ为3时,投票域范围较小,在有效提取区内三组断层骨架的同时,保留了大量的局部特征细节,不连续性特征边界线(即断裂)之间的连接样式和交接关系清楚。随着σ增大,不连续性特征更加平滑,增强了主干信息,部分细节特征被弱化。当投票尺度持续增大时,细节信息被压制,则只见三组断层的整体轮廓。张量投票算法通过σ控制投票域范围,投票结果存在着增强主要信息与压制局部特征的矛盾。因此,在实际生产应用中,可通过循环遍历投票尺度参数(数值范围设定为1~30)进行部分数据处理测试,再结合工区已有资料,选择最优参数进行全工区的数据处理。
|
图 12 σ对RMS属性的不连续性特征增强处理结果 (a)RMS属性;(b)σ=3;(c)σ=5;(d)σ=8 |
相干属性和方差属性可以识别断层、岩性边界以及地层不连续变化等特征,并且能够用来自动拾取地震数据中的地质信息,是最常用的断层识别方法,对于同相轴错断较大的断层识别效果较好,具有较强的抗噪性。一般在地下地质结构中,连续性越差,对应的方差值越高,相干值越低。在这些属性基础上进行张量投票处理能够增强不连续性特征,提高提取的断层骨架的完整度。如图 13所示,从方差切片和相干切片上基本可以看到断层的分布形态及变化趋势,但识别的断层特征连续性较差,分辨率较低,增加了多解性,不利于断层的精细解释。通过张量投票增强处理后,在方差切片和相干切片基础上进一步增强了特征信息,有效地将人类视觉感知到的信息可视化;同时,得到的断裂信息连续性更加完整,增加了提取的断裂骨架的可靠性。对比常规属性(图 13a、图 13c)与张量投票处理后(图 13b、图 13d)的效果可见,无论是细节刻画还是整体轮廓,应用张量投票方法后断裂带更加清晰,能够帮助地质人员更好地进行人机交互解释,为后续的断层建模提供可靠的依据。

|
图 13 不同属性切片及张量投票处理结果对比 (a)相干属性切片;(b)对图a进行张量投票处理;(c)方差体切片;(d)对图c进行张量投票处理 |
裂缝及断层、地质体边界检测是地震资料解释中的一项主要内容,为此,本文在地震属性基础上,提出了一种基于张量投票的特征骨架提取方法,并通过模型试算和实际资料处理,取得了良好的应用效果,得到以下几点认识。
(1) 张量投票方法能够增强地震属性中构造不连续特征信息,提高提取的特征骨架的完整性。小尺度投票能够很好地刻画细节特征,大尺度投票重点刻画较完整的断层轮廓。
(2) 通过张量投票处理结果与相干属性、方差属性的对比分析,表明了本文方法能够挖掘属性中隐藏的不连续性特征,特征骨架具有较高的完整度;在描述断层信息的连续性方面比方差、相干属性更加清晰,能够突显微弱的细节特征。
(3) 本文方法的投票尺度选取非自适应,难以实现在增强断层信息的连续性的同时保留细节信息的自动优化,如何针对复杂的地震数据进行分尺度参数自适应调整以及提高运行效率,是下一步算法优化的方向。
| [1] |
Gersztenkorn A, Marfurt K J. Eigenstructure based coherence computations as an aid to 3-D structural and stratigraphic mapping[J]. Geophysics, 1999, 64(5): 1468-1479. DOI:10.1190/1.1444651 |
| [2] |
李婷婷, 侯思宇, 马世忠, 等. 断层识别方法综述及研究进展[J]. 地球物理学进展, 2018, 33(4): 1507-1514. LI Tingting, HOU Siyu, MA Shizhong, et al. Overview and research progress of fault identification method[J]. Progress in Geophysics, 2018, 33(4): 1507-1514. |
| [3] |
苑书金. 地震相干体技术的研究综述[J]. 勘探地球物理进展, 2007, 30(1): 7-15. YUAN Shujin. A review of seismic coherence techniques[J]. Progress in Exploration Geophysics, 2007, 30(1): 7-15. |
| [4] |
Randen T, Monsen E, Signer C, et al. Three-dimensional texture attributes for seismic data analysis[C]. SEG Technical Program Expanded Abstracts, 2000, 19: 668-671.
|
| [5] |
Pedersen S I, Skov T, Hetlelid A, et al. New paradigm of fault interpretation[C]. SEG Technical Program Expanded Abstracts, 2003, 22: 350-353.
|
| [6] |
Jacquemin P, Mallet J L. Automatic faults extraction using double hough transform[C]. SEG Technical Program Expanded Abstracts, 2005, 24: 755-759.
|
| [7] |
代荣获, 尹成, 张旭东. 自适应边缘保持平滑滤波[C]. 北京: CPS/SEG北京2018国际地球物理会议, 2018, 3. DAI Ronghuo, YIN Cheng, ZHANG Xudong. Adaptive edge-preserving smoothing filter[C]. CPS/SEG International Geophysical Conference, Beijing, 2018, 3. |
| [8] |
王研博. 基于边缘检测技术的地层边界和地层倾角提取[D]. 吉林长春: 吉林大学, 2018. WANG Yanbo. Extraction of Formation Boundaries and Dips Using Edge Detection Techniques[D]. Jilin University, Changchun, Jilin, 2018. |
| [9] |
周钰邦, 李勇, 王孟修, 等. GST算法在地震属性的研究[C]. 北京: CPS/SEG北京2018国际地球物理会议, 2018, 4. ZHOU Yubang, LI Yong, WANG Mengxiu, et al. A study of GST method in the seismic attributes[C]. CPS/SEG International Geophysical Conference, Beijing, 2018, 4. |
| [10] |
崔正伟, 程冰洁, 徐天吉, 等. 基于构造导向滤波与梯度结构张量相干属性的储层裂缝预测方法及应用[J]. 石油地球物理勘探, 2021, 56(3): 555-563. CUI Zhengwei, CHENG Bingjie, XU Tianji, et al. Reservoir fracture prediction method and application based on structure-oriented filtering and coherent attributes of gradient structure tensor[J]. Oil Geophysical Prospecting, 2021, 56(3): 555-563. |
| [11] |
刘宏杰, 毛海波, 杨晓海, 等. 基于三维各向异性拉普拉斯滤波的随机噪声压制方法及应用[J]. 石油地球物理勘探, 2019, 54(3): 522-528. LIU Hongjie, MAO Haibo, YANG Xiaohai, et al. 3D anisotropic Laplacian filtering based random seismic noise suppression[J]. Oil Geophysical Prospecting, 2019, 54(3): 522-528. |
| [12] |
刘艺璇, 尹成, 丁峰, 等. 一种改进滤波技术在海上油田勘探中的应用[J]. 化工设计通讯, 2019, 45(12): 248-249. LIU Yixuan, YIN Cheng, DING Feng, et al. Application of an improved filtering technique in offshore oil field exploration[J]. Chemical Engineering Design Communications, 2019, 45(12): 248-249. DOI:10.3969/j.issn.1003-6490.2019.12.165 |
| [13] |
张栋, 黄旭日, 丁峰, 等. 河流相储层构型不连续界限横向预测方法[C]. 江苏南京: SPG/SEG南京2020年国际地球物理会议, 2020, 4. ZHANG Dong, HUANG Xuri, DING Feng, et al. Discontinuity detection method of fluvial reservoir architecture in horizontal direction[C]. SPG/SEG International Geophysical Conference, Nanjing, Jiangsu, 2020, 4. |
| [14] |
许辉群, 桂志先, 孙赞东. 边缘检测技术在地震属性中的应用[J]. 石油地球物理勘探, 2011, 46(1): 126-128. XU Huiqun, GUI Zhixian, SUN Zandong. Application of edge detection technique in seismic attribute analysis[J]. Oil Geophysical Prospecting, 2011, 46(1): 126-128. |
| [15] |
苟量, 彭真明. 小波多尺度边缘检测及其在裂缝预测中的应用[J]. 石油地球物理勘探, 2005, 40(3): 309-313. GOU Liang, PENG Zhenming. Multi-scale edge detection of wavelet and application in fracture prediction[J]. Oil Geophysical Prospecting, 2005, 40(3): 309-313. |
| [16] |
Guy G. Inference of Multiple Curves and Surfaces from Sparse Data[D]. University of Southern California, 1995.
|
| [17] |
Martinez-Sanchez A, Garcia I, Asano S, et al. Robust membrane detection based on tensor voting for electron tomography[J]. Journal of Structural Biology, 2014, 186(1): 49-61. DOI:10.1016/j.jsb.2014.02.015 |
| [18] |
Bayro-Corrochano E. Geometric Algebra Applications, Vol. I: Computer Vision, Graphics and Neurocompu-ting[M]. Springer, 2019.
|
| [19] |
King B J. Range Data Analysis by Free-space Mode-ling and Tensor Voting[D]. Rensselaer Polytechnic Institute, USA, 2008.
|
| [20] |
Medioni G, Tang C K. Tensor voting: Theory and applications[EB/OL]. [2013-12-29]. https://www.docin.com/p-747939511.html.
|
| [21] |
Jia J Y, Tang C K. Image repairing: Robust image synthesis by adaptive ND tensor voting[C]. 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Proceedings, 2003, 643-650.
|
| [22] |
Kim H S, Choi H K, Lee K H. Feature detection of triangular meshes based on tensor voting theory[J]. Computer-Aided Design, 2009, 41(1): 47-58. |
| [23] |
王莉, 苏李君. 一种面向图像线特征提取的改进投票域的张量投票算法[J]. 河南理工大学学报(自然科学版), 2021, 40(1): 133-137. WANG Li, SU Lijun. A tensor voting algorithm for image line feature extraction based on improved vo-ting field[J]. Journal of Henan Polytechnic University(Natural Science), 2021, 40(1): 133-137. |
| [24] |
秦和娟. 基于张量投票的机载LiDAR数据道路骨架线提取研究[D]. 江苏南京: 南京信息工程大学, 2020. QIN Hejuan. Road Centerlines Extraction Based on Tensor Voting Using Airborne LiDAR Data[D]. Nanjing University of Information Science & Techno-logy, Nanjing, Jiangsu, 2020. |
| [25] |
Moreno R, Pizarro L, Burgeth B, et al. Adaptation of Tensor Voting to Image Structure Estimation[M]//New Developments in the Visualization and Processing of Tensor Fields, Mathematics and Visualization. Springer, Berlin, 2012, 29-50.
|
| [26] |
Tong W S, Tang C K, Mordohai P, et al. First order augmentation to tensor voting for boundary inference and multiscale analysis in 3D[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(5): 594-611. |
| [27] |
左西年, 刘来福, 王心丽, 等. 基于Tensor Voting的蚁蛉翅脉修补[J]. 北京师范大学学报(自然科学版), 2005, 41(2): 135-138. ZUO Xinian, LIU Laifu, WANG Xinli, et al. Reparation of Myrmeleontidae's venation based on tensor voting[J]. Journal of Beijing Normal University(Na-tural Science), 2005, 41(2): 135-138. |
| [28] |
Wu X M, Zhu Z H. Methods to enhance seismic faults and construct fault surfaces[J]. Computers and Geosciences, 2017, 107: 37-48. |
| [29] |
邱康. 基于Tensor Voting的CT影像导丝检测[D]. 贵州贵阳: 贵州大学, 2019. QIU Kang. Guide Wire of CT Image Detection Based on Tensor Voting[D]. Guizhou University, Guiyang, Guizhou, 2019. |
| [30] |
吴春林, 吴凌燕, 郭维波, 等. 基于张量投票法的路面裂缝检测应用[J]. 仪表技术, 2019(4): 36-37. WU Chunlin, WU Lingyan, GUO Weibo, et al. Application of pavement crack detection based on tensor voting[J]. Instrumentation Technology, 2019(4): 36-37. |
| [31] |
童亨茂. 岩石圈脆性断层作用力学模型[J]. 自然杂志, 2013, 35(1): 56-63. TONG Hengmao. Mechanical model of brittle faulting in lithosphere[J]. Chinese Journal of Nature, 2013, 35(1): 56-63. |



 崔晓庆, 四川省成都市新都区新都大道8号西南石油大学地球科学与技术学院, 610500。Email:
崔晓庆, 四川省成都市新都区新都大道8号西南石油大学地球科学与技术学院, 610500。Email: