② 中海石油(中国)有限公司上海分公司, 上海 200335
② Shanghai Branch of CNOOC Ltd., Shanghai 200335, China
曲流河砂体是陆相沉积中最主要的油气储集体之一。伴随河道形态变化和反复沉积、侵蚀,平原区曲流河河谷内残留点坝复合沉积体[1-3]。识别曲流河点坝对于研究曲流河演化特征、指导油气藏开发等具有重要意义[4-5]。然而,曲流河往往经历多期改造而形成复合微相单元,如何利用地震资料准确预测砂体厚度的变化并识别复合体内部的单一点坝,是曲流河储层预测的关键。围绕上述问题形成了一系列的地震储层预测技术(如地层切片[6-10]、地震属性分析[11-13]及地震反演[14]等技术),其中地震属性分析是最简单、有效且发展迅速的方法。新的单一属性类型的研发和多属性融合是地震属性分析技术发展的两大方向。近年来,以分频属性融合技术[15]、基于机器学习的多属性分析[16-18]等为代表的地震属性融合分析技术广泛应用于河流相储层的研究。
极限学习机(ELM)是一种基于前馈神经网络构建的机器学习方法,它优化了隐层节点的调整,采用随机神经元和随机连接,在学习速度上显著优于支持向量机(SVM)和深度学习方法[19-20],而且泛化能力强,预测误差小[21]。陈芊澍等[22]和Wang等[23]利用极限学习机算法进行地震多属性分析,在煤层及裂缝带预测方面取得了良好的效果,但是在储层研究领域的其他方面的应用尚未见文献报道。
本文选取渤海湾盆地济阳坳陷孤东油田馆陶组高弯度曲流河,将极限学习机算法应用于地震多属性融合中以预测砂体分布,按照“井震结合,动(生产动态资料)静(地震、地质等资料)结合”的思路识别曲流带内复合点坝沉积体中的单一点坝,揭示高弯度曲流河内部结构。
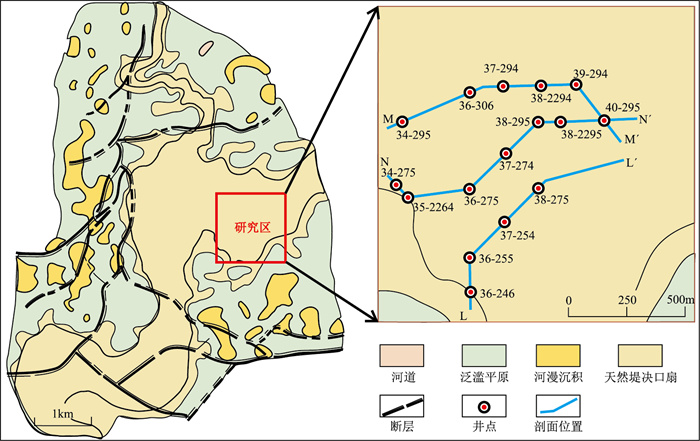
1 研究区概况孤东油田紧邻黄河入海口,是渤海湾盆地济阳坳陷沾化凹陷内的一个大型披覆背斜构造整装油藏,主要的油气层为新近系馆陶组。研究区发育典型的高弯度曲流河沉积[9, 24-25],但近年来的新井钻探和注水开发成果揭示曲流河点坝沉积微相内部具有强非均质性,其中单一点坝认识不清成为当前制约油气开发的关键因素。研究区面积为2.45km2,共完钻井60余口(图 1)。三维地震资料覆盖全区,道间距为25m。目的层平均深度约为1260m,地震纵波平均速度为2150m/s。目的层段地震资料主频为35Hz,垂向分辨率(按照1/4λ计算)约为15.4m。
|
图 1 研究区沉积背景 |
每种地震属性都包含了复杂的地质信息,但是在理论上地震属性与地质参数之间缺乏确定性对应关系。从多种地震属性中获得需要的地质信息是地质和地球物理人员共同的目标。在这种大信息量、非线性的分析中,神经网络具有独特的优势。本文采用基于前馈神经网络构建的极限学习机算法进行地震多属性分析,实现多属性融合,预测砂体厚度及分布。
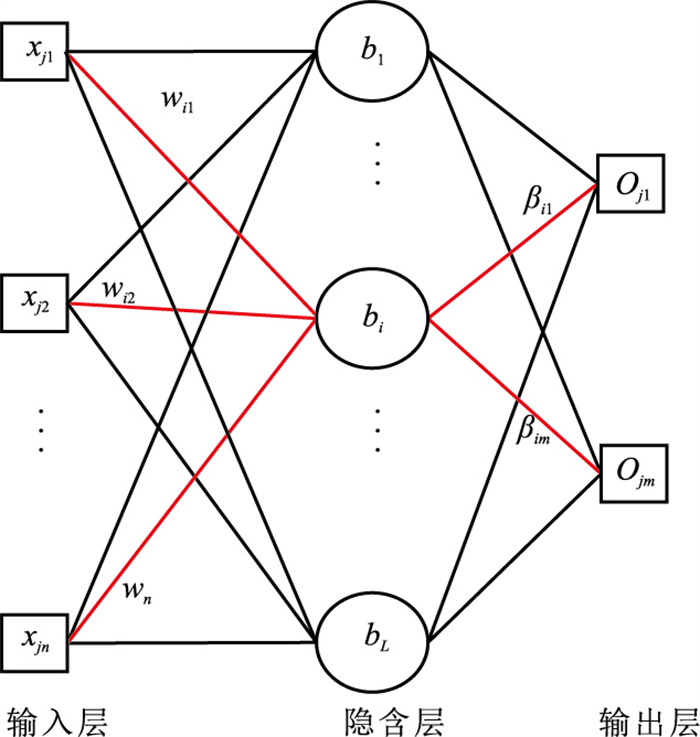
2.1 极限学习机算法极限学习机是Huang等[26]提出的一种前馈神经网络,由输入层、隐含层和输出层组成(图 2)。
|
图 2 前馈神经网络结构 |
在利用极限学习机进行多属性分析时,将来自不同井点的数据形成样本集合。例如对于N个不同样本形成集合{(Xj, tj)},其中,j=1, 2, …, N,Xj=xj1, xj2, …, xjnT∈ Rn,tj= tj1, tj2, …,tjmT∈ Rm。当隐含层节点数量为L个时,激励函数为g(x)的前馈神经输出Oj可表示为
| $ \sum\limits_{i = 1}^L {{\mathit{\boldsymbol{\beta }}_i}g({\mathit{\boldsymbol{W}}_i} \bullet {\mathit{\boldsymbol{X}}_j} + {b_i}) = {\mathit{\boldsymbol{O}}_j}} $ | (1) |
式中:Wi= wi1, wi2, …winT表示输入层到第i个隐含层节点的输入权值;bi为第i个隐含层节点的偏差;βi= βi1, βi2, …βimT是连接第i个隐含层节点与输出层的权值。
网络的学习目标是使输出的误差最小,即
| $ \sum\limits_{i = 1}^L {{\mathit{\boldsymbol{\beta }}_i}g({\mathit{\boldsymbol{W}}_i} \bullet {\mathit{\boldsymbol{X}}_j} + {b_i}) = {\mathit{\boldsymbol{t}}_j}} $ | (2) |
可简化为
| $ \mathit{\boldsymbol{H\beta }} = \mathit{\boldsymbol{T}} $ | (3) |
其中
| $ \begin{array}{c} \mathit{\boldsymbol{H}}({\mathit{\boldsymbol{W}}_1}, \cdots {\mathit{\boldsymbol{W}}_L}, {b_1}, \cdots , {b_L}, {\mathit{\boldsymbol{X}}_1}, \cdots {\mathit{\boldsymbol{X}}_L}) = \\ {\left( {\begin{array}{*{20}{c}} {g({\mathit{\boldsymbol{W}}_1} \bullet {\mathit{\boldsymbol{X}}_1} + {b_1})}& \cdots &{g({\mathit{\boldsymbol{W}}_L} \bullet {\mathit{\boldsymbol{X}}_1} + {b_L})}\\ \vdots &{}& \vdots \\ {g({\mathit{\boldsymbol{W}}_1} \bullet {\mathit{\boldsymbol{X}}_N} + {b_1})}& \cdots &{g({\mathit{\boldsymbol{W}}_L} \bullet {\mathit{\boldsymbol{X}}_N} + {b_L})} \end{array}} \right)_{N \times L}} \end{array} $ |
| $ \mathit{\boldsymbol{\beta }} = [\mathit{\boldsymbol{\beta }}_1^{\rm{T}} \cdots \mathit{\boldsymbol{\beta }}_L^{\rm{T}}]_{L \times m}^{\rm{T}} $ |
| $ \mathit{\boldsymbol{T}} = [\mathit{\boldsymbol{T}}_1^{\rm{T}} \cdots \mathit{\boldsymbol{T}}_L^{\rm{T}}]_{N \times m}^{\rm{T}} $ |
在极限学习机中,输入权重Wi和隐含层的偏差bi(由算法随机给定),使隐含层的输出矩阵H被唯一确定。因此,训练问题转化为求解输出权值矩阵的最小二乘解的问题,输出权值矩阵为
| $ \mathit{\boldsymbol{\hat \beta }} = {\mathit{\boldsymbol{H}}^{† }}\mathit{\boldsymbol{T}} $ | (4) |
式中
在计算过程中,只需调整隐含层神经元结点数,不需要迭代。因此,相比传统基于梯度下降的迭代方法,极限学习机算法能够解决收敛速度慢、容易陷入局部极小值的问题,具有极端“快速”的特点[27],可明显缩短学习时间;同时,所得解为唯一最优解,网络的泛化性能得到了保证[28]。
2.2 基于极限学习机的多属性融合将地震属性分析技术与机器学习方法相融合,可预测砂体厚度。其中有两个关键问题:一是如何选取地震属性;二是如何融合地震属性预测砂体。为此,本文设计的解决路径包含四个部分(图 3),即地震属性提取与优选(流程A)、特征变量与目标变量的统计(流程B)、地震属性与地质参数关系的建立(流程C)及砂体厚度的地质解释(流程D)。其中流程A和B针对第一个关键问题,解决地震属性的选取问题;流程C针对第二个关键问题,解决属性的融合与地质参数的预测问题。

|
图 3 基于极限学习机的多属性融合方法流程 |
需要特别说明的是,在流程A中,需要对数据进行预处理和属性优选,具体分为以下四步。
(1) 单一地震属性提取。为了减少属性类型选取的盲目性,需要根据研究区砂体发育特点(厚度、组合模式、沉积相类型等)和地震属性的物理意义进行选择。需要强调的是,充分利用前人的经验是一个有效的途径。
(2) 地震属性标准化处理。不同地震属性物理意义和值域存在差异,开展属性融合分析之前,需要对训练集和测试集中的地震属性进行标准化处理,以避免数值较大的地震属性对融合结果产生过度影响。
(3) 单一属性与井点砂岩厚度之间的相关性分析及筛选。计算每种地震属性与井点砂岩厚度之间的相关性,筛除相关性差的地震属性类型。
(4) 属性聚类分析进行再次筛选。一些在物理意义上相近的地震属性与砂岩厚度之间相关性都较高时,容易形成信息重复。为了避免这一情况,实现数据有效降维,需要对上一步筛选后的地震属性进行聚类分析,在聚类结果中选择与砂岩厚度相关性最高的属性。
经过上述属性处理与优选后,使用极限学习机算法,构建多属性融合预测砂岩厚度的网络模型,最后将全区的地震属性分析数据作为特征变量输入最优模型,预测砂体厚度及分布。
3 应用实例 3.1 模型正演根据河道的迁移特征,曲流河道间的横向组合可以划分为两种类型、三种模式,即点坝起始端与废弃河道叠加、废弃河道与废弃河道叠加两大类。其中前一类又可进一步细分为废弃河道泥岩保留和不保留两种模式。
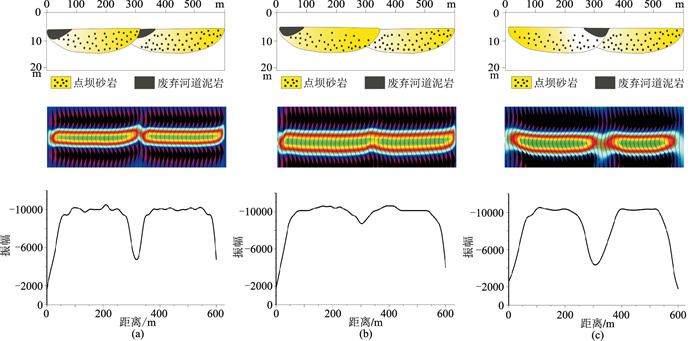
对上述三种模型开展正演模拟(图 4)。根据井点信息,设置点坝主体位置砂岩厚度为12m,废弃河道处砂岩厚度为7m,砂岩速度为2160m/s,泥岩速度为2500m/s,子波为35Hz雷克子波。对正演结果进行-90°相位转换。
|
图 4 不同点坝叠置模式正演模拟 (a)两期河道同向叠加(保留泥岩);(b)两期河道同向叠加(不保留泥岩);(c)两期河道相向叠加。上为地质模型,中为正演剖面(-90°相移),下为振幅 |
模式一(图 4a)为两期河道同向迁移叠加,后期河道起始端紧邻前一期并部分侵蚀前一期废弃河道,但前期废弃河道泥岩保留。在点坝叠置部位砂体厚度快速减小,正演模拟结果可见振幅快速减弱。
模式二(图 4b)同样为两期河道同向迁移叠加,但后期河道完全侵蚀前一期的废弃河道,甚至侵蚀部分河道砂岩,前一期废弃河道细粒沉积部分没有残留。在这种情况下,点坝叠置位置砂体厚度减小速度慢、程度弱,振幅较两侧相对减弱。
模式三(图 4c)为距离较远的两期河道相向迁移,后期河道侵蚀了前期河道而在两条河道之间保留了后期的废弃河道。点坝叠置部分砂体厚度由两侧向中间快速减小,振幅快速减弱至低值。
三种叠置模式的正演响应特征的相同点是在点坝叠置部位振幅减弱,不同点是砂体减薄方式导致的振幅减弱程度的差异和波形错动的位置。从振幅变化可以看出,振幅与砂岩厚度变化有良好的对应关系,这就意味着振幅能够较好地反映砂体的厚度变化。
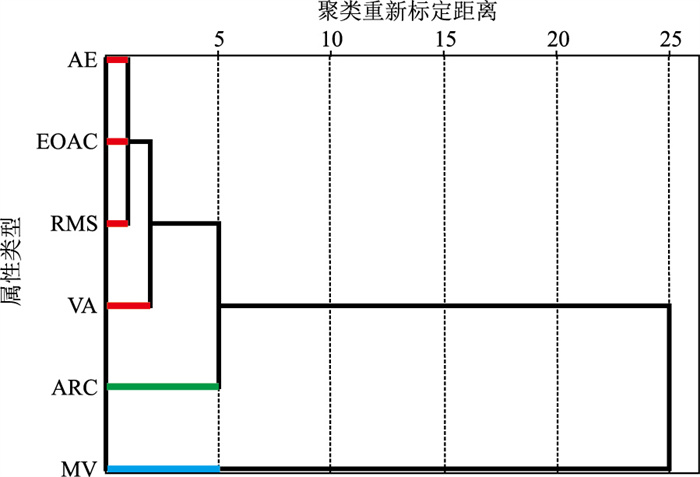
3.2 多属性融合过程对目的层段提取振幅类、频谱类、相位类等共计16种常见的地震属性,计算各属性与砂体厚度的相关系数,初步优选出6种与砂体厚度相关系数大于0.5的地震属性(表 1)。对6种初选地震属性聚类分析,结果显示可为三大类(图 5)。平均能量(AE)、能量自相关(EOAC)、振幅平方差(VA)、均方根振幅(RMS)四者距离在2以下,为第一类;弧长(ARC)和最小振幅值(MV)分别作为第二类和第三类,它们与第一类距离大于5且彼此距离也大于5。选取每类中与砂体厚度相关系数最高的地震属性,即最终选择RMS、ARC和MV属性作为参与下一步机器学习的特征变量来源。
|
|
表 1 井点砂体厚度及地震属性之间的相关系数 |
|
图 5 聚类分析树形图 |
选取拟合优度(R2)和均方根误差(RMSE)作为评价预测结果准确性的参数。拟合优度越接近于1则模型预测效果越好;均方根误差越接近于0则说明预测准确性越高。
训练集多属性融合预测与实际砂体厚度的R2为0.8237,RMSE为0.5813m(图 6a);单一属性(RMS)预测与实际砂体厚度的R2为0.6562,RMSE为0.9546m(图 6b)。测试集预测与实际砂体厚度R2为0.8275,RMSE为0.5921m(图 6c);单一属性(RMS)预测与实际砂体厚度的R2为0.6787,RMSE为0.9906m(图 6d)。上述结果表明,基于极限学习机的多属性融合预测结果比单一属性预测结果准确度更高。

|
图 6 基于极限学习机的多属性融合技术与单属性预测技术的预测结果 (a)多属性训练集;(b)单属性训练集;(c)多属性测试集;(d)单属性测试集 |
研究区大部分钻井揭示,均方根振幅单一地震属性与砂岩厚度之间具有较高的相关性,但局部存在与实钻不吻合的异常区,这降低了单一属性预测砂岩厚度的可靠性,因而需要采用多属性预测砂岩厚度。
研究区36-255井区的6口井存在地震属性与砂岩厚度关系异常(图 7红色虚线框内)。钻井揭示6口井钻遇点坝主体,砂体厚度均为10m左右。单一地震属性表现为低值,根据单一地震属性预测为砂岩不发育区(图 7b),这与实钻结果不符。采用极限学习机多属性融合预测的6口井的砂岩厚度与实际砂岩厚度的R2为0.6639,RMSE为0.2961m(图 8a)。而单一的均方根振幅属性预测的砂岩厚度与实际砂岩厚度R2为0.4104,RMSE为1.0987m(图 8b)。
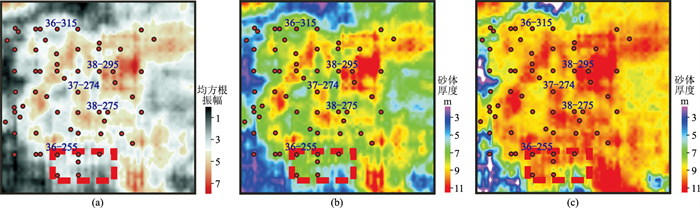
|
图 7 属性异常区两种方法预测结果对比 (a)均方根振幅;(b)单属性(RMS)预测;(c)机器学习驱动的多属性预测 |
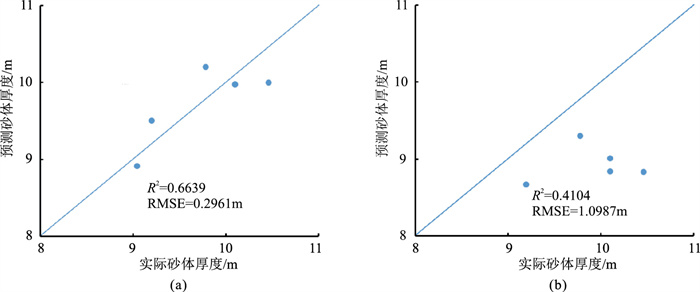
|
图 8 属性异常区两种技术的预测结果比较 (a)机器学习驱动的多属性预测;(b)单属性预测 |
如上所述,极限学习机驱动的多属性预测方法明显优于单属性预测方法。
3.3.3 不同机器学习方法对比选取研究区资料齐全的30口井建立对照组,比较ELM、BP神经网络和SVM算法进行多属性融合预测的效果。以砂岩厚度预测误差10%作为标准,预测误差小于10%为吻合,大于10%为不吻合,统计三种不同方法的砂岩厚度预测单井吻合率。结果(表 2)显示,ELM方法的单井吻合率为93.3%,SVM算法为86.7%,而BP神经网络预测单井吻合率为83.3%,这表明极限学习机驱动的多属性融合方法(本文方法)效果更好。
|
|
表 2 不同方法预测的砂体厚度样本检验结果 |
应用本文方法预测的砂岩厚度及分布(图 9)可以确定在泥岩沉积背景下发育的条带状河道,厚度大值区对应的点坝复合体被砂体不发育的“月牙形”(泥岩发育带)分割。结合钻井标定可以识别出五个单一点坝,即点坝A~点坝E。
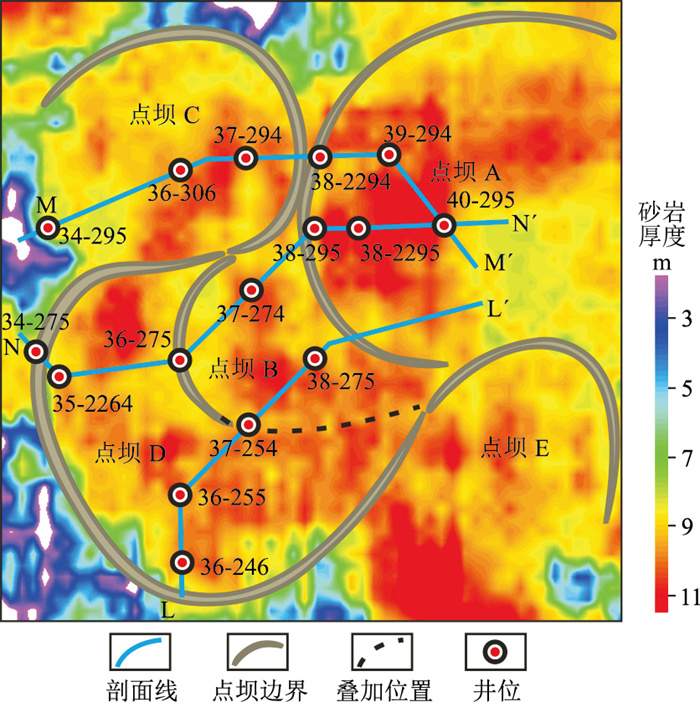
|
图 9 单一点坝综合划分结果 |
测线LL′(图 10a)上可见侧积方向相同的两个单期叠置点坝(点坝D和点坝B),前一期废弃河道完全被后期河道侵蚀,并且没有残留,属于模式二(图 4)。37-254井两侧反射同相轴连续性较好,但是该井东侧的反射振幅更强(图 10a)。钻井显示两期砂体叠置(图 10b),与地震反射的振幅变化一致。
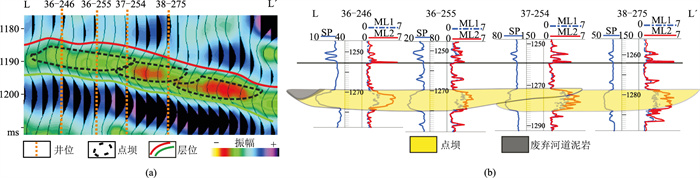
|
图 10 剖面LL′河道同向叠加(泥岩未保留)的地震(a)及测井(b)特征 SP为自然电位,单位为mV;ML1、ML2分别为微梯度电阻率、微电位电阻率,单位均为Ω·m。 |
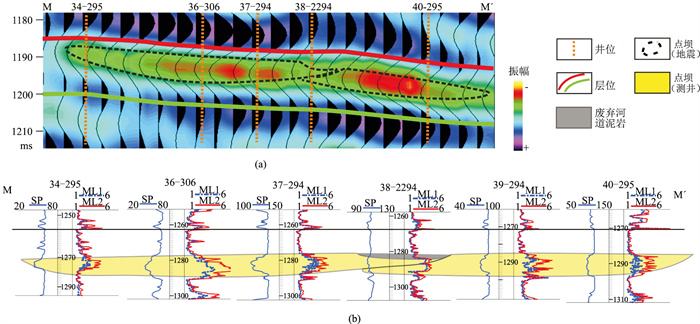
测线MM′(图 11a)上可见两个侧积方向相对的单期叠置点坝,即点坝C与点坝A(属于图 4中的模式三)。38-2294井位于点坝叠置区(图 9),处于弱振幅区,反射同相轴略向下凹,显示了时间厚度减小的特点(图 11a)。这是由于该井所在位置为废弃河道叠置区、砂岩厚度减小造成的。从连井剖面(图 11b)可见,38-2294井砂岩厚度减小且砂体顶面低于两侧其他井,说明了这是河道废弃造成的。
|
图 11 剖面MM′河道相向叠加的地震(a)及测井(b)特征 SP为自然电位,单位为mV;ML1、ML2分别为微梯度电阻率、微电位电阻率,单位均为Ω·m。 |
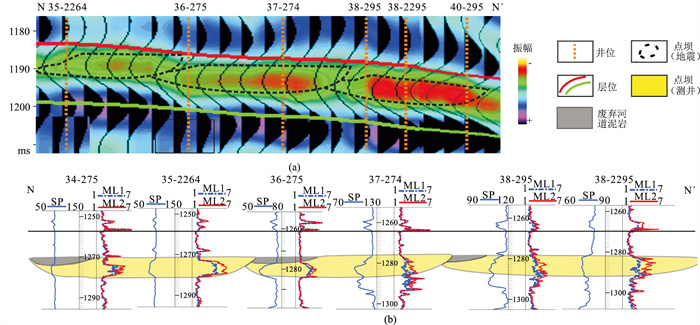
测线NN′(图 12a)上可见三个侧积方向大致相同的单期点坝(点坝D、点坝B和点坝A),36-275井和38-295井处于单期点坝的叠置区。测井资料揭示发育废弃河道残留的特征(图 12b),该点坝组合属于模式一(图 4)。前述两井点处的振幅变化以及同相轴揭示的高程关系表明,自东向西三个单一点坝发育时间由老逐渐变新,这与钻井结果一致。
|
图 12 剖面NN′河道同向叠加(泥岩保留)的地震(a)及测井(b)特征 SP为自然电位,单位为mV;ML1、ML2分别为微梯度电阻率、微电位电阻率,单位均为Ω·m。 |
综上所述,研究区发育高弯度曲流河的点坝复合体,北部和西南部发育泛滥平原,点坝复合体内部被残留的废弃河道将曲流带分为五个单一点坝(图 13a)。其中,点坝C与点坝A侧积方向相对;点坝A、点坝B和点坝D侧积方向相近,点坝B末期的废弃河道泥岩部分保留。点坝C、点坝D和点坝E的废弃河道在平面上连续,发育稳定,结合现代河流沉积特征(图 13b)可判断为同期河道沉积的三个连续点坝。

|
图 13 沉积微相图及现代沉积实例 |
新钻38-C295井是38-295井的侧钻井,在F靶点钻遇目的层,在G靶点出目的层。本文砂岩厚度预测及单一点坝解释结果表明,该井目的层段处于废弃河道内(图 14a)。随钻自然伽马曲线(图 14b)显示38-C295井目的层顶部发育厚度3.00m的泥质沉积,砂岩厚度为8.10m,而平面上与之紧邻的37-274井砂岩厚度为10.24m,从而揭示了38-C295井在目的层顶部钻遇废弃河道,验证了单一点坝的地震解释结果的合理性。

|
图 14 单一点坝识别结果的新钻井检验 (a)砂岩厚度预测结果及单一点坝解释;(b)测井曲线特征 |
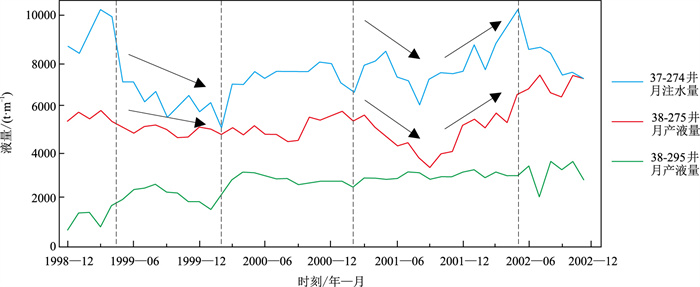
开发动态资料可以反映井间砂体的连通性,可以检验储层内部结构的预测结果。图 14a所示的三口井位于同一个开发井组,其中37-274井为注水井,38-275井和38-295井为开发井,二者与注水井37-274井的距离均约为250m。根据本文方法单一点坝识别结果,37-274井与38-275井位于点坝B内,而38-295井则位于点坝A(图 9,图 14a)。注采资料显示,37-274井注水量的变化与38-275井的产液量有良好的对应性。例如,1999年4月至2000年2月,随着37-274井注水量的降低,对应的采油井38-275井的液量发生了降低;而2001年2月至2002年5月,37-274井注水量经历了先调减后调增的措施变化,38-275井的产液量出现了一致性的变化,这两口注采对子井的变化趋势和时间具有一致性。而同期注水井37-274井与邻近的采油井38-295井的产液量变化并无对应性(图 15)。从生产动态信息来看,37-274井与38-275井的井间砂体连通性要远远好于37-274井与38-295井,这从砂体井间连通性方面验证了本文方法单一点坝识别结果的准确性。
|
图 15 三口注采井的生产曲线(井点位置见图 14a) |
(1) 基于极限学习机的多属性融合技术比单一属性对砂体厚度的预测更准确,在实例区的单井吻合率达到93.3%,高于支持向量机和BP神经网络算法。
(2) 孤东油田馆陶组曲流带发育三种单一点坝组合模式,即相向迁移点坝叠置模式、同向迁移废弃河道残留模式和同向迁移废弃河道无残留模式,三种模式的地震反射差异主要为横向连续性的变化和振幅幅度的差异。
| [1] |
林志鹏, 单敬福, 陈乐, 等. 基于地貌形态学交融的现代曲流河道迁移构型表征[J]. 沉积学报, 2018, 36(3): 427-445. LIN Zhipeng, SHAN Jingfu, CHEN Le, et al. Geomorphology processes of channel planform migration on modern meandering rivers[J]. Acta Sedimentologica Sinica, 2018, 36(3): 427-445. |
| [2] |
Yousefi S, Pourghasemi H R, Hooke J, et al. Changes in morphometric meander parameters identified on the Karoon River, Iran, using remote sensing data[J]. Geo-morphology, 2016, 271: 55-64. |
| [3] |
Morais E S, Rocha P C, Hooke J. Spatiotemporal variations in channel changes caused by cumulative factors in a meandering river: The lower Peixe River, Brazil[J]. Geomorphology, 2016, 273: 348-360. DOI:10.1016/j.geomorph.2016.07.026 |
| [4] |
胡光义, 范廷恩, 陈飞, 等. 从储层构型到"地震构型相"——一种河流相高精度概念模型的表征方法[J]. 地质学报, 2017, 91(2): 465-478. HU Guangyi, FAN Ting'en, CHEN Fei, et al. From reservoir architecture to seismic architecture facies: characteristic method of a high-resolution fluvial fa-cies model[J]. Acta Geologica Sinica, 2017, 91(2): 465-478. DOI:10.3969/j.issn.0001-5717.2017.02.012 |
| [5] |
Miall A D. Architectural-element analysis: A new me-thod of facies analysis applied to fluvial deposits[J]. Earth Science Reviews, 1985, 22(4): 261-308. DOI:10.1016/0012-8252(85)90001-7 |
| [6] |
Tan M X, Zhu X M, Liu Q H, et al. Multiple fluvial styles in Late Miocene post-rift successions of the offshore Bohai Bay Basin (China): Evidence from a seismic geomorphological study[J]. Marine and Petro-leum Geology, 2020, 113: 104173. DOI:10.1016/j.marpetgeo.2019.104173 |
| [7] |
Hossain S, Imranuzzaman M. Identification of the architecture and evolution of fluvial system using seismic geomorphology: A case study from Gulf of Thailand[J]. Journal of Natural Gas Geoscience, 2019, 4(1): 29-46. DOI:10.1016/j.jnggs.2019.02.001 |
| [8] |
刘海, 林承焰, 董春梅, 等. 基于地震沉积学的复杂曲流带沉积相研究[J]. 中国石油大学学报(自然科学版), 2018, 42(6): 30-39. LIU Hai, LIN Chengyan, DONG Chunmei, et al. Sedi-mentary facies of complex meandering belt based on seismic sedimentology[J]. Journal of China University of Petroleum (Edition of Natural Science), 2018, 42(6): 30-39. DOI:10.3969/j.issn.1673-5005.2018.06.004 |
| [9] |
Sun Z, Lin C, Zhang X, et al. Architectural analysis of subsurface meander-belt sandstones: A case study of a densely drilled oil field, Zhanhua sag, east of Bohai Bay Basin[J]. AAPG Bulletin, 2020, 104(8): 1649-1677. DOI:10.1306/04272017239 |
| [10] |
马佳国, 周卿, 王波, 等. "富砂型"河流相沉积储层砂体精细刻画[J]. 石油物探, 2021, 60(3): 461-470. MA Jiaguo, ZHOU Qing, WANG Bo, et al. Fine description of a sandbody in a sand-rich fluvial sedimentary reservoir[J]. Geophysical Prospecting for Petroleum, 2021, 60(3): 461-470. DOI:10.3969/j.issn.1000-1441.2021.03.012 |
| [11] |
周连敏, 何书梅, 赵郁文, 等. 复合曲流河道内的单河道识别[J]. 石油地球物理勘探, 2019, 54(1): 175-181. ZHOU Lianmin, HE Shumei, ZHAO Yuwen, et al. Single channel identification in a meandering river with compound channels[J]. Oil Geophysical Prospecting, 2019, 54(1): 175-181. |
| [12] |
Zeng H L, Zhu X M, Liu Q H, et al. An alternative, seismic-assisted method of fluvial architectural-element analysis in the subsurface: Neogene, Shaleitian area, Bohai Bay Basin, China[J]. Marine and Petro-leum Geology, 2020, 118: 104435. DOI:10.1016/j.marpetgeo.2020.104435 |
| [13] |
陈亮, 白雪峰, 李静, 等. 三维可视化和属性分析技术在Doshan地区的应用[J]. 石油地球物理勘探, 2018, 53(增刊2): 256-260. CHEN Liang, BAI Xuefeng, LI Jing, et al. 3D visua-lization and attribute analysis applied in seismic data interpretation of Doshan Area[J]. Oil Geophysical Prospecting, 2018, 53(S2): 256-260. |
| [14] |
徐立恒, 马耀军, 朱遂珲, 等. 油田开发后期井间砂体识别[J]. 石油地球物理勘探, 2019, 54(2): 390-397. XU Liheng, MA Yaojun, ZHU Suihui, et al. Cross-well sand-body identification in the oilfield development late stage[J]. Oil Geophysical Prospecting, 2019, 54(2): 390-397. |
| [15] |
岳大力, 李伟, 王军, 等. 基于分频融合地震属性的曲流带预测与点坝识别——以渤海湾盆地埕岛油田馆陶组为例[J]. 古地理学报, 2018, 20(6): 941-950. YUE Dali, LI Wei, WANG Jun, et al. Prediction of meandering belt and point-bar recognition based on spectral-decomposed and fused seismic attributes: A case study of the Guantao Formation, Chengdao Oilfield, Bohai Bay Basin[J]. Journal of Palaeogeography, 2018, 20(6): 941-950. |
| [16] |
Li W, Yue D, Wang W, et al. Fusing multiple frequency-decomposed seismic attributes with machine lear-ning for thickness prediction and sedimentary facies in-terpretation in fluvial reservoirs[J]. Journal of Petroleum Science and Engineering, 2019, 177: 1087-1102. DOI:10.1016/j.petrol.2019.03.017 |
| [17] |
Ao Y, Li H, Zhu L, et al. A SCiForest based semi-supervised learning method for the seismic interpretation of channel sand-body[J]. Journal of Applied Geophysics, 2019, 167: 51-62. DOI:10.1016/j.jappgeo.2019.04.019 |
| [18] |
蔡义峰, 熊婷, 姚卫江, 等. 地震多属性分析技术在薄层砂体预测中的应用[J]. 石油地球物理勘探, 2017, 52(增刊2): 140-145. CAI Yifeng, XIONG Ting, YAO Weijiang, et al. Thin sandstone prediction with seismic multi-attribute analysis[J]. Oil Geophysical Prospecting, 2017, 52(S2): 140-145. |
| [19] |
Huang G B, Chen L, Siew C K. Universal approximation using incremental constructive feed forward networks with random hidden nodes[J]. IEEE Transactions on Neural Networks, 2006, 17(4): 879-892. DOI:10.1109/TNN.2006.875977 |
| [20] |
Xie Z G, Xu K, Shan W, et al. Projective feature lear-ning for 3D shapes with multi-view depth images[J]. Computer Graphics Forum, 2015, 34(7): 1-11. DOI:10.1111/cgf.12740 |
| [21] |
Bai Z, Kasun L, Huang G B. Generic object recognition with local receptive fields based extreme learning machine[J]. Procedia Computer Science, 2015, 53(1): 391-399. |
| [22] |
陈芊澍, 文晓涛, 何健, 等. 基于极限学习机的裂缝带预测[J]. 石油物探, 2021, 60(1): 149-156. CHEN Qianshu, WEN Xiaotao, HE Jian, et al. Prediction of a fracture zone using an extreme learning machine[J]. Geophysical Prospecting for Petroleum, 2021, 60(1): 149-156. DOI:10.3969/j.issn.1000-1441.2021.01.014 |
| [23] |
Wang X, Li Y, Chen T J, et al. Quantitative thickness prediction of tectonically deformed coal using extreme learning machine and principal component analysis: A case study[J]. Computers and Geosciences, 2017, 101: 38-47. DOI:10.1016/j.cageo.2017.02.001 |
| [24] |
孙志峰, 林承焰, 董春梅. 复杂曲流带识别标志及其内部点坝叠加接触模式[J]. 沉积学报, 2018, 36(2): 366-375. SUN Zhifeng, LIN Chengyan, DONG Chunmei. Boundary distinction mark of the complicated meander belt and stacking mode between point-bar sandbodies within the belt[J]. Acta Sedimentologica Sinica, 2018, 36(2): 366-375. |
| [25] |
Zhang X, Zhang T, Lin C, et al. Reservoir architecture and evolution of meandering belt: A subsurface case in the Jiyang Depression, eastern China[J]. Journal of Petroleum Science and Engineering, 2020, 193: 107380. DOI:10.1016/j.petrol.2020.107380 |
| [26] |
Huang G, Zhu Q, Siew C. Extreme learning machine: Theory and applications[J]. Neurocomputing, 2006, 70(1-3): 489-501. DOI:10.1016/j.neucom.2005.12.126 |
| [27] |
刘学艺, 李平, 郜传厚. 极限学习机的快速留-交叉验证算法[J]. 上海交通大学学报, 2011, 45(8): 1140-1145. LIU Xueyi, LI Ping, GAO Chuanhou. Fast leave-one-out cross-validation algorithm for extreme lear-ning machine[J]. Journal of Shanghai Jiaotong Univer-sity, 2011, 45(8): 1140-1145. DOI:10.3969/j.issn.1674-8115.2011.08.021 |
| [28] |
潘华贤, 程国建, 蔡磊. 极限学习机与支持向量机在储层渗透率预测中的对比研究[J]. 计算机工程与科学, 2010, 31(2): 131-134. PAN Huaxian, CHENG Guojian, CAI Lei. Comparison of the extreme learning machine with the support vector machine for reservoir permeability prediction[J]. Computer Engineering & Science, 2010, 31(2): 131-134. DOI:10.3969/j.issn.1007-130X.2010.02.036 |



 张宪国, 山东省青岛市长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
张宪国, 山东省青岛市长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: 