② 中国石油大学(华东), 山东青岛 266580
② China University of Petroleum (East China), Qingdao, Shandong 266580, China
碳酸盐岩地区由于溶蚀作用,断层往往伴有缝洞。研究断层及其伴生的缝洞,对储层预测具有重要意义。边缘检测方法众多,如方差体方法、蚂蚁追踪方法[1]、曲率属性方法及其他方法[2-4]、多代相干体算法[5-7]、Canny算子边缘检测方法、sobel算子边缘检测算法等,最新的方法有相似属性方法、Likelihood属性方法、混乱属性相干方法等。其中相似属性方法、Likelihood属性方法及多代相干体方法实质上也是相干方法。上述方法是非常有效的断层检测方法,取得了很好的应用效果[8-14],但也有其自身的不足和边缘检测能力的限制,特别是对噪声干扰、多边缘干涉及弱小目标边缘的检测效果不理想。曲率属性方法、Canny算子和sobel算子边缘检测方法涉及梯度计算,严重放大了噪声,检测结果的可靠性差。
压缩感知理论是近年来新的信号处理理论,在数据压缩、传输领域得到广泛应用。压缩感知理论的稀疏重建理论[15-17]为信号重建提供了新的理论方法,在图像重建领域普遍获得较好效果[18-21];在地震勘探领域,人们利用压缩感知理论去噪[22]、数据重建[23]、拓频处理,取得了较好效果。
针对边缘检测存在的问题,本文首先分析断层边缘和缝洞边缘的空间分布特征,根据断层边缘和缝洞边缘的地震响应特征,把低秩稀疏分析理论引入边缘检测,研究边缘信息、背景信息及噪声信息的低秩稀疏分解与重建;为了提高边缘检测能力和分辨率,在压缩感知稀疏表示基础上,对地震资料进行深度稀疏化表示,结合向量稀疏表示和矩阵稀疏表示,通过低秩稀疏分析理论[24-25],形成一种全新的边缘检测方法。
1 基本框架理论 1.1 信号分析低秩表示模型低秩表示思想是构建一个能够表示所有样本能力的字典,并且每个样本都可以用字典中的原子线性表示,同类样本的表示系数具有相关性,故整个表示系数矩阵是一个低秩矩阵。该模型可以更好地挖掘数据的结构信息,较好地解决多线性子空间聚类和分离问题。由于矩阵满足低秩条件,所以可以保证同类数据样本聚集到相同的子空间。
在复杂的地震资料边缘检测中,相似背景和稀疏目标组成了地震响应的所有成分,背景又由多种子背景构成。背景和局部目标也是相对的,若研究目标是断层,则地层相对于断层为背景;若研究目标是断层中的缝洞,则断层相对于缝洞为背景。
1.2 低秩稀疏表示根据低秩稀疏分解理论,假设地震信号S由区域相似信息和局部信息构成,则可以分解为低秩矩阵B和稀疏矩阵D两部分,即:S=B+D,其中B为背景部分(低秩部分或相似部分),D为高秩部分(稀疏部分)。可利用信息主成分分析求解最优低秩矩阵B,即求解下列优化问题
| $ {\rm{mi}}{{\rm{n}}_{\mathit{\boldsymbol{B}},\mathit{\boldsymbol{D}}}}{\left\| \mathit{\boldsymbol{S}} \right\|_{\rm{F}}}\;{\rm{满足}}\;{\rm{rank}}(\mathit{\boldsymbol{B}}) \le \mathit{r},\mathit{\boldsymbol{S}} = \mathit{\boldsymbol{B}} + \mathit{\boldsymbol{D}} $ | (1) |
式中:r为矩阵的秩;‖S‖F为Frobenius范数。
通过此约束问题,可以找到矩阵S在一个R维线性子空间的投影。当矩阵D的元素服从独立高斯分布时,对S进行奇异值分解,便可得到式(1)的最优解。如果D不满足以上条件,式(1)无解或误差较大。于是利用稳健的主成分分析方法解决这个问题。引入正则化参数μ,得到新的优化问题
| $ {\rm{min}}[{\rm{rank}}(\mathit{\boldsymbol{B}}) + \mathit{\mu }{\left\| \mathit{\boldsymbol{D}} \right\|_{\rm{F}}}]\;{\rm{满足}}\;\mathit{\boldsymbol{S}} = \mathit{\boldsymbol{B}} + \mathit{\boldsymbol{D}} $ | (2) |
上述优化问题是一个NP-hard问题,因此对目标函数进行松弛,即将非凸函数问题转化为凸函数问题,利用核范数代替矩阵的秩,如L1范数代替L0范数。此时的凸优化问题为
| $ {\rm{min}}[{\left\| \mathit{\boldsymbol{B}} \right\|_1} + \mathit{\mu }{\left\| \mathit{\boldsymbol{D}} \right\|_1}]\;{\rm{满足}}\;\mathit{\boldsymbol{S}} = \mathit{\boldsymbol{B}} + \mathit{\boldsymbol{D}} $ | (3) |
利用压缩感知理论,将式(3)改为
| $ {\rm{min}}{\left\| {\mathit{\boldsymbol{S}} - \mathit{\boldsymbol{A}}(\mathit{\boldsymbol{B}} + \mathit{\boldsymbol{D}})} \right\|_{\rm{F}}}\;{\rm{满足}}\;{\left\| \mathit{\boldsymbol{B}} \right\|_2} \le \mathit{r},{\left\| \mathit{\boldsymbol{D}} \right\|_0} \le \mathit{k} $ | (4) |
式中:A为字典矩阵;k为稀疏目标的稀疏度,取决于稀疏目标的大小和数目,而低秩化程度估计的准确度直接影响背景的抑制效果。由式(4)可知,模型在矩阵的秩和向量的稀疏度约束下求目标函数的最优解。通过求解以上最优问题,使背景相似信息和局部稀疏信息最佳分离,有效分离地质体边缘信息、地层信息及噪声,从而进行边缘检测。
1.3 向量信号稀疏与矩阵低秩稀疏特征分析信号的稀疏分解可以是一维向量,如一维小波分解,也可以是二维矩阵,如曲波分解。矩阵的秩刻画了矩阵不相关行或列的数目,一个矩阵中的不相关的行或列越少,则该矩阵的秩越小,反之亦然。矩阵奇异值分解能够提取高维数据的局部特征及约减维数,其本质是将分类能力弱的数据集合(矩阵)的类间方差增大,提高分类能力。矩阵的奇异值个数越少,奇异值分解越稀疏,因此稀疏和低秩是一致的,反映数据的压缩能力。
2 地震资料低秩稀疏边缘检测方法基于压缩感知原理和假设,可以将边缘检测问题转化为压缩与矩阵的低秩稀疏分解问题。通过低秩稀疏分解方法压制地层信息,从而分离边缘信息。通过数据的矩阵结构变换,把地层信息变换为低秩部分,把边缘信息变换为稀疏部分,利用奇异值分解压制地层信息进而分离边缘信息。信号重建的可靠性、精度及分辨率都和信号的稀疏化分解程度有关。由低秩稀疏分解理论[24-25]可知,要得到唯一的分解结果,要求稀疏部分独立和高度稀疏。实际地震记录的边缘信息、地层信息及噪声等远不能满足高度稀疏与独立的条件。
2.1 地震信号向量稀疏表示及去噪优化地震资料稀疏表示是提高边缘检测能力的关键环节之一。利用压缩感知理论对地震信号向量稀疏表示,采用平稳小波分解方法对地震信号进行多尺度小波分解,建立小波稀疏表示字典。有效信号压缩重建就是稀疏系数优化和稀疏系数加权组合的过程。含噪信号通过某种基分解,使信号和噪声的特征不同而分离。通常情况下,噪声系数呈均匀分布,信号系数呈幂律分布。对于能量较大信号,稀疏分解使有效信号的能量强于噪声,可根据压缩感知理论的优化方法压制噪声;对于能量较小信号,稀疏分解使有效信号与噪声能量水平相当,此时压缩感知理论优化方法对噪声的压制效果不理想。假设在横向上信号稀疏分解后有效信号系数相关,而噪声系数不相关,则可采用横向相关法对稀疏系数去噪处理。
2.2 矩阵低秩稀疏表示及优化方法以上分析了信号在某种正交基下的稀疏表示方法。为了充分挖掘数据结构方面的信息,以下从矩阵秩角度讨论稀疏化问题。
2.2.1 张量奇异值分解矩阵稀疏分解有很多方式,为了更好地分析低秩问题,本文采用奇异值分解稀疏表示方法。数据矩阵的秩既与数据本身尺度有关,还与数据的排列方式(数据结构)有关。地质体是三维的,地质体地震响应信息也是三维的,把三维数据分解成二维矩阵进行奇异值稀疏分解,涉及张量分析及高阶奇异值分解。一般奇异值分解针对2阶张量矩阵,对于高阶张量,奇异值分解是高阶奇异值分解。高阶奇异值分解难以分析其低秩稀疏特征,为了研究简便,这里采用张量分解的方法,即把一个子数据体块分解成一系列二维矩阵,对于不同的分解模型,通过分析每个矩阵的低秩稀疏特征,构建具有最优低秩稀疏结构信息的张量分解模型。
2.2.2 矩阵低秩优化(1) 矩阵张量构建与优化
对于一个数据集合,不同矩阵组建方式有不同的矩阵分解特征,从而有不同的信息表示能力。根据多线性代数理论,张量是一个N维数组,则张量的阶数也为N。向量是一阶张量,矩阵是2阶张量,立体矩阵是3阶张量。数据信息包括能量信息、结构信息等。立体矩阵包含了全面的结构信息,为了充分挖掘结构信息,对三维地震数据进行立体矩阵分析建模。将子块三维数据分解成二维矩阵的模式很多,如果把所有分解模式都列出计算,计算量太大而不适合于实际分析。在断层和缝洞检测中,断层在二维情况下具有线状特征,洞边缘在二维情况下具有等轴(近似圆)特性。根据检测的两类边缘信息,分别构建行、列数不同的矩阵和行、列数相同的矩阵。对于断层检测问题,在纵向构建非方阵,即线、道及45°线方向共四个二维矩阵,在横向构建方阵,即过计算点的一个方阵;对于缝洞检测问题,在纵、横向均构建方阵。
(2) 奇异值分解去噪优化
矩阵低秩优化包括矩阵建模和奇异值分解去噪,以下讨论矩阵去噪优化。矩阵低秩优化就是通过某种方式尽可能获得具有最小秩的表示矩阵,也就是寻找一个最佳的低秩表示,达到矩阵低秩稀疏优化的目的,从而提高算法的准确性和边缘检测的分辨率。无论采用何种矩阵建模,都不能直接消除数据集合中噪声的影响。矩阵分析理论表明,矩阵中个别元素的突变会使矩阵的数目和大小发生明显变化,这种变化与该元素和矩阵的方差呈线性关系。矩阵奇异值分解去噪低秩优化问题就是使矩阵秩最小化问题。
为了使式(2)的稀疏模型对噪声更稳键,本文将λ‖D‖F刻画的残差矩阵分解为稀疏目标矩阵和噪声矩阵,即
| $ \begin{array}{c} {\rm{min}}[{\rm{rank}}(\mathit{\boldsymbol{AZ}}) + \mathit{\lambda }{\left\| \mathit{\boldsymbol{T}} \right\|_1} + \mathit{\beta }\left\| \mathit{\boldsymbol{P}} \right\|_2^2]\;{\rm{满足}}\;\\ \mathit{\boldsymbol{S}}{\rm{ = }}\mathit{\boldsymbol{AZ}}{\rm{ + }}\mathit{\boldsymbol{T}}{\rm{ + }}\mathit{\boldsymbol{P}} \end{array} $ | (5) |
式中:B=AZ是分解字典矩阵,Z是系数矩阵;T为稀疏目标;P为噪声;λ、β为两个待定参数。
将式(5)写为
| $ \begin{array}{c} {\rm{min}}[{\left\| {\mathit{\boldsymbol{AZ}}} \right\|_2} + \mathit{\lambda }{\left\| \mathit{\boldsymbol{T}} \right\|_1} + \mathit{\boldsymbol{\beta }}\left\| \mathit{\boldsymbol{P}} \right\|_2^2]{\rm{MZ}}\\ \mathit{\boldsymbol{S}}{\rm{ = }}\mathit{\boldsymbol{AZ}}{\rm{ + }}\mathit{\boldsymbol{T}}{\rm{ + }}\mathit{\boldsymbol{P}} \end{array} $ | (6) |
通过增广拉格朗日乘子方法,将式(6)的约束优化问题转化为一个无约束优化问题,优化目标函数为
| $ \begin{array}{l} \mathit{L}(\mathit{\boldsymbol{Z}},\mathit{\boldsymbol{T}},\mathit{\boldsymbol{P}},\mathit{\gamma }) = {\left\| {\mathit{\boldsymbol{AZ}}} \right\|_2} + \mathit{\lambda }{\left\| \mathit{\boldsymbol{T}} \right\|_1} + \mathit{\beta }\left\| \mathit{\boldsymbol{P}} \right\|_2^2 + \\ \;\;\left\| {\mathit{\gamma }(\mathit{\boldsymbol{S}} - \mathit{\boldsymbol{AZ}} - \mathit{\boldsymbol{T}} - \mathit{\boldsymbol{P}})} \right\|_2^2 + \frac{\mathit{\rho }}{2}\left\| {\mathit{\boldsymbol{S}} - \mathit{\boldsymbol{AZ}} - \mathit{\boldsymbol{T}} - \mathit{\boldsymbol{P}}} \right\|_2^2 \end{array} $ | (7) |
式中:等式右边第1项代表奇异值分解;第2项代表压缩感知稀疏分解重建;第3项代表噪声,主要为奇异值分解的噪声,压缩感知的噪声已去除;第4项和第5项为信号自身的约束,γ、ρ为惩罚参数。后三项都是2范数,以保证计算过程既要压制噪声,又要保证新的重建信号是期望信号(去除噪声的原始信号)。式(7)综合了小波向量稀疏优化、矩阵稀疏优化及各种约束问题,利用现有的固定变量迭代方法求解,根据研究问题的特点和算法实现要求,采用阈值迭代方法进行优化。
3 算法实现步骤由稀疏分解、稀疏系数去噪优化及矩阵建模等一系列方法得到多尺度的优化小波系数,并进行张量矩阵建模。对张量建模分解矩阵进行奇异值分解,再对矩阵奇异值进行低秩优化,根据优化后的奇异值结果重建边缘信息。具体算法步骤如下。
(1) 地震资料平稳小波分解。利用平稳小波变换方法对地震资料进行多尺度小波分解,得到地震资料的小波稀疏字典。
(2) 多尺度小波系数优化。为了最大程度地压制噪声,利用有效信号和噪声的分解系数分布特征,利用压缩感知中的MP算法和系数特征拟合方法,优选最优小波系数去噪;利用优选的分解系数通过横向相邻点进行相关计算,再次选出相关系数大的小波系数。
(3) 根据多尺度优化小波系数建立张量矩阵并进行建模。通过张量建模,构建地震数据边缘信息分类最优的矩阵表示模式。
(4) 张量矩阵奇异值分解。对三维地震数据子块(立体矩阵)进行二维矩阵分解,并对各个分解矩阵进行奇异值分解。
(5) 矩阵奇异值低秩优化。根据目标函数(式(7)),采用阈值迭代方法优化计算,以提高矩阵的低秩稀疏优化程度,从而压制奇异值分解噪声。
(6) 双稀疏和双优化结果融合与重建。将小波分解稀疏、矩阵奇异值分解稀疏和小波系数优化、矩阵低秩稀疏优化结果进行双稀疏、双优化与重建。
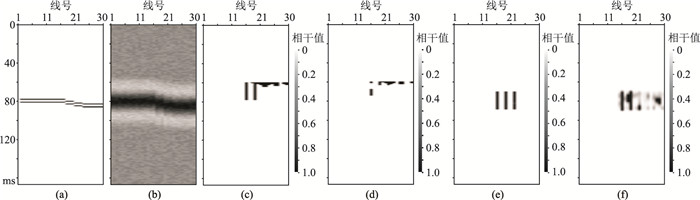
4 模型分析为了测试、分析低秩稀疏边缘检测方法(下文简称本文方法)对边缘信息的识别能力及方法适应性,分别对小断层理论模型和实际模型进行测试、分析。图 1为小断层反射系数模型及其边缘检测结果。由图可见,本文方法(图 1e、图 1f)清晰地识别了三条小断层,对小断层的识别效果明显好于相干方法(图 1c、图 1d),其中对主频为20Hz雷克子波合成的含噪记录(图中没有展示)的相干检测结果(图 1d)中没有断层显示。上述结果说明本文方法的抗噪性较强。
|
图 1 小断层反射系数模型及其边缘检测结果 (a)小断层反射系数模型;(b)主频为25Hz雷克子波与图a褶积形成的含噪记录;(c)相干(25Hz);(d)相干(20Hz);(e)本文方法(25Hz);(f)本文方法(20Hz)。模型中存在三条小断层,断距分别为3个采样点(30m)、2个采样点(20m)和1和个采样点(10m) |
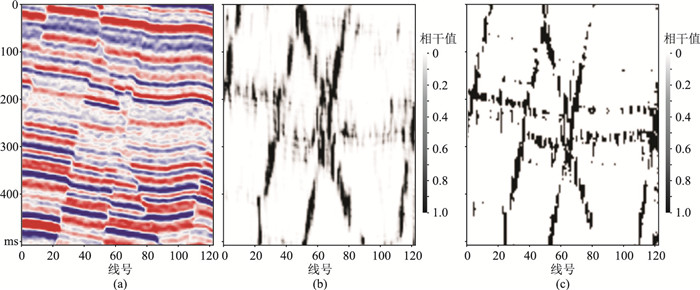
图 2为实际断层模型及其边缘检测结果。由图可见,本文方法很好地指示了常规断层(图 2c),同时在断层模型剖面(图 2a)上未能指示应出现断层的部位,相干结果较模糊、散乱(图 2b),但本文方法较清晰地揭示了断层并且断层连续性好(图 2c)。上述结果说明本文方法的适用性较强。
|
图 2 实际断层模型及其边缘检测结果 (a)断层模型剖面;(b)相干方法;(c)本文方法 |
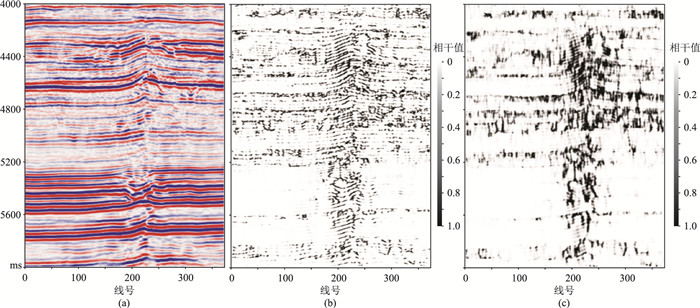
利用实际资料验证本文方法的应用效果。图 3为不同规模矩阵的直接奇异值检测结果。由图可见:7×5阶矩阵(横向的窗口尺度大于纵向)检测结果对地层边缘压制效果差(图 3b);5×17阶矩阵检测结果清楚显示了断层,地层压制效果较好(图 3c)。因此,对于同样的方法,不同规模矩阵的直接奇异值检测结果不同。矩阵行、列元素(横、纵向窗口的尺度)的关系体现了低秩化揭示横、纵向方向特性结构信息的能力,同时说明矩阵建模对于揭示结构信息的重要性。上述分析表明,直接对地震信号进行奇异值分解,只能揭示较大的断层,不能揭示小断层,并且检测结果模糊、不清晰。
|
图 3 不同规模矩阵直接奇异值检测结果 (a)地震剖面;(b)7×5阶;(c)5×17阶 |
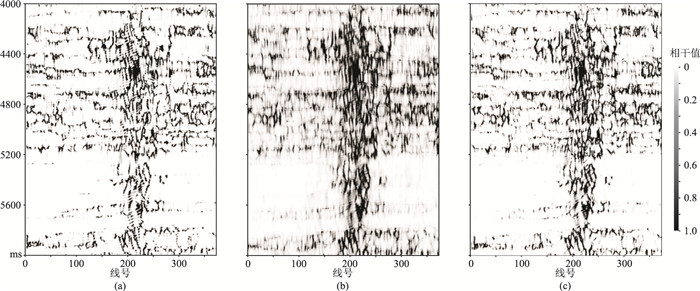
图 4为不同尺度组合双稀疏边缘检测结果,其计算过程是对地震信号进行小波稀疏分解后再进行奇异值分解,在计算过程中对地震信号进行5级分解,通过把多尺度信息与双稀疏(小波分解与矩阵分解)分析融合到算法实现,极大地提高了断层尤其是小断层的检测能力。由图 4可见:①信号向量的稀疏分解稀疏度越大,奇异值分解低秩度也越大,即实际检测结果分辨率提高,地层信息得到压制。②在高频边缘信息具有完备性,低频边缘信息具有冗余性;向量稀疏促进了矩阵低秩稀疏,再次说明双稀疏对提高边缘检测能力的意义。
|
图 4 不同尺度组合双稀疏边缘检测结果 (a)第2尺度;(b)第2、第3尺度组合;(c)所有尺度组合 |
相似背景组成的矩阵具有低秩特征,突变信号与噪声具有稀疏特征。如果相似背景有噪声干扰,则背景的低秩化程度大大降低,背景越“干净”其组成的矩阵相似性越高,矩阵低秩化程度越大,稀疏化程度也越大。“干净”背景下存在断层或缝洞等边缘信息时,分离效果最好。本文的研究主旨是通过稀疏分解压制噪声、增强稀疏化、最佳低秩化,从而最大程度地分离背景信息和边缘信息,增强边缘检测能力。
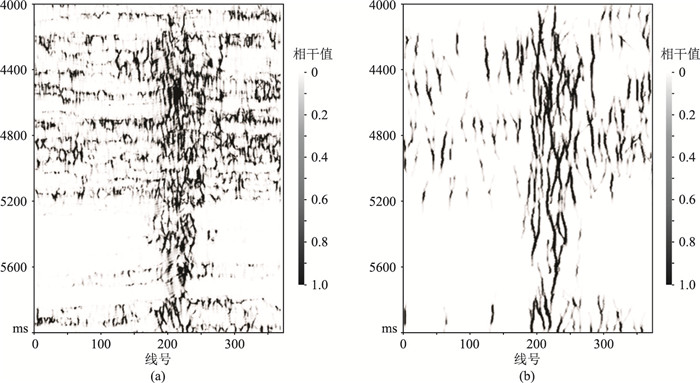
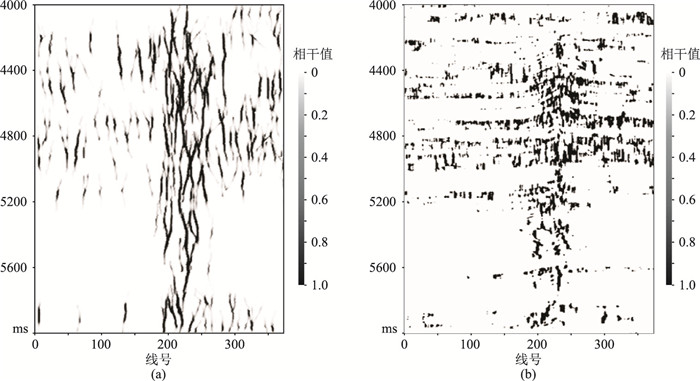
图 5为优化前、后边缘检测结果。由图可见,联合优化结果明显、清晰,极大地压制了噪声(图 5b)。图 6为本文方法与相干法边缘检测结果对比。由图可见,在小断层检测能力、分辨率及断层的连续性方面,本文方法的边缘检测效果都明显优于相干方法。图 7为洞边缘层切片,由图可见,与相干法洞边缘层切片(图 7b)相比,本文方法洞边缘层切片(图 7c)对洞边缘的识别效果更好。
|
图 5 优化前(a)、后(b)边缘检测结果 |
|
图 6 本文方法(a)与相干法(b)边缘检测结果 |

|
图 7 洞边缘层切片 (a)原始切片;(b)相干方法;(c)本文方法 |
断层和缝洞边缘检测实质上是利用地震资料压制地层信息和噪声、突出边缘信息的过程。地层信息具有低秩特性,噪声和边缘信息具有稀疏特性。提高边缘检测与识别能力,就是提高边缘信息的类间分类能力和噪声压制能力。根据噪声和有效信号的稀疏域分布特征,利用幂律特征约束,通过拟合方法对能量相近的噪声和有效信号系数再次优化。为了挖掘数据结构信息,提高边缘检测能力,围绕相似背景目标和稀疏目标分离,利用张量矩阵建模和奇异值分解方法,通过双稀疏和双优化,即小波分解稀疏、矩阵分解稀疏和小波系数优化、矩阵低秩优化,增强了尺度分析的正交性和类间分类能力,提高了重建结果分辨率和精度。与相干方法相比,本文方法对于断层和缝洞边缘具有更好的刻画能力,较全面地揭示了较小的缝洞和小断层信息。
| [1] |
温睿, 刘国昌, 冉扬. 压缩感知地震数据重建中的三个关键因素分析[J]. 石油地球物理勘探, 2018, 53(4): 682-693. WEN Rui, LIU Guochang, RAN Yang. Three key factors in seismic data reconstruction based on compressive sensing[J]. Oil Geophysical Prospecting, 2018, 53(4): 682-693. |
| [2] |
王雄文, 王华忠. 基于压缩感知的高分辨率平面波分解方法研究[J]. 地球物理学报, 2014, 57(9): 2946-2960. WANG Xiongwen, WANG Huazhong. A research of high-resolution plane-wave decomposition based on compressed sensing[J]. Chinese Journal of Geophy-sics, 2014, 57(9): 2946-2960. |
| [3] |
张军华, 张彬彬, 张在金, 等. 地震低频信息缺失特征分析及拓频方法研究[J]. 应用地球物理, 2015, 12(2): 212-220. ZHANG Junhua, ZHANG Binbin, ZHANG Zaijin, et al. Low-frequency data analysis and expansion[J]. Applied Geophysics, 2015, 12(2): 212-220. |
| [4] |
丁燕, 杜启振, 刘力辉, 等. 基于压缩感知和宽带俞式低通整形滤波器的地震低频信息特征分析与补偿[J]. 地球物理学报, 2019, 62(6): 2267-2275. DING Yan, DU Qizhen, LIU Lihui, et al. Feature analysis and compensation of seismic low-frequency based on compressed sensing and broad-band Yu-type low-passing shaping filter[J]. Chinese Journal of Geophysics, 2019, 62(6): 2267-2275. |
| [5] |
蔡涵鹏, 胡光岷, 贺振华, 等. 基于非线性变时窗相干算法的不连续性检测方法[J]. 石油地球物理勘探, 2016, 51(2): 371-375. CAI Hanpeng, HU Guangmin, HE Zhenhua, et al. Subtle discontinuity delection with nonlinear variable-time window coherency algorithm[J]. Oil Geophysical Prospecting, 2016, 51(2): 371-375. |
| [6] |
Van B, Pepper R. Seismic signal processing method and apparatus: Canada, CA2318224 C[P]. 2004.
|
| [7] |
汪杰, 汪锐. 基于方差相干体的断层识别方法[J]. 工程地球物理学报, 2016, 13(1): 46-51. WANG Jie, WANG Rui. Fault identification method based on variance-coherence cubes[J]. Chinese Journal of Engineering Geophysics, 2016, 13(1): 46-51. DOI:10.3969/j.issn.1672-7940.2016.01.008 |
| [8] |
Marc D, Ciprian D, Yannick B, et al. New fault attri-bute based on robust directional scheme[J]. Geophy-sics, 2007, 72(4): P39-P46. |
| [9] |
Olivier L, Sorin P, Christian G, et al. Seismic fault preserving diffusion[J]. Journal of Applied Geophysics, 2006, 61(2): 132-141. |
| [10] |
Israel C, Nicholas C, Anthony A V. Detection and extraction of fault surfaces in 3D seismic data[J]. Geophysics, 2006, 71(4): P21-P27. DOI:10.1190/1.2215357 |
| [11] |
Wu X M, Zhu Z H. Methods to enhance seismic faults and construct fault surfaces[J]. Computers & Geosciences, 2017, 107(10): 37-48. |
| [12] |
Dave H. Dynamic warping of seismic images[J]. Geophysics, 2013, 78(2): S105-S115. DOI:10.1190/geo2012-0327.1 |
| [13] |
Wu X M, Dave H. 3D seismic image processing for faults[J]. Geophysics, 2016, 81(2): IM1-IM11. DOI:10.1190/geo2015-0380.1 |
| [14] |
Dave H. Methods to compute fault images, extract fault surfaces, and estimate fault throws from 3D seismic images[J]. Geophysics, 2013, 78(2): O33-O43. DOI:10.1190/geo2012-0331.1 |
| [15] |
郭念民, 陈猛, 冯雪梅, 等. 基于压缩感知理论的地震数据重建方法[C]. SPG/SEG北京2016国际地球物理会议电子文集, 2016, P631.44. GUO Nianmin, CHEN Meng, FENG Xuemei, et al. Seismic data reconstruction method based compressed sensing theory[C]. SPG/SEG 2016 International Geophysical Conference, Beijing, China, 2016, P631.44. |
| [16] |
赵子越, 李振春, 张敏. 利用压缩感知技术的离散正交S变换地震数据重建[J]. 石油地球物理勘探, 2020, 55(1): 29-35. ZHAO Ziyue, LI Zhenchun, ZHANG Min. Seismic data reconstruction using discrete orthonormal S-transform based on compressive sensing[J]. Oil Geophysical Prospecting, 2020, 55(1): 29-35. |
| [17] |
朱丹, 刘天佑, 李宏伟. 利用数据低秩性和稀疏性的位场分离[J]. 石油地球物理勘探, 2019, 54(4): 925-936. ZHU Dan, LIU Tianyou, LI Hongwei. Potential field separation based on the low rank and sparse characteristics[J]. Oil Geophysical Prospecting, 2019, 54(4): 925-936. |
| [18] |
Felix J H, Gilles H. Non-parametric seismic data recovery with curvelet frames[J]. Geophysical Journal International, 2008, 173(1): 233-248. DOI:10.1111/j.1365-246X.2007.03698.x |
| [19] |
白兰淑, 刘伊克, 卢回忆, 等. 基于压缩感知的Curvelet域联合迭代地震数据重建[J]. 地球物理学报, 2014, 57(9): 2937-2945. BAI Lanshu, LIU Yike, LU Huiyi, et al. Curvelet-domain joint iterative seismic data reconstruction based on compressed sensing[J]. Chinese Journal of Geophysics, 2014, 57(9): 2937-2945. |
| [20] |
宋维琪, 张宇, 吴彩端, 等. 多道联合压缩感知弱小反射地震信号提取处理方法[J]. 地球物理学报, 2017, 60(8): 3238-3245. SONG Weiqi, ZHANG Yu, WU Caiduan, et al. The method of weak seismic reflection signal processing and extracting baesd on multitrace joint compressed sensing[J]. Chinese Journal of Geophysics, 2017, 60(8): 3238-3245. |
| [21] |
Al-Dossary S, Marfurt K J. 3D volumetric multispectral estimates of reflector curvature and rotation[J]. Geophysics, 2006, 71(5): P41-P51. DOI:10.1190/1.2242449 |
| [22] |
Lin L M, Zhang G Z, Li J K. Compressed sensing KSVD dictionary learning method application in seismic denoising[C]. International Geophysical Conference, Qingdao, China, 2017.
|
| [23] |
Li H S, Yang W Y, and Yong X S. Sparse reconstruction of 3D stochastic trace missing seismic data[C]. Beijing 2014 International Geophysical Conference & Exposition, Beijing, China, 2014.
|
| [24] |
AlBinHassan N M, Marfurt K J. Fault detection using Hough transforms[J]. SEG Technical Program Expanded Abstracts, 2003, 22: 1719-1721. |
| [25] |
Arthur E B. A filter to improve seismic discontinuity data for fault interpretation[J]. Geophysics, 2006, 71(3): P1-P4. DOI:10.1190/1.2195988 |



 宋维琪, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
宋维琪, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: 