② 东方地球物理公司研究院, 河北涿州 072750;
③ 北京中恒利华石油技术研究所, 北京 100102
② BGP Inc., CNPC, Zhuozhou, Hebei 072750, China;
③ ZHLH Petroleum Technology Research Institute, Beijing 100102, China
页岩气藏的特征、形成机理与常规天然气藏不同,对页岩气的评价参数一般分为地质甜点和工程甜点两大类。其中地质甜点包括构造埋深、页岩物性、优势页岩厚度、总有机碳含量(TOC)、有机质成熟度等。工程甜点可为后期水平井压裂、储层改造提供技术支撑,包括脆性、裂缝、页岩力学性质等参数。目前中国对页岩气的勘探、开发主要集中在四川盆地南部和渝西地区,其主力产层是古生界奥陶系五峰组(O3w)至志留系龙马溪组。由于页岩气具有源储一体、大面积连续成藏、无气/水界面等特征,对页岩气的甜点储层预测难度大[1]。近年来,页岩气的勘探深度由小于3500m逐步转变为3500~ 4500m。随着埋深、地层压力的增大,储层孔隙结构趋于复杂,深层及优质页岩定量预测难度越来越大。四川盆地多年的勘探、开发经验表明,要取得页岩气高产,水平井轨迹保持在最佳层段龙马溪组一亚段1-2小层(S1l11-2)是关键,但S1l11-2很薄(厚度为3~6m),定量预测储层难度大。由于受地震分辨率影响,常规的确定性反演方法无法有效识别优质页岩储层(TOC>2%,且主要位于S1l11-2);另外,实际生产中大多基于密度或者纵横波速度比反演结果的线性或非线性拟合预测页岩气地质甜点参数(TOC、孔隙度、含气性等),进一步增加了甜点参数预测的多解性,给深层页岩气的评层选区带来一定难度。
从前人研究成果看,薄储层预测从地质综合研究(沉积环境、成岩作用、分布规律等)和叠后定量研究逐步走向叠前多参数定量研究,地震反演技术是薄储层定量预测的最主要方法之一[2]。高分辨率叠前地震反演是定量评价页岩气层弹性、物性及有利甜点区空间展布范围的重要方法。基于统计学理论的随机反演方法或概率化反演算法在获取高分辨率模型参数最优解的同时,可以有效地评价反演结果和先验信息的不确定性,能更好地定量解释储层参数。以贝叶斯反演框架为例,业界针对模型参数先验信息构建、后验概率密度分布构建、随机采样算法优选进行了大量研究。Eide等[3]从概率角度出发,假设先验概率密度函数以及和井震有关的条件似然函数均符合高斯分布,基于贝叶斯公式推导出与储层参数有关的后验概率密度函数,通过对后验概率密度函数多次采样最终得到反演结果。Escobar等[4]基于贝叶斯理论和Zoeppritz近似方程求取纵横波阻抗的后验分布,用新的序贯算法对后验概率进行抽样,最终提出一种层序网格内的超快速叠前随机反演方法。为了加快随机反演计算速度,Contreras等[5]引入马尔科夫链—蒙特卡洛(MCMC)技术,通过联合模拟纵波和横波阻抗将其扩展为对多个部分叠加道集的反演,将随机反演推向叠前。Smith等[6]利用MCMC方法获取模型参数的后验分布,利用MCMC方法逼近贝叶斯统计分析中出现的积分运算。大量文献研究成果表明,基于协克里金、序贯高斯、模拟退火等地质统计学算法的随机反演能够随机模拟薄储层[7-11]。近年来,基于地质统计学反演的地震波形指示反演方兴未艾[12-15],由于地震波形的变化反映了沉积环境和岩性组合的空间变化,将这种变化定义为储层构型,可以利用波形变化间接推断储层空间的相变特征。该技术在空间结构化数据指导下不断寻优,利用地震波形的横向变化和空间距离代替变差函数进行样本选样,使反演结果在横向上更符合地质沉积规律。
基于叠后地震波形指示反演在薄储层预测方面的优势,以及叠前弹性参数较叠后弹性参数信息更丰富、对储层的敏感性更高的特点,本文基于岩石物理资料,应用地震驱动+储层构型约束的高精度叠前随机反演方法,探寻定量表征优质薄页岩的技术,为深层页岩气地质甜点预测提供技术支撑。
1 方法原理常规叠前反演主要通过岩石物理建模技术计算弹性参数建立参数模型,再根据AVO响应特征建立道集与弹性参数的关系,利用Zoeppritz近似方程或者弹性阻抗方程建立目标函数迭代求解参数模型。针对深层优质页岩定量预测技术难题,本文在叠后波形指示反演基础上,充分利用叠前多参数相似特征和岩相组合的指示作用,利用波形相似性和空间距离多参数优选模拟样本,以建立样本空间(图 1)。叠后波形指示反演根据波形相似性优选统计样本,对比预测道地震波形与所有已知井旁道地震波形,优选最相似的若干井样本,再比较这些井的不同频段的滤波曲线,寻找共性结构特征并建立初始模型[8]。在叠前,该方法利用道集波形和AVO特征,基于道集波形相似性、AVO特征和空间距离的三变量优选方法提取结构相似的井数据作为空间估值样本,建立待判别道集初始模型,然后在贝叶斯框架下开展MCMC模拟,补充确定性叠前反演缺失的高频成分。该模拟算法的核心是根据实际概率分布得到统计意义上正确的随机样点分布,实现全局优化的多个等概率模拟结果[16-17]。由钻/测井数据、岩相地质数据及已有的确定性反演数据, 结合地层框架模型建立的目的层概率密度函数和纵横向变差函数获得地质统计学信息,降低了MCMC模拟的不确定性,在反演过程中加入地震数据约束,进一步降低了地质统计学反演的不确定性,可保证等概率结果的相似性。

|
图 1 叠前波形特征选样分析示意图(AVO属性平面图) vP、vS、Den分别代表纵波速度、横波速度、密度 |
首先,通过叠前道集特征矩阵建立测井曲线样本数据集,其中叠前道集特征矩阵是由道集波形特征动态矩阵、AVO特征指示因子矩阵和距离权重因子矩阵组成,描述了待预测点与样本点的井旁道波形相似度、AVO特征相似度和空间距离等3个井震相关性特征。道集波形特征动态矩阵由对比预测点与各样本点的近、中、远分角度叠加地震波形获得,AVO特征指示因子矩阵由对比预测点与各样本点的AVO特征获得,距离权重因子矩阵由对比预测点与各样本点的距离获得。其次,在小波域进行频率分解,提取样本集曲线的共性结构作为初始模型。对于不同的共性结构相关截止频率l应用
| $ \begin{aligned} O(l) &=\arg \left(\min \|\boldsymbol{W}-\overline{\boldsymbol{W}}\|_{1}\right) \\ &=\arg \left(\min \left\|\int_{0}^{l} g(\omega, t) \mathrm{d} \omega-\overline{\boldsymbol{W}}\right\|_{1}\right) \end{aligned} $ | (1) |
提取具有共性结构的弹性参数样本并进行分类。式中:W为样本井集测井曲线;W为样本井集测井曲线平均值;g(ω, t)为小波函数,ω、t分别为角频率和时间。
在道集优化的基础上计算道集波形特征参数,利用奇异值分解进行波形分类,建立地震道集波形与不同结构特征的井上弹性参数曲线样本的映射关系。首先建立初始样本集
| $ \boldsymbol{D}=\boldsymbol{U} \boldsymbol{\varSigma} \boldsymbol{V}^{*} $ | (2) |
式中:U和V分别为n×n阶地震波形数据正交矩阵和m×m阶井点属性正交矩阵,V*为V的共轭转置;Σ为n×m阶非负实数对角矩阵,表征井上曲线样本与地震波形的相关性。定义U为叠前道集矩阵,则
| $ \boldsymbol{U}=\left[\begin{array}{lll} \boldsymbol{\alpha} & \boldsymbol{\beta} & \boldsymbol{\gamma} \end{array}\right] $ | (3) |
式中:α为采集数据波形特征参数;β为AVO特征因子参数;γ为距离加权因子参数。
1.2 基于贝叶斯框架的随机反演针对反演优化问题,本文在贝叶斯框架下构建了待反演模型参数的后验概率密度分布(PDF)及目标泛函。贝叶斯推断为在当前观测地震数据的情况下,结合观测数据之前对待反演模型参数的先验知识计算模型参数PDF的统计学习方法,是一种将先验信息和似然函数转化为后验信息的方法,其数学基础是贝叶斯定理[18-19]。假设未知模型参数服从某种类型的概率密度分布,即所谓的先验知识,它的引入是对带限地震数据的修正,贝叶斯公式为
| $ p(\boldsymbol{m} \mid \boldsymbol{d})=\frac{p(\boldsymbol{d} \mid \boldsymbol{m}) p(\boldsymbol{m})}{\int_{-\infty}^{+\infty} p(\boldsymbol{d} \mid \boldsymbol{m}) p(\boldsymbol{m}) \mathrm{d} \boldsymbol{m}} \approx p(\boldsymbol{d} \mid \boldsymbol{m}) p(\boldsymbol{m}) $ | (4) |
式中:p(m|d)为待反演模型参数的PDF;p(d|m)为观测地震数据的似然函数;p(m)为待反演模型参数的先验分布。贝叶斯反演是从已知数据d中估计弹性参数模型m的PDF的过程。假设观测地震数据的噪声分布服从高斯概率密度分布
| $ \begin{aligned} &p\left(\boldsymbol{d} \mid \boldsymbol{m}, \boldsymbol{C_{d}}\right) \propto \frac{1}{(2 {\rm{ \mathit{ π} }})^{N / 2} \sqrt{\left|\boldsymbol{C_{d}}\right|}} \times \\ &\quad \exp \left[-\frac{1}{2}(\boldsymbol{d}-\boldsymbol{G} \boldsymbol{m})^{\mathrm{T}} \boldsymbol{C_{d}}^{-1}(\boldsymbol{d}-\boldsymbol{G} \boldsymbol{m})\right] \end{aligned} $ | (5) |
式中:G为地震数据的正演矩阵;Cd为弹性阻抗数据体的协方差矩阵。通过测井数据统计分析待反演模型参数的先验信息,得到模型参数的先验概率密度分布
| $ \begin{aligned} P(\boldsymbol{m}) &=\frac{1}{(2 {\rm{ \mathit{ π} }})^{N / 2} \sqrt{\left|\boldsymbol{C_{m}}\right|}} \times \\ &{\exp \left[-\frac{1}{2}\left(\boldsymbol{m}-\boldsymbol{\mu_{m}}\right)^{\mathrm{T}}\left(\boldsymbol{C_{m}}\right)^{-1}\left(\boldsymbol{m}-\boldsymbol{\mu_{m}}\right)\right]} \end{aligned} $ | (6) |
式中:Cm为模型参数的协方差矩阵;μm为模型参数的先验均值。将式(6)代入贝叶斯公式,可以求取模型参数的p(m|d)
| $ \begin{array}{c} p(\boldsymbol{m} \mid \boldsymbol{d}) \approx \kappa \cdot \exp \left[-\frac{1}{2}(\boldsymbol{d}-\boldsymbol{G} \boldsymbol{m})^{\mathrm{T}} \boldsymbol{C_{d}}^{-1}(\boldsymbol{d}-\boldsymbol{G} \boldsymbol{m})\right] \\ \cdot \exp \left[-\frac{1}{2}\left(\boldsymbol{m}-\boldsymbol{\mu_{m}}\right)^{\mathrm{T}} \boldsymbol{C_{m}}^{-1}\left(\boldsymbol{m}-\boldsymbol{\mu_{m}}\right)\right] \end{array} $ | (7) |
其中
| $ \kappa=\frac{1}{(2 {\rm{ \mathit{ π} }})^{N / 2} \sqrt{\left|\boldsymbol{C_{d}}\right|}} \frac{1}{(2 {\rm{ \mathit{ π} }})^{N / 2} \sqrt{\left|\boldsymbol{C_{m}}\right|}} $ |
对式(7)两边取对数,得到等价的目标泛函
| $ \begin{aligned} O(\boldsymbol{m} \mid \boldsymbol{d}) \sim & \arg \min _{\boldsymbol{m}}\left[(\boldsymbol{d}-\boldsymbol{G} \boldsymbol{m})^{\mathrm{T}} \boldsymbol{C_{d}}^{-1}(\boldsymbol{d}-\boldsymbol{G} \boldsymbol{m})+\right.\\ &\left.\left(\boldsymbol{m}-\boldsymbol{\mu}_{\boldsymbol{m}}\right)^{\mathrm{T}} \boldsymbol{C}_{\boldsymbol{m}}^{-1}\left(\boldsymbol{m}-\boldsymbol{\mu}_{\boldsymbol{m}}\right)\right] \end{aligned} $ | (8) |
令lnO(m|d)=0,得到反演方程
| $ \left[\boldsymbol{G}^{\mathrm{T}} \boldsymbol{C_{d}}^{-1} \boldsymbol{G}+\boldsymbol{C_{m}}^{-1}\right] \boldsymbol{m}=\boldsymbol{G}^{\mathrm{T}} \boldsymbol{C_{d}}^{-1} \boldsymbol{d}+\boldsymbol{C_{m}}^{-1} \boldsymbol{\mu_{m}} $ | (9) |
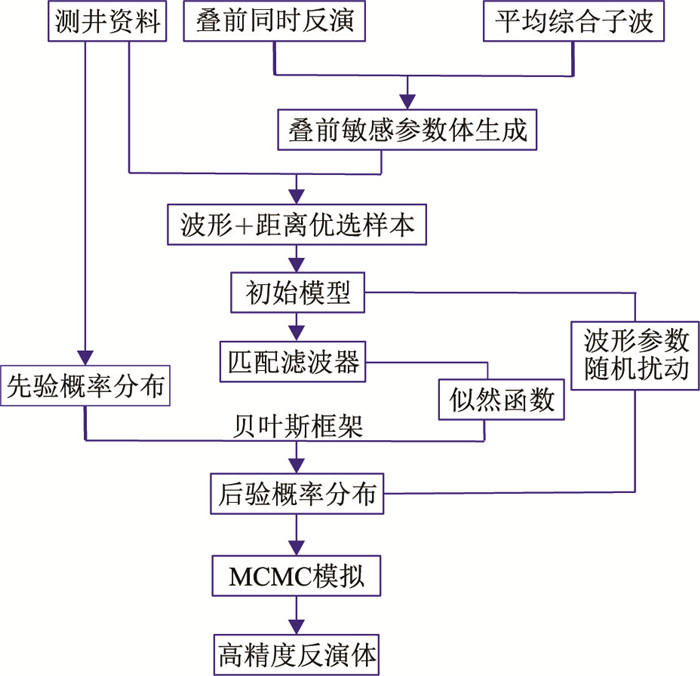
利用式(9)可以求出贝叶斯推断中的最大后验概率解,可以采用迭代重加权最小二乘算法求解,也可以利用蒙特卡洛仿真模拟和马尔科夫链模型获取模型参数的随机解。由于基于统计学和随机采样的反演算法可以有效提高反演分辨率,因此本文利用贝叶斯概率解评价模型参数的最优解和不确定性。此外,本文基于叠前高精度反演结果,通过建立道集与弹性参数曲线的样本模型寻找待预测区与已知样本井数据的共性结构(截距、梯度、振幅、相位等),在相似共性结构的道集组合约束下获得高分辨率的反演结果(图 2)。
|
图 2 叠前多参数相似性高精度反演流程 |
MCMC采用的算法为Metropolis-Hasting算法,通过该算法不断对由波形优选样本建立的地震波形指示的初始模型进行随机扰动,从而得到贝叶斯推断中的最大后验概率解,取多次可行实现的均值作为期望值输出,具体步骤如下。
(1) 根据初始模型选择一个初值m0i,并令i=0;
(2) 利用建议分布q(m0i, m*)产生一个状态变换m0i→ m*,m*表示建议分布生成的模型参数候选点;
(3) 产生随机数μ,其中μ~U(0, 1);
(4) 计算对数接受概率α(m0i, m*)
| $ \begin{aligned} &\alpha\left(\boldsymbol{m}_{0}^{i}, \boldsymbol{m}^{*}\right)= \\ &\min \left\{\ln \left[p\left(\boldsymbol{m}^{*}, \boldsymbol{d}\right)\right]+\ln \left[q\left(\boldsymbol{m}^{*}, \boldsymbol{m}_{0}^{i}\right)\right]-\right. \\ &\left.\quad \ln \left[p\left(\boldsymbol{m}_{0}^{i}, \boldsymbol{d}\right)\right]-\ln \left[q\left(\boldsymbol{m}_{0}^{i}, \boldsymbol{m}^{*}\right)\right], 0\right\} \end{aligned} $ | (10) |
(5) 若lnμ≤α(m0i, m*),那么mi+1= m*,否则mi+1= m0i;
(6) 令i=i+1,返回步骤(2)、迭代直至平稳状态(总迭代次数为N)。
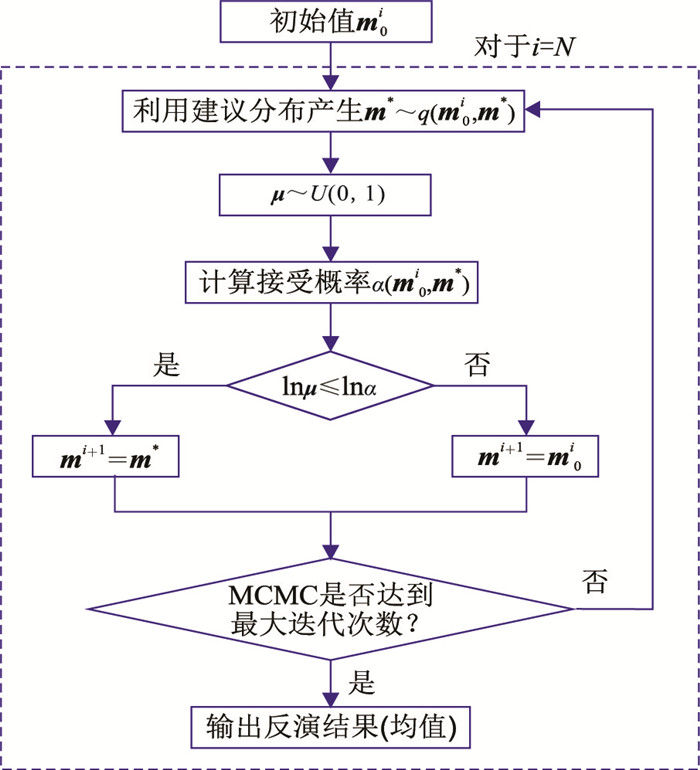
可以证明以此种方式构建的接受概率是满足细致平衡条件的,算法实现流程见图 3。
|
图 3 算法流程 |
由于无法直接反演页岩气甜点参数(TOC、含气量、孔隙度等物性参数),目前主要基于单参数或多参数回归分析建立预测模型预测甜点参数。这种方法往往预测精度较低,且多解性强,对于指导页岩气评层选区意义不大。波形的变化特征能有效指示岩相组合的弹性参数变化特征,利用其波形特征优选模拟样本建立样本空间(也称波形变差函数),在贝叶斯框架下开展随机模拟,补充确定性叠前反演纵横波速度比时缺失的高频成分[20-21]。
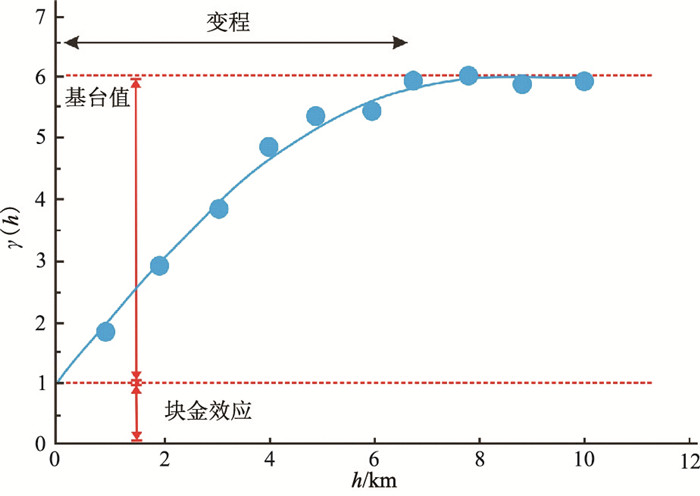
地质统计学由区域变量抽取的样本值估算方差,通过变程反映变量的影响范围。经典变差函数中滞后距h代表区域空间两点之间的距离,变差函数值γ(h)代表区域空间两点参数值的差(图 4)。经典变差函数描述的是参数随实际区域空间距离而变化的规律。假设有样本A、B,则滞后距h=|AB|。
|
图 4 变差函数相关性分析示意图 |
对于一维区域空间,即A=(x1),B=(x2),则
| $ |\boldsymbol{A B}|=\left|x_{1}-x_{2}\right| $ | (11) |
对于二维区域空间,即A=(x1,y1),B=(x2,y2),则
| $ |\boldsymbol{A B}|=\sqrt{\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}} $ | (12) |
对于三维区域空间,即A=(x1,y1,z1),B=(x2,y2,z2),则
| $ |\boldsymbol{A B}|=\sqrt{\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}} $ | (13) |
通过计算波形空间两点之间的距离得到变差函数滞后距h。假设波形空间是四维空间,波形空间中的点自然是四维点。设有两点的地震波形,质心、均值、方差、变方差分别为C、A、V、Vv,则
| $ h=|\boldsymbol{A B}|=\sqrt{\left(C_{1}-C_{2}\right)^{2}+\left(A_{1}-A_{2}\right)^{2}+\left(V_{1}-V_{2}\right)^{2}+\left(V_{v 1}-V_{v 2}\right)^{2}} $ | (14) |
式中下标1、2表示地震波序号。甜点参数模拟思想基于子波不变假设,认为地震弹性参数差异与井特征参数结果变化密切相关,即地震弹性参数随井位而变化。根据质心、均值、方差、变方差等四种属性描述地震特征参数差异的特征向量,利用测井参数的统计变量与井的特征参数垂向变差函数表征井垂向结构变化相对地震差异的变化量。最后统计预测道地震特征参数的特征向量,利用波形变差函数模拟预测道(井)的特征参数实现特征参数模拟。该模拟方法有效结合地震、地质和测井信息,利用地震信息指导井参数高频模拟,利用波形横向变化与井特征参数相对变化关系,建立特征向量变差函数模型,实现井震协同高频模拟。
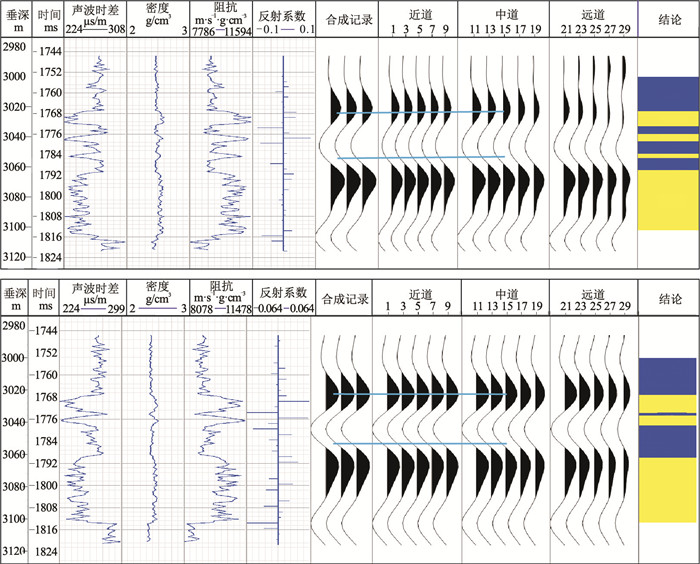
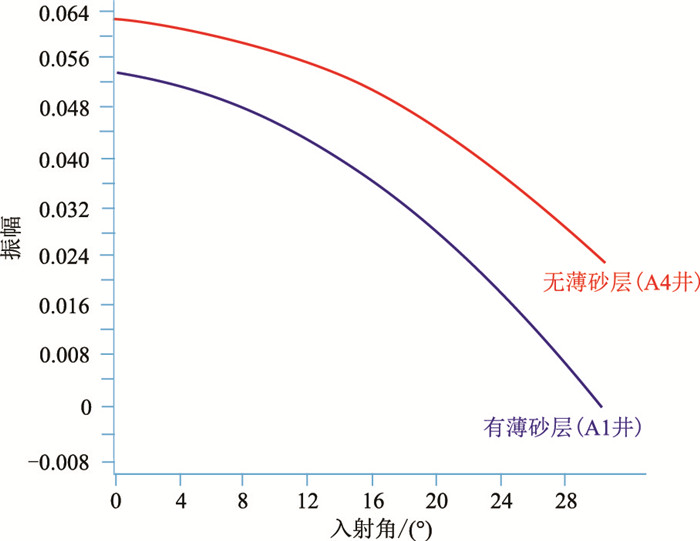
2 模型验证为了验证所提方法的有效性和对薄层的纵、横向识别能力,首先对比薄砂层与厚砂层的叠前道集特征,选取A1、A4井开展正演分析。由正演模拟的近、中、远道集(图 5)可见:道集波形特征发生明显变化;两口井在零炮检距处均表现为强振幅、正极性AVO特征,振幅呈减小趋势,但随着入射角增大,两口井AVO特征逐渐发生变化,且远道集更能体现波形的差异性(图 6)。
|
图 5 A1井(上)和A4井(下)正演道集 A1井同时存在薄砂层与厚砂层,A4井只存在厚砂层。结论中蓝色代表泥岩,黄色代表砂岩 |
|
图 6 A1和A4井AVO响应特性 |
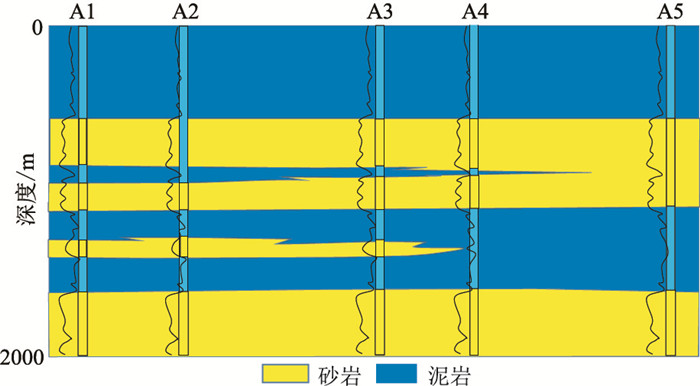
进一步设计了砂泥岩薄互层地质模型(图 7)。为了便于开展波形相似性反演,在该模型上建立5口虚拟井(A1~A5)提取不同的储层特征。利用主频为40~100Hz的零相位雷克子波作为震源进行正演模拟,选取低频(40Hz)、中频(70Hz)和高频(100Hz)地震正演剖面开展不同反演方法实验。
|
图 7 砂泥岩薄互层地质模型 泥岩背景中由上至下发育4组薄互层砂体,其中前两套砂体为叠置砂体,第三套砂体最薄(厚度为4m),砂岩、泥岩速度分别为3500、2800 m/s,密度分别为2.65、2.26g/cm3 |
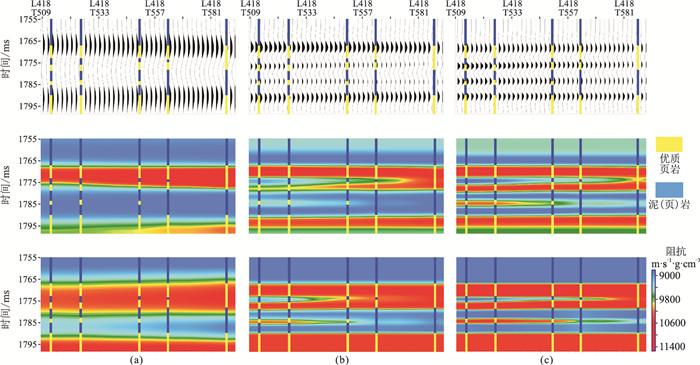
图 8为40Hz、70Hz和100Hz地震正演、稀疏脉冲反演和多参数波形相似性反演剖面。由图可见:① 40Hz地震正演剖面由于分辨率较低,完全无法识别薄互层砂体,由于砂体组合不同,地震波形差异也较大(图 8a上);70Hz地震正演剖面只能识别叠置砂体(图 8b上);100Hz地震正演剖面可以识别每一个薄砂体(图 8c上)。②稀疏脉冲反演剖面与地震正演剖面的分辨率特征相似,如40Hz稀疏脉冲反演剖面完全无法识别薄互层砂体(图 8a中),70Hz稀疏脉冲反演剖面可以分辨叠置的两套砂体(图 8b中),100Hz稀疏脉冲反演剖面可以分辨第3套薄砂体(图 8c中)。③多参数波形相似性反演剖面的分辨率明显高于稀疏脉冲反演(图 8a下、图 8b下、图 8c下),并且在70Hz时就能完全识别薄砂体(图 8b下)。
|
图 8 40Hz(a)、70 Hz(b)和100Hz(c)地震正演 图 8(上)、稀疏脉冲反演(中)和多参数波形相似性反演(下)剖面 |
研究区位于重庆渝西地区,构造位置为川南古坳中隆低陡构造带北部,属于华蓥山褶皱带向南呈帚状的低陡背斜群,由北往南发育雁行排列的梳状背斜构造,褶皱强度由北往南逐渐减弱,向斜区面积不断增大。根据该区内断层及埋深特征,O3w底界埋深主要集中于3500~4500m,埋深较大,构造整体较平缓,但内部小断层发育。断层主要以北东向为主,该区西部也发育近南北向断层,向斜内主要发育中、小断层,以小断层为主,大断层主要发育于大背斜构造两翼。从单井岩相解释成果看,龙一段一亚段1-3小层(S1l11-3)主要发育碳质泥棚微相,其中1小层(S1l11)、2小层(S1l12)层理发育,硅质含量高,为硅质岩相类型。大量水平井数据揭示,水平井靶体段为优质页岩段(Ⅰ类,O3w-S1l11-2)。单井综合解释结果表明,S1l11-2厚度为3~6m不等。因此,要想精准预测S1l11-2优质页岩厚度,必须借助高分辨率地震优质页岩参数精细划分、对比及预测页岩小层。
3.2 叠前道集优化处理多参数波形相似性反演技术的关键是道集优化处理、敏感参数体生成、样本选取、截止频率确定等流程。基于新生成的叠前敏感参数体,再利用其波形相似性和空间距离多参数优选模拟样本,建立波形与弹性参数曲线的样本模型,在贝叶斯框架下开展随机模拟,补充确定性叠前反演缺失的高频成分,寻找待预测区与已知样本的共性结构(振幅、频率、相位等),在相似共性结构的道集组合约束下反演,从而获得高分辨率的薄层反演成果。
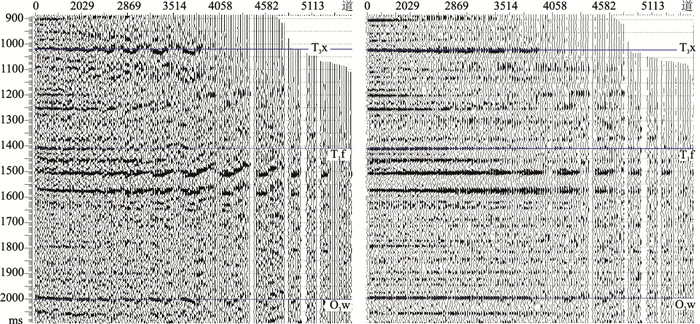
研究区叠前时间偏移CRP道集上存在明显的随机噪声和远炮检距剩余时差,前者影响叠前道集的信噪比,后者导致道集不平、AVO规律不明确。由于叠前高精度反演对道集质量要求较高,为此制定了道集优化流程。首先,在利用射线追踪方法将炮检距转换为入射角时需要质控和优化地震速度,使其满足射线追踪的需求;其次,在道集优化中需考虑随机噪声压制与多次波问题;最后,在去除噪声的道集上,针对远道进行剩余时差校正。图 9为拉平前、后道集。由图可见:①由于道集中存在较多的随机噪声且远炮检距道集不平,尤其在远炮检距处,原始道集与合成记录的相关性较差,O3w的AVO规律也较差(图 9左)。②利用Radon变换和移动积分道集拉平技术优化处理后的道集资料明显提高了信噪比,同时大幅提高了叠前道集的质量(图 9右),为后续高精度反演提供了可靠的道集资料;利用优化后的道集进一步开展井震标定,优化后的道集与合成记录的相关性得到明显改善,同时O3w底部AVO曲线与井上正演道集的AVO曲线更吻合。
|
图 9 拉平前(左)、后(右)道集 T3x为须家河组,T1f为飞仙关组 |
由岩石物理敏感参数分析直方图(图 10)看出,

|
图 10 龙马溪组优质页岩密度分析直方图 |
密度能够较好地筛选优质页岩,因此将密度作为敏感参数。进一步将页岩分为Ⅰ、Ⅱ、Ⅲ类:密度小于2.57g/cm3的为Ⅰ类(优质页岩);密度为2.57~2.65g/cm3的为Ⅱ类(优质页岩);密度大于2.65g/cm3的为Ⅲ类。对比地质统计学反演与多参数波形相似性反演的密度剖面(图 11)可见:地质统计学反演结果的横向变化不稳定,不符合页岩分布地质规律,无法有效识别Ⅰ类页岩;多参数波形相似性反演结果的纵向分辨率高,反演信息更丰富,且能有效区分Ⅰ、Ⅱ类页岩。

|
图 11 地质统计学反演(上)与多参数波形相似性反演(下)的密度剖面 P2l为龙潭组,P1l为梁山组,S1l2为龙二段 |
正则化可理解为对带限观测数据的补充,通过引入正则化乘法项,将不适定的地震反演问题转化为适定的反问题求解,以获取待反演模型参数的最优解或近似解[22]。为了均衡预测样本井点与非样本井点弹性参数的相关性,需求取样本井点的弹性阻抗与预测地震中频弹性阻抗的直接匹配系数,因而设置正则化因子参数。通过正则化因子加强约束,进行地震趋势(振幅、频率、相位)控制,防止过度拟合。引入弹性阻抗模型作为先验信息,可以修正反演结果,能够满足样本要求而且稳定。目标函数为
| $ J = \left\| {\mathit{\boldsymbol{Lm}} - \mathit{\boldsymbol{d}}} \right\|_2^2 + \lambda R(\mathit{\boldsymbol{m}}) $ | (15) |
式中:λ为正则化因子,也称为平衡参数或阻尼系数;R(m) 为正则化方程的权重。如果选取λ值过大,反演结果会偏重于正则化条件,完全基于地震趋势,样本井无法起到井约束效果;如果选取λ值过小,则大部分权重分配给差异条件
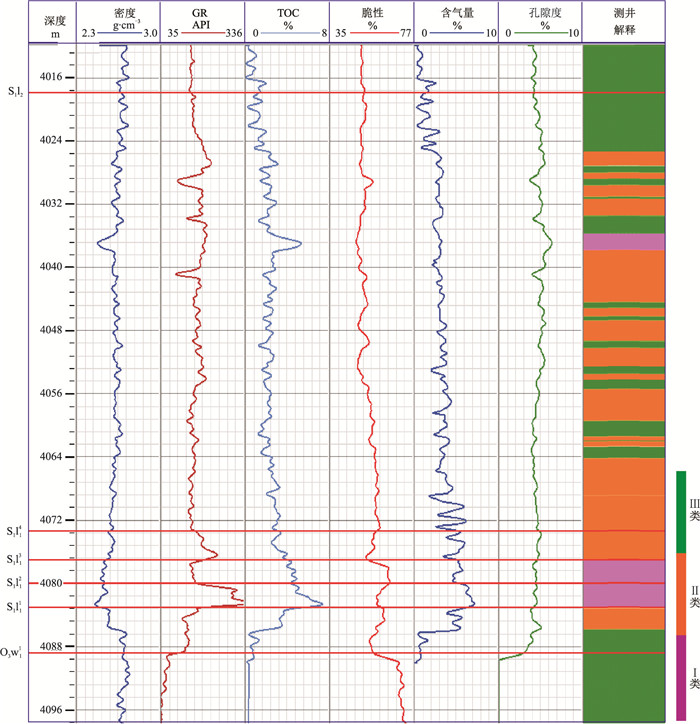
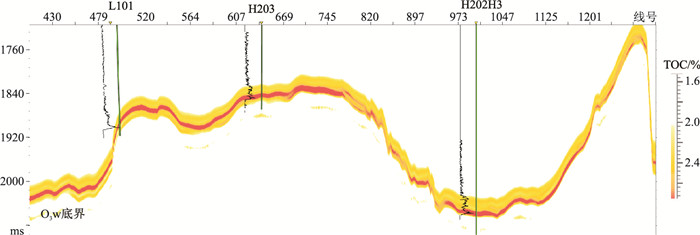
本文通过特征参数模拟直接预测页岩气的地质甜点参数,提高了甜点参数的预测精度。图 12为H202井测井综合解释图。由图可见,优质页岩的测井响应表现为低密度、高GR、高TOC、高含气量、高孔隙度、中高脆性等特征。图 13为过L101-H203-H202H3井TOC模拟图。由图可见,TOC模拟结果与测井曲线吻合度较高,横向变化趋势合理,其中向斜平缓区TOC相对较高。以高品质OVT域处理的三维地震资料为基础,基于岩石物理分析,将弹性参数转化为储层指标,利用叠前波形指示反演预测优质页岩厚度和基于波形变差函数模拟方法直接预测TOC甜点参数(表 1),能准确识别水平井的油藏目标,为水平井布署提供技术支撑。
|
图 12 H202井测井综合解释图 |
|
图 13 过L101-H203-H202H3井TOC模拟图 |
|
|
表 1 S1l11优质页岩预测结果对井分析表 |
(1) 波形驱动多参数约束高精度叠前反演方法,在叠后波形指示反演基础上进行创新,采用“地震驱动+储层构型约束”的方式分析储层空间变化,利用道集波形和AVO特征,基于道集波形相似性、AVO特征和空间距离的三变量优选方法提取结构相似的井数据进行空间选样,有效预测了S1l11-2优质页岩厚度。
(2) 基于特征参数的井震高频模拟,精确模拟了S1l11-2地质甜点参数。实际应用表明,该方法同时提高了纵、横向反演分辨率,增强了反演结果确定性,降低了页岩气地质甜点预测的多解性,为页岩气评层选区起到了良好的支撑作用,提高了钻探成功率。
| [1] |
刘振武, 撒利明, 杨晓, 等. 页岩气勘探开发对地球物理技术的需求[J]. 石油地球物理勘探, 2011, 46(5): 810-818. LIU Zhenwu, SA Liming, YANG Xiao, et al. Needs of geophysical technologies for shale gas exploration[J]. Oil Geophysical Prospecting, 2011, 46(5): 810-818. |
| [2] |
印兴耀, 李龙. 基于岩石物理模型的纵、横波速度反演方法[J]. 石油物探, 2015, 54(3): 249-253. YIN Xingyao, LI Long. P-wave and S-wave velocities inversion based on rock physics model[J]. Geophysical Prospecting for Petroleum, 2015, 54(3): 249-253. DOI:10.3969/j.issn.1000-1441.2015.03.001 |
| [3] |
Eide A L, Ursin B L, Omre H L. Stochastic simulation of porosity and acoustic impedance conditioned to seismic data and well data[C]. SEG Technical Program Expanded Abstracts, 1997, 16: 1614-1617.
|
| [4] |
Escobar I, Williamson P, Cherrett A, et al. Fast geostatistical stochastic inversion in astratigraphic grid[C]. SEG Technical Program Expanded Abstracts, 2006, 25: 2067-2071.
|
| [5] |
Contreras A, Kvien K, Fasnach T, et al. T-15 AVA stochastic inversion of pre-stack seismic data and well logs for 3D reservoir modeling[C]. Extended Abstracts of 67th EAGE Conference & Exhibition, 2005, doi: https://doi.org/10.3997/2214-4609-pdb.1.F014.
|
| [6] |
Smith A F M, Roberts G O. Bayesian computation via the Gibbs sampler and related Markov Chain Monte Carlo methods[J]. Journal of the Royal Statistical Society, 1993, 55(1): 3-23. |
| [7] |
印兴耀, 张世鑫, 张繁昌, 等. 利用基于Russell近似的弹性波阻抗反演进行储层描述和流体识别[J]. 石油地球物理勘探, 2010, 45(3): 373-380. YIN Xingyao, ZHANG Shixin, ZHANG Fanchang, et al. Utilizing Russell approximation-based elastic wave impedance inversion to conduct reservoir description and fluid identification[J]. Oil Geophysical Prospecting, 2010, 45(3): 373-380. |
| [8] |
孙思敏, 彭仕宓. 地质统计学反演方法及其在薄层砂体预测中的应用[J]. 西安石油大学学报(自然科学版), 2007, 22(1): 41-48. SUN Simin, PENG Shimi. Geostatistical inversion method and its application in the prediction of thin reservoirs[J]. Journal of Xi'an Shiyou University(Natural Science Edition), 2007, 22(1): 41-48. DOI:10.3969/j.issn.1673-064X.2007.01.010 |
| [9] |
印兴耀, 张洪学, 宗兆云. OVT数据域五维地震资料解释技术研究现状与进展[J]. 石油物探, 2018, 57(2): 155-178. YIN Xingyao, ZHANG Hongxue, ZONG Zhaoyun. Research status and progress of 5D seismic data interpretation in OVT domain[J]. Geophysical Prospecting for Petroleum, 2018, 57(2): 155-178. DOI:10.3969/j.issn.1000-1441.2018.02.001 |
| [10] |
强敏, 周义军, 钟艳, 等. 基于部分叠加数据的叠前同时反演技术的应用[J]. 石油地球物理勘探, 2010, 45(6): 895-898. QIANG Min, ZHOU Yijun, ZHONG Yan, et al. App-lication of pre-stack simultaneous inversion based on partial stack data[J]. Oil Geophysical Prospecting, 2010, 45(6): 895-898. |
| [11] |
王西文, 刘全新, 周嘉玺, 等. 精细储层预测技术在板南5-3井区的应用[J]. 石油物探, 2003, 42(3): 389-394. WANG Xiwen, LIU Quanxin, ZHOU Jiaxi, et al. App-lication of fine reservoir prediction techniques in Bannan 5-3 oilfied[J]. Geophysical Prospecting for Petroleum, 2003, 42(3): 389-394. DOI:10.3969/j.issn.1000-1441.2003.03.023 |
| [12] |
顾雯, 徐敏, 王铎翰, 等. 地震波形指示反演技术在薄储层预测中的应用——以准噶尔盆地B地区薄层砂岩气藏为例[J]. 天然气地球科学, 2016, 27(11): 2064-2069. GU Wen, XU Min, WANG Duohan, et al. Application of seismic motion inversion technology in thin reservoir prediction: A case study of the thin sandstone gas reservoir in the B area of Junggar Basin[J]. Natural Gas Geoscience, 2016, 27(11): 2064-2069. DOI:10.11764/j.issn.1672-1926.2016.11.2064 |
| [13] |
顾雯, 章雄, 徐敏, 等. 强屏蔽下薄储层高精度预测研究——以松辽盆地三肇凹陷为例[J]. 石油物探, 2017, 56(3): 439-448. GU Wen, ZHANG Xiong, XU Min, et al. High precision prediction of thin reservoir under strong shielding effect and its application: a case study from Sanzhao Depression, Songliao Basin[J]. Geophysical Prospecting for Petroleum, 2017, 56(3): 439-448. DOI:10.3969/j.issn.1000-1441.2017.03.014 |
| [14] |
胡玮, 齐鹏, 杨江峰, 等. 波形指示反演在超深层致密砂岩薄储层中的应用[J]. 地球物理学进展, 2018, 33(2): 620-624. HU Wei, QI PENG, YANG Jiangfeng, et al. Application of seismic motion inversion in identification of tight thin super deep reservoirs[J]. Progress in Geophysics,, 2018, 33(2): 620-624. |
| [15] |
Vapnik V N, 著, 张学工, 译. 统计学习理论的本质[M]. 北京: 清华大学出版社, 2000.
|
| [16] |
苏小军, 管仁顺, 王利田, 等. 波形差异反演方法及其在气藏描述中的应用[J]. 地球物理学进展, 2007, 22(5): 1578-1584. SU Xiaojun, GUAN Renshun, WANG Litian, et al. The inverse of wave different and its applition in the forecast of gas[J]. Progress in Geophysics, 2007, 22(5): 1578-1584. DOI:10.3969/j.issn.1004-2903.2007.05.036 |
| [17] |
李宁. 基于模拟退火的地质统计学反演方法研究[D]. 山东青岛: 中国石油大学(华东), 2013.
|
| [18] |
孙瑞莹. 先验信息构建与地震随机反演方法研究[D]. 山东青岛: 中国石油大学(华东), 2015.
|
| [19] |
潘新朋. 优化MCMC方法在地震反演中的应用研究[D]. 山东青岛: 中国石油大学(华东), 2016.
|
| [20] |
王小丹, 印兴耀, 金惠, 等. 叠前地震随机反演方法及实际资料应用[J]. 地球物理学进展, 2018, 33(6): 2471-2476. WANG Xiaodan, YIN Xingyao, JIN Hui, et al. Prestack seismic stochastic inversion and application on real data[J]. Progress in Geophysics, 2018, 33(6): 2471-2476. |
| [21] |
潘新朋, 张广智. 裂缝-孔隙型含气储层流体与裂缝参数贝叶斯地震反演方法[J]. 中国科学(地球科学), 2019, 49(5): 796-810. PAN Xinpeng, ZHANG Guangzhi. Bayesian seismic inversion for estimating fluid content and fracture parameters in a gas-saturated fractured porous reservoir[J]. Scientia Sinica(Terrae), 2019, 49(5): 796-810. |
| [22] |
李坤, 印兴耀. 混合概率模型驱动的叠前地震反演方法[J]. 石油地球物理勘探, 2020, 55(4): 839-853. LI Kun, YIN Xingyao. Prestack seismic inversion driven by mixture probabilistic models[J]. Oil Geophysical Prospecting, 2020, 55(4): 839-853. |



 印兴耀, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266555。Email:
印兴耀, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266555。Email: 