② 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071
② Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266071, China
地震反演是获得地下介质弹性参数、物性参数及含流体性质参数的重要方法,是定量描述含油气储层的核心地震技术。根据不适定地球物理反问题求解方式的差异,地震反演分为确定性反演和随机反演两大类。基于最小化原理求解反问题最优解或近似解的方法,通常称为确定性反演,其估计结果是一个相对平滑的唯一解。依据统计学理论的随机反演方法充分考虑了观测数据及反演过程的不确定性,消除了确定性反演中的平滑性,能够得到地下介质随机模型的多个实现,从而获得多个反演结果[1-6],在获取反演最优解的同时有效评价反演结果的不确定性。
地下介质普遍存在非均质特征,含油气储层的非均质特征主要表现为储层空间分布范围变化大,因此储层的弹性、物性及含流体性质在空间上是变化而不均匀的[7-8]。通常使用统计学的随机介质模型描述地下复杂非均匀介质,利用均值、方差、自相关函数等参数表征地下介质空间变化的统计特性[9-12]。为精细研究地下介质特性及其参数变化,需要借助随机介质模型描述地下介质的小尺度非均匀特性,进而有效刻画地下油气藏的细节信息。相比确定性反演,地震随机反演方法融合了地层格架、测井、地震等多尺度信息,可以获得更丰富的地下地层信息,使反演结果的分辨率更高[13-15],可以描述非均质复杂储层。
近几年,随机反演方法在储层预测、流体检测及页岩甜点预测等方面获得了较好的效果。前人[16-19]利用随机反演方法求取储层弹性参数、物性参数以及流体因子。郭同翠等[20]利用叠前地质统计学反演方法预测页岩甜点的空间展布。Azevedo等[21]利用叠前地震随机反演获得纵横波速度、密度及岩相数据。De Figueiredo等[22-23]基于岩石物理先验模型的联合贝叶斯反演获得了弹性参数、物性参数等储层特征参数。Mohamed等[24]结合地震属性与叠后地震随机反演获得了砂岩相预测模型。
以贝叶斯推断为基础的地震随机反演方法整合了未知模型参数的先验概率密度分布信息,通过似然函数建立模型参数与观测地震数据间的关系,获得待反演参数的后验概率密度函数[22, 24-29]。在反演过程中,先验信息模型用于描述地下地质体的空间变化特征,对于获得准确的反演结果非常重要,有利于缩小模型参数的求解空间。但常规的地震随机反演方法以测井数据为硬数据,利用变差函数表征地下地质体的空间展布特征[13-16, 24-26, 30-31]。然而,基于测井数据的随机模拟不能描述复杂地下地质体的空间变化特征,从而降低了非均质储层地震定量表征的稳定性和可靠性。
为了充分利用已知地震、测井数据中蕴含的地下地层空间结构信息,本文基于随机介质理论,依据地震和测井数据得到精确表征地层空间变化特征的非均匀介质特征参数,构建非均匀介质特征参数模型作为后续随机反演的先验信息模型,通过优化算法求解后验概率密度函数,形成了基于非均匀介质特征参数的地震随机反演方法。
1 方法原理本文引入随机介质构建贝叶斯随机反演的先验模型,利用混合型自相关函数表征非均匀介质的空间分布特征,从已知地震、测井数据中估算纵向、横向自相关长度及自相关角度等非均匀介质特征参数,获得反映地下复杂储层小尺度空间变化特征的信息,为后续反演提供先验模型。
1.1 随机介质基本原理随机介质是利用统计方法描述地下介质不同尺度非均匀性的介质模型,一般可以用均值、标准差和自相关函数等一阶、二阶统计量表征地下介质的空间随机变化特征。随机介质模型可以表征地下复杂介质的非均匀特性,有效反映含油气储层的小尺度变化特征。在二阶平稳假设条件下,随机介质模型定义为[9-11]
| $ \mathit{m}(\mathit{t},\mathit{x}) = {\mathit{m}_0}(\mathit{t},\mathit{x}) + {\mathit{\sigma }_\mathit{m}}(\mathit{t},\mathit{x}) $ | (1) |
其中
| $ {\mathit{\sigma }_\mathit{m}}(\mathit{t},\mathit{x}) = {\mathit{\delta }_m}(\mathit{t},\mathit{x})\mathit{f}(\mathit{t},\mathit{x}) $ | (2) |
式中:m0(t, x)为模型的均值,可描述介质的平均特性,表征介质的大尺度非均匀性,x为横坐标,t为时间;σm(t, x)描述平均特性上的随机扰动,表征介质的小尺度非均匀性;δm(t, x)一般为测井数据的标准差;f(t, x)为空间分布特征,是满足二维自相关函数R(t, x)的均值为0、标准差为1的二维随机序列。因此,可以使用均值为零的平稳空间随机过程表示地下介质的小尺度非均匀性。
1.2 非均匀介质特征参数混合型自相关函数表征地下介质的小尺度空间分布特征,通过引入粗糙度因子,混合型自相关函数综合了高斯型和指数型的特点。高斯型自相关函数较好地描述了单尺度平滑的非均匀介质。指数型自相关函数描述了随机介质的多尺度、自相似的特性,能更好地表征实际介质的多尺度特性。混合型自相关函数则更灵活地描述地下介质,适用性更强[9-10]。因此,本文采用混合型自相关函数R(t, x)描述非均匀介质的空间变化特征,即
| $ \begin{array}{l} \mathit{R}(\mathit{t},\mathit{x}) = {\rm{exp}}\left\{ { - \left[ {\frac{{{{(\mathit{x}{\rm{cos}}\mathit{\theta } + \mathit{t}{\rm{sin}}\mathit{\theta })}^2}}}{{{\mathit{a}^2}}}} \right.} \right. + \\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {{{\left. {\frac{{{{(\mathit{x}{\rm{sin}}\mathit{\theta } + \mathit{t}{\rm{cos}}\mathit{\theta })}^2}}}{{{\mathit{b}^2}}}} \right]}^{\frac{1}{{1 + \mathit{\eta }}}}}} \right\} \end{array} $ | (3) |
式中:a、b分别为横向(x方向)、纵向(t方向)自相关长度;θ为自相关角度;η为粗糙度因子,η=0为高斯型自相关函数,η=1为指数型自相关函数。
综合式(1)~式(3)可知,描述地下非均匀介质的特征参数包括均值、标准差、纵向和横向自相关长度及自相关角度等,通过这些参数可以模拟产生满足相应的自相关函数且具有指定均值和标准差的随机介质模型。
1.3 非均匀介质特征参数的估计及建模为从实际地震数据中获得地下地层空间结构特征参数,首先建立地震记录、地震子波与统计特征参数模型之间的函数关系[11]。根据随机介质理论可知,在连续介质中,波阻抗Z(t, x)与反射系数r(t, x)的关系为
| $ \mathit{r}(\mathit{t},\mathit{x}) = \frac{1}{2}\frac{\partial }{{\partial \mathit{t}}}{\rm{lg}}\left\{ {{\mathit{Z}_{\rm{o}}}(\mathit{t},\mathit{x})[1 + {\mathit{\delta }_\mathit{z}}(\mathit{t},\mathit{x})]} \right\} $ | (4) |
式中:Z0(t, x)为表征低频分量的背景波阻抗;δz(t, x)为表征高频分量的扰动量。
由式(4)、线性褶积模型以及卷积的微分性质可知,地震数据功率谱Ss(ω, kx)满足
| $ {\left| {{\mathit{S}_{\rm{s}}}(\mathit{\omega },{\mathit{k}_\mathit{x}})} \right|^2} \approx {\left| {{\mathit{S}_{{\mathit{\delta }_{\rm{Z}}}}}(\mathit{\omega },{\mathit{k}_\mathit{x}})} \right|^2} \cdot {\left| {{\mathit{S}_\mathit{\psi }}(\mathit{\omega })} \right|^2} $ | (5) |
式中:SδZ(ω, kx)为随机介质的功率谱,ω为角频率,kx为波数;Sψ(ω)为ψ(t)的功率谱,
对SδZ(ω, kx)进行傅里叶反变换得到随机介质的自相关函数R(t, x),进而估算出纵向、横向自相关长度和自相关角度等参数。
利用估算的特征参数求取二维自相关函数及其功率谱,得到非均匀介质的振幅谱,在区间[0,2π)产生均匀分布的随机相位信息。综合振幅谱和相位谱得到非均匀随机介质的频谱函数,由傅里叶反变换得到二维随机序列,对其进行标准化,使其均值为零、标准差为1,再结合由测井数据得到的标准差和均值,从而构建非均匀随机介质模型[12]。
2 非均匀介质特征参数分析由于均值表征介质的大尺度平均特性,标准差反映偏离平均值的程度,为更好地突显小尺度非均匀特性,本文给定具体的均值和方差,讨论不同纵向、横向自相关长度以及不同自相关角度对非均匀波阻抗介质模型的影响。
图 1为不同纵向、横向自相关长度及不同自相关角度的非均匀介质模型。由图可见:①自相关函数反映介质在空间的相关程度,a展示了介质在水平方向的相关范围,反映介质的横向尺度;b展示了介质在垂向的相关范围,反映介质的纵向尺度(图 1a、图 1b)。②θ反映随机介质模型的扰动方向(图 1c、图 1d),通过θ模拟地下介质层位的方向变化。
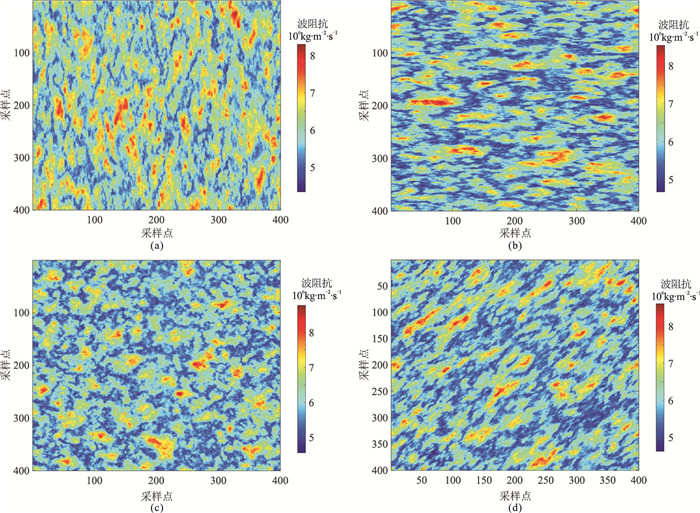
|
图 1 不同纵向、横向自相关长度及不同自相关角度的非均匀介质模型 (a)a=10, b=30, θ=0°;(b)a=30, b=10, θ=0°;(c)a= b=15,θ=0°;(d)a= b=15,θ=20°构建的随机介质模型的网格数为400×400,网格间距为dx=dt=1,波阻抗均值为6×106kg·m-2·s-1,标准差为6×105kg·m-2·s-1 |
总之,通过分析不同尺度的非均匀介质参数可知,纵向、横向自相关长度和自相关角度等统计量描述了介质弹性参数的空间扰动,可以刻画介质的空间变化特性。因此,借助非均质介质特征参数构建的模型反映了地下介质的非均质特性,为后续反演提供了更可靠的先验信息。
3 基于非均匀介质参数的随机反演基于上述方法原理构建表征地下介质非均质特性的先验信息模型,在贝叶斯理论框架下,联合似然函数得到反演目标函数,进而利用优化算法求解目标函数,最终形成基于非均匀介质特征参数的随机反演方法。
3.1 贝叶斯理论贝叶斯理论融合了待反演参数模型和已知数据的先验信息,通过似然函数转化为后验信息,得到模型参数的概率估计,其后验概率密度函数为[32]
| $ \mathit{p}(\mathit{\boldsymbol{m}}|\mathit{\boldsymbol{d}}) = \frac{{\mathit{p}(\mathit{\boldsymbol{m}})\mathit{p}(\mathit{\boldsymbol{d}}|\mathit{\boldsymbol{m}})}}{{\mathit{p}(\mathit{\boldsymbol{d}})}} \propto \mathit{p}(\mathit{\boldsymbol{m}})\mathit{p}(\mathit{\boldsymbol{d}}|\mathit{\boldsymbol{m}}) $ | (6) |
式中:p(m | d)为模型参数m的后验概率密度函数,表示观测数据d已知时m的分布规律;p(m)为m的先验概率密度函数,表示d未知时m的分布规律;p(d | m)为似然函数,表示m与d的拟合程度;p(d)为d的分布情况。
3.2 目标函数本文以构建的非均匀介质模型为地质统计先验模型,并结合待反演参数与地震数据之间的正演关系构建似然函数,进而以贝叶斯理论为基础[32],得到表征最终反演结果的后验概率密度函数。为减少反演结果的不确定性,增加了非均匀介质特征参数的约束项。因此,最终建立的目标函数为
| $ \begin{array}{l} J = \sum\limits_{k = 1}^N {{{\left( {{s^k} - s_{{\rm{obs}}}^k} \right)}^2}} + \alpha \sum\limits_{k = 1}^N {{{\left( {{R^k} - R_0^k} \right)}^2}} + \\ \;\;\;\;{\alpha _1}\sum\limits_{k = 1}^N {{{\left( {{a^k} - a_{{\rm{obs}}}^k} \right)}^2}} + {\alpha _2}\sum\limits_{k = 1}^N {{{\left( {{b^k} - b_{{\rm{obs}}}^k} \right)}^2}} + \\ \;\;\;\;{\alpha _3}\sum\limits_{k = 1}^N {{{\left( {{\theta ^k} - \theta _{{\rm{obs}}}^k} \right)}^2}} \end{array} $ | (7) |
式中:sk为模拟地震记录;sobsk为观测地震数据;Rk为反演参数;R0k为根据测井数据构建的平滑约束信息;α、α1、α2、α3表示加权系数;ak、bk和θk分别为反演过程估计的横向、纵向自相关长度和自相关角度;aobsk、bobsk和θobsk为由估计地震数据得到的特征参数。
3.3 非常快速量子退火优化算法非常快速量子退火(Very Fast Quantum Annealing,VFQA)算法是量子退火算法(Quantum Annealing,QA)的改进算法,采用依赖于温度的似Cauchy分布产生新的扰动模型,可以加快算法的收敛速度。
为提高随机反演的计算效率,本文采用VFQA算法扰动更新模型数据,扰动方式为
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{y}_\mathit{i}} = \mathit{T}{\rm{sgn}}(\mathit{u} - 0.5)\left[ {{{\left( {1 + \frac{1}{\mathit{T}}} \right)}^{\left| {2\mathit{u} - 1} \right|}} - 1} \right]}\\ {{\mathit{m}_\mathit{j}} = {\mathit{m}_\mathit{i}} + {\mathit{y}_\mathit{i}}({\mathit{B}_\mathit{i}} - {\mathit{A}_\mathit{i}})} \end{array}} \right. $ | (8) |
式中:mj∈ Ai, Bi为修改后模型参数,Ai, Bi ∈ Nx, Nt为模型的搜索空间,j∈ Nx, Nt,Nx×Nt为模型的大小;mi为修改前模型参数,i∈ Nx, Nt;yi为由u产生的随机变量,u∈[0, 1]为均匀分布的随机数;T为当前温度。
根据Metropolis接受准则:当模型更新前、后的目标函数之差ΔE < 0时,接受扰动后的模型;当ΔE≥0时,以
| $ p = \left\{ {\begin{array}{*{20}{l}} {1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\Delta \mathit{E} < 0}\\ {{\rm{exp}}\left( {\frac{{ - \Delta \mathit{E}}}{{\mathit{kL}}}} \right)\;\;\;\;\;\;\Delta \mathit{E} \ge \mathit{0}} \end{array}} \right. $ | (9) |
式中k、L均为可调参数。
3.4 基于非均匀介质特征参数的随机反演由地震数据和测井数据估计非均匀介质参数,基于估计的参数构建随机介质模型作为反演的先验信息;结合地震数据与待反演参数之间的关系构建似然函数;然后在贝叶斯理论框架下得到待反演参数的后验概率分布函数,进而得到反演目标函数;最后利用VFQA优化算法优化目标函数得到最终的反演结果(图 2)。

|
图 2 基于非均匀介质特征参数的随机反演流程 |
为验证上述方法的有效性,选用二维波阻抗模型(图 3)测试、分析,该模型具有很明显的非均匀特征。在具体反演过程中,分别在第10、20、30和40道处抽取四口伪井,并给定主频为30Hz的雷克子波,将计算得到的模型的合成地震记录作为实际地震数据进行反演。图 4为估计的b、a及θ。由图可见,估计的三个参数与模型数据吻合较好,如在第250个采样点处,θ(图 4c)与模型数据的角度变化趋势一致,b(图 4a)和a(图 4b)也能反映两个薄层的空间变化特征。
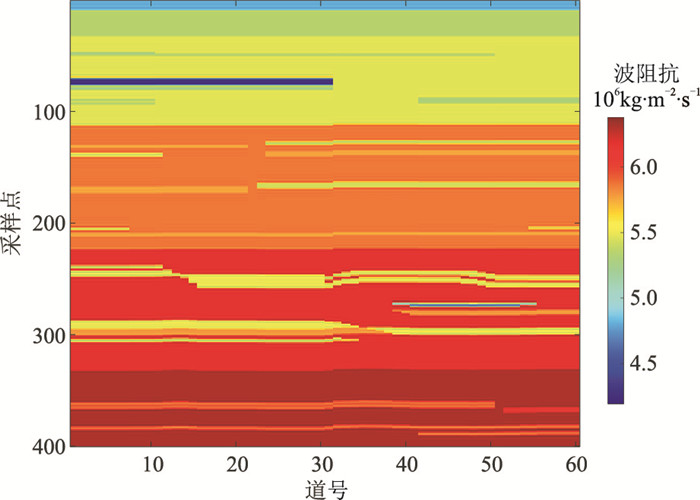
|
图 3 波阻抗模型数据 在第250个采样点附近有两个薄层 |
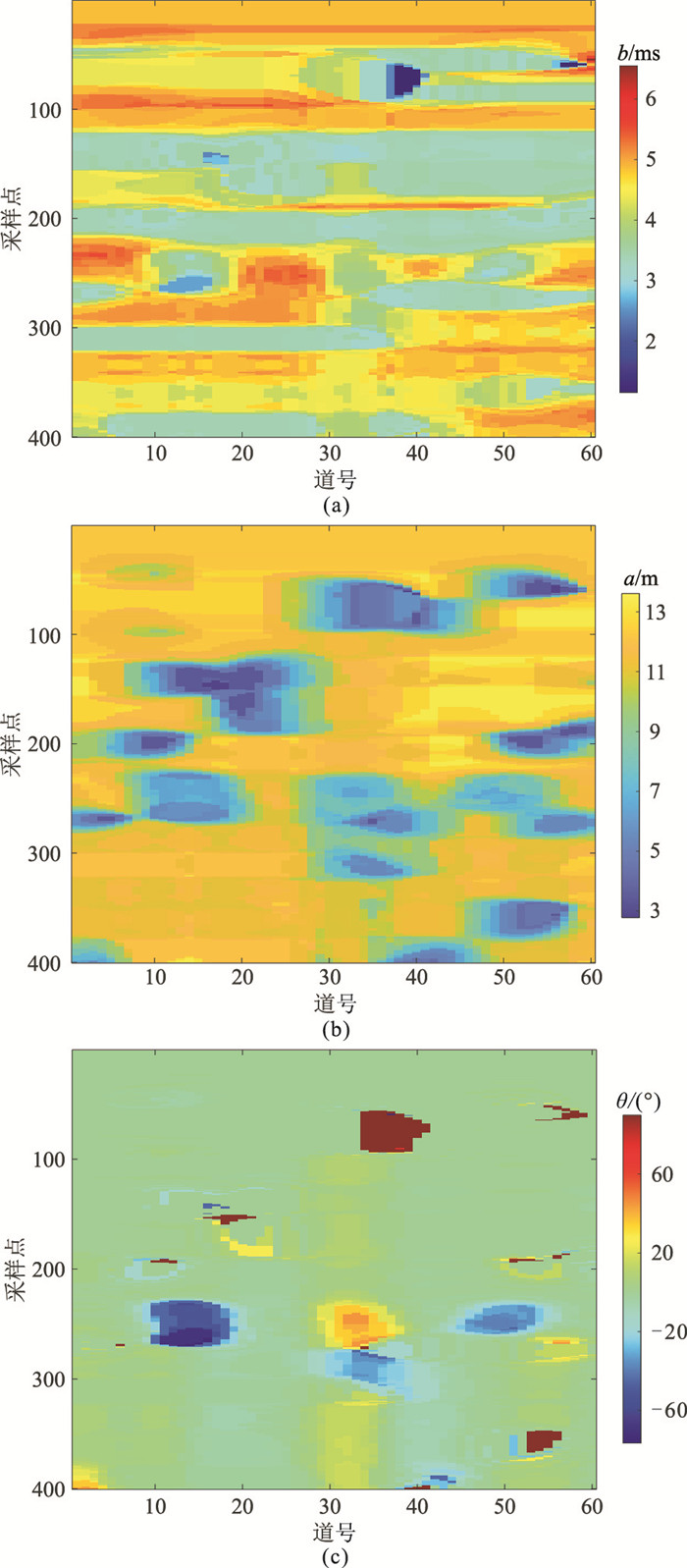
|
图 4 估计的b(a)、a(b)及θ(c) |
另外,考虑到模型的非均质性,在参数估计时采用加窗处理,由地震数据目标层段的非均质特性确定滑动窗口的尺度,得到的特征参数相当于在窗口范围内对模型进行了平滑处理。因此,估计的参数不能与模型数据完全一致,但已足够反映模型数据的空间趋势变化特征。
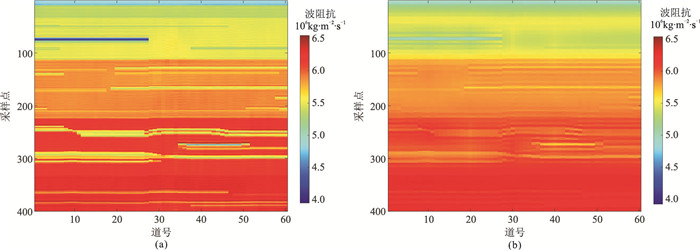
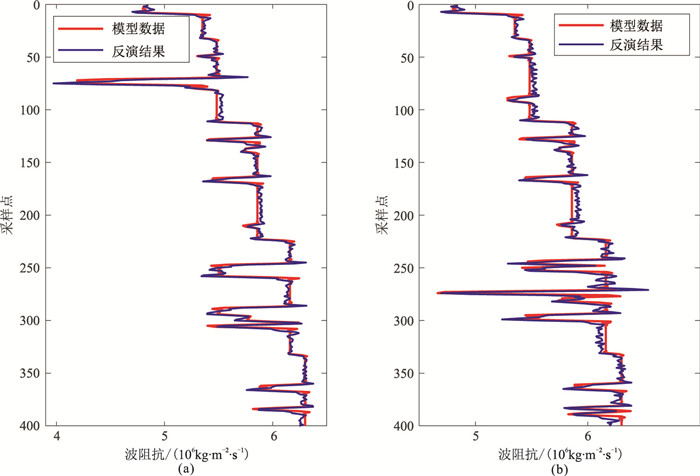
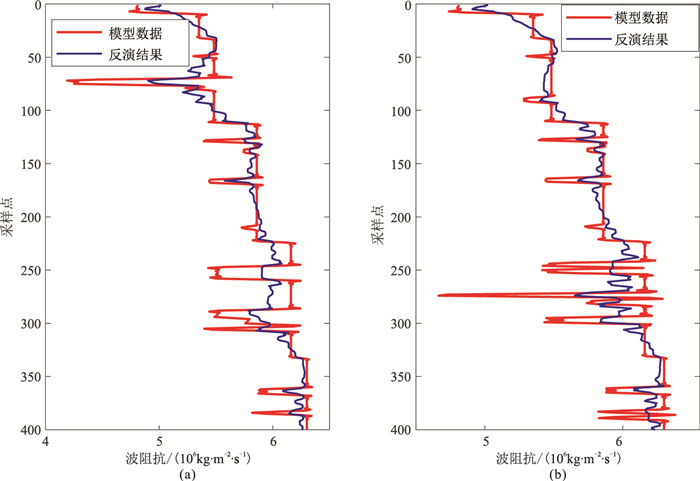
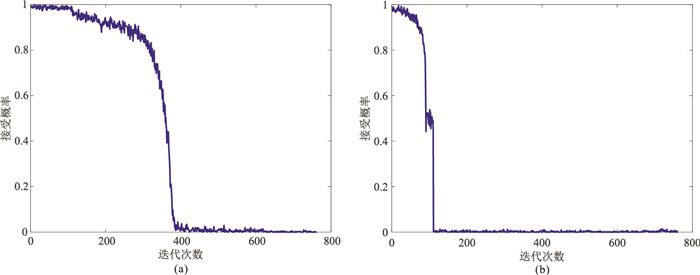
基于上述非均匀介质模型的构建方法构建非均匀介质先验信息模型(图 5),其反映了模型数据(图 3)的空间展布特征。图 6为模型数据的随机反演结果与常规稀疏约束脉冲确定性反演结果。由图可见,随机反演结果的分辨率更高(图 6a)。图 7、图 8分别为第20道和第40道的随机反演结果、常规确定性反演结果与原始模型数据对比。可见,相对于确定性反演结果(图 8),随机反演结果在幅值和形状上均与模型数据匹配较好(图 7)。图 9为QA算法、VFQA算法接受概率随迭代次数的变化曲线。
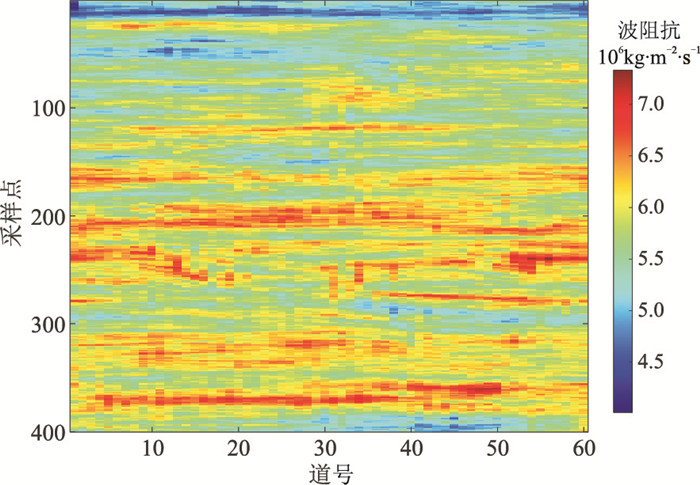
|
图 5 非均匀介质先验信息模型 |
|
图 6 模型数据的随机反演结果(a)与常规稀疏约束脉冲确定性反演结果(b) |
|
图 7 第20道(左)和第40道(右)随机反演结果和原始模型数据对比 |
|
图 8 第20道(左)和第40道(右)确定性反演结果和原始模型数据对比 |
|
图 9 QA算法(a)、VFQA算法(b)接受概率随迭代次数的变化曲线 |
由图可见,VFQA算法在迭代约100次时即可收敛(图 9b),而QA算法则需要迭代近400次才可收敛(图 9a)。
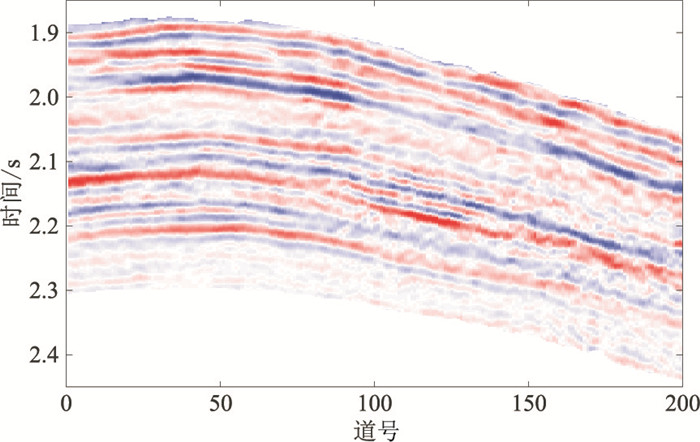
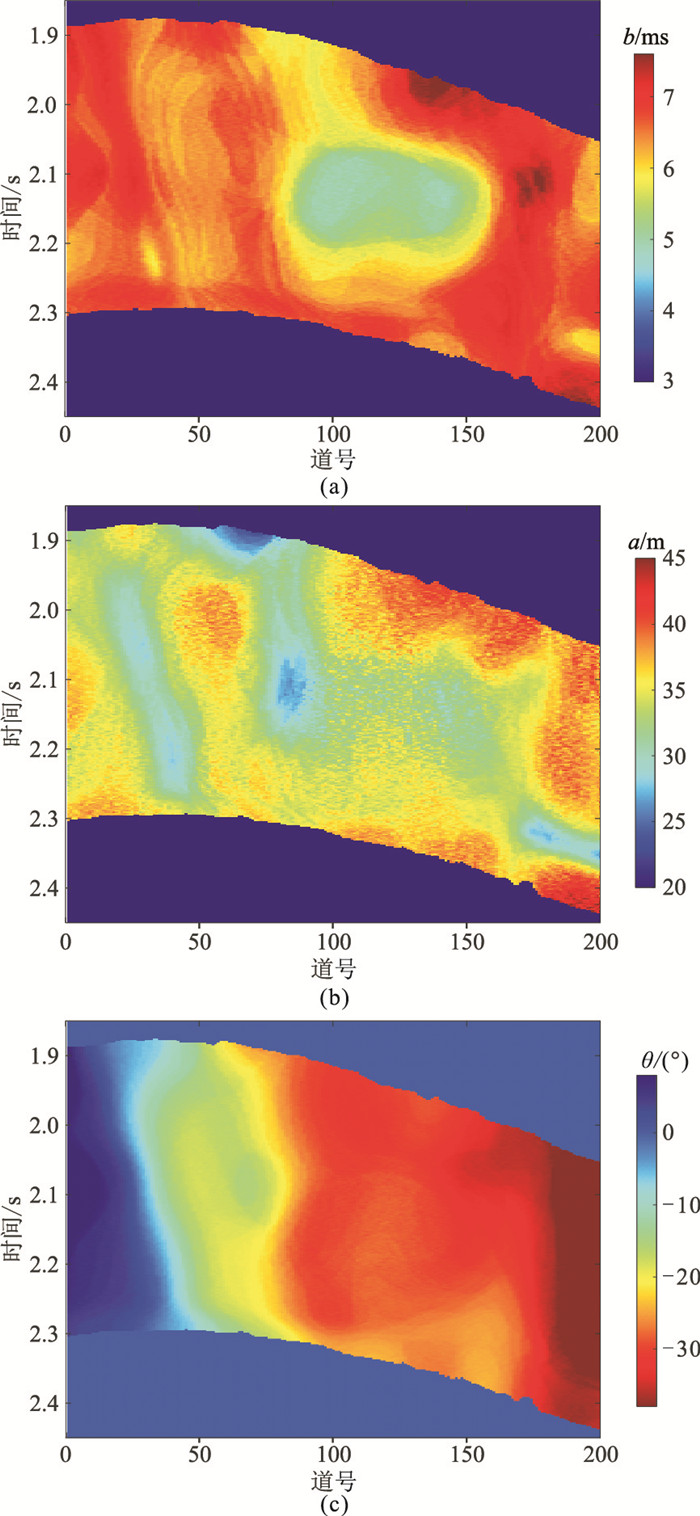
4.2 实例分析本文选取中国M油田叠后地震数据(图 10)测试、分析,其中间部分反射同相轴变细,局部分辨率较高。图 11为对图 10估计的b、a及θ。由图可见:在图 10的局部分辨率较高位置处,b的中间部分数值偏小(图 11a),这是由于非均质体的纵向尺度减小所致;a反映了同相轴的横向变化(图 11b);θ反映了同相轴的倾斜变化,显示地震同相轴先趋于平缓,然后随着道数增加倾角逐渐增大(图 11c)。
|
图 10 叠后地震数据 纵向采样间隔为4ms,时间范围为1.8~2.5s,共有200道,井位于第100道处 |
|
图 11 对图 10估计的b(a)、a(b)及θ(c) |
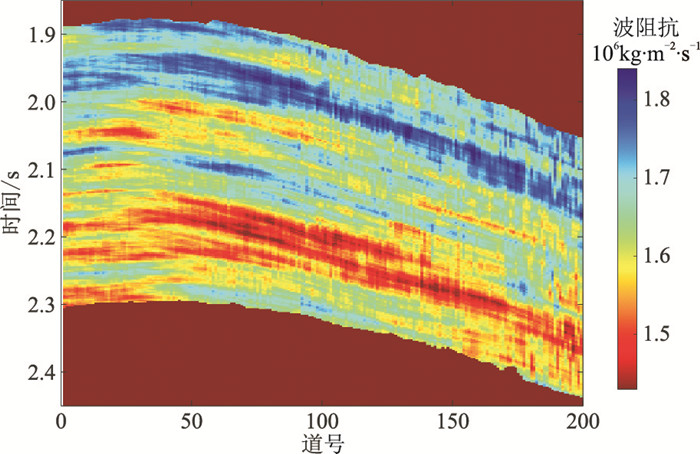
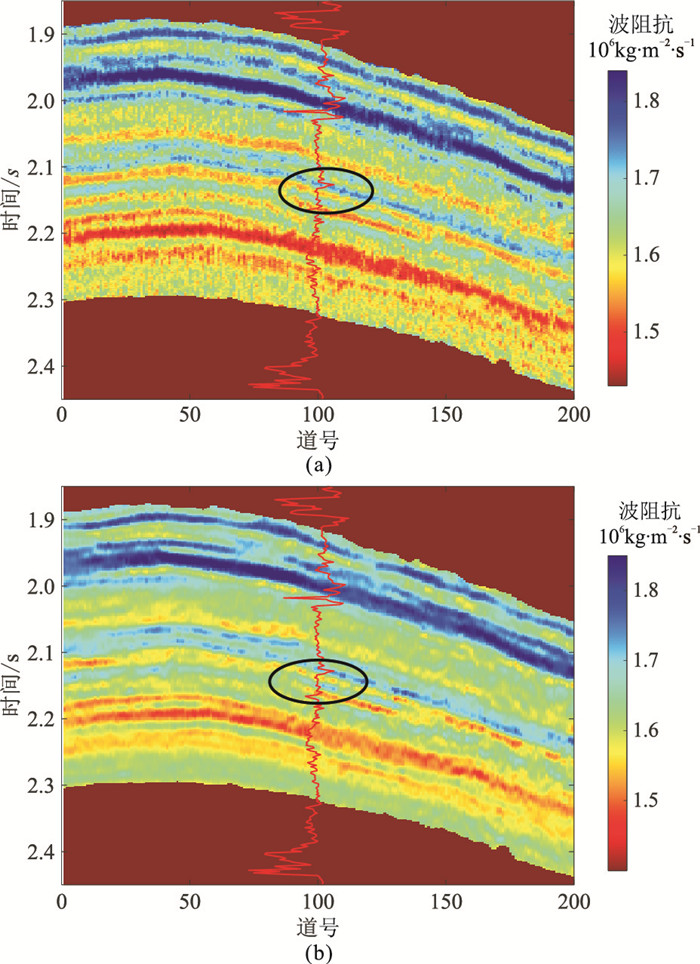
首先计算测井数据的标准差等参数,然后由克里金插值建立测井数据插值模型作为均值,进而利用上述建模方法估计特征参数构建地质统计随机介质模型(图 12)。该模型充分融合了已知测井和地震数据蕴含的地下地质信息,可以作为后续反演的先验信息模型。图 13为实际数据随机反演与常规确定性反演结果。由图可见,相对于常规确定性反演结果(图 13b),基于非均匀介质统计特征参数的随机反演结果的分辨率较高,且横向连续性也较好,更准确地指示了含气储层的位置(图 13a黑色椭圆处)。
|
图 12 构建的非均匀介质先验信息模型 |
|
图 13 实际数据随机反演(a)与常规确定性反演(b)结果 |
地震随机反演是描述地下复杂储层的一种非常有效的方法,可以获得高分辨率的储层弹性参数数据体。本文提出了一种基于非均匀介质特征参数的随机反演方法,借助随机介质理论从已知地震和测井数据中提取描述储层非均质特性的纵向、横向自相关长度和自相关角度等统计特征参数,为后续随机反演提供可靠的先验信息模型,实现了波阻抗高分辨率反演。模型试算和实例分析表明,由于充分融合了已知地震和测井数据中蕴含的地下信息,估计的非均匀介质特征参数描述了非均质储层弹性参数的空间扰动特性,反映了储层的空间结构特征,为随机反演提供了可靠的地质统计先验信息,高分辨率随机反演的精度较高。但是,由于需要从地震数据中估计特征参数,地震数据的品质影响反演效果。另外,由于加窗处理使估计的特征参数与地震数据不完全一致,也会影响后续反演精度。因此,需要进一步研究利用地震数据估计特征参数的有效方法。
| [1] |
Bosch M, Mukerji T, Gonzalez E F. Seismic inversion for reservoir properties combining statistical rock physics and geostatistics: a review[J]. Geophysics, 2010, 75(5): A165-A176. |
| [2] |
Cooke D, Cant J. Model-based seismic inversion: comparing deterministic and probabilistic approaches[J]. CSEG Recorder, 2010, 35(4): 28-39. |
| [3] |
Francis A. Limitations of deterministic seismic inversion data as input for reservoir model conditioning[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 2396-2400.
|
| [4] |
Francis A. Limitations of deterministic and advantages of stochastic seismic inversion[J]. CSEG Recorder, 2005, 30(2): 5-11. |
| [5] |
Sams M. Comparison of lithology and net pay uncertainty between deterministic and geostatistical inversion workflows[J]. First Break, 2010, 28(2): 35-44. |
| [6] |
李坤, 印兴耀. 混合概率模型驱动的叠前地震反演方法[J]. 石油地球物理勘探, 2020, 55(4): 839-853. LI Kun, YIN Xingyao. Prestack seismic inversion driven by mixture probabilistic models[J]. Oil Geophysical Prospecting, 2020, 55(4): 839-853. |
| [7] |
Fokker P A, Borello E S, Serazio C, et al. Estimating reservoir heterogeneities from pulse testing[J]. Journal of Petroleum Science and Engineering, 2012. DOI:10.1016/j.petrol.2012.03.017 |
| [8] |
陈欢庆, 王珏, 杜宜静. 储层非均质性研究方法进展[J]. 高校地质学报, 2017, 23(1): 104-116. CHEN Huanqing, WANG Jue, DU Yijing. Advances of research methods on reservoir heterogeneity[J]. Geological Journal of China Universities, 2017, 23(1): 104-116. |
| [9] |
Ikelle LT, Yung S K, Daube F. 2-D random media with ellipsoidal autocorrelation functions[J]. Geophysics, 1993, 58(9): 1359-1372. DOI:10.1190/1.1443518 |
| [10] |
奚先, 姚姚. 随机介质模型的模拟与混合型随机介质[J]. 地球科学——中国地质大学学报, 2002, 27(1): 67-71. XI Xian, YAO Yao. Simulations of random medium model and interimxed random medium[J]. Earth Science-Journal of China University of Geosciences, 2002, 27(1): 67-71. |
| [11] |
顾元, 朱培民, 李辉, 等. 二维叠后地震数据的平稳随机介质参数估计[J]. 地球物理学报, 2014, 57(7): 2291-2301. GU Yuan, ZHU Peimin, LI Hui, et al. Estimation of 2D stationary random medium parameters from post-stack seismic data[J]. Chinese Journal of Geophysics, 2014, 57(7): 2291-2301. |
| [12] |
奚先, 姚姚. 非平稳随机介质模型[J]. 石油地球物理勘探, 2005, 40(1): 71-75. XI Xian, YAO Yao. Non-stationary random medium model[J]. Oil Geophysical Prospecting, 2005, 40(1): 71-75. |
| [13] |
李祺鑫, 罗亚能, 张生, 等. 高分辨率波阻抗贝叶斯序贯随机反演[J]. 石油地球物理勘探, 2020, 55(2): 389-397. LI Qixin, LUO Yaneng, ZHANG Sheng, et al. High-resolution Bayesian sequential stochastic inversion[J]. Oil Geophysical Prospecting, 2020, 55(2): 389-397. |
| [14] |
纪永祯, 张渝悦, 朱立华, 等. 多道随机稀疏反射系数反演[J]. 石油物探, 2020, 59(6): 912-917. JI Yongzhen, ZHANG Yuyue, ZHU Lihua, et al. Multi-trace stochastic sparse-spike inversion for reflectivity[J]. Geophysical Prospecting for Petroleum, 2020, 59(6): 912-917. DOI:10.3969/j.issn.1000-1441.2020.06.009 |
| [15] |
Debeye H W, Sabbah E, Made P M. Stochastic inversion[C]. SEG Technical Program Expanded Abstracts, 1996, 15: 1212-1215.
|
| [16] |
Yin X Y, Sun R Y, Wang B L, et al. Simultaneous inversion of petrophysical parameters based on geostatistical a priori information[J]. Applied Geophysics, 2014, 11(3): 321-330. DOI:10.1007/s11770-014-0447-z |
| [17] |
王保丽, 印兴耀, 丁龙翔, 等. 基于FFT-MA谱模拟的快速随机反演方法研究[J]. 地球物理学报, 2015, 58(2): 664-673. WANG Baoli, YIN Xingyao, DING Longxiang, et al. Study of fast stochastic inversion based on FFT-MA spectrum simulation[J]. Chinese Journal of Geophy-sics, 2015, 58(2): 664-673. |
| [18] |
孙瑞莹, 印兴耀, 王保丽, 等. 基于随机地震反演的Russell流体因子直接估算方法[J]. 地球物理学报, 2016, 59(3): 1143-1150. SUN Ruiying, YIN Xingyao, WANG Baoli, et al. A direct estimation method for the Russell fluid factor based on stochastic seismic inversion[J]. Chinese Journal of Geophysics, 2016, 59(3): 1143-1150. |
| [19] |
王保丽, 孙瑞莹, 印兴耀, 等. 基于Metropolis抽样的非线性反演方法[J]. 石油地球物理勘探, 2015, 50(1): 111-117. WANG Baoli, SUN Ruiying, YIN Xingyao, et al. Nonlinear inversion based on Metropolis sampling algorithm[J]. Oil Geophysical Prospecting, 2015, 50(1): 111-117. |
| [20] |
郭同翠, 姜明军, 纪迎章, 等. 叠前地质统计学反演在页岩甜点和薄夹层预测中的应用——以西加拿大盆地W区块为例[J]. 石油地球物理勘探, 2020, 55(1): 167-175. GUO Tongcui, JIANG Mingjun, JI Yingzhang, et al. The application of prestack geostatistical inversion in the prediction of shale sweet spots and thin interbeds: a case study of Block W in Western Canada Basin[J]. Oil Geophysical Prospecting, 2020, 55(1): 167-175. |
| [21] |
Azevedo L, Nunes R. Geostatistical seismic AVO inversion directly for facies: real case application[C]. Extended Abstracts of 77th EAGE Conference & Exhibition, 2015, 423-426.
|
| [22] |
De Figueiredo L P, Grana D, Bordignon F, et al. Joint Bayesian inversion based on rock-physics prior modeling for the estimation of spatially correlated reservoir properties[J]. Geophysics, 2018, 83(5): M49-M61. DOI:10.1190/geo2017-0463.1 |
| [23] |
De Figueiredo L P, Grana D, Santos M, et al. Bayesian seismic inversion based on rock-physics prior modeling for the joint estimation of acoustic impedance, porosity and lithofacies[J]. Journal of Computational Physics, 2017, 336(5): 128-142. |
| [24] |
Mohamed I A, John P, Mohamed S E, et al. Integrated seismic attributes and stochastic inversion for reservoir characterization: Insights from Wadi field[J]. Journal of African Earth Sciences, 2020. DOI:10.1016/j.jafrearsci.2019.103661 |
| [25] |
张繁昌, 肖张波, 印兴耀. 地震数据约束下的贝叶斯随机反演[J]. 石油地球物理勘探, 2014, 49(1): 176-182. ZHANG Fanchang, XIAO Zhangbo, YIN Xingyao. Bayesian stochastic inversion constrained by seismic data[J]. Oil Geophysical Prospecting, 2014, 49(1): 176-182. |
| [26] |
Pereira P, Azevedo L, Nunes R. Integrating of initial guess models into geostatistical seismic inversion methodologies[C]. SEG Technical Program Expanded Abstracts, 2016, 35: 326-330.
|
| [27] |
Erasmus K O, James I, Thomas H. Basis-constrained Bayesian Markov-chain Monte Carlo diffe-rence inversion for geoelectrical monitoring of hydrogeologic processes[J]. Geophysics, 2019, 84(4): M37-M42. |
| [28] |
Heidi K, Ragnar H, Odd K. Bayesian Monte Carlo method for seismic predrill prospect assessment[J]. Geophysics, 2010, 75(2): O9-O19. DOI:10.1190/1.3339678 |
| [29] |
Grana D. Bayesian petroelastic inversion with multiple prior models[J]. Geophysics, 2020, 85(5): M57-M71. DOI:10.1190/geo2019-0625.1 |
| [30] |
Francis A. Understanding stochastic inversion: Part 1[J]. First Break, 2006, 24(11): 69-77. |
| [31] |
Francis A. Understanding stochastic inversion: Part 2[J]. First Break, 2006, 24(12): 79-84. |
| [32] |
Tarantola A. Inverse Problem Theory and Methods for Model Parameter Estimation[M]. Paris: SIAM, 2005.
|



 王保丽, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
王保丽, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: 