② 中国石油大学(北京)地球物理学院, 北京 102249;
③ 中石油长庆油田分公司勘探开发研究院, 陕西西安 710018
② College of Geophysics, China University of Petroleum (Beijing), Beijing 102249, China;
③ Research Institute of Exploration and Development, Changqing Oilfield Company, PetroChina, Xi'an, Shaanxi 710018, China
随着油气勘探、开发的不断深入,常规流体识别技术无法满足勘探需求,因此利用与频率有关的地震信息识别流体成为研究热点[1-3]。考虑到“低频阴影”以及优势频率等半定量频率相关流体检测方法[4-5]受限于多解性以及分辨率低,因此不具有普适性。将常规反演与频率相关的流体识别技术有机结合的AVF反演能充分利用反射系数随频率的变化信息定量地获取频散属性,多解性更低,分辨率更高,可更有效地识别流体[6-7]。
近十年来,AVF反演理论趋于完善。一方面,基于衰减与频散的岩石物理机理研究正逐步完善,为利用衰减、频散特性识别流体奠定了理论基础[8-10]。另一方面,AVF正演分析方法从早期的单一界面假设[11]向层状介质假设过渡,更合理地将地震反射响应与衰减、频散联系起来。流体性质、衰减特性、反射响应三者关系密切,可利用反射系数随频率的变化信息估计频散,进而利用频散属性指示流体变化。
Wilson等[12]基于Smith-Gidlow频率域反射系数近似公式[13],首次提出由地震反射数据定量反演频散属性的方法,并利用模型数据验证方法的有效性。该频散反演方法的流程为:①利用谱分解方法(如短时傅里叶变换[14]、小波变换[15]、S变换[16]等)计算地震记录的时频谱;②基于地震记录提取子波,并结合谱均衡技术消除地震数据中的子波叠印,从而获取反射系数的时频谱[16];③选取合适的参考频率点以及参与计算的频率点反演频散属性。基于不同的正演近似公式以及谱分解技术[17-19],该方法在实际资料测试中取得一定效果。
纵波衰减与频散是PP波地震记录衰减的主要原因[8],因此理论上只需利用PP波叠后地震资料即可进行AVF反演,以获取纵波频散因子指示流体[20]。但基于传统单界面的AVF反演方法并不令人满意且在很多方面仍然存在争议。第一,衰减与频散都可以导致AVF现象[21],而常规频散反演仅考虑界面的频散。实际上介质传播过程中的AVF效应远远大于界面的AVF效应。第二,常规方法合成的地震数据仅包含一次反射波信息,忽略了透射损失、层间多次波的影响,造成流体识别错误。第三,需要进一步提升常规反演方法的精度和分辨率。
针对上述问题,本文提出利用一维零炮检距黏滞声波方程解析解的AVF反演方法,其正演算子是非线性的,AVF反演过程需要求解地震数据对模型数据的导数(即Fréchet导数)[22]。基于Kolsky-Futterman衰减介质模型[23-24],通过链式法则,利用反演的纵波阻抗构建高精度的Fréchet导数矩阵,在此基础上反演的频散属性更精确、且分辨率更高。最后,通过模型以及实际数据验证方法的有效性和实用性。
1 基本理论 1.1 正演在N层水平黏滞声学介质假设下,双界面介质模型[25-26]的相邻层反射响应递归公式为
| $ r_{i}(\omega)=\frac{r_{i+1}(\omega)+R_{i}(\omega)}{1+R_{i}(\omega) r_{i+1}(\omega)} \mathrm{e}^{-2 {\rm{j}} \omega h_{i} / v_{i}(\omega)} $ | (1) |
式中:rn(ω)为第n(n=i、i+1)反射界面以下的总反射响应,ω为角频率;hn和vn(ω)分别为第n层的介质厚度和复速度;
若输入的模型参数为时间域阻抗参数,则式(1)改写为
| $ r_{i}(\omega)=\frac{r_{i+1}(\omega)+R_{i}(\omega)}{1+R_{i}(\omega) r_{i+1}(\omega)} \mathrm{e}^{-\mathrm{j} \omega \tau_{i}(\omega)} $ | (2) |
式中:τi(ω)表示第i层双程复旅行时;
根据Kolsky-Futterman模型,得
| $ \frac{1}{v_{i}(\omega)}=\frac{1}{\bar{v}_{i}}\left(1-\frac{1}{{\rm{ \mathit{ π} }} Q_{i}} \ln \left|\frac{\omega}{\omega_{\mathrm{r}}}\right|-\frac{\mathrm{j}}{2 Q_{i}}\right) $ | (3) |
式中:ωr为参考角频率;vi为第i层实数域速度;Qi为第i层品质因子。于是
| $ \begin{aligned} \tau_{i}(\omega) &=\frac{2 h_{i}}{v_{i}(\omega)}=\frac{2 h_{i}}{\bar{v}_{i}}\left(1-\frac{1}{{\rm{ \mathit{ π} }} Q_{i}} \ln \left|\frac{\omega}{\omega_{\mathrm{r}}}\right|-\frac{\mathrm{j}}{2 Q_{i}}\right) \\ &=\mathrm{d} t\left(1-\frac{1}{{\rm{ \mathit{ π} }} Q_{i}} \ln \left|\frac{\omega}{\omega_{\mathrm{r}}}\right|-\frac{\mathrm{j}}{2 Q_{i}} \right) \end{aligned} $ | (4) |
式中dt为时间采样间隔。由于Qi≫1,因此
| $ v_{i}(\omega) \approx \bar{v}_{i}\left|\frac{\omega}{\omega_{\mathrm{r}}}\right|^{\frac{1}{{\rm{ \mathit{ π} }} Q_{i}}} \mathrm{e}^{\frac{\mathrm{j}}{2 Q_{i}}} \approx \bar{v}_{i}\left(1+\frac{1}{{\rm{ \mathit{ π} }} Q_{i}} \ln \left|\frac{\omega}{\omega_{\mathrm{r}}}\right|+\frac{\mathrm{j}}{2 Q_{i}}\right) $ | (5) |
式中:
则复波阻抗为
| $ \begin{aligned} I_{i}(\omega) &=\rho_{i} \bar{v}_{i}\left(1+\frac{1}{{\rm{ \mathit{ π} }} Q_{i}} \ln \left|\frac{\omega}{\omega_{\mathrm{r}}}\right|+\frac{\mathrm{j}}{2 Q_{i}}\right) \\ &=\bar{I}_{i}\left(1+\frac{1}{{\rm{ \mathit{ π} }} Q_{i}} \ln \left|\frac{\omega}{\omega_{\mathrm{r}}}\right|+\frac{\mathrm{j}}{2 Q_{i}}\right) \end{aligned} $ | (6) |
式中Ii为输入的实数域波阻抗。
由于最深层(第N层)不存在反射,因此rN=0。由式(2)得到总反射响应函数r0。由
| $ g(t)=\frac{1}{2 {\rm{ \mathit{ π} }}} \int_{-\infty}^{\infty} W(\omega) r_{0}(\omega) \mathrm{e}^{\mathrm{j} \omega t} \mathrm{~d} \omega $ | (7) |
进行傅里叶反变换,可获得地震记录g(t)。式中W(ω)为频率域子波。
综上所述,输入已知的波阻抗以及品质因子,即可模拟一维零炮检距黏滞声波波动方程解析解,求解波场信息过程中考虑了衰减(包括除一次反射波以外的多次波以及层间透射损失)。考虑到孔隙介质的衰减特性与黏弹介质的衰减特性可以互相等效表征[27-28],因此基于Kolsky-Futterman模型进行AVF正演分析。
1.2 AVF反演根据AVF理论可知,反射系数随频率的变化信息反映频散特征,其数学基础是在频率域进行泰勒展开。此时正演方法为非线性映射,可用非线性算子G表示。已知反射系数
| $ \boldsymbol{r}_{0}=\boldsymbol{R}(t, f)=\boldsymbol{G}[\boldsymbol{m}(t, f)] $ | (8) |
式中:r0为r0的矩阵形式;R(t, f)为反射系数的时频谱,t、f分别为时间、频率;m为模型参数(波阻抗)。首先,在选定的参考频率f0处对反射系数进行一阶泰勒近似
| $ \begin{aligned} &\boldsymbol{R}(t, f) \approx \boldsymbol{G}\left[\boldsymbol{m}\left(t, f_{0}\right)\right]+ \\ &\left.\left.\frac{\partial \boldsymbol{G}[\boldsymbol{m}(t, f)]}{\partial \boldsymbol{m}(t, f)}\right|_{\boldsymbol{m}(t, f)=\boldsymbol{m}\left(t, f_{0}\right)} \frac{\partial \boldsymbol{m}(t, f)}{\partial f}\right|_{f=f_{0}}\left(f-f_{0}\right) \end{aligned} $ | (9) |
式中G[m(t, f0)]= R(t, f0)。模型参数相对于频率的导数即频散程度,记作
| $ \boldsymbol{R}(t, f)-\boldsymbol{R}\left(t, f_{0}\right)=\left(f-f_{0}\right) \operatorname{Fr} H_{\mathrm{p}} $ | (10) |
求解式(10)需要已知R(t, f),因此首先利用时频分解方法获取地震记录时频谱
| $ \boldsymbol{S}(t, f)=\boldsymbol{R}(t, f) \boldsymbol{W}(f) $ | (11) |
联立式(10)、式(11),得
| $ \begin{aligned} \boldsymbol{S}(t,& f) \boldsymbol{W}\left(f_{0}\right)-\boldsymbol{S}\left(t, f_{0}\right) \boldsymbol{W}(f) \\ &=\boldsymbol{W}\left(f_{0}\right) \boldsymbol{W}(f)\left(f-f_{0}\right) \operatorname{Fr} H_{\mathrm{p}} \end{aligned} $ | (12) |
利用上述公式可消除地震数据的子波叠印,该过程称为谱均衡。
通过链式求导法计算Fr,即
| $ \frac{\partial \boldsymbol{r}_{0}(\omega)}{\partial \bar{I}_{i}}=\frac{\partial \boldsymbol{r}_{0}(\omega)}{\partial \boldsymbol{r}_{1}(\omega)} \frac{\partial \boldsymbol{r}_{1}(\omega)}{\partial \boldsymbol{r}_{2}(\omega)} \cdots \frac{\partial \boldsymbol{r}_{i-2}(\omega)}{\partial \boldsymbol{r}_{i-1}(\omega)} \frac{\partial \boldsymbol{r}_{i-1}(\omega)}{\partial \bar{I}_{i}} $ | (13) |
其中
| $ \left\{\begin{array}{l} \frac{\partial r_{i-2}(\omega)}{\partial r_{i-1}(\omega)}=\frac{1-R_{i-2}^{2}}{\left[1+R_{i-2} r_{i-1}(\omega)\right]^{2}} \mathrm{e}^{-\mathrm{j} \omega \tau_{i-2}(\omega)} \\ \frac{\partial r_{i-1}(\omega)}{\partial \bar{I}_{i}}=\frac{\frac{\partial R_{i-1}}{\partial \bar{I}_{i}}\left[1-r_{i}^{2}(\omega)\right]+\frac{\partial r_{i}(\omega)}{\partial \bar{I}_{i}}\left(1-R_{i-1}^{2}\right)}{\left[1+R_{i-1} r_{i}(\omega)\right]^{2}} \mathrm{e}^{-\mathrm{j} \omega \tau_{i-1}(\omega)} \end{array}\right. $ | (14) |
式中:rl(l=i-2、i-1、i)、Rk(k=i-2、i-1)分别为rl、Rk的标量形式;∂Ri-1/∂Ii=-2Ii-1/(Ii-1+Ii)2。由于∂ri+1(ω)/∂Ii=0,因此
| $ \frac{\partial r_{i}(\omega)}{\partial \bar{I}_{i}}=\frac{\frac{\partial R_{i}}{\partial \bar{I}_{i}}\left[1-r_{i+1}^{2}(\omega)\right]}{\left[1+R_{i} r_{i+1}(\omega)\right]^{2}} \mathrm{e}^{-\mathrm{j} \omega \tau_{i}(\omega)} $ | (15) |
基于式(12),即可求解Hp获得纵波频散属性。求取Hp的过程利用了振幅随频率变化的信息,故整个过程称作AVF反演。至此,本文基于黏滞声波方程解析解的相关理论,建立了更完善的AVF反演方法,其流程(图 1)为:①利用时频谱方法等计算地震记录的时频谱;②基于地震记录提取子波,消除地震数据中子波叠印获取反射系数的时频谱;③基于黏滞声波方程进行波阻抗反演(附录A),获得更准确的阻抗参数计算Fréchet导数;④根据导数矩阵建立AVF反演方程,选取合适的参考频率点以及参与计算的频率点反演高精度频散属性。
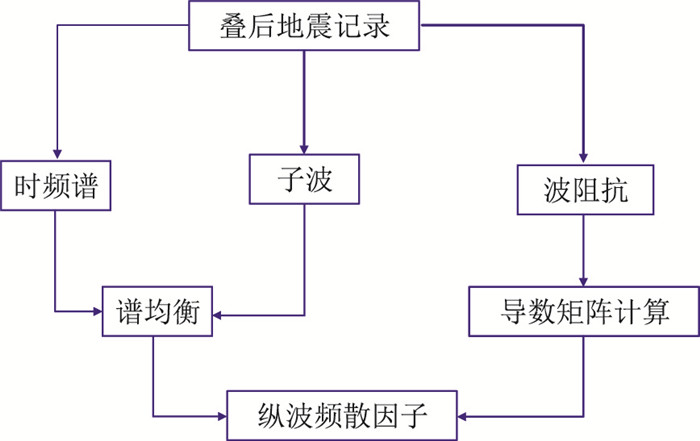
|
图 1 基于黏滞声波解析解的频散反演流程 |
首先根据式(5)模拟衰减效应。图 2为振幅衰减与频散。由图可见,相对于原始子波,振幅衰减+频散后的子波的振幅和相位均发生变化,其中衰减仅导致振幅变化,频散仅导致相位变化。因此,振幅衰减与频散关系密切,不能单独分析。
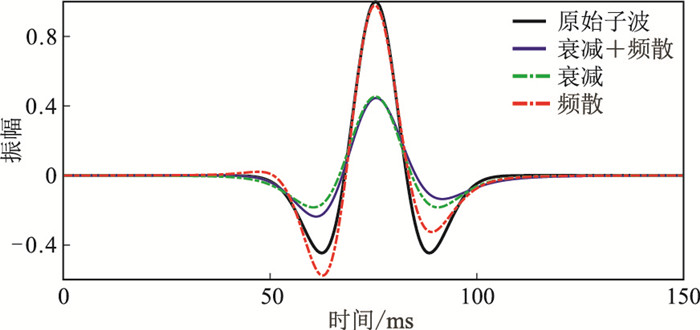
|
图 2 振幅衰减与频散 |
为验证所提方法的正演优越性,设计薄互层波阻抗模型(图 3a),利用常规单界面方法及解析解方法进行正演模拟(图 3b)。由于两种波场模拟方法的物理完备性不同,因此所得数据的振幅、相位和分辨率差异很大。可见:由于透射损失和衰减效应,不同深度的一次反射波振幅差异明显,且深度越大振幅差异越大(图 3b红色虚线框处);在底部基岩层(430~700ms)的黏滞声波方程解析解数据中可见明显的层间多次波,因此模拟结果更真实。进一步利用谱分解方法提取图 3b红色箭头处的数据,经过谱均衡得到AVF曲线(图 4)。不难发现:①基于界面的AVF效应并不明显,基于黏滞声波方程解析解方法提取的AVF曲线衰减特征更符合实际情况。②界面的AVF效应远远小于传播过程中的AVF效应,因此传播过程中不能忽略衰减。③如果执行单界面AVF反演,不能完全消除传播过程引起的振幅衰减,些许误差将对最终反演结果造成很大影响。因此,利用综合考虑两种效应的基于黏滞声波方程解析解的AVF反演更有效。
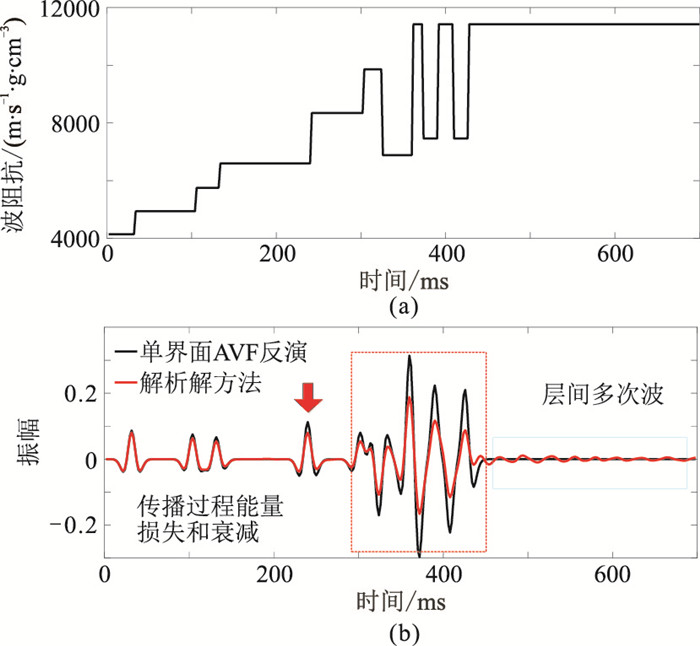
|
图 3 薄互层波阻抗模型(a) 及合成的地震道(b) 设置400ms处为薄互层位置,以突出层间多次波。Q=80,采用30Hz的雷克子波作为震源 |
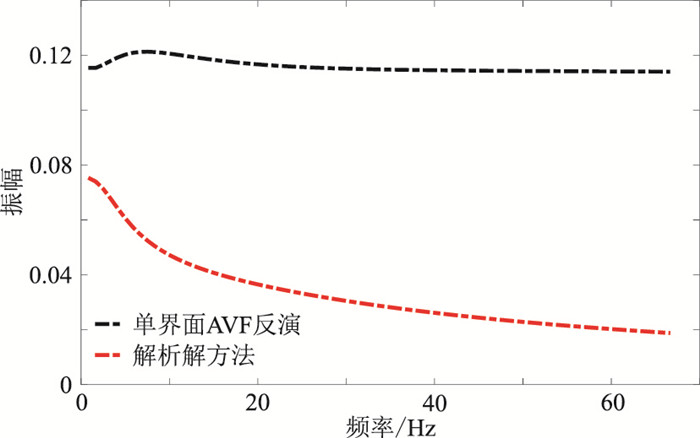
|
图 4 图 3b红色箭头处的AVF曲线 |
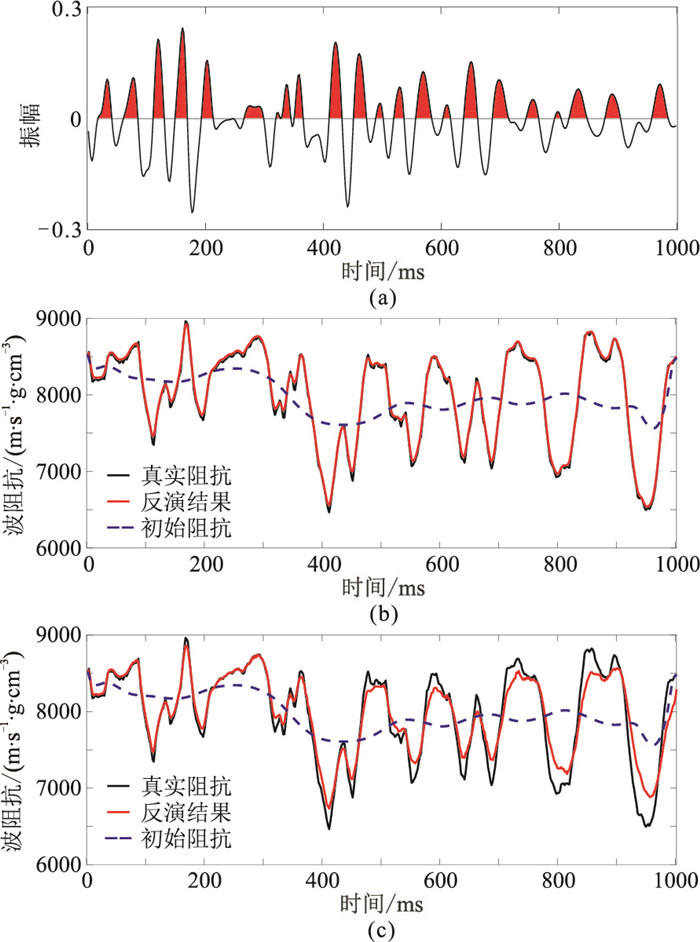
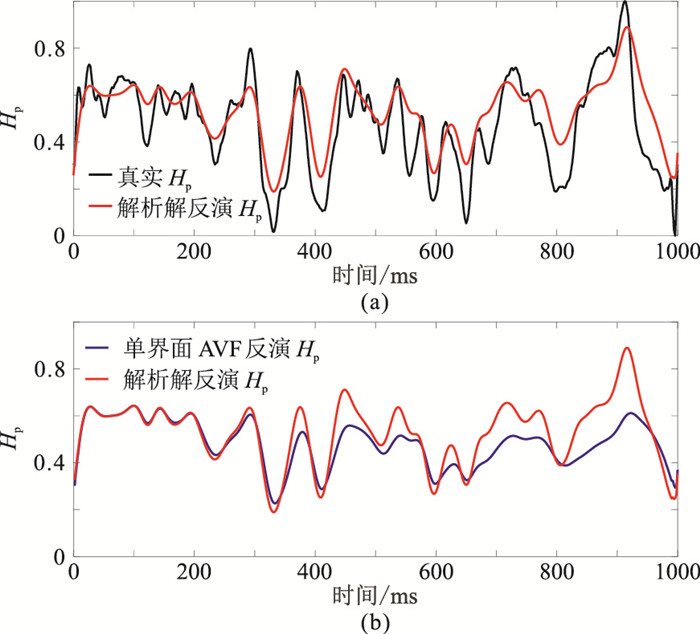
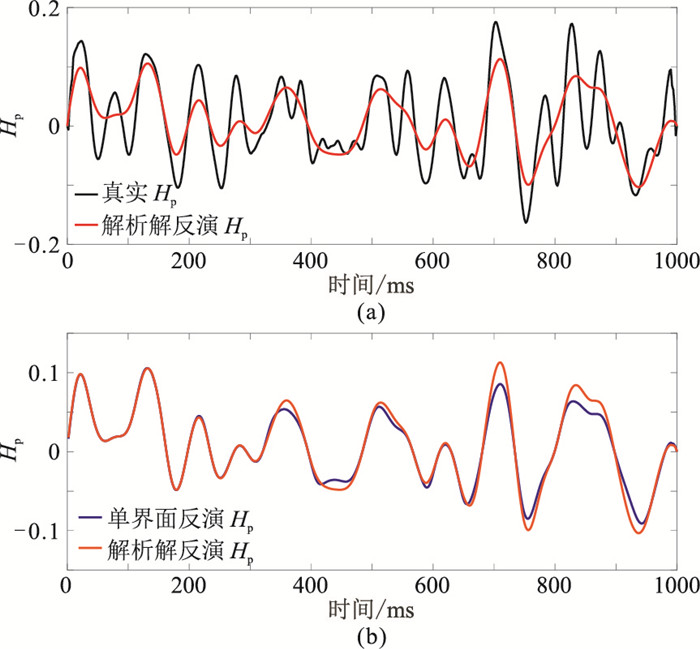
利用解析解合成带衰减的全波场信息(包括透射损失、多次波等)作为真实地震数据。分别对基于测井数据合成的地震记录(图 5a)进行黏滞声波解析解反演(图 5b)以及常规阻抗反演(图 5c)。由反演结果可见,由于传播效应的影响,随着时间增加,与基于测井数据合成的地震记录(图 5a)相比,常规阻抗反演精度和分辨率损失较严重(图 5c),黏滞声波解析解反演结果(图 5b)与图 5a的一致性较好,从而验证了黏滞声波解析解反演的有效性。进一步对图 5a进行黏滞声波解析解AVF反演以及常规单界面AVF反演,对比不同反演结果表明:①由于时频分析方法的分辨率限制(测不准准则)、子波带限影响(频率带限)、参与计算的频率点选择(斜率近似)以及频散反演过程中的等效近似(泰勒展开)等因素,导致黏滞声波解析解AVF反演的频散属性仅能大致反映纵波频散,与真实频散属性存在一定差异(图 6a)。②相对于常规单界面AVF反演,黏滞声波解析解AVF反演结果明显提高了精度和分辨率(图 6b)。图 7为弱衰减条件的反演频散属性对比。由图可见:黏滞声波解析解AVF反演的频散属性与真实频散属性同样存在一定差异(图 7a),但由于衰减效应较弱,常规单界面AVF反演结果与黏滞声波解析解AVF反演结果的差异较小(图 7b),仅在深部存在一定差异。综上所述,基于黏滞声波解析解的AVF反演效果明显好于常规AVF反演方法,可较好地识别流体变化造成的强衰减效应。因此文中提出的基于黏滞声波方程解析解的AVF反演方法是有效的。
|
图 5 对由解析解合成的带衰减的地震记录的反演结果 (a)基于测井数据合成的地震记录;(b)黏滞声波解析解反演;(c)常规阻抗反演 |
|
图 6 反演频散属性对比 (a)黏滞声波解析解AVF反演频散属性与真实频散属性;(b)黏滞声波解析解AVF反演频散属性与常规单界面AVF反演频散属性 |
|
图 7 弱衰减条件的反演频散属性对比 (a)黏滞声波解析解AVF反演频散属性与真实频散属性;(b)黏滞声波解析解AVF反演频散属性与常规单界面AVF反演频散属性 |
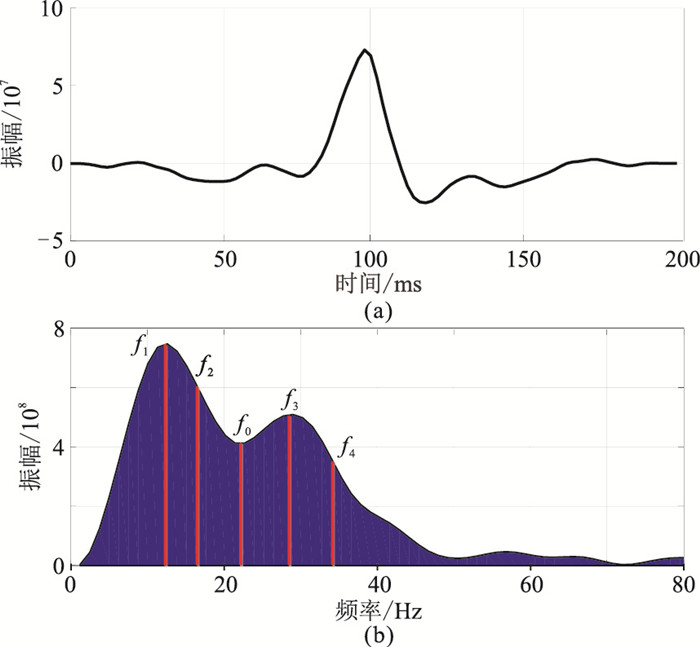
实际数据为中国北方X区的叠后地震剖面(图 8),基于黏滞声波解析解的频散反演流程(图 1),首先利用统计原理提取子波及其振幅谱(图 9)。利用振幅谱信息选取参考频率与特征计算频率。根据频散属性定义

|
图 8 X区叠后地震剖面 采样间隔为2ms |
|
图 9 基于统计理论估计的子波(a)及其振幅谱(b) f1=13Hz、f2=18Hz、f3=28Hz、f4=34Hz为特征计算频率 |
|
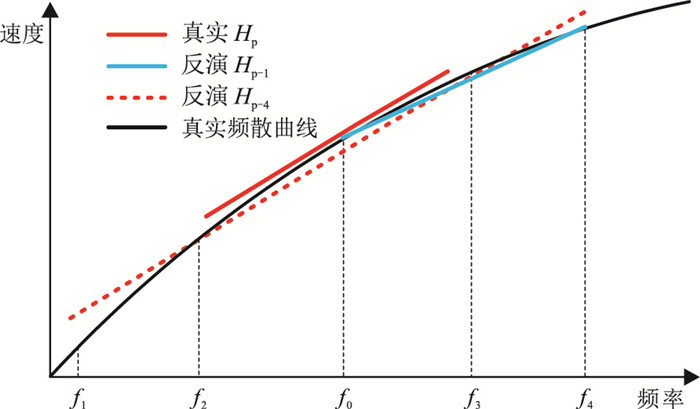
图 10 频散属性反演中的频率影响示意图 |
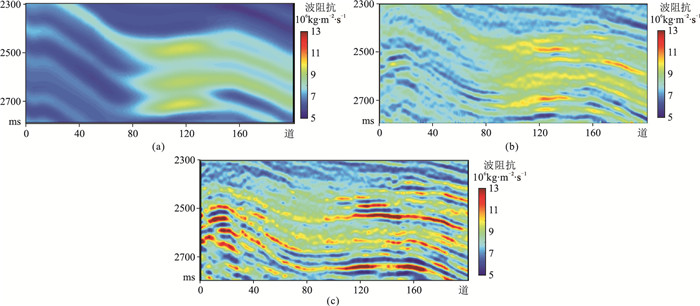
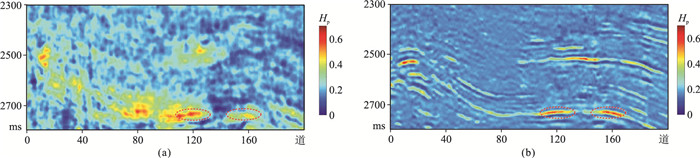
进一步利用实际数据进行波阻抗反演,利用所拾取的层位结合测井信息插值得到初始阻抗模型(图 11a),并进行常规反演(图 11b)与基于黏滞声波解析解反演(图 11c)。结果表明,基于黏滞声波解析解反演考虑了衰减效应,因此最终反演结果(图 11c) 的分辨率高于常规反演结果(图 11b),并且横向变化更符合地质规律。图 12为常规单界面AVF反演结果与基于黏滞声波解析解AVF反演结果。可见:常规单界面AVF反演结果与地震剖面的一致性较差(图 12a);基于黏滞声波解析解AVF反演属于单道反演,从而保证反演结果与地震剖面的一致性较好,确定的流体异常位置与钻井验证结果一致(图 12b红色椭圆处)。因此两种频散属性反演结果的分辨率存在较大差异,即基于黏滞声波解析解AVF反演效果(图 12b)优于常规单界面AVF反演(图 12a)。X区测试结果表明,基于黏滞声波解析解的AVF反演方法更有效、可靠。
|
图 11 X区波阻抗反演结果 (a)初始阻抗模型;(b)常规阻抗反演;(c)基于黏滞声波解析解反演 |
|
图 12 常规单界面AVF反演结果(a)与基于黏滞声波解析解AVF反演结果(b) |
本文仅利用叠后资料进行基于黏滞声波解析解的非线性纵波频散反演指示流体,在处理衰减与频散的同时,充分考虑透射损失、多次波影响,在正演方面更具优越性。通过对比常规方法和新方法的合成记录、AVF曲线差异,发现界面频散对地震记录的影响很小,且传播过程的AVF效应远大于界面频散造成的AVF效应。合成数据和实际数据AVF反演测试均表明,新方法的精度和分辨率明显高于常规单界面AVF反演。但新方法仍存在以下不足:
(1) 受AVF方法的固有流程所限,最终的频散反演结果与真实频散存在差异。
(2) 尽管传播过程的AVF效应远大于界面频散造成的AVF效应,但由于动校拉伸、部分叠加、多次波干涉等也可能产生AVF效应。因此,一方面,在常规处理过程中应避免数值原因造成的AVF现象。另一方面,要结合常规流体因子判别频散反演结果的合理性,从而降低流体指示错误风险。
(3) 基于固定的孔隙介质岩石物理模型,频散属性与储层物性参数存在明确的表达式,因此应选取不同的参考频率计算不同频率的频散属性。理论上,可利用不同参考频率的频散属性获取储层物性参数信息。
附录A 黏滞声波方程波阻抗反演根据非线性反演流程[29],解析解为
| $ \boldsymbol{d}=\boldsymbol{G}(\boldsymbol{m}) $ | (A-1) |
式中:d为观测数据向量;m为模型的参数向量;G(m)为m映射到d的非线性算子,文中G(m) 为解析法正演结果。基于贝叶斯推理框架[30],假设模型服从高斯分布,可构建目标函数
| $ \begin{aligned} J(\boldsymbol{m}) &=[\boldsymbol{d}-\boldsymbol{G}(\boldsymbol{m})]^{\mathrm{T}}[\boldsymbol{d}-\boldsymbol{G}(\boldsymbol{m})]+\\ &\boldsymbol{\mu}_{\mathrm{a}}(\boldsymbol{m}-\boldsymbol{\mu})^{\mathrm{T}} \boldsymbol{\sigma}_{\boldsymbol{m}}^{-2}(\boldsymbol{m}-\boldsymbol{\mu}) \end{aligned} $ | (A-2) |
式中:超参数μa为先验信息权重;σm2为模型参数的方差;μ为模型均值,可由构建的初始模型代替。可使用高斯—牛顿算法求解式(A-2),即按
| $ \left\{\begin{array}{l} \boldsymbol{H}\left(\boldsymbol{m}^{k}\right) \Delta \boldsymbol{m}=-\boldsymbol{\gamma}\left(\boldsymbol{m}^{k}\right) \\ \boldsymbol{m}^{k+1}=\boldsymbol{m}^{k}+\Delta \boldsymbol{m} \end{array}\right. $ | (A-3) |
迭代求解。其中
| $ \left\{\begin{array}{l} \boldsymbol{\gamma}\left(\boldsymbol{m}^{k}\right)=\left(\boldsymbol{g}^{k}\right)^{\mathrm{T}}\left[\boldsymbol{G}\left(\boldsymbol{m}^{k}\right)-\boldsymbol{d}\right]+\boldsymbol{\mu}_{\mathrm{a}} \boldsymbol{\sigma_{m}}^{-2}\left(\boldsymbol{m}^{k}-\boldsymbol{m}\right) \\ \boldsymbol{H}\left(\boldsymbol{m}^{k}\right) \approx\left(\boldsymbol{g}^{k}\right)^{\mathrm{T}} \boldsymbol{g}^{k}+\boldsymbol{\mu}_{\mathrm{a}} \boldsymbol{\sigma_{m}}^{-2} \boldsymbol{E} \end{array}\right. $ | (A-4) |
式中:gk=∂G(mk)/∂m表示对应正演问题的Fréchet导数矩阵(式(13)~式(15)),mk为模型第k次迭代结果;E为单位矩阵;Δm为扰动量。通过反复迭代,即可获得精确的波阻抗信息。
| [1] |
Castagna J P. Petrophysical imaging using AVO[J]. The Leading Edge, 1993, 12(3): 172-178. DOI:10.1190/1.1436939 |
| [2] |
Odebeatu E, Zhang J, Chapman M, et al. Application of spectral decomposition to detection of dispersion anomalies associated with gas saturation[J]. The Leading Edge, 2006, 25(2): 206-210. DOI:10.1190/1.2172314 |
| [3] |
赵万金, 杨午阳, 张巧凤, 等. 一种频率域AVO油气检测方法[J]. 石油地球物理勘探, 2012, 47(3): 436-441. ZHAO Wanjin, YANG Wuyang, ZHANG Qiaofeng, et al. A frequency AVO method for hydrocarbon detection[J]. Oil Geophysical Prospecting, 2012, 47(3): 436-441. |
| [4] |
陈学华, 贺振华, 黄德济, 等. 时频域油气储层低频阴影检测[J]. 地球物理学报, 2009, 52(1): 215-221. CHEN Xuehua, HE Zhenhua, HUANG Deji, et al. Low frequency shadow detection of gas reservoirs in time-frequency domain[J]. Chinese Journal of Geophysics, 2009, 52(1): 215-221. |
| [5] |
刘杰, 张懿疆, 王秀玲, 等. 利用反褶积广义S变换提取流体流度属性[J]. 石油地球物理勘探, 2019, 54(3): 617-623. LIU Jie, ZHANG Yijiang, WANG Xiuling, et al. Re-servoir fluid mobility extraction based on the deconvolution generalized S-transform[J]. Oil Geophysical Prospecting, 2019, 54(3): 617-623. |
| [6] |
张震, 印兴耀, 郝前勇. 基于AVO反演的频变流体识别方法[J]. 地球物理学报, 2014, 57(12): 4171-4184. ZHANG Zhen, YIN Xingyao, HAO Qianyong. Frequency-dependent fluid identification method based on AVO inversion[J]. Chinese Journal of Geophysics, 2014, 57(12): 4171-4184. DOI:10.6038/cjg20141228 |
| [7] |
罗鑫, 陈学华, 张杰, 等. 基于依赖频率AVO反演的高含气饱和度储层预测方法[J]. 石油地球物理勘探, 2019, 54(2): 356-364. LUO Xin, CHEN Xuehua, ZHANG Jie, et al. High gas-saturation reservoir prediction based on frequency-dependent AVO inversion[J]. Oil Geophysical Prospecting, 2019, 54(2): 356-364. |
| [8] |
White J E. Computed seismic speeds and attenuation in rocks with partial gas saturation[J]. Geophysics, 1975, 40(2): 224-232. DOI:10.1190/1.1440520 |
| [9] |
Johnson D L. Theory of frequency dependent acoustics in patchy-saturated porous media[J]. The Journal of the Acoustical Society of America, 2001, 110(2): 682-694. DOI:10.1121/1.1381021 |
| [10] |
李博南, 刘财, 郭智奇. 基于等效介质模型和频变AVO反演的裂缝储层参数估算方法[J]. 吉林大学学报(地球科学版), 2017, 47(1): 234-244. LI Bonan, LIU Cai, GUO Zhiqi. Estimation of fractured reservoir parameters based on equivalent media model and frequency-dependent AVO inversion[J]. Journal of Jilin University (Earth Science Edition), 2017, 47(1): 234-244. |
| [11] |
Ren H, Goloshubin G, Hilterman F J. Poroelastic analysis of permeability effects in thinly layered po-rous media[J]. Geophysics, 2009, 74(6): N49-N54. DOI:10.1190/1.3223185 |
| [12] |
Wilson A, Chapman M, and Li X Y. Frequency-depen-dent AVO inversion[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 341-345.
|
| [13] |
Smith G C, Gidlow P M. Weighted stacking for rock property estimation and detection of gas[J]. Geophy-sical Prospecting, 1987, 35(9): 993-1014. DOI:10.1111/j.1365-2478.1987.tb00856.x |
| [14] |
Partyka G, Gridley J, Lopez J. Interpretational applications of spectral decomposition in reservoir cha-racterization[J]. The Leading Edge, 1999, 18(3): 353-360. DOI:10.1190/1.1438295 |
| [15] |
Sinha S, Routh P S, Anno P D, et al. Spectral decomposition of seismic data with continuous-wavelet transform[J]. Geophysics, 2005, 70(6): P19-P25. DOI:10.1190/1.2127113 |
| [16] |
Stockwell R G, Mansinha L, Lowe R P. Localization of the complex spectrum: the S transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001. DOI:10.1109/78.492555 |
| [17] |
Burnett M D, Castagna J P, Méndez-Hernández E, et al. Application of spectral decomposition to gas basins in Mexico[J]. The Leading Edge, 2003, 22(11): 1130-1134. DOI:10.1190/1.1634918 |
| [18] |
程冰洁, 徐天吉, 李曙光. 频变AVO含气性识别技术研究与应用[J]. 地球物理学报, 2012, 55(2): 608-613. CHENG Bingjie, XU Tianji, LI Shuguang. Research and application of frequency dependent AVO analysis for gas recognition[J]. Chinese Journal of Geophy-sics, 2012, 55(2): 608-613. |
| [19] |
Wu X, Chapman M, Li X Y, et al. Quantitative gas saturation estimation by frequency-dependent amplitude-versus-offset analysis[J]. Geophysical Prospecting, 2014, 62(6): 1224-1237. DOI:10.1111/1365-2478.12179 |
| [20] |
张世鑫, 印兴耀, 张广智, 等. 纵波速度频散属性反演方法研究[J]. 石油物探, 2011, 50(3): 219-224. ZHANG Shixin, YIN Xingyao, ZHANG Guangzhi, et al. Inversion method for the velocity dispersion-dependent attribute of P-wave[J]. Geophysical Prospecting for Petroleum, 2011, 50(3): 219-224. DOI:10.3969/j.issn.1000-1441.2011.03.002 |
| [21] |
钟晗, 刘洋. 频变AVO影响因素分析[J]. 石油地球物理勘探, 2017, 52(4): 783-796. ZHONG Han, LIU Yang. Influence factors on frequency-dependent AVO[J]. Oil Geophysical Prospecting, 2017, 52(4): 783-796. |
| [22] |
Backus G E, Gilbert J F. Numerical applications of a formalism for geophysical inverse problems[J]. Geophysical Journal International, 1967, 13(1-3): 247-276. DOI:10.1111/j.1365-246X.1967.tb02159.x |
| [23] |
Kolsky H. The propagation of stress pulses in visco-elastic solids[J]. Philosophical Magazine, 1956. DOI:10.1080/14786435608238144 |
| [24] |
Futterman W I. Dispersive body waves[J]. Journal of Geophysical Research, 1962. DOI:10.1029/JZ067i013p05279 |
| [25] |
Oliveira S, Loures L, Moraes F, et al. Nonlinear impedance inversion for attenuating media[J]. Geophy-sics, 2009, 74(6): R111-R117. |
| [26] |
李远强, 霍志周, 李景叶, 等. 基于波动方程解析解的块约束广义声阻抗反演[J]. 石油地球物理勘探, 2020, 55(5): 1073-1083. LI Yuanqiang, HUO Zhizhou, LI Jingye, et al. Genera-lized impedance blocky inversion based on analytic solution to wave equation[J]. Oil Geophysical Prospecting, 2020, 55(5): 1073-1083. |
| [27] |
Masson Y J, Pride S R. Poroelastic finite difference modeling of seismic attenuation and dispersion due to mesoscopic-scale heterogeneity[J]. Journal of Geophysical Research, 2007, 112(12): 3-24. |
| [28] |
Sidler R, Rubino J G, Holliger K. Quantitative comparison between simulations of seismic wave propagation in heterogeneous poro-elastic media and equivalent visco-elastic solids for marine-type environments[J]. Geophysical Journal International, 2013, 193(1): 463-474. DOI:10.1093/gji/ggs125 |
| [29] |
Li Y, Li J, Song W, et al. Impedance inversion based on the analytical solution of wave equation with attenu-ation[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 744-748.
|
| [30] |
Buland A, Omre H. Bayesian linearized AVO inversion[J]. Geophysics, 2003, 68(1): 185-198. DOI:10.1190/1.1543206 |



 李远强, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院, 102249。Email:
李远强, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院, 102249。Email: 