② 长安大学地质工程与测绘学院地球物理系, 陕西西安 710054;
③ 哈利法科学与技术大学地球科学系, 阿布扎比 2533
② Institute of Geophysics, School of Geological Engineering and Geomatics, Chang'an University, Xi'an, Shaanxi 710054, China;
③ Department of Earth Sciences, Khalifa University of Science and Technology, Abu Dhabi 2533, UAE
地震波场数值模拟不仅是了解地震波传播规律和解释地震数据的重要工具,也是地震成像的基础。随着计算机技术快速发展,各种地震波场数值模拟算法日趋完善,如有限差分法[1]、有限元法[2]、边界元法[3]、伪谱法[4-5]、谱元法[6]、有限体积法[7]等。尽管3D波场数值解相对于2D更符合实际观测记录,然而巨大的内存需求和运算量使得实际3D大尺度波场数值模拟及波形反演面临计算资源的巨大挑战。因此,目前更多的实际应用则在2D或小尺度的3D空间开展,如逆时偏移成像[8]和全波形反演[9]。
虽然2D数值模拟相较于3D高效,但引入了线源假设代替实际的点源激发。这种线源假设意味着震源激发大小沿走向不变,模拟的波场也是2D,其结果很难与实际观测的3D地震记录相匹配[10-11]。当然可采用3D到2D地震数据转换方法,将实际的点源数据(3D)转换成线源数据(2D),但目前这些转换方法只适用于简单的地质模型,例如均匀介质和水平层状介质,并且需要满足远场近似和无波场重叠等苛刻条件[12],不利于实际复杂介质的成像。
鉴于此,为了克服2D波场模拟中线源假设带来的失真和3D波场模拟中效率低下的不足,人们提出了2.5D波场模拟方法[13]。2.5D地震波场数值模拟方法假设地质模型沿走向方向模型属性不变,因此可以沿走向方向做傅里叶变换将3D问题简化为重复的2D问题,从而大大提高了计算效率,且与3D解析解高度吻合[14]。如:Song等[13]在频率域通过有限差分法重构了3D地震波场;Zhou等[15]给出了精确的2.5D吸收边界条件,并采用有限元法得到了频率域2.5D波场数值解;Maokun等[16]则利用近似最佳正交有限差分算法进行了2.5D弹性波数值模拟;Takenaka等[17]给出了时间域平面波入射下2.5D弹性波动力学方程的求解过程;Novais等[18]改进了时间域2.5D地震波场有限差分数值模拟方法的波数采样方法。Xiong等[19]首先将空间域弹性波方程转换为波数域弹性波方程,然后采用交错网格有限差分求解波数域方程。
然而,上述时间域或频率域2.5D地震波场数值模拟方法只针对单一的弹性、黏弹性或各向异性介质,并没有一种较为普适的算法,即可同时满足不同介质属性(弹性、黏弹性、各向异性)和不同边界条件(声波自由地表,固体自由地表和固—液边界)下的2.5D波场数值模拟算法。本文提出一种适合复杂多种介质混合模型下时间域广义2.5D一阶波动方程及数值解法,适用于混合(声波、弹性各向同性、弹性各向异性)介质和各种边界条件(声波自由地表、固体自由地表和固—液边界)的地震波场数值模拟。
另一方面,为了适应复杂地表起伏模型中的数值模拟,本文采用曲网格进行模型剖分,并采用低频散、低耗散的同位网格MacCormack有限差分法格式[20]离散时间域广义2.5D一阶波动方程,从而得到高精度的数值解。最后,应用数值模拟算例验证了本文2.5D数值模拟方法的正确性和有效性。
1 时间域2.5D广义一阶速度—应力波动方程首先建立广义2.5D一阶速度—应力波动方程,并分析该方程的普适性问题。2.5D地震波场数值模拟是3D地震波场数值模拟的一种特殊情况,其假设地质模型沿走向(y方向)具有不变的物理性质,则2.5D地震波动方程可以通过对3D地震波动方程沿y方向做傅里叶变换得到[21]。
1.1 弹性各向异性介质波动方程三维弹性各向异性介质中,地震波的控制方程[22]为
| $ \rho \ddot{u}_{j}=\sigma_{i j, i}+F_{j} $ | (1) |
式中:ρ表示密度;uj和Fj分别为位移和震源的j方向分量;j为uj关于时间t的二阶导数;σij为应力张量,σij, i为σij关于i方向的偏导数;i、j为x、y或z。根据胡克定理,有
| $ \mathit{\boldsymbol{\sigma }} = \mathit{\boldsymbol{cu}} $ | (2) |
式中c为刚度矩阵。假设地质模型沿y方向物理性质不变,且有速度与位移的关系vj=
| $ \left\{\begin{array}{l} \dot{\widetilde{v}}_{x}=\frac{\tilde{\sigma}_{x x, x}+\tilde{\sigma}_{x z, z}+\mathrm{i} k_{y} \tilde{\sigma}_{x y}+\tilde{s}_{x}}{\rho} \\ \dot{\tilde{v}}_{y}=\frac{\tilde{\sigma}_{x y, x}+\tilde{\sigma}_{y z, z}+\mathrm{i} k_{y} \tilde{\sigma}_{y y}+\tilde{s}_{y}}{\rho} \\ \dot{\widetilde{v}}_{z}=\frac{{\tilde{\sigma}_{x z, x}}{+\tilde{\sigma}_{z z, z}}+\mathrm{i} k_{y} \tilde{\sigma}_{y z}+\tilde{s}_{z}} {\rho} \end{array}\right. $ | (3) |
和
| $ \left\{\begin{array}{l} \begin{aligned} \dot{\tilde{\sigma}}_{x x}=&c_{11} \tilde{v}_{x, x}+c_{15} \widetilde{v}_{x, z}+c_{16} \tilde{v}_{y, x}+c_{14} \widetilde{v}_{y, z}+c_{15} \tilde{v}_{z, x}+ \\ & c_{13} \tilde{v}_{z, z}+\mathrm{i} k_{y}\left(c_{16} \tilde{v}_{x}+c_{12} \widetilde{v}_{y}+c_{14} \tilde{v}_{z}\right) \end{aligned}\\ \begin{aligned} \dot{\tilde{\sigma}}_{x y}=&c_{16} \widetilde{v}_{x, x}+c_{56} \widetilde{v}_{x, z}+c_{66} \widetilde{v}_{y, x}+c_{46} \widetilde{v}_{y, z}+c_{56} \widetilde{v}_{z, x}+ \\ &c_{36} \widetilde{v}_{z, z}+\mathrm{i} k_{y}\left(c_{66} \widetilde{v}_{x}+c_{26} \widetilde{v}_{y}+c_{46} \widetilde{v}_{z}\right) \end{aligned}\\ \begin{aligned} \dot{\tilde{\sigma}}_{y y}=&c_{12} \tilde{v}_{x, x}+c_{25} \tilde{v}_{x, z}+c_{26} \tilde{v}_{y, x}+c_{24} \widetilde{v}_{y, z}+c_{25} \tilde{v}_{z, x}+ \\ &c_{23} \tilde{v}_{z, z}+\mathrm{i} k_{y}\left(c_{26} \tilde{v}_{x}+c_{22} \tilde{v}_{y}+c_{24} \tilde{v}_{z}\right) \end{aligned}\\ \begin{aligned} \dot{\widetilde{\sigma}}_{x z}=&c_{15} \widetilde{v}_{x, x}+c_{55} \widetilde{v}_{x, z}+c_{56} \widetilde{v}_{y, x}+c_{45} \widetilde{v}_{y, z}+c_{55} \widetilde{v}_{z, x}+\\ &c_{35} \widetilde{v}_{z, z}+\mathrm{i} k_{y}\left(c_{56} \widetilde{v}_{x}+c_{25} \widetilde{v}_{y}+c_{45} \widetilde{v}_{z}\right)\\ \dot{\widetilde{\sigma}}_{y z}=&c_{14} \widetilde{v}_{x, x}+c_{45} \widetilde{v}_{x, z}+c_{46} \widetilde{v}_{y, x}+c_{44} \widetilde{v}_{y, z}+c_{45} \widetilde{v}_{z, x}+\\ &c_{34} \tilde{v}_{z, z}+\mathrm{i} k_{y}\left(c_{46} \tilde{v}_{x}+c_{24} \tilde{v}_{y}+c_{44} \widetilde{v}_{z}\right)\\ \dot{\widetilde{\sigma}}_{z z}=&c_{13} \widetilde{v}_{x, x}+c_{35} \widetilde{v}_{x, z}+c_{36} \widetilde{v}_{y, x}+c_{34} \widetilde{v}_{y, z}+c_{35} \widetilde{v}_{z, x}+\\ &c_{33} \tilde{v}_{z, z}+\mathrm{i} k_{y}\left(c_{36} \widetilde{v}_{x}+c_{23} \tilde{v}_{y}+c_{34} \widetilde{v}_{z}\right) \end{aligned} \end{array}\right. $ | (4) |
式中:
| $ \left\{\begin{array}{l} \tilde{\boldsymbol{v}}=\left(\widetilde{v}_{x}, \widetilde{v}_{y}, \widetilde{v}_{z}\right)^{\mathrm{T}} \\ \tilde{\boldsymbol{s}}=\frac{1}{\rho}\left(\tilde{s}_{x}, \tilde{s}_{y}, \tilde{s}_{z}\right)^{\mathrm{T}} \\ \tilde{\boldsymbol{\sigma}}_{1}=\left(\tilde{\sigma}_{x x}, \tilde{\sigma}_{x y}, \tilde{\sigma}_{y y}\right)^{\mathrm{T}} \\ \tilde{\boldsymbol{\sigma}}_{2}=\left(\tilde{\sigma}_{x z}, \tilde{\sigma}_{y z}, \tilde{\sigma}_{z z}\right)^{\mathrm{T}} \\ \tilde{\boldsymbol{Y}}^{(\mathrm{S})}=\left(\tilde{\boldsymbol{v}}^{\mathrm{T}}, \tilde{\boldsymbol{\sigma}}_{1}^{\mathrm{T}}, \tilde{\boldsymbol{\sigma}}_{2}^{\mathrm{T}}\right)^{\mathrm{T}} \\ \tilde{\boldsymbol{s}}{}^{(\mathrm{S})}=(\tilde{\boldsymbol{s}}, 0,0)^{\mathrm{T}} \end{array}\right. $ | (5) |
式中上标“(S)”表示弹性各向同性或弹性各向异性的固体介质。式(3)和式(4)可简写为矩阵形式
| $ \dot{\tilde{\boldsymbol{Y}}}{}^{(\mathrm{S})}=\boldsymbol{A}^{(\mathrm{S})} \partial_{x} \tilde{\boldsymbol{Y}}{}^{(\mathrm{S})}+\boldsymbol{B}^{(\mathrm{S})} \partial_{z} \tilde{\boldsymbol{Y}}{}^{(\mathrm{S})}+\boldsymbol{C}^{(\mathrm{S})} \tilde{\boldsymbol{Y}}{}^{(\mathrm{S})}+\tilde{\boldsymbol{s}}^{(\mathrm{S})} $ | (6) |
上式为任意弹性各向异性介质中的2.5D地震波控制方程,系数矩阵A(S)、B(S)、C(S)的具体表达式见附录A。
1.2 声波介质波动方程在声波介质中,应力满足切向应力为零和法向应力的轴向分量等于液体压力
| $ \sigma_{i j}=-\delta_{i j} P $ | (7) |
P可表示为
| $ P=-K u_{j, j}+s(t) \delta\left(\boldsymbol{x}-\boldsymbol{x}_{\mathrm{s}}\right) $ | (8) |
式中:K为体积模量;s(t)为xs处的震源函数。将式(7)代入式(1),可得
| $ \dot{v}_{j}=-\frac{P_{, j}}{\rho} $ | (9) |
对式(8)求时间导数,可得
| $ \dot{P}=-K v_{j, j}+\dot{s}(t) \delta\left(\boldsymbol{x}-\boldsymbol{x}_{\mathrm{s}}\right) $ | (10) |
根据式(9),式(10)可以表示为
| $ \dot{P}=-K\left(\partial_{x} v_{x}+\partial_{y} v_{y}+\partial_{z} v_{z}\right)+\dot{s}(t) \delta\left(\boldsymbol{x}-\boldsymbol{x}_{\mathrm{s}}\right) $ | (11) |
对式(9)和式(11)做关于y的傅里叶变换,可得
| $ \left\{\begin{array}{l} \dot{\tilde{v}}_{x}=-\frac{\partial_{x} \widetilde{P}}{\rho} \\ \dot{\tilde{v}}_{y}=-\frac{\mathrm{i} k_{y} \widetilde{P}}{\rho} \\ \dot{\tilde{v}}_{z}=-\frac{\partial_{z} \widetilde{P}}{\rho} \end{array}\right. $ | (12) |
| $ \dot{\widetilde{P}}=-K\left(\partial_{x} {\widetilde{v}}_{x}+\mathrm{i} k_{y} {\tilde{v}}_{y}+\partial_{z} \widetilde{v}_{z}\right)+\dot{\widetilde{s}}(t) \delta\left(x-x_{\mathrm{s}}\right) $ | (13) |
定义
| $ \left\{\begin{array}{l} \tilde{\boldsymbol{Y}}{}^{(\mathrm{W})}=\left(\widetilde{v}_{x}, \widetilde{v}_{y}, \tilde{v}_{z}, \widetilde{P}\right)^{\mathrm{T}} \\ \tilde{\boldsymbol{s}}{}^{(\mathrm{W})}=\left[0,0,0, \dot{\widetilde{s}}(t) \delta\left(\boldsymbol{x}-\boldsymbol{x}_{\mathrm{s}}\right)\right]^{\mathrm{T}} \end{array}\right. $ | (14) |
可得式(12)和式(13)的矩阵形式
| $ \dot{\tilde{\boldsymbol{Y}}}{}^{(\mathrm{W})}=\boldsymbol{A}^{(\mathrm{W})} \partial_{x} \tilde{\boldsymbol{Y}}{}^{(\mathrm{W})}+\boldsymbol{B}^{(\mathrm{W})} \partial_{z} \tilde{\boldsymbol{Y}}{}^{(\mathrm{W})}+\boldsymbol{C}^{(\mathrm{W})} \tilde{\boldsymbol{Y}}{}^{(\mathrm{W})}+\tilde{\boldsymbol{s}}{}^{(\mathrm{W})} $ | (15) |
式中:上标“(W)”表示声波介质;系数矩阵A(W)、B(W)、C(W)的具体表达式见附录B。上式为声波介质中的2.5D地震波控制方程。
1.3 声波自由地表声波自由地表边界条件需要满足地表处液体压力P=0,代入式(12)和式(13),可得
| $ \left\{\begin{array}{l} \dot{\tilde{v}}_{x}=-\frac{\partial_{x} \widetilde{P}}{\rho} \\ \dot{\tilde{v}}_{y}=0 \\ \dot{\tilde{v}}_{z}=-\frac{-\partial_{z} \widetilde{P}}{\rho} \\ \dot{\tilde{P}}=0 \end{array}\right. $ | (16) |
| $ \begin{aligned} \dot{\tilde{\boldsymbol{Y}}}{}^{(\mathrm{AW})}=& \boldsymbol{A}^{(\mathrm{AW})} \partial_{x} \tilde{\boldsymbol{Y}}{}^{(\mathrm{AW})}+\boldsymbol{B}^{(\mathrm{AW})} \partial_{z} \tilde{\boldsymbol{Y}}{}^{(\mathrm{AW})}+\\ & \boldsymbol{C}^{(\mathrm{AW})} \tilde{\boldsymbol{Y}}{}^{(\mathrm{AW})}+\tilde{\boldsymbol{s}}{}^{(\mathrm{AW})} \end{aligned} $ | (17) |
式中:上标“(AW)”表示声波自由地表;系数矩阵A(AW)、B(AW)、C(AW)分别为
| $ \boldsymbol{A}^{(\mathrm{AW})}=-\rho^{-1}\left(\begin{array}{llll} 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right) $ | (18) |
| $ \boldsymbol{B}^{(\text {AW })}=-\rho^{-1}\left(\begin{array}{llll} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{array}\right) $ | (19) |
| $ \boldsymbol{C}^{(\text {AW })}=\bf{0} $ | (20) |
对比式(18)~式(20)与附录B,可以发现式(17)是式(15)的特例。
1.4 固体自由地表固体自由地表边界条件需要满足地表处法向应力为0,即
| $ \boldsymbol{\sigma} \cdot \boldsymbol{n}=0 $ | (21) |
展开为
| $ \left\{\begin{array}{l} \sigma_{x x} n_{1}+\sigma_{x y} n_{2}+\sigma_{x z} n_{3}=0 \\ \sigma_{x y} n_{1}+\sigma_{y y} n_{2}+\sigma_{y z} n_{3}=0 \\ \sigma_{x z} n_{1}+\sigma_{y z} n_{2}+\sigma_{z z} n_{3}=0 \end{array}\right. $ | (22) |
式中n =(n1,n2,n3)表示界面的法向向量。将式(22)写成矩阵形式
| $ \left(\begin{array}{cccccc} n_{1} & n_{2} & 0 & n_{3} & 0 & 0 \\ 0 & n_{1} & n_{2} & 0 & n_{3} & 0 \\ 0 & 0 & 0 & n_{1} & n_{2} & n_{3} \end{array}\right)\left(\begin{array}{l} \sigma_{x x} \\ \sigma_{x y} \\ \sigma_{y y} \\ \sigma_{x z} \\ \sigma_{y z} \\ \sigma_{z z} \end{array}\right)=0 $ | (23) |
将上式写为子矩阵格式
| $ \boldsymbol{\varGamma}_{2} \boldsymbol{\sigma}_{2}=-\boldsymbol{\varGamma}_{1} \boldsymbol{\sigma}_{1} $ | (24) |
式中
| $ \left\{\begin{array}{l} \boldsymbol{\sigma}_{1}=\left(\sigma_{x x}, \sigma_{x y}, \sigma_{y y}\right) \\ \boldsymbol{\sigma}_{2}=\left(\sigma_{x z}, \sigma_{y z}, \sigma_{z z}\right) \end{array}\right. $ | (25) |
| $ \left\{\begin{array}{l} \boldsymbol{\varGamma}_{1}=\left(\begin{array}{lll} n_{1} & n_{2} & 0 \\ 0 & n_{1} & n_{2} \\ 0 & 0 & 0 \end{array}\right) \\ \boldsymbol{\varGamma}_{2}=\left(\begin{array}{ccc} n_{3} & 0 & 0 \\ 0 & n_{3} & 0 \\ n_{1} & n_{2} & n_{3} \end{array}\right) \end{array}\right. $ | (26) |
定义
| $ \begin{aligned} \boldsymbol{S} &=-\boldsymbol{\varGamma}_{2}^{-1} \boldsymbol{\varGamma}_{1} \\ &=\left(\begin{array}{ccc} n_{3}^{-1} & 0 & 0 \\ 0 & n_{3}^{-1} & 0 \\ -n_{1} n_{3}^{-2} & -n_{2} n_{3}^{-2} & n_{3}^{-1} \end{array}\right)\left(\begin{array}{ccc} n_{1} & n_{2} & 0 \\ 0 & n_{1} & n_{2} \\ 0 & 0 & 0 \end{array}\right) \\ &=\left(\begin{array}{ccc} -n_{1} n_{3}^{-1} & -n_{2} n_{3}^{-1} & 0 \\ 0 & -n_{1} n_{3}^{-1} & -n_{2} n_{3}^{-1} \\ n_{1}^{2} n_{3}^{-2} & 2 n_{1} n_{2} n_{3}^{-2} & n_{2}^{2} n_{3}^{-2} \end{array}\right) \end{aligned} $ | (27) |
式(23)可改写为
| $ \boldsymbol{\sigma}_{2}=\boldsymbol{S} \boldsymbol{\sigma}_{1} $ | (28) |
由上式可知,应力分量σ2可由σ1和表面法向分量n得到,只有应力分量σ1未知。假设自由地表由z=z0(x)给出,其坡度为tanα=z0′(x),法向分量为n =(-sinα, 0, cosα),则式(27)变为
| $ \boldsymbol{S}=\left(\begin{array}{ccc} z_{0}^{\prime}(x) & 0 & 0 \\ 0 & z_{0}^{\prime}(x) & 0 \\ {\left[z_{0}^{\prime}(x)\right]^{2}} & 0 & 0 \end{array}\right) $ | (29) |
根据式(28)和式(29)可得
| $ \left\{\begin{array}{l} \dot{\boldsymbol{\sigma}}_{2}=\boldsymbol{S}\dot{\boldsymbol{\sigma}}_{1} \\ \partial_{x} \boldsymbol{\sigma}_{2}=\partial_{x} \boldsymbol{S} \boldsymbol{\sigma}_{1}+\boldsymbol{S} \partial_{x} \boldsymbol{\sigma}_{1} \\ \partial_{z} \boldsymbol{\sigma}_{2}=\boldsymbol{S} \partial_{z} \boldsymbol{\sigma}_{1} \end{array}\right. $ | (30) |
将上式代入式(3),可得
| $ \left\{\begin{aligned} \dot{\tilde{v}}_{x}=&\left[\tilde{\sigma}_{x x, x}+z_{0}^{\prime}(x) \tilde{\sigma}_{x x, z}+\mathrm{i} k_{y} \tilde{\sigma}_{x y}+\tilde{s}_{x}\right] / \rho \\ \dot{\tilde{v}}_{y}=&\left[\tilde{\sigma}_{x y, x}+z_{0}^{\prime}(x) \tilde{\sigma}_{x y, z}+\mathrm{i} k_{y} \tilde{\sigma}_{y y}+\tilde{s}_{y}\right] / \rho \\ \dot{\tilde{v}}_{z}=&\left\{z_{0}^{\prime}(x) \tilde{\sigma}_{x x, x}+\left[z_{0}^{\prime}(x)\right]^{2} \tilde{\sigma}_{x x, z}+\right.\\ &\left.\mathrm{i} k_{y} z_{0}^{\prime}(x) \tilde{\sigma}_{x y}+z_{0}^{\prime \prime}(x) \tilde{\sigma}_{x x}+\tilde{s}_{z}\right\} / \rho \end{aligned}\right. $ | (31) |
由式(4)可得
| $ \left\{\begin{array}{l} \dot{\widetilde{\sigma}}_{x x}=c_{11} \tilde{v}_{x, x}+c_{15} \tilde{v}_{x, z}+c_{16} \widetilde{v}_{y, x}+c_{14} \widetilde{v}_{y, z}+c_{15} \widetilde{v}_{z, x}+c_{13} \widetilde{v}_{z, z}+\mathrm{i} k_{y}\left(c_{16} \widetilde{v}_{x}+c_{12} \widetilde{v}_{y}+c_{14} \widetilde{v}_{z}\right) \\ \dot{\widetilde{\sigma}}_{x y}=c_{16} \widetilde{v}_{x, x}+c_{56} \widetilde{v}_{x, z}+c_{66} \widetilde{v}_{y, x}+c_{46} \widetilde{v}_{y, z}+c_{56} \widetilde{v}_{z, x}+c_{36} \widetilde{v}_{z, z}+\mathrm{i} k_{y}\left(c_{66} \widetilde{v}_{x}+c_{26} \widetilde{v}_{y}+c_{46} \widetilde{v}_{z}\right) \\ \dot{\widetilde{\sigma}}_{y y}=c_{12} \widetilde{v}_{x, x}+c_{25} \widetilde{v}_{x, z}+c_{26} \widetilde{v}_{y, x}+c_{24} \widetilde{v}_{y, z}+c_{25} \widetilde{v}_{z, x}+c_{23} \widetilde{v}_{z, z}+\mathrm{i} k_{y}\left(c_{26} \widetilde{v}_{x}+c_{22} \widetilde{v}_{y}+c_{24} \widetilde{v}_{z}\right) \end{array}\right. $ | (32) |
定义
| $ \left\{\begin{array}{l} \tilde{\boldsymbol{Y}}{}^{(\mathrm{AS})}=\left(\widetilde{v}_{x}, \widetilde{v}_{y}, \widetilde{v}_{z}, \tilde{\sigma}_{x x}, \tilde{\sigma}_{x y}, \tilde{\sigma}_{y y}\right)^{\mathrm{T}} \\ \tilde{\boldsymbol{s}}{}^{(\mathrm{AS})}=\rho^{-1}\left(\tilde{s}_{x}, \tilde{s}_{y}, \tilde{s}_{z}, 0,0,0\right)^{\mathrm{T}} \end{array}\right. $ | (33) |
则式(30)和式(31)可简写为
| $ \begin{gathered} \dot{\tilde{\boldsymbol{Y}}}{}^{(\mathrm{AS})}=\boldsymbol{A}^{(\mathrm{AS})} \partial_{x} \tilde{\boldsymbol{Y}}{}^{(\mathrm{AS})}+\boldsymbol{B}^{(\mathrm{AS})} \partial_{z} \tilde{\boldsymbol{Y}}{}^{(\mathrm{AS})}+ \\ \boldsymbol{C}^{(\mathrm{AS})} \tilde{\boldsymbol{Y}}{}^{(\mathrm{AS})}+\tilde{\boldsymbol{s}}{}^{(\mathrm{AS})} \end{gathered} $ | (34) |
式中:上标“(AS)”表示固体自由地表边界;系数矩阵A(W)、B(W)、C(W)的具体表达式见附录C。式(34)为固体自由地表处的2.5D地震波控制方程。与式(5)、式(6)相比,式(33)、式(34) 根据固体自由地表边界条件消除了应力分量
在固—液边界上,例如由z=z0(x)定义的二维海底界面,边界条件需要满足法向应力和法向速度分量连续,并且切向应力分量为0,即
| $ \tilde{\boldsymbol{\sigma}}\left[t, x, z_{0}(x)\right] \cdot \boldsymbol{n}=-\widetilde{P}\left[t, x, z_{0}(x)\right] \cdot \boldsymbol{n} $ | (35) |
| $ \tilde{\boldsymbol{v}}{}^{(\mathrm{S})}\left[t, x, z_{0}(x)\right] \cdot \boldsymbol{n}=\tilde{\boldsymbol{v}}{}^{(\mathrm{W})}\left[t, x, z_{0}(x)\right] \cdot \boldsymbol{n} $ | (36) |
| $ \left\{\begin{array}{l} \tilde{\boldsymbol{\sigma}}\left[t, x, z_{0}(x)\right] \cdot \boldsymbol{\tau}^{(1)}=0 \\ \tilde{\boldsymbol{\sigma}}\left[t, x, z_{0}(x)\right] \cdot \boldsymbol{\tau}^{(2)}=0 \end{array}\right. $ | (37) |
式中:
| $ \left\{\begin{array}{l} \boldsymbol{\tau}^{(1)}=(0,1,0)^{\mathrm{T}} \\ \boldsymbol{\tau}^{(2)}=(\cos \alpha, 0, \sin \alpha)^{\mathrm{T}} \end{array}\right. $ | (38) |
将式(38)代入(37),可得
| $ \left\{\begin{array}{l} \tilde{\sigma}_{12}=\tilde{\sigma}_{22}=\tilde{\sigma}_{23}=0 \\ \tilde{\sigma}_{11}=-z^{\prime}{}_{0}(x) \tilde{\sigma}_{13} \\ \tilde{\sigma}_{13}=-z^{\prime}{}_{0}(x) \tilde{\sigma}_{33} \end{array}\right. $ | (39) |
式(39)表明只有
| $ \tilde{\sigma}_{33}=\frac{-1}{1+\left[z_{0}^{\prime}(x)\right]^{2}} \widetilde{P} $ | (40) |
上式说明
| $ \dot{\tilde{P}}=-\left\{1+\left[z_{0}^{\prime}(x)\right]^{2}\right\} \dot{\widetilde{\sigma}}_{33} $ | (41) |
为了表示简单,假设固液边界上没有施加震源,将式(4)和式(13)代入(41),可得
| $ \begin{aligned} &\partial_{x} \tilde{v}_{x}^{(\mathrm{W})}+\mathrm{i} k_{y} \tilde{v}_{y}^{(\mathrm{W})}+\partial_{z} \tilde{v}_{z}^{(\mathrm{W})} \\ &=\frac{1+\left[z_{0}^{\prime}(x)\right]^{2}}{K}\left[\left(c_{13}, c_{36}, c_{35}\right) \cdot \partial_{x} \tilde{\boldsymbol{v}}^{(\mathrm{S})}+\right. \\ &\left.\left(c_{35}, c_{34}, c_{33}\right) \cdot \partial_{x} \tilde{\boldsymbol{v}}^{(\mathrm{S})}+\mathrm{i} k_{y}\left(c_{36}, c_{23}, c_{34}\right) \cdot \tilde{\boldsymbol{v}}^{(\mathrm{S})}\right] \end{aligned} $ | (42) |
上式对于任意ky成立,可得
| $ \tilde{v}_{y}^{(\mathrm{W})}=\frac{1+\left[z_{0}^{\prime}(x)\right]^{2}}{K}\left[c_{36} \widetilde{v}_{x}^{(\mathrm{S})}+c_{23} \widetilde{v}_{y}^{(\mathrm{S})}+c_{34} \widetilde{v}_{z}^{(\mathrm{S})}\right] $ | (43) |
由式(35)可知
| $ \widetilde{v}_{z}^{(\mathrm{W})}=z_{0}^{\prime}(x)\left[\widetilde{v}_{x}^{(\mathrm{W})}-\widetilde{v}_{x}^{(\mathrm{S})}\right]+\widetilde{v}_{z}^{(\mathrm{S})} $ | (44) |
式(43)和式(44)表明液体侧速度分量
将式(42)代入式(4),可得
| $ \begin{aligned} &\dot{\tilde{P}}=-\left\{1+\left[z_{0}^{\prime}(x)\right]^{2}\right\}\left[\left(c_{13}, c_{36}, c_{35}\right) \cdot \partial_{x} \tilde{\boldsymbol{v}}^{(\mathrm{S})}+\right. \\ &\left.\left(c_{35}, c_{34}, c_{33}\right) \cdot \partial_{z} \tilde{\boldsymbol{v}}^{(\mathrm{S})}+\mathrm{i} k_{y}\left(c_{36}, c_{23}, c_{34}\right) \cdot \tilde{\boldsymbol{v}}^{(\mathrm{S})}\right] \end{aligned} $ | (45) |
将式(39)和式(40)代入式(3),可得
| $ \left\{\begin{array}{l} \dot{\widetilde{v}}_{x}^{(\mathrm{S})}=\rho_{\mathrm{S}}^{-1} \frac{z_{0}^{\prime}(x)}{\left[z_{0}^{\prime}(x)\right]^{2}+1}\left\{-z_{0}^{\prime}(x) \partial_{x} \widetilde{P}+\right. \\ \ \ \ \ \ \ \ \ \ \ \ \left.\partial_{z} \widetilde{P}+\frac{-2 z_{0}^{\prime \prime}(x)}{\left[z_{0}^{\prime}(x)\right]^{2}+1} \widetilde{P}\right\} \\ \dot{v}_{y}^{(\mathrm{S})}=\rho_{\mathrm{S}}^{-1}\left[-z_{0}^{\prime}(x) \partial_{z} \tilde{\sigma}_{12}+\partial_{z} \tilde{\sigma}_{23}\right] \\ \dot{v}_{z}^{(\mathrm{S})}=\rho_{\mathrm{S}}^{-1} \frac{1}{\left[z_{0}^{\prime}(x)\right]^{2}+1}\left\{-z_{0}^{\prime}(x) \partial_{x} \widetilde{P}-\right. \\ \ \ \ \ \ \ \ \ \ \ \ \left.\partial_{z} \widetilde{P}+\frac{-z_{0}^{\prime \prime}(x)\left[1-\left(z_{0}^{\prime}(x)\right)^{2}\right]}{\left[z_{0}^{\prime}(x)\right]^{2}+1}\widetilde{P}\right\} \end{array}\right. $ | (46) |
式中ρS为固体密度。由式(12)可知
| $ \dot{\tilde{v}}{}_{x}^{(\mathrm{W})}=\rho_{\mathrm{W}}^{-1}\left(-\partial_{x} \widetilde{P}\right) $ | (47) |
式中ρW为液体密度。定义
| $ \left\{\begin{array}{l} \tilde{\boldsymbol{Y}}{}^{(\mathrm{WS})}=\left[\tilde{\boldsymbol{v}}^{(\mathrm{WS})}, \tilde{\mathrm{P}}, \tilde{\sigma}_{12}, \tilde{\sigma}_{23}\right]^{\mathrm{T}} \\ \tilde{\boldsymbol{v}}{}^{(\mathrm{WS})}=\left[\widetilde{v}_{x}^{(\mathrm{W})}, \widetilde{v}_{x}^{(\mathrm{S})}, \widetilde{v}_{y}^{(\mathrm{S})}, \widetilde{v}_{z}^{(\mathrm{S})}\right] \\ \tilde{\boldsymbol{s}}{}^{(\mathrm{WS})}=\left\{\begin{array}{l} {\left[0,0,0,0, \dot{\widetilde{s}}(t) \delta\left(\boldsymbol{x-x}_{s}\right), 0,0\right]^{\mathrm{T}}(\text { 液体中 })} \\ \left(0, \tilde{s}_{x}, \tilde{s}_{y}, \tilde{s}_{z}, 0,0,0\right)^{\mathrm{T}} \text { (固体中) } \end{array}\right. \end{array}\right. $ | (48) |
将式(45)~式(47)写成矩阵形式
| $ \begin{gathered} \dot{\tilde{\boldsymbol{Y}}}{}^{(\mathrm{WS})}=\boldsymbol{A}^{(\mathrm{WS})} \partial_{x} \tilde{\boldsymbol{Y}}{}^{(\mathrm{WS})}+\boldsymbol{B}^{(\mathrm{WS})} \partial_{z} \tilde{\boldsymbol{Y}}{}^{(\mathrm{WS})}+ \\ \boldsymbol{C}^{(\mathrm{WS})} \tilde{\boldsymbol{Y}}{}^{(\mathrm{WS})}+\tilde{\boldsymbol{s}}{}^{(\mathrm{WS})} \end{gathered} $ | (49) |
式中:上标“(WS)”表示固—液体边界;系数矩阵A(WS)、B(WS)、C(WS)的具体表达式见附录D。求解式(49)后,固液边界固体侧应力分量
至此,获得了2.5D广义一阶速度—应力波动方程
| $ \dot{\tilde{\boldsymbol{Y}}}=\boldsymbol{A} \partial_{x} \tilde{\boldsymbol{Y}}+\boldsymbol{B} \partial_{z} \tilde{\boldsymbol{Y}}+{\boldsymbol{C}}\tilde{\boldsymbol{Y}}+\tilde{\boldsymbol{s}} $ | (50) |
式中的各个参量可根据不同介质或不同边界条件而有所不同。
2 曲线网格有限差分算法 2.1 曲线坐标系与直角坐标系的转换关系为了使网格线与物理空间的边界线重合,避免传统矩形网格由于阶梯状近似产生的虚假散射问题,应用曲线网格(贴体网格)对地质模型进行剖分,然后将实际的非规则物理空间变换到一个规则的计算空间[23]。假设物理空间的坐标(x, z)和计算空间的坐标(ξ, η)之间映射关系(图 1)为
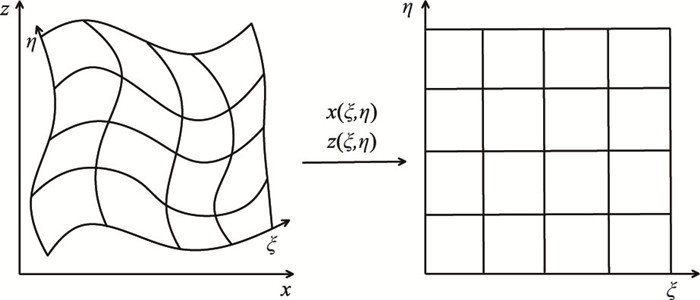
|
图 1 曲线网格和计算网格的变换关系示意图 |
| $ \left\{\begin{array}{l} x=x(\xi, \eta) \\ z=z(\xi, \eta) \end{array}\right. $ | (51) |
由链式求导法则可得
| $ \left\{\begin{array}{l} 1=x_{, \xi} \xi_{, x}+x_{, \eta} \eta_{, x} \\ 0=x_{, \xi} \xi_{, z}+x_{, \eta} \eta_{, z} \\ 0=z_{, \xi} \xi_{, x}+z_{, \eta} \eta_{, x} \\ 1=z_{, \xi} \xi_{, z}+z_{, \eta} \eta_{, z} \end{array}\right. $ | (52) |
整理可得到坐标转换系数
| $ \left\{\begin{array}{l} \xi_{, x}=\frac{1}{J} z_{, \eta} \\ \xi_{, z}=-\frac{1}{J} x_{, \eta} \\ \eta_{, x}=-\frac{1}{J} z_{, \xi} \\ \eta_{, z}=\frac{1}{J} x_{, \xi} \end{array}\right. $ | (53) |
式中J=x, ξz, η-x, ηz, ξ。为了避免网格非均匀引发的虚假震源项,x, ξ、x, η、z, ξ、z, η均采用数值方法计算,所采用的数值法与下文求解波动方程空间导数的数值算法相同。
2.2 曲线坐标系中的广义一阶速度—应力波动方程根据求导的链式法则,广义一阶速度—应力弹性波方程的矩阵形式在曲线坐标系中的表达式为
| $ \begin{aligned} \dot{\tilde{\boldsymbol{Y}}}=&\left(\partial_{x} \xi \boldsymbol{A}+\partial_{z} \xi \boldsymbol{B}\right) \partial_{\xi} \tilde{\boldsymbol{Y}}+\\ &\left(\partial_{x} \eta \boldsymbol{A}+\partial_{z} \eta \boldsymbol{B}\right) \partial_{\eta} \widetilde{\boldsymbol{Y}}+\boldsymbol{C} \widetilde{\boldsymbol{Y}}+\widetilde{\boldsymbol{s}} \end{aligned} $ | (54) |
Hixon等[24]采用Tam等[25]提出的DRP (Dispersion Relation Preserving)方法对同位MacCormack格式的系数进行了优化,得到了低频散、低耗散的DRP/opt MacCormack格式,本文采用该格式有限差分算子离散方程。
同位网格MacCormack格式的两个偏心差分格式——向前和向后差分格式分别为
| $ L_{\xi}^{\mathrm{F}}(\tilde{\boldsymbol{Y}})_{i}=\frac{1}{\Delta \xi} \sum\limits_{j=-1}^{3} a_{j} \tilde{\boldsymbol{Y}}_{i+j} $ | (55) |
| $ L_{\mathtt{ξ}}^{\mathrm{B}}(\tilde{\boldsymbol{Y}})_{i}=\frac{1}{\Delta \xi} \sum\limits_{j=-1}^{3}-a_{j} \tilde{\boldsymbol{Y}}_{i-j} $ | (56) |
差分系数为
| $ \left\{\begin{array}{l} a_{-1}=-0.30874 \\ a_{0}=-0.63260 \\ a_{1}=1.23300 \\ a_{2}=-0.33340 \\ a_{3}=0.04168 \end{array}\right. $ | (57) |
采用DRP/opt MacCormack有限差分格式,式(54)空间导数可以离散为
| $ \left\{\begin{array}{l} \hat{L}{}^{\mathrm{FF}}(\tilde{\boldsymbol{Y}})=\left(\partial_{x} \xi \boldsymbol{A}+\partial_{z} \xi \boldsymbol{B}\right) L_{\xi}^{\mathrm{F}}(\tilde{\boldsymbol{Y}})+\left(\partial_{x} \eta \boldsymbol{A}+\partial_{z} \eta \boldsymbol{B}\right) L_{\eta}^{\mathrm{F}}(\tilde{\boldsymbol{Y}}) \\ \hat{L}{}^{\mathrm{BB}}(\tilde{\boldsymbol{Y}})=\left(\partial_{x} \xi \boldsymbol{A}+\partial_{z} \xi \boldsymbol{B}\right) L_{\xi}^{\mathrm{B}}(\tilde{\boldsymbol{Y}})+\left(\partial_{x} \eta \boldsymbol{A}+\partial_{z} \eta \boldsymbol{B}\right) L_{\eta}^{\mathrm{B}}(\tilde{\boldsymbol{Y}}) \\ \hat{L}{}^{\mathrm{FB}}(\tilde{\boldsymbol{Y}})=\left(\partial_{x} \xi \boldsymbol{A}+\partial_{z} \xi \boldsymbol{B}\right) L_{\xi}^{\mathrm{F}}(\tilde{\boldsymbol{Y}})+\left(\partial_{x} \eta \boldsymbol{A}+\partial_{z} \eta \boldsymbol{B}\right) L_{\eta}^{\mathrm{B}}(\tilde{\boldsymbol{Y}}) \\ \hat{L}{}^{\mathrm{BF}}(\tilde{\boldsymbol{Y}})=\left(\partial_{x} \xi \boldsymbol{A}+\partial_{z} \xi \boldsymbol{B}\right) L_{\xi}^{\mathrm{B}}(\tilde{\boldsymbol{Y}})+\left(\partial_{x} \eta \bf{A}+\partial_{z} \eta \boldsymbol{B}\right) L_{\eta}^{\mathrm{F}}(\tilde{\boldsymbol{Y}}) \end{array}\right. $ | (58) |
在时间方向上采用四阶Runge-Kutta法[26],结合DRP/opt MacCormack有限差分算子,波场可以从时间步长第N步更新到第N+4步[20],具体过程如下。
第一步,已知
| $ \left\{\begin{array}{l} \boldsymbol{h}^{(1)}=\Delta t \hat{L}{}^{\mathrm{FF}}\left(\tilde{\boldsymbol{Y}}{}^{N}\right) \\ \boldsymbol{h}^{(2)}=\Delta t \hat{L}{}^{\mathrm{BB}}\left[\tilde{\boldsymbol{Y}}{}^{N}+\alpha_{1} \boldsymbol{h}^{(1)}\right] \\ \boldsymbol{h}^{(3)}=\Delta t \hat{L}{}^{\mathrm{FF}}\left[\tilde{\boldsymbol{Y}}{}^{N}+\alpha_{2} \boldsymbol{h}^{(2)}\right] \\ \boldsymbol{h}^{(4)}=\Delta t \hat{L}{}^{\mathrm{BB}}\left[\tilde{\boldsymbol{Y}}{}^{N}+\alpha_{3} \boldsymbol{h}^{(3)}\right] \\ \tilde{\boldsymbol{Y}}{}^{N+1}=\tilde{\boldsymbol{Y}}{}^{N}+\beta_{1} \boldsymbol{h}^{(1)}+\beta_{2} \boldsymbol{h}^{(2)}+\beta_{3} \boldsymbol{h}^{(3)}+\beta_{4} \boldsymbol{h}^{(4)} \end{array}\right. $ | (59) |
第二步,已知
| $ \left\{\begin{array}{l} \boldsymbol{h}^{(1)}=\Delta t \hat{L}{}^{\mathrm{FB}}\left(\tilde{\boldsymbol{Y}}{}^{N+1}\right) \\ \boldsymbol{h}^{(2)}=\Delta t \hat{L}{}^{\mathrm{BF}}\left[\tilde{\boldsymbol{Y}}{}^{N+1}+\alpha_{1} \boldsymbol{h}^{(1)}\right] \\ \boldsymbol{h}^{(3)}=\Delta t \hat{L}{}^{\mathrm{FB}}\left[\tilde{\boldsymbol{Y}}{}^{N+1}+\alpha_{2} \boldsymbol{h}^{(2)}\right] \\ \boldsymbol{h}^{(4)}=\Delta t \hat{L}{}^{\mathrm{BF}}\left[\tilde{\boldsymbol{Y}}{}^{N+1}+\alpha_{3} \boldsymbol{h}^{(3)}\right] \\ \tilde{\boldsymbol{Y}}{}^{N+2}=\tilde{\boldsymbol{Y}}{}^{N+1}+\beta_{1} \boldsymbol{h}^{(1)}+\beta_{2} \boldsymbol{h}^{(2)}+\beta_{3} \boldsymbol{h}^{(3)}+\beta_{4} \boldsymbol{h}^{(4)} \end{array}\right. $ | (60) |
第三步,已知
| $ \left\{\begin{array}{l} \boldsymbol{h}^{(1)}=\Delta t \hat{L}{}^{\mathrm{BB}}\left(\tilde{\boldsymbol{Y}}{}^{N+2}\right) \\ \boldsymbol{h}^{(2)}=\Delta t \hat{L}{}^{\mathrm{FF}}\left[\tilde{\boldsymbol{Y}}{}^{N+2}+\alpha_{1} \boldsymbol{h}^{(1)}\right] \\ \boldsymbol{h}^{(3)}=\Delta t \hat{L}{}^{\mathrm{BB}}\left[\tilde{\boldsymbol{Y}}{}^{N+2}+\alpha_{2} \boldsymbol{h}^{(2)}\right] \\ \boldsymbol{h}^{(4)}=\Delta t \hat{L}{}^{\mathrm{FF}}\left[\tilde{\boldsymbol{Y}}{}^{N+2}+\alpha_{3} \boldsymbol{h}^{(3)}\right] \\ \tilde{\boldsymbol{Y}}{}^{N+3}=\tilde{\boldsymbol{Y}}{}^{N+2}+\beta_{1} \boldsymbol{h}^{(1)}+\beta_{2} \boldsymbol{h}^{(2)}+\beta_{3} \boldsymbol{h}^{(3)}+\beta_{4} \boldsymbol{h}^{(4)} \end{array}\right. $ | (61) |
第四步,已知
| $ \left\{\begin{array}{l} \boldsymbol{h}^{(1)}=\Delta t \hat{L}{}^{\mathrm{BF}}\left(\tilde{\boldsymbol{Y}}{}^{{N}+3}\right) \\ \boldsymbol{h}^{(2)}=\Delta t \hat{L}{}^{\mathrm{FB}}\left[\tilde{\boldsymbol{Y}}{}^{{N}+3}+\alpha_{1} \boldsymbol{h}^{(1)}\right] \\ \boldsymbol{h}^{(3)}=\Delta t \hat{L}{}^{\mathrm{BF}}\left[\tilde{\boldsymbol{Y}}{}^{{N}+3}+\alpha_{2} \boldsymbol{h}^{(2)}\right] \\ \boldsymbol{h}^{(4)}=\Delta t \hat{L}{}^{\mathrm{FB}}\left[\tilde{\boldsymbol{Y}}{}^{{N}+3}+\alpha_{3} \boldsymbol{h}^{(3)}\right] \\ \tilde{\boldsymbol{Y}}{}^{{N}+4}=\tilde{\boldsymbol{Y}}{}^{{N}+3}+\beta_{1} \boldsymbol{h}^{(1)}+\beta_{2} \boldsymbol{h}^{(2)}+\beta_{3} \boldsymbol{h}^{(3)}+\beta_{4} \boldsymbol{h}^{(4)} \end{array}\right. $ | (62) |
式中:α1=0.5;α2=0.5;α3=1.0;β1=1/6;β2=1/3;β3=1/3;β4=1/6。
3 震源、人工边界和波数域采样 3.1 震源和吸收边界本文在网格点上施加集中力源,并使用Ricker子波做为震源
| $ s(t)=\left[1-2 {\rm{ \mathit{ π} }}^{2} f_{\mathrm{c}}^{2}\left(t-t_{0}\right)^{2}\right] \exp \left[-{\rm{ \mathit{ π} }}^{2} f_{\mathrm{c}}^{2}\left(t-t_{0}\right)^{2}\right] $ | (63) |
式中:震源中心频率fc=30Hz;延迟时间t0=30ms。为了消除人工边界产生的边界反射,本文采用新近提出的广义刚度衰减法(The Generalized Stiffness Reduction Method,GSRM)[27],吸收效果优于最佳匹配层方法,适用于各种介质,如声波介质、各向同性和各向异性介质。
3.2 波数域采样方法采用曲线网格有限差分法求解式(54),可得到ky域地震波波场在离散时刻tN=NΔt的数值解
| $ \begin{aligned} \boldsymbol{Y}\left(t_{{N}}, x, y, z\right) \approx & \frac{2 k_{y}^{\mathrm{c}}}{{\rm{ \mathit{ π} }}\left(M_{k y}-1\right)} \sum\limits_{m=1}^{M_{k y}} \tilde{\boldsymbol{Y}}\left(t_{{N}}, x, k_{y}^{m}, z\right) \mathrm{e}^{\mathrm{i} k_{y}^{m} y} \\ & k_{y}^{m} \in\left[-k_{y}^{\mathrm{c}}, k_{y}^{\mathrm{c}}\right] \end{aligned} $ | (64) |
式中:kyc=π/Δx;Mky=Mx,其中Δx和Mx分别为x方向网格离散间距和网格点数[18]。
根据波场向量Y的定义,速度分量(
| $ v_{i j}\left(t_{N}, x, y, z\right)= \begin{cases}\frac{k_{y}^{\mathrm{c}}}{{\rm{ \mathit{ π} }}\left(N_{k y}-1\right)} \sum\limits_{m=1}^{M_{k y}} \tilde{v}_{i j}\left(t_{N}, x, k_{y}^{m}, z\right) \cos \left(k_{y}^{m} y\right) & i+j \text { 为偶数 } \\ \frac{k_{y}^{\mathrm{c}}}{{\rm{ \mathit{ π} }}\left(N_{k y}-1\right)} \sum\limits_{m=1}^{M_{k y}} {\rm{i}}\tilde{v}_{i j}\left(t_{N}, x, k_{y}^{m}, z\right) \sin \left(k_{y}^{m} y\right) & i+j \text { 为奇数 }\end{cases} $ | (65) |
式中vij表示施加i方向集中力源时得到的j方向速度分量。
同理,声波介质中ky域压力
| $ \begin{gathered} P\left(t_{N}, x, y, z\right)=\frac{k_{y}^{\mathrm{c}}}{{\rm{ \mathit{ π} }}\left(M_{k y}-1\right)} \times \\ \sum\limits_{m=1}^{M_{k y}} \widetilde{P}\left(t_{N}, x, k_{y}^{m}, z\right) \cos \left(k_{y}^{m} y\right) \end{gathered} $ | (66) |
为了检验本文2.5D波场数值模拟方法的正确性和计算效率,同时考虑到所提方法的普适性,本文选择三个(声波、弹性各向同性和弹性VTI-1)地表水平均匀介质模型进行试算,2D模型尺寸为500m×500m,3D模型尺寸为500m×500m×500m。分别将模拟的2.5D数值解与3D解析解[22, 28]、3D数值解进行对比,3D数值解采用本文相同的数值方法求解3D声波方程和弹性波方程得到。三个均匀介质模型的网格剖分间距Δx=Δy=Δz=2m,震源位于模型中心,检波器位于(100m,0,100m)。三个模型的主要弹性参数如表 1所示,其余参数根据介质性质可由主要参数导出。对于各向同性弹性介质,c12=c13=c23= c11-2c44,c22=c33=c11,c55=c66=c44;对于VTI-1介质,c12=c11-2c66,c13=c23=c11-2c44,c22=c33=c11,c55=c44;对于VTI-2介质,c12=c11-2c66,c22=c11,c23=c13,c55=c44。VTI-1和VTI-2介质是Vavryčuk[28]为了得到解析解而给出的两种简化各向异性介质。
|
|
表 1 介质弹性参数 |
图 2为三个地表水平均匀介质模型的2.5D数值解的波场快照,从图中可以清晰地看到波场的P、S波波前。为了验证本文方法模拟得到的2.5D数值解的计算精度和正确性,将2.5D数值解与对应的3D解析解及3D数值解进行对比(图 3),三者匹配良好,验证了本文算法的计算精度和正确性。
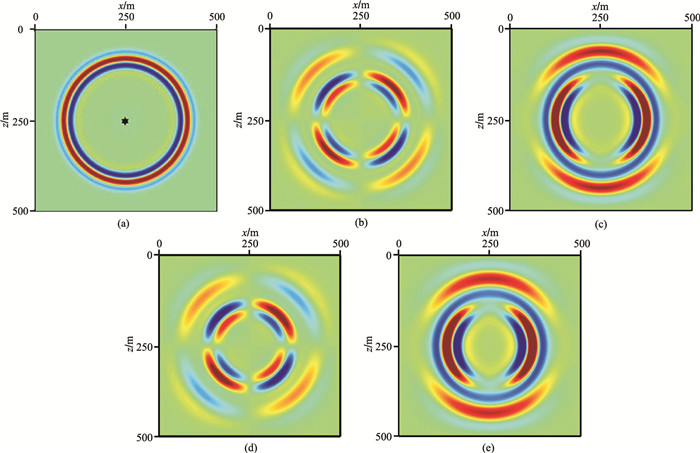
|
图 2 地表水平均匀介质模型2.5D模拟的波场快照 (a)声波介质的P分量,0.15s;(b)、(c)分别为各向同性介质的vx和vz分量,0.09s;(d)、(e)分别为VTI-1介质的中vx和vz分量,0.08s |
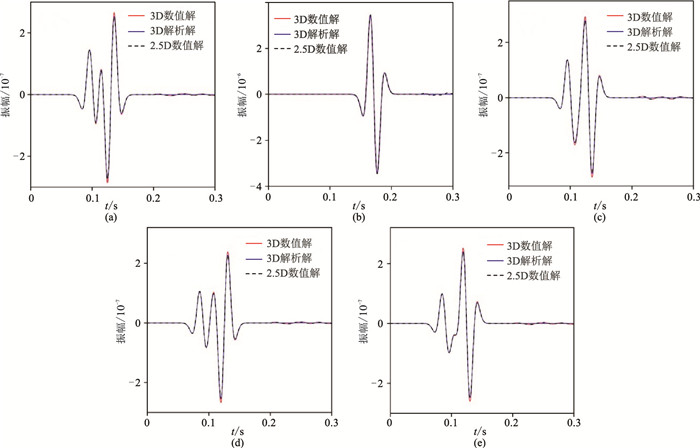
|
图 3 地表水平均匀介质模型2.5D数值解与3D数值解、3D解析解的对比 (a)声波介质中P分量;(b)、(c)分别为各向同性介质的vx和vz分量;(d)、(e)分别为VTI-1介质的vx和vz分量 |
2.5D与3D数值模拟计算机内存占用和CPU运行时间的对比如表 2所示,可以看出,2.5D数值模拟所需CPU时间和计算机内存都远小于3D,特别是计算机内存。所以本文的2.5D波场数值模拟方法则具有较高的实际应用价值,可以直接应用于地震数据反演方法。
|
|
表 2 2.5 D与3D数值模拟用时和内存占用对比 |
应用起伏地表声波、弹性各向同性和弹性VTI-1均匀介质模型(图 4)验证本文施加自由地表边界算法的正确性。网格剖分间距Δx=Δz=2m,震源位于(500m,400m),检波器位于(300m,500m),模型参数见表 1。
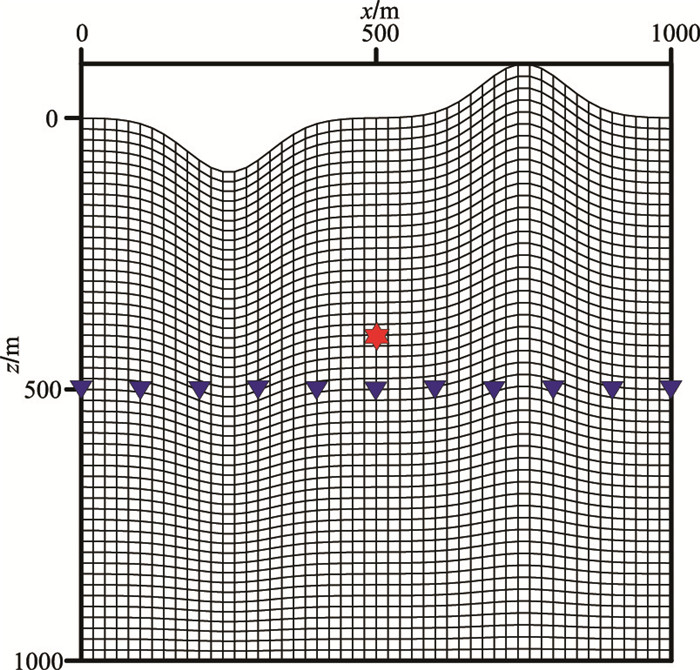
|
图 4 模型网格剖分示意图 红星和蓝三角分别为震源和检波器 |
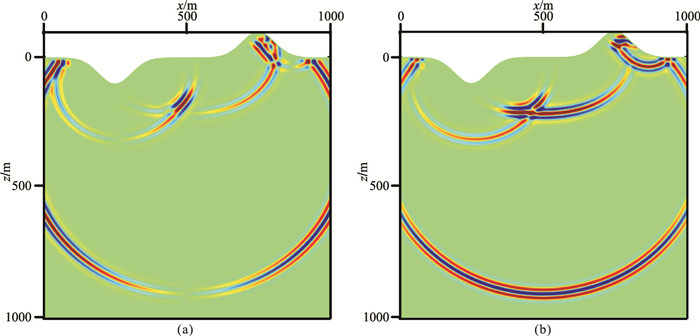
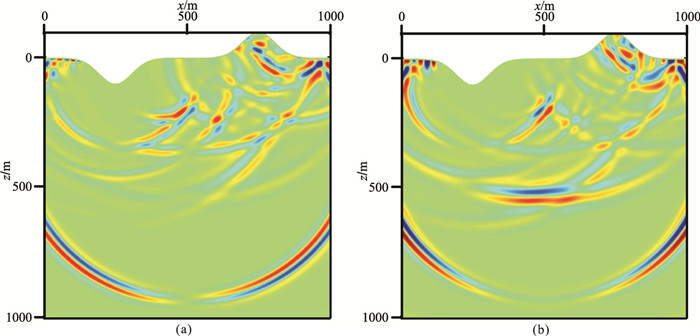
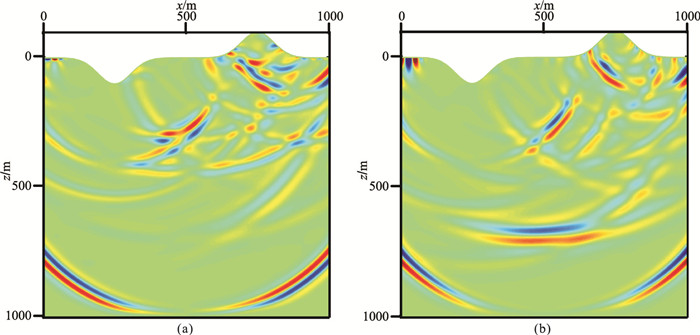
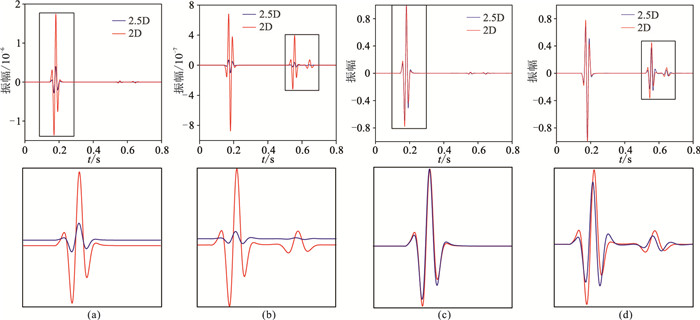
图 5、图 6、图 7分别为起伏地表声波、弹性各向同性和弹性VTI-1均匀介质模型的2.5D数值解的vx和vz分量波场快照,从中可以清楚地看到直达P波及自由地表产生的反射波。图 8、图 9、图 10为三个起伏地表模型2.5D与2D数值解的波形对比,其中2D数值解是令式(50)中ky=0后采用本文相同方法获得。2.5D数值解和2D数值解之间不仅存在着明显的振幅差异,还存在相移。
|
图 5 起伏地表声波均匀介质模型2.5D数值解vx(a)和vz(b)分量在0.4s的波场快照 |
|
图 6 起伏地表各向同性均匀弹性介质模型2.5D数值解vx(a)和vz(b)分量在0.32s的波场快照 |
|
图 7 起伏地表均匀VTI-1介质模型2.5D数值解vx(a)和vz(b)分量在0.32s的波场快照 |
|
图 8 起伏地表声波均匀介质模型2.5D与2D数值解对比 (a)vx分量;(b)vz分量;(c)图a的归一化显示;(d)图b的归一化显示。下图为上图方框的放大显示 |
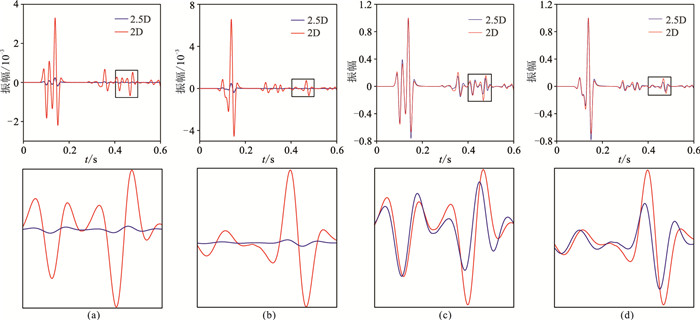
|
图 9 起伏地表均匀各向同性弹性介质模型2.5D与2D数值解的对比 (a)vx分量;(b)vz分量;(c)图a的归一化显示;(d)图b的归一化显示。下图为上图方框的放大显示 |
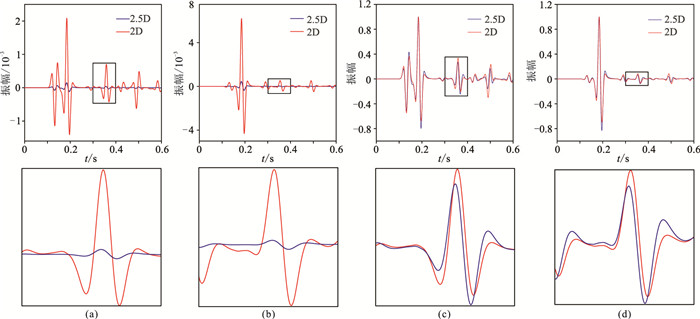
|
图 10 起伏地表均匀VTI-1介质模型2.5D与2D数值解的对比 (a)vx分量;(b)vz分量;(c)图a的归一化显示;(d)图b的归一化显示。下图为上图方框的放大显示 |
建立一个正弦起伏固—液耦合界面模型(图 11)验证本文的2.5D数值模拟方法适用性。模型尺寸为1000m×1000m,网格间距为2m,第一层为声波介质,第二次为各向同性介质(参数见表 1)。震源位于(500m,300m),5个检波器等间距布置于(300m,0m)与(300m,400m)之间。图 11为2.5D数值解的0.28s时刻波场照,从图中可以观察到直达P波经过固—液界面产生了清晰的透射P波和S波;图 12是2.5D与2D数值解的波形对比,可以看出2.5D与2D数值解之间同样存在着明显的振幅差异和相移现象。
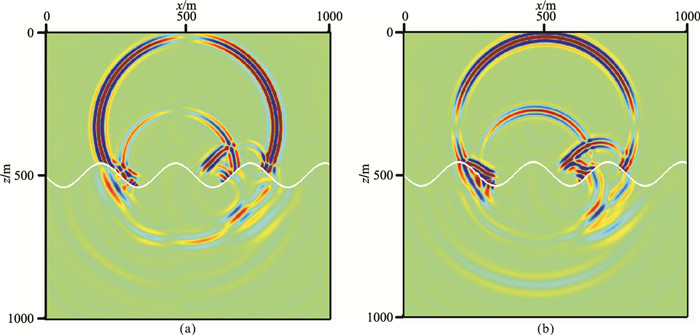
|
图 11 固—液耦合模型2.5D数值解vx(a)和vz(b)分量在0.28s的波场快照 图中起伏曲线为正弦起伏界面 |
|
图 12 固—液耦合模型2.5D与2D数值解波形对比 (a)vx分量;(b)vz分量 |
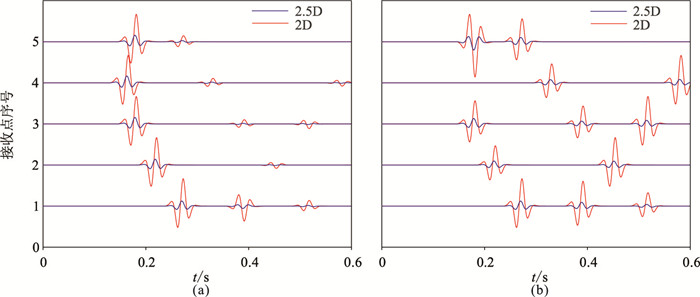
为了检验本文2.5D波场数值模拟方法对于复杂介质的适用性,选择一个三层模型(图 13)进行实验。该模型第一层为声波介质(水),第二层为弹性各向同性介质,第三层为VTI弹性介质(VTI-2),各层弹性参数见表 1。震源位于(1000m,450m);三个检波器分别位于(500m,200m)、(500m,500m)、(500m,800m),每层各有一个。图 14为三层模型2.5D数值解vx分量在不同时刻的波场快照,可以看出清晰的反射波、转换波、透射波和多次波。由图 14a、图 14b可以看出,当P波和S波到达固—液边界时,透射和转换后的P波出现在第一层(声波介质)中,而反射和转换后的P波和SV波在第二层(各向同性介质)中向下传播;在第三层(VTI-2介质)中出现P波和S波穿过固—固界面产生的透射和转换波。由图 14c~图 14f可以发现,当波传播到自由表面产生了反射的P波,在第二层介质中出现了清晰的多次波。图 15、图 16、图 17分别为三个检波器的2.5D与2D模拟记录对比,可以看出,无论检波器位于何种介质中,二者存在明显的振幅差异和相移。
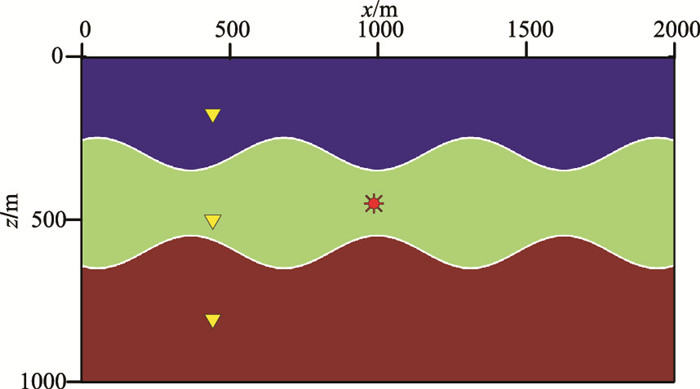
|
图 13 三层模型示意图 星和三角分别表示震源和接收器点位置 |
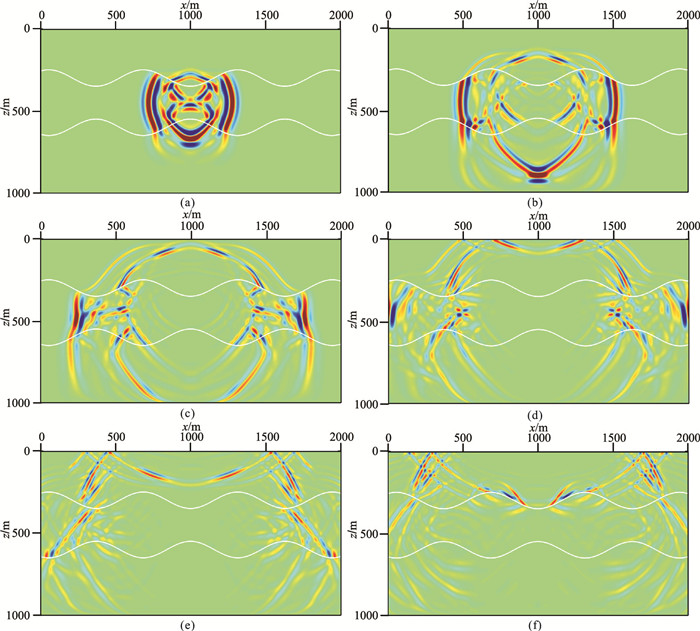
|
图 14 三层模型2.5D数值解vx分量在不同时刻的波场快照 (a)0.12s;(b)0.20s;(c)0.28s;(d)0.36s;(e)0.44s;(f)0.52s |
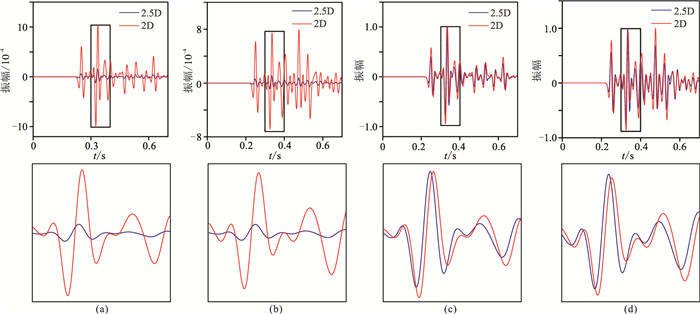
|
图 15 三层模型第一个检波器的2.5D与2D数值模拟记录对比 (a)vx分量;(b)vz分量;(c)图a的归一化显示;(d)图b的归一化显示。下图为上图方框的放大显示 |
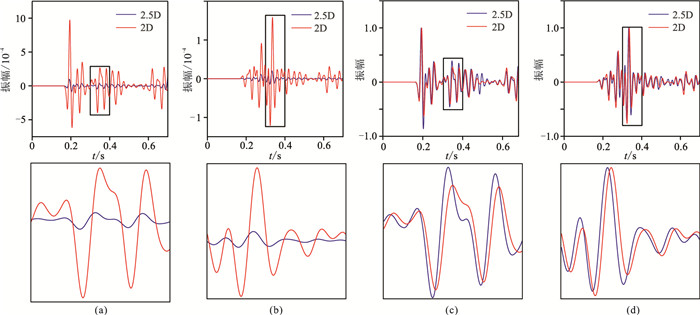
|
图 16 三层模型第二个检波器的2.5D与2D数值模拟记录对比 (a)vx分量;(b)vz分量;(c)图a的归一化显示;(d)图b的归一化显示。下图为上图方框的放大显示 |
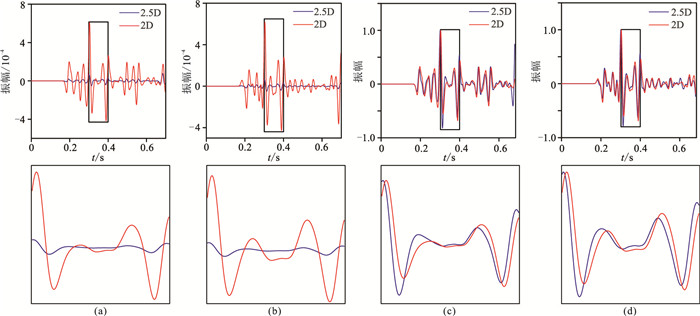
|
图 17 三层模型第三个检波器的2.5D与2D数值模拟记录对比 (a)vx分量;(b)vz分量;(c)图a的归一化显示;(d)图b的归一化显示。下图为上图方框的放大显示 |
三层混合模型模拟结果表明,本文方法适用于复杂介质2.5D地震波数值模拟。
6 结论本文通过推导、整理得到了一个矩阵形式的2.5D广义一阶速度—应力波动方程,该方程不仅适用于声波介质和一般各向异性介质,而且适用于不同的边界条件(声波自由地表、固体自由地表和固—液边界条件)。通过定义不同的波场矢量,并根据模型离散点介质参数的变化给出了三个系数矩阵,在压力或应力矢量上施加点源后采用数值方法求解,可以用一个计算机程序实现复杂介质中的2D或2.5D地震波场数值模拟。为了更好地贴合起伏地形,本文选择曲线网格有限差分法求解波动方程,数值模拟实验表明,在不同的介质中本文方法模拟得到的2.5D数值解与3D解析解非常匹配,并且适用于不同的边界条件。除此之外,本文验证了2.5D数值方法的计算效率远优于3D数值方法。这种2.5D数值模拟方法可以直接用于实际点源地震数据的逆时偏移成像。
附录A 弹性各向异性介质中波动方程的系数矩阵将式(3)、式(4)写成矩阵形式,则式(6)中的系数矩阵可表示为
| $ \boldsymbol{A}^{(\mathrm{S})}=\left(\begin{array}{ccc} 0 & \boldsymbol{U}_{1} & \boldsymbol{U}_{2} \\ \boldsymbol{W}_{1} & 0 & 0 \\ \boldsymbol{W}_{4} & 0 & 0 \end{array}\right) $ | (A-1) |
| $ \boldsymbol{B}^{(\mathrm{S})}=\left(\begin{array}{ccc} 0 & 0 & \boldsymbol{U}_{3} \\ \boldsymbol{W}_{2} & 0 & 0 \\ \boldsymbol{W}_{5} & 0 & 0 \end{array}\right) $ | (A-2) |
| $ \boldsymbol{C}^{(\mathrm{S})}=\left(\begin{array}{ccc} 0 & \boldsymbol{U}_{4} & \boldsymbol{U}_{5} \\ \boldsymbol{W}_{3} & 0 & 0 \\ \boldsymbol{W}_{6} & 0 & 0 \end{array}\right) $ | (A-3) |
式中
| $ \boldsymbol{U}_{1}=\rho^{-1}\left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array}\right) $ | (A-4) |
| $ \boldsymbol{U}_{2}=\rho^{-1}\left(\begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \end{array}\right) $ | (A-5) |
| $ \boldsymbol{U}_{3}=\rho^{-1}\left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right) $ | (A-6) |
| $ \boldsymbol{U}_{4}={\rm{i}} k_{y} \rho^{-1}\left(\begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{array}\right) $ | (A-7) |
| $ \boldsymbol{U}_{5}=\mathrm{i} k_{y} \rho^{-1}\left(\begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 1 & 0 \end{array}\right) $ | (A-8) |
| $ \boldsymbol{W}_{1}=\left(\begin{array}{ccc} c_{11} & c_{16} & c_{15} \\ c_{16} & c_{66} & c_{56} \\ c_{12} & c_{26} & c_{25} \end{array}\right) $ | (A-9) |
| $ \boldsymbol{W}_{2}=\left(\begin{array}{lll} c_{15} & c_{14} & c_{13} \\ c_{56} & c_{46} & c_{36} \\ c_{25} & c_{24} & c_{23} \end{array}\right) $ | (A-10) |
| $ \boldsymbol{W}_{3}=\mathrm{i} k_{y}\left(\begin{array}{ccc} c_{16} & c_{12} & c_{14} \\ c_{66} & c_{26} & c_{46} \\ c_{26} & c_{22} & c_{24} \end{array}\right) $ | (A-11) |
| $ \boldsymbol{W}_{4}=\left(\begin{array}{lll} c_{15} & c_{56} & c_{55} \\ c_{14} & c_{46} & c_{45} \\ c_{13} & c_{36} & c_{35} \end{array}\right) $ | (A-12) |
| $ \boldsymbol{W}_{5}=\left(\begin{array}{lll} c_{55} & c_{45} & c_{35} \\ c_{45} & c_{44} & c_{34} \\ c_{35} & c_{34} & c_{33} \end{array}\right) $ | (A-13) |
| $ \boldsymbol{W}_{6}=\mathrm{i} k_{y}\left(\begin{array}{ccc} c_{56} & c_{25} & c_{45} \\ c_{46} & c_{24} & c_{44} \\ c_{36} & c_{23} & c_{34} \end{array}\right) $ | (A-14) |
将式(12)和式(13)写成矩阵形式,则式(15)的系数矩阵为
| $ \boldsymbol{A}^{(\mathrm{W})}=\left(\begin{array}{cccc} 0 & 0 & 0 & -\rho^{-1} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ -K & 0 & 0 & 0 \end{array}\right) $ | (B-1) |
| $ \boldsymbol{B}^{(\mathrm{W})}=\left(\begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & -\rho^{-1} \\ 0 & 0 & -K & 0 \end{array}\right) $ | (B-2) |
| $ \boldsymbol{C}^{(\mathrm{W})}=-\mathrm{i} k_{y}\left(\begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & \rho^{-1} \\ 0 & 0 & 0 & 0 \\ 0 & K & 0 & 0 \end{array}\right) $ | (B-3) |
将式(31)和式(32)写成矩阵形式,则式(34)系数矩阵可表示为
| $ \boldsymbol{A}^{(\mathrm{AS})} =\left(\begin{array}{cc} 0 & \boldsymbol{A}_{1}^{(\mathrm{AS})} \\ \boldsymbol{A}_{2}^{(\mathrm{AS})} & 0 \end{array}\right) $ | (C-1) |
| $ \boldsymbol{B}^{(\mathrm{AS})} =\left(\begin{array}{cc} 0 & \boldsymbol{B}_{1}^{(\mathrm{AS})} \\ \boldsymbol{B}_{2}^{(\mathrm{AS})} & 0 \end{array}\right) $ | (C-2) |
| $ \boldsymbol{C}^{(\mathrm{AS})} =\left(\begin{array}{cc} 0 & \boldsymbol{C}_{1}^{(\mathrm{AS})} \\ \boldsymbol{C}_{2}^{(\mathrm{AS})} & 0 \end{array}\right) $ | (C-3) |
式中:
| $ \boldsymbol{A}_{1}^{(\mathrm{AS})}=\rho^{-1}\left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ \partial_{x} z_{0} & 0 & 0 \end{array}\right) $ | (C-4) |
| $ \boldsymbol{A}_{2}^{(\mathrm{AS})}=\left(\begin{array}{ccc} c_{11} & c_{16} & c_{15} \\ c_{16} & c_{66} & c_{56} \\ c_{12} & c_{26} & c_{26} \end{array}\right) $ | (C-5) |
| $ \boldsymbol{B}_{1}^{(\mathrm{AS})}=\rho^{-1}\left(\begin{array}{ccc} \partial_{x} z_{0} & 0 & 0 \\ 0 & \partial_{x} z_{0} & 0 \\ \left(\partial_{x} z_{0}\right)^{2} & 0 & 0 \end{array}\right) $ | (C-6) |
| $ \boldsymbol{B}_{2}^{(\mathrm{AS})}=\left(\begin{array}{ccc} c_{15} & c_{14} & c_{13} \\ c_{56} & c_{46} & c_{36} \\ c_{25} & c_{24} & c_{23} \end{array}\right) $ | (C-7) |
| $ \boldsymbol{C}_{1}^{(\mathrm{AS})}=\rho^{-1}\left(\begin{array}{ccc} 0 & \mathrm{i} k_{y} & 0 \\ 0 & 0 & \mathrm{i} k_{y} \\ \partial_{x x} z_{0} & \mathrm{i} k_{y} \partial_{x} z_{0} & 0 \end{array}\right) $ | (C-8) |
| $ \boldsymbol{C}_{2}^{(\mathrm{AS})}=\mathrm{i} k_{y}\left(\begin{array}{lll} c_{16} & c_{12} & c_{14} \\ c_{66} & c_{26} & c_{46} \\ c_{26} & c_{22} & c_{24} \end{array}\right) $ | (C-9) |
将式(45)~式(47)联合写成一个矩阵形式,可导出式(49)的系数矩阵,为
| $ \boldsymbol{A}^{(\mathrm{WS})} =\left(\begin{array}{cc} \bf{0} & \boldsymbol{A}_{1}^{(\mathrm{WS})} \\ \boldsymbol{A}_{2}^{(\mathrm{WS})} & \bf{0} \end{array}\right) $ | (D-1) |
| $ \boldsymbol{B}^{(\mathrm{WS})} =\left(\begin{array}{cc} \bf{0} & \boldsymbol{B}_{1}^{(\mathrm{WS})} \\ \boldsymbol{B}_{2}^{(\mathrm{WS})} & \bf{0} \end{array}\right) $ | (D-2) |
| $ \boldsymbol{C}^{(\mathrm{WS})} =\left(\begin{array}{cc} \bf{0} & \boldsymbol{C}_{1}^{(\mathrm{WS})} \\ \boldsymbol{C}_{2}^{(\mathrm{WS})} & \bf{0} \end{array}\right) $ | (D-3) |
式中:
| $ \boldsymbol{A}_{1}^{(\mathrm{WS})}=\left(\begin{array}{ccc} -\rho_{\mathrm{w}}^{-1} & 0 & 0 \\ \frac{-\rho_{\mathrm{s}}^{-1}\left(\partial_{x} z_{0}\right)^{2}}{\left(\partial_{x} z_{0}\right)^{2}+1} & 0 & 0 \\ 0 & 0 & 0 \\ \frac{-\rho_{\mathrm{s}}^{-1} \partial_{x} z_{0}}{\left(\partial_{x} z_{0}\right)^{2}+1} & 0 & 0 \end{array}\right) $ | (D-4) |
| $ \boldsymbol{A}_{2}^{(\mathrm{WS})}=-K\left(\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right) $ | (D-5) |
| $ \boldsymbol{B}_{1}^{(\mathrm{WS})}=\rho_{\mathrm{s}}^{-1}\left(\begin{array}{ccc} 0 & 0 & 0 \\ \frac{\partial_{x} z_{0}}{\left(\partial_{x} z_{0}\right)^{2}+1} & 0 & 0 \\ 0 & -\partial_{x} z_{0} & 1 \\ \frac{-1}{\left(\partial_{x} z_{0}\right)^{2}+1} & 0 & 0 \end{array}\right) $ | (D-6) |
| $ \boldsymbol{B}_{2}^{(\mathrm{WS})}=K\left(\begin{array}{cccc} -\partial_{x} z_{0} & \partial_{x} z_{0} & 0 & -1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right) $ | (D-7) |
| $ \boldsymbol{C}_{1}^{(\mathrm{WS})}=\frac{-\rho_{\mathrm{s}}^{-1}}{\left[\left(\partial_{x} z_{0}\right)^{2}+1\right]^{2}}\left(\begin{array}{ccc} 0 & 0 & 0 \\ -2 \partial_{x} z_{0} \partial_{x x} z_{0} & 0 & 0 \\ 0 & 0 & 0 \\ \partial_{x x} z_{0}\left[1-\left(\partial_{x} z_{0}\right)^{2}\right] & 0 & 0 \end{array}\right) $ | (D-8) |
| $ \boldsymbol{C}_{2}^{(\mathrm{WS})}=-\mathrm{i} k_{y}\left[\left(\partial_{x} z_{0}\right)^{2}+1\right]\left(\begin{array}{cccc} 0 & c_{36} & c_{23} & c_{34} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right) $ | (D-9) |
| [1] |
李青阳, 吴国忱, 段沛然. 准规则网格高阶有限差分法非均质弹性波波场模拟[J]. 石油地球物理勘探, 2019, 54(3): 539-550. LI Qingyang, WU Guochen, DUAN Peiran. Elastic wavefield forward modeling in heterogeneous media based on the quasi-regular grid high-order finite difference[J]. Oil Geophysical Prospecting, 2019, 54(3): 539-550. |
| [2] |
Zhu J, Dorman J. Two-dimensional, three-component wave propagation in a transversely isotropic medium with arbitrary-orientation-finite-element modelling[J]. Geophysics, 2000, 65(3): 934-942. DOI:10.1190/1.1444789 |
| [3] |
Ge Z, Chen X. An efficient approach for simulating wave propagation with the boundary element method in multilayered media with irregular interfaces[J]. Bulletin of the Seismological Society of America, 2008, 98(6): 3007-3016. DOI:10.1785/0120080920 |
| [4] |
谭文卓, 吴帮玉, 李博, 等. 梯形网格伪谱法地震波场模拟[J]. 石油地球物理勘探, 2020, 55(6): 1282-1291. TAN Wenzhuo, WU Bangyu, LI Bo, et al. Seismic wave simulation using a trapezoid grid pseudo-spectral method[J]. Oil Geophysical Prospecting, 2020, 55(6): 1282-1291. |
| [5] |
张庆朝, 朱国维, 周俊杰, 等. TTI介质qP波伪谱法正演模拟[J]. 石油地球物理勘探, 2019, 54(2): 302-311. ZHANG Qingchao, ZHU Guowei, ZHOU Junjie, et al. qP-wave numerical simulation in TTI media with pseudo-spectral method[J]. Oil Geophysical Prospecting, 2019, 54(2): 302-311. |
| [6] |
Zhou B, Greenhalgh S A. 3-D frequency-domain seismic wave modelling in heterogeneous, anisotropic media using a Gaussian quadrature grid approach[J]. Geophysical Journal International, 2011, 184(1): 507-526. DOI:10.1111/j.1365-246X.2010.04859.x |
| [7] |
Dormy E, Tarantola A. Numerical simulation of elastic wave propagation using a finite volume method[J]. Journal of Geophysical Research: Solid Earth, 1995, 100(B2): 2123-2133. DOI:10.1029/94JB02648 |
| [8] |
Zhang Y, Duan L, Xie Y. A stable and practical implementation of least-squares reverse time migration[J]. Geophysics, 2015, 80(1): V23-V31. DOI:10.1190/geo2013-0461.1 |
| [9] |
Li Y E, Demanet L. Full-waveform inversion with extrapolated low-frequency data[J]. Geophysics, 2016, 81(6): R339-R348. DOI:10.1190/geo2016-0038.1 |
| [10] |
Zhou B, Greenhalgh S A, Hansruedi M. 2.5-D frequency-domain seismic wave modelling in heteroge-neous, anisotropic media using a Gaussian quadrature grid technique[J]. Computer and Geosciences, 2012, 39(1): 18-33. |
| [11] |
Auer L, Nuber A M, Greenhalgh S A, et al. A critical appraisal of asymptotic 3D-to-2D data transformation in full-waveform seismic crosshole tomography[J]. Geophysics, 2013, 78(6): R235-R247. DOI:10.1190/geo2012-0382.1 |
| [12] |
Williamson P R, Pratt R G. A critical review of the acoustic wave modelling procedure in 2.5 dimensions[J]. Geophysics, 1995, 60(2): 591-595. DOI:10.1190/1.1443798 |
| [13] |
Song Z, Williamson P R. Frequency-domain acoustic-wave modeling and inversion of crosshole data: Part I, 2.5-D modeling method[J]. Geophysics, 1995, 60(3): 784-795. DOI:10.1190/1.1443817 |
| [14] |
Zhou B, Greenhalgh S A. An adaptive wavenumber sampling strategy for 2.5D seismic-wave modelling in the frequency-domain[J]. Pure and Applied Geophysics, 2006, 163(7): 1399-1416. DOI:10.1007/s00024-006-0081-7 |
| [15] |
Zhou B, Greenhalgh S A. A damping method for the computation of the 2.5-D Green's function for arbitrary acoustic media[J]. Geophysical Journal International, 1998, 133(1): 111-120. DOI:10.1046/j.1365-246X.1998.1331474.x |
| [16] |
Maokun L, Vladimir D, Aria A, et al. A 2.5D finite-difference algorithm for elastic wave modeling using near-optimal quadratures[J]. Geophysics, 2016, 81(4): T155-T162. DOI:10.1190/geo2015-0550.1 |
| [17] |
Takenaka H, Kennett B L N. A 2.5-D time-domain elastodynamic equation for plane-wave incidence[J]. Geophysical Journal International, 1996, 125(2): F5-F9. DOI:10.1111/j.1365-246X.1996.tb00001.x |
| [18] |
Novais A, Santos L T. 2.5D finite-difference solution of the acoustic wave equation[J]. Geophysical Prospecting, 2005, 53(4): 523-531. DOI:10.1111/j.1365-2478.2005.00488.x |
| [19] |
Xiong J L, Lin Y, Abubakar A, et al. 2.5-D forward and inverse modelling of full-waveform elastic seismic survey[J]. Geophysical Journal International, 2013, 193(2): 938-948. DOI:10.1093/gji/ggt013 |
| [20] |
Zhang W, Chen X F. Traction image method for irregular free surface boundaries in finite difference seismic wave simulation[J]. Geophysical Journal International, 2006, 167(1): 337-353. DOI:10.1111/j.1365-246X.2006.03113.x |
| [21] |
李芳, 曹思远, 孙建国, 等. 2.5D傅氏变换法声波方程数值模拟及精度分析[J]. 石油地球物理勘探, 2009, 44(3): 276-281. LI Fang, CAO Siyuan, SUN Jianguo, et al. Numeric simulation and precision analysis of acoustic equation by 2.5D Fourier transform[J]. Oil Geophysical Prospecting, 2009, 44(3): 276-281. |
| [22] |
Aki K, Richards P G. Quantitative Seismolog(2nd Edition)[M]. Sausalito, CA: University Science Books, 2002.
|
| [23] |
蒋丽丽, 孙建国. 基于Poisson方程的曲网格生成技术[J]. 世界地质, 2008, 27(3): 298-305. JIANG Lili, SUN Jianguo. Source terms of elliptic system in grid generation[J]. Global Geology, 2008, 27(3): 298-305. DOI:10.3969/j.issn.1004-5589.2008.03.011 |
| [24] |
Hixon R, Turkel E. Compact implicit MacCormack-type schemes with high accuracy[J]. Journal of Computational Physics, 2000, 158(1): 51-70. DOI:10.1006/jcph.1999.6406 |
| [25] |
Tam C K, Webb J C. Dispersion-relation-preserving finite difference schemes for computational acoustics[J]. Journal of Computational Physics, 1993, 107(2): 262-281. DOI:10.1006/jcph.1993.1142 |
| [26] |
Hixon R. Evaluation of a high-accuracy MacCormack-type scheme using benchmark problems[J]. Journal of Computational Acoustics, 1997, 6(3): 291-305. |
| [27] |
Zhou B, Moosoo W, Greenhalgh S, et al. Generalized stiffness reduction method to remove the artificial edge-effects for seismic wave modelling in elastic anisotropic media[J]. Geophysical Journal Internatio-nal, 2020, 220(2): 1394-1408. DOI:10.1093/gji/ggz529 |
| [28] |
Vavryuk V. Asymptotic green's function in homoge-neous anisotropic viscoelastic media[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2007, 463(2): 2689-2707. |



 白超英, 陕西省西安市雁塔路南段126号长安大学地质工程与测绘学院地球物理系, 710054。Email:
白超英, 陕西省西安市雁塔路南段126号长安大学地质工程与测绘学院地球物理系, 710054。Email: 