地震拓频技术大致可分为两类,一类是时间域拓频,主要包括反褶积[1]、盲反褶积[2]、反Q滤波[3]、盲源分离[4]、压缩感知[5]等。反褶积通过压缩地震子波提高时间分辨率,计算过程中往往需要假设地震子波为最小相位,以及反射系数为高斯白噪,或是需要子波的参与。为了克服这些问题,盲反褶积应运而生,盲反褶积不需要或者是弱化了对子波和反射系数的先验假设,因而可以应用于时变系统和非最小相位系统,但是由于其对噪声较为敏感,因此并没有得到较好的应用。反Q滤波通过补偿地层的黏弹性衰减,从而提高地震资料的分辨率,但易受噪声、Q值误差等多种因素影响。盲源分离利用围岩反射在各地震道的相似性和目标储层弱信号的差异性分离地震弱信号,以达到提高地震资料分辨率的目的,往往需要对相邻的地震道做出一定的假设。
另一类是频率域拓频,主要包括谱白化[6]、谱蓝化[7]、有色反演[8]、谱反演[9-10]等。谱白化通过对地震数据频谱进行补偿,以达到拓宽地震频带的目的。但现实中很难得到完全白化的频谱,因此谱蓝化技术得到了更为广泛的应用。有色反演实际上是一种测井约束频率域拓频,其核心是用地震的频谱和井的波阻抗频谱相匹配,从而拓宽地震数据的频谱。谱反演是在谱分解的基础上,通过反演使频率域目标函数达到极小而得到反射系数的方法,由于谱反演法能分辨调谐厚度以下的薄层,因而得到了较为广泛的应用。
最小二乘法在地震勘探中的应用十分广泛。约束最小二乘地震反演[11]使用最小二乘方法构建目标函数,反演过程稳定、计算效率高;最小二乘偏移[12-13]把成像问题当作一个反问题处理,以寻求更接近于真实的地下反射;最小二乘横波估计[14]通过最小二乘将横波估计目标函数的最优化问题转化为求解线性矩阵方程组问题,从而大大提高了横波估计的效率和稳定性;最小二乘时频分析方法[15-17]将时频分析转换成一个求解反问题的过程,通过求解矩阵方程组进而得到信号的高分辨率时频分析结果。
本文开发了复数域约束最小二乘谱蓝化拓频(Constrained Complex-domain Least-squares Spectrum Blueing,简记为Y-SpecB)技术,其核心思想是设计一个宽频的约束目标谱[18],在复数域最小二乘[19-21]的思路下,将原始地震频谱向约束目标谱靠近,进而达到提高地震资料主频、拓宽频带的目的。
1 数学模型及其解考虑复数域矩阵方程
| $ \boldsymbol{E}(\omega) \boldsymbol{D}(\omega)+\boldsymbol{N}(\omega)=\boldsymbol{F}(\omega) $ | (1) |
式中:E(ω)为频率域拓频算子;D(ω)为地震数据的谱;F(w)为宽频约束目标谱;N(ω)为白噪声的谱;ω为频率。其中D(ω)和F(ω)为已知项,E(ω)为未知待求项。
式(1)即为Y-SpecB的正演数学模型,其意义为,用拓频算子去拓宽原始地震谱,加上白噪声谱,从而逼近宽频约束目标谱。
复数矩阵E(ω)、D(ω)、F(ω)的具体形式为
| $ \boldsymbol{E}(\omega)=\left[\begin{array}{c} e_{\mathrm{R} 1}+\mathrm{i} e_{\mathrm{I} 1} \\ e_{\mathrm{R} 2}+\mathrm{i} e_{\mathrm{I} 2} \\ \vdots \\ e_{\mathrm{R} n}+\mathrm{i} e_{\mathrm{I} n} \end{array}\right] $ | (2) |
| $ \boldsymbol{D}(\omega)=\left[\begin{array}{llll} d_{\mathrm{R} 1}+\mathrm{i} d_{\mathrm{I} 1} & & & \\ & d_{\mathrm{R} 2}+\mathrm{i} d_{\mathrm{I} 2} & & \\ & & \ddots & \\ & & & d_{\mathrm{R} n}+\mathrm{i} d_{\mathrm{I} n} \end{array}\right] $ | (3) |
| $ \boldsymbol{F}(\omega)=\left[\begin{array}{c} f_{\mathrm{R} 1}+\mathrm{i} f_{\mathrm{I} 1} \\ f_{\mathrm{R} 2}+\mathrm{i} f_{\mathrm{I} 2} \\ \vdots \\ f_{\mathrm{R} n}+\mathrm{i} f_{\mathrm{I} n} \end{array}\right] $ | (4) |
式中:下标“R”表示复数的实部;下标“I”表示复数的虚部;n为待拓频地震道的频率域样点数。
将E(ω)定义为下式的最优解
| $ \|\boldsymbol{E}(\omega) \boldsymbol{D}(\omega)-\boldsymbol{F}(\omega)\|^{2} \Rightarrow \min $ | (5) |
显然,该式为复数域的最优化问题。令
| $ \left\{\begin{array}{l} \boldsymbol{E}=\boldsymbol{E}_{\mathrm{R}}+\mathrm{i} \boldsymbol{E}_{\mathrm{I}} \\ \boldsymbol{D}=\boldsymbol{D}_{\mathrm{R}}+\mathrm{i} \boldsymbol{D}_{\mathrm{I}} \\ \boldsymbol{F}=\boldsymbol{F}_{\mathrm{R}}+\mathrm{i} \boldsymbol{F}_{\mathrm{I}} \end{array}\right. $ | (6) |
则式(1)可以写为
| $ \left[\begin{array}{cc} \boldsymbol{D}_{\mathrm{R}} & -\boldsymbol{D}_{\mathrm{I}} \\ \boldsymbol{D}_{\mathrm{I}} & \boldsymbol{D}_{\mathrm{R}} \end{array}\right]\left[\begin{array}{c} \boldsymbol{E}_{\mathrm{R}} \\ \boldsymbol{E}_{\mathrm{I}} \end{array}\right]=\left[\begin{array}{c} \boldsymbol{F}_{\mathrm{R}} \\ \boldsymbol{F}_{\mathrm{I}} \end{array}\right] $ | (7) |
用矩阵方程组式(7)中的系数矩阵的转置左乘该矩阵方程,有
| $ \begin{gathered} {\left[\begin{array}{cc} \boldsymbol{D}_{\mathrm{R}}^{\mathrm{T}} & \boldsymbol{D}_{\mathrm{I}}^{\mathrm{T}} \\ -\boldsymbol{D}_{\mathrm{I}}^{\mathrm{T}} & \boldsymbol{D}_{\mathrm{R}}^{\mathrm{T}} \end{array}\right]\left[\begin{array}{cc} \boldsymbol{D}_{\mathrm{R}} & -\boldsymbol{D}_{\mathrm{I}} \\ \boldsymbol{D}_{\mathrm{I}} & \boldsymbol{D}_{\mathrm{R}} \end{array}\right]\left[\begin{array}{c} \boldsymbol{E}_{\mathrm{R}} \\ \boldsymbol{E}_{\mathrm{I}} \end{array}\right]} \\ =\left[\begin{array}{cc} \boldsymbol{D}_{\mathrm{R}}^{\mathrm{T}} & \boldsymbol{D}_{\mathrm{I}}^{\mathrm{T}} \\ -\boldsymbol{D}_{\mathrm{I}}^{\mathrm{T}} & \boldsymbol{D}_{\mathrm{R}}^{\mathrm{T}} \end{array}\right]\left[\begin{array}{c} \boldsymbol{F}_{\mathrm{R}} \\ \boldsymbol{F}_{\mathrm{I}} \end{array}\right] \end{gathered} $ | (8) |
进一步可表示为
| $ \left[\begin{array}{cc} \boldsymbol{P} & \boldsymbol{Q} \\ -\boldsymbol{Q} & \boldsymbol{P} \end{array}\right]\left[\begin{array}{c} \boldsymbol{E}_{\mathrm{R}} \\ \boldsymbol{E}_{\mathrm{I}} \end{array}\right]=\left[\begin{array}{cc} \boldsymbol{D}_{\mathrm{R}}^{\mathrm{T}} & \boldsymbol{D}_{\mathrm{I}}^{\mathrm{T}} \\ -\boldsymbol{D}_{1}^{\mathrm{T}} & \boldsymbol{D}_{\mathrm{R}}^{\mathrm{T}} \end{array}\right]\left[\begin{array}{c} \boldsymbol{F}_{\mathrm{R}} \\ \boldsymbol{F}_{\mathrm{I}} \end{array}\right] $ | (9) |
式中
| $ \left\{\begin{array}{l} \boldsymbol{P}=\boldsymbol{D}_{\mathrm{R}}^{\mathrm{T}} \boldsymbol{D}_{\mathrm{R}}+\boldsymbol{D}_{\mathrm{I}}^{\mathrm{T}} \boldsymbol{D}_{\mathrm{I}} \\ \boldsymbol{Q}=\boldsymbol{D}_{\mathrm{l}}^{\mathrm{T}} \boldsymbol{D}_{\mathrm{R}}-\boldsymbol{D}_{\mathrm{R}}^{\mathrm{T}} \boldsymbol{D}_{\mathrm{I}} \end{array}\right. $ | (10) |
则式(9)的解可以写为
| $ \left[\begin{array}{c} \boldsymbol{E}_{\mathrm{R}} \\ \boldsymbol{E}_{\mathrm{I}} \end{array}\right]=\left[\begin{array}{cc} \boldsymbol{P} & \boldsymbol{Q} \\ -\boldsymbol{Q} & \boldsymbol{P} \end{array}\right]^{-1}\left[\begin{array}{cc} \boldsymbol{D}_{\mathrm{R}}^{\mathrm{T}} & \boldsymbol{D}_{1}^{\mathrm{T}} \\ -\boldsymbol{D}_{1}^{\mathrm{T}} & \boldsymbol{D}_{\mathrm{R}}^{\mathrm{T}} \end{array}\right]\left[\begin{array}{c} \boldsymbol{F}_{\mathrm{R}} \\ \boldsymbol{F}_{\mathrm{I}} \end{array}\right] $ | (11) |
实际计算中,为了提高解的稳定性,需要对目标函数的最优化过程进行约束[22-24],则目标函数式(5)变为
| $ \|\boldsymbol{E}(\omega) \boldsymbol{D}(\omega)-\boldsymbol{F}(\omega)\|^{2}+\operatorname{Regu} [\boldsymbol{E}(\omega)] \Rightarrow \min $ | (12) |
式中Regu[E(ω)]为正则化项。由于L2范数正则化可以有解析形式的解,易于求解,因此在求解式(12)时选用L2范数正则化约束,则式(11)变为
| $ \begin{gathered} {\left[\begin{array}{c} \boldsymbol{E}_{\mathrm{R}} \\ \boldsymbol{E}_{\mathrm{I}} \end{array}\right]=\left\{\left[\begin{array}{cc} \boldsymbol{P} & \boldsymbol{Q} \\ -\boldsymbol{Q} & \boldsymbol{P} \end{array}\right]+\left[\begin{array}{cc} \mu \boldsymbol{I} & 0 \\ 0 & \mu \boldsymbol{I} \end{array}\right]\right\}^{-1} \times} \\ {\left[\begin{array}{cc} \boldsymbol{D}_{\mathrm{R}}^{\mathrm{T}} & \boldsymbol{D}_{1}^{\mathrm{T}} \\ -\boldsymbol{D}_{1}^{\mathrm{T}} & \boldsymbol{D}_{\mathrm{R}}^{\mathrm{T}} \end{array}\right]\left[\begin{array}{c} \boldsymbol{F}_{\mathrm{R}} \\ \boldsymbol{F}_{\mathrm{I}} \end{array}\right]} \end{gathered} $ | (13) |
式中:μ≥0,为控频因子;I为单位对角矩阵。
将式(13)的解表示为
| $ \boldsymbol{E}_{\mathrm{O}}(\omega)=\boldsymbol{E}_{\mathrm{R}}(\omega)+\mathrm{i} \boldsymbol{E}_{\mathrm{I}}(\omega) $ | (14) |
将求解的拓频算子EO(ω)与原始地震频谱D(ω)相乘,可得拓频后的地震数据频谱
| $ \boldsymbol{D}_{\mathrm{Y}}(\omega)=\boldsymbol{E}_{\mathrm{O}}(\omega) \boldsymbol{D}(\omega) $ | (15) |
对其进行傅里叶反变换,可得拓频后的时间域地震数据
| $ \boldsymbol{d}_{\mathrm{Y}}=\operatorname{IFFT}\left[\boldsymbol{D}_{\mathrm{Y}}(\omega)\right] $ | (16) |
式中IFFT表示傅里叶反变换。
2 宽频约束目标谱的设计宽频约束目标谱的设计是本文方法的关键点之一,常用两种目标谱的设计方法,一是理论目标谱,二是实际目标谱。
理论目标谱基于各种窗函数进行设计,常用的理论目标谱如图 1所示。一般来说,海宁窗和高斯窗具有窄频的特征,梯形窗和广义高斯窗具有宽频的特征,而梯形窗函数具有频率突变点,不利于最小二乘的拟合效果。理论目标谱的优点是设计灵活,可控性高。

|
图 1 常用理论目标谱 (a)海宁窗;(b)梯形窗;(c)高斯窗;(d)广义高斯窗 |
为了更好地拓展地震资料的高低频,一般会采用广义高斯窗形状的理论目标谱(图 1d),广义高斯目标谱Gg定义为
| $ G_{\mathrm{g}}=\left\{\begin{array}{c} \exp \left[-\frac{\left(\omega-\omega_{\mathrm{L}}\right)^{2}}{2 \sigma_{\mathrm{L}}^{2}}\right] & \omega \leqslant \omega_{\mathrm{L}} \\ 1 & \omega_{\mathrm{L}}<\omega<\omega_{\mathrm{H}} \\ \exp \left[-\frac{\left(\omega-\omega_{\mathrm{H}}\right)^{2}}{2 \sigma_{\mathrm{H}}^{2}}\right] & \omega \geqslant \omega_{\mathrm{H}} \end{array}\right. $ | (17) |
式中:ωL表示低截频率;ωH表示高截频率;σL表示低截标准差;σH表示高截标准差。
实际目标谱的设计来自具体研究区实际测井资料,多采用波阻抗的频谱作为实际目标谱,这和有色反演思路较为类似。图 2为M地区一口井波阻抗的频谱(去掉部分低频信息后),可以看出,井资料频谱很宽,即使到了500Hz仍然有能量,并且振幅谱的变化较大,因此,实际目标谱往往不太稳定和统一。
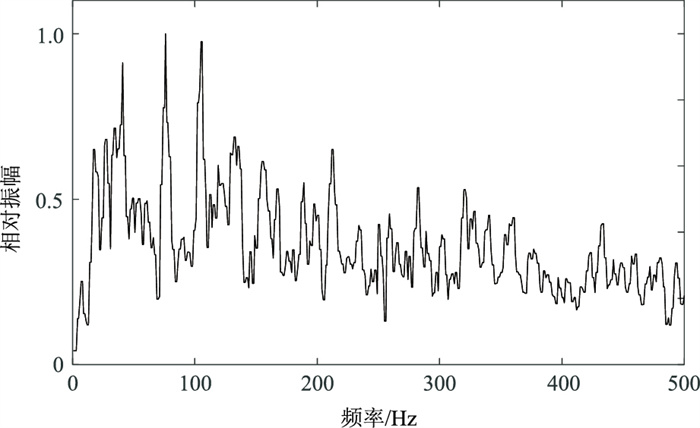
|
图 2 实际井资料的波阻抗频谱 |
上述约束目标谱的设计主要是针对目标谱的振幅谱。Y-SpecB方法不改变拓频后地震数据的相位谱,具体做法是:首先对地震道进行傅里叶变换,然后保留相位谱,将相位谱所对应的振幅谱修正为所设计的目标谱的振幅谱,即可得到包含了振幅谱和相位谱的约束目标谱。此时,通过反演求得的拓频算子为零相位,在时间域对称。
需要说明的是,不论采用理论目标谱还是实际目标谱,对拓频结果的影响并不大,这主要是因为本文方法并不是让拓频后的频谱去拟合目标谱,而是在控频因子μ的控制下向目标谱靠近,拓展原始地震数据微弱的低频和高频信息,进而拓宽频带,提高地震资料的分辨率。
实际应用中,可以尝试不同的理论目标谱和实际目标谱分别进行拓频,从中选择效果更好的目标谱,进而开展全区的拓频处理。
3 模型验证通过模型数据说明本文方法的准确性和有效性。设计如图 3所示的抽象前积体地质模型[25],红色和黄色表示前积砂体,绿色表示泥岩,岩性地层单元的时间厚度约20ms,前积体时间厚度约5ms,共11期。
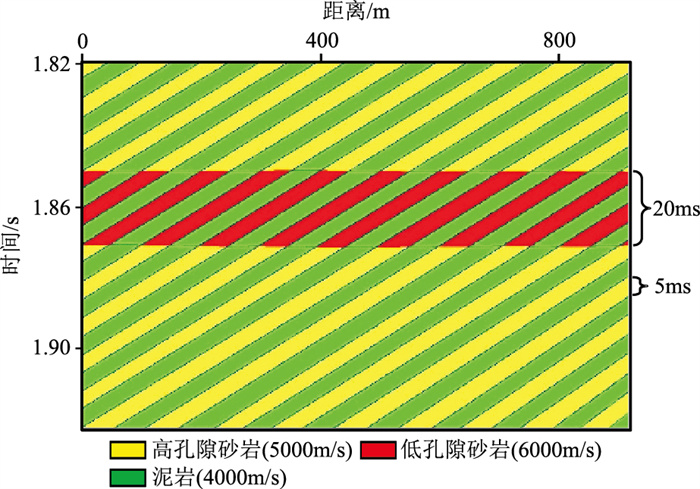
|
图 3 前积体地质模型 |
分别采用不同主频的Ricker子波进行地震正演,结果如图 4所示。可以看出,30Hz合成记录主频较低,频带较窄,无法分辨岩性界面内部的11期前积砂体,而只能反映大套的岩性地层界面,50Hz合成记录主频较高,频带较宽,可以较好地分辨这11期前积砂体。
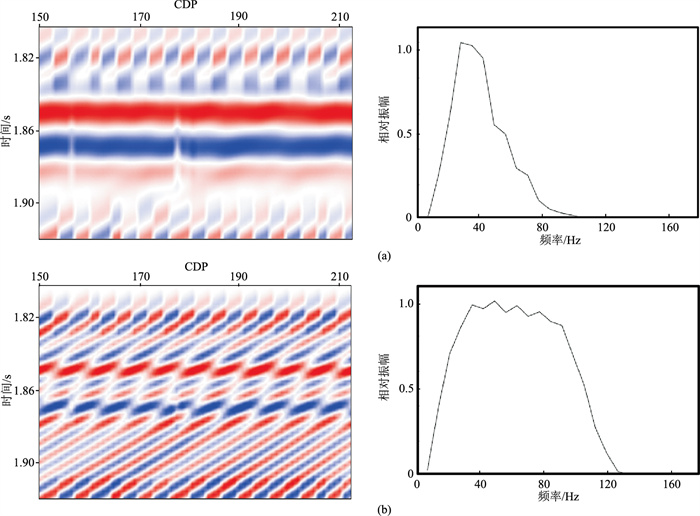
|
图 4 前积体模型不同主频子波地震正演结果(左)及其频谱(右) (a)30Hz;(b)50Hz |
选择广义高斯目标谱,用本文方法对30Hz合成记录进行拓频处理,并分析不同的控频因子μ对拓频结果的影响。经过反复测试,发现当ωL=18Hz、ωH=110Hz、σL=10Hz、σH=30Hz时,拓频效果最佳。图 5为使用不同控频因子μ拓频结果,可以看出,本文方法不仅能增加高频端的能量,同时也能拓展低频段的能量,随着μ变小,拓频后地震记录的主频逐渐变高,频带逐渐变宽,前积砂体也逐渐变得清晰可识别;当μ=0.0001时,拓频结果能够较为真实地恢复50Hz的合成记录,岩性界面中的10期砂体得以重建,如图 6所示。
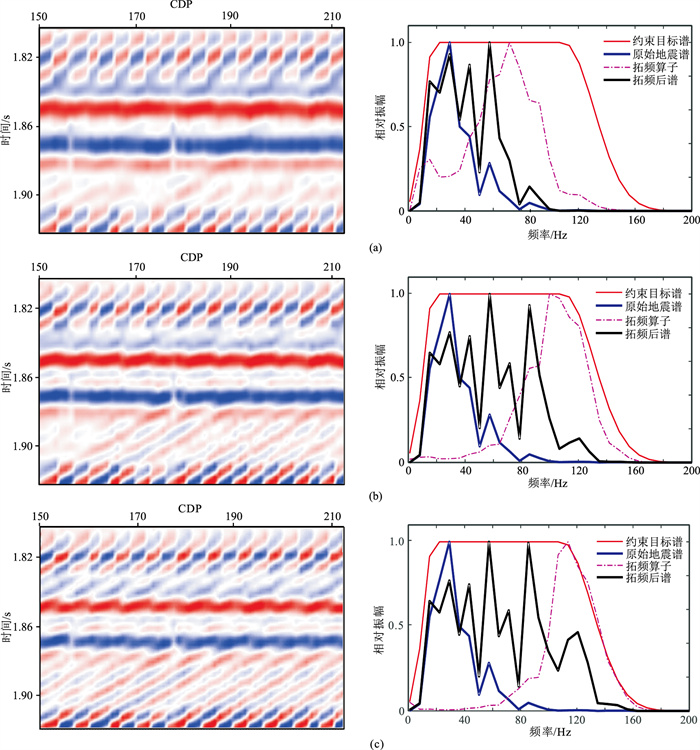
|
图 5 前积体模型不同控频因子μ的拓频后剖面(左)及CDP=180单道频谱(右)的对比 (a)μ=0.01;(b)μ=0.001;(b)μ=0.0001 |

|
图 6 50Hz记录(上)与30Hz记录拓频后(下)的对比 |
频率域拓频算子类似于一个带通滤波器,对其进行傅里叶反变换,可以得到时间域拓频算子,如图 7所示。该算子关于零时刻对称,相位为零,保证了拓频不会改变原始地震数据的相位信息,进而保证拓频后的地震数据的准确性。
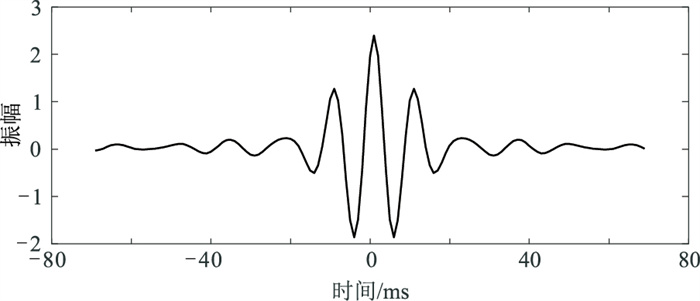
|
图 7 时间域拓频算子 |
进一步分析拓频前、后数据与高频合成记录的相关性。30Hz合成地震道在经过拓频后同相轴增多,与50Hz合成地震道的同相轴具有很好的一致性(图 8);30Hz合成地震道与50Hz合成地震道互相关最大值为0.45,而30Hz拓频后地震道与50Hz合成地震道互相关最大值为0.87,相关性提高了0.93倍(图 9)。由图 10可以看出,30Hz合成地震道相位谱和拓频后地震道相位谱在有效频带范围内并没有改变,进而保证了拓频结果的可靠性。
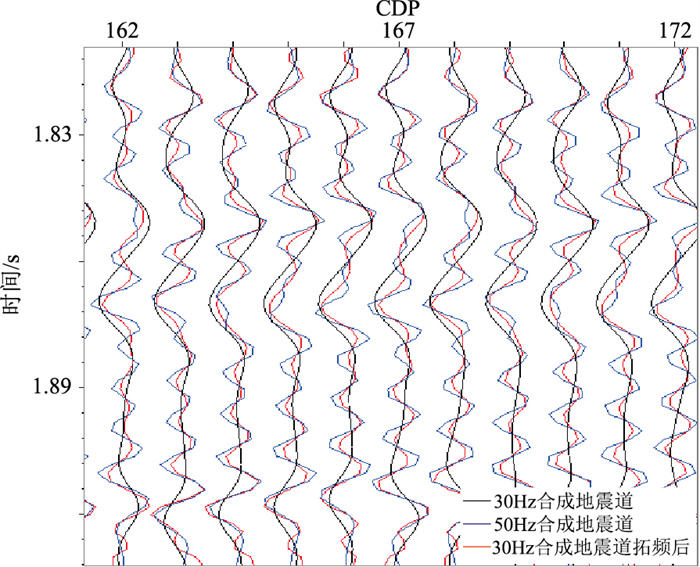
|
图 8 30Hz合成记录拓频前、后与50Hz合成记录的波形对比 |
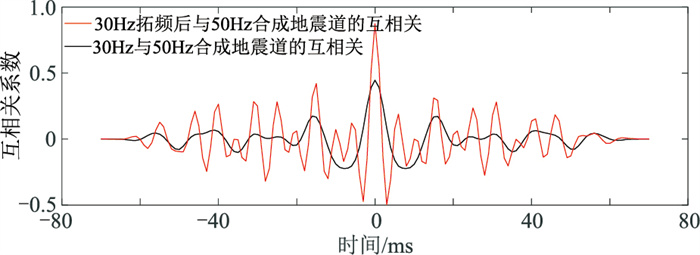
|
图 9 30Hz合成记录拓频前、后与50Hz合成记录相关性分析(CDP165) |
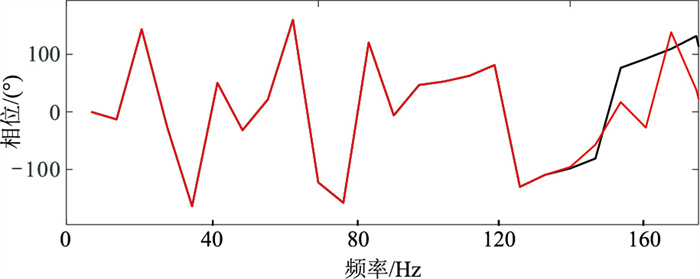
|
图 10 30Hz合成记录拓频前(黑色)、后(红色)相位谱对比 |
关于约束目标谱参数ωL、ωH、σL、σH及控频因子μ如何设置,并没有一个具体的要求,一般的原则是,约束目标谱要完全包含原始地震道的频谱,为保证拓频效果,ωH可适当高一些;在此基础上,μ越小,拓频后的频谱越接近目标谱。缺省值为ωL=18Hz、ωH=100Hz、σL=10Hz、σH=30Hz、μ=0.0001,在此基础上,可以不断调试这些参数,直到达到满意的拓频效果。
模型试算结果表明,本文方法可以在基本不改变相位谱的基础上,通过调节控频因子μ,有效地补偿地震数据的低频信息,增强高频信息,保证了拓频结果的客观、准确性。
4 实际应用 4.1 薄互层识别济阳坳陷CD油田古近系东营组4砂组(Ed4)以浊积沉积为主,储量丰富,是寻找优质储量的重点攻关层系。该层较深,和泥岩呈互层分布,总体较薄,由部分井测井曲线可知,平均速度约为3600m/s。在地震剖面上目的层主频约为25Hz,地震数据的分辨率较低,大约为18m,同相轴出现相互叠置现象,导致大多砂体无法有效分辨。
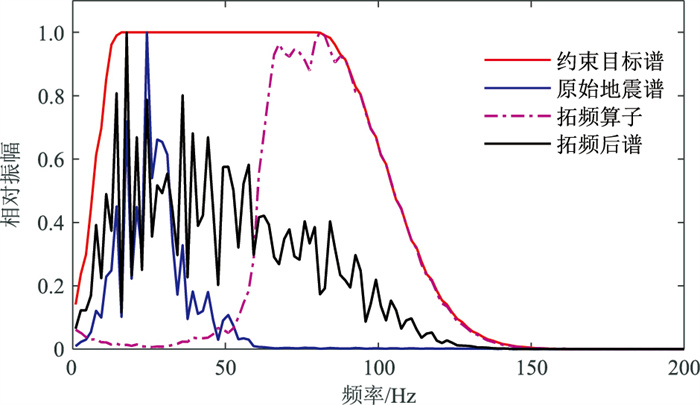
在开展Y-SpecB拓频前,首先要设计目标谱。对地震数据的主频、带宽和有效信号占比(ESR)进行分析,最终选择广义高斯窗的理论目标谱,如图 11所示,参数ωL=15Hz、ωH=80Hz、σL=10Hz、σH=30Hz。对μ的取值进行试验,反复设定不同值并观察拓频后地震数据的保真度和ESR,最终确定μ=0.0001。
|
图 11 CD油田约束目标谱、拓频算子、原始单道及拓频后的频谱对比 |
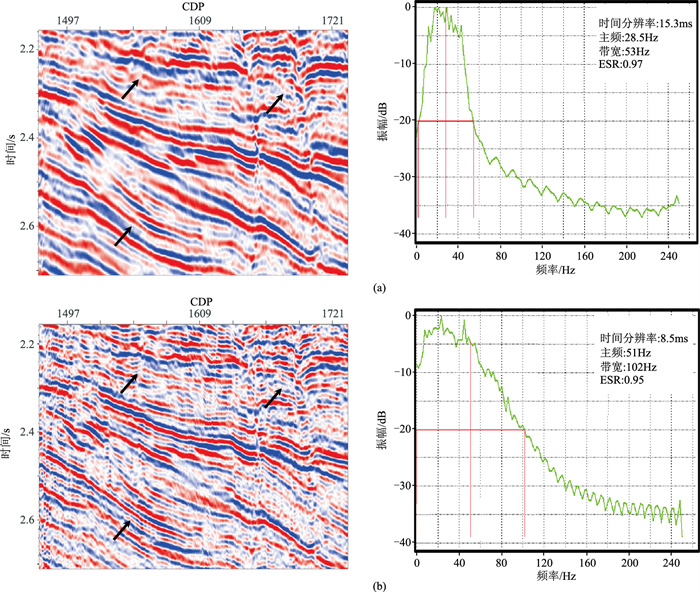
图 12为Line1783拓频前、后的剖面及频谱对比,可以看出,拓频后地震数据主频由28.5Hz提高到51Hz,带宽由53Hz增加到102Hz,由该区地层速度计算,拓频后的地震资料对于地层的绝对分辨率由18m左右提高到8.7m左右,大大提高了地震资料的分辨能力,拓频后的地震剖面能量均衡,中、高频信息丰富,分辨率明显提高(箭头所示),总体效果较好。
|
图 12 拓频前(a)、后(b)Line1783地震剖面(左)及其频谱(右)的对比 |
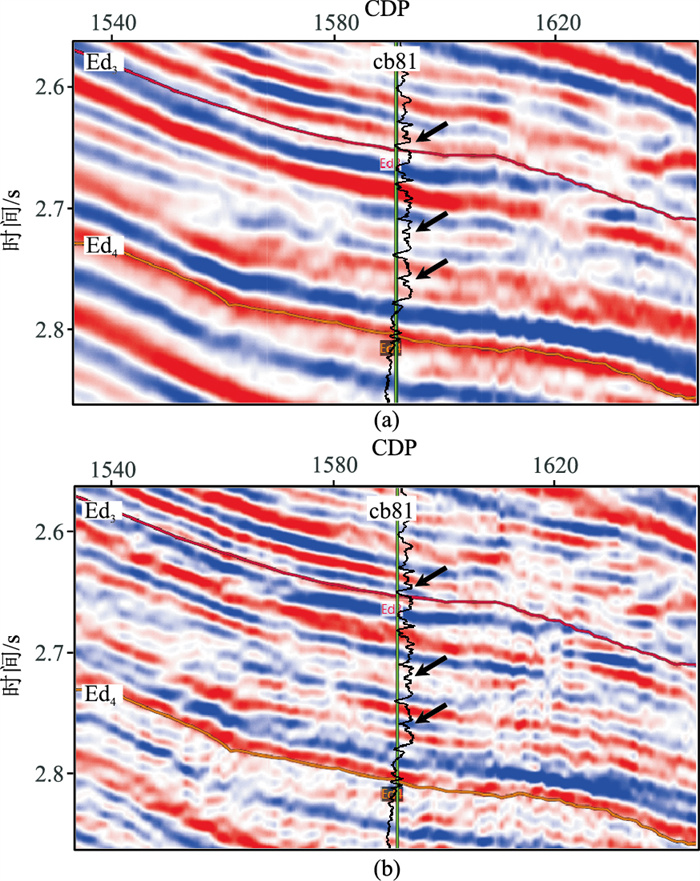
图 13为过cb81井地震剖面拓频前、后对比,其中黑色井曲线为波阻抗,目的层段速度具有砂高泥低的特点,黑色箭头处为几套薄层砂体或砂泥岩薄互层的组合。从上往下的第一、第三箭头处砂体组合,由于储层之间的泥岩隔层较薄,在原始剖面上两套砂岩与泥岩隔层的同相轴出现了相互干涉的现象,而在拓频后的地震剖面上,这两套砂体被清楚地分辨了出来。中间箭头处为一套砂泥岩薄互层,在原始剖面上表现为一个地震同相轴,而在拓频后的地震剖面上,隐约可以看到多个同相轴,分辨率得到了明显提高。
|
图 13 过cb81井地震剖面拓频前(a)、后(b)的对比 |
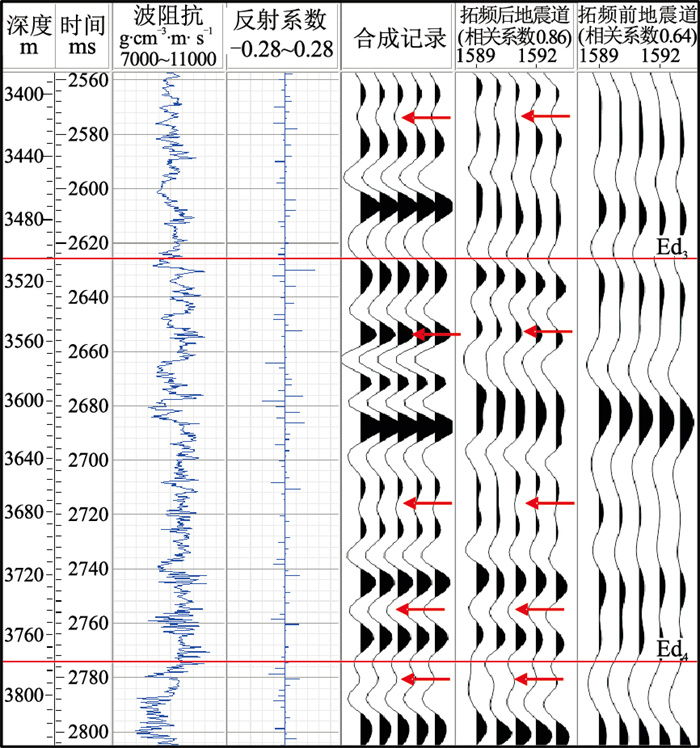
进一步通过井震标定分析本文方法拓频结果的准确性。根据拓频后数据的主频范围,选择主频45Hz的Ricker子波制作合成记录,进行井震标定。从图 14中的红色箭头处可以看出,在拓频后的剖面上可以较为清晰的看到原始地震剖面上没有的地震同相轴。将合成记录和拓频前、后的地震剖面进行对比,合成记录和拓频后的地震剖面的相关性更好,相关系数由0.64提高到了0.86,即用拓频后的地震数据进行井震标定,可提高标定结果的准确性,进一步说明本文方法拓频结果的客观性、准确性。
|
图 14 cb81井拓频前、后井震标定对比 |
济阳坳陷GB洼陷南斜坡古近系沙三段(Es3)以发育地层超覆油气藏为主,已发现多套含油层,是该区最主要的储量层系。在构造研究基础上,开展地层展布规律分析,通过北东向的井间地层对比,发现在古地貌坡折处,井间存在地层超覆尖灭现象。
通过分析和试算,选择Zh243井的实际目标谱作为约束目标普。由于实际目标谱的变化较大且不稳定(图 2),因此对原始的实际目标谱进行了去直流和平滑处理,结果如图 15所示。经过反复实验,取μ=0.001。
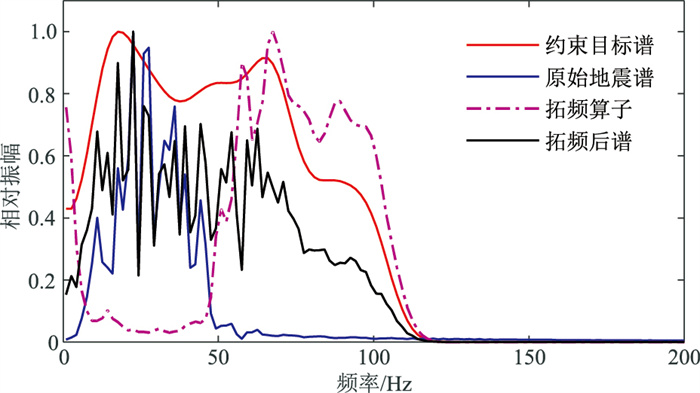
|
图 15 GB洼陷原始地震单道频谱、约束目标谱、拓频算子及拓频后频谱对比 |
图 16为连井剖面拓频前、后对比。在原始地震剖面上,由于原始地震资料分辨率较低,Es3的12砂组3小层(Es312-3)超覆尖灭点难以直接刻画,同时,Zh243井Es3底部的两套砂体(2400ms处)对应地震地震剖面上的一个同相轴,无法有效地分辨(图 16a)。在经过拓频后,地震数据主频由27.5Hz提高到49Hz,带宽由47Hz拓展到98Hz,时间分辨率由15.8ms提高到8.9ms,拓频后的剖面能量均衡,频谱的高频端得到扩展,低频能量也得到一定的补偿,提高了分辨率。

|
图 16 拓频前(a)、后(b)连井剖面(左)及其频谱(右)的对比 |
从拓频后的地震剖面(图 16b)可以看出,Es312-3地层超覆尖灭点更加清楚,向Zh245井的方向偏移了5道左右,约62m(道间距为12.5m),同时,Zh243井Es3底部的两套砂体所对应的地震同相轴被分开,Es312-3砂体尖灭点的位置也得到了清晰的识别,从而提高了地层尖灭点以及小层砂体尖灭点的识别精度。地质人员在拓频资料的基础上开展超覆线精细解释,在Es312-3描述了5个超覆圈闭,面积约2.5km2,应用本文拓频技术扩大了该层系的储量规模;同时可以看出,Es312-3地层超覆尖灭点和砂体尖灭点的位置不同,这也为井位部署、提高探井成功率提供了更为准确的基础数据。
为验证本文方法的客观性、准确性,对拓频后地震剖面进行梯形带通滤波,滤波器参数设置为0~20~30~50Hz,带通滤波后的地震数据(图 17)和原始数据(图 16a)非常接近。

|
图 17 拓频结果的带通滤波后地震剖面 |
本文建立了复数域约束最小二乘拓频方法的正演数学模型,在宽频目标谱的约束下,通过复数域最小二乘方法,实现了地震数据频率域的拓频处理。模型验证表明,本文方法可以在不改变地震信号相位谱的情况下,有效增强地震数据的低频和高频信息,并可以通过设定不同的控频因子来调节拓频后地震数据的频谱和目标频谱之间的距离,以得到不同分辨率的拓频结果。实际应用结果表明,本文方法可以提高地震主频、拓宽频带,有效地提高了地震资料对薄互层以及尖灭点的识别能力,可以为地震地质综合研究提供高分辨率的地震资料。
| [1] |
Porsani M J, Ursin B. Mixed phase deconvolution[J]. Geophyscis, 1998, 63(2): 637-647. DOI:10.1190/1.1444363 |
| [2] |
潘树林, 闫柯, 李凌云, 等. 自适应步长FISTA算法稀疏脉冲反褶积[J]. 石油地球物理勘探, 2019, 54(4): 737-743. PAN Shulin, YAN Ke, LI Lingyun, et al. Sparse-spike deconvolution based on adaptive step FISTA algorithm[J]. Oil Geophysical Prospecting, 2019, 54(4): 737-743. |
| [3] |
吴吉忠, 杨晓利, 龙洋. 一种稳定高效的等效Q值反Q滤波算法及应用[J]. 石油地球物理勘探, 2016, 51(1): 63-70. WU Jizhong, YANG Xiaoli, LONG Yang. A robust approach of inversion Q filtering with equivalent Q[J]. Oil Geophysical Prospecting, 2016, 51(1): 63-70. |
| [4] |
穆星. 基于盲信号处理技术的地震弱信号分离方法[J]. 油气地质与采收率, 2012, 19(5): 47-49. MU Xing. Seismic weak signal separation based on blind signal processing[J]. Petroleum Geology and Recovery Efficiency, 2012, 19(5): 47-49. DOI:10.3969/j.issn.1009-9603.2012.05.012 |
| [5] |
赵子越, 李振春, 张敏. 利用压缩感知技术的离散正交S变换地震数据重建[J]. 石油地球物理勘探, 2020, 55(1): 29-35. ZHAO Ziyue, LI Zhenchun, ZHANG Min. Seismic data reconstruction using discrete orthonormal S-transform based on compressive sensing[J]. Oil Geophysical Prospecting, 2020, 55(1): 29-35. |
| [6] |
陈传仁, 周熙襄. 小波谱白化方法提高地震资料的分辨率[J]. 石油地球物理勘探, 2000, 35(6): 703-709. CHEN Chuanren, ZHOU Xixiang. Improving resolution of seismic data using wavelet spectrum whitening[J]. Oil Geophysical Prospecting, 2000, 35(6): 703-709. DOI:10.3321/j.issn:1000-7210.2000.06.003 |
| [7] |
刘建伟, 高秋菊, 师涛. 谱蓝化技术在大王庄油田储层预测中的应用[J]. 复杂油气藏, 2016, 9(1): 31-34. LIU Jianwei, GAO Qiuju, SHI Tao. Application of spectral bluing frequence technology in reservoir prediction of Dawangzhuang area[J]. Complex Hydrocarbon Reservoirs, 2016, 9(1): 31-34. |
| [8] |
毕俊凤, 杨培杰. 有色反演技术在少井区岩性体预测中的应用[J]. 物探与化探, 2014, 38(3): 558-565. BI Junfeng, YANG Peijie. The application of colored inversion to reservoir prediction in sparse well zone[J]. Geophysical and Geochemical Exploration, 2014, 38(3): 558-565. |
| [9] |
Puryear C I, Castagna J P. Layer-thickness determination and stratigraphic interpretation using spectral inversion[J]. Geophysics, 2008, 73(2): R37-R48. DOI:10.1190/1.2838274 |
| [10] |
刘万金, 周辉, 袁三一, 等. 谱反演在地震属性解释中的应用[J]. 石油地球物理勘探, 2013, 48(3): 423-428. LIU Wanjin, ZHOU Hui, YUAN Sanyi, et al. Application of spectral inversion in the seismic attribute interpretation[J]. Oil Geophysical Prospecting, 2013, 48(3): 423-428. |
| [11] |
林恬, 孟小红, 张致付. 基于约束最小二乘与信赖域的储层参数反演方法[J]. 地球物理学报, 2017, 60(10): 3969-3983. LIN Tian, MENG Xiaohong, ZHANG Zhifu. The petrophysical parameter inversion method based on constrained least squares and trust region approach[J]. Chinese Journal of Geophysics, 2017, 60(10): 3969-3983. |
| [12] |
Aoki N, Schuster G T. Fast least squares migration with a deblurring filter[J]. Geophysics, 2009, 74(6): WCA83-WCA93. |
| [13] |
杨勤勇, 段心标. 最小二乘偏移研究现状及发展趋势[J]. 石油物探, 2018, 57(6): 795-802. YANG Qinyong, DUAN Xinbiao. Research status and development trend of least square migration[J]. Geophysical Prospecting for Petroleum, 2018, 57(6): 795-802. |
| [14] |
罗水亮, 杨培杰, 胡光明, 等. 基于变形P-L模型的矩阵方程迭代精细横波预测[J]. 地球物理学报, 2016, 59(5): 1839-1848. LUO Shuiliang, YANG Peijie, HU Guangming, et al. S-wave velocity prediction based on the modified P-L model and matrix equation iteration[J]. Chinese Journal of Geophysics, 2016, 59(5): 1839-1848. |
| [15] |
Vaníek P. Approximate spectral analysis by least-squares fit[J]. Astrophysics and Space Science, 1969, 4: 387-391. DOI:10.1007/BF00651344 |
| [16] |
Puryear C I, Tai S, Castagna J P, et al. Constrained least-squares spectral analysis: Application to seismic data[J]. Geophysics, 2012, 77(5): Ⅴ143-Ⅴ167. |
| [17] |
杨培杰, 随风贵. 一种改进的最小二乘时频分析方法[J]. 石油物探, 2020, 59(5): 815-822. YANG Peijie, SUI Fenggui. An improved least squares time-frequency analysis[J]. Geophysical Prospecting for Petroleum, 2020, 59(5): 815-822. |
| [18] |
Kazemeini S H, Fomel S. Prestack spectral blueing: A tool for increasing seismic resolution[C]. SEG Technical Program Expanded Abstracts, 2008, 23: 854-857.
|
| [19] |
Miller K S. Complex linear least squares[J]. Society for Industrial and Applied Mathematics, 1973, 15(4): 706-726. |
| [20] |
谷湘潜, 康红文, 曹洪兴. 复数域内的最小二乘法[J]. 自然科学进展, 2006, 16(1): 49-54. GU Xiangqian, KANG Hongwen, CAO Hongxing. Least square method in complex field[J]. Progress in Natural Science, 2006, 16(1): 49-54. |
| [21] |
Bydder M. Solution of a complex least squares problem with constrained phase[J]. Linear Algebra and Its Applications, 2010, 433: 1719-1721. |
| [22] |
Stephen B, Vandenberghe L. Convex Optimization[M]. New York: Cambridge University Press, 2004.
|
| [23] |
Tibshirani R. Regression Shrinkage and Selection via the Lasso[D]. University of Toronto, Toronto, 1994.
|
| [24] |
Ulrych T J, Sacchi M D, Woodbury A. A Bayes tour of inversion: a tutorial[J]. Geophysics, 2001, 66(1): 55-69. |
| [25] |
Zeng H L, Kerans C. Seismic frequency control on carbonate seismic stratigraphy: A case study of the Kingdom Abo sequence, west Texas[J]. AAPG Bulletin, 2003, 87(2): 273-293. |



 杨培杰, 山东省东营市聊城路2号中国石化胜利油田分公司勘探开发研究院, 257015。Email:
杨培杰, 山东省东营市聊城路2号中国石化胜利油田分公司勘探开发研究院, 257015。Email: 