随着渤海油田油气勘探开发的不断深入,储层预测所面临的地质地震条件也变得日益复杂。在河流相岩性油气藏储层预测中,当高速粉砂质泥岩、低速欠压实泥岩等特殊岩性存在时,目标储层与围岩波阻抗差异明显增大,导致在地震剖面上产生较强的反射同相轴,形成“假亮点”,从而使地震反射振幅的相对强弱不能有效表征储层发育的真实变化情况,加大了储层预测难度。因此,采用合理有效的预测方法准确预测强反射掩盖下的储层信息,就显得尤为重要。
目前,针对强反射掩盖下的储层预测的技术方法较为单一,应用较多的是地震多子波分解与重构方法[1-6]。该方法首先把地震道分解为一系列不同振幅和不同频率的子波集合,然后根据不同地质异常体,选择一定范围内的子波振幅和频率进行重构,能有效去除干扰信号的影响。李海山等[4]利用基于匹配追踪算法的多子波分解与重构方法,揭示了煤层强反射之下的含气层的有效反射信息。朱博华等[5]针对油页岩强反射屏蔽储层有效信号的问题,采用基于匹配追踪算法的多子波分解与重构方法对油页岩形成的强反射进行分离,使储层弱反射信号得到了有效增强,井点吻合率显著提高。然而,匹配追踪算法[7]是一种贪婪算法,它不苛求整体最优解,而是试图尽快找到某种意义上的局部最优解。因此,地震多子波分解与重构方法虽在煤层、页岩层等强反射层发育区的储层预测中取得了一定效果,但该方法很难利用地震振幅和频率信息,从根本上解决因不同围岩间波阻抗差异大导致的储层干涉加强而出现的强反射“假亮点”问题,应用效果有限。
针对现有技术存在的上述缺点,本文研究一种基于地震相位分解的自适应强反射分离方法,通过对地震信号相位稳定分解与最优化组合不同相位分量,实现地震信号的重构,可有效去除由特殊围岩等因素产生的强反射对目标储层的干扰影响。然而,目前鲜见关于地震相位分解方法及其应用的文献[8],其主要原因是常规谱分解方法(如连续小波变换和S变换等)得到的相位谱都很复杂,难以解释,限制了对相位谱的有效应用[9]。
本文采用稀疏反演复谱分解方法对地震数据进行时频分析。相对于常规谱分解方法,稀疏反演复谱分解方法不仅能产生高分辨率能量谱,同时也可产生准确的相位谱,因此能为地震相位分解方法的实现提供更准确、可靠的基础数据。在此基础上,实现了地震数据相位稳定分解与重构,构建出一种新的地震地质解释维度。然后,通过正演模拟技术,分析了在受围岩差异影响时产生强反射干扰的复杂地质地震条件下地层的地震响应特征和机理,建立了不同地层地震响应特征的波形信息与对应的相位信息和地质信息之间的联系,为创新利用相位信息解决因不同围岩间波阻抗差异大导致的储层干涉加强而形成的强反射“假亮点”问题奠定了理论基础,进而提出一种基于地震相位分解的自适应围岩强反射分离方法。最后,理论合成数据和实际数据的应用结果表明,新方法可有效去除特殊围岩等因素产生的强反射干扰相位分量而突显目标储层,解决了受围岩差异影响时储层地震响应“失真”的问题。相对于利用地震振幅和频率信息的地震多子波分解与重构方法,新方法显著提高了储层预测的精度,为油田的精细岩性勘探和高效精准开发提供了有力保障。
1 地震相位分解方法及其实现 1.1 稀疏反演复谱分解方法稀疏反演复谱分解[10]是一种高分辨率地震信号时频分析方法,将谱分解描述为一个线性反演问题,再用稀疏约束正则化策略求解该线性反演问题,最终得到一个具有高分辨率的时频谱。该高分辨率稀疏反演复谱分解法的数学模型可表示[11-12]为
| $ \mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{n}} = \left( {{\mathit{\boldsymbol{W}}_1}{\mathit{\boldsymbol{W}}_2} \ldots {\rm{ }}{\mathit{\boldsymbol{W}}_N}} \right)\left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{r}}_1}}\\ {{\mathit{\boldsymbol{r}}_2}}\\ \vdots \\ {{\mathit{\boldsymbol{r}}_N}} \end{array}} \right) + \mathit{\boldsymbol{n}} = \mathit{\boldsymbol{s}} $ | (1) |
式中:s为地震记录;Wi是主频为fi且与频率相关的复子波褶积矩阵;ri为与Wi对应且与频率相关的复反射系数;N为参与计算的频率个数,且i=1, 2, …, N;A为复子波卷积矩阵库;x为与频率相关的复反射系数矩阵;n为随机噪声。
式(1)中矩阵x的元素个数远大于地震记录s的元素个数,因此式(1)线性反演问题是一个欠定问题。为了降低解的不确定性并获得稀疏时频谱,需对x执行稀疏约束,进而将线性反演问题(式(1))转化为基追踪去噪问题[13]进行求解,即有
| $ \mathop {{\rm{min}}}\limits_{x \in {C^n}} {\left\| \mathit{\boldsymbol{x}} \right\|_1} + \frac{1}{{2\mu }}\left\| {\mathit{\boldsymbol{Ax}} - \mathit{\boldsymbol{s}}} \right\|_2^2 $ | (2) |
式中:权重参数μ>0,用于最小化过程中控制式(2)前后两项的相对权重;Cn表征n维复数域。
采用高效且鲁棒的交替方向优化算法[14]求解无约束基追踪去噪问题(式(2))后,便可得到高分辨率时频谱x,对时频谱x做进一步运算,便可得到相应的时频能量谱Fs和时频相位谱θs
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{F}}_{\rm{s}}} = {\left| \mathit{\boldsymbol{x}} \right|^2}\\ {\mathit{\boldsymbol{\theta }}_{\rm{s}}} = {\rm{arctan}}\left( \mathit{\boldsymbol{x}} \right) \end{array} \right. $ | (3) |
式中|·|表示求模运算。
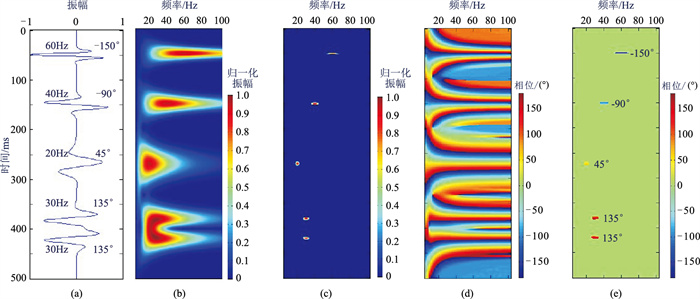
图 1a展示由不同频率和相位的Ricker子波合成的一道地震信号,以说明高分辨率稀疏反演复谱分解法不仅能产生高分辨率的能量谱,同时也可产生准确的相位谱。从该图可见:第一个子波的主频和相位分别为60Hz和-150°;第二、第三个子波的主频和相位分别为40Hz和-90°、20Hz和45°;第四与第五个子波的主频和相位相同,都是30Hz和135°。
|
图 1 稀疏反演复谱分解方法与连续小波变换方法关于时频谱的分辨率和准确性比较 (a)不同频率和相位的Ricker子波合成的一道地震信号;(b)、(d)分别为利用连续小波变换方法获得的时频能量谱和时频相位谱;(c)、(e)分别为利用稀疏反演复谱分解方法获得的时频能量谱和时频相位谱 |
分别用连续小波变换方法和稀疏反演复谱分解方法求取时频谱,且两种方法均选用Ricker子波构建子波库,同时两种方法的计算参数均是经多次测试后选取的最优参数。首先,利用连续小波变换方法获得了时频能量谱(图 1b),它代表常规谱分解方法的分辨率水平;而从利用相同方法获得的时频相位谱(图 1d)中,却难以提取有效的子波相位信息。然后,利用稀疏反演复谱分解方法分别求得时频能量谱(图 1c)和时频相位谱(图 1e),该结果与合成地震信号真实情况一致。比较这两种谱分解方法得到的结果,可见相对于常规谱分解方法,稀疏反演复谱分解方法不仅能产生高分辨率的能量谱,同时也可准确地计算时变子波的相位信息。显然,稀疏反演复谱分解方法的这些优势能为地震相位分解方法的实现提供强有力的技术保障。
1.2 地震相位分解方法的实现地震道S(t)的相位分解数学模型公式[15]为
| $ {S^\prime }\left( {\theta ,t} \right) = \int_{{f_2}}^{{f_1}} {{S^\prime }\left( {f,\theta ,t} \right){\rm{d}}f} $ | (4) |
式中:f1~f2为反变换设定的频率范围;S′(f, θ, t)为利用稀疏反演复谱分解方法对原始地震道S(t)进行计算得到的时频分析结果,其中f为频率,θ为相位,t为时间;S′(θ, t)为地震道S(t)相位分解后对应的相位道集,显示地震振幅和相位随时间变化的分布。相位道集可直观地解释为地震道中单个相位分量的振幅与时间的关系;同时,可根据下式对地震信号中特定相位分量进行重构
| $ {S^\prime }\left( t \right) = \int_{{\theta _2}}^{{\theta _1}} {{S^\prime }\left( {\theta ,t} \right){\rm{d}}\theta } {\rm{ }} $ | (5) |
式中θ1~θ2对应于相位道集叠加所选定的相位范围。当所有相位和频率都处于计算范围内时,则有S′(t)=S(t),即原始地震道可以通过式(5)无损地重构。
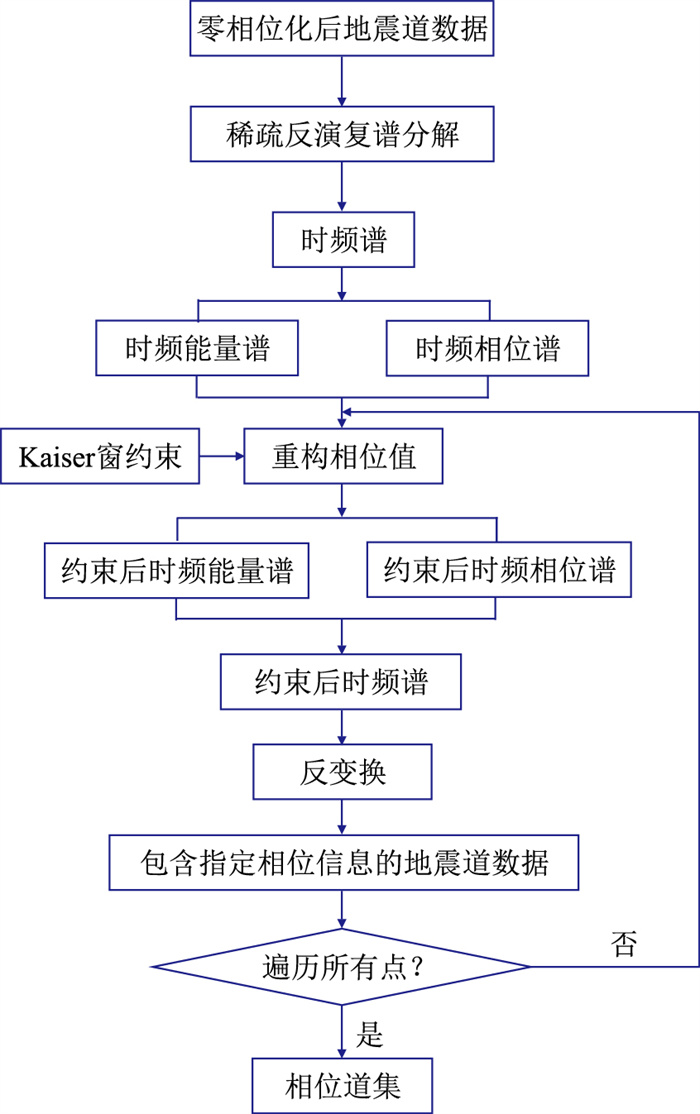
具体地,基于稀疏反演复谱分解的地震相位分解方法的主要实现步骤如图 2所示:首先对零相位化后的地震道数据进行稀疏反演复谱分解,得到高分辨率的能量谱和准确的相位谱(统称为时频谱);然后针对指定的待重构的相位值运用Kaiser窗[16]进行约束搜索,得到约束后的能量谱和相位谱(统称为约束后的时频谱);在此基础上做反变换,便可重构得到只包含指定相位信息的地震道数据;最后对时频谱沿着相位轴[-180°,180°]逐点进行上述操作,即可完成对一维时间域地震道数据的相位分解,得到对应的二维时间—相位域的相位道集,构建出一种新的地震地质解释维度。
|
图 2 基于稀疏反演复谱分解的地震相位分解法实现流程 |
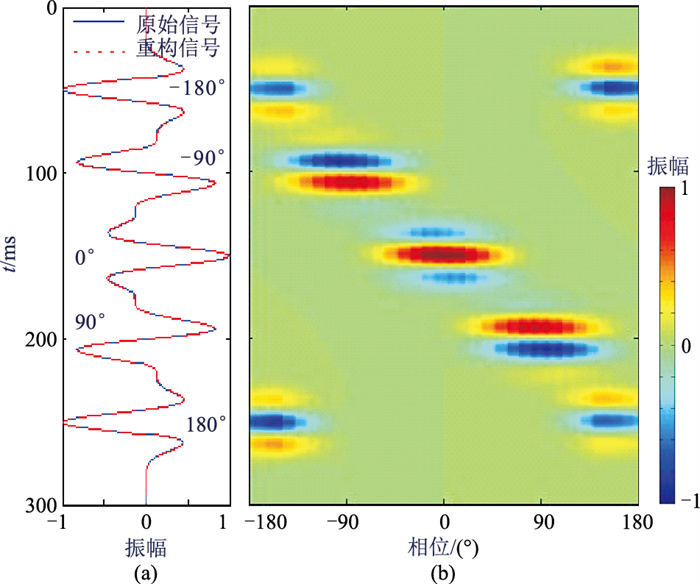
图 3展示一个合成地震信号的相位分解与重构效果。针对由不同相位(已标注)Ricker子波合成的一道地震信号(图 3a),通过相位分解得到相位道集(图 3b),可见所得相位道集与原始合成地震信号中的相位信息对应关系良好,也能准确重构信号,表明本文所提的相位分解与重构方法的准确性。另外,相位道集不同于相位谱或属性,可同时显示振幅和相位信息。
|
图 3 地震相位分解与重构 (a)不同相位Ricker子波合成的信号;(b)相位分解后所得相位道集 |
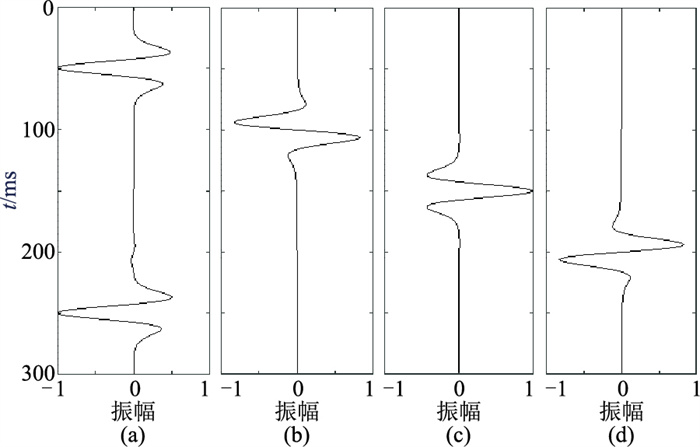
为了验证地震相位分解方法的有效性,对图 3a信号进行地震相位分解,并对该信号进行指定相位的提取与重构,即分别重构出180°、-90°、0°和90°相位分量的波形信号(图 4)。此4个相位分量分别只包含了合成信号中对应的单一相位分量波形成分。通过对比,可以看出重构的4个相位分量信号与原始信号对应的分量信号的波形和时间位置一致,表明本文所提地震相位分解方法的有效性和准确性。同时,也说明了相位分解是一种潜在的强大的解释工具,可用于压制或突显具有特定地质意义的地震反射。
|
图 4 合成信号不同相位分量的提取与重构 (a)180°;(b)-90°;(c)0°;(d)90° |
研究发现,地震数据中不同相位分量具有不同的地质地球物理意义,如0°相位分量可表示厚层高阻抗地层顶界地震响应,180°相位分量可表示厚层低阻抗地层顶界地震响应,90°和-90°相位分量分别对应薄层高阻抗和低阻抗地层的地震响应,其他地层组合关系也可用另外的对应相位分量表示(图 5),这就为创新利用相位信息解决因不同围岩间波阻抗差异大而导致的强反射“假亮点”问题奠定了理论基础。本文提出基于地震相位分解的自适应围岩强反射分离方法,正是基于此认识,即通过对地震信号相位稳定分解与最优化组合不同相位分量,实现地震信号的重构,可有效去除由特殊围岩等因素产生的强反射对目标储层的干扰。

|
图 5 不同地层地震响应特征的波形信息与对应相位信息和地质信息之间的关系 |
基于地震相位分解的自适应强反射分离方法的主要实现步骤(图 6)如下。
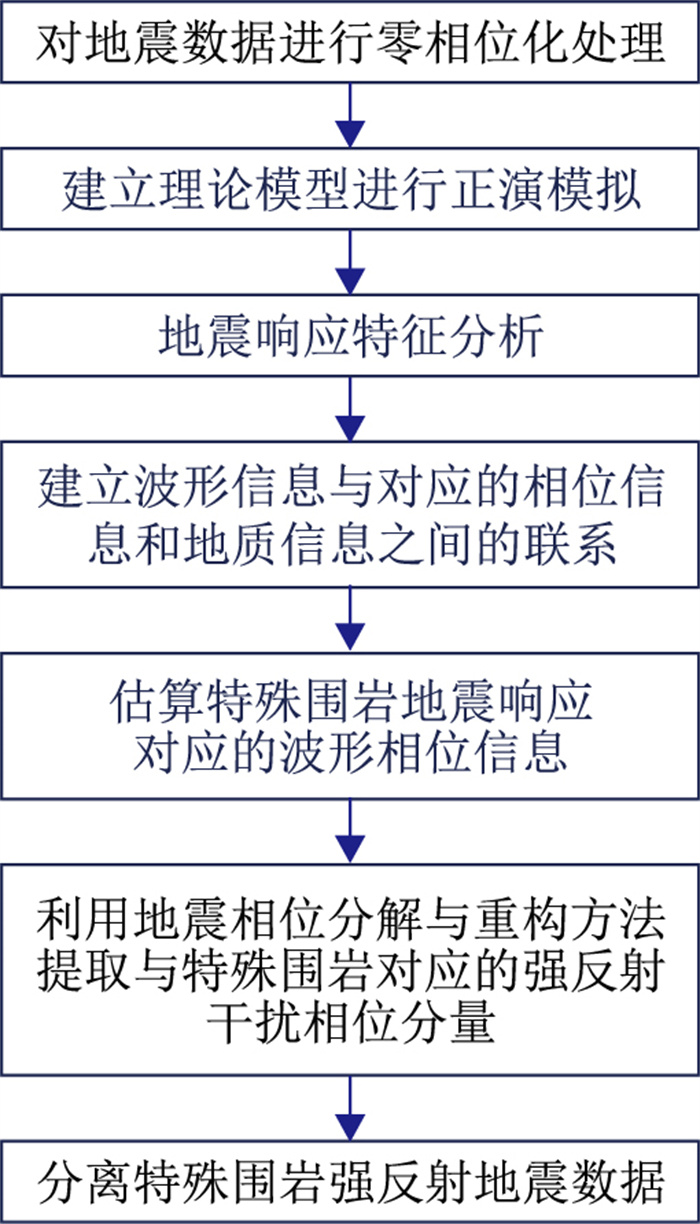
|
图 6 基于地震相位分解的自适应强反射分离方法流程 |
(1) 对研究区内的地震数据进行零相位化处理,为后续的地震信号相位分解与重构处理准备好基础数据。
(2) 结合实际地质情况,根据测井及岩石物理资料建立理论模型,通过正演模拟进行地震响应特征分析,建立不同地层地震响应的波形信息与对应相位信息和地质信息之间的联系。
(3) 根据正演数据和实际数据地震响应特征分析结果,采用基于相似系数准则的相位估算方法求取与背景围岩有明显差异处的特殊围岩地震响应的波形相位信息。
(4) 在目标储层位置上下开一时窗,选取时窗内零相位化后地震数据,利用基于稀疏反演复谱分解的地震相位分解方法进行自适应相位分解与重构,提取与特殊围岩对应的强反射干扰相位分量。
(5) 将提取的与特殊围岩对应的强反射干扰相位分量从零相位化后的地震数据中分离,即可得到突出目标储层有效反射信息的地震数据
| $ {S^{\rm{c}}}\left( t \right) = S\left( t \right) - {S^\prime }_\theta \left( t \right) $ | (6) |
式中:Sc(t)为去除特殊围岩强反射干扰后的地震数据;S(t)为原始零相位化后地震数据;S′θ(t)为提取的与特殊围岩对应的强反射干扰相位分量。在实际应用中,当最终得到的去除特殊围岩强反射干扰后的地震数据噪声明显、同相轴横向连续性较差时,可利用扩散滤波技术进行处理,且在压制噪声的同时能增强地震同相轴的横向连续性。
2.2 理论模型测试为了验证基于地震相位分解的自适应强反射分离方法的有效性,利用理论模型合成数据进行测试和验证。结合实际地质情况,根据测井及岩石物理资料,设计一个典型二维模型(图 7a)作为地震相位分解去围岩强反射的实施模型,其中储层岩性为砂岩,背景围岩为常规泥岩,特殊围岩为高速粉砂质泥岩。表 1给出了该典型二维模型具体参数。

|
图 7 二维典型围岩差异影响模型正演示意图 (a)二维典型围岩差异影响模型;(b)基于褶积模型的正演模拟记录 |
|
|
表 1 模型参数 |
根据模型参数,基于褶积模型,选用主频为30Hz的零相位Ricker子波进行正演模拟。图 7b为正演得到的地震记录,当围岩和储层不变时,储层的地震响应振幅强度应是一致的,但从图 7b的正演记录中可看到右侧储层由于上覆高速粉砂质泥岩的存在且较厚,在波的干涉影响导致下方储层的地震响应振幅异常强,属于“假亮点”,该现象将影响后续储层预测结果的准确性。
对地震响应特征做深入分析,并基于相似系数准则的相位估算方法求取地震响应波形相位信息。通常,在调谐厚度附近或小于调谐厚度时,不受特殊围岩影响时低阻抗储层顶、底地震响应分别对应的是波谷和波峰,其综合地震响应波形相当于-90°相位子波(图 8a)。而受特殊围岩影响后的综合地震响应可看作是由上覆特殊高阻抗泥岩的地震响应和下伏低阻抗储层的地震响应组成,相当于180°相位子波(图 8b)。单纯的特殊高阻抗泥岩顶、底地震响应分别对应波峰和波谷,其综合地震响应波形相当于90°相位子波(图 8c)。因此,首先通过采用地震相位分解方法将地震数据自适应地分解为不同相位分量,进而提取与特殊围岩对应的90°强反射干扰相位分量,然后将其从原始地震数据中分离,即可得到突出目标储层有效反射信息的数据。
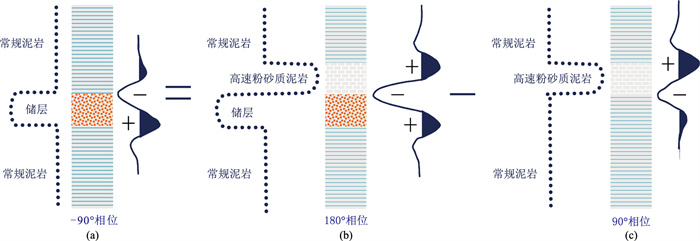
|
图 8 围岩差异影响分析示意图 (a)不受特殊围岩影响时低阻抗储层地震响应;(b)受特殊围岩影响的综合地震响应;(c)单纯的特殊高阻抗泥岩地震响应 |
在本次理论模型测试中,为了进一步突显基于地震相位分解的自适应强反射分离方法的有效性和优势,首先利用商业软件对图 7b记录进行地震多子波分解与重构去围岩强反射处理。从所得结果剖面(图 9a)可见:在目标储层位置处地震响应波形产生明显畸变,表明地震多子波分解与重构方法不适用于去除因不同围岩间波阻抗差异大而导致的储层干涉加强出现的强反射“假亮点”。图 9b是采用基于地震相位分解的自适应强反射分离方法得到的地震剖面,较彻底地去除了受围岩差异影响时给储层地震响应带来的假象,使储层地震响应的振幅相对强弱能更准确地反映其真实发育情况,效果明显。
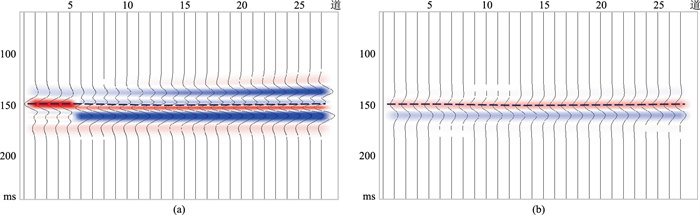
|
图 9 基于地震多子波分解与重构去围岩强反射方法(a)与地震相位分解的自适应围岩强反射分离方法(b)效果对比 |
渤海BZ油田新近系河流相储层是该区主要目的层系。由于河流相沉积环境中主河道延伸距离远、泥岩粉砂质含量变化快,导致目标储层的围岩波阻抗差异大,易形成围岩差异干涉带来的假象,从而使振幅相对强弱不能有效地表征储层发育的真实变化情况,储层预测难度大。因此,将本文提出的基于地震相位分解的自适应强反射分离方法应用于该油田实际资料处理,以压制围岩差异影响来突显目标储层,从而达到精细预测储层的目的。这对于处在滚动评价阶段的渤海BZ油田的井位科学部署和扩大储量规模,均具有重大意义。
该区已钻井A在S砂体钻遇3.8m储层,测井解释为油层;在过S砂体的连井原始地震剖面(图 10a)和对应的S砂体振幅属性平面图(图 10b)上,可见已钻井A和设计井B在S砂体处的地震响应振幅差异较小,是否预示设计井B在该砂体处储层不发育?从地质和地球物理角度分析后发现,由于研究区储层受围岩差异影响,导致已钻井A和设计井B在S砂体处的地震响应振幅差异较小,从而使振幅相对强弱不能有效表征储层的真实变化情况。

|
图 10 S砂体地震相位分解去围岩强反射结果 (a)过S砂体原始连井剖面;(b)S砂体原始振幅属性平面图;(c)过S砂体处理后连井剖面;(d)S砂体处理后振幅属性平面图 |
为了厘清A井区S砂体东侧的储层发育情况,在钻前将本文所提方法应用于该区实际资料处理。从处理后所得地震剖面(图 10c)和对应的振幅属性平面图(图 10d)中看到,本文方法可较彻底地去除围岩差异影响带来的“假亮点”,进一步突显已钻井A与设计井B在S砂体处的振幅差异,即B井处振幅明显强于A井,表明S砂体在B井处要比A井处的储层发育。该新处理结果推动了设计井B的部署和钻探,后期实钻在该砂体位置钻遇12.7m储层,测井解释为油层,钻后探明储量增加了600多万方,显著增大了A井区潜在储量规模。
4 结论与讨论地震相位分解技术可将复合地震信号分解成不同的相位分量,每个相位分量具有不同的地质和地球物理意义。该技术适用于某些特殊地质条件下的储层预测,如围岩差异明显、火成岩发育区等,能产生强反射干扰的复杂地震地质条件。在此情形下,假设地震资料为零相位,调谐厚度附近或小于调谐厚度的特殊高阻抗泥岩或火成岩在90°相位分量上检测效果最好,而此厚度的低阻抗砂岩储层在-90°相位分量上检测效果最好。同时,该技术也适用于无井情况,尤其适用于海上油气勘探。但钻井数据可用来校准原始地震数据的相位,这对于精细解释至关重要。
对理论合成数据和实际数据的应用结果表明,本文提出的基于地震相位分解的自适应强反射分离方法可有效去除特殊围岩等因素产生的强反射干扰相位分量,并突显目标储层,解决了受围岩差异影响时储层地震响应“失真”的问题。相对于利用地震振幅和频率信息的常规地震多子波分解与重构方法,本文方法显著提高了储层预测精度,可为后续准确预测储层厚度、物性、含油气性等提供可靠的数据基础,进而为油田的精细岩性勘探和高效精准开发提供有力保障。
需要提醒的是,当目标储层薄、物性变化快,且纵横向叠置关系复杂时,该方法适用性变差。
| [1] |
张军华, 刘振, 刘炳杨, 等. 强屏蔽层下弱反射储层特征分析及识别方法[J]. 特种油气藏, 2012, 19(1): 23-26. ZHANG Junhua, LIU Zhen, LIU Bingyang, et al. Analysis and identification of reservoir characteristics of weak reflectors under strong shielding layer[J]. Special Oil & Gas Reservoirs, 2012, 19(1): 23-26. DOI:10.3969/j.issn.1006-6535.2012.01.004 |
| [2] |
秦雪霏, 李巍. 大牛地气田煤系地层去煤影响储层预测技术[J]. 吉林大学学报: 地球科学版, 2014, 44(3): 1048-1054. QIN Xuefei, LI Wei. Research of identification and trimming of coal-bed interference in Daniudi gas field[J]. Journal of Jilin University: Earth Science Edition, 2014, 44(3): 1048-1054. |
| [3] |
Wang Y H. Multichannel matching pursuit for seismic trace decomposition[J]. Geophysics, 2010, 75(4): Ⅴ61-Ⅴ66. |
| [4] |
李海山, 杨午阳, 田军, 等. 匹配追踪煤层强反射分离方法[J]. 石油地球物理勘探, 2014, 49(5): 866-870. LI Haishan, YANG Wuyang, TIAN Jun, et al. Coal seam strong reflection separation with matching pursuit[J]. Oil Geophysical Prospecting, 2014, 49(5): 866-870. |
| [5] |
朱博华, 向雪梅, 张卫华. 匹配追踪强反射层分离方法及应用[J]. 石油物探, 2016, 55(2): 280-287. ZHU Bohua, XIANG Xuemei, ZHANG Weihua. Strong reflection horizons separation based on ma-tching pursuit algorithm and its application[J]. Geophysical Prospecting for Petroleum, 2016, 55(2): 280-287. DOI:10.3969/j.issn.1000-1441.2016.02.014 |
| [6] |
杨子鹏, 宋维琪, 刘军, 等. 多道联合约束的匹配追踪强反射轴压制方法[J]. 石油地球物理勘探, 2021, 56(1): 77-85. YANG Zipeng, SONG Weiqi, LIU Jun, et al. A me-thod of combining multi-channel signals to suppress the strong reflection through matching pursuit[J]. Oil Geophysical Prospecting, 2021, 56(1): 77-85. |
| [7] |
Wang Y H. Seismic time-frequency spectral decompo-sition by matching pursuit[J]. Geophysics, 2007, 72(1): Ⅴ13-Ⅴ20. |
| [8] |
杨培杰, 罗红梅, 王金铎. 地震数据分相位重构方法[J]. 石油地球物理勘探, 2019, 54(3): 594-599. YANG Peijie, LUO Hongmei, WANG Jinduo. Seismic data phase reconstruction[J]. Oil Geophysical Prospecting, 2019, 54(3): 594-599. |
| [9] |
张生强, 张志军, 谭辉煌, 等. 流体流度与时频相位融合的油气检测方法及应用[J]. 石油地球物理勘探, 2019, 54(4): 853-859. ZHANG Shengqiang, ZHANG Zhijun, TAN Hui-huang, et al. Hydrocarbon detection with fluid-mobility and time-frequency phase fusion[J]. Oil Geophysical Prospecting, 2019, 54(4): 853-859. |
| [10] |
Bonar D C, Sacchi M D. Complex spectral decomposition via inversion strategies[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 1408-1412.
|
| [11] |
张生强, 韩立国, 李才, 等. 基于高分辨率反演谱分解的储层流体流度计算方法研究[J]. 石油物探, 2015, 54(2): 142-149. ZHANG Shengqiang, HAN Liguo, LI Cai, et al. Computation method for reservoir fluid mobility based on high-resolution inversion spectral decomposition[J]. Geophysical Prospecting for Petroleum, 2015, 54(2): 142-149. |
| [12] |
张生强, 张志军, 郭军, 等. 时频空间域低频约束AVO响应校正方法[J]. 石油地球物理勘探, 2021, 56(1): 137-145. ZHANG Shengqiang, ZHANG Zhijun, GUO Jun, et al. AVO response correction constrained by low-frequency components in time-frequency-space domain[J]. Oil Geophysical Prospecting, 2021, 56(1): 137-145. |
| [13] |
Chen S S, Donoho D L, Saunders M A. Atomic decomposition by basis pursuit[J]. SIAM Journal on Scientific Computing, 1998, 20(1): 33-61. DOI:10.1137/S1064827596304010 |
| [14] |
Yang J F, Zhang Y. Alternating direction algorithms for L1-problems in compressive sensing[J]. SIAM Journal on Scientific Computing, 2011, 33(1): 250-278. DOI:10.1137/090777761 |
| [15] |
Castagna J, Oyem A, Portniaguine O, et al. Phase de-composition[J]. Interpretation, 2016, 4(3): SN1-SN10. |
| [16] |
高云鹏, 滕召胜, 曾博, 等. 基于Kaiser窗频谱校正的介质损耗因数测量[J]. 电工技术学报, 2009, 24(5): 203-208. GAO Yunpeng, TENG Zhaosheng, ZENG Bo, et al. Dielectric loss factor measurement based on Kaiser window spectral correction[J]. Transactions of China Electro Technical Society, 2009, 24(5): 203-208. |



 张生强, 天津市滨海新区海川路2121号中海石油(中国)有限公司天津分公司渤海石油研究院, 300459。Email:
张生强, 天津市滨海新区海川路2121号中海石油(中国)有限公司天津分公司渤海石油研究院, 300459。Email: 