② 东方地球物理公司国际勘探事业部, 河北涿州 072751;
③ 东方地球物理公司研究院, 河北涿州, 072751
② BGP Intl., CNPC, Zhuozhou, Hebei 072751, China;
③ Geophysical Research Institute, BGP, CNPC, Zhuozhou, Hebei 072751, China
地震数据重建是地震信号分析领域的一个重要研究方向。地震数据采集时由于采集环境以及采集成本等因素[1],采集到的数据通常呈现不规则或稀疏分布,不完整的地震数据缺失部分地球物理信息,据其不能准确地预测地下岩层的性质。因此,为保证满足后续地震资料处理对数据完整性的要求,必须恢复缺失的地震数据,以提高储层预测的准确性,促进油气的勘探与开发。显然,重建缺失的地震数据具有非常重要的现实意义。
传统的地震数据重建方法主要有基于滤波的重建方法[2-4]、基于波动方程的重建方法[5-7]以及基于变换函数的重建方法[8-11]等三种类型。滤波重建法是通过褶积插值滤波器实现地震数据重建,主要用于重建规则采样地震数据,且计算量大。波动方程法是通过Kirchhoff积分算子实现地震数据重建[12],该方法需地下信息作为先验条件,在地下信息未知或精度低时对重建结果影响很大。变换函数法是利用最小二乘法将信号变换到某一新的变换域,再通过反变换重构地震数据。常用的变换函数有傅里叶变换、曲波变换、离散余弦变换等。变换函数法结构简单,计算复杂度低,可实现规则和非规则采样地震数据的重建,且不需将地下地层信息作为先验条件,但该方法对采样率要求较高,造成采集成本高昂,且要求地震数据的采集规模较大。
压缩感知理论[13-16](Compressive sensing,CS)的应用,克服了传统地震数据重建方法的缺陷,解决了对采样率要求较高的问题[17],使稀疏信号可在低于奈奎斯特采样频率的条件下用稀疏优化算法重建完整信号。压缩感知地震数据重建主要分为稀疏表示阶段和稀疏重建阶段,重建阶段相当于稀疏优化问题。白兰淑等[18]结合稀疏促进的曲波恢复迭代算法和Bregman迭代阈值算法提出改进的联合迭代算法,在压缩感知理论框架下,用Curvelet变换稀疏表示地震数据,该改进算法能稀疏优化重建地震数据,具有收敛快、重建信噪比高的优点,但其计算量大、计算复杂度高。周亚同等[19]提出压缩感知下K-SVD字典学习自适应稀疏表示地震数据、正则化正交匹配追踪(Regularized orthogonal matching pursuit,ROMP)稀疏优化重建地震数据的方法,能加快复杂实际地震数据重建速度。但该稀疏优化算法得到的不是全局最优解,故重建精度较低。
交替乘子方向算法(Alternating direction method of multipliers,ADMM)[20-22]具有简化复杂性、高重建速度和良好重建质量的优点,在地震数据领域引起了广泛关注。Sternfels等[23]将ADMM算法与压缩感知理论结合实现含噪地震数据的降噪。Zhang等[24]将ADMM算法应用于缺失地震数据的恢复,实现压缩感知地震数据的精确重构。李慧等[25]在此基础上提出压缩感知框架下K-SVD字典学习稀疏表示地震数据,利用ADMM算法优化重建地震数据,达到提高地震数据重建精度的目的。
尽管ADMM算法在地震数据重建中效果显著,但由于该算法中平衡因子无法根据地震数据自适应地进行调整,易损害重建精度。另外,在基于ADMM算法的压缩感知地震数据重建模型中,由于输入训练样本较少,算法参数较多以及模型复杂度较高等问题,容易出现过拟合现象。针对上述问题,本文对ADMM算法进行改进,提出平方正则交替乘子方向算法(Square regular-alternating direction method of multipliers,SR-ADMM)。一方面在ADMM算法迭代中加入平方正则项;另一方面自适应选取平衡因子。最终将SR-ADMM算法与压缩感知理论相结合,实现基于压缩感知的SR-ADMM算法地震数据重建。通过模拟地震数据、实际单炮数据以及大庆油田实际地震数据对本文所提算法进行了验证。
1 压缩感知基本理论压缩感知理论具有三个重要的前提条件:地震数据的稀疏性、测量矩阵的不相干性以及合适的优化算法。压缩感知的数据重建模型为
| $ \mathit{\boldsymbol{y = \varPhi x}} $ | (1) |
式中:x∈RN,为原始信号;Φ∈RM×N,为测量矩阵;y∈RM,为测量矩阵下原始信号的观测值。该式表示原始信号从N维信号降维到M维获得观测值,信号降维过程可用图 1所示图像表示。

|
图 1 原始信号降维 |
由于式(1)为欠定方程,有无穷多的解,很难直接通过观测值y恢复出原始信号x。因此可用一个与测量矩阵不相关的变换矩阵对原始信号做稀疏表示,得到稀疏矩阵。其数学表达式为
| $ \mathit{\boldsymbol{x = D\varTheta }} $ | (2) |
式中:D∈RN×N,为稀疏变换矩阵;Θ为稀疏系数,是长度为N的一维向量。式(2)的原始信号稀疏表示过程可用图 2所示图像表示。

|
图 2 信号的稀疏表示 |
因此观测值y可以表示为
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{\varPhi x}} = \mathit{\boldsymbol{\varPhi \varPhi \varTheta }} = \mathit{\boldsymbol{A\varTheta }} $ | (3) |
式中A=ΦD,为M×N阶感知矩阵。A满足约束等距性质,即可通过求解L0范数优化问题很好地从观测值y中恢复出原始信号x
| $ \min {\left\| \mathit{\boldsymbol{\varTheta }} \right\|_0}\quad {\rm{ s}}{\rm{.t}}{\rm{. }}\quad \mathit{\boldsymbol{y = A\varTheta }} $ | (4) |
式中稀疏系数Θ的L0范数表示该向量中所有非零元素的个数。但L0范数的最优化问题是一个非确定性多项式问题,在稀疏变换矩阵D与测量矩阵Φ不相干时,求解Θ的L0范数问题等价于求解Θ的L1范数,故可将式(4)转化为求解L1范数优化问题
| $ \min {\left\| \mathit{\boldsymbol{\varTheta }} \right\|_1}\quad {\rm{ s}}{\rm{.t}}{\rm{. }}\quad \mathit{\boldsymbol{y = A\varTheta }} $ | (5) |
式(5)与式(4)等价,即求解满足约束条件的最稀疏Θ转换为求解满足约束条件的元素绝对值和最小Θ。通过求解式(5)得到最稀疏系数
| $ \tilde{\boldsymbol{x}}=\tilde{\boldsymbol{D}} \tilde{\boldsymbol{\varTheta}} $ | (6) |
适用的重构算法是压缩感知精确重构的重要前提。ADMM算法的优点在于将对偶上升法的可分解性与乘子法的收敛性质结合起来,通过对偶上升法使线性稀疏项不断接近最优解,保证在惩罚参数较小的情况下满足精度要求;克服乘子法中变量二次项无法拆分的问题,将原始问题拆分求解,可实现并行运算且提高运算效率。使用ADMM算法求解压缩感知地震数据重建问题的数学模型为
| $ \widetilde{\boldsymbol{\varTheta}}=\operatorname{argmin} \frac{1}{2}\|\boldsymbol{A} \boldsymbol{\varTheta}-\boldsymbol{y}\|_{2}^{2}+\boldsymbol{\lambda}\|\boldsymbol{\varTheta}\|_{1} $ | (7) |
式中λ表示平衡因子,用于控制前、后两项之间的权重。
引入辅助变量Z
| $ \begin{gathered} \widetilde{\boldsymbol{\varTheta}}=\operatorname{argmin} \frac{1}{2}\|\boldsymbol{A} \boldsymbol{\varTheta}-\boldsymbol{y}\|_{2}^{2}+\boldsymbol{\lambda}\|\boldsymbol{Z}\|_{1} \\ \text { s.t. } \quad \boldsymbol{\varTheta}-\boldsymbol{Z}=0 \end{gathered} $ | (8) |
该式的增广拉格朗日函数为
| $ \begin{gathered} L_{\rho}(\boldsymbol{\varTheta}, \boldsymbol{Z}, \boldsymbol{y})=\frac{1}{2}\|\boldsymbol{A} \boldsymbol{\varTheta}-\boldsymbol{y}\|_{2}^{2}+\boldsymbol{\lambda}(\boldsymbol{\varTheta}-\boldsymbol{Z})+ \\ \frac{\rho}{2}\|\boldsymbol{\varTheta}-\boldsymbol{Z}\|_{2}^{2} \end{gathered} $ | (9) |
根据上式可知,Θ的更新就是在固定参数Z和λ的情况下,求解增广拉格朗日函数的最小值问题,即
| $ \boldsymbol{L}^{\prime}{}_{\boldsymbol{\varTheta}}=\boldsymbol{A}^{\mathrm{T}}\left(\boldsymbol{A} \boldsymbol{\theta}^{k+1}-\boldsymbol{y}\right)+\boldsymbol{\lambda}^{k}+\rho\left(\boldsymbol{\theta}^{k+1}-\boldsymbol{z}^{k}\right) $ | (10) |
求解可知ADMM算法第k+1次的迭代表达式为
| $ \left\{\begin{array}{l} \boldsymbol{\theta}^{k+1}=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}+\rho \boldsymbol{I}\right)\left[\boldsymbol{A}^{\mathrm{T}} \boldsymbol{y}+\rho\left(\boldsymbol{z}^{k}-\boldsymbol{\lambda}^{k}\right)\right] \\ \boldsymbol{z}^{k+1}=\boldsymbol{S}_{\boldsymbol{\lambda} / \rho}\left(\boldsymbol{\theta}^{k+1}+\frac{\boldsymbol{\lambda}^{k}}{\rho}\right) \\ \boldsymbol{u}^{k+1}=\boldsymbol{u}^{k}+\left(\boldsymbol{\theta}^{k+1}-\boldsymbol{z}^{k+1}\right) \end{array}\right. $ | (11) |
式中:u=λ/ρ,其中ρ表示惩罚参数;Sλ/ρ为软阈值函数,定义为
| $ \boldsymbol{S}_{\boldsymbol{\lambda} / \rho}(x)= \begin{cases}x-k & x>k \\ 0 & |x| \leqslant k \\ x+k & x<-k\end{cases} $ | (12) |
以K-SVD字典学习对地震数据进行稀疏表示,并用ADMM算法解决稀疏优化问题,构成基于ADMM算法和K-SVD字典学习的压缩感知地震数据重建模型。在该模型中,由于存在输入训练样本较少、ADMM算法迭代参数较多及模型复杂度较高等问题,容易出现过拟合现象,因此增加平方邻近项正则化式中的子问题,防止过拟合。正则化交替乘子方向算法公式如下
| $ \left\{\begin{array}{l} \boldsymbol{\theta}^{k+1}=\left(\boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}+\rho \boldsymbol{I}\right)\left[\boldsymbol{A}^{\mathrm{T}} \boldsymbol{y}+\rho\left(\boldsymbol{z}^{k}-\boldsymbol{\lambda}^{k}\right)\right] \\ \boldsymbol{z}^{k+1}=\boldsymbol{S}_{\boldsymbol{\lambda} / \rho}\left(\boldsymbol{\theta}^{k+1}+\frac{\boldsymbol{\lambda}^{k}}{\rho}\right)+\frac{1}{2}\left\|\boldsymbol{z}-\boldsymbol{z}^{k}\right\|^{2} \\ \boldsymbol{u}^{k+1}=\boldsymbol{u}^{k}+\left(\boldsymbol{\theta}^{k+1}-\boldsymbol{z}^{k+1}\right)+\frac{1}{2}\left\|\boldsymbol{u}-\boldsymbol{u}^{k}\right\|^{2} \end{array}\right. $ | (13) |
另外,由于ADMM算法中平衡因子的取值只能根据经验选取,若平衡因子λ较大,则说明稀疏项权重更大,所求值更稀疏而不会过多考虑约束;反之,重建数据更接近于原始信号。为了使λ更精确,从而获得更高重建精度,本文将λ的选取改进为可自适应方式。对平衡因子的改进方案如下
| $ \boldsymbol{\lambda}_{1, a}=\boldsymbol{\lambda} \times \alpha^{l}, \boldsymbol{\lambda}_{2, a}=\boldsymbol{\lambda} \times \alpha^{l-1}, \cdots $ | (14) |
| $ \boldsymbol{\lambda}_{1, b}=\boldsymbol{\lambda} / \alpha^{l}, \boldsymbol{\lambda}_{2, b}=\boldsymbol{\lambda} / \alpha^{l-1}, \cdots $ | (15) |
首先根据经验设定初始平衡因子λ。两式中α的作用是选取λ的邻近值,可选择略大于1或略小于1的数,如α=0.95。式(14)和式(15)分别表示对初始平衡因子做乘法和除法,获得多个近似值。接着分别用所获近似值以式(13)进行迭代实现重建,选取使地震数据重建误差最小的平衡因子为最优平衡因子,通过一轮迭代就可得到平衡因子最优值;之后,继续完成后续迭代过程。两式中常数l表征近似解的个数,若l取值越大,就能获得数量更多的平衡因子近似值,理论上重建效果更好。但l过大,会造成时间空间负荷,因此需根据地震数据实情选取。
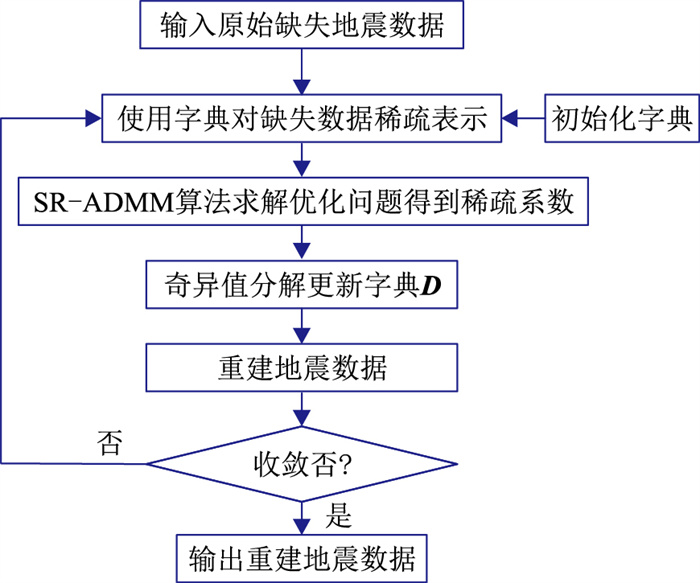
3 基于压缩感知的SR-ADMM地震数据重建本文基于压缩感知的SR-ADMM算法地震数据重建的流程如图 3所示。
|
图 3 重建流程图 |
在压缩感知框架下,以K-SVD字典学习对地震数据做稀疏表示,用SR-ADMM算法稀疏优化实现缺失地震数据重建。缺失数据重建具体步骤为:
(1) 输入训练样本,对重建模型进行训练,得到初始字典D0、初始稀疏系数Θ0;
(2) 输入原始缺失地震数据x,用初始字典D0对该地震数据进行稀疏表示;
(3) 用SR-ADMM算法求解最优化问题(式(7)),得到初步稀疏近似
(4) 以K-SVD字典学习算法更新稀疏变换字典D,用更新后的字典D对步骤(3)初步重建地震数据做稀疏表示;
(5) 用SR-ADMM算法求解更新得到稀疏近似
(6) 将步骤(3)迭代得到的地震数据替换为下一次迭代的输入数据,重复步骤(4)~步骤(5),直到收敛;输出迭代后的重建地震数据
将信噪比作为地震数据重建性能的评判指标
| $ \mathrm{SNR}=10 \lg \frac{\|\boldsymbol{x}\|_{2}^{2}}{\|\boldsymbol{x}-\tilde{\boldsymbol{x}}\|_{2}^{2}} $ | (16) |
式中
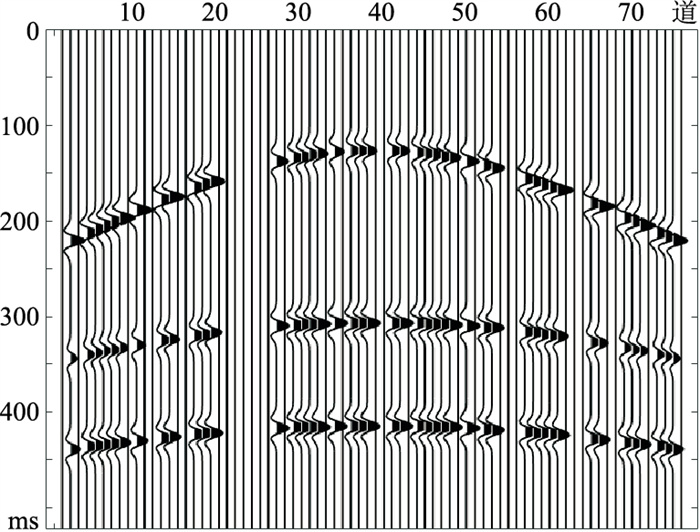
验证模型的模拟地震数据(图 4)共76道,522个采样点,采样间隔为1ms。图 5为该炮点集随机采样数据。ADMM算法中平衡因子根据多次实验后得出,选取λ=0.15;SR-ADMM算法平衡因子则根据模拟地震数据自适应地选取。

|
图 4 原始模拟地震数据 |
|
图 5 随机采样模拟地震数据 |
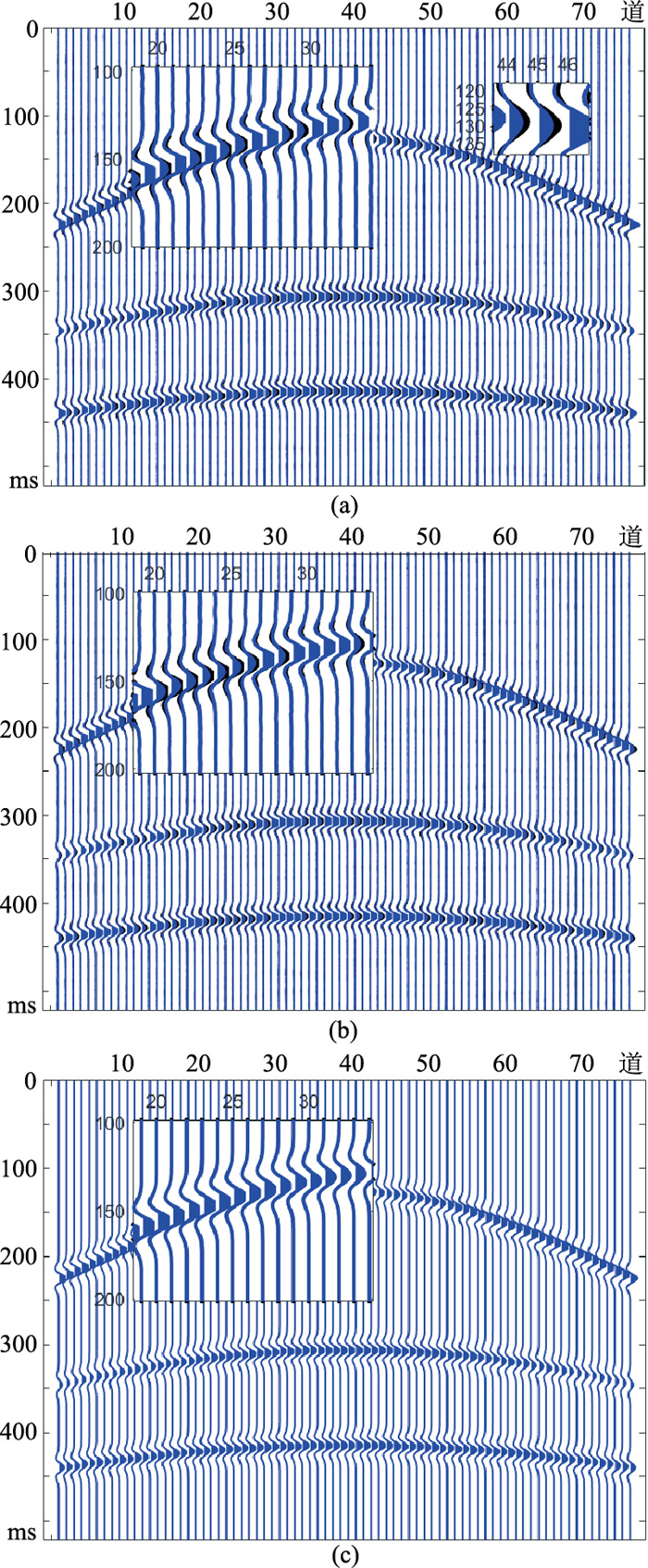
OMP算法是压缩感知框架下常用于解决优化问题的一种稀疏优化算法。分别采用OMP(图 6a)、ADMM(图 6b)和SR-ADMM(图 6c)三种算法对图 5所示随机采样模拟地震数据进行重建。
|
图 6 三种算法重建结果与原始数据对比 (a)OMP; (b)ADMM; (c)SR-ADMM |
上述三种算法的重建信噪比和均方误差如表 1所示。将这三种算法重建结果(图 6,深蓝色波形)与原始地震数据(黑色波形)进行对比,并将缺失较严重的第19~第33道数据进行局部放大。可见对于该随机缺失模拟地震数据,基于压缩感知理论的三种算法都能实现数据重建,OMP算法(图 6a)重建效果一般,从随机缺失的第21道~第26道数据,易见缺失部分重建振幅与原始振幅存在误差,且该算法对于未缺失部分(如第45道)数据产生影响,重建的均方误差相对其他两种方法较大,重建信噪比相对其他两种方法最低;ADMM算法(图 6b)重建效果较好,不会对未缺失部分数据产生影响,但缺失数据的振幅尚未得到完全恢复;SR-ADMM算法(图 6c)重建的效果最好,对数据细节的恢复更完备,同相轴清晰可见,重建数据振幅与原始地震数据振幅一致,且该算法重建信噪比最高,重建均方误差最小。
|
|
表 1 模拟数据重建信噪比和均方误差 |
由于SR-ADMM算法中平衡因子是根据地震数据自适应地选取,所选平衡因子使数据重建误差最小,从而达到提高重建精度的目的。而且,基于该算法的压缩感知数据重建模型防止了数据的过拟合现象,一定程度上也提高了数据重建精度。因此,针对随机缺失模拟地震数据,采用SR-ADMM算法重建的信噪比高于OMP和ADMM算法,即SR- ADMM算法的重建精度高于经典ADMM算法。
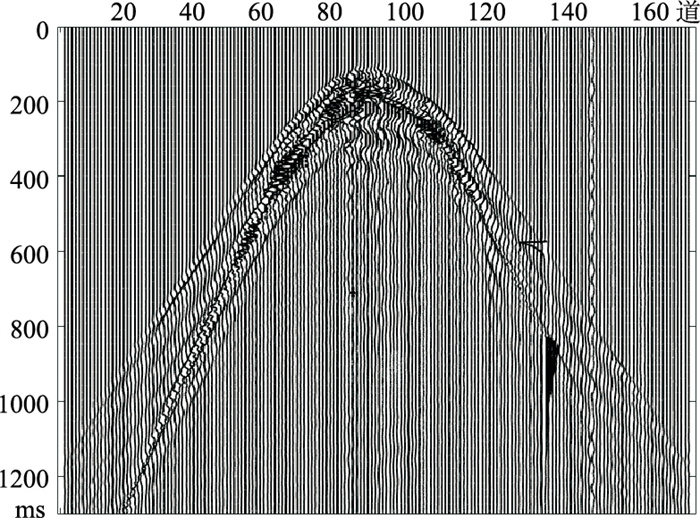
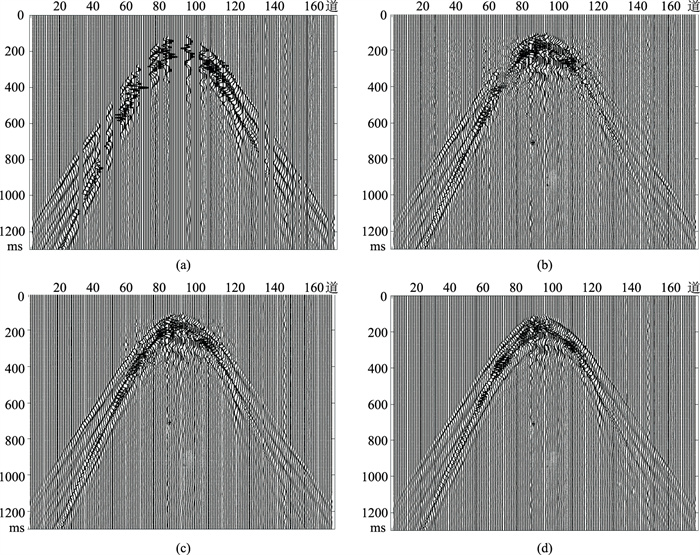
4.2 实际地震数据仿真验证选取的M油田实际单炮地震数据(图 7)共有170道,采样点数为1300,时间采样率为1ms;其缺失率为40%的单炮地震数据如图 8a所示。分别使用OMP、ADMM及SR-ADMM三种算法对缺失数据(图 8a)进行重建(图 8b~图 8d)。ADMM算法中平衡因子据多次试验后设定为λ=0.17,SR-ADMM算法的平衡因子据实际地震数据自适应地选取。三种算法对应的重建信噪比和均方误差如表 2所示。
|
图 7 实际地震数据单炮记录 |
|
图 8 实际缺失地震数据及三种算法重建后单炮记录 (a)实际缺失数据;(b)、(c)、(d)对应OMP、ADMM、SR-ADMM算法 |
|
|
表 2 实际数据重建信噪比和均方误差 |
结合表 2和图 8b~图 8d可看出:OMP算法(图 8b)重建效果欠理想,同相轴连续性较差,重建信噪比较低,均方误差较大;ADMM算法(图 8c)重建效果比OMP算法稍好,大致实现了缺失数据的重建,但重建后的数据附近出现抖动,重建信噪比较高,均方误差中等;SR-ADMM算法(图 8d)重建效果很好,同相轴更光滑,重建振幅连续性良好,在三种算法中重建信噪比最高,均方误差最小。
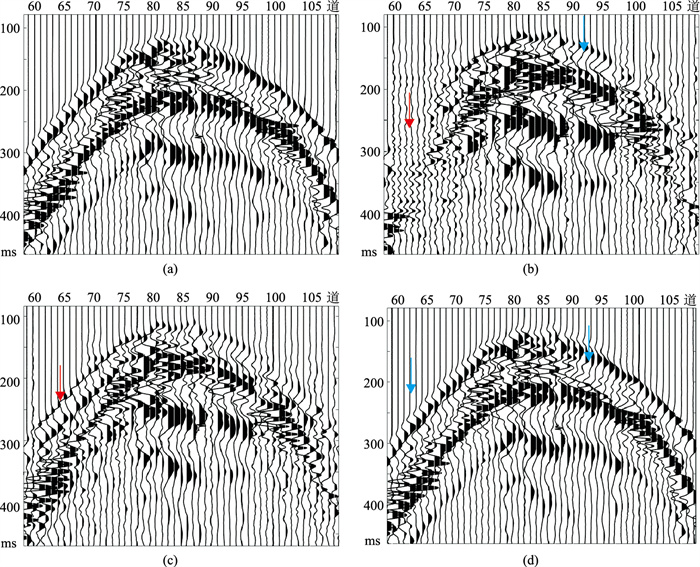
为了更直观地对比三种优化算法的重建效果,将随机采样原始数据中缺失较多的第59~第109道进行局部放大(图 9a),其中第59~第67道、第72~第74道、第76道、第78~第87道、第90~第95道、第100道及第104道为缺失数据。分别采用OMP(图 9b)、ADMM(图 9c)和SR-ADMM(图 9d)三种算法得到相应重建结果的局部放大图。
|
图 9 原始数据及OMP、ADMM、SR-ADMM三种算法重建结果局部放大 (a)原始地震数据局部放大;(b)、(c)、(d)对应OMP、ADMM、SR-ADMM三种算法重建结果的局部放大 |
对比图 9a与图 9b可看出部分缺失数据实现了重建(图 9b蓝色箭头所指),部分缺失数据未得到恢复(红色箭头所指),且重建数据振幅与原始数据有差距;对比图 9a与图 9c可见,缺失数据虽得到了恢复(图 9c蓝色箭头),但重建后的振幅与原始数据存在误差;对比图 9a与图 9d发现,所有缺失数据都得到有效恢复(图 9d蓝色箭头),且重建数据振幅与原始数据一致。
因此,采用SR-ADMM算法可以很好地重建实际地震数据复杂的细节,重建性能较好。
4.3 三维实际地震数据应用上述模拟和实际地震单炮记录验证了本文方法的有效性,进一步将本文方法应用于中国石油大庆油田实际三维数据。从该三维地震数据的一条测线中选取200道(图 10),时间采样率为1ms,采样点为500个。图 11a为随机缺失30%的该三维数据实例。ADMM算法中平衡因子据多次实验后设定为λ=0.20,SR-ADMM算法的平衡因子基于实际地震数据自适应地选取。

|
图 10 三维地震数据实例 |

|
图 11 实际缺失三维地震数据及三种算法重建结果 (a)实际缺失数据;(b)、(c)、(d)对应OMP、ADMM、SR-ADMM算法 |
同样分别采用OMP、ADMM及SR-ADMM三种算法对随机采样实际三维地震数据进行重建,得到相应的重建结果(图 11b~图 11d)。可见OMP算法的数据重建(图 11b)效果一般,未能很好地实现缺失数据的恢复重建,同相轴欠连续;ADMM算法重建数据(图 11c)效果相对较好,同相轴连续性提高,但存在同相轴抖动现象;SR-ADMM算法很好地实现了三维数据重建(图 11d),缺失位置的数据与相邻位置同相轴的走向相符合,且很连续。
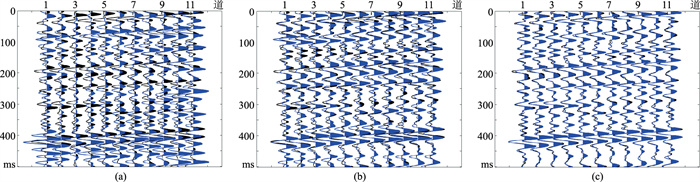
为便于比较三种算法重建效果,将三种重建结果的第50~第60道与原始数据进行放大对比(图 12)。三种算法的重建信噪比及均方误差如表 3所示。
|
图 12 三种算法重建结果(蓝色)与原始数据(黑色)的波形对比 (a)OMP; (b)ADMM; (c)SR-ADMM |
|
|
表 3 三维实际数据重建信噪比和均方误差 |
综合分析表 3和图 12所示局部放大图,可以看出OMP算法恢复地震数据(图 12a)的振幅与原始地震数据(黑色)相差较大,且重建信噪比较低,均方误差较大;ADMM算法重建(图 12b)的振幅与原始地震数据更契合,其重建信噪比高于OMP算法,均方误差较小;而SR-ADMM算法重建后(图 12c)振幅与原始地震数据几乎一致,重建信噪比最高,均方误差最小。显然,SR-ADMM算法在实际三维地震数据重建中也有效,且可提高实际三维地震数据的重建精度。
5 结束语本文提出基于压缩感知的SR-ADMM算法地震数据重建方法。该算法在原始ADMM算法基础上加入正则项正则化迭代中子问题,并且自适应地选取平衡因子,利用该算法解决最优化问题实现缺失地震数据的重建。仿真验证表明利用本文算法能有效地实现缺失地震数据,且其重建精度高于常规压缩感知地震数据重建优化算法。
需要指出的是,数据的稀疏性是压缩感知数据重建的前提,对重建效果有很大影响,数据越稀疏,重建效果越好。因此,如何更好的对地震数据进行稀疏表示是下一步的研究方向。
| [1] |
张怀榜. 复杂地表区高精度地震特殊采集方法研究及应用[D]. 四川成都: 成都理工大学, 2020. ZHANG Huaibang. Research and Application of Special High Precision Seismic Acquisition Method in Complex Surface Areas[D]. Chengdu University of Technology, Chengdu, Sichuan, 2020. |
| [2] |
Spitz S. Seismic trace interpolation in the F-X domain[J]. Geophysics, 1991, 56(6): 785-794. DOI:10.1190/1.1443096 |
| [3] |
国九英, 周兴元. F-K域等道距道内插[J]. 石油地球物理勘探, 1996, 31(2): 211-218. GUO Jiuying, ZHOU Xingyuan. Iso-spaced trace interpolation in F-K domain[J]. Oil Geophysical Prospecting, 1996, 31(2): 211-218. |
| [4] |
Claerbout J F, Nichols D. Interpolation beyond alia-sing by (tau, x)-domain PEFs[C]. Extended Abstracts of 53rd EAGE Conference & Exhibition, 1991, CP42.
|
| [5] |
Liu B, Sacchi M D. Minimum weighted norm interpolation of seismic records[J]. Geophysics, 2004, 69(6): 1560-1568. DOI:10.1190/1.1836829 |
| [6] |
Canning A, Gardner G H F. Regularizing 3D data sets with DMO[J]. Geophysics, 1996, 61(4): 1103-1114. DOI:10.1190/1.1444031 |
| [7] |
Ronen J. Wave equation trace interpolation[J]. Geophysics, 1987, 52(7): 973-984. DOI:10.1190/1.1442366 |
| [8] |
王天野. 基于傅里叶变换的反泄漏地震数据重建方法[D]. 黑龙江大庆: 东北石油大学, 2017. WANG Tianye. Research on Seismic Data Reconstruction Based on Fourier Transform[D]. Northeast Petroleum University, Daqing, Heilongjiang, 2017. |
| [9] |
常凯, 张海江, 林叶. 基于样条插值与曲波变换压缩感知的井下微地震监测数据重建[J]. 物探化探计算技术, 2016, 38(6): 788-795. CHANG Kai, ZHANG Haijiang, LIN Ye. Downhole microseismic monitoring data reconstruction based on spline interpolation and curvelet-based compressive sensing[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2016, 38(6): 788-795. DOI:10.3969/j.issn.1001-1749.2016.06.12 |
| [10] |
Naghizadeh M and Sacchi M D. Beyond alias hierarchical scale curvelet interpolation of regularly and irregularly sampled seismic data[J]. Geophysics, 2010, 75(6): WB189-WB202. DOI:10.1190/1.3509468 |
| [11] |
赵子越, 李振春, 张敏. 利用压缩感知技术的离散正交S变换地震数据重建[J]. 石油地球物理勘探, 2020, 55(1): 29-35. ZHAO Ziyue, LI Zhenchun, ZHANG Min. Seismic data reconstruction using discrete orthonormal S-transform based on compressive sensing[J]. Oil Geophysical Prospecting, 2020, 55(1): 29-35. |
| [12] |
Kuehl H. Least-squares Wave-equation Migration/Inversion[D]. University of Alberta, 2002.
|
| [13] |
Dohono D L. Compressed sensing[J]. IEEE Transactions on information theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [14] |
Candes E J, Romberg J, Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. DOI:10.1109/TIT.2005.862083 |
| [15] |
Baraniuk R. Compressive Sensing[J]. IEEE Signal Processing Magazine, 2007, 24(4): 118-121. DOI:10.1109/MSP.2007.4286571 |
| [16] |
温睿, 刘国昌, 冉扬. 压缩感知地震数据重建中的三个关键因素分析[J]. 石油地球物理勘探, 2018, 53(4): 682-693. WEN Rui, LIU Guochang, RAN Yang. Three key factors in seismic data reconstruction based on compressive sensing[J]. Oil Geophysical Prospecting, 2018, 53(4): 682-693. |
| [17] |
黄小刚. 海上压缩感知地震仿真采集设计与处理[J]. 石油地球物理勘探, 2020, 55(2): 248-256. HUANG Xiaogang. A simulation of acquisition design and data processing for offshore compressive sensing seismic[J]. Oil Geophysical Prospecting, 2020, 55(2): 248-256. |
| [18] |
白兰淑, 刘伊克, 卢回忆, 等. 基于压缩感知的Curvelet域联合迭代地震数据重建[J]. 地球物理学报, 2014, 57(9): 2937-2945. BAI Lanshu, LIU Yike, LU Huiyi, et al. Curvelet-domain joint iterative seismic data reconstruction based on compressed sensing[J]. Chinese Journal of Geophysics, 2014, 57(9): 2937-2945. |
| [19] |
周亚同, 王丽莉, 蒲青山. 压缩感知框架下基于K-奇异值分解字典学习的地震数据重建[J]. 石油地球物理勘探, 2014, 49(4): 652-662. ZHOU Yatong, WANG Lili, PU Qingshan. Seismic data reconstruction based on K-SVD dictionary lear-ning under compressive sensing framework[J]. Oil Geophysical Prospecting, 2014, 49(4): 652-660. |
| [20] |
Boyd S, Parikh N, Chu E, et al. Distributed optimization and statistical learning via alternating direction method of multipliers[J]. Foundations and Trends Machine Learning, 2011, 3(1): 1-122. |
| [21] |
钟轶君. 范数最优化问题的交替方向乘子算法[D]. 辽宁大连: 大连理工大学, 2013. ZHONG Yijun. Norm Optimization via Alternating Direction Method of Multipliers[D]. Dalian University of Technology, Dalian, Liaoning, 2013. |
| [22] |
贾慧敏. 求解最优化问题的ADMM算法的研究[D]. 湖北武汉: 华中科技大学, 2016. JIA Huimin. The Research of the ADMM Algorithm for Solving the Optimization Problem[D]. Huazhong University of Science and Technology, Wuhan, Hubei, 2016. |
| [23] |
Sternfels R, Viguier G, Gondoin R, et al. Multi-dimensional simultaneous random plus erratic noise attenuation and interpolation for seismic data by joint low-rank and sparse inversion[J]. Geophysics, 2015, 80(6): WD129-WD141. DOI:10.1190/geo2015-0066.1 |
| [24] |
Zhang L, Han L G, Liu Z G, et al. Recovery of seismic data based on compressed sensing-based alternating direction multiplier algorithm[C]. 2017 China Earth Sciences Joint Academic Annual Conference.
|
| [25] |
李慧, 韩立国, 张良, 等. 基于字典学习和ADMM的地震数据重建[J]. 石油物探, 2019, 58(3): 419-426. LI Hui, HAN Liguo, ZHANG Liang, et al. Seismic data reconstruction using dictionary learning and the alternating direction method of multipliers[J]. Geophysical Prospecting for Petroleum, 2019, 58(3): 418-426. |



 段中钰, 北京市朝阳区北四环中路35号北京信息科技大学健翔桥校区信息与通信工程学院, 100101。Email:
段中钰, 北京市朝阳区北四环中路35号北京信息科技大学健翔桥校区信息与通信工程学院, 100101。Email: 