② 中国石油西南油气田分公司, 四川成都 610041
② PetroChina Southwest Oil & Gasfield Company, Chengdu, Sichuan 610041, China
受地形、地表条件限制,山地地震勘探难以使用可控震源产生地震波,通常采用炸药作为激发震源,即在地表选定的激发点位置用钻机钻挖一口深约5~30m的井孔。作为钻井动力的柴油机,在驱动钻杆时产生持续强烈的振动,使钻头在钻进过程中与地层发生摩擦碰撞也产生振动。柴油机与钻机通过支架连接起来安置于地面,从而形成一个在地表连续振动的噪声源,该近地表振动噪声以井架为中心,向四周辐射传播,其传播规律与近地表的速度结构[1-4]密切相关。在这些设备中占突出地位的是柴油机,其振动强烈且持续不断。
事实上,地球表面始终存在一种微弱振动,通常称之为微动或环境噪声,它源于自然界和人类的各种活动。所有这些振动的能量以波的形式通过地球介质散射到达接收点,其中含有各种体波,但能量传播的主要形式是面波,即所谓的被动源面波。
Aki[5]于1957年提出一种被称为空间自相关(Spatial autocorrelation,SPAC)的被动源面波勘探方法,用于从微动中提取面波频散曲线。地震波干涉法是处理被动源面波数据的另一种方法,Clearbout[6]是此项研究的先驱者(1968年)。对于利用两检波器的道集记录做互相关运算得到的序列信号,他认为可将其视为以其中一道为(虚拟)震源点,而在另一道接收的地震记录。基于地震干涉原理的尾波技术应用于天然地震资料的分析。在全球地壳结构层析成像中获得成功应用的背景噪声互相关(Noise correlation function,NCF)也是一种地震干涉法。通过数学分析和物理模型试验,证明SPAC方法与NCF方法的物理原理是一致的[7]。
从背景噪声中提取面波格林函数的数据处理方法[8]现已较成熟。近年来,环境噪声反演成像在天然地震和工程地质勘查领域获得了大量的应用。Zhang等[9]利用地震干涉法基于城市背景噪声开展近地表调查[10-11],通过30m的排列获得了50m深度的地表结构数据。
在地震勘探炮井的钻进过程中,柴油机与钻机通过支架形成的连接体可看作一个位置明确的噪声源,它产生的近地表振动噪声连续向四周辐射传播。本文针对这两个特点,建立了在以该连接体为中心的一条辐射线上布置一系列检波器以调查近地表速度结构[12-14]的方法:采用第1道与其余各道的连续记录地表振动信号互相关构建面波的经验格林函数,并通过多道数据分析法提取面波频散曲线[15-16],从而反演得到近地表地层的速度结构[17-19]。在现场试验中还开展了多道瞬态面波采集和三分量微测井的对比分析,这三方面的结果对应一致。
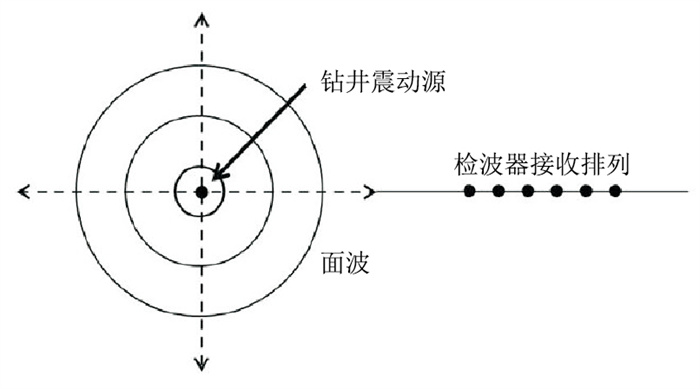
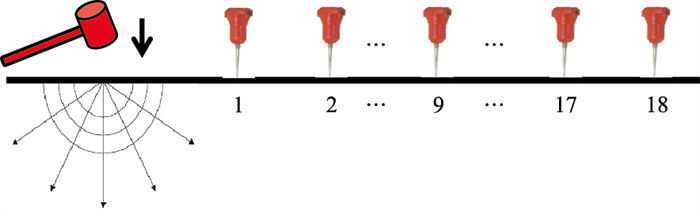
1 方法原理 1.1 采集观测系统为了用地震干涉法准确地估算面波速度,背景噪声需要在各个方向上均匀分布或接收排列在背景噪声传播的主要路径上。地震炮井钻进引起的地表振动属于传播方向明确的噪声源,因此在以噪声源为中心的一条辐射线上布置直线型接收排列是最佳观测方式(图 1)。对于山地地震勘探而言,一般在炮井附近很难找到一块长度或宽度超过30m的平地,最大偏离距常被限制在30m范围内。这样,为了能对低频(即长波长)面波分量进行充分采样,使用低频的检波器就显得尤为重要。
|
图 1 随钻振动信号的采集观测系统示意图 |
炮井钻进过程中柴油机高速运转,活塞在气缸内气体爆发压力作用下,对气缸壁进行强烈撞击,产生活塞敲击振动,这是柴油机振动的主要原因。活塞在气缸中周期性地往复运动,其频率控制了柴油机、钻头和连接支架的振动频率,因此记录到的地表振动是周期性非平稳信号,具有如下特征。
(1) 同一地震道中信号的周期长短具有一定的随机性。这是因为钻头在不同岩层中钻进速度和摩擦阻力不同,造成柴油机、钻头和连接支架的总体振动周期呈现随机性,而且不同周期中振动的幅度也呈现非平稳特征,这种性质也直接影响了地表的振动特点。
(2) 由于近地表压实程度低,对地震波衰减强,造成不同炮检距接收的振动信号振幅变化大。因此,为了避免引起地震道之间信号互相关计算误差,需做地震道信号振幅归一化处理。
1.3 随钻振动信号数据处理理论计算和众多实际观测数据表明,两点间噪声场的互相关函数与格林函数非常相似。因此,对两个检波点记录的长时间钻井地表噪声进行互相关,可提取它们之间近地表地震波场,即经验格林函数。然而,直接利用两道的地表噪声信号进行互相关计算,通常很难得到高信噪比的格林函数,这主要是因为地表振动噪声的频谱存在优势频率,其较强的能量抑制了其他频段的信号;此外,接收排列附近的人为活动等干扰源和不同道之间噪声信号振幅差异对互相关结果的影响也较大。为了减少这些不利因素的影响,首先要对原始地表振动噪声记录进行预处理,然后再进行互相关计算。其数据处理可分为三个主要步骤。
1.3.1 单道数据预处理通常一口炮井的完钻时长约为60~120min。为了提高互相关结果的信噪比,将每道的长时间记录划分为多段,每段的时长可根据记录信号的质量和总的记录道长度综合确定。一般来说,每段5min时长的信号能在互相关结果中提取到面波,段数越多,越有利于提高互相关结果的信噪比。
每段数据分别进行预处理:去均值,去趋势,带通滤波,时间域归一化和谱白化。其中最重要一步是时间域归一化处理,目的是消除排列附近的人动等干扰,并使不同道的信号振幅达到均衡。由于地震干涉法使用远场背景噪声计算格林函数,近场的不规则强能量干扰(如人动等)引起的强振幅干扰会影响计算结果的精度。因此,避免接收排列附近的强能量干扰就显得尤为重要。
滑动绝对平均值法是一种有效的时域归一化方法[8]。假定一个离散事件序列dj,利用下式
| $ {\omega _n} = \frac{1}{{2N + 1}}\sum\limits_{j = n - N}^{n + N} {\left| {{d_j}} \right|} $ | (1) |
计算一个时窗内波形数据绝对振幅的平均值,即时间点n的归一化因子ωn。逐段移动时窗,用dn除以该点的权重ωn,得到归一化的时间序列
| $ {\tilde d_n} = \frac{{{d_n}}}{{{\omega _n}}} $ | (2) |
时窗长度(2N +1)决定了有多少振幅信息可保留。
1.3.2 分段振动信号互相关与叠加设K个地震道中每个地震道都划分为M段,距离钻机最近的一道信号与其余各道信号逐段对应做互相关计算,得到M(K-1)个相关函数xk1(t)、xk2(t)、…、xkM(t)(k=1,…, K-1), 对各地震道的M个函数取平均,由于相关函数有正、负两支延迟时,将两支对应时刻的相关函数再取平均,最终得到以离钻机最近一道为震源、其余各道为接收点的地震波场经验格林函数EG,即
| $ {C_k}\left( t \right) = \frac{1}{M}\sum\limits_{i = 1}^M {{x_{ki}}\left( t \right)} $ | (3) |
| $ {\rm{EG}} = \frac{1}{2}\sum\limits_{t = 0}^{{T_d}} {\left[ {{C_k}\left( t \right) + {C_k}\left( { - t} \right)} \right]} $ | (4) |
式中Td为相关函数的最大延迟时。
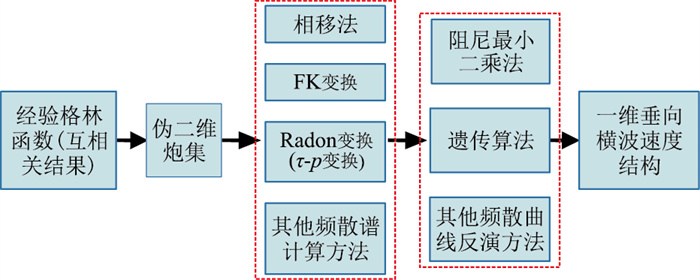
1.3.3 频散曲线的计算与反演可将从式(3)、式(4)得到的经验格林函数看作是一个二维单炮记录,应用相移法、FK及Radon(τ-p)变换等面波频散谱分析法可得到拟面波频散曲线,然后进行阻尼最小二乘法或遗传算法反演就可求得近地表的横波速度场[15, 19]。计算流程如图 2所示。
|
图 2 随钻拟面波频散曲线的计算与反演流程 |
在四川盆地秋林北地区三维地震勘探项目中对上述方法进行了试验。整个工区的近地表为第四系土壤(厚度约10m)覆盖下的砂泥岩互层结构,地震钻井深度一般为15~20m,使用的钻机类型包括空气钻机、水钻和顿钻等。试验现场如图 3所示,为山地斜坡上的一小块平地。在以钻机为起点的一条直线上布设随钻振动信号接收排列,图中红色的小盒子为能长时间连续记录的节点仪,节点仪间距为1m,共布放18个接收节点,排列总长为17m,第1道节点仪距离钻机3m。钻机于13∶46启动,直到15∶16结束,井深为15.4m。

|
图 3 随钻振动信号接收排列 |
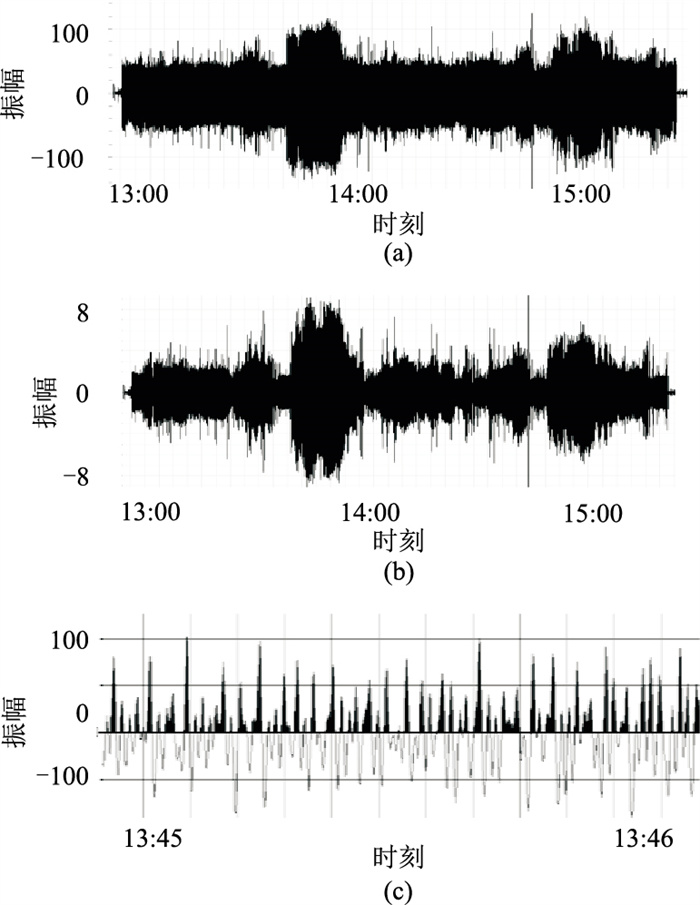
图 4展示了距离钻机最近道(图 4a,即第1道)和最远道(图 4b,即第18道)记录(90min)的近地表振动信号。它们所反映的钻井过程中近地表振动特征规律基本一致,但由于地震波传播衰减,后者的振幅小于前者。图 4c为第1道信号局部显示,可见在强振幅之间夹有一小段弱振幅,各个强振幅的幅度和间隔呈现随机性特征,表明了随钻振动信号的非平稳特征。
|
图 4 持续90min的随钻近地表振动信号 (a)、(b)分别为第1、第18道的随钻振动信号;(c)13∶45~13∶46时段的第1道信号 |
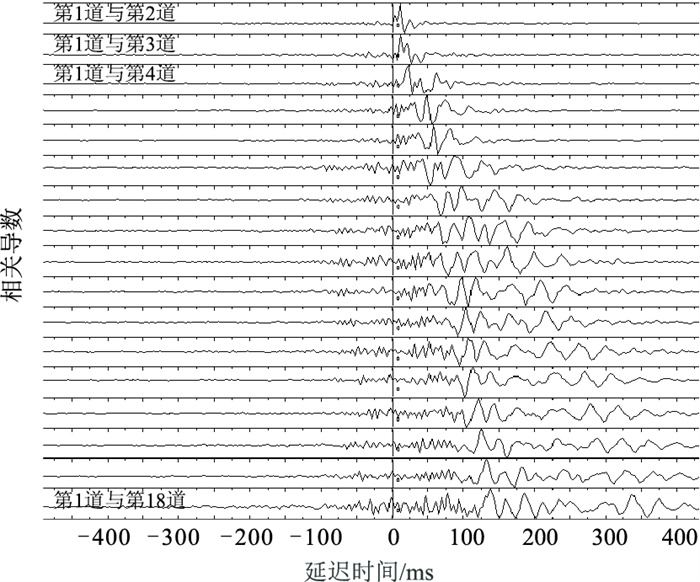
对记录的18道地震数据每道分割成15段,每段时长为6min,分段进行去均值、去趋势、时间域归一化和频率域归一化等处理,再将第1道分别与其余17道对应段数据进行互相关计算和叠加,最终得到17条互相关曲线。将相关结果对延迟时求导,并对这些导数曲线按照与第1道距离从小到大的顺序排列(图 5)。由于钻机的振动以辐射状向四周传播,接收排列布置在以钻机为中心的辐射线上,接收到的振动传播方向性明确,即从第1道向第18道沿直线传播。因此,互相关时间导数曲线的极大值集中在相关零延迟时刻的右侧,它们实际上就代表了随钻振动激发面波的经验格林函数。
|
图 5 第1道与其余17道的互相关结果对延迟时的导数 |
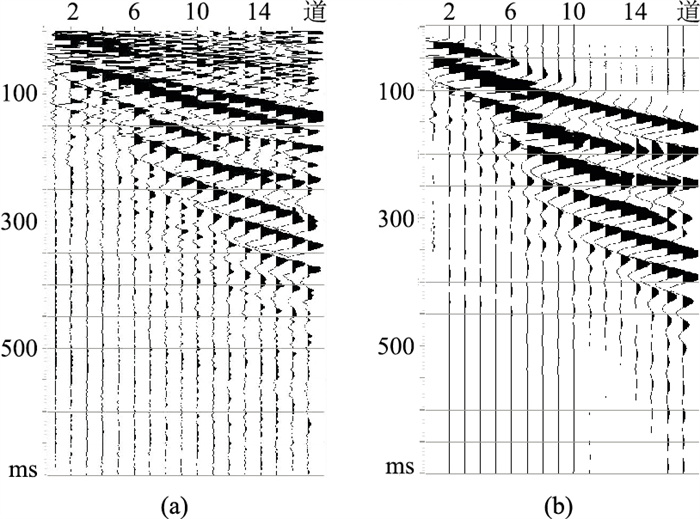
对相关零延迟时刻左、右两侧对称点的相关值取平均,并选取0~700ms时段数据,就得到图 6a所示的随钻振动激发的拟面波地震记录,它相当于震源在第1道位置处激发产生的拟面波波场。
|
图 6 随钻振动拟面波(a)和多道瞬态面波(b)记录 |
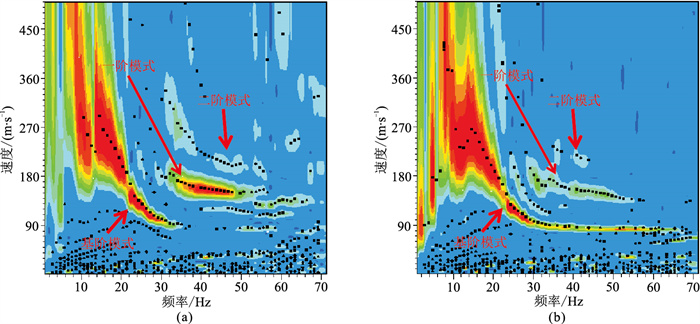
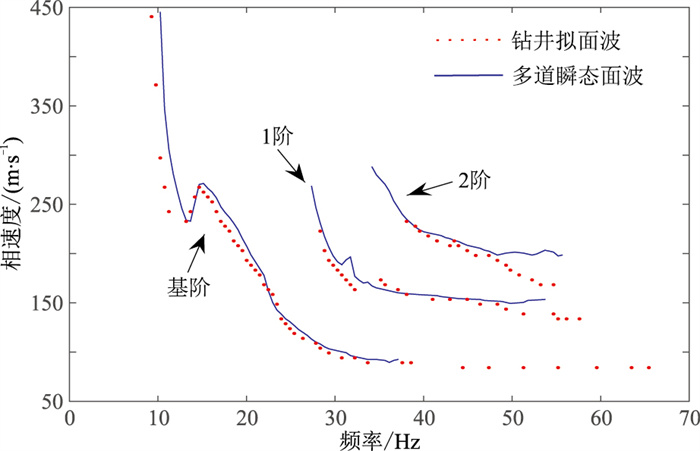
由于图 6a的拟面波波场的震源相当于在第1道位置,为了便于对比,在第1道位置使用重锤敲击(图 7),按照多道瞬态方式采集实际的面波波场,接收排列为记录随钻振动的同一个排列,得到的多道瞬态面波记录如图 6b所示。通过对比,可见两个波场非常相似,其面波同相轴出现的时间和数量也基本一致,但随钻振动拟面波记录(图 6a)中的高频成分相对多一些。对这两条记录分别进行图 8所示的频散谱分析:图中黑点表示谱振幅的局部极大值,面波的频散点就位于这些局部极大值中;在谱强振幅(红色)区域黑点代表的局部极大值点即为真正的面波频散点。从图 8还可看见基阶、1阶和2阶三种面波,它们的频散曲线基本一致(图 9),但随钻振动拟面波的1阶、2阶面波要强些,而多道瞬态面波的基阶面波更强些。
|
图 7 多道瞬态方式采集实际面波波场 |
|
图 8 随钻拟面波(a)和多道瞬态面波(b)相移法频散谱分析 |
|
图 9 随钻拟面波与多道瞬态面波频散曲线比较 |
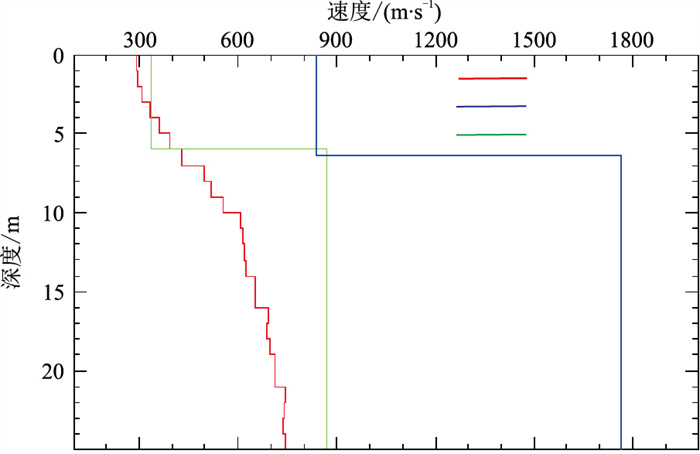
同时,还开展了数字三分量微测井对比试验,得到相应的横波(图 10中绿线)与纵波(蓝线)速度的微测井解释成果。应用阻尼最小二乘法对上述随钻振动拟面波频散曲线(图 8a)进行反演,反演初始模型采用由频散曲线计算得到的半波长模型。从反演结果(图 10中红线)可见,面波反演得到的横波速度与微测井测出的横波速度基本相符。
|
图 10 第1道与其余17道的互相关结果对延迟时的导数 |
本文现场试验的结果表明,按照被动源面波的处理方式能够从随钻振动信号中提取面波信息,反演的近地表横波速度结构与实际情况基本一致。
由于山地地形起伏变化,在炮井周边平地长(或宽)度一般不超过30m,因此排列长度被限制在30m范围内。对低频信号可能存在采样不足问题,从而影响探测深度,这是有待后续进一步研究的课题。
由于多道瞬态面波频散曲线高频段相对丰富,而随钻振动拟面波频散曲线的低频段信息相对充分,因此可对两者的频散曲线进行拼接、合并,从而拓宽频散曲线的频带范围,达到主动源方法与被动源方法联合勘探的目的。
| [1] |
金昌昆, 王延光, 尚新民, 等. 微测井与方位加权插值精细近地表速度建模技术[J]. 石油地球物理勘探, 2020, 55(2): 257-265. JIN Changkun, WANG Yanguang, SHANG Xinmin, et al. Near-surface velocity modeling based on micro-log and azimuth-weighted interpolation[J]. Oil Geophysical Prospecting, 2020, 55(2): 257-265. |
| [2] |
郭振波, 孙鹏远, 钱忠平, 等. 快速回转波近地表速度建模方法[J]. 石油地球物理勘探, 2019, 54(2): 261-267. GUO Zhenbo, SUN Pengyuan, QIAN Zhongping, et al. Fast near-surface model building with turning wave[J]. Oil Geophysical Prospecting, 2019, 54(2): 261-267. |
| [3] |
王孝, 曾华会, 刘文卿, 等. 基于微测井分步约束的近地表速度层析反演[J]. 石油地球物理勘探, 2018, 53(增刊1): 69-74. WANG Xiao, ZENG Huahui, LIU Wenqing, et al. Near-surface velocity tomographic inversion with a joint stepped-constraint of uphole and firstbreak information[J]. Oil Geophysical Prospecting, 2018, 53(S1): 69-74. |
| [4] |
赵玲芝, 谷跃民, 张建中. 多信息融合的近地表速度建模技术及应用[J]. 石油地球物理勘探, 2017, 52(1): 34-41. ZHAO Lingzhi, GU Yuemin, ZHANG Jianzhong. Near-surface model building with multi-discipline information fusion[J]. Oil Geophysical Prospecting, 2017, 52(1): 34-41. |
| [5] |
Aki K. Space and time spectra of stationary stochastic waves, with special reference to micro tremors[J]. Bulletin of the Earthquake Research Institute, University of Tokyo, 1957, 35: 415-456. |
| [6] |
Claerbout J F. Synthesis of a layered medium from its acoustic transmission response[J]. Geophysics, 1968, 33(2): 264-269. DOI:10.1190/1.1439927 |
| [7] |
Yokoi T, Margaryan S. Consistency of the spatial autocorrelation method with seismic interferometry and its consequence[J]. Geophysical Prospecting, 2008, 56(3): 435-451. DOI:10.1111/j.1365-2478.2008.00709.x |
| [8] |
Bensen G D, Ritzwoller M H, Barmin M P, et al. Processing seismic ambient noise data to obtain reliable broad-band surface wave dispersion measurements[J]. Geophysical Journal International, 2007, 169(3): 1239-1260. DOI:10.1111/j.1365-246X.2007.03374.x |
| [9] |
Zhang Y, Li Y E, Zhang H, et al. Optimized passive seismic interferometer for bedrock detection: A Singapore case study[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 2506-2510.
|
| [10] |
于承业, 周志才. 利用双井微测井资料估算近地表Q值[J]. 石油地球物理勘探, 2011, 46(1): 89-92. YU Chengye, ZHOU Zhicai. Estimation of near surface Q value based on the datasets of the uphole survey in double hole[J]. Oil Geophysical Prospecting, 2011, 46(1): 89-92. |
| [11] |
张海新, 丁伟, 刘秀玉, 等. 永新地区近地表校正方法[J]. 石油地球物理勘探, 2008, 43(增刊2): 63-66. ZHANG Haixin, DING Wei, LIU Xiuyu, et al. Near-surface correction method in Yongxin area[J]. Oil Geophysical Prospecting, 2008, 43(S2): 63-66. |
| [12] |
赵秋芳, 云美厚, 朱丽波, 等. 近地表Q值测试方法研究进展与展望[J]. 石油地球物理勘探, 2019, 54(6): 1397-1418. ZHAO Qiufang, YUN Meihou, ZHU Libo, et al. Progress and outlook of near-surface quality factor Q measurement and inversion[J]. Oil Geophysical Prospecting, 2019, 54(6): 1397-1418. |
| [13] |
苏勤, 曾华会, 田彦灿, 等. 表层Q值确定性求取与空变补偿方法[J]. 石油地球物理勘探, 2019, 54(5): 988-996. SU Qin, ZENG Huahui, TIAN Yancan, et al. Near-surface Q value estimation and quantitative amplitude compensation[J]. Oil Geophysical Prospecting, 2019, 54(5): 988-996. |
| [14] |
李伟娜, 云美厚, 党鹏飞, 等. 基于微测井资料的双线性回归稳定Q估计[J]. 石油物探, 2017, 56(4): 483-490. LI Weina, YUN Meihou, DANG Pengfei, et al. Stability Q estimation by dual linear regression based on uphole survey data[J]. Geophysical Prospecting for Petroleum, 2017, 56(4): 483-490. DOI:10.3969/j.issn.1000-1441.2017.04.003 |
| [15] |
Park C B, Miller R D, Xia J. Imaging dispersion curves of surface waves on multi-channel record[C]. SEG Technical Program Expanded Abstracts, 1998, 17: 1377-1380.
|
| [16] |
姜福豪, 李培明, 张翊孟, 等. 多道面波频散分析在实际大炮数据中的应用[J]. 石油地球物理勘探, 2018, 53(1): 17-24. JIANG Fuhao, LI Peiming, ZHANG Yimeng, et al. Frequency dispersion analysis of MASW in real seismic data[J]. Oil Geophysical Prospecting, 2018, 53(1): 17-24. |
| [17] |
沈鸿雁, 王鑫, 李欣欣. 近地表结构调查及参数反演综述[J]. 石油物探, 2019, 58(4): 471-485. SHEN Hongyan, WANG Xin, LI Xinxin. Near-surface structure survey and parameter inversion review[J]. Geophysical Prospecting for Petroleum, 2019, 58(4): 471-485. DOI:10.3969/j.issn.1000-1441.2019.04.001 |
| [18] |
李宇, 杨德义, 邓辉, 等. 初至旅行时层析反演近地表模型精度分析[J]. 石油地球物理勘探, 2011, 46(2): 221-225. LI Yu, YANG Deyi, DENG Hui, et al. Analysis on inversion accuracy of near-surface model inversed by first break traveltime tomography[J]. Oil Geophysical Prospecting, 2011, 46(2): 221-225. |
| [19] |
Xia J, Miller R D, Park C B. Estimation of near-surface shear-wave velocity by inversion of Rayleigh waves[J]. Geophysics, 1999, 64(3): 691-700. DOI:10.1190/1.1444578 |



 李彪, 四川省成都市华阳大道一段216号中国石油集团东方地球物理公司西南分公司, 610213。Email:
李彪, 四川省成都市华阳大道一段216号中国石油集团东方地球物理公司西南分公司, 610213。Email: 