② 东华理工大学江西省核地学数据科学与系统工程技术研究中心, 江西南昌 330013;
③ 东华理工大学江西省放射性地学大数据技术工程实验室, 江西南昌 330013;
④ 中国石油新疆油田分公司百口泉采油厂, 新疆克拉玛依 834000;
⑤ 东华理工大学软件学院, 江西南昌 330013
② Jiangxi Engineering Technology Research Center of Nuclear Geoscience Data Science and System, East China University of Technology, Nanchang, Jiangxi 330013, China;
③ Jiangxi Engineering Laboratory on Radioactive Geoscience and Big Data Technology, East China University of Technology, Nanchang, Jiangxi 330013, China;
④ Baikouquan Oil Production Plant of Petrochina Xinjiang Oilfield Branch, Karamay, Xinjiang 834000, China;
⑤ School of Software, East China University of Technology, Nanchang, Jiangxi 330013, China
在地震资料处理中,分辨率一直是评判处理结果的关键指标之一。特别是在开发地震中,分辨率显得尤为重要。如高分辨率处理是薄储层、低幅度构造、小断层等小尺度地质体勘探的关键技术。
常用的提高分辨率方法主要有反褶积、Q补偿、谱白化、小波变换和广义S变换等。
赵玉敏[1]认为传统反褶积技术无法较大幅度提高地震资料分辨率,同时反褶积方法是针对单道处理,容易破坏同相轴的横向连续性,且在有噪声时处理效果不稳定,因而提出一种信噪比约束下的提高分辨率方法。李红彩等[2]先应用地表一致性稳健反褶积提高叠前地震数据分辨率,再对该叠后数据应用短时窗傅里叶变换,综合应用叠前、叠后两种提高分辨率方法,为墩塘地区岩性油气藏或隐蔽油气藏勘探提供物探支撑。魏忠宇[3]提出一种径向道域反褶积方法,并应用于实际地震资料的高分辨率处理。
余连勇等[4]基于地下介质的水平层状假设,根据叠前地震记录和VSP记录观测系统的特点,给出叠前地震记录反Q滤波和VSP记录(零井源距和非零井源距)反Q滤波的统一算法和公式,并通过模型验证了方法的有效性。董相杰等[5]根据零井源距VSP下行初至波最大振幅随时间的变化趋势,将地层划分为强衰减和弱衰减两类,提出VSP强衰减地层反Q滤波。张固澜等[6]基于Futterman提出的地震波振幅衰减和相速度频散表达式,从井震匹配角度出发,阐明了反Q滤波相位补偿的必要性;并且提出一种自适应增益限的反Q滤波振幅补偿方法[7]。程志国等[8]采用改进的谱比法技术系列从VSP下行波场准确提取Q值,利用井控约束建立三维Q场,最后使用稳定的反Q滤波对叠前数据进行处理,补偿后的剖面分辨率得到提高。陈树民等[9]通过引入描述黏性吸收的等效Q值参数,发展了补偿介质吸收的叠前时间偏移方法,即基于地表观测数据建立等效Q值模型,应用补偿因子的光滑性阈值控制介质黏性吸收补偿的稳定性,提高了成像分辨率。孙明等[10]针对冀东南堡4号中浅层河道砂体识别,采用VSP井驱动Q补偿、高保真分频去噪、分频剩余静校正、井约束反褶积及优势频带反褶积等技术手段,拓宽了频带、提高了信噪比及分辨率。赵秋芳等[11]基于S变换的谱比法,探讨了获得理想Q估算值的最小含气储层厚度应不小于地震子波的主波长。周衍等[12]运用稳定化反Q滤波方法对塔河三维地震数据进行提高分辨率处理,同步实施振幅补偿和子波相位校正,展示该方法能提高对碳酸盐岩缝洞储集体特征描述的精度。
王季[13]利用Hilbert-Huang变换对地震信号进行时频分解,再通过白化滤波器对其Hilbert谱进行谱白化,增强了地震信号时域和频域的分辨率,使剖面更连续和清晰。颜中辉等[14]对地震记录进行固有模态分解(EMD),得到不同尺度的IMF分量;再利用常规谱白化方法对各分量根据瞬时频率进行合理的振幅均衡;将均衡后的IMF分量做反变换重构地震记录,从而得到高分辨地震数据。
路鹏飞等[15]根据薄互层地质特点和地震响应特征,提出一种利用小波变换提高地震资料分辨率的方法,提高了老爷庙油田地震资料分辨率。黄捍东等[16]基于广义S变换研究提高地震资料分辨率的方法。杨子鹏等[17]将广义S变换理论与压缩感知理论相结合,提出一种新的叠后地震资料处理方法,并给出补偿计算公式。本文参考了该补偿计算公式,并做了相应改进。
通过上述调研发现,反褶积方法很容易破坏同相轴的横向连续性,且有噪声存在时,该方法很不稳定[1]。反Q滤波法可补偿地震波振幅衰减,校正地震波的相位特征,从而改善地震资料同相轴的连续性,增强弱反射波的能量,提高地震资料分辨率,但现有的反Q滤波法因其补偿公式的缺陷,补偿后的地震记录会出现吉布斯效应及背景高频噪声被抬升等现象,导致地震资料信噪比降低[18]。谱白化方法可提高地震资料分辨率,但在提频同时往往会放大噪声。应用小波变换可提高地震资料分辨率,且计算速度非常快。但该类方法易对资料中的低频弱振幅信号的特征造成损害,而这些信号所蕴含的信息往往与地质体的含油气特征息息相关[19]。
在小波分析理论基础上,近年来相继出现了Ridgelet、Curvelet、Contourlet、Shearlet等变换的多尺度分析方法,其中Shearlet变换以优越的多分辨率、多尺度和多方向性特征,发展迅速,已广泛应用于信号和图像处理领域,并取得了良好的效果。同时,Shearlet变换在地学领域也有广泛应用,如数据重建[20]、面波压制[21]、随机噪声去除[22-26]、河道检测[27],被认为是目前对地震信号最优表达方式之一。
已有的提高地震分辨率方法在提高地震信号分辨率的同时往往会放大噪声,降低地震资料的信噪比,需要噪声去除辅助工作。本文根据已有提高地震资料分辨率方法的优缺点,通过Shearlet变换将地震资料转换到Shearlet域,在Shearlet域将有效信号与随机噪声分开;同时,在Shearlet域将有效信号分解成多个尺度、多个分辨率和多个方向性信号。结合Shearlet变换这两个特点,首先舍弃Shearlet域随机噪声的系数,且仅对优势尺度(频带)和代表地层方向有效范围的Shearlet域系数做提频处理。这样既提高了地震资料分辨率,又保持了信噪比。合成数据和实际资料的处理结果表明,本文方法可有效提高叠后地震资料分辨率。
1 Shearlet变换提高地震资料分辨率 1.1 二维Shearlet变换原理在二维空间,信号f的Shearlet变换为
| $ {\rm{S}}{{\rm{H}}_\mathit{\Phi }}(f) = \left\langle {f,{\mathit{\Phi }_{a,s,\mathit{\boldsymbol{p}}}}} \right\rangle $ | (1) |
式中:a、s、p分别为对应尺度、方向、位置的参数;Φa, s, p为Shearlet母函数,且满足
| $ \varPhi_{a, s, \boldsymbol{p}}(x)=\left|\operatorname{det} \boldsymbol{M}_{a, s}\right|^{\frac{-1}{2}} \varPhi\left(\boldsymbol{M}_{a, s}^{-1} x-\boldsymbol{p}\right) $ | (2) |
式中:a∈R+,s∈R,p∈R2,且R+、R、R2分别表示正实数集、实数集及二维实向量集;x为自变量;中间矩阵
| $ \boldsymbol{M}_{a, s}=\left(\begin{array}{ll} a & \sqrt{a} s \\ 0 & \sqrt{a} \end{array}\right) $ | (3) |
式中Ma, s=SsAa,其中Ss为剪切矩阵,Aa为各向异性扩散矩阵,且有
| $ \boldsymbol{S}_{s}=\left(\begin{array}{ll} 1 & s \\ 0 & 1 \end{array}\right) \quad \boldsymbol{A}_{a}=\left(\begin{array}{lc} a & 0 \\ 0 & \sqrt{a} \end{array}\right) $ | (4) |
Shearlet反变换为
| $ f=\int_{\boldsymbol{R}^{2}} \int_{-\infty}^{\infty} \int_{0}^{\infty}\left\langle f, \varPhi_{a, s, \boldsymbol{p}}\right\rangle \varPhi_{a, s, \boldsymbol{p}} \frac{\mathrm{d} a}{a^{3}} \mathrm{~d} s \mathrm{~d} \boldsymbol{p} $ | (5) |
连续Shearlet变换可离散化。由于∀a>0,b∈A,可得对应的离散化尺度矩阵A和剪切矩阵B
| $ \boldsymbol{A}=\left(\begin{array}{cc} a & 0 \\ 0 & \sqrt{a} \end{array}\right) \quad \boldsymbol{B}=\left(\begin{array}{ll} 1 & b \\ 0 & 1 \end{array}\right) $ | (6) |
当a=4,b=1时,
令a=2-j,s=-l,则有
| $ \varPhi_{j, l, \boldsymbol{k}}=\left|\operatorname{det} \boldsymbol{A}_{0}\right|^{\frac{j}{2}} \varPhi\left(\boldsymbol{B}_{0}^{l} \boldsymbol{A}_{0}^{j} \boldsymbol{x}-\boldsymbol{k}\right) $ | (7) |
式中:j, l∈Z,k∈Z2,离散化Shearlet变换为
| $ {\rm{S}}{{\rm{H}}_\mathit{\Phi }}(f) = \left\langle {f,{\mathit{\Phi }_{j,l,\mathit{\boldsymbol{k}}}}} \right\rangle $ | (8) |
其反变换为
| $ f = \left\langle {f,{\mathit{\Phi }_{j,l,\mathit{\boldsymbol{k}}}}} \right\rangle {\mathit{\Phi }_{j,l,\mathit{\boldsymbol{k}}}} $ | (9) |
地震数据s(t, x, y)经Shearlet变换,可表示为
| $ {c_{j,l,\mathit{\boldsymbol{k}}}} = \left\langle {s,{\mathit{\Phi }_{j,l,\mathit{\boldsymbol{k}}}}} \right\rangle $ | (10) |
式中cj, l, k是Shearlet变换后尺度为j、方向为l、位置为k的Shearlet域系数。
地震数据可从Shearlet域系数反变换得到
| $ s = \sum\limits_{j,l,\mathit{\boldsymbol{k}}} {\left\langle {s,{\mathit{\Phi }_{j,l,\mathit{\boldsymbol{k}}}}} \right\rangle } {\mathit{\Phi }_{j,l,\mathit{\boldsymbol{k}}}} = \sum\limits_{j,l,\mathit{\boldsymbol{k}}} {{c_{j,l,\mathit{\boldsymbol{k}}}}} {\mathit{\Phi }_{j,l,\mathit{\boldsymbol{k}}}} $ | (11) |
对M×N个数据点的地震数据进行Shearlet变换,其变换后各尺度方向上的Shearlet系数都是M×N,Shearlet系数与原始地震数据在位置上具有一一对应的关系。因此,Shearlet变换对尺度方向表征更细腻,变换系数的物理意义更明确。
从式(11)可看到,对Shearlet域系数进行相应的处理,可得到新的地震数据。
地震波在地下传播过程中,若没有地层吸收和地震波频率及能量等的衰减,深、浅层反射波具有相同频宽的振幅谱,相位谱仅差一线性相位。如果把地震记录分成不同的频率(尺度)和不同的方向,所对应时间及空间的能量分布关系具有相似性,即对所有频率(尺度)而言,深层反射的能量与同一频率浅层反射能量之比应相同,所不同的只是各频率的绝对能量大小不一样。但由于地层的吸收及地震波的衰减,造成各频率能量对时间及空间的分布不同,在Shearlet域给表征地层的域系数乘以补偿因子,就起到了对地层吸收及地震波衰减的补偿作用。通过对Shearlet系数进行相应处理,可实现提高地震资料分辨率的目的。具体方法如下:
(1) 对地震数据进行Shearlet变换,得到Shearlet域系数。
(2) 因随机噪声本身无方向性且服从高斯分布,故随机噪声分解后,其Shearlet域系数值低且也是随机分布、无方向性,这在Shearlet域系数剖面中很易识别,应将该部分的域系数置为零。
(3) 分离完噪声与有效信号后,需对新的优势频带范围内的Shearlet域系数c′j, l, k做能量补偿和提频处理。在Shearlet域系数中,最后一个Shearlet域系数数据代表原始信号的低频信息。为了提高中高频信号,不需对最后一个Shearlet域系数数据进行处理。地震数据的中低频信息能量相对较强,而中高频(尤其是高频)信息的能量相对较弱,但这些中高频信号含有更丰富的地层信息。通常,地震数据变换到Shearlet域,在Shearlet域中反映厚度较大地层的中低频信息域系数相对较强,反映厚度较薄地层信息的域系数较弱,需在Shearlet域对该部分信号进行补偿,使补偿后其能量与低、中频信号能量尽可能接近,从而拓宽地震信号的频宽,抬升中高频信号,进而提高地震资料的分辨率。
在Shearlet域补偿计算公式为
| $ {c''_{j,l,\mathit{\boldsymbol{k}}}} = {c'_{j,l,\mathit{\boldsymbol{k}}}} \times \left( {\frac{{{\rm{MM}}}}{{(1 - \alpha )\left| {{{c'}_{j,l,\mathit{\boldsymbol{k}}}}} \right| + \alpha \times {\rm{MM}}}}} \right) $ | (12) |
式中:MM=max(|c′j, l, k|);α为提高分辨率因子,其取值视实情而定,通常的取值范围是0,1。α的取值主要考虑地震资料的信噪比和待分辨地层的厚度,若地震资料信噪比低,则α相对要大些;若地震资料信噪比较高,且要区分相对较薄地层,则α相对要小些。
(4) 对补偿后Shearlet域系数c″j, l, k进行反变换,得到提高分辨率后的地震数据
| $ {s_0} = \sum\limits_{j,l,\mathit{\boldsymbol{k}}} {{{c''}_{j,l,\mathit{\boldsymbol{k}}}}} {\mathit{\Phi }_{j,l,\mathit{\boldsymbol{k}}}} $ | (13) |
应用上述方法,既提高了地震资料分辨率,又保持了处理后信号的信噪比。
2 理论模型试验为了验证此方法的可行性,设计了理论模型。测试重点是基于Shearlet变换提频方法的高频成分恢复能力。
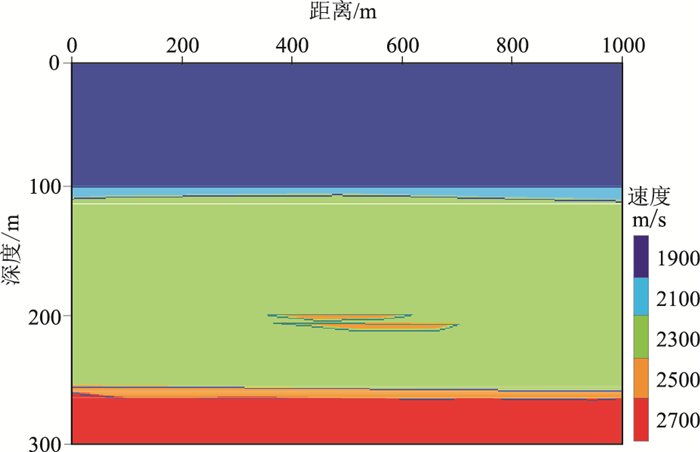
构建如图 1所示的理论模型,横向范围是0~1000m,深度范围是0~300m。在模型100m处嵌入一套速度为2100m/s的砂岩体,砂岩体厚度范围是10~21m。在模型200m处嵌入两个叠置的速度为2500m/s的砂岩透镜体1和砂岩透镜体2。
|
图 1 理论模型 |
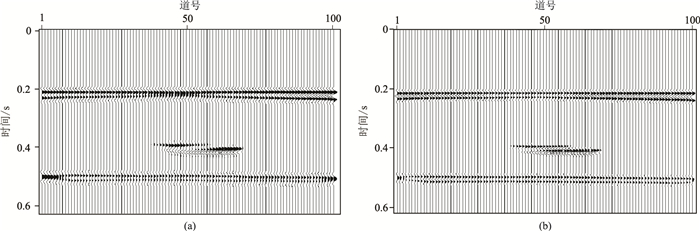
图 2分别用主频为30Hz和45Hz的零相位Ricker子波进行正演,得到子波合成记录。通过对图 2的正演剖面做Shearlet变换提频处理以验证该方法的有效性。
|
图 2 30Hz(a)和45Hz(b)零相位Ricker子波合成记录 |
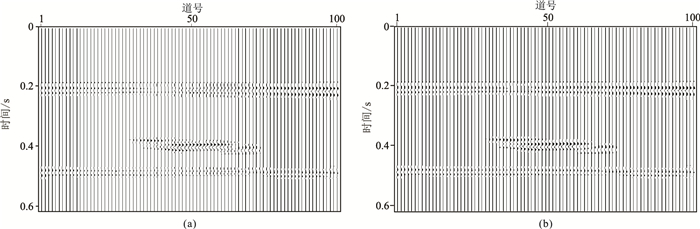
将正演剖面进行Shearlet变换,其中Shearlet变换的尺度数为4,变换后形成49个域系数剖面。在该剖面中选取能在一定程度上反映砂体细节信息的Shearlet域系数,并用本文方法进行补偿(图 3),可见在Shearlet域经本文方法补偿后(图 3b)的薄层信息体现得更清晰。
|
图 3 补偿前(a)、后(b)的经Shearlet变换第33个域系数剖面 |
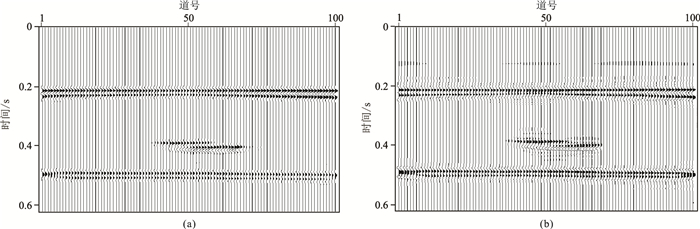
将补偿后的Shearlet域系数反变换得到提频后剖面(图 4a)。与图 2a相比,可见第一套砂体最薄处砂体边界完全分开:速度为2100m/s的砂体在第30~第52道之间地震同相轴已完全分开;速度为2500m/s的砂体在第32~第40道之间、第68~第87道之间地震同相轴也已完全分开;透镜体1和透镜体2的边界特征也与原模型匹配较好,两个透镜体细节信息也很好地展示出来。Shearlet变换提高分辨率方法效果(图 4a)与直接用45Hz主频子波正演的剖面(图 2b)基本一致。
|
图 4 对图 2a应用本文方法(a)和小波变换方法(b)处理后结果 |
另外,将此方法与小波变换提频进行对比,可见图 4b的第41~第51道之间速度为2500m/s的砂体地震同相轴未分开。应用小波变换后,两个透镜体附近的噪声干扰有所增强(图 4b)。
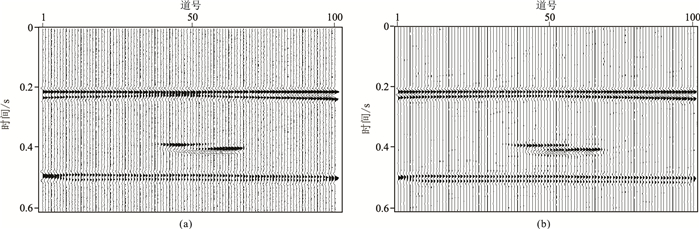
在理论模型中加入10%的随机噪声(图 5a),验证该方法对随机噪声的稳定性。本文方法仍能分离出所有砂体的反射地震轴(图 5b),并减少了噪声影响。而小波变换提频后噪声成分有所增强(图 6)。
|
图 5 加入10%高斯白噪声(a)和应用本文方法提高分辨率处理后结果(b) |

|
图 6 对图 5a应用小波变换方法提高分辨率处理后结果 |
为了比较Shearlet变换中不同分解尺度对提高地震资料分辨率的影响,分别以图 2的数据为试验对象,依次测试了尺度数为3、4、5的情形。图 7a和图 7c分别是尺度数为3和尺度数为5的处理结果,可见尺度为4是较合适(图 7b)。

|
图 7 不同分解尺度提高分辨率后地震数据对比 (a)尺度数为3;(b)尺度数为4;(c)尺度数为5 |
从该模型试验可知,利用Shearlet变换提高分辨率处理方法能有效补偿有效地震波能量,有效提高薄砂体识别能力,提高地震资料分辨率。
3 实际资料应用M区块前期已有地震数据无法满足现阶段的开发地质需求,因此将本文方法应用到该区块实际叠后地震数据,通过提频处理后再进行谱分解等属性提取及后续综合地质研究。
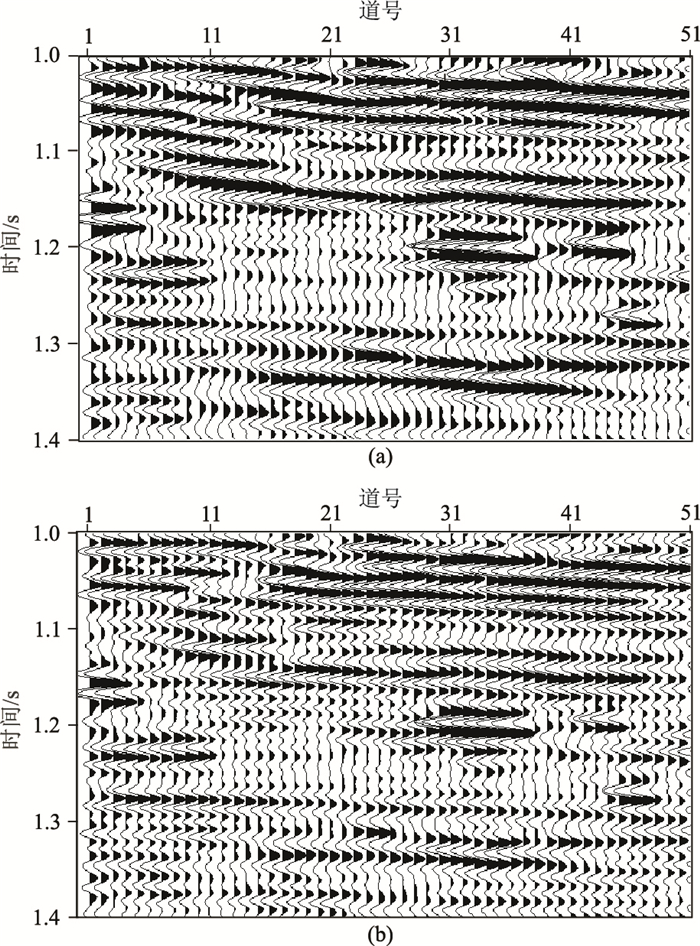
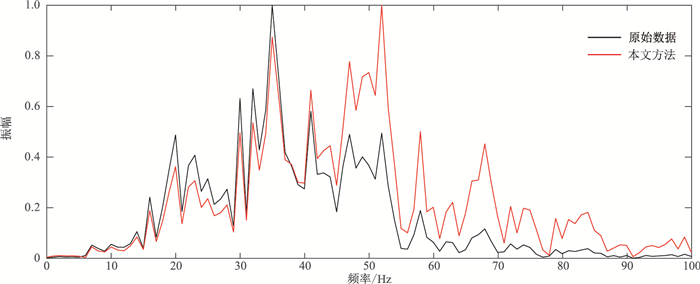
针对该区原始地震数据(图 8a),应用本文方法提高分辨率后(图 8b),地层波组特征更清晰,在组段内部,地质信息变得丰富,薄层及砂层组、单砂体呈现得更明显。从分辨率扩展前、后的频谱(图 9)可以看到,提频前的频带是8~70Hz,主频约35Hz,提频后的频带是8~90Hz,主频提高到约52Hz,提频后频带明显拓宽。
|
图 8 提高分辨率前(a)、后(b)地震数据对比 |
|
图 9 提频前、后地震数据频谱对比 |
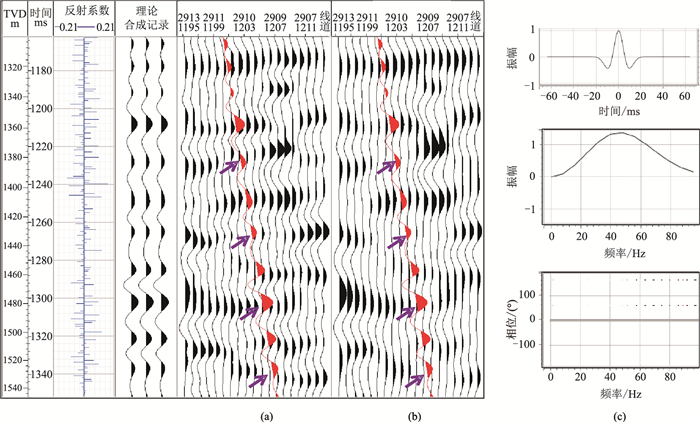
在图 10所示井旁合成地震记录中,地震子波是主频为45Hz的零相位Ricker子波。将井与原始地震数据及提高分辨率后地震数据分别进行比较,可见本文方法较好地提高了分辨率,且与井中信息吻合得较好。
|
图 10 过井合成记录对比及所采用子波 (a)提高分辨率后地震数据;(b)原始地震数据;(c)子波波形(上)及其振幅谱(中)、相位谱(下) |
通过对比、分析提高分辨率前、后地震数据的谱分解属性剖面(图 11),可以看出本文方法显著地提高了三维地震资料的空间分辨率,属性剖面上河道(箭头处)特征更易于识别。

|
图 11 提高分辨率前(a)、后(b)谱分解属性剖面 |
本文根据Shearlet变换的特点、地震资料中有效信号及优势频带与随机噪声在Shearlet域的差异,同时基于地层吸收及地震波衰减补偿原理,在Shearlet域对地层吸收及地震波衰减进行补偿。理论模型及实际地震数据的应用表明,利用Shearlet变换方法可以提高地震资料分辨率,并且此方法能保持较高信噪比。从实际资料的处理结果可看出,提高分辨率后剖面上地层和砂体特征变得更清晰,复波被有效分离,高频成分明显加强,低频部分也得到保持,在谱分解属性剖面上河道更清晰易辨,有利于后续开发地震及地质工作的开展。
| [1] |
赵玉敏. 信噪比约束下的提高分辨率方法研究[D]. 北京: 中国石油大学(北京), 2017. ZHAO Yumin. Research on Resolution Enhancement Method with Adaptive Lateral Constraint Based on Denoising Filter[D]. China University of Petroleum(Beijing), Beijing, 2017. |
| [2] |
李红彩, 罗军梅. 提高分辨率处理技术在墩塘地区的应用[J]. 工艺技术, 2019, 9: 227-228. LI Hongcai, LUO Junmei. Application of processing technology to improve resolution in Duntang area[J]. Process technology, 2019, 9: 227-228. |
| [3] |
魏忠宇. 径向道域反褶积提高地震资料分辨率方法研究[D]. 吉林长春: 吉林大学, 2020. WEI Zongyu. The Radial Trace Domain Deconvolution to Improve the Resolution of Seismic Data[D]. Jinlin University, Changchun, Jilin, 2020. |
| [4] |
余连勇, 胡光义, 赵岩, 等. 稳定的反Q滤波统一算法及其在地震资料高分辨率处理中的应用[J]. 中国海上油气, 2014, 26(4): 29-33. YU Lianyong, HU Guangyi, ZHAO Yan, et al. A unified algorithm of stable inverse Q filtering and its application to high resolution processing of seismic data[J]. China Offshore Oil and Gas, 2014, 26(4): 29-33. |
| [5] |
董相杰, 余杰, 王珊, 等. 强衰减地层VSP反Q滤波方法[J]. 石油地球物理勘探, 2014, 49(5): 871-876. DONG Xiangjie, YU Jie, WANG Shan, et al. VSP inverse Q filtering in strong attenuation formation[J]. Oil Geophysical Prospecting, 2014, 49(5): 871-876. |
| [6] |
张固澜, 贺振华, 王熙明, 等. 地震波频散效应与反Q滤波相位补偿[J]. 地球物理学报, 2014, 57(5): 1655-1663. ZHANG Gulan, HE Zhenhua, WANG Ximing, et al. Seismic wave dispersion effects and inverse Q filter phase compensation[J]. Chinese Journal of Geophy-sics, 2014, 57(5): 1655-1663. |
| [7] |
张固澜, 林进, 王熙明, 等. 一种自适应增益限的反Q滤波[J]. 地球物理学报, 2015, 58(7): 2525-2535. ZHANG Gulan, LIN Jin, WANG Ximing, et al. A self-adaptive approach for inverse Q filtering[J]. Chinese Journal of Geophysics, 2015, 58(7): 2525-2535. |
| [8] |
程志国, 娄兵, 姚茂敏, 等. VSP井控Q值提取和补偿方法在玛湖地区的应用[J]. 物探化探计算技术, 2015, 37(6): 749-753. CHENG Zhiguo, LOU Bing, YAO Maomin, et al. Application of VSP well controlled Q extraction and compensation method in Mahu area[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2015, 37(6): 749-753. DOI:10.3969/j.issn.1001-1749.2015.06.13 |
| [9] |
陈树民, 刘礼农, 张剑锋, 等. 一种补偿介质吸收叠前时间偏移技术[J]. 石油物探, 2018, 57(4): 576-583. CHEN Shumin, LIU Linong, ZHANG Jianfeng, et al. A deabsorption prestack time migration technology[J]. Geophysical Prospecting for Petroleum, 2018, 57(4): 576-583. DOI:10.3969/j.issn.1000-1441.2018.04.011 |
| [10] |
孙明, 赵宝银, 陈伟超, 等. 针对冀东南堡4号中浅层河道砂体识别的提高分辨率处理[J]. 物探化探计算技术, 2018, 40(4): 417-424. SUN Ming, ZHAO Baoyin, CHEN Weichao, et al. High resolution seismic data processing aimed at channel sand body recognition in middle shallow layers, Jidong Nanpu 4 structure[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2018, 40(4): 417-424. DOI:10.3969/j.issn.1001-1749.2018.04.02 |
| [11] |
赵秋芳, 党鹏飞, 云美厚, 等. 不同时频变换谱比法品质因子Q估算效果对比分析[J]. 地球物理学进展, 2018, 33(5): 2097-2101. ZHAO Qiufang, DANG Pengfei, YUN Meihou, et al. Comparative analysis of quality factor Q estimated by spectral ratio method based on different time frequency transform[J]. Progress in Geophysics, 2018, 33(5): 2097-2101. |
| [12] |
周衍, 饶莹. 地震反Q滤波应用于碳酸盐岩储层特征描述[J]. 地球物理学报, 2018, 61(1): 284-292. ZHOU Yan, RAO Ying. Seismic inverse Q filtering for carbonate reservoir characterization[J]. Chinese Journal of Geophysics, 2018, 61(1): 284-292. |
| [13] |
王季. 基于Hilbert谱白化的高分辨率地震资料处理[J]. 煤炭学报, 2012, 37(1): 50-54. WANG Ji. High resolution seismic processing based on whitening of Hilbert spectrum[J]. Journal of China Coal Society, 2012, 37(1): 50-54. |
| [14] |
颜中辉, 方刚, 徐华宁, 等. 希尔伯特谱白化方法在海洋地震资料高分辨率处理中的应用[J]. 海洋地质与第四纪地质, 2018, 38(4): 212-220. YAN Zhonghui, FANG Gang, XU Huaning, et al. The application of Hilbert spectral whitening method to high resolution processing of marine seismic data[J]. Marine Geology & Quaternary Geology, 2018, 38(4): 212-220. |
| [15] |
路鹏飞, 郭爱华, 赵宝银, 等. 利用小波分析技术提高老爷庙油田地震资料分辨率[J]. 石油地球物理勘探, 2012, 47(2): 272-276. LU Pengfei, GUO Aihua, ZHAO Baoyin, et al. Seismic data resolution improvement in Laoyemiao by wavelet analysis[J]. Oil Geophysical Prospecting, 2012, 47(2): 272-276. |
| [16] |
黄捍东, 冯娜, 王彦超, 等. 广义S变换地震高分辨率处理方法研究[J]. 石油地球物理勘探, 2014, 49(1): 82-88. HUANG Handong, FENG Na, WANG Yanchao, et al. High resolution seismic processing based on gene-ralized S transform[J]. Oil Geophysical Prospecting, 2014, 49(1): 82-88. |
| [17] |
杨子鹏, 宋维琪, 刘军, 等. 联合广义S变换和压缩感知提高地震资料分辨率[J/OL]. 地球物理学进展(网络首发), 2020: 1-11. YANG Zipeng, SONG Weiqi, LIU Jun, et al. Combine generalized S transform with compressed sensing to improve the resolution of seismic data[J/OL]. Progress in Geophysics, 2020: 1-11. |
| [18] |
宋鑫磊. 地震资料反Q滤波法研究及应用[D]. 四川成都: 成都理工大学, 2019. SONG Xinlei. The Study and Application of Inverse Q-filtering for Seismic Data[D]. Chengdu University of Technology, Chengdu, Sichuan, 2019. |
| [19] |
李曙光, 唐建明, 徐天吉, 等. 几种提高地震资料分辨率的方法及效果分析[J]. 勘探地球物理进展, 2010, 33(5): 323-327. LI Shuguang, TANG Jianming, XU Tianji, et al. Methods for improving seismic data resolution[J]. Progress in Exploration Geophysics, 2010, 33(5): 323-327. |
| [20] |
王常波. 基于Shearlet稀疏变换基的压缩感知重建技术[J]. 地球物理学进展, 2018, 33(6): 2441-2449. WANG Changbo. Compressed sensing seismic data reconstruction with Shearlet transformation[J]. Progress in Geophysics, 2018, 33(6): 2441-2449. |
| [21] |
王德营, 李振春, 董烈乾. Shearlet域和TT域联合压制面波方法[J]. 石油地球物理勘探, 2014, 49(1): 53-60. WANG Deying, LI Zhenchun, DONG Lieqian. Surface wave joint suppression based on Shearlet transformation and time-time transformation[J]. Oil Geophysical Prospecting, 2014, 49(1): 53-60. |
| [22] |
李民, 周亚同, 李梦瑶, 等. Shearlet域基于非局部均值的地震信号去噪[J/OL]. 重庆大学学报(网络首发), 2019. LI Min, ZHOU Yatong, LI Mengyao, et al. Denoising of seismic signals based on non-local mean in Shearlet domain[J/OL]. Journal of Chongqing University, 2019. |
| [23] |
童思友, 高航, 刘锐, 等. 基于Shearlet变换的自适应地震资料随机噪声压制[J]. 石油地球物理勘探, 2019, 54(4): 744-750. TONG Siyou, GAO Hang, LIU Rui, et al. Seismic random noise adaptive suppression based on the Shearlet transform[J]. Oil Geophysical Prospecting, 2019, 54(4): 744-750. |
| [24] |
董新桐, 马海涛, 李月. 丘陵地带地震资料随机噪声压制新技术: 高阶加权阈值函数的Shearlet变换[J]. 地球物理学报, 2019, 62(10): 4039-4046. DONG Xintong, MA Haitao, LI Yue. The new technology for suppression of hilly land seismic random noise: Shearlet transform and the high order weighted threshold function[J]. Chinese Journal of Geophysics, 2019, 62(10): 4039-4046. DOI:10.6038/cjg2019M0582 |
| [25] |
程浩, 王德利, 王恩德, 等. 尺度自适应三维Shearlet变换地震随机噪声压制[J]. 石油地球物理勘探, 2019, 54(5): 970-978. CHENG Hao, WANG Deli, WANG Ende, et al. Seismic random noise suppression based on scale adaptive 3D Shearlet transform[J]. Oil Geophysical Prospecting, 2019, 54(5): 970-978. |
| [26] |
薛林, 程浩, 巩恩普, 等. Shearlet域自适应阈值地震数据随机噪声压制[J]. 石油地球物理勘探, 2020, 55(2): 282-291. XUE Lin, CHENG Hao, GONG Enpu, et al. Random noise suppression using adaptive threshold in Shearlet domain[J]. Oil Geophysical Prospecting, 2020, 55(2): 282-291. |
| [27] |
Karbalaali H, Javaherian A, Dahlke S, et al. Seismic channel edge detection using 3D Shearlets-a study on synthetic and real channelized 3D seismic data[J]. Geophysical Prospecting, 2018, 66(7): 1272-1289. DOI:10.1111/1365-2478.12629 |



 路鹏飞, 江西省南昌市经开区广兰大道418号东华理工大学信息工程学院, 330013。Email:
路鹏飞, 江西省南昌市经开区广兰大道418号东华理工大学信息工程学院, 330013。Email: 