② 中国地质大学(武汉)湖北省地球内部多尺度成像重点实验室, 湖北武汉 430074
② Hubei Subsurface Multi-scale Imaging Lab(SMIL), China University of Geosciences, Wuhan, Hubei 430074, China
英国学者Rayleigh于1887年发现瑞雷面波,并论证了它在均匀半空间内的存在。早期瑞雷波常被视作干扰波;但随着瑞雷波的频散等特性被发现,它逐渐被用于地球物理勘查中。与其他常用地球物理勘探方法相比[1-2],瑞雷波勘探具有快速、轻便、无损等优点[3],所以近年来在浅地表地球物理工程和无损检测等领域获得了广泛应用[4-5]。
通过反演瑞雷波频散曲线可获得各层的横波速度和地层厚度,进而进行地质结构分层[6-7]。然而,瑞雷波频散曲线反演是一个典型的高度非线性、多参数、多极值地球物理优化问题。这些常用反演方法可分成两大类:局部线性化反演与非线性化反演。局部线性反演算法有:最小二乘法、OCCAM算法[8]和最速下降法[9]等。该类方法利用泰勒级数展开,近似地将瑞雷波方程线性化,并用扰动法计算雅可比矩阵,因此对初始模型依赖性强,只有当初始模型接近真实模型时才能获得较好的反演结果,否则容易导致反演过程失败;同时,雅可比矩阵的计算精度也将直接影响反演结果的质量。非线性全局优化算法有:蒙特卡洛算法、遗传算法和模拟退火算法等[10]。该类算法尽管放松了对初始模型的选取,然而也存在计算量大,收敛速度慢、精度较低、容易出现早熟收敛等情况[11-12]。
近年来对人工神经网络的研究与应用成为热点,它具有自组织、求得最优解而不是精确解、容错性强等优点,因此已在地球物理反演领域崭露头角。曹旭等[11]、周晓华等[13]尝试将人工神经网络用于瑞雷波频散曲线反演,并进行了简单速度递增型理论模型试算和两层递增型实例分析。利用人工神经网络进行反演的最关键环节是建立训练样本集,这将直接影响人工神经网络的反演精度和效率。然而,此前的研究在建立训练样本集时假定地下地质模型类型已知(如两层递增模型),通过给定待反演参数(即各层横波速度和地层厚度)、固定步长的增量建立训练样本集,这不仅极大增加了样本数量和网络训练时间,而且建立的样本集代表性差,不能有效刻画地下可能出现的各种地质模型。因此,该类方法在瑞雷波频散曲线理论模型试算和实测资料反演中有很大局限性。
针对建立人工神经网络反演训练样本集的困难性,本文通过给定待反演参数搜索范围,在该范围内随机生成各种训练样本,进而建立多样训练样本集。这种建立方法不仅有效降低了训练样本数和网络训练时间,而且训练样本集代表性强,能有效刻画地下可能出现的各种地质模型,且无需预先已知地质结构类型。通过对实际近地表勘查中三种典型理论模型的试算和算法抗噪性测试,检验了本文设计的人工神经网络反演方案的可行性和有效性;通过实例分析,并与其他遗传算法对比,进一步检验了人工神经网络算法的实用性和优越性。
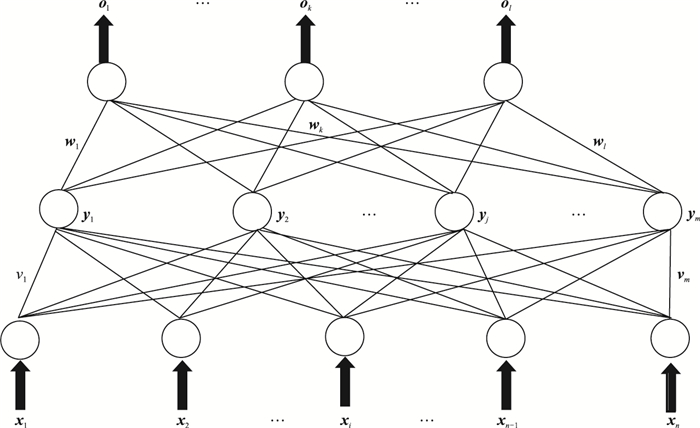
1 BP神经网络基本原理、算法及反演流程 1.1 BP神经网络模型图 1为最普遍应用的单隐层神经网络模型,包括输入层、隐含层和输出层,故也被称为三层感知器。
|
图 1 BP神经网络模型 |
输入向量为X=(x1, x2, …,xi, …, xn)T;
隐含层输出向量为Y=(y1, y2, …,yj, …, ym)T;
输出层输出向量为O=(o1, o2, …,ok, …, ol)T;
期望输出向量为d=(d1, d2, …,dk, …, dl)T。
输入层到隐层之间的权值矩阵用V=(v1, v2, …,vj, …, vm)表示,其中列向量vj为隐含层第j个神经元对应的权向量。
隐含层到输出层之间的权值矩阵用W=(w1, w2, …,wk, …, wl)表示,其中列向量wk为输出层第k个神经元对应的权向量。
各层信号之间有如下数学关系。
隐含层有
| $ \begin{cases}\boldsymbol{y}_{j}=f\left(\operatorname{net}_{j}\right) & j=1,2, \cdots, m \\ \text {net}_{j}=\sum\limits_{i=0}^{n} v_{i j} \boldsymbol{x}_{i} & j=1,2, \cdots, m\end{cases} $ | (1) |
输出层有
| $ \begin{cases}\boldsymbol{o}_{k}=f\left(\operatorname{net}_{k}\right) & k=1,2, \cdots, l \\ \text {net}_{k}=\sum\limits_{j=0}^{m} w_{j k} \boldsymbol{y}_{j} & k=1,2, \cdots, l\end{cases} $ | (2) |
式(1)和式(2)中,变换函数f(x)通常均为单极性sigmoid函数
| $ f(x)=\frac{1}{1+\mathrm{e}^{-x}} $ | (3) |
sigmoid函数具有连续、可导的特点。根据需要,也可采用双极性sigmoid函数(或称双曲线正切函数)。为降低计算复杂度,必要时输出层也可采用线性函数。BP神经网络所采用的传递函数均是可微的单调递增函数。
1.2 BP神经网络学习算法BP人工神经网络的基本思想是:输入待训练样本,从输入层前向传播至隐含层再到输出层,若输出结果不满足期望值,输出结果再从隐含层反向传播到输入层,此过程将误差分担至各层各个单元,不断修正权值和阈值,以使输出结果趋向于期望值;网络各层的权值改变量由传播到该层的误差大小决定。此修正过程一直持续到输出结果满足期望值,或达到预先设定的训练次数。
本文使用三层BP神经网络的学习算法如下。
(1) 网络的误差
当网络输出不等于期望输出时,表示成误差
| $ E=\frac{1}{2} \sum\limits_{k=1}^{l}(\boldsymbol{d}-\boldsymbol{O})^{2}=\frac{1}{2} \sum\limits_{k=1}^{l}\left(\boldsymbol{d}_{k}-\boldsymbol{o}_{k}\right)^{2} $ | (4) |
对以上误差展开至隐层,就有
| $ \begin{aligned} E &=\frac{1}{2} \sum\limits_{k=1}^{l}\left[\boldsymbol{d}_{k}-f\left(\operatorname{net}_{k}\right)\right]^{2} \\ &=\frac{1}{2} \sum\limits_{k=1}^{l}\left[\boldsymbol{d}_{k}-f\left(\sum\limits_{j=0}^{m} w_{j k} \boldsymbol{y}_{j}\right)\right]^{2} \end{aligned} $ | (5) |
进一步展开至输出层,可得
| $ \begin{aligned} E &=\frac{1}{2} \sum\limits_{k=1}^{l}\left\{\boldsymbol{d}_{k}-f\left[\sum\limits_{j=0}^{m} w_{j k} f\left(\operatorname{net}_{j}\right)\right]\right\}^{2} \\ &=\frac{1}{2} \sum\limits_{k=1}^{l}\left\{\boldsymbol{d}_{k}-f\left[\sum\limits_{j=0}^{m} w_{j k} f\left(\sum\limits_{i=0}^{n} v_{i j} \boldsymbol{x}_{i}\right)\right]\right\}^{2} \end{aligned} $ | (6) |
(2) 基于梯度下降的网络权值调整(系数η)为
| $ \begin{aligned} \Delta& w_{j k}=-\eta \frac{\partial E}{\partial w_{j k}} \\ &j=0,1,2, \cdots, m ; k=1,2, \cdots, l \end{aligned} $ | (7) |
| $ \begin{aligned} \Delta &v_{i j}=-\eta \frac{\partial E}{\partial v_{i j}} \\ &i=0,1,2, \cdots, n ; j=1,2, \cdots, m \end{aligned} $ | (8) |
式(7)与式(8)仅是对权值调整思路的数学表达,而不是具体的权值调整计算式。在全部推导过程中,对输出层均有j=0, 1, 2, …, m; k=1, 2, …, l。同时,对隐含层均有i=0, 1, 2, …, n; j=1, 2, …, m。进而可得
| $ \Delta w_{j k}=-\eta \frac{\partial E}{\partial w_{j k}}=-\eta \frac{\partial E}{\partial{\rm{n e t}}_{k}} \frac{\partial{\rm{n e t}}_{k}}{\partial w_{j k}} $ | (9) |
| $ \Delta v_{i j}=-\eta \frac{\partial E}{\partial v_{i j}}=-\eta \frac{\partial E}{\partial \operatorname{net}_{j}} \frac{\partial \mathrm{net}_{j}}{\partial v_{i j}} $ | (10) |
对输出层和隐含层各定义一个误差信号,令
| $ \boldsymbol{\delta}_{k}^\boldsymbol{o}=-\frac{\partial E}{\partial \operatorname{net}_{k}} $ | (11) |
| $ \boldsymbol{\delta}_{j}^\boldsymbol{y}=-\frac{\partial E}{\partial \operatorname{net}_{j}} $ | (12) |
综合应用式(2)和式(11),可将式(9)改写为
| $ \Delta w_{j k}=\eta \boldsymbol{\delta}_{k}^\boldsymbol{o} \boldsymbol{y}_{j} $ | (13) |
综合应用式(3)求导结果和式(12),可将式(10)改写为
| $ \Delta v_{i j}=-\eta \boldsymbol{\delta}_{j}^\boldsymbol{y} \boldsymbol{x}_{i} $ | (14) |
输出层δko、隐含层δjy分别展开为
| $ \boldsymbol{\delta}_{k}^\boldsymbol{o}=-\frac{\partial E}{\partial \operatorname{net}_{k}}=-\frac{\partial E}{\partial \boldsymbol{o}_{k}} \frac{\partial \boldsymbol{o}_{k}}{\partial \operatorname{net}_{k}}=-\frac{\partial E}{\partial \boldsymbol{o}_{k}} f^{\prime}\left(\operatorname{net}_{k}\right) $ | (15) |
| $ \boldsymbol{\delta}_{j}^\boldsymbol{y}=-\frac{\partial E}{\partial \operatorname{net}_{j}}=-\frac{\partial E}{\partial \boldsymbol{y}_{j}} \frac{\partial \boldsymbol{y}_{j}}{\partial{\mathrm{net}}_{j}}=-\frac{\partial E}{\partial \boldsymbol{y}_{j}} f^{\prime}\left(\operatorname{net}_{j}\right) $ | (16) |
求取式(15)、式(16)中网络误差对各层输出的偏导。
输出层:利用式(4)求偏导可得
| $ \frac{\partial E}{\partial \boldsymbol{o}_{k}}=-\left(\boldsymbol{d}_{k}-\boldsymbol{o}_{k}\right) $ | (17) |
隐含层:利用式(16)可求得
| $ \frac{\partial E}{\partial \boldsymbol{y}_{j}}=-\sum\limits_{k=1}^{l}\left(\boldsymbol{d}_{k}-\boldsymbol{o}_{k}\right) f^{\prime}\left(\operatorname{net}_{k}\right) w_{j k} $ | (18) |
将式(17)、式(18)分别代入式(15)和式(16),并将式(3)的求导公式中的f′(x)替换为f′(net),就可得到
| $ \boldsymbol{\delta}_{k}^\boldsymbol{o}=\left(\boldsymbol{d}_{k}-\boldsymbol{o}_{k}\right) \boldsymbol{o}_{k}\left(\boldsymbol{I}-\boldsymbol{o}_{k}\right) $ | (19) |
| $ \begin{aligned} \boldsymbol{\delta}_{j}^\boldsymbol{y} &=\left[\sum\limits_{k=1}^{l}\left(\boldsymbol{d}_{k}-\boldsymbol{o}_{k}\right) f^{\prime}\left(\operatorname{net}_{k}\right) w_{j k}\right] f^{\prime}\left(\operatorname{net}_{j}\right) \\ &=\left(\sum\limits_{k=1}^{l} \boldsymbol{\delta}_{k}^\boldsymbol{o} w_{j k}\right) \boldsymbol{y}_{j}\left(\boldsymbol{I}-\boldsymbol{y}_{j}\right) \end{aligned} $ | (20) |
式(19)~式(20)中I为单位矩阵。将该两式代入式(13)和式(14),可得学习算法权值调整的计算式
| $ \Delta w_{j k}=\eta \boldsymbol{\delta}_{k}^\boldsymbol{o} \boldsymbol{y}_{j}=\eta\left(\boldsymbol{d}_{k}-\boldsymbol{o}_{k}\right) \boldsymbol{o}_{k}\left(\boldsymbol{I}-\boldsymbol{o}_{k}\right) \boldsymbol{y}_{j} $ | (21) |
| $ \Delta v_{i j}=\eta \boldsymbol{\delta}_{j}^\boldsymbol{y} x_{i}=\eta\left(\sum\limits_{k=1}^{l} \boldsymbol{\delta}_{k}^\boldsymbol{o} w_{j k}\right) \boldsymbol{y}_{j}\left(\boldsymbol{I}-\boldsymbol{y}_{j}\right) \boldsymbol{x}_{i} $ | (22) |
(3) BP学习算法的向量形式
针对输出层:假设Y=(y1, y2, …,yj, …, ym)T, δo=(δ1o, δ2o,…,δko, …, δlo)T, 则隐含层到输出层之间的权值矩阵调整量为
| $ \Delta \boldsymbol{W}=\eta\left(\boldsymbol{\delta}^\boldsymbol{o} \boldsymbol{Y}^{\mathrm{T}}\right)^{\mathrm{T}} $ | (23) |
对于隐含层:再设X=(x1, x2, …,xj, …, xm)T, δy=(δ1y, δ2y,…,δky, …, δly)T, 则输入层到隐含层之间的权值矩阵调整量为
| $ \Delta \boldsymbol{V}=\eta\left(\boldsymbol{\delta}^{y} \boldsymbol{X}^{\mathrm{T}}\right)^{\mathrm{T}} $ | (24) |
常规反演方法是利用实测频散曲线和已有的地质资料构建初始模型,再正演计算频散曲线。若实测频散曲线和正演频散曲线偏差在误差范围内,则正演模型即为反演结果;否则,修正模型继续正演计算频散曲线,并做对比分析,直到正演计算的频散曲线与实测频散曲线较好地吻合。这种反演方法结果较准确,其缺点是对初始模型依赖性强,若初始模型不合适,则反演工作量很大。而采用BP人工神经网络方法则避免了这种复杂运算量大且精确性较差的计算方式。现今计算层状介质中瑞雷波频散曲线的主流方法包括Haskell算法、快速Schwab-Knopoff算法等。自2001年以来,凡友华等[14-15]对瑞雷波算法深入研究分析后,基于快速Delta矩阵算法的基本思想在柱坐标系下得到快速矢量传递算法。该传递算法避免了以往方法中同一矩阵各元素的数量级相差较大、出现复数运算的缺陷,提高了计算的精度及稳定性[14]。因此,本文采用快速矢量传递算法进行瑞雷波频散曲线正演模拟计算。
建立神经网络反演的步骤:
(1) 利用快速矢量传递算法进行瑞雷波频散曲线正演模拟,求取大量不同的地质(随机)模型的频散曲线,将频散曲线作为网络输入、地质模型作为网络输出。
(2) 研究结果表明,对于由均匀各向同性介质构成的层状介质来说,对瑞雷波频散最敏感的因素是各层介质的厚度和横波速度[16]。因此在瑞雷波频散曲线反演中,一般只反演横波速度和地层厚度。瑞雷波频散方程的其他参数,像纵波速度是通过纵横波与泊松比之间的关系式,用横波速度和泊松比换算的,而泊松比是根据地层参数近似估算的。不同地层具有不同的泊松比值范围,通过前期地质调查确定具体地层之后再给定近似泊松比。
(3) 训练神经网络。神经网络必须有训练样本作为学习网络的依据才能完成学习过程,该训练样本的可靠性对整个神经网络学习算法的精确度有决定性的影响。随后,通过BP神经网络进行频散曲线反演。
1.4 BP神经网络训练网络样本的选取方法大致可归纳为两类:一是利用已知的观测数据及相应解释资料;二是通过计算机进行正演,生成训练样本。基于瑞雷波频散特性,本文采用第二种方法获取训练样本。在频散曲线非线性反演中,神经网络的输入即为利用不同的地层模型参数得到的频散曲线,神经网络的输出则是与其对应的地层模型。使用不同类型的层状模型正演产生训练样本,并通过训练构建神经网络反演模型。
2 理论模型试算针对实际近地表瑞雷波勘探中经常遇到的典型地质结构,设计具有代表性的四层地质模型, 测试神经网络算法的有效性。考虑到大多数情况下,基阶波是能量最强、最易观测到的,也是实际应用最广泛的,利用设计的地质模型通过快速矢量算法正演模拟产生基阶瑞雷波频散曲线(频点数为35,频带范围为0~100Hz),再以理论产生的频散曲线做反演。
选择四层介质模型是为了在不增大计算量的情况下尽量贴合实际。构建三种四层地质模型:速度递增型、含低速软夹层型、含高速硬夹层型[17]。夹层对层状岩体稳定性的影响及作用机理,对含夹层矿床开采、边坡稳定性控制及冲击地压的防治都具有重大的现实意义。
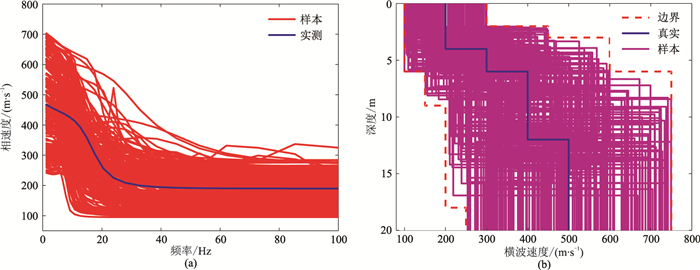
2.1 速度递增模型(模型1)反演在设定搜索范围内随机生成490种四层地质模型(图 2b,表 1);正演模拟出用于网络训练的490条频散曲线(图 2a)。将频散曲线上35个点作为神经网络输入,模型对应的7个参数作为输出;利用BP神经网络构建一个多输入、多输出的模型,从而达到建立网络的过程,为随后的训练做准备。
|
图 2 模型1搜索范围内随机生成的490个模型样本集 (a)频散曲线;(b)横波速度剖面 |
|
|
表 1 模型1参数及搜索范围 |
网络的隐含层选取40个神经元,选用带反弹的BP训练函数trainrp,学习速率是0.0001,训练次数为15000,其余参数均为默认值。对共计20次反演取平均值作为最后反演结果,可见每次的迭代收敛曲线及反演结果(图 3,表 2)。

|
图 3 模型1人工神经网络算法执行过程 (a)每次训练误差记录及其平均值;(b)多次反演结果横波速度剖面 |
|
|
表 2 模型1反演结果 |
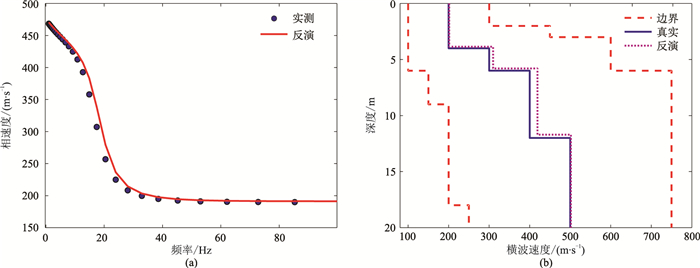
从模型1通过人工神经网络算法反演的频散曲线和横波速度剖面(图 4)可见,模型真实值被精确地反演与重建。
|
图 4 人工神经网络算法反演结果 (a)实测的和反演拟合的频散曲线;(b)真实的和反演的横波速度剖面 |
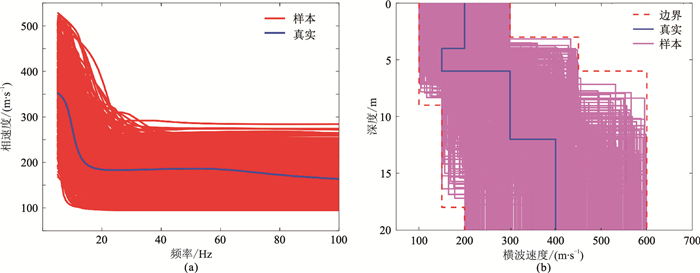
针对模型2,同样在搜索范围内随机生成490种四层地质模型(图 5b,表 3);正演模拟出用于网络训练的490条频散曲线(图 5a)。将频散曲线上35个点作为神经网络输入,模型对应的7个参数作为输出,通过BP神经网络建立一个多输入、多输出的模型,并准备后续的训练。
|
图 5 模型2搜索范围内随机生成的490个模型样本集 (a)频散曲线;(b)横波速度剖面 |
|
|
表 3 模型2参数及搜索范围 |
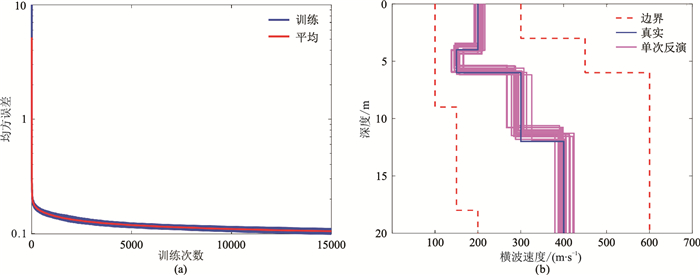
网络的隐含层选取45个神经元,训练函数、学习速率、训练次数均与上面相同,其余参数也为默认值。将共计20次反演的平均值作为最后反演结果,可见每次迭代的收敛曲线及反演结果(图 6,表 4)。
|
图 6 模型2人工神经网络算法执行过程 (a)每次训练误差记录及其平均值;(b)多次反演结果横波速度剖面 |
|
|
表 4 模型2反演结果 |
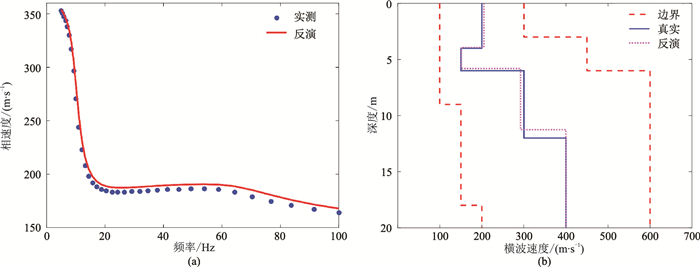
从模型2的人工神经网络算法反演的频散曲线和横波速度剖面(图 7)可见,模型真实值被精确地反演与重建。
|
图 7 模型2人工神经网络算法反演结果 (a)实测的和反演拟合的频散曲线;(b)真实的和反演的横波速度剖面 |
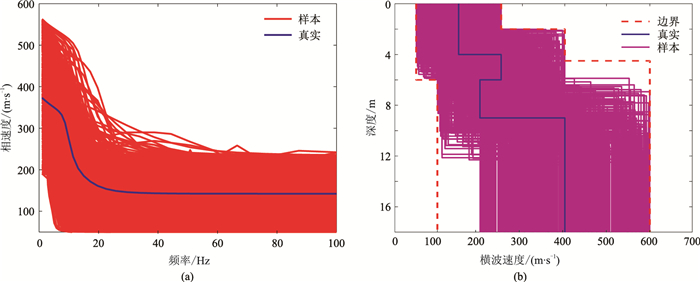
针对模型3,仍然以同样方式生成了490种四层地质模型(图 8b,表 5)、模拟出用于网络训练的490条频散曲线(图 8a)。采用对应相同的神经网络输入、输出,构建一个多输入、多输出的模型,以供后续训练。
|
图 8 模型3搜索范围内随机生成的490个模型样本集 (a)频散曲线;(b)横波速度剖面 |
|
|
表 5 模型3参数及搜索范围 |
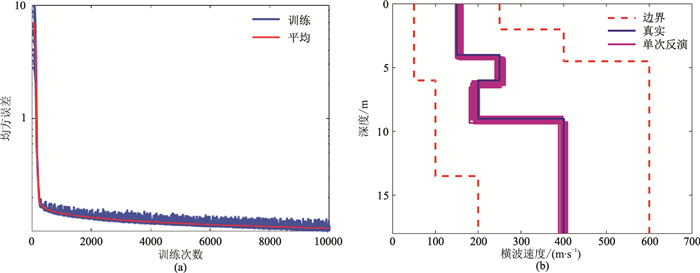
网络的隐含层选取30个神经元,选用上述相同的训练函数和学习速率,训练次数为10000,其余参数仍选默认值。以20次反演平均值作为最终反演结果,可看到每次的迭代收敛曲线及反演结果(图 9,表 6)。
|
图 9 模型3人工神经网络算法执行过程 (a)每次训练误差记录及其平均值;(b)多次反演结果横波速度剖面 |
|
|
表 6 模型3反演结果 |
观察模型3通过人工神经网络算法反演的频散曲线和横波速度剖面(图 10),依然可见模型真实值被精确地反演与重建。

|
图 10 模型3人工神经网络算法反演结果 (a)实测的和反演拟合的频散曲线;(b)真实的和反演的横波速度剖面 |
实际勘探采集的数据通常都是掺杂了很多其他无规律的噪声,这样在计算分析时,不可避免地会产生偏差甚至是错误。对于一种新算法,能否不随外界因素影响,保持较强抗噪性或其他优良特性是至关重要的。
为了能仿真实测资料,但又不至于太过复杂且能最大程度地说明算法的抗噪性,期望利用一个简单的随机函数找到一种噪声加到理论频散曲线上,得到的是统一标准噪声的频散曲线。给出
| $ \begin{aligned} \text { Data }=& \text { Signal }+2 \times(0.5-\mathrm{RND}) \times \\ & \text { Signal } \times \text { Noise } \end{aligned} $ | (25) |
式中:可变的是Signal,即是理论频散曲线;RND是一个随机数,增加了噪声的随机性。本次将添加的噪声取值设为10%,通过在不同模型中取得的反演效果,进行分析、讨论。
针对包含四层介质的模型1、模型2、模型3,表 7~表 9分别为加入10%噪声情况下三种模型的参数及其反演结果统计,图 11~图 13则是相应的频散曲线和横波速度。
|
|
表 7 含噪10%的模型1数据反演结果统计 |
|
|
表 8 含噪10%的模型2数据反演结果统计 |
|
|
表 9 含噪10%的模型3数据反演结果统计 |
|
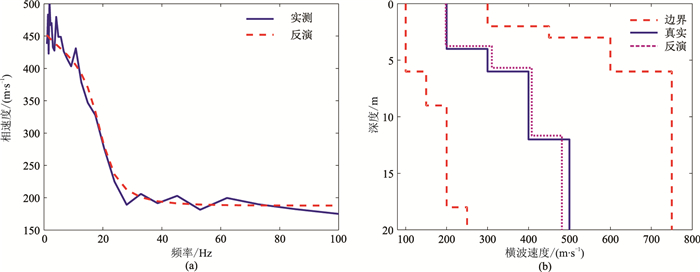
图 11 模型1加噪10%人工神经网络算法反演结果 (a)实测的和反演拟合的频散曲线;(b)真实的和反演的横波速度剖面 |
|
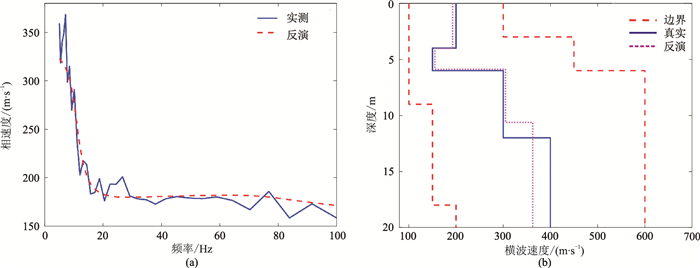
图 12 模型2加噪10%人工神经网络算法反演结果 (a)实测的和反演拟合的频散曲线;(b)真实的和反演的横波速度剖面 |
|
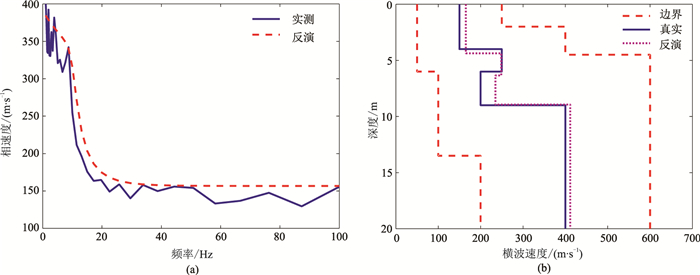
图 13 模型3加噪10%人工神经网络算法反演结果 (a)实测的和反演拟合的频散曲线;(b)真实的和反演的横波速度剖面 |
从以上反演模拟响应可见,人工神经网络算法对四层模型上含有10%噪声数据的反演仍具有稳定性,反演模型的频散曲线均与理论值基本拟合。三个典型四层模型参数平均误差分别为2.82%、4.96%、5.73%,表明该算法的稳定性和抗噪性较好。
4 实例分析针对瑞雷波频散曲线反演具有高度非线性、多参数、多极值的特点,前面已利用人工神经网络算法进行了理论模型试算和抗噪能力测试,检验了此算法用于瑞雷波频散曲线非线性反演的有效性及程序的正确性。现以意大利东北部一个废物处理场的典型实例[18],进一步检验人工神经网络算法反演实际频散曲线的能力。
4.1 实例背景介绍意大利东北边的废物处理场的松散堆积物厚约18m,基岩是灰岩。通过钻孔数据可得到其厚度分层情况。与前面理论无噪声数据分析所用方法相似,保持密度和泊松比与实际值一样,只考虑其横波速度和厚度。利用人工神经网络算法对真实数据的非线性反演所需的搜索空间、泊松比和密度等参数列于表 10。
|
|
表 10 现场实测数据的模型搜索范围参数 |
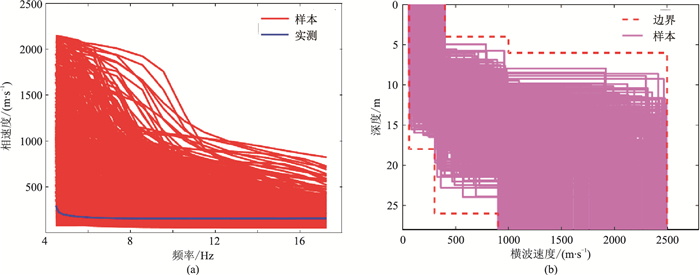
应用上节同样方法,在搜索范围内随机生成630个五层地质模型(图 14b);正演模拟出用于网络训练的630条频散曲线(图 14a)。将频散曲线上15个点作为神经网络输入,模型对应的9个参数作为输出,通过BP网络建立一个多输入、多输出模型,然后展开训练。
|
图 14 实测资料搜索范围内随机生成的630个模型样本集 (a)频散曲线;(b)横波速度剖面 |
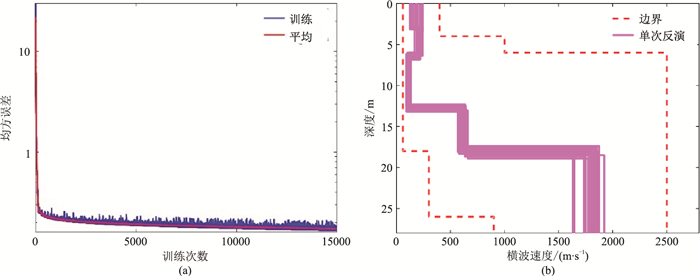
网络的隐含层选取55个神经元,选用带反弹的BP训练函数traingda,学习速率是0.00005,训练次数为15000,其余参数均为默认值。将共计20次反演的平均值作为最终反演结果,可见每次的迭代收敛曲线及反演结果(图 15)。
|
图 15 实测资料人工神经网络算法执行过程 (a)每次训练误差记录及其平均值;(b)多次反演结果横波速度剖面 |
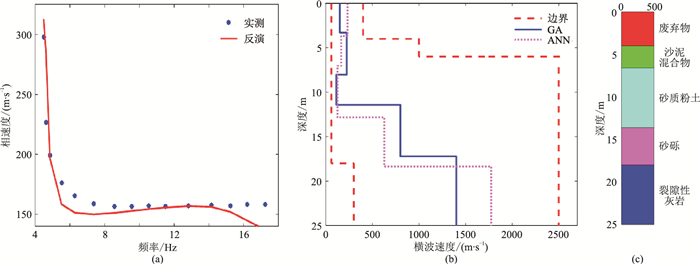
将反演所得模型进行正演,得到的频散曲线(图 16a)与实测频散点拟合较好,虽无真实横波速度剖面数据,但可与前人利用其他算法得到的反演值进行对比(图 16b)。发现除第一层外其他各层横波速度大致相同,误差较小。而通过钻孔资料发现第三层沙土横波速度小于第二层混砂黏土速度,故认为通过ANN反演的横波速度更接近真实情况。再通过与钻孔地层柱状图(图 16c)细致对比,可知第一层、第二层的厚度基本一致;ANN(人工神经网络)反演得到的第三层、第四层的厚度较GA(遗传算法)反演值更接近实际厚度。
|
图 16 实测资料人工神经网络算法反演结果对比 (a)实测和反演拟合的频散曲线;(b)GA算法和人工神经网络算法对应的横波速度剖面;(c)钻孔地层柱状图[18] |
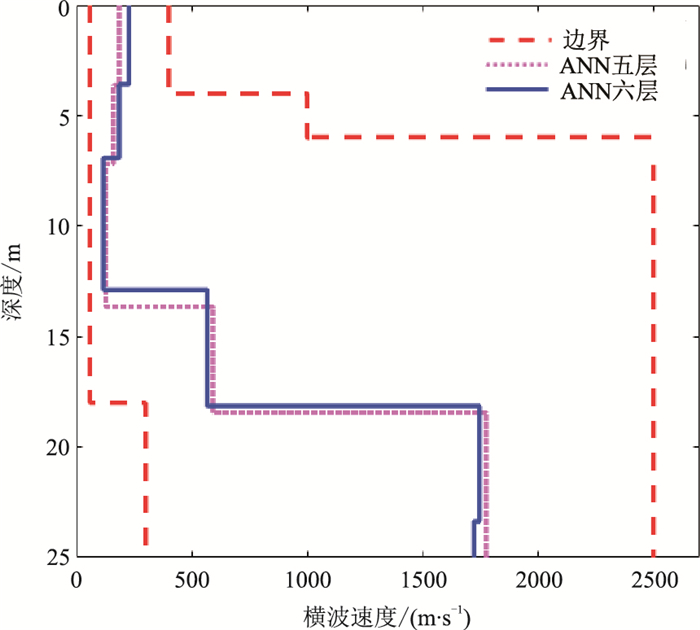
在实际反演过程中,有时地层层数是未知的。为了模拟这种情况,本文将该实例假设为六层模型,利用本文设计的人工神经网络算法重新做反演(图 17蓝色实线)。可知五层模型反演结果与六层模型结果很接近,且都能与钻孔资料较好地吻合,进而验证了本文设计的人工神经网络算法具有较强非线性反演映射能力。当然,在实际反演中,并不是将地层剖分的越细越好,通常需在地层分辨率与模型反演精度之间做折中选取。
|
图 17 五层、六层地层反演结果对比 |
(1) 利用快速矢量传递算法,对近地表典型四层模型进行了基阶瑞雷波正演模拟。由于瑞雷波反演的大部分时间用于正演模拟计算上,又因训练样本集的质量将直接影响反演精度和效率,因此正演和训练样本集的建立成为反演的关键因素。
(2) 应用BP神经网络对理论模型进行反演试算的结果表明:BP人工神经网络算法是一种不依赖于初始模型的全局优化算法,计算精度高、具有较强的抗干扰能力。加入噪声的理论模型反演结果进一步表明,BP神经网络具有稳定性和较强抗噪性。
(3) 针对实际资料进行瑞雷波频散曲线反演,并与遗传算法进行对比,结果表明BP人工神经网络反演方法具有可行性与实用性。
| [1] |
邵广周, 李庆春. 联合应用τ-p变换法和相移法提取面波频散曲线[J]. 石油地球物理勘探, 2010, 45(6): 836-840. SHAO Guangzhou, LI Qingchun. Joint application of τ-p and phase-shift stacking method to extract ground wave dispersion curve[J]. Oil Geophysical Prospecting, 2010, 45(6): 836-840. |
| [2] |
鲁来玉, 张碧星, 汪承灏. 基于瑞利波高阶模式反演的实验研究[J]. 地球物理学报, 2006, 49(4): 1082-1091. LU Laiyu, ZHANG Bixing, WANG Chenghao. Experiment and inversion studies on Rayleigh wave considering higher modes[J]. Chinese Journal of Geophy-sics, 2006, 49(4): 1082-1091. DOI:10.3321/j.issn:0001-5733.2006.04.021 |
| [3] |
宋先海, 张学强, 王一鸣, 等. 近地表弹性介质瑞雷波勘探研究进展与展望[J]. 地质科技通报, 2020, 39(5): 173-182. SONG Xianhai, ZHANG Xueqiang, WANG Yiming, et al. Recent advances and prospects of near surface elastic Rayleigh waves[J]. Bulletin of Geological Science and Technology, 2020, 39(5): 173-182. |
| [4] |
Xu Y X, Xia J H, Miller R D. Numerical investigation of implementation of air-earth boundary by acoustic-elastic boundary approach[J]. Geophysics, 2007, 72(5): SM147-SM153. DOI:10.1190/1.2753831 |
| [5] |
高静怀, 何洋洋, 马逸尘. 黏弹性与弹性介质中Rayleigh面波特性对比研究[J]. 地球物理学报, 2012, 55(1): 207-218. GAO Jinghuai, HE Yangyang, MA Yichen. Comparison of the Rayleigh wave in elastic and viscoelastic media[J]. Chinese Journal of Geophysics, 2012, 55(1): 207-218. DOI:10.6038/j.issn.0001-5733.2012.01.020 |
| [6] |
夏江海, 高玲利, 潘雨迪, 等. 高频面波方法的若干新进展[J]. 地球物理学报, 2015, 58(8): 2591-2605. XIA Jianghai, GAO Lingli, PAN Yudi, et al. New fin-dings in high frequency surface wave method[J]. Chinese Journal of Geophysics, 2015, 58(8): 2591-2605. |
| [7] |
Chai H Y, Cui Y J, Wei C F. A parametric study of effective phase velocity of surface waves in layered media[J]. Computers & Geotechnics, 2012, 44(June): 176-184. |
| [8] |
Zhang S X, Chan L S, Chen C Y, et al. Apparent phase velocities and fundamental-mode phase velocities of Rayleigh waves[J]. Soil Dynamics and Earthquake Engineering, 2003, 23(7): 563-569. DOI:10.1016/S0267-7261(03)00069-1 |
| [9] |
Li J, Lin F C, Allam A, et al. Wave equation dispersion inversion of surface waves recorded on irregular topography[J]. Geophysical Journal International, 2019, 217(1): 346-360. DOI:10.1093/gji/ggz005 |
| [10] |
杨博, 熊章强, 张大洲, 等. 利用自适应混沌遗传粒子群算法反演瑞雷面波频散曲线[J]. 石油地球物理勘探, 2019, 54(6): 1217-1227. YANG Bo, XIONG Zhangqiang, ZHANG Dazhou, et al. Rayleigh surface-wave dispersion curve inversion based on adaptive chaos genetic particle swarm optimization algorithm[J]. Oil Geophysical Prospecting, 2019, 54(6): 1217-1227. |
| [11] |
曹旭, 熊章强, 张大洲. 基于BP神经网络的瑞雷面波智能优化反演[J]. 工程地球物理学报, 2015, 12(4): 514-519. CAO Xu, XIONG Zhangqiang, ZHANG Dazhou. The Rayleigh surface wave intelligent inversion based on the BP artificial neural network[J]. Chinese Journal of Engineering Geophysics, 2015, 12(4): 514-519. DOI:10.3969/j.issn.1672-7940.2015.04.017 |
| [12] |
于东凯, 宋先海, 张学强, 等. 蚱蜢算法在瑞雷波频散曲线反演中的应用[J]. 石油地球物理勘探, 2019, 54(2): 288-301. YU Dongkai, SONG Xianhai, ZHANG Xueqiang, et al. Rayleigh wave dispersion inversion based on grasshopper optimization algorithm[J]. Oil Geophysical Prospecting, 2019, 54(2): 288-301. |
| [13] |
周晓华, 林君, 陈祖斌, 等. 改进的神经网络反演微动面波频散曲线[J]. 吉林大学学报(地球科学版), 2011, 41(3): 900-906. ZHOU Xiaohua, LIN Jun, CHEN Zubin, et al. Iterative inversion of microtremor surface wave dispersion curves by improved neural network[J]. Journal of Jilin University(Earth Science Edition), 2011, 41(3): 900-906. |
| [14] |
凡友华, 刘家琦, 肖柏勋. 计算瑞利波频散曲线的快速矢量传递算法[J]. 湖南大学学报(自然科学版), 2002, 29(5): 25-30. FAN Youhua, LIU Jiaqi, XIAO Boxun. Fast vector-transfer algorithm for computation of Rayleigh wave dispersion curves[J]. Journal of Hunan University(Natural Sciences), 2002, 29(5): 25-30. DOI:10.3321/j.issn:1000-2472.2002.05.006 |
| [15] |
凡友华, 陈晓非, 刘雪峰, 等. Rayleigh波的频散方程高频近似分解和多模式激发数目[J]. 地球物理学报, 2007, 50(1): 233-239. FAN Youhua, CHEN Xiaofei, LIU Xuefeng, et al. Approximate decomposition of the dispersion equation at high frequencies and the number of multimodes for Rayleigh waves[J]. Chinese Journal of Geophysics, 2007, 50(1): 233-239. DOI:10.3321/j.issn:0001-5733.2007.01.029 |
| [16] |
尹晓菲, 胥鸿睿, 郝晓菡, 等. 水平层状模型中多模式瑞雷波和拉夫波相速度频散曲线的灵敏度分析[J]. 石油地球物理勘探, 2020, 55(1): 136-146. YIN Xiaofei, XU Hongrui, HAO Xiaohan, et al. Sensitivity analysis of multi-mode Rayleigh and Love wave phase-velocity dispersion curves in horizontal layered models[J]. Oil Geophysical Prospecting, 2020, 55(1): 136-146. |
| [17] |
张碧星, 肖柏勋, 杨文杰, 等. 瑞利波勘探中"之"形频散曲线的形成机理及反演研究[J]. 地球物理学报, 2000, 43(4): 557-567. ZHANG Bixing, XIAO Boxun, YANG Wenjie, et al. Mechanism of zigzag dispersion curves in Rayleigh exploration and its inversion study[J]. Chinese Journal of Geophysics, 2000, 43(4): 557-567. DOI:10.3321/j.issn:0001-5733.2000.04.017 |
| [18] |
Dal Moro G, Pipan M, Gabrielli P. Rayleigh wave dispersion curve inversion via genetic algorithms and marginal posterior probability density estimation[J]. Journal of Applied Geophysics, 2007, 61(1): 39-55. DOI:10.1016/j.jappgeo.2006.04.002 |



 宋先海, 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉)地球物理与空间信息学院应用地球物理系, 430074。Email:
宋先海, 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉)地球物理与空间信息学院应用地球物理系, 430074。Email: 