② 中国海洋石油总公司, 北京 116503
② China National Offshore Oil Corporation, Beijing 116503, China
反射地震学利用地面接收到的反射数据反演地下介质的特性[1]。在反射地震学中,地震子波的估计对于处理地震数据具有重要意义[2]。频域地震子波等于振幅谱与相位谱的乘积,因此地震子波估计包括两部分内容,即振幅谱和相位谱。
现有的地震子波估计方法可以分为两大类,即确定型方法和统计型方法。Walden等[3]提出一种谱分析方法,利用测井数据与地震记录的功率谱和交互功率谱在一定时窗内估计子波;Tan[4]提出一种基于波动方程估计子波振幅谱的方法,该方法假设子波为最小相位;Edgar等[5]提出了一种匹配子波估计法,利用地震数据拟合出子波振幅谱,将相位置零得到初始零相位子波,结合测井反射系数可得到合成地震记录,不断调整子波的相位和振幅,使真实值与合成地震记录达到最佳匹配,此时对应的子波即为估计结果。这些确定型方法利用精确的地震子波振幅谱可加速算法收敛。另一类是统计型方法,这类方法通常假设反射系数序列具有白噪非高斯性。Wiggins[6]提出峰态最大化准则,用于衡量序列非高斯性的参数;Van der Baan等[7-9]对Wiggins的方法进行改进,提出了非稳态子波估计方法。Ro-binson等[10-11]提出地震记录的时变褶积模型,即地震子波随地震波的传播而变化,不同的旅行时具有不同的子波,Margrave等[12]称之为非平稳褶积模型。作为时变褶积模型的一种近似方法,高静怀等[13]、Gao等[14-15]和Wang等[16]提出一种非平稳地震记录的自适应划分方法,将非平稳地震记录划分为近似平稳的多个时间间隔。对于这些方法,找到每一个时间区间的等效子波振幅谱是关键。
在假设反射系数序列服从白噪分布的前提下,学者们提出了一些子波振幅谱估计方法,比如对数谱平均(LSA)法[17]及谱模拟(SS)法[18]。其中,LSA法不适用于地下介质在横向上不连续的情况;SS法假定子波振幅谱满足一种函数多项式,其中的参数可通过地震记录振幅谱与函数自变量之间的最小二乘拟合确定。在实际应用中,选择合适的函数形式比较困难,且这些方法对子波振幅谱的形态有明确限制,得到的是类似于Ricker子波的单峰光滑曲线。此外,大量实际测井数据表明,反射系数序列不满足随机分布,其振幅谱符合蓝色特征,即反射系数振幅谱随频率增大而逐渐增强,且沿频率方向强度会发生变化,呈现出非白色分布的趋势[19],这使上述方法在实际中难以应用。为了解决该问题,Gao等[20]提出一种压缩映射算子方法,通过地震数据的统计关系估计子波振幅谱。该方法对非白反射系数序列十分有效,且不需要预估函数形式,但需要选择合适的拟合频率范围。
机器学习作为一种数据驱动方法,可在不需要物理理论知识的情况下处理非线性问题。机器学习最初是在视觉领域发展起来的,并逐渐在地球物理领域取得了较好的应用效果。目前,人工神经网络(ANN)及其最新的变体网络(即深度学习)可通过大量训练数据学习、拟合复杂非线性函数,效果非常好。Wang等[21]利用Hopfield神经网络实现了最小预测误差反褶积和地震子波的估计。Chen等[22]提出一种模型驱动交替耦合的深度网络结构,实现了地震子波与反射系数的反演。唐杰等[23]基于多分辨率的U-Net神经网络实现了地震数据断层检测,准确率较高。
本文提出一种融入先验信息的卷积神经网络估计地震子波振幅谱的新方法,将子波振幅谱的光滑性作为先验信息,对地震数据进行预处理,拟合得到的结果更准确。将本文方法获得的子波谱与广泛使用的谱模拟方法[18]获得的子波谱进行比较,发现前者对于白色和非白反射系数均适用,且当子波谱为非单峰(如可控震源子波)时也可准确估计。最后,将本文方法应用于一个叠后地震剖面,结果表明该方法可有效提高地震数据的分辨率。
1 方法原理 1.1 褶积模型常用的地震数据处理方法基于传统的褶积模型,有赖于六个基本假设[24]。若假设子波是紧支撑的,则地震记录在时域中可表示为
| $ s(t)=\int r(\tau) w(t-\tau) \mathrm{d} t+n(t) $ | (1) |
式中:s(t)表示地震记录,t为时间;w(t)表示地震子波;r(t)为反射系数序列;n(t)是随机噪声; τ表示积分运算中的位移量。其中w(t)、r(t)和n(t)均属于L2(R)空间。对式(1)两端同时进行傅里叶变换,可得
| $ S(\omega)=W(\omega) R(\omega)+\hat{n}(w) $ | (2) |
式中S(ω)、W(ω)、R(ω)和
通常地,地震子波振幅谱由地震记录振幅谱经非线性运算获得,因此对式(2)等号两端同时求振幅谱,即可得到地震记录的振幅谱
| $ |S(\omega)|=|R(\omega)| \times|W(\omega)|+|\hat{n}(\omega)| $ | (3) |
为了使深度神经网络向正确的梯度更新方向进行训练,并充分学习子波振幅谱信息,可利用子波振幅谱的一些先验信息。Neidell[25]指出,地震子波振幅谱基本为光滑、有限支集的函数(正频率或负频率)。基于这一先验信息,在已知子波振幅谱满足光滑分布的前提下,对式(3)得到的地震数据进行预处理,并将处理结果作为输入数据融入神经网络。
由于地震记录谱是不规则的,因此根据Gao等[20]提出的压缩映射算子法,通过累积分布函数中的积分运算,可实现地震数据的预处理,从而得到一个相对光滑的地震子波谱。预处理的具体过程可表示为
| $ S_{0}(\omega)=\frac{|S(\omega)|}{\max [|S(\omega)|]} $ | (4) |
| $ F_{0}(\omega)=\int_{0}^{\omega} S_{0}(\xi) \mathrm{d} \xi $ | (5) |
式(4)是对式(3)得到的地震记录振幅谱|S(ω)|进行归一化处理,然后利用式(5)对归一化结果S0(ω)进行积分运算,得到平滑后的地震记录振幅谱F0(ω)。该预处理过程具有低通滤波的作用。
预处理之后,将F0(ω)作为神经网络的输入数据,经卷积神经网络的非线性拟合,最终可估计出较准确的地震子波振幅谱。
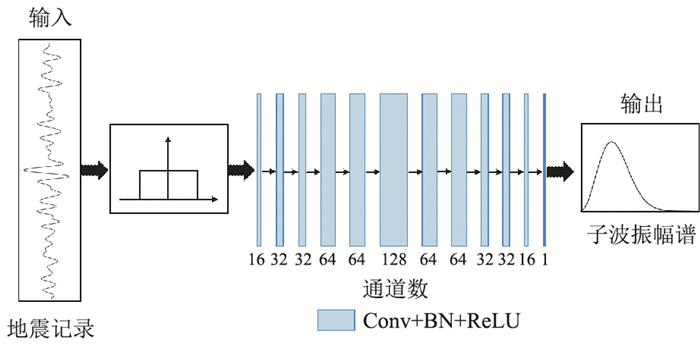
本文搭建的深度网络结构如图 1所示。网络的输入层为551×1的平滑地震记录谱,得到的网络输出为551×1的子波振幅谱。需特别注意的是,该网络的输入、输出可随输入长度的大小进行调整。这里的卷积步长为1,卷积核大小为5×1,采用较大的卷积核可增强对输入信号的平滑效果。由于线性整流函数(Rectified Linear Unit, ReLU)相比于Sigmoid和双曲正切(Tanh)激活函数的收敛更快,不易产生梯度消失,更适用于深度神经网络。因此,在除最后一层以外的每层卷积操作后,都使用ReLU函数进行激活。
|
图 1 DNN估计子波振幅谱结构图 |
模型参数优化的目标函数为
| $ L(\boldsymbol{\varTheta})=\frac{1}{2} \sum\limits_{i=1}^{N}\left\|W_{i}(\omega)-\hat{W}_{i}(\omega)\right\|_{2}^{2} $ | (6) |
式中:Θ表示参数集;W(ω)表示真实的地震子波振幅谱;
损失函数选用均方误差(MSE)函数,该函数易训练且具有稳定解,而且与所要解决问题的目标函数形式一致。
梯度下降选用自适应矩估计(Adaptive Moment Estimation, Adam)梯度最速下降法。
通过深度学习网络,由地震数据得到地震子波振幅谱的过程可描述为
| $ \hat{W}(\omega)=G_{\boldsymbol{\varTheta}}\left[F_{0}(\omega)\right] $ | (7) |
式中GΘ是非线性拟合算子。该算子通过一个12层深度神经网络(DNN)在训练过程中不断优化参数集Θ。增加神经网络的深度可以增加网络的参数种类,以便更好地学习目标特征。但是,过多地增加网络层数会出现梯度消失、过拟合等问题。因此,在同时考虑网络训练和测试精度的情况下,将输入层、12个卷积层(Conv)、归一化层(BN)、输出层依次连接,构成一个12层的深度卷积网络(图 1)。估计子波振幅谱的算法实现流程如表 1所示。
|
|
表 1 融入先验信息的基于DNN的子波振幅谱估计流程 |
深度学习是一种数据驱动的方法,因此需要生成数据集对网络进行训练和测试。为增强算法的泛化性与可靠性,采用四种不同类型的地震子波及服从高斯白噪分布和非白噪分布的两种不同类型的反射系数序列生成数据集。
本文模型数据采用的样本地震子波分别为Ricker子波、广义地震子波[26]、可控震源子波和带通子波,参数设置见表 2。其中,根据Wang[26]提出的广义地震子波公式,对参考频率ω0、时域子波中心点τ0以及分数值u进行设置。表中的前两个子波属于单峰子波,后两个属于非单峰子波,且子波振幅谱在形态上差异较大。本文暂且不考虑时变子波的情况。
|
|
表 2 地震子波参数设置 |
样本中的反射系数序列分别采用高斯白噪声随机数序列、蓝色噪声序列[27-28]及服从α-stable分布的随机数序列[29-31]。第一种反射系数序列服从高斯白噪分布,后两者属于服从非白噪分布的反射系数序列。其中,蓝色噪声可用白噪声经过一个ARMA(1, 1)系统[28]模拟,本文取ARMA(1, 1)系统为
| $ H(Z)=\frac{1-0.69 Z^{-1}}{1-0.28 Z^{-1}} $ | (8) |
此外,根据Pavel等[30]提出的产生α-stable分布随机数的方法,生成反射系数序列。
根据褶积模型将地震子波与反射系数序列进行褶积计算,可得到合成地震记录。
2 应用效果 2.1 模型数据采用合成地震记录对DNN进行训练,将估计的子波振幅谱与Rosa等[18]提出的谱模拟方法(SS法)得到的结果进行比较。定义误差函数
| $ \varDelta_{\mathrm{ASSW}}=\frac{\mathrm{ASSW}_{\text {estimated }}}{\| \text { ASSW }_{\text {estimated }} \|}-\frac{\text { ASSW }_{\text {true }}}{\| \mathrm{ASSW}_{\text {true }} \|} $ | (9) |
衡量估计得到的子波谱与真实子波谱的相似程度。式中:ASSW表示子波谱;下标“estimated”和“true”分别表示估计值和真实值。误差函数的最大值定义为
| $ \bar{\varDelta}_{\mathrm{ASSW}}=\max \limits_{f}\left[\left|\varDelta_{\mathrm{ASSW}}(f)\right|\right] $ | (10) |
下面分析不同类型反射系数序列情况下得到的估计子波振幅谱。
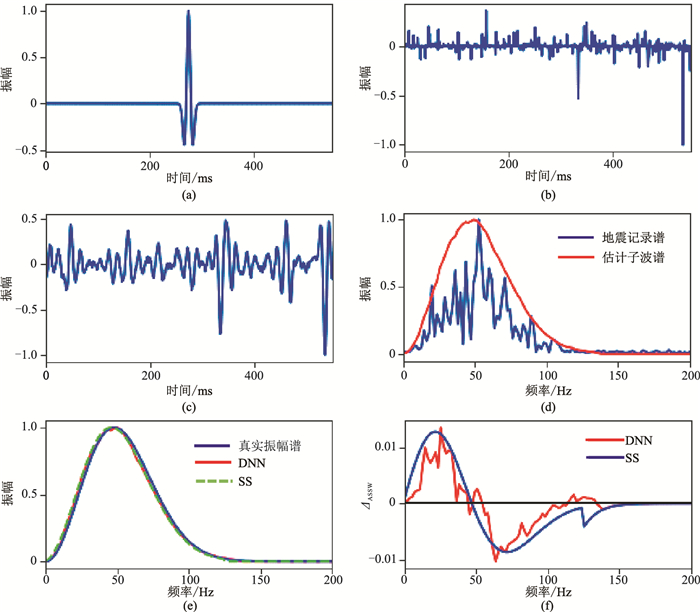
2.1.1 满足白噪分布的反射系数序列图 2是反射系数序列服从白噪分布的子波振幅谱估计结果,其中图 2e对比了DNN法与SS法估计的子波振幅谱,图 2f是图 2e对应的误差函数。从图 2b可以看出,在反射系数序列满足高斯白噪分布的前提下,图 2e中SS法(绿线)与本文提出的DNN法(红线)所得的子波振幅谱均与真实子波振幅谱(蓝线)有较高的一致性;图 2f中的误差函数值均在较小的振幅值范围内变化,二者的
|
图 2 反射系数序列服从白噪分布的子波振幅谱估计 (a)零相位Ricker子波;(b)服从高斯白噪的反射系数序列;(c)合成地震记录;(d)DNN法得到的地震子波振幅谱;(e)真实子波振幅谱及分别用DNN法和SS法估计得到的子波振幅谱;(f)真实值与估计子波谱之间的ΔASSW |
上述分析表明,当反射系数序列服从高斯白噪分布时,利用DNN法和SS法均可从地震记录振幅谱中提取较准确的子波振幅谱。然而,更多的实验表明,SS法对地震记录振幅谱的有效频率及位置十分敏感,且在真实子波未知的情况下,该方法中多项式里的拟合参数较难确定,为子波振幅谱的估计带来很大限制。
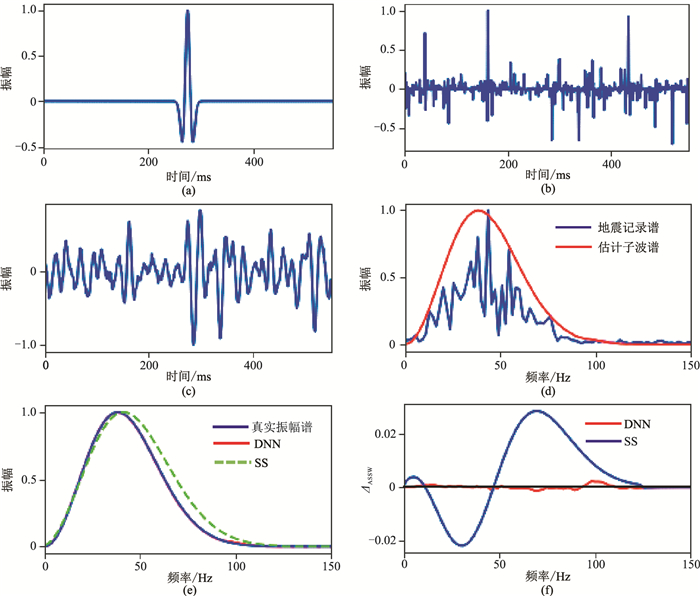
2.1.2 满足非白噪分布的反射系数序列图 3展示了一种非白噪分布反射系数序列的算例结果,其中图 3e对比了DNN法和SS法估计的子波振幅谱。对比图 3e与图 2e可以发现,无论在反射系数序列服从白噪分布还是非白噪分布两种情况下,DNN法估计的子波谱与真实子波谱均能保持较高的一致性;而SS法的拟合效果明显不同,即对于满足非白噪分布的反射系数序列估计的子波谱效果不及满足白噪分布的反射系数序列的估计结果:在子波谱的高频段(45~100Hz)出现了较大的拟合偏差。这说明传统的SS法不适用于反射系数序列服从非白噪分布时的子波谱估计。从图 3e的误差函数曲线可以看出,DNN法的ΔASSW约为0.004,而SS法的ΔASSW约为0.03。由此可见,若反射系数序列服从蓝色噪声分布,DNN法能更准确地估计地震子波振幅谱。
|
图 3 反射系数序列服从蓝噪分布时的子波振幅谱估计 (a)零相位Ricker子波;(b)服从蓝色噪声分布的反射系数序列;(c)合成地震记录;(d)DNN法得到的地震子波振幅谱;(e)真实子波振幅谱以及分别用DNN法和SS法估计得到的子波振幅谱;(f)DNN法和SS法估计子波振幅谱的ΔASSW |
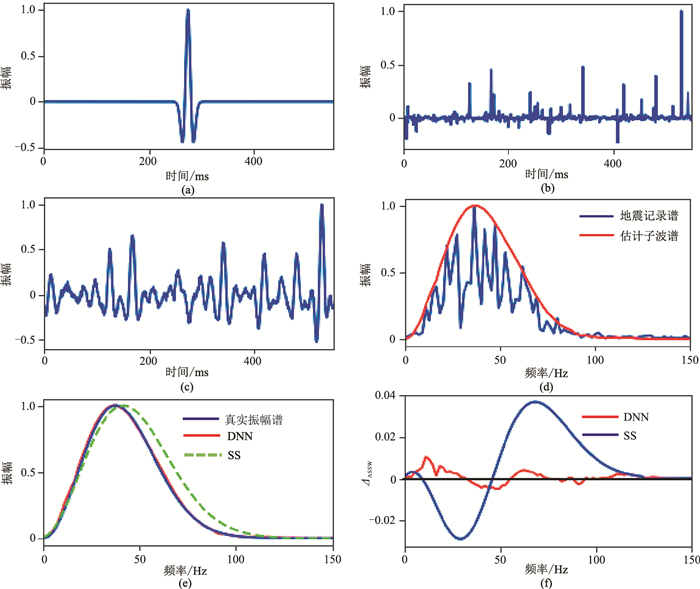
图 4是一种反射系数服从α-stable分布的子波振幅谱估计结果。Painter等[32]研究发现,实际数据的反射系数序列更接近于对称的α-stable分布。图 4e展示了DNN法和SS法估计得到的子波振幅谱,图 4f是对应的误差函数。可以发现,本文所提的DNN法提取子波振幅谱效果较好,拟合误差较小,ΔASSW值约为0.01;而传统的SS法拟合结果与真实子波谱之间误差相对较大,ΔASSW约为0.04,不能准确地估计地震子波振幅谱,尤其在50~100Hz频段内偏差较大。
|
图 4 反射系数序列服从α-stable分布时的子波振幅谱估计结果 (a)零相位Ricker子波;(b)服从α-stable分布的反射系数序列;(c)合成地震记录;(d)DNN法得到的地震子波振幅谱;(e)真实子波振幅谱以及分别用DNN法和SS法估计得到的子波振幅谱;(f)DNN法和SS法估计子波振幅谱的ΔASSW |
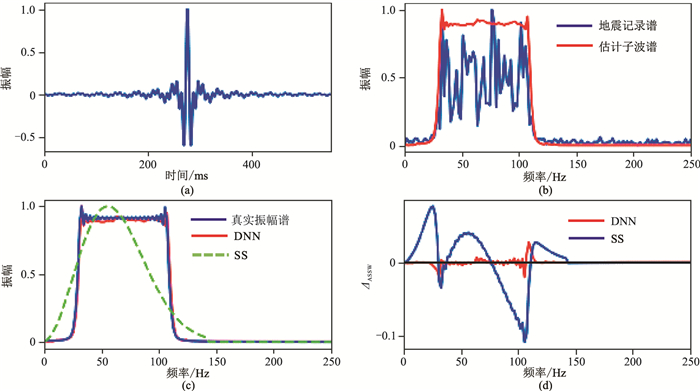
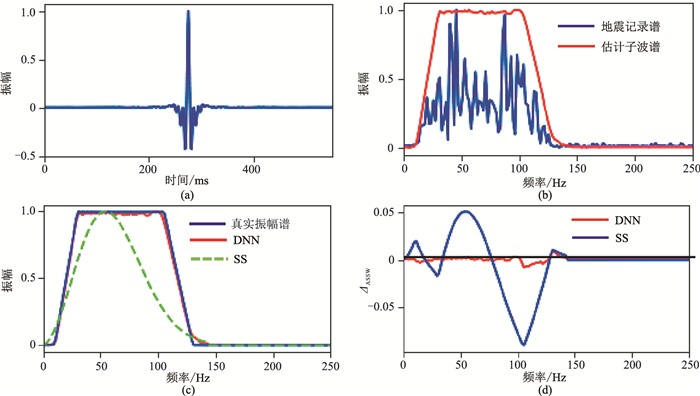
上述测试主要针对单峰子波振幅谱的估计,本节分析本文算法对于非单峰子波振幅谱的估计效果。图 5和图 6分别是可控震源子波和带通子波两种非单峰子波振幅谱的估计结果。
|
图 5 可控震源子波振幅谱估计 (a)可控震源子波;(b)DNN法得到的非单峰地震子波振幅谱;(c)真实子波振幅谱以及分别用DNN法和SS法估计得到的子波振幅谱;(d)真实子波谱与估计子波谱的ΔASSW |
|
图 6 带通子波振幅谱估计 (a)带通子波;(b)DNN法得到的非单峰地震子波振幅谱;(c)真实子波振幅谱以及分别用DNN法和SS法估计得到的子波振幅谱;(d)真实子波谱与估计子波谱之间的ΔASSW |
对比图 5c和图 6c所示可控震源子波和带通子波的振幅谱估计结果可发现,传统的SS法对于此类非单峰子波振幅谱的估计会失真,而本文提出的DNN方法与真实子波谱有较高的一致性。图 5d和图 6d中由DNN法产生的误差函数值ΔASSW远小于SS法产生的误差。究其原因,传统的SS法是基于统计方法提出的多项式拟合函数,所以对地震子波波形有很大限制,只能估计类似于Ricker子波的单峰子波振幅谱,对于非单峰子波谱的估计则不准确;而本文提出的DNN法是基于深度学习,通过数据驱动在神经网络实现的非线性关系下,能够学习各种不同形状的子波,具有较好的泛化性,且对反射系数序列的分布类型不敏感。由此可见,本文提出的DNN法可实现不同的非单峰子波振幅谱的估计,且准确性较高。
综上所述,无论是高斯白噪,还是蓝色噪声或α-stable分布的反射系数序列,本文提出的DNN法都能较准确地估计地震子波振幅谱,尤其能够实现非单峰子波振幅谱的准确估计,而现有的其他地震子波振幅谱估计方法则无法实现。
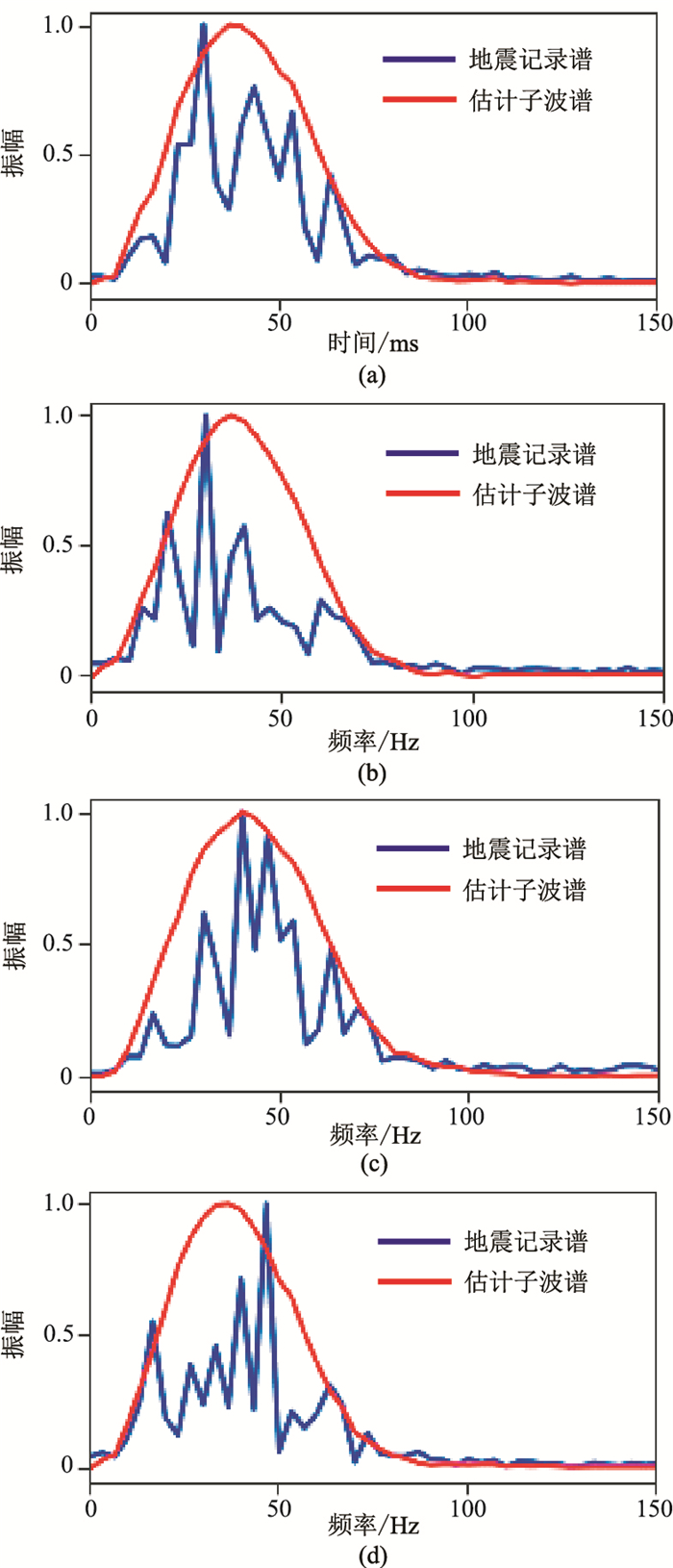
2.2 实际数据为了检验本文提出的DNN方法对实际数据的处理效果,对中国海洋石油总公司的一个实际叠后地震剖面进行高分辨处理。该叠后地震剖面的时间采样点为551,采样间隔为2ms,共1001个地震道。对于每个地震道取其中150个采样点近似为平稳的地震数据。将实际资料作为测试数据,并利用基于模型数据训练好的网络进行子波提取效果测试。随机抽取了实际资料中的4道数据,进行子波振幅谱估计。
图 7展示不同地震道的估计子波振幅谱。可以发现,DNN法从实际地震资料得到的拟合包络合理、准确,能够较好地描述地震子波形态。将该子波振幅谱用于维纳反褶积[33],可得到高分辨率结果(图 8)。本文只采用子波振幅进行反褶积,即零相位反褶积。
|
图 7 实际资料DNN法估计的地震子波振幅谱 (a)第40道;(b)第324道;(c)第413道;(d)第584道 |
|
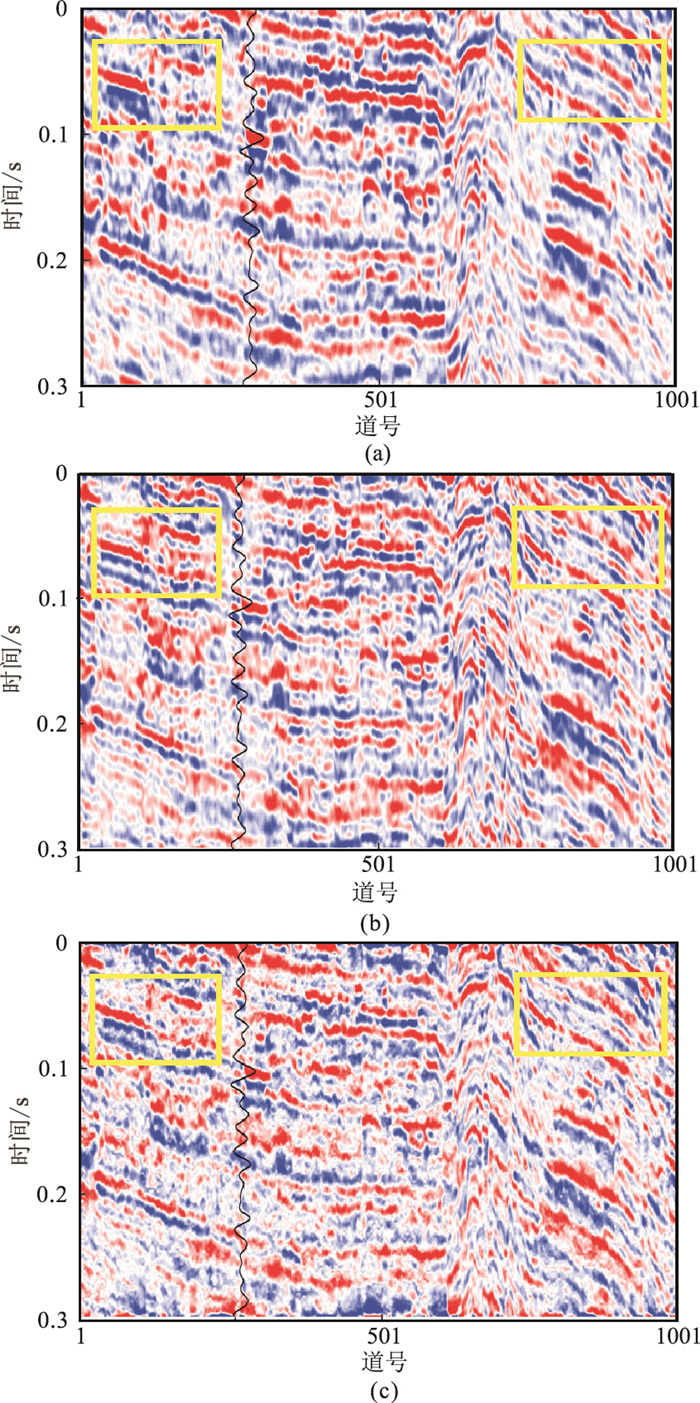
图 8 实际资料地震剖面反褶积结果 (a)实际地震剖面数据;(b)DNN法处理结果;(c)SS法处理结果第270道为测井数据 |
图 8是该实际地震剖面的高分辨率处理结果,其中第270道为测井数据,用以验证处理结果的准确性。由图 8b可以看出,采用DNN法估计的子波振幅谱经反褶积处理后,资料的纵向分辨率得到明显提高,与测井数据有较好的一致性,尤其是黄色方框区域,展现出较好的横向连续性。从图 8c所示的传统方法处理结果可见,剖面上存在明显的横向不连续现象及噪声,对实际资料的纵向分辨率没有明显改善。
因此,经本文方法处理的资料分辨率得到明显提高,横向连续性也好,实现了对地震资料的保真高分辨率处理。
3 结束语本文提出一种融入先验信息的深度学习地震子波振幅谱估计方法。首先通过已知地震子波振幅谱光滑这一先验信息,对地震数据进行预处理;然后,经过一个12层的卷积神经网络,对输入地震数据进行非线性拟合;最后,提取地震子波振幅谱。得到以下结论。
(1) 在本文DNN子波振幅谱估计方法中,需要对地震数据进行必要的预处理,因为实际的测井数据既包含噪声,也包含测量误差[34]。
(2) 本文方法不需要任何假设,不仅能够对单峰和非单峰地震子波振幅谱进行很好的估计,还避免了各种多项式的参数估计以及有效频段估计所带来的计算误差,具有较好的抗噪性能。模型算例和实际数据的测试都证明了这一点。
(3) 由于传统的地震子波振幅谱估计方法是基于统计学提出的,因此对于不同分布特征的反射系数以及子波的形态有一定限制;深度学习作为一种数据驱动方法,不依赖于地震数据的统计特性,因此不需要对反射系数类型作假设。
尚需指出,本文方法虽能准确地估计地震子波振幅谱,但仍具有以下几方面发展空间:
(1) 本文提出的融合先验信息的深度神经网络是一种有监督的机器学习方法,其估计精度依赖于训练样本中地震子波种类的个数,若训练样本中地震子波的类型不够充足,则训练的模型泛化性不能得到保证。笔者单位拟与油田合作,根据多块实际数据工区重新建立子波样本标签,针对实际中复杂的地震数据,以使该方法具有更好的泛化性;
(2) 本文方法无需考虑时变子波振幅谱的提取,因此对于非平稳地震数据,可采用非平稳地震数据划分[16]等方法对实际地震数据先作分段处理,在后续的研究中则需考虑时变性;
(3) 反射系数序列服从非白分布情况下的子波振幅谱估计对于Q值的提取也至关重要,需做进一步的研究。
| [1] |
Symes W W. The seismic reflection inverse problem[J]. Inverse Problems, 2009, 25(12): 123008. DOI:10.1088/0266-5611/25/12/123008 |
| [2] |
Chen H L, Gao J H, Liu N H, et al. Multi-trace semi-blind nonstationary deconvolution[J]. IEEE Geo-science and Remote Sensing Letters, 2019, 16(8): 1195-1199. DOI:10.1109/LGRS.2019.2893924 |
| [3] |
Walden A T, White R E. Seismic wavelet estimation: a frequency domain solution to a geophysical noisy input-output problem[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(1): 287-297. DOI:10.1109/36.655337 |
| [4] |
Tan T H. Wavelet spectrum estimation[J]. Geophy-sics, 1999, 64(6): 1836-46. |
| [5] |
Edgar J A, Van der Baan M. How reliable is statistical wavelet estimation?[J]. Geophysics, 2011, 76(4): V59-V68. DOI:10.1190/1.3587220 |
| [6] |
Wiggins R A. Minimum entropy deconvolution[J]. Geo-exploration, 1978, 16(1-2): 21-35. |
| [7] |
Van der Baan M. Time-varying wavelet estimation and deconvolution by kurtosis maximization[J]. Geo-physics, 2008, 73(2): V11-V18. |
| [8] |
Van der Baan M, Fomel S. Nonstationary phase estimation using regularized local kurtosis maximization[J]. Geophysics, 2009, 74(6): A75-A80. DOI:10.1190/1.3213533 |
| [9] |
Van der Baan M, Fomel S, Perz M. Nonstationary phase estimation: A tool for seismic interpretation[J]. The Leading Edge, 2010, 29(9): 1020-1026. DOI:10.1190/1.3485762 |
| [10] |
Robinson E A, Treitel S. Geophysical Signal Analysis[M]. Prentice-Hall, 2000.
|
| [11] |
Robinson E A, Treitel S. Digital imaging and deconvolution[C]. The ABCs of Seismic Exploration and Processing, 2008.
|
| [12] |
Margrave G F, Lamoureux M P, Henley D C. Gabor deconvolution: estimating reflectivity by nonstationary deconvolution of seismic data[J]. Geophysics, 2011, 76(3): W15-W30. DOI:10.1190/1.3560167 |
| [13] |
高静怀, 汪玲玲, 赵伟. 基于反射地震记录变子波模型提高地震道分辨率[J]. 地球物理学报, 2009, 52(5): 1289-1300. GAO Jinghuai, WANG Lingling, ZHAO Wei. Enhancing resolution of seismic traces based on the changing wavelet model of the seismogram[J]. Chinese Journal of Geophysics, 2009, 52(5): 1289-1300. DOI:10.3969/j.issn.0001-5733.2009.05.018 |
| [14] |
Gao J H, Yang S L, Wang D X, et al. Estimation of quality factor Q from the instantaneous frequency at the envelope peak of a seismic signal[J]. Journal of Computational Acoustics, 2011, 19(1): 155-179. |
| [15] |
Gao J H, Zhang B. Estimation of seismic wavelets based on the multivariate scale mixture of Gaussians model[J]. Entropy, 2010, 12(1): 14-33. |
| [16] |
Wang L L, Gao J H, Zhao W, et al. Enhancing resolution of nonstationary seismic data by molecular-Gabor transform[J]. Geophysics, 2013, 78(1): V31-V41. DOI:10.1190/geo2011-0450.1 |
| [17] |
Otis R M, Smith R B. Homomorphic deconvolution by log spectral averaging[J]. Geophysics, 1977, 42(6): 1146-1157. DOI:10.1190/1.1440780 |
| [18] |
Rosa A L R, Ulrych T J. Processing via spectral mo-deling[J]. Geophysics, 1991, 56(8): 1244-1251. DOI:10.1190/1.1443144 |
| [19] |
唐博文, 赵波, 吴艳辉, 等. 一种实现谱模拟反褶积的新途径[J]. 石油地球物理勘探, 2010, 45(增刊1): 66-70. TANG Bowen, ZHAO Bo, WU Yanhui, et al. A new way to realize spectral modeling deconvolution[J]. Oil Geophysical Prospecting, 2010, 45(S1): 66-70. |
| [20] |
Gao J H, Zhang B, Han W M, et al. A new approach for extracting the amplitude spectrum of the seismic wavelet from the seismic traces[J]. Inverse Problems, 2017, 33(10): 103012. |
| [21] |
Wang L X, Mendel J M. Adaptive minimum prediction-error deconvolution and source wavelet estimation using Hopfield neural networks[J]. Geophysics, 1992, 57(5): 882-840. |
| [22] |
Chen H L, Gao J H, Jiang X D, et al. Optimization-inspired deep learning high-resolution inversion for seismic data[J]. Geophysics, 2021, 86(3): A27-A57. DOI:10.1190/geo2020-0299.1 |
| [23] |
唐杰, 孟涛, 韩盛元, 等. 基于多分辨率U-Net网络的地震数据断层检测方法[J]. 石油地球物理勘探, 2021, 56(3): 436-445. TANG Jie, MENG Tao, HAN Shengyuan, et al. A fault detection method of seismic data based on MultiRes-Unet[J]. Oil Geophysical Prospecting, 2021, 56(3): 436-445. |
| [24] |
Yilmaz O. Seismic Data Processing[M]. SEG Press, 1987.
|
| [25] |
Neidell N S. Could the processed seismic wavelet be simpler than we think?[J]. Geophysics, 1991, 56(4): 681-690. |
| [26] |
Wang Y H. Generalized seismic wavelets[J]. Geophysical Journal International, 2015, 203: 1172-1178. DOI:10.1093/gji/ggv346 |
| [27] |
Walden A T, Hosken J W J. The nature of the non-Gaussianity of primary reflection coefficients and its significance for deconvolution[J]. Geophysical Prospecting, 1986, 34(5): 1038-1066. |
| [28] |
Saggaf M M, Robinson E A. A unified framework for the deconvolution of traces of nonwhite reflectivity[J]. Geophysics, 2000, 65(6): 1660-1676. |
| [29] |
Samorodnitsky G, Taqqu M S. Stable Non-Gaussian Random Processes Stochastic Models with Infinite Variance[M]. New York: Chapman and Hall, 1994.
|
| [30] |
Pavel C, Wolfgang H, Weron R. Statistical Tools for Finance and Insurance[M]. Berlin: Springer, 2005.
|
| [31] |
Weron R. On the Chambers-Mallows-Stuck method for simulating skewed stable random variables[J]. Statistics & Probability Letters, 1996, 28(2): 165-171. |
| [32] |
Painter S, Beresford G, Paterson L. On the distribution of seismic reflection coefficients and seismic amplitudes[J]. Geophysics, 1995, 60(5): 1187-1194. |
| [33] |
宋常州, 张旭明. 地震资料高分辨率处理技术应用[J]. 石油地球物理勘探, 2009, 44(1): 44-48. SONG Changzhou, ZHANG Xuming. Seismic data high resolution processing technique and its application[J]. Oil Geophysical Prospecting, 2009, 44(1): 44-48. |
| [34] |
杨培杰, 印兴耀. 地震子波提取方法综述[J]. 石油地球物理勘探, 2008, 43(1): 123-128. YANG Peijie, YIN Xingyao. Summary of seismic wavelet pick-up[J]. Oil Geophysical Prospecting, 2008, 43(1): 123-128. DOI:10.3321/j.issn:1000-7210.2008.01.021 |



 高静怀, 陕西省西安市咸宁西路28号西安交通大学信息与通信工程学院, 710049。Email:
高静怀, 陕西省西安市咸宁西路28号西安交通大学信息与通信工程学院, 710049。Email: 