② 青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266100
② Evaluation and Detection Technology Laboratory of Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266100, China
地震勘探在地下地质构造研究、油气资源勘查等领域起着重要的作用。在实际地震资料采集过程中,有效信息通常与复杂的背景干扰混合在一起,因此需要处理之后地震资料才可用于地质解释。噪声压制是地震资料处理中的重要一环,目的是提高地震数据的信噪比,改善成像质量。而随机噪声是一种不规则噪声,频率、传播方向不固定,很难直接去除。因此,随机噪声压制的研究具有重要的意义。
目前,地震数据随机噪声压制方法大致可分为两类,即基于模型驱动和基于数据驱动。基于模型驱动的去噪方法有f-x域预测去噪[1-3]、S变换去噪[4-5]、曲波变换去噪[6-7]、小波阈值去噪[8-14]等。该类方法提出时间较早,以较为常用的小波阈值去噪方法为例,其发展至今已有二十余年。1995年,Donoho[8]首次提出小波阈值去噪方法,奠定了小波变换在信号去噪领域的地位。之后,张宇等[9]、王勇等[10]利用小波阈值去噪方法完成了地震数据随机噪声的压制。在此基础上,不同学者对小波阈值去噪方法进行了不同程度的改进。付燕[11]在小波阈值去噪基础上,对随机噪声控制的尺度一上的小波系数进行第二次多尺度小波变换,并将二次小波变换后的尺度一上的小波系数置零,完成了对随机噪声的压制。刘军等[12]将广义交叉验证函数作为一种新的阈值函数,优化了小波阈值的选取过程。除了对小波阈值去噪方法进行改进外,还有学者将小波阈值去噪方法与其他理论相结合,对地震资料进行联合去噪。夏洪瑞等[13]将小波阈值去噪与加权叠加理论相结合,提出了小波时空域变阈值去噪方法。赵迎等[14]将小波阈值去噪与完备总体经验模态分解理论相结合,提出了一种相对保幅、有效的去噪方法。
不论是小波阈值去噪方法,还是其他基于模型驱动的去噪方法,其发展时间相对较长,技术逐渐趋于成熟。但是,压制噪声的初始条件及数学原理均是从频率差异、区域统计规律、振幅差异等某一特定角度出发,因此,方法本身存在一定的局限性。
近年来,随着计算机硬件水平的提高,基于数据驱动的去噪方法得到了较快发展。主要代表为不同深度学习框架下的噪声去除方法,如韩卫雪等[15]提出了基于深度学习卷积神经网络的地震数据随机噪声去除算法,并通过对不同类型实际地震数据去噪测试,验证了算法的可行性和有效性;王钰清等[16]改进了卷积神经网络的训练策略,提出了基于数据增广和卷积神经网络的地震随机噪声压制方法;李海山等[17]将残差卷积神经网络应用于叠前随机噪声压制,取得了较好的效果。卷积神经网络主要依靠卷积层提取地震数据的纹理特征压制噪声,但当网络层深度增加时,会导致非凸目标函数产生局部最优解。另外,由于卷积神经网络自身结构相对简单,存在模型训练速度慢、对训练样本要求高等问题[18]。生成对抗网络(Generative Adversarial Networks, GAN)[19]在一定程度上解决了这些问题。生成对抗网络作为一种新的无监督学习算法,具有较强的自主学习和生成样本能力,降低了对训练样本的要求[20-21]。Wang等[22]、Dong等[23]将GAN用于地震数据的噪声压制,取得了一定的效果。Radford等[24]将卷积神经网络与GAN相结合,提出了深度卷积GAN,此网络具有更强的特征学习能力及生成能力,但网络训练不稳定。针对此问题,Zhu等[25]在GAN的基础上提出循环一致性生成对抗网络(CycleGAN),通过引入循环一致性损失强化训练过程的稳定性,从而更好地实现网络对抗学习的过程。
因此,本文提出一种基于CycleGAN的地震数据随机噪声压制方法。通过对简单模型、复杂模型的地震剖面及实际地震数据的测试,并与经典的小波阈值去噪方法对比,验证本文方法的可行性和有效性。
1 基本原理 1.1 生成对抗网络GAN由Goodfellow等[19]提出,是一个通过对抗过程估计深度学习中生成模型的新框架。GAN主框架由一个生成器G(Generator)和一个判别器D(Discriminator)组成(图 1)。

|
图 1 GAN基本结构 |
GAN的基本思想来源于博弈论中的一个经典问题——“零和博弈”。在GAN中,参与“零和博弈”的双方为生成器G和判别器D,主要通过对抗学习的方式训练、优化模型,达到纳什平衡[26],此时模型参数达到最优。GAN目标函数为
| $ \min\limits_{G} \max\limits_{D} V(D, G)=E_{\boldsymbol{y} \sim P_{\text {data }}(\boldsymbol{y})}[\lg D(\boldsymbol{y})]+ \\ E_{\boldsymbol{x} \sim P_{\boldsymbol{x}}(\boldsymbol{x})}\{\lg [1-D(G(\boldsymbol{x}))]\} $ | (1) |
式中:V(D, G)表示关于G和D的价值函数;y为输入的真实数据;x为服从高斯分布的随机变量;Px(x)为x的概率分布;Pdata(y)为y的概率分布;x~Px(x)表示随机变量服从Px(x)的采样;y~Pdata(y)表示真实数据服从Pdata(y)的采样;D(y)、D[G(x)]分别表示将y、G(x)判别为真实数据的概率,其中G(x)为x经生成器G后生成的数据;Ex(·)表示在x采样下“·”的期望值。
目标函数可以是最大化判别器判定正确的可能性,同时训练生成器使lg{1-D[G(x)]}最小。
1.2 循环一致性生成对抗网络CycleGAN的设计初衷是在不需要其他额外信息的前提下,将图像从源领域映射到目标领域。相较于传统GAN,CycleGAN主要有两点改进[25]:
(1) 在CycleGAN里,输入数据可以为不成对的训练数据,无须建立训练数据间一对一的映射,即可实现输入数据到目标数据之间的转换;
(2) 引入循环一致性损失函数强化训练过程。
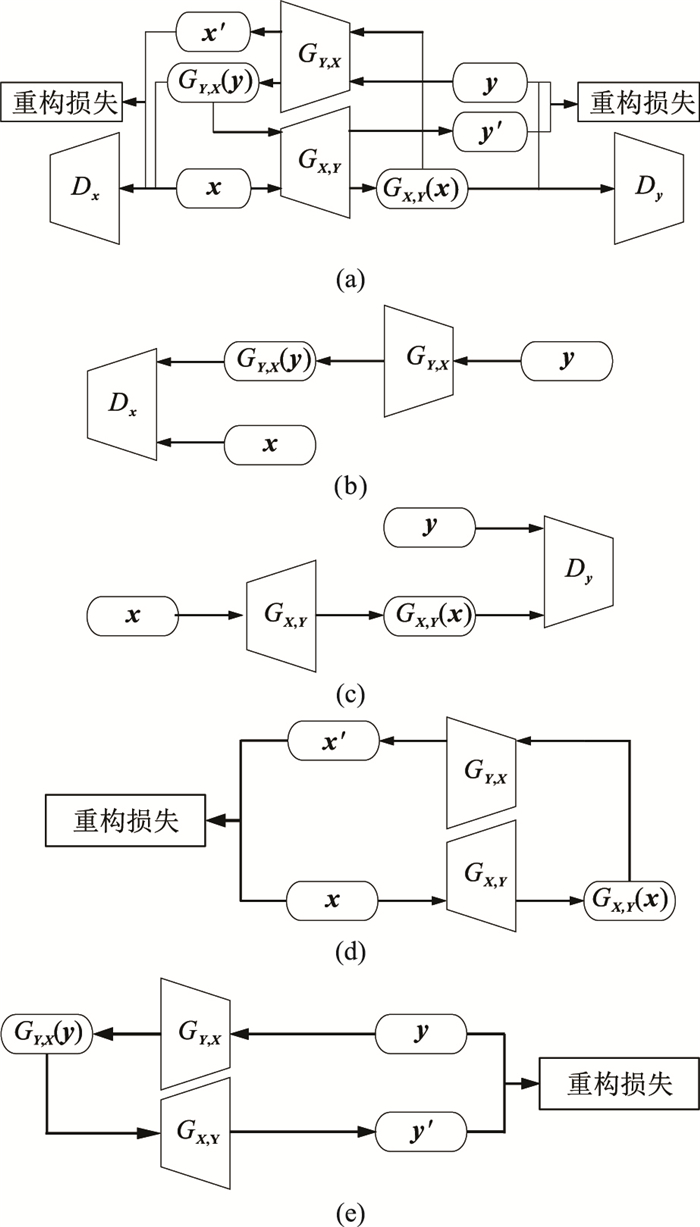
CycleGAN的基本结构是由两个GAN组成,并且构成一个环形网络(图 2a)。在CycleGAN内的两个GAN(图 2b、图 2c)共享两个生成器GX, Y、GY, X(GX, Y表示该生成器作用是将X域内的数据转换至Y域,下标“X, Y”不具有实际物理意义,仅为一种命名方式,GY, X同理),并且各自带一个判别器Dx、Dy。其中,为避免生成器GX, Y、GY, X将域内的所有数据都转换为另一个域内的某一数据,CycleGAN使用循环一致性损失(Cycle Consistency Loss)作为约束,即x和y从源域转换到目标域后,同样也可以从目标域返回源域[27]。
|
图 2 CycleGAN基本结构及不同模块构成 (a)CycleGAN基本结构;(b)GAN1;(c)GAN2;(d)前向循环一致性损失;(e)后向循环一致性损失 |
由于CycleGAN的结构发生变化,目标函数也随之发生变化。CycleGAN的目标函数由对抗损失和循环一致性损失两部分组成。
(1) 对抗损失。在CycleGAN中,对于GAN1,目标函数为
| $ \operatorname{los}_{\mathrm{GAN} 1}\left(G_{\boldsymbol{X}, \boldsymbol{Y}}, D_{\boldsymbol{y}}, \boldsymbol{x}, \boldsymbol{y}\right)=E_{\boldsymbol{y} \sim P_{\text {data }}(\boldsymbol{y})}\left[\lg D_{\boldsymbol{y}}(\boldsymbol{y})\right]+ \\ E_{\boldsymbol{x} \sim P_{\boldsymbol{x}}(\boldsymbol{x})}\left\{\lg \left[1-D_{\boldsymbol{y}}\left(G_{\boldsymbol{X}, \boldsymbol{Y}}(\boldsymbol{x})\right)\right]\right\} $ | (2) |
同理,对于GAN2,目标函数为
| $ \operatorname{loss}_{\mathrm{GAN} 2}\left(G_{\boldsymbol{X}, \boldsymbol{Y}}, D_{\boldsymbol{x}}, \boldsymbol{y}, \boldsymbol{x}\right)=E_{\boldsymbol{x }\sim P_{\text {data }}(\boldsymbol{x})}\left[\lg D_{\boldsymbol{x}}(\boldsymbol{x})\right]+ \\ E_{\boldsymbol{y} \sim P_{\boldsymbol{y}}(\boldsymbol{y})}\left\{\lg \left[1-D_{\boldsymbol{x}}\left(G_{\boldsymbol{Y}, \boldsymbol{X}}(\boldsymbol{y})\right)\right]\right\} $ | (3) |
(2) 循环一致性损失。在对GAN1、GAN2进行对抗训练时,仅使用对抗损失不能保证学习得到的映射会将一个输入x生成期望的输出y。为了进一步提高对抗训练的准确性,减少可能的映射函数空间,学习得到的映射函数GX, Y(·)、GY, X(·)还应满足循环一致性条件,如图 2d所示,将X域(含噪声数据)内的数据x转换至Y域(去噪后数据)后,再转换为x′,即x→GX, Y(x)→GY, X[GX, Y(x)]→x′,使得x与x′接近,甚至相同,这样可以避免模型网络将所有X域内数据转换为Y域内某一固定数据;同理如图 2e,将Y域内的数据y转换至X域后,再转换为y′,即y→GY, X(y)→GX, Y[GY, X(y)]→y′。循环一致性损失为
| $ \operatorname{loss}_{\text {cycle }}\left(G_{\boldsymbol{X}, \boldsymbol{Y}}, G_{\boldsymbol{Y}, \boldsymbol{X}}\right)= \\ \mathrm{E}_{\boldsymbol{x} \sim P_{\mathrm{data}}(\boldsymbol{x})}\left\{\left\|G_{\boldsymbol{Y}, \boldsymbol{X}}\left[G_{\boldsymbol{X}, \boldsymbol{Y}}(\boldsymbol{x})\right]-\boldsymbol{x}\right\|_{1}\right\}+ \\ E_{\boldsymbol{y} \sim P_{\text {data }}(\boldsymbol{y})}\left\{\left\|G_{\boldsymbol{X}, \boldsymbol{Y}}\left[G_{\boldsymbol{Y}, \boldsymbol{X}}(\boldsymbol{y})\right]-\boldsymbol{y}\right\|_{1}\right\} $ | (4) |
式中‖·‖1表示L1范数。
循环一致性损失使输入的x、y与输出的x′、y′之间保持高度一致性,从而使生成器的学习更具有目标性,可防止网络对抗性学习的退化[28]。
最终的损失函数由上述三部分组成,即
| $ \operatorname{loss}_{\mathrm{all}}\left(G_{\boldsymbol{X}, \boldsymbol{Y}}, G_{\boldsymbol{Y}, \boldsymbol{X}}, D_{\boldsymbol{x}}, D_{\boldsymbol{y}}\right)=\operatorname{loss}_{\mathrm{GAN} 1}\left(G_{\boldsymbol{X}, \boldsymbol{Y}}, D_{\boldsymbol{y}}, \boldsymbol{x}, \boldsymbol{y}\right)+ \\ \operatorname{loss}_{\mathrm{GAN} 2}\left(G_{\boldsymbol{Y}, \boldsymbol{X}}, D_{\boldsymbol{x}}, \boldsymbol{y}, \boldsymbol{x}\right)+\lambda \operatorname{loss}_{\mathrm{cycle}}\left(G_{\boldsymbol{X}, \boldsymbol{Y}}, \mathrm{G}_{\boldsymbol{Y}, \boldsymbol{X}}\right) $ | (5) |
式中λ为控制系数(通常为10),用来控制对抗损失和循环一致性损失在最终损失中的比重。最终的目标函数为
| $ \min\limits_{G_{\boldsymbol{X}, \boldsymbol{Y}}, G_{\boldsymbol{Y}, \boldsymbol{X}}} \max\limits_{D_{\boldsymbol{x}}, D_{\boldsymbol{y}}} \operatorname{loss}_\text{all}\left(G_{\boldsymbol{X}, \boldsymbol{Y}}, G_{\boldsymbol{Y}, \boldsymbol{X}}, D_{\boldsymbol{x}}, D_{\boldsymbol{y}}\right)= \\ \operatorname{loss}_{\mathrm{GAN} 1}\left(G_{\boldsymbol{X}, \boldsymbol{Y}}, \mathrm{D}_{\boldsymbol{y}}, \boldsymbol{x}, \boldsymbol{y}\right)+\operatorname{loss}_{\mathrm{GAN} 2}\left(G_{\boldsymbol{Y}, \boldsymbol{X}}, D_{\boldsymbol{x}}, \boldsymbol{y}, \boldsymbol{x}\right)+ \\ \lambda \text { loss }_{\text {cycle }}\left(G_{\boldsymbol{X}, \boldsymbol{Y}}, \mathrm{G}_{\boldsymbol{Y}, \boldsymbol{X}}\right) $ | (6) |
在CycleGAN中,本文用深度残差网络[29](Deep Residual Network,ResNet)构建生成器网络,用马尔柯夫判别器[30](PatchGAN)构建判别器网络。
2.1 生成器网络在深度学习过程中,卷积神经网络通过不断堆叠卷积层进行特征提取,并且随着层数增大,特征也变得更丰富。但是,层数与准确率并不是单纯的正比关系,即不是神经网络中卷积层数越大越好,因为当达到一定层数时会出现网络退化现象。而ResNet可有效解决此问题。
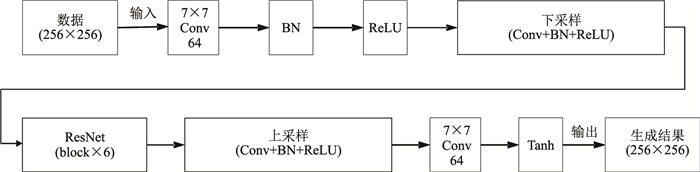
本文利用ResNet网络构建CycleGAN的生成器(图 3),与图像处理领域中的RGB三通道数据不同,地震数据类似于单通道灰度图。因此,网络的输入数据为256×256的矩阵,使用64个7×7大小的卷积核(Conv)进行卷积处理,经批量标准化(BN)、ReLU激活函数、下采样,进入由6个残差块组成的ResNet网络;然后经过上采样、64个7×7大小的卷积核进行卷积处理及Tanh激活函数,输出数据为256×256的矩阵。
|
图 3 本文CycleGAN生成器网络结构 |
普通GAN判别器输出一个实数,是对输入数据整体进行判别的结果;而PatchGAN输出一个矩阵,矩阵中的每个元素代表输入数据中某一部分的判别结果,因而具有更高的分辨率及准确性。
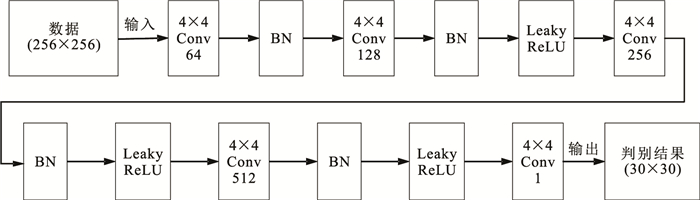
本文判别器(图 4)使用PatchGAN,与生成器网络输入数据相同,判别器网络的输入数据大小同样为256×256的矩阵,使用不同层深、卷积核大小均为4×4的卷积层处理,每次卷积处理后,需经批量标准化、斜率为0.2的Leaky ReLU激活函数处理,最终输出30×30的矩阵,该矩阵的每个元素值代表某部分输入数据为真实数据的概率。
|
图 4 本文CycleGAN判别器网络结构 |
本文研究使用Dell台式工作站,Linux64位操作系统,版本为Ubuntu.18.04,GPU为NVIDIA. GTX1070。为验证CycleGAN对地震数据随机噪声的去除效果,分别利用理论数据(简单模型、复杂模型)和实际数据进行测试,同时对上述地震数据进行小波阈值去噪(综合对比应用不同小波及不同阈值的去噪结果,本文最终选用了sym3小波、固定式阈值、软阈值函数,小波分解层数为3层,见附录A),通过结合不同的信号去噪效果评估指标(本文使用信噪比SNR、均方根误差RMSE两种评估方法,见附录B),对比、评估地震剖面噪声压制效果;并抽取单道数据进行频谱分析,通过剖面细节进一步明确CycleGAN方法的噪声压制效果。
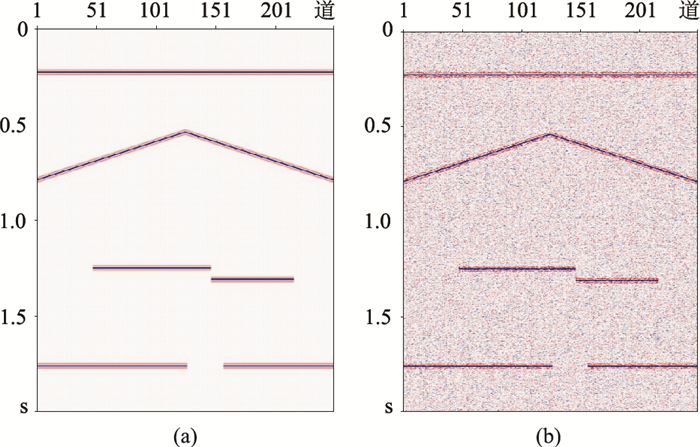
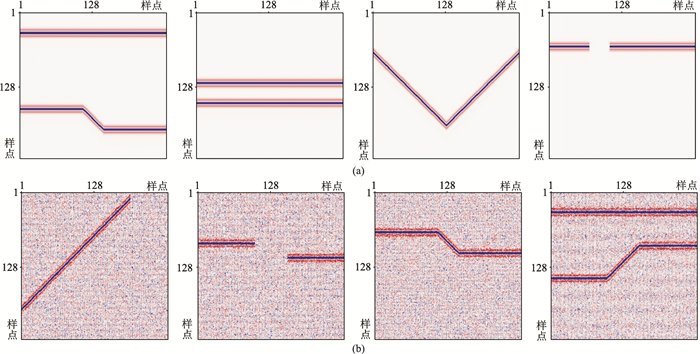
3.1 理论数据测试 3.1.1 简单模型数据测试简单模型无噪声剖面如图 5a所示,添加一定程度的高斯白噪声得到含噪声剖面(图 5b,SNR为0.31)。剖面共250道,每道时长2000ms,包含水平、倾斜、不连续和孤立等多种同相轴。对于Cycle-GAN算法,需建立合适的训练集进行训练,在对模型进行去噪试验时,训练集样本分别选取2750幅无噪声和含随机噪声剖面(图 6)。其中,含噪声剖面与无噪声剖面无需一一对应,每幅训练集剖面中含有水平、倾斜、不连续和孤立等不同类型同相轴。
|
图 5 简单模型地震剖面 (a)无噪声;(b)含噪声 |
|
图 6 简单模型训练集样本示例 (a)无噪声剖面;(b)含噪声剖面 |
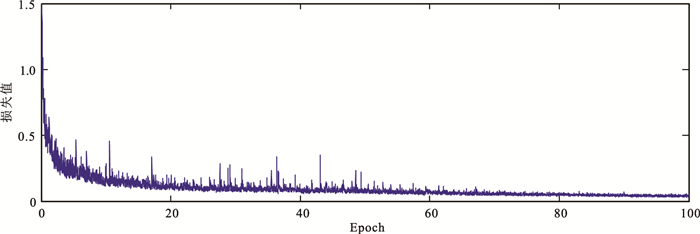
利用制作好的训练样本集,经历100Epoch,用时约40h,可得到训练好的网络结构,通过该网络对含噪剖面进行随机噪声压制测试。图 7为该网络的损失函数曲线。由图也可看出,本文网络中的各部分达到了一种相对平衡的状态,网络可以完成对剖面内随机噪声的压制。
|
图 7 CycleGAN损失函数曲线 |
从图 8可以看出,小波阈值去噪方法与Cycle-GAN去噪方法均对噪声进行了一定程度的压制,但后者去噪效果明显优于前者。由表 1可知,Cycle-GAN去噪后数据SNR为10.38,明显大于小波阈值,RMSE也小于小波阈值。

|
图 8 简单模型地震剖面两种方法去噪效果对比 (a)小波阈值去噪结果;(b)CycleGAN去噪结果;(c)小波阈值法去除的噪声;(d)CycleGAN法去除的噪声 |
|
|
表 1 简单模型地震剖面去噪效果对比 |
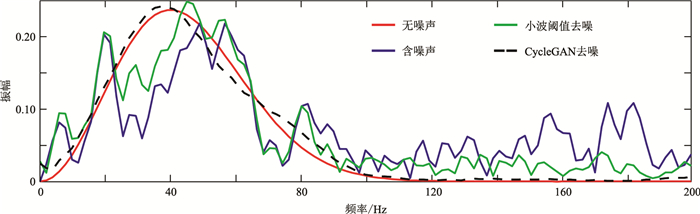
对比剖面细节,图 8b红框内同相轴在去噪后形态存在部分畸变,对比剖面内其他同相轴及训练集样本,可知是由训练集内与其类似剖面训练样本较少,导致网络对于该形态的同相轴去噪能力不够所致。抽取每幅剖面第60道数据进行频谱分析,结果如图 9所示。由图可见,原始无噪声地震数据的频谱较为光滑,而加入随机噪声之后的含噪声地震数据频谱发生了较大变化;通过小波阈值去噪后,频谱虽有所改善,但仍与原始数据频谱差别较大;而CycleGAN去噪后的数据频谱毛刺状干扰基本消除,并且频谱特征与原始地震剖面基本一致。
|
图 9 简单模型地震剖面第60道去噪前后频谱对比 |
使用Overthrust模型(图 10a)的反射系数与主频为40Hz的Ricker子波进行褶积得到无噪声地震剖面(图 10b),剖面共500道,每道时长640ms。对无噪声数据添加高斯白噪声得到含噪声数据(图 10c,SNR为0.65)。为了制作足够数量的训练样本,可将数据进行一系列的处理,如上下倒转、左右倒转、插值等。由于此噪声模型相对复杂,需要选取比简单模型更多的训练样本,本文选取10000幅含随机噪声剖面和10000幅无噪声剖面作为训练样本,图 11为部分训练样本示例。

|
图 10 Overthrust模型及地震剖面 (a)Overthrust模型;(b)无噪声;(c)含噪声 |

|
图 11 复杂模型训练集样本示例 (a)无噪声剖面;(b) 含噪声剖面 |
利用训练好的网络,对含噪声数据进行去噪测试,结果如图 12所示。对比图 12a与图 12b可知,在图 10c中受随机噪声影响较为严重的同相轴(图 10c中红色箭头处),经过两种去噪方法处理后情况均有所改善,但CycleGAN去噪效果明显优于小波阈值;对比图 12c与图 12d可见,图 12c中除随机噪声外,还存在部分同相轴,可知小波阈值去噪算法将部分有效信息去除,而CycleGAN去噪结果中无此现象。同样,由表 2也可以看出,本文去噪算法性能更佳。

|
图 12 Overthrust模型地震剖面去噪效果对比 (a)小波阈值去噪结果;(b)CycleGAN去噪结果;(c)小波阈值去除的噪声;(d)CycleGAN去除的噪声 |
|
|
表 2 Overthrust模型地震剖面去噪效果对比 |
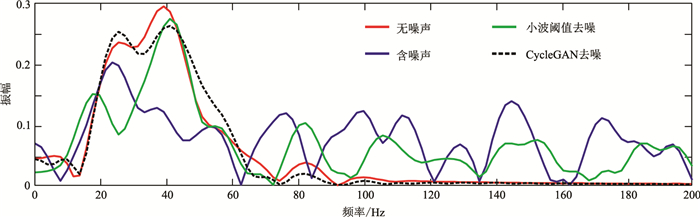
对于Overthrust模型地震剖面的细节部分,如图 12a和图 12b中红框内区域,抽取第240道数据进行频谱(图 13)分析,在90~180Hz范围内,可发现CycleGAN去噪方法几乎完全消除了随机噪声;在0~90Hz范围内,CycleGAN去噪方法也能够很好地保留有效信号,最大限度地消除了随机噪声的影响。
|
图 13 Overthrust模型地震剖面第240道去噪前后频谱对比 |
选用中国东部A工区实际地震数据进行测试。对于受噪声影响较小的数据进行常规噪声压制处理,即可获得成像较为清晰的地震剖面。从中选取10幅作为训练集中无噪声剖面,图 14为其中的两幅剖面,每幅剖面有250道,每道时长为1024ms。通过对无噪声剖面进行上下反转、左右反转及插值处理,扩充训练数据集数量,得到5000幅无噪声剖面。对无噪声剖面添加一定程度高斯白噪声,得到5000幅含噪声剖面。利用上述数据作为训练集进行网络训练。取该工区内另一随机噪声严重的剖面(图 15a,SNR为0.55)为测试数据,测试数据共250道,每道时长为1024ms,去噪结果如图 15b、图 15c所示。

|
图 14 A工区高信噪比叠后地震剖面经常规噪声压制处理后效果示例 (a)剖面一;(b)剖面二 |
|
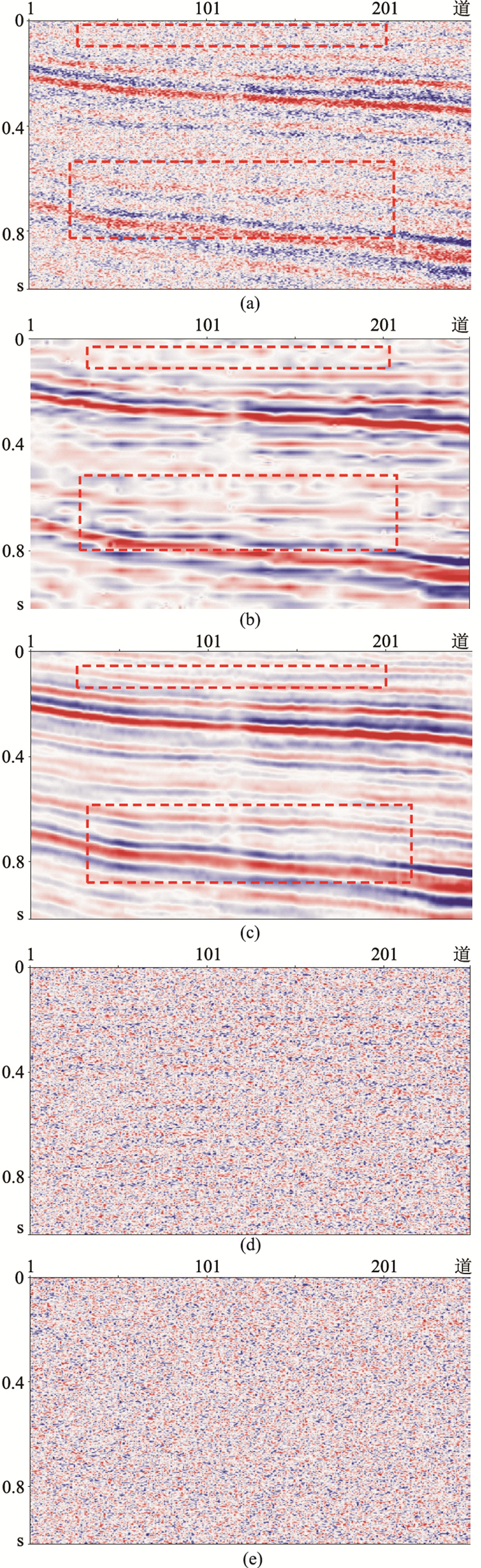
图 15 A工区叠后地震数据及去噪效果对比 (a)叠后地震剖面;(b)小波阈值去噪结果;(c)CycleGAN去噪结果;(d)小波阈值去除的噪声;(e)CycleGAN去除的噪声 |
对比图 15b、15c可以发现,由于原始数据在进行小波阈值去噪时,小波分解得到的小波系数无法对有效信号进行完美的表达,因此,虽然“雪花状”随机噪声得到压制,但其中部分连续同相轴变为多个不连续块状同相轴(如图 15a、15b内红框内部分),有效信号损失较为严重。图 15d、图 15e分别为两种方法去除的噪声,其中,小波阈值去噪方法去除的噪声(图 15d)存在类似条状同相轴,相比之下,CycleGAN在压制随机噪声的同时,有效信息也得到了最大程度的保留。表 3为实际地震数据去噪效果对比,由表 3也可以看出,本文去噪方法性能更佳。
|
|
表 3 实际地震数据去噪效果对比 |
本文提出一种适用于地震数据随机噪声压制的循环一致性生成对抗网络,该网络生成器由ResNet网络构成,有效避免了梯度爆炸(消失)及网络退化问题;判别器由PatchGAN构成,可以更好地对生成结果进行识别;同时,该网络在传统对抗损失的基础上引入循环一致性损失,提高了训练过程的稳定性。通过训练好的网络分别对简单模型数据、复杂模型数据及实际地震数据进行随机噪声压制测试,并以常规去噪算法(本文应用小波阈值去噪方法)作为对照组,利用去噪前后数据信噪比、均方根误差等参数,证明了本文构建的网络去噪方法优于小波阈值去噪方法;通过对比单道频谱分析结果进一步说明CycleGAN去噪效果优于常规去噪算法,验证了本文方法在地震数据随机噪声压制方面的可行性。
目前,深度学习算法在地震资料处理领域的应用才刚刚起步,还存在许多问题亟待加以改进。本研究下一步工作是:如何在维持当前去噪效果的同时,缩短网络训练时间,改善CycleGAN去噪的泛化能力,提高本文方法的实用性。
附录A 固定式阈值和软阈值函数计算公式文中小波阈值去噪的阈值计算规则为固定式阈值,阈值函数为软阈值函数。
去噪过程中首先需要估计阈值,然后保留大于阈值的系数,舍弃小于阈值的系数。阈值选择过大则可能去除有效信号,过小则不能完全消除噪声,因此需要选择一个合适的阈值规则。文中固定式阈值为
| $ \lambda=\sigma \sqrt{2 \ln N} $ | (A-1) |
式中:σ为噪声的标准方差;N为信号的长度。
在完成阈值计算后,需要阈值函数对小波系数进行处理,文中使用的软阈值函数计算公式为
| $ \hat{\omega}(j, k)= \begin{cases}0 & |\omega(j, k)|<\lambda \\ |\omega(j, k)-\lambda| \operatorname{sgn}[\omega(j, k)] & |\omega(j, k)| \geqslant \lambda\end{cases} $ | (A-2) |
式中:
信噪比(Signal to Noise Ratio,SNR)是有效信号能量与噪声能量之比,为振幅比的平方。假设有效信号为s(t),去噪后信号为g(t),则
| $ \mathrm{SNR}=\frac{E_{\mathrm{s}}}{E_{\mathrm{n}}}=\frac{\sum\limits_{i=1}^{N} s^{2}(t)}{\sum\limits_{i=1}^{N}[g(t)-s(t)]^{2}} $ | (B-1) |
式中Es、En分别为有效信号能量、噪声能量。通常认为,SNR越高,去噪后的信号残留噪声能量越小,去噪效果越好。
均方根误差(Root Mean Squared Error,RMSE)是均方误差的算术平方根,用来表示有效信号与去噪后信号之间的差异
| $ \mathrm{RMSE}=\sqrt{\frac{1}{N} \sum\limits_{i=1}^{N}[g(t)-s(t)]^{2}} $ | (B-2) |
通常认为,RMSE越小,去噪效果越好。
| [1] |
国九英, 周兴元. 用f-x域预测技术消除随机噪音[J]. 石油地球物理勘探, 1992, 27(5): 655-661. GUO Jiuying, ZHOU Xingyuan. Random noise elimination using f-x domain prediction[J]. Oil Geophysical Prospecting, 1992, 27(5): 655-661. |
| [2] |
Gan S W, Wang S D, Chen Y K, et al. Improved random noise attenuation using f-x empirical mode decomposition and local similarity[J]. Applied Geophy-sics, 2016, 13(1): 127-134. DOI:10.1007/s11770-016-0545-1 |
| [3] |
国胧予, 刘财, 刘洋, 等. 基于f-x域流式预测滤波器的地震随机噪声衰减方法[J]. 地球物理学报, 2020, 63(1): 329-338. GUO Longyu, LIU Cai, LIU Yang, et al. Seismic random noise attenuation based on streaming prediction filter in the f-x domain[J]. Chinese Journal of Geophysics, 2020, 63(1): 329-338. |
| [4] |
赵淑红, 朱光明. S变换时频滤波去噪方法[J]. 石油地球物理勘探, 2007, 42(4): 402-406. ZHAO Shuhong, ZHU Guangming. Time frequency filtering to denoising by S transorm[J]. Oil Geophysical Prospecting, 2007, 42(4): 402-406. DOI:10.3321/j.issn:1000-7210.2007.04.008 |
| [5] |
曹鹏涛, 张敏, 李振春. 基于广义S变换及高斯平滑的自适应滤波去噪方法[J]. 石油地球物理勘探, 2018, 53(6): 1128-1136. CAO Pengtao, ZHANG Min, LI Zhenchun. An adaptive filtering denoising method based on genera-lized S-transform and Gaussian smoothing[J]. Oil Geophysical Prospecting, 2018, 53(6): 1128-1136. |
| [6] |
孙苗苗, 李振春, 曲英铭, 等. 基于曲波域稀疏约束的OVT域地震数据去噪方法研究[J]. 石油物探, 2019, 58(2): 208-218. SUN Miaomiao, LI Zhenchun, QU Yingming, et al. A seismic denoising method based on curvelet transform with sparse constraint in OVT domain[J]. Geophysical Prospecting for Petroleum, 2019, 58(2): 208-218. DOI:10.3969/j.issn.1000-1441.2019.02.006 |
| [7] |
张华, 刁塑, 温建亮, 等. 应用二维非均匀曲波变换压制地震随机噪声[J]. 石油地球物理勘探, 2019, 54(1): 16-23. ZHANG Hua, DIAO Su, WEN Jianliang, et al. A random noise suppression with 2D non-uniform curvelet transform[J]. Oil Geophysical Prospecting, 2019, 54(1): 16-23. |
| [8] |
Donoho D L. De-nosing by soft-thresholding[J]. IEEE Transactions on Information Theory, 1995, 41(3): 613-627. DOI:10.1109/18.382009 |
| [9] |
张宇, 张关泉. 小波变换用于去除高频随机噪声[J]. 石油地球物理勘探, 1997, 32(3): 327-337. ZHANG Yu, ZHANG Guanquan. High-frequency random noise elimination using wavelet transform[J]. Oil Geophysical Prospecting, 1997, 32(3): 327-337. |
| [10] |
王勇, 郦军, 张奎凤. 基于小波变换的地震信号降噪处理[J]. 石油物探, 1998, 37(3): 72-76. WANG Yong, LI Jun, ZHANG Kuifeng. The noise elimination processing of seismic signal based on wavelet transform[J]. Geophysical Prospecting for Petroleum, 1998, 37(3): 72-76. |
| [11] |
付燕. 基于二次小波变换的地震信号去噪方法[J]. 石油地球物理勘探, 2005, 40(2): 154-157. FU Yan. Noise-elimination method for seismic signal based on second wavelet transform[J]. Oil Geophysical Prospecting, 2005, 40(2): 154-157. DOI:10.3321/j.issn:1000-7210.2005.02.013 |
| [12] |
刘军, 郑成龙, 吴新华, 等. 基于改进混沌果蝇优化小波阈值法地震信号随机噪声压制[J]. 地质与勘探, 2017, 53(4): 765-772. LIU Jun, ZHENG Chenglong, WU Xinhua, et al. Suppression of seismic random noise based on the improved wavelet threshold method using chaotic fruit fly optimization[J]. Geology and Exploration, 2017, 53(4): 765-772. |
| [13] |
夏洪瑞, 葛川庆, 彭涛. 小波时空变阈值去噪方法在可控震源资料处理中的应用[J]. 石油地球物理勘探, 2010, 45(1): 23-27. XIA Hongrui, GE Chuanqing, PENG Tao. Application of wavelet time-space-varying threshold denoising method in vibroseis data processing[J]. Oil Geophysical Prospecting, 2010, 45(1): 23-27. |
| [14] |
赵迎, 乐友喜, 黄健良, 等. CEEMD与小波变换联合去噪方法研究[J]. 地球物理学进展, 2015, 30(6): 2870-2877. ZHAO Ying, YUE Youxi, HUANG Jianliang, et al. CEEMD and wavelet transform jointed denoising method[J]. Progress in Geophysics, 2015, 30(6): 2870-2877. |
| [15] |
韩卫雪, 周亚同, 池越. 基于深度学习卷积神经网络的地震数据随机噪声去除[J]. 石油物探, 2018, 57(6): 72-79. HAN Weixue, ZHOU Yatong, CHI Yue. Deep lear-ning convolutional neural networks for random noise attenuation in seismic data[J]. Geophysical Prospecting for Petroleum, 2018, 57(6): 72-79. |
| [16] |
王钰清, 陆文凯, 刘金林, 等. 基于数据增广和CNN的地震随机噪声压制[J]. 地球物理学报, 2019, 62(1): 427-439. WANG Yuqing, LU Wenkai, LIU Jinlin, et al. Random seismic noise attenuation based on data augmentation and CNN[J]. Chinese Journal of Geophysics, 2019, 62(1): 427-439. |
| [17] |
李海山, 陈德武, 吴杰, 等. 叠前随机噪声深度残差网络压制方法[J]. 石油地球物理勘探, 2020, 55(3): 493-503. LI Haishan, CHEN Dewu, WU Jie, et al. Pre-stack random noise suppression with residual network[J]. Oil Geophysical Prospecting, 2020, 55(3): 493-503. |
| [18] |
梁俊杰, 韦舰晶, 蒋正锋. 生成对抗网络GAN综述[J]. 计算机科学与探索, 2020, 14(1): 1-17. LIANG Junjie, WEI Jianjing, JIANG Zhengfeng. Generative adversarial networks GAN overview[J]. Journal of Forntiers of Computer Science and Technology, 2020, 14(1): 1-17. |
| [19] |
Goodfellow I J, Pouget Abadie J, Mirza M, et al. Ge-nerative adversarial nets[C]. International Conference on Neural Information Processing Systems, 2014, 2672-2680.
|
| [20] |
杨懿男, 齐林海, 王红, 等. 基于生成对抗网络的小样本数据生成技术研究[J]. 电力建设, 2019, 40(5): 71-77. YANG Yinan, QI Linhai, WANG Hong, et al. Research on generation technology of small sample data based on generative adversarial network[J]. Electric Power Construction, 2019, 40(5): 71-77. |
| [21] |
桑亮, 高爽, 尹增山. 基于生成对抗网络的运动模糊图像复原[J]. 计算机工程与应用, 2019, 55(6): 173-177. SANG Liang, GAO Shuang, YIN Zengshan. Motion deblurring based on generative adversarial networks[J]. Computer Engineering and Applications, 2019, 55(6): 173-177. |
| [22] |
Wang H, Li Y, DONG X. Generative adversarial network for desert seismic data denoising[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020. DOI:10.1109/TGRS.2020.3030692 |
| [23] |
Dong X T, LI Y. Denoising the optical fiber seismic data by using convolutional adversarial network based on loss balance[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020. DOI:10.1109/TGRS.2020.3036065 |
| [24] |
Radford A, Metz L, Chintala S. Unsupervised representation learning with deep convolutional generative adversarial networks[C]. Machine Learning, 2016. arXiv. org > cs > arXiv: 1511.06434.
|
| [25] |
Zhu J Y, Park T, Isola P, et al. Unpaired image-to-image translation using cycle-consistent adversarial networks[C]. IEEE International Conference on Computer Vision, 2017, 2242-2251.
|
| [26] |
Ratliff L J, Burden S A, Sastry S S. Characterization and computation of local Nash equilibria in continuous games[C]. Communication, Control, & Computing, 2006, 917-924.
|
| [27] |
刘华超, 张俊然, 刘云飞. 引入特征损失对CycleGAN的影响研究[J]. 计算机工程与应用, 2020, 56(22): 217-223. LIU Huachao, ZHANG Junran, LIU Yunfei. The influence of identity loss on CycleGAN[J]. Computer Engineering and Applications, 2020, 56(22): 217-223. DOI:10.3778/j.issn.1002-8331.1910-0405 |
| [28] |
Li C Y, Liu H, Chen C Y, et al. ALICE: towards understanding adversarial learning for joint distribution matching[C]. 31st Annual Conference on Neural Information Processing Systems (NIPS), 2017, 1-13.
|
| [29] |
He K M, Zhang X Y, Ren S Q, et al. Deep residual learning for image recognition[C]. Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition, 2016, 770-778.
|
| [30] |
Isola P, Zhu J Y, Zhou T, et al. Image-to-image translation with conditional adversarial networks[C]. Proceedings of the IEEE Computer Vision and Pattern Recognition, 2017, 1125-1134.
|



 张会星, 山东省青岛市崂山区松岭路238号中国海洋大学海底科学与探测技术教育部重点实验室, 266100。Email:
张会星, 山东省青岛市崂山区松岭路238号中国海洋大学海底科学与探测技术教育部重点实验室, 266100。Email: 