② 中国石油大港油田公司勘探开发研究院, 天津 300280
② Research Institute of Exploration & Development, Dagang Oilfield Company, PetroChina, Tianjin 300280, China
在地震资料解释中,人工识别断层耗时、费力,且人为因素往往容易增加断层解释结果的不确定性。如何高效率、准确地识别断层,特别是在发育大量、复杂断层的勘探区,是一个难题。
在过去几十年中,利用计算机辅助识别断层方面的技术发展很快。李军等[1]、王静等[2]利用各向异性扩散滤波方法识别断层,效果较好。Wu[3]提出的方向性结构张量相干算法对小断层的识别效果较好。Qi等[4]提出了多角度相干算法,可以提高相干属性识别断层的精度。Duan等[5]提出的振幅谱方差相干算法更能突出小断裂。Wang等[6]提出三维构造导向复相干属性,从理论模型和实际资料的应用两方面证明了其在断裂识别方面的有效性。Yan等[7]采用多方向特征值相干属性检测断层等不连续性。Chopra等[8]利用曲率属性解释断层。霍志周等[9]提出了一种高精度结构曲率的提取方法,对高陡构造及断层的刻画精度更高,更有利于构造解释。Di等[10]、Ashraf等[11]、Philips等[12]提出将边缘检测算法用于断层识别,增强断层边缘信息,可提高断层识别的准确性。Pedersen等[13]系统提出了蚂蚁追踪的流程。李楠等[14]利用高清蚂蚁体解释复杂断裂带,能在提高信噪比的同时增强断层连续性。上述滤波方法、属性类算法、边缘检测方法和蚂蚁追踪算法等在实际中应用广泛,但计算参数的设置以及解释人员的经验往往会影响断层识别的准确性。
近年来,随着人工智能的快速发展,机器学习和深度学习方法越来越多地应用于地球物理领域,多种基于卷积神经网络的算法开始应用于断层识别。Huang等[15]将多种地震属性作为卷积神经网络的输入进行模型的训练和断层的自动识别。Di等[16]提出一种基于多层感知机(Multilayer Perceptron,MLP)的断层识别方法,将多种地震属性作为训练样本,断层识别效果较好。Xiong等[17]将卷积神经网络预测的断层与相干属性方法进行对比,证明了前者的断层识别效果更好。Guo等[18]直接将二维地震数据和人工标注的断层标签输入卷积神经网络中,提高了断层识别的效率。Zhao等[19]结合卷积神经网络与构造导向滤波技术,并应用于实际地震资料的断层识别,效果较好。Wu等[20]应用基于卷积神经网络的像素分类方法,可以同时识别断层的分布和预测断层倾角,并提出了一种更为高效的三维U-Net断层识别方法[21],即利用多个理论合成的地震数据体进行模型训练,进而用于实际地震数据的断层预测。Pochet等[22]指出,将地震振幅数据作为卷积神经网络的输入可以避免多属性技术带来的计算量大的问题。Cunha等[23]利用合成的地震数据训练卷积神经网络模型,然后引入迁移学习的理念,对模型进行微调后,再应用到实际地震资料中,可提高断层识别的准确性。Di等[24]在卷积神经网络中应用解释性约束条件,提高了断层识别的准确性。张政等[25]结合深度残差网络与迁移学习方法,增强了网络的泛化能力,优化了识别结果。常德宽等[26]提出一种基于深度卷积神经网络的断层识别方法,断层识别的准确性和效率明显优于常规相干算法。
为了进一步提高断层识别的准确性,本文将三维U-Net与深度残差网络相结合,引入多层深度监督的机制,构建基于三维深度监督网络的断层检测方法。网络的设计思想是:在U-Net的编码部分和解码部分的卷积块之间增加残差连接,简化网络的学习目标,降低网络训练难度;在解码部分利用多层深度监督机制,更有效地结合断层的多尺度信息,进一步提高断层识别的准确性。具体的实现过程不同于常德宽等[26]提出的深度卷积神经网络方法,本文方法无需根据实际地震资料进行训练,而是采用Wu等[27]提出的方法,自动生成大量、不同类型的断层样本用于训练,可以减少人工标注断层的时间成本。与Wu等[20]提出的三维U-Net网络的断层检测结果对比,本文方法断层识别精度更高。
1 方法原理 1.1 残差网络结构增加神经网络的深度可以增加网络的参数种类,因而可以更好地学习目标特征。但是,简单地增加网络层数会出现梯度消失、梯度爆炸、过拟合等问题,造成网络退化、训练精度和测试精度下降。He等[28]提出利用残差模块的方法,可以解决深层网络的退化问题。
残差模块基本结构如图 1所示。假设神经网络的输入为x,期望输出为H(x),实际输出为F(x)。与常规的卷积模块(图 1a)结构不同,在残差网络中,通过跳跃连接的方式可以直接把输入x传到输出作为初始结果,则输出结果变为H(x)=F(x)+x。这相当于残差模块改变了学习目标,不再是学习一个完整的输出,而是目标值H(x)与x的差值,即残差F(x)=H(x)-x。

|
图 1 不同模块结构对比 (a)卷积模块;(b)残差模块。ReLU为激活函数 |
He等[28]指出,如果网络层数超过最佳层数,残差网络会将多余层训练为F(x)=0,即这些层的输入与输出相同,从而变为恒等映射。恒等映射函数允许将较深层中的梯度值快速传递至较浅层,可解决网络训练过程中梯度爆炸或梯度消失的问题。因此,网络层数加深不会造成网络退化,从而可以提高网络训练过程的稳定性和效率。
1.2 三维深度监督网络构建本文构建的三维深度监督网络(简称本文网络,下同)的结构(图 2)类似于Wu等[21]提出的三维U-Net,由编码器和解码器两部分组成。编码器子网络分析输入的地震数据并学习断层的特征;解码器子网络学习不同尺度的特征信息,并可以进行端到端训练,实现断层的语义分割。在分辨率相等的层之间建立的跳跃连接可以将来自解码器的深层高级特征与来自编码器的浅层低级特征进行融合,从而提高断层识别的准确性。

|
图 2 三维深度监督网络(本文网络)结构 长方体右侧数字表示每个步骤后输出特征图的数量(上)和大小(下) |
与三维U-Net不同,本文网络引入了残差学习模块和多层次的深度监督。残差模块的引入能够简化网络的学习目标,降低训练难度;多层次的深度监督能够为网络提供更多的反馈,减轻训练过程中潜在的梯度消失,使解码器子网络更有效地整合多尺度信息,从而进一步提高断层识别的准确性。
如图 2所示,本文网络为四层结构,由四个编码器和四个解码器组成,每个编码器、解码器均包含一个残差学习模块。残差模块(图 1b)由两个3×3×3的三维卷积层和一个跳跃连接构成,卷积层之后添加批量归一化(Batch Normalization)[29]和Leaky ReLU激活函数,并引入失活层(Dropout)防止过拟合问题的出现。批量归一化对每个层的输入数据作归一化处理,使其满足标准正态分布,这可以降低内部协变量偏移,提高模型训练的效率[30];Leaky ReLU激活函数可解决梯度消失问题,不仅可以缩短神经网络训练周期,提升对应模型的收敛速度,而且能够增强模型的鲁棒性及稳定性。
在编码器部分,每一层残差模块之后采用步幅为2的2×2×2的最大池化对数据进行降维,扩大后续的卷积层对地震数据的感受野。在解码器部分,每一层残差模块之后采用步幅为2的2×2×2的上采样,使上采样后的数据能够更准确地重建断层特征。
在U-Net的特征提取阶段,即编码器子网络部分,浅层结构可以抓取断层的简单特征,而深层结构因为感受野的扩大以及多次卷积操作,可以捕获到断层的抽象特征。浅层特征和深层特征对于断层的检测都起着至关重要的作用,而原始U-Net结构仅在解码器子网络的最后一层进行输出,没有利用不同层级解码器输出的特点。为了弥补U-Net的这一缺陷并取得更好的断层检测效果,本文引入多层深度监督机制,即对解码器子网络的每一层均进行输出,具体实现过程为:在每个解码器阶段的最后一层,通过一个3×3×3的卷积操作和一个步幅为2的2×2×2上采样操作,用以匹配不同层级解码器输出的尺寸;将每一层解码器的输出逐层相加,最终利用Sigmoid激活函数输出断层概率值,取值范围为[0, 1]。本文构建的多层深度监督的网络,可以充分学习到不同尺度的断层语义信息,在网络训练过程中可以充分利用不同尺度的断层特征,使最终用于断层检测的信息更丰富,从而有助于提高断层细分的准确性以及断层检测的精度。
2 网络训练和模型测试 2.1 训练样本生成利用本文网络训练模型检测断层需要大量的断层样本。手动标记或解释三维地震数据中的断层非常耗时且受人为因素影响较大。不正确的人工解释,即标记错误或者未被标记的断层,往往会误导整个网络的学习过程。为了避免这些问题,本文应用Wu等[27]提出的方法,生成多个包含不同类型断层的合成地震数据,作为训练样本用以训练和验证本文网络。断层样本的生成(图 3)步骤如下。
|
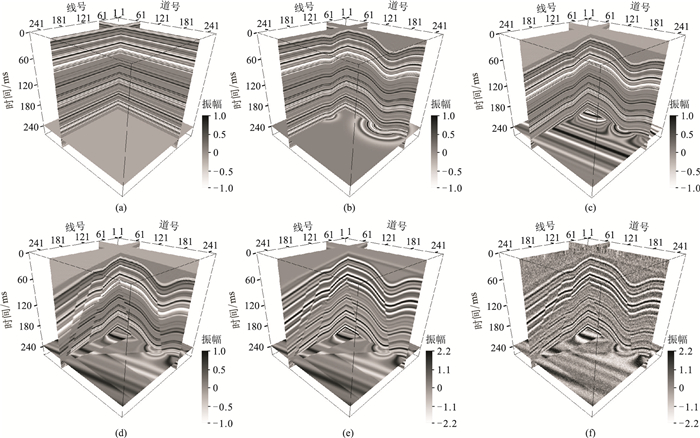
图 3 断层样本生成流程 (a)反射系数模型;(b)添加褶皱构造;(c)添加平面剪切构造;(d)添加断层;(e)与雷克子波褶积;(f)添加随机噪声 |
(1) 随机生成一维水平反射系数模型(图 3a),反射系数范围为[-1, 1]。
(2) 在反射系数模型中,通过垂直剪切模型增加褶皱构造(图 3b),生成褶皱构造的方法为
| $ S_{1}(x, y, z)=a+\frac{1.5}{N_{z}} \sum\limits_{k=1}^{N_{g}} b_{k} \mathrm{e}^{\frac{\left(x-c_{k}\right)^{2}+\left(y-d_{k}\right)^{2}}{2 \sigma_{k}^{2}}} $ | (1) |
式中:Nz代表z方向所有的采样点数量;a代表垂向剪切在z方向的位置,a∈0,15;bk表示垂向褶皱的大小,bk∈0, 15;ck和dk分别代表褶皱在x和y方向的位置,因为本文生成的模型大小为256×256×256,所以二者的取值范围均为0, 256;σk表示褶皱的半径,σk∈[10, 30];Ng代表褶皱构造的控制点数。通过在预定义的取值范围内随机选择每个参数值,可以生成大量具有特定褶皱结构的模型。
(3) 为了进一步增加模型结构的复杂性,利用
| $ S_{2}(x, y, z)=e+f x+g y $ | (2) |
对步骤(2)生成的褶皱模型添加平面剪切构造,生成如图 3c所示的模型。式中:e表示褶皱构造在z方向上位移量;f表示平面在x方向的斜率;g表示平面在y方向上的斜率。三个参数的取值范围分别为:e∈[0, 5],f∈[0, 0.2],g∈[0, 0.2]。
(4) 在模型中添加断层,尽管所有断层都是平面的,但是断层的方向(倾角和走向)和位移都互不相同,而每个断层的断距沿着走向和倾向在空间上变化。根据实际工区的断层资料,定义断层断距的范围为[10, 70],断层倾角范围为[50°, 80°]和[-80°, -50°],其中,正角度代表正断层,负角度代表逆断层。添加断层后的模型如图 3d所示。
(5) 将生成的模型同雷克子波褶积得到合成地震记录(图 3e),子波频率的预设范围为[20Hz, 35Hz]。值得注意的是,在模型中添加褶皱和断层构造后,再与雷克子波褶积,可以模糊断层边界比较尖锐的不连续性,从而使断层看上去更为真实。
(6) 为了使合成地震数据更为贴近实际,对其添加高斯随机噪声(信噪比的取值范围为[3, 6]),得到如图 3f所示的地震记录。
通过随机选择褶皱、断层、子波峰值频率和噪声等参数,利用该方法最终生成300对大小为256×256×256的合成地震数据和断层标签数据用于模型训练,并随机生成了30对数据集用于模型验证。图 4展示了6对典型的合成地震数据及其对应的断层标签数据剖面,包括阶梯式断层、“X”形断层、“Y”形断层、“入”字形断层等。
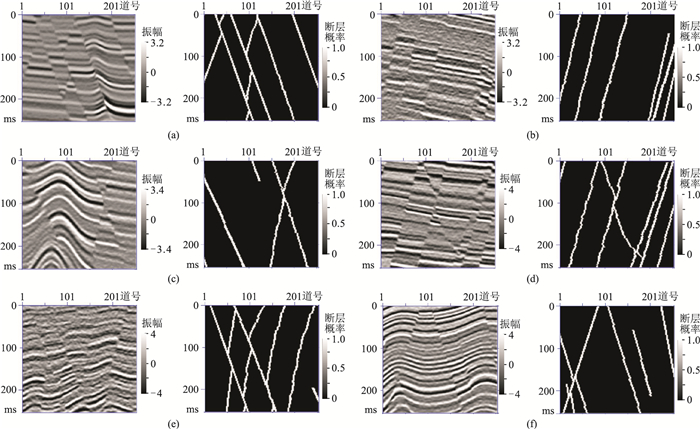
|
图 4 典型合成地震数据(左)及其断层标签样式(右) (a)正向阶梯状断层;(b)反向阶梯状断层;(c)“X”形断层;(d)“Y”形断层;(e)“入”字形断层;(f)地垒式断层 |
不同地震数据的振幅值可能有很大差异,需要对所有的数据集进行归一化处理,即将每个图像减去其平均值再除以其标准偏差。为了进一步增加训练和验证数据集的多样性,本文对原始数据进行了两种类型的数据扩展处理。第一种方法为数据增强,即将图像绕垂直轴旋转0°、90°、180°和270°,从而将训练数据集的数量增加4倍;第二种方法是随机地从原始数据体中切割出较小的子数据体,然后使用这些子数据训练网络。每个原始数据的尺寸大小为256×256×256,在网络训练过程中,本文从较大的数据中随机剪切了大小为128×128×128的子数据,确保不同迭代周期的训练数据集是不同的。这两种方式可以增加训练数据集的数量和多样性,而且用较小的图像训练卷积神经网络,可以大大减少训练期间的GPU内存需求和计算成本。
2.2 网络训练参数设置在构建本文网络时,每一层的参数都是随机初始化的,因此需要对其进一步更新,以创建输入地震数据体到输出断层概率体之间的良好映射网络。在模型训练的过程中需要使用优化算法迭代更新参数,直至输出的断层数据与断层标签之间的误差收敛到最佳为止。本文使用Adam(Adaptive Moment Estimation)方法[31]优化网络参数。
因为断层检测涉及到二进制图像分割问题,常用的损失函数是二进制交叉熵(Binary Cross Entropy)LBCE[32],即
| $ L_{\mathrm{BCE}}=-\frac{1}{N_{\mathrm{s}}} \sum\limits_{i=1}^{N_{\mathrm{s}}}\left[y_{i} \ln p_{i}+\left(1-y_{i}\right) \ln \left(1-p_{i}\right)\right] $ | (3) |
式中:Ns是三维输出图像或标签图像中样本的数量;yi和pi分别表示第i个图像样本的断层二进制标签值和预测值。
当损失函数设定为二进制交叉熵时,断层识别会出现类别不均衡的问题,这是因为在实际地震资料中,断层点占比远远小于非断层点。数据样本分布的不均衡会影响网络模型的训练,并且样本在比例失衡的情况下会导致网络模型性能下降,最终导致断层检测的准确性降低。因此,本文在二进制交叉熵的基础上,引入Focal Loss损失函数[33],可以解决断层检测中断层点与非断层点比例失衡的问题,其表达式为
| $ L_{\mathrm{Focal}}=-\frac{1}{N_{\mathrm{s}}} \sum\limits_{i=1}^{\mathrm{N}_{\mathrm{s}}}\left[\alpha\left(1-p_{i}\right)^{\gamma} y_{i} \ln p_{i}+\right. \\ \left.(1-\alpha)\left(1-y_{i}\right) p_{i}^{\gamma} \ln \left(1-p_{i}\right)\right] $ | (4) |
式中:α是平衡系数,取值为0.5;γ为调节因子,通常取2。
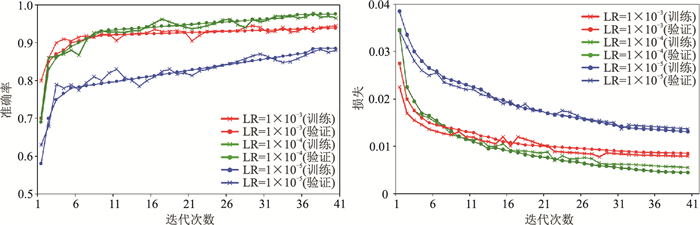
为了选择合适的学习率(Learning Rate,LR),本文进行了不同的试验(图 5)。由图 5可见,学习率为1×10-4时,训练的损失最小,准确率最高,所以本文设置学习率为1×10-4。
|
图 5 不同学习率计算得到的准确率(左)和损失(右) |
学习率为1×10-4时,不同迭代次数(20、40、60和80)得到的断层检测结果如图 6所示。可以看出,当迭代次数为20时,断层检测精度低,不能准确识别断层交叉点(蓝色箭头所示);当迭代次数为40、60和80时,得到的结果相差不大。为了提高网络训练效率,本文选定迭代次数为40。

|
图 6 不同迭代次数的断层检测结果 (a)合成地震数据;(b)断层标签;(c)20次迭代;(d)40次迭代;(e)60次迭代;(f)80次迭代 |
用相同的参数(学习率为1×10-4,迭代次数为40,训练平台为Google Colab)分别训练三维U-Net和本文网络,训练完成后保存模型,然后在30个验证数据集上进行测试(验证数据集未参与网络训练,大小为128×128×128),并对断层预测结果进行量化评价。
断层的预测属于二分类问题,在二分类的问题中,两种类别通常被定义为正类(Positive)和负类(Negative)。在这类问题中,又可以细分为四种情况:假如一个样本是正类也被预测成正类,就叫做真正类(True Positive,TP),反之,若是负类却被当作正类的话,就被称作假正类(False Positive,FP);类似地,当样本是负类而被预测为负类,那么就是真负类(True Negative,TN),而正类被预测为负类就是假负类(False Negative,FP),对应的断层预测的相关可能性见表 1。
|
|
表 1 断层预测的相关可能性分类 |
根据断层预测的相关可能性,采用准确率(A)、召回率(R)、F1值(衡量二分类模型精度的一种指标,同时兼顾了精确率和召回率)和交并比IOU(Intersection Over Union)四种指标可以量化评价断层检测效果。主要指标定义如下。
TP的数量(QTP)与QTP和FP数量(QFP)之和的比率为精确率,即
| $ P=\frac{Q_{\mathrm{TP}}}{Q_{\mathrm{TP}}+Q_{\mathrm{FP}}} $ | (5) |
P表示的是预测为正的样本中有多少是对的,值越大,预测效果越好。
QTP与QTP和FN数量(QFN)之和的比率为召回率,即
| $ R=\frac{Q_{\mathrm{TP}}}{Q_{\mathrm{TP}}+Q_{\mathrm{FN}}} $ | (6) |
R表示样本里的正类被正确预测的比例。
F1值是精确率与召回率的调和平均值,即
| $ F_{1}=\frac{2 P R}{P+R} $ | (7) |
对于给定的相关数据集,分类器正确识别的样本数除以总样本数,即可得准确率
| $ A=\frac{Q_{\mathrm{TP}}+Q_{\mathrm{TN}}}{Q_{\mathrm{TP}}+Q_{\mathrm{FP}}+Q_{\mathrm{FN}}+Q_{\mathrm{TN}}} $ | (8) |
交并比为
| $ \mathrm{IOU}=\frac{S\left(y_{\text {true }} \cap y_{\text {pre }}\right)}{S\left(y_{\text {true }} \cup y_{\text {pre }}\right)} $ | (9) |
式中:ytrue表示断层标签;ypre表示网络模型预测的断层;S(·)表示面积。IOU介于0与1之间,越接近于1,表示断层重叠面积越大,识别效果越好。
分别利用三维U-Net和本文网络预测30个验证数据的断层,三维U-Net的断层检测结果A、R、F1、IOU分别为0.945~0.968、0.678~0.821、0.668~0.862、0.540~0.741;而本文网络A、R、F1、IOU分别为0.961~0.989、0.710~0.881、0.699~0.921、0.571~0.810。
选择其中一个测试模型展示断层预测效果(图 7),对应的量化评价结果见表 2。从图 7可以看出,三维U-Net和本文网络基本能识别出断层形态及展布,但在断层交叉位置处(图 7c蓝色箭头所示),三维U-Net不能对其有效检测,识别出的断层结果与断层标签偏差较大;而本文网络可以清晰、准确地检测出断层交叉点的位置。从表 2可以看出,本文网络的各个评价指标均优于三维U-Net网络。
|
图 7 验证数据的断层预测效果 (a)合成地震数据;(b)断层标签;(c)三维U-Net预测;(d)本文网络预测 |
|
|
表 2 两种网络检测断层的量化评价结果 |
为了验证本文网络在实际地震资料中的应用效果,将本文网络训练得到的模型应用于大港油田自来屯工区的三维地震资料。选取的三维地震数据纵测线号为1975~2230,横测线号为1100~2124,时间为1000~1800ms,采样间隔为1ms。工区内断层比较发育,特别是“Y”形、交叉小断层较多。大部分断层的倾角为50°~80°,断距大致为10~70m。
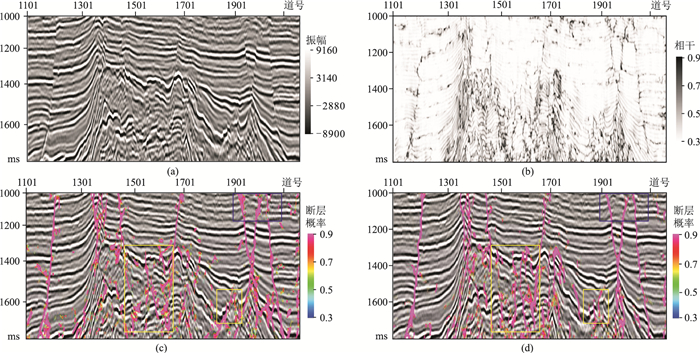
分别采用三维U-Net和本文网络训练得到的模型对该地震数据进行断层检测。从纵测线检测结果(图 8、图 9)可以看出,相干体属性基本可以指示大断层的位置以及展布形态,但连续性较差,且非断层区域干扰较多,小断层杂乱,难以准确识别。三维U-Net和本文网络识别出的大断层特征更清晰,小断层的细节特征也更丰富,表明了两种网络的断层预测结果(图 8c、图 8d、图 9c、图 9d)均优于相干体属性(图 8b、图 9b)。同时,相较于三维U-Net网络,本文网络检测的大断层连续性更好,断层边缘更清晰(图 8c和图 8d的蓝色框内),而且本文网络检测到的小断层特征更明显,并能有效减少小断层的漏识别和错误识别的概率(图 8c、图 8d、图 9c和图 9d的黄色框内)。
|
图 8 Inline2060地震剖面断层检测结果对比 (a)原始地震剖面;(b)相干属性剖面;(c)三维U-Net识别;(d)本文网络识别 |

|
图 9 Inline2150地震剖面断层检测结果对比 (a)原始地震剖面;(b)相干属性剖面;(c)三维U-Net识别;(d)本文网络识别 |
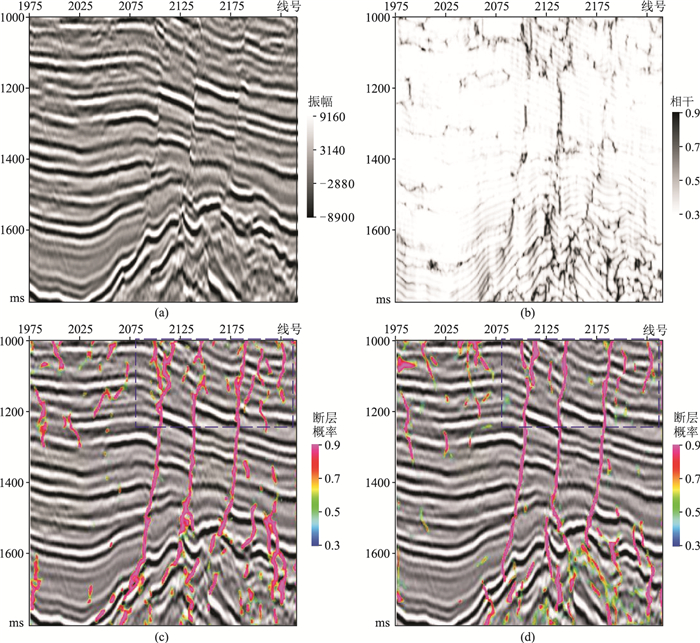
横测线方向上显示大断层较多,且类似于阶梯状(图 10a),小断层较少。相干体属性识别出的大断层连续性较差(图 10b),小断层基本不能有效识别。三维U-Net网络的断层识别精度有了明显提高,但相较于本文网络检测结果,个别大断层连续性差(图 10c和图 10d的蓝色框内)。
|
图 10 Crossline1300地震剖面断层检测结果对比 (a)原始地震剖面;(b)相干属性剖面;(c)三维U-Net识别;(d)本文网络识别 |
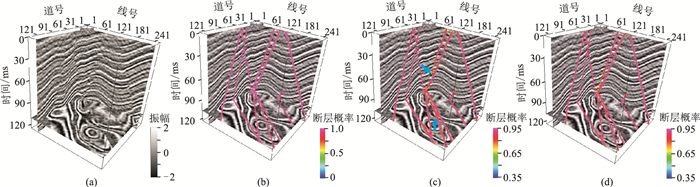
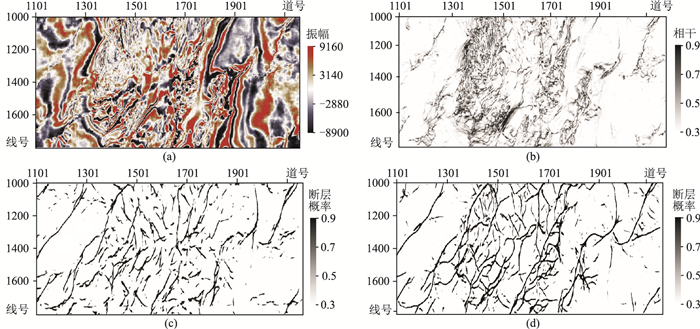
从相干属性时间切片(图 11a)可以看出,大断层展布形态较清晰,但小断层难以准确识别。三维U-Net网络检测的断层(图 11c)识别精度有了明显提高,且背景干扰减少,但某些区域的断层连续性差。本文网络检测断层(图 11d)形态和展布更为清晰,大断层连续性更好,小断层特征更丰富,断层识别精度有了很大提高。
|
图 11 1400ms时间切片断层检测结果对比 (a)原始地震数据;(b)相干属性;(c)三维U-Net识别;(d)本文网络识别 |
综上所述,本文网络的断层检测精度更高,特别是在小断层的识别方面更具优势,这也证明了本文方法的有效性。
4 结论与认识本文将三维U-Net和残差学习模块结合在一起,并引入多层深度监督的机制,构建了基于三维深度监督网络识别断层的方法。该方法可以更有效地结合断层的多尺度信息,提高断层识别的准确性。理论模型测试和实际地震资料的应用表明,与常规三维U-Net相比,本文方法能够更加准确地识别断层,预测的断层连续性更好,小断层的识别准确率也更高。
在三维深度监督网络的实际应用中,以下三点需要重点关注。
(1) 三维深度监督网络的层数可以选择三层或四层(本文为四层)。多次实验证实,在实际地震数据的断层特征较为简单的情况下,三层网络可以满足实际的断层检测要求。
(2) 在生成断层训练样本时,尽量根据实际地震资料的断层特征设置参数,特别是断层倾角、断距、子波频率和信噪比这几个参数对模型的适用性影响较大。
(3) 关于迭代次数的选择,多组随机选择的断层样本训练证明,迭代次数选择40的时候验证数据的断层预测准确率可以达到0.96,继续增加迭代次数,准确率的提高程度有限,对实际数据的断层检测影响较小。考虑到网络训练的时间成本和计算效率,迭代次数不必选择太大。
| [1] |
李军, 张军华, 刘杨, 等. 图像熵各向异性扩散保边滤波方法及在断层识别中的应用[J]. 石油地球物理勘探, 2019, 54(2): 365-370. LI Jun, ZHANG Junhua, LIU Yang, et al. Anisotropic diffusion edge-preserved filter based on image entropy and application in fault identification[J]. Oil Geophy-sical Prospecting, 2019, 54(2): 365-370. |
| [2] |
王静, 张军华, 冯德永, 等. 利用不连续性的各向异性扩散滤波方法识别断层[J]. 石油地球物理勘探, 2020, 55(6): 1349-1357. WANG Jing, ZHANG Junhua, FENG Deyong, et al. Fault identification based on a discontinuous anisotropic diffusion filter[J]. Oil Geophysical Prospecting, 2020, 55(6): 1349-1357. |
| [3] |
Wu X M. Directional structure-tensor-based coherence to detect seismic faults and channels[J]. Geophysics, 2017, 82(2): A13-A17. DOI:10.1190/geo2016-0473.1 |
| [4] |
Qi J, Li F Y, Marfut K. Multiazimuth coherence[J]. Geophysics, 2017, 82(6): O83-O89. DOI:10.1190/geo2017-0196.1 |
| [5] |
Duan Y T, Wu C D, Zheng X D, et al. Coherence based on spectral variance analysis[J]. Geophysics, 2018, 83(3): O55-O66. DOI:10.1190/geo2017-0158.1 |
| [6] |
Wang S X, Yuan S Y, Wang T Y, et al. Three-dimensional geosteering coherence attributes for deep-formation discontinuity detection[J]. Geophysics, 2018, 83(6): O105-O113. DOI:10.1190/geo2017-0642.1 |
| [7] |
Yan B P, Fang R R, Huang X G, et al. Multidirection-al eigenvalue-based coherence attribute for discontinuity detection[J]. Geophysics, 2021, 86(3): O29-O36. DOI:10.1190/geo2020-0354.1 |
| [8] |
Chopra S, Marfurt K J. Volumetric curvature attri-butes add value to 3D seismic data interpretation[J]. The Leading Edge, 2007, 26(7): 856-867. DOI:10.1190/1.2756864 |
| [9] |
霍志周, 刘喜武, 莫莉, 等. 高精度结构曲率提取方法在潜江凹陷构造解释中的应用[J]. 石油物探, 2020, 59(6): 961-969. HUO Zhizhou, LIU Xiwu, MO Li, et al. Application of high-precision structural curvature extracting on the structural interpretation of Jianghan-Qianjiang Depression[J]. Geophysical Prospecting for Petro-leum, 2020, 59(6): 961-969. DOI:10.3969/j.issn.1000-1441.2020.06.014 |
| [10] |
Di H, Gao D. Gray-level transformation and Canny edge detection for 3D seismic discontinuity enhancement[J]. Computers and Geosciences, 2014, 72: 192-200. DOI:10.1016/j.cageo.2014.07.011 |
| [11] |
Ashraf H, Mousa W A, AI Dossary S. Sobel filter for edge detection of hexagonally sampled 3D seismic data[J]. Geophysics, 2016, 81(6): N41-N51. DOI:10.1190/geo2015-0495.1 |
| [12] |
Philips M, Formel S. Plane-wave sobel attribute for discontinuity enhancement in seismic images[J]. Geo-physics, 2017, 82(6): WB63-WB69. |
| [13] |
Pedersen S I, Randen T, Sonneland L, et al. Automatic fault extraction using artificial ants[C]. SEG Technical Program Expanded Abstracts, 2002, 21: 512-515.
|
| [14] |
李楠, 王龙颖, 黄胜兵, 等. 利用高清蚂蚁体精细解释复杂断裂带[J]. 石油地球物理勘探, 2019, 54(1): 182-190. LI Nan, WANG Longying, HUANG Shengbing, et al. 3D seismic fine structural interpretation in complex fault zones based on the high-definition ant-tracking attribute volume[J]. Oil Geophysical Prospecting, 2019, 54(1): 182-190. |
| [15] |
Huang L, Dong X, Clee T E. A scalable deep learning platform for identifying geologic features from seismic attributes[J]. The Leading Edge, 2017, 36(3): 249-256. DOI:10.1190/tle36030249.1 |
| [16] |
Di H, Shafiq M, Alregib G. Patch-level MLP classification for improved fault detection[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 2211-2215.
|
| [17] |
Xiong W, Ji X, Ma Y, et al. Seismic fault detection with convolutional neural network[J]. Geophysics, 2018, 83(5): O97-O103. DOI:10.1190/geo2017-0666.1 |
| [18] |
Guo B, Li L, Luo Y. A new method for automatic seismic fault detection using convolutional neural network[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 1951-1955.
|
| [19] |
Zhao T, Pradip M. A fault detection workflow using deep learning and image processing[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 1966-1969.
|
| [20] |
Wu X, Shi Y, Fomel S, et al. Convolutional neural networks for fault interpretation in seismic images[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 1946-1950.
|
| [21] |
Wu X, Liang L, Shi Y, et al. FaultSeg3D: Using synthetic data sets to train an end-to-end convolutional neural network for 3D seismic fault segmentation[J]. Geophysics, 2019, 84(3): IM35-IM45. DOI:10.1190/geo2018-0646.1 |
| [22] |
Pochet A, Diniz P H B, Lopes H, et al. Seismic fault detection using convolutional neural networks trained on synthetic poststacked amplitude maps[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(3): 352-356. DOI:10.1109/LGRS.2018.2875836 |
| [23] |
Cunha A, Pochet A, Lopes H, et al. Seismic fault detection in real data using transfer learning from a convolutional neural network pre-trained with synthetic seismic data[J]. Computers and Geosciences, 2020, 135: 1-9. |
| [24] |
Di H, Li C, Smith S, et al. Imposing interpretational constraints on a seismic interpretation convolutional neural network[J]. Geophysics, 2021, 86(3): IM63-IM71. DOI:10.1190/geo2020-0449.1 |
| [25] |
张政, 严哲, 顾汉明. 基于残差网络与迁移学习的断层自动识别[J]. 石油地球物理勘探, 2020, 55(5): 950-956. ZHANG Zheng, YAN Zhe, GU Hanming. Automatic fault recognition with residual network and transfer learning[J]. Oil Geophysical Prospecting, 2020, 55(5): 950-956. |
| [26] |
常德宽, 雍学善, 王一惠, 等. 基于深度卷积神经网络的地震数据断层识别方法[J]. 石油地球物理勘探, 2021, 56(1): 1-8. CHANG Dekuan, YONG Xueshan, WANG Yihui, et al. Seismic fault interpretation based on deep convolutional neural networks[J]. Oil Geophysical Prospecting, 2021, 56(1): 1-8. |
| [27] |
Wu X, Hale D. 3D seismic image processing for faults[J]. Geophysics, 2016, 81(2): IM1-IM11. DOI:10.1190/geo2015-0380.1 |
| [28] |
He K, Zhang X, Ren S, et al. Deep residual learning for image recognition[C]. Proceedings of the IEEE International Conference on Computer Vision, 2016, 770-778.
|
| [29] |
Noh H, Hong S, Han B. Learning deconvolution network for semantic segmentation[C]. Proceedings of the IEEE International Conference on Computer Vision, 2015, 1520-1528.
|
| [30] |
卢新瑞, 黄捍东, 李帅, 等. 基于U-Net的盐体识别方法[J]. 计算物理, 2019, 37(3): 327-334. LU Xinrui, HUANG Handong, LI Shuai, et al. Saltbody classification method based on U-Net[J]. Chinese Journal of Computational Physics, 2019, 37(3): 327-334. |
| [31] |
Kingma D and Ba J. Adam: A method for stochastic optimization[C]. International Conference on Learning Representations, 2015.
|
| [32] |
Golik P, Doetsch P, Ney H. Cross-entropy vs. squared error training: a theoretical and experimental compa-rison[C]. Interspeech, 2013.
|
| [33] |
Lin T Y, Goyal P, Girshick R, et al. Focal loss for dense object detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020, 42(2): 318-327. DOI:10.1109/TPAMI.2018.2858826 |



 张军华, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
张军华, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: 