② 青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266061;
③ 星环信息科技(上海)有限公司, 上海 200030
② Evaluation and Detection Technology Laboratory of Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266061, China;
③ Shanghai Transwarp Co. Ltd, Shanghai 200030, China
地震速度建模影响地震波成像精度,对地质构造解释具有指导作用。人们基于地震波形和走时数据提出了多种地震速度建模方法。其中,叠加速度分析是油气勘探中最为常用的速度建模方法,该方法可以建立平缓层状构造的地震速度模型,但基于水平层状速度结构的假设,它在地层非水平、横向速度变化、含低速层等情况下精度不高[1]。偏移速度分析是一种将速度分析与偏移成像相结合的速度建模方法,基于射线理论的偏移速度建模虽然效率高、稳定性强,但在复杂构造情况下精度较低[2]。走时层析成像是一种适用于速度变化平缓的复杂构造的速度建模方法,一般用于浅部速度建模[3-5]。采用大炮检距地震初至旅行时的走时层析成像可以对深部速度结构建模[6-9],但对速度突变和小尺度异常的构造成像效果不佳。为了解决复杂速度结构的建模问题,Tarantola[10]提出了波形反演方法,并从理论研究推广到实际应用。全波形反演利用地震波场的运动学和动力学信息构建地下速度模型,建模精度高且可以实现多参数建模[11]。但迭代的方式使全波形反演强烈依赖于初始模型和先验信息,容易受实际数据中低频信息缺失的影响[12],且迭代过程较复杂,耗时较长[13-14]。另外,随着勘探区块地下结构复杂程度的增加,高密度采集、节点地震采集和广角宽方位三维地震采集等技术得到了推广应用,地震数据量也快速增大。因此,有必要进一步提高速度建模方法的稳定性和精度,并提高其在数据量增大情况下的计算效率。
深度学习为速度建模提供了一种高效且可以准确利用大量地震数据的手段。Araya-polo等[15]采用速度谱作为数据集,基于常规的卷积神经网络提出了一种将深度学习引入地震速度建模的方法。Mosser等[16]基于深度卷积生成对抗网络的深度学习方法,将反演问题看作不同域之间的转换,实现了地震数据域与速度模型域之间的转换。Li等[17]基于深度神经网络的地震反演网络(SeisInvNet),使用所有地震道数据和全局地震剖面重构速度模型。Zhang等[18]开发了一种基于实时数据驱动技术的速度建模对抗网络(VelocityGAN),用以提高速度模型精度。Yuan等[19]在已知初始速度和数据的情况下,用全卷积神经网络(FCN)实现了时移数据与目标速度变化之间的映射。Yang等[20]基于FCN提出了直接使用全波形地震数据建立速度模型的方法。Park等[21]实现了用卷积神经网络和迁移学习进行自动速度分析的工作流程。Fabien-ouellet等[22]基于深度卷积神经网络,利用共中心点道集反演均方根速度和层速度。Wang等[23]基于FCN的井间观测系统,利用纵波速度建模。Chen等[24]提出了一种用骨架化数据求解波动方程的速度建模方法。孙宇航等[25]基于GRU神经网络,提出了一种用储层参数预测横波速度的方法。张昊等[26]提出了一种基于深度学习的地震速度谱自动拾取方法。张玉玺[27]等用深度学习方法实现了对盐丘的自动识别。
上述深度学习速度建模方法通过神经网络框架对数据空间进行全局搜索,克服了线性反演方法中初始模型准确度和先验信息的限制,是一种非常有应用前景的地震速度建模技术。另外,深度学习还是一种高效的速度建模手段,深度神经网络模型只需要训练一次就可以开展多次速度建模,而建模过程耗时很少,在需要大量开展速度建模的地区可以有效减少速度建模所需时间,相比于传统方法计算效率更高。
然而,上述深度学习速度建模方法所采用的数据集会降低建模精度和稳定性。如果直接使用地震波形作为数据集,深度学习速度建模会出现不稳定的问题[19];如果仅采用速度谱作为数据集,那么速度谱的水平地层假设条件将限制其对横向变化速度结构的估计能力,难以刻画速度模型的细节[15]。速度谱通过地震反射数据水平叠加实现了地震记录中层状速度结构信息的稀疏化表达,将其作为数据集有助于提高速度建模的稳定性。鉴于速度谱训练集有助于提高建模稳定性、地震波形数据集有助于提高建模精度,因而可以把速度谱和地震数据波形融合为统一的深度学习特征数据集,以同时提高速度建模的稳定性和精度。
另外,深度学习速度建模对训练集的要求较高,即要求训练集能够体现模型中的关键细节。常规的做法是通过生成大量的随机训练样本,增加训练集的特征覆盖能力。Wang等[23]在设计训练集模型时,采用了完全随机的方式,基于随机的照片生成大量的训练样本,保证了速度建模方法可以应用于任意地质条件,在井间数值实验中取到了较好的效果,但对于地震数据集的要求较高,预测结果主要依赖直达波。人们在利用深度学习进行地震速度建模时,多是先确定训练集样本速度模型的种类(如层状模型、断层模型等),然后在这一类模型中设置不同的参数,随机生成大量的训练样本[15, 17-18, 20],这样可以使训练样本包含同一类型速度模型的多种情况,从而得到丰富的样本特征。由于预测结果依赖于训练集速度模型,因此训练集应尽量包含较多的特征以增强速度建模的准确性和稳定性。层析成像中的多尺度参数化方法[28]将速度模型分解为包含不同尺度网格的子模型,每个子模型覆盖整个模型区域,单个子模型中网格大小不同。这种参数化方法考虑了不同大小异常体适应不同网格的情况,使层析反演可以更好地刻画异常体的边界。本文结合层析成像中的多尺度参数化方式采用常规分类生成随机训练集的方法,将速度模型中的特征进行多尺度分解,生成包含不同尺度特征的训练集速度模型,构建多尺度训练集。这种方法增加了训练集的特征覆盖能力,一定程度上缓解了深度学习对于训练集的依赖,提高了建模精度。
1 方法原理 1.1 深度神经网络架构利用深度神经网络构建地震数据与速度模型之间的映射关系,可以实现基于深度学习的地震速度建模。
FCN将传统卷积神经网络的全连接层替换为卷积层,支持任意尺寸的输入数据,在图像识别领域达到了可预测单个像素的精度[29]。基于FCN改进的U-Net具有编码—解码的“U”型结构,它先通过下采样提取输入数据的特征,然后通过上采样将特征信息传递给后面分辨率更高的层,得到更精细的结果[30]。地震速度建模是从地震资料中提取地下速度信息的过程,与U-Net提取输入数据特征信息的特点十分契合。因此,本文选取U-Net作为深度学习速度建模的基础神经网络框架。同时,改进原始U-Net,使针对图像识别领域设计的U-Net适用于地震速度建模。
首先,针对输入地震数据与输出速度模型之间大小不一致的问题,利用U-Net实现了不对称大小之间的映射。常规用于图像识别的U-Net的输入和输出都在图像域,且需要大小相同。然而,地震速度建模的输入数据在时间域,而输出的速度模型在深度域,这就造成了输入与输出数据之间的不匹配。在基于深度学习的地震速度建模过程中,地震数据被映射为速度模型,而输入与输出数据之间的不匹配会导致神经网络的输入与输出在大小和存储方式上的明显差异,因此神经网络难以完成训练。针对该问题,联合地震反射波形和速度谱作为深度神经网络的输入,并将它们通过重采样的方式统一到与输出神经网络的速度模型相近的大小。地震反射波形由地震记录去除直达波得到;速度谱通过地震反射数据水平叠加得到。速度谱可以看作是层状速度结构信息的稀疏化表达,将其作为深度学习的特征有利于提高神经网络模型训练的稳定性。将反射波形数据和速度谱分别以多个炮集和多个共中心点集的格式存储,再通过重采样调整它们的长度和宽度,将每个炮集反射波形数据和每个共中心点集速度谱统一为相同大小的二维矩阵,然后将所有二维矩阵联合成为一个三维矩阵。最后就可以实现将不同炮集的反射波形数据和不同共中心点位置的速度谱从不同的通道联合输入深度神经网络。U-Net在编码、解码的过程中训练自身,完成了地震数据向速度模型的映射,可以实现基于数据驱动的深度学习速度建模。虽然神经网络的输入和输出分别是时间域的数据和深度域的速度模型,但是该方法通过从时间域输入数据提取信息,用深度神经网络建立了时间域信息与模型域采样点之间的映射,没有明显时深问题建模的局限。
其次,为了防止深度学习速度建模产生过拟合,在U-Net中添加了两个随机失活(Dropout)层,从而提高了深度神经网络模型的泛化能力。神经网络的隐层是除输入层和输出层外的其他层,它是对输入特征多层次的抽象,但神经元较多的隐层更容易让神经网络的预测结果产生过拟合。而Dropout层在训练过程中将深度神经网络隐层的神经元根据相应的概率随机重置为0,从而使网络模型更具鲁棒性,降低过拟合。同时,还可以降低网络整体结构的复杂程度,大大减少运算量。
在深度神经网络中添加和取消Dropout层可以分析Dropout层对过拟合现象的影响。用相同的层状模型训练集分别采用添加和不添加Dropout层的深度神经网络进行训练。然后用两组测试样本进行实验。第一组测试样本包含25个与训练样本重复的速度模型,第二组测试样本包含25个与训练样本不重复的速度模型。两组测试样本的预测结果与真实模型之间的归一化均方根误差(NRMS,指相对误差)如表 1所示。在不添加Dropout层时,与训练样本不重复的测试样本的建模结果误差大于与训练样本重复的测试样本。这说明在没有Dropout层的情况下,深度神经网络存在过拟合现象,此时深度学习过程倾向于输出与训练集中模型比较相近的模型。而在添加了Dropout层后,无论测试样本是否与训练样本重复,建模结果的误差都相差不大,因而可以降低过拟合。因此,添加Dropout层可以改善网络结构,提高地震速度建模的准确性。
|
|
表 1 添加Dropout层前后预测模型与真实模型的归一化均方根误差 |
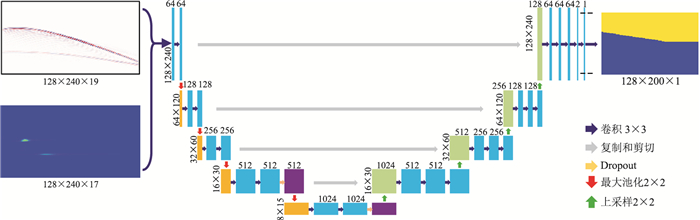
本文构建的深度学习速度建模的神经网络架构如图 1所示。该网络的输入是由19个大小为128×240的地震反射波形数据和17个大小为128×240的速度谱联合而成的大小为128×240×36的三维矩阵。神经网络的输出是大小为128×200的二维地震速度模型。共有24个卷积层(蓝色矩形)、4个池化层(黄色矩形)、4个上采样层(绿色矩形)、2个Dropout层(紫色矩形)和1个裁剪层(黑色虚线)。卷积层采用ReLU激活函数,卷积核大小为3×3。最大池化层中的下采样因子大小为2×2。上采样层中的上采样因子大小为2×2。Dropout层以50%的概率重置隐层中神经元。深度神经网络共有4个下采样过程和4个上采样过程,既保证了网络有足够的深度,可以对速度特征进行提取,又不会使网络模型过于复杂。
|
图 1 改进的全卷积神经网络架构 不同颜色的矩形代表深度神经网络中的不同层。其中,蓝色代表卷积层;黄色代表池化层;紫色代表Dropout层;绿色代表上采样层。蓝色矩形(卷积层)中的黑色虚线代表裁剪操作;矩形左侧数字代表层的大小,上侧数字代表层数,箭头代表层与层之间的操作。左上图代表炮集反射波形数据,左下图代表速度谱;右上图代表地震速度模型 |
将包含N个数据样本的数据集表示为{X(i), V(i)}i=1N,其中,X(i)代表地震反射波形和速度谱构成的数据集,它由第i个速度模型V(i)正演得到。在速度建模过程中,输入神经网络的多个通道(通道数等于共炮集个数与速度谱数量之和)的数据同时被用于网络参数的训练,以提高数据冗余度。
在深度学习中,直接对神经网络的最优解进行求取是十分困难的,常规的做法是通过迭代的方式逼近最优解。因此深度学习的本质可以看作是建立最优化模型,通过最优化方法迭代求出损失函数的最小值,从而训练出最佳的网络模型。这个过程可以表示为
| $ \hat{\boldsymbol{\omega}}=\arg \min L\left[\boldsymbol{V}^{(i)}, \hat{\boldsymbol{V}}^{(i)}\right] $ | (1) |
式中:
式(1)给出了损失函数最小情况下参数ω的取值。本文采用二范数度量真实速度模型与预测速度模型之间的误差,式(1)可写为
| $ \hat{\boldsymbol{\omega}}=\arg \min \sum\limits_{i=1}^{N}\left[\boldsymbol{V}^{(i)}-\hat{\boldsymbol{V}}^{(i)}\right]^{2} $ | (2) |
梯度下降法是深度学习中最常用的一种优化算法。它的基本思想是:用当前位置最快下降的方向,即当前位置的负梯度方向作为搜索方向去接近目标值,从而使损失函数逐渐减小,最终达到最小值。
假设一个深度学习问题中的损失函数L是每一个样本损失函数l的总和,即
| $ L(\boldsymbol{\omega})=\sum\limits_{i=1}^{N} l\left\{h_{\boldsymbol{\omega}}\left[\boldsymbol{X}^{(i)}\right], \boldsymbol{V}^{(i)}\right\} $ | (3) |
式中:hω[X(i)]是第i个训练样本的输入信号X(i)经过参数为ω的神经网络后的输出,即预测速度模型
| $ \nabla_{\boldsymbol{\omega}}[\mathrm{L}(\boldsymbol{\omega})]=\sum\limits_{i=1}^{N} \nabla_{\boldsymbol{\omega}}^{(i)}(l)\left\{h_{\boldsymbol{\omega}}\left[X^{(i)}\right], V^{(i)}\right\} $ | (4) |
梯度下降法更新神经网络的参数ω的过程可以表示为
| $ \boldsymbol{\omega}_{t+1}=\boldsymbol{\omega}_{t}-\eta \nabla_{\boldsymbol{\omega}}(L) \\ =\boldsymbol{\omega}_{t}-\eta \sum\limits_{i=1}^{N} \nabla_{\boldsymbol{\omega}^{(i)}}(l) $ | (5) |
式中:ωt代表第t次迭代后的神经网络参数;η为学习率,是一个小常数。
从式(5)可以看出,每次进行迭代更新网络参数ω时,都要对全部N个样本进行计算。而在深度学习中,神经网络参数的数量十分庞大,同时为了逼近网络的最优解,迭代次数往往也很大,这使梯度下降法在应用于深度学习时运算量巨大。因此,随机梯度下降法[31]应运而生。随机梯度下降法的基本思路是:通过随机提取小批量的样本B={X(1), …, X(M)}获取梯度,从而对神经网络参数进行更新。M是小批量样本的总个数,一般取值较小,且不随迭代次数变化,因此在很大程度上减少了运算成本。随机梯度下降法中梯度为
| $ \nabla_{\boldsymbol{\omega}} L[(\boldsymbol{\omega})]=\sum\limits_{i=1}^{M} \nabla_{\boldsymbol{\omega}}^{(i)}(l)\left\{h_{\boldsymbol{\omega}}\left[\boldsymbol{X}^{(i)}\right], \boldsymbol{V}^{(i)}\right\} $ | (6) |
随机梯度下降法更新神经网络的参数ω的过程可以表示为
| $ \boldsymbol{\omega}_{t+1}=\boldsymbol{\omega}_{t}-\eta \nabla_{\boldsymbol{\omega}}(L) \\ =\boldsymbol{\omega}_{t}-\eta \sum\limits_{i=1}^{M} \nabla_{\boldsymbol{\omega}}^{(i)}(l) $ | (7) |
与梯度下降法不同,随机梯度下降法在每次迭代时,只计算当前的一小批样本,它的下降方向在局部上并不稳定,但在整体上却是稳定的,结果会出现在全局最优的附近。这种方法计算效率高,且对内存的需求较小,但样本在输入前需要打乱顺序,保证足够的随机性。
本文采用随机梯度下降法对深度神经网络模型参数的最优化问题进行求解。
2 训练集模型和数据集的构建将地震速度模型作为深度学习的标签,即深度神经网络的输出;将地震波形和速度谱作为深度学习的特征数据集,即深度神经网络的输入,可以构建深度神经网络的训练集。本文首先针对沉积地层和孤立异常速度体两种类型,分别设置简单的数值实验;然后截取BP盐丘模型[32]生成深度学习地震速度建模的训练集,测试本文方法在复杂构造情况下的建模效果。
2.1 训练集模型在设计的数值实验中,地震速度模型被离散化为二维离散网格,每个网格大小相同。模型的横向和垂向网格数分别为200和128,单个网格尺寸为20m×20m。根据实际界面形态和异常速度体分布,改变地震速度模型的速度界面形态和异常体的大小、位置,构成训练集。
针对不同的地下地质结构,在数值实验中把速度模型训练集分为三组,分别是简单的层状模型、孤立异常体模型以及含有两者特征的复杂模型。
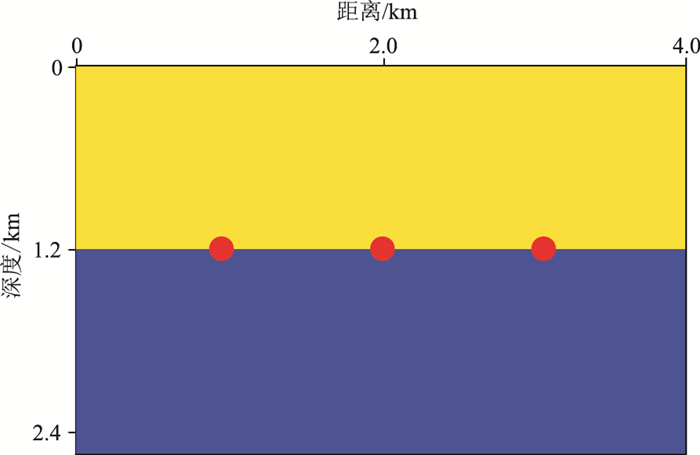
(1) 第一组数值实验(针对沉积地层)。训练集由73个双层速度模型构成,所有模型的上层速度均为2000m/s,下层速度均为3500m/s。系统改变地层界面的位置、形状和倾角三个参数,生成一系列不同的层状速度模型。首先,在地层界面上选择3个控制点,坐标分别为(1.0km,1.2km)、(2.0km,1.2km)和(3.0km,1.2km)(图 2中的三个红点);然后,顺序改变界面的三个控制点的位置,并按照0.15的斜率间隔改变控制点两侧地层界面的倾斜程度;最后,通过不同控制点位置和地层界面斜率的组合,形成包含73个双层地震速度模型的训练集。
|
图 2 层状速度模型训练集示意图 红点代表选取的界面拐点 |
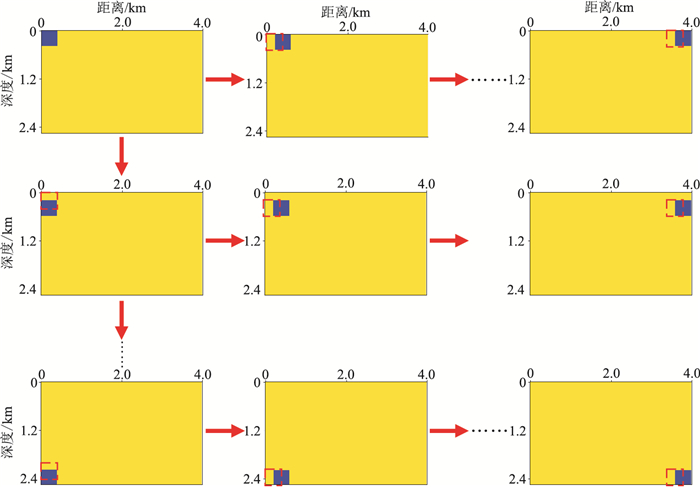
(2) 第二组数值实验(针对孤立异常速度体)。训练集由654个包含单个矩形异常体的速度模型构成。图 3展示了速度模型的生成过程,即设定矩形异常体尺寸,并将其按一定方向移动,每移动一次产生一个速度模型;改变异常体大小,并重复上述过程,就可以生成不同尺寸的训练集速度模型。该生成训练集的过程类似于地震层析成像的多尺度参数化[28],因此称这样的训练集为多尺度训练集。
|
图 3 孤立异常体速度模型训练集示意图 红色虚线方框代表生成的前一个速度模型中异常体(蓝色方块)的位置 |
该训练集中异常体速度值和背景速度值都可以改变,不失一般性,把异常体的速度均设为3500m/s,背景速度均设为2000m/s。异常体包括边长分别为400、800、1200、1600和2400m的正方形和大小为4000m×2560m(整个速度模型区域)的矩形。
第一个模型中异常体的左上角位于(0,0)处,之后依次向右移动10个网格,即200m的距离,直到异常体的右边界到达模型的右边界;然后把异常体移至最左侧,再向下移动10个网格的距离,并按照前面相同的右移步骤完成一次水平向移动;依此类推,直到异常体的下边界超过模型的下边界。其他尺度的孤立异常体速度模型也按照相同的方式生成。多个包含不同单尺度孤立异常体模型的训练集构成了多尺度模型训练集。为了与多尺度速度模型训练集的结果进行对比,本研究还建立了只包含边长为400m异常体的单尺度速度模型训练集。
(3) 第三组数值实验(针对较为复杂的含有沉积地层和孤立异常体两种类型的BP盐丘模型)。如图 4所示,分别采用3个不同尺度的矩形窗口在图 4c中顺序移动,共截取得到450个速度模型。不同尺度的矩形窗口在截取速度模型时都从图 4c的左上角开始,然后按照从左到右、从上到下的顺序移动相同的距离,一直截取到图 4c的右下角。最后将截取到的每个速度模型都抽取为128×200的相同大小。

|
图 4 BP盐丘速度模型训练集示意图 (a)沉积地层(背景速度)模型;(b)孤立盐丘模型;(c)在图a上加入图b中盐丘的速度模型。红色方框代表截取速度模型的三个不同尺度的窗口 |
根据训练集中的地震速度模型,通过伪谱法声波正演模拟[33-34]可以生成地震反射波形和速度谱联合的特征数据集。正演模拟采用主频为15Hz的雷克子波作为震源子波,时间采样间隔为2ms,每道记录的长度为3.2s。共采用19个炮点和240个检波点,炮间距为200m,道间距为20m。正演模拟获得共炮集地震记录后,去除每个地震记录中的直达波,形成反射波形数据;然后,抽取共中心点集,将x轴800m处选作第一个共中心点位置,沿模型x轴方向每隔200m确定一个共中心点,一直到4000m处,总共得到17个共中心点道集;对共中心点道集进行动校叠加,动校正的速度扫描范围为1500~5500m/s,由此得到与共中心点道集对应的17个速度谱;之后,对每个共炮集地震反射波形数据和每个速度谱归一化,使其值范围为[-1, 1];最后,在时间域重新采样,联合波形数据和速度谱,生成一系列128×240×36的三维矩阵,从而建立特征数据集。
3 数值实验和结果分析为了测试本文方法优越性,分别将没有联合的地震波形数据和速度谱作为特征进行训练,并将训练结果与本文(联合)方法进行比较。没有联合的情况下,地震波形特征数据集和速度谱特征数据集分别是大小为128×240×19和128×240×17的三维矩阵。
本文设计的三组训练集分别用于训练深度神经网络,得到三个不同的神经网络参数。训练时,采用的迭代次数(Epochs)为500次,批大小(Batch Size)为32。
用三组测试集分别对训练好的三个网络模型进行测试。测试集速度模型是未用于训练神经网络的速度模型,它与训练集速度模型不重复,仅只是用于测试深度神经网络的速度建模效果。假设测试集地震速度模型未知,将速度模型正演得到的反射波形数据和速度谱经处理后输入到训练好的深度神经网络中,得到预测地震速度模型。深度学习地震速度建模的效果可以通过对比预测模型与真实模型进行评价,二者之间的误差用NRMS值表示。NRMS值越小,说明真实模型与预测模型之间的误差越小,速度建模结果越准确。真实模型与预测模型之间的NRMS值为
| $ e_{\mathrm{NRMS}}=\frac{\sum\limits_{i=1}^{k}\left(V_{i}^{\mathrm{Test}}-\hat{V}_{i}^{\mathrm{Test}}\right)^{2}}{\sum\limits_{i=1}^{k}\left(V_{i}^{\mathrm{Test}}\right)^{2}} $ | (8) |
式中:ViTest是测试集真实模型第i个网格中的速度值;
本文深度神经网络架构基于以Tensorflow为后端的Keras框架进行搭建,并用Python代码进行编译。硬件环境配置为:CPU Intel-Core-i9-9900k@3.5GHz;内存32G;显卡GFORCE GTX2080Ti。
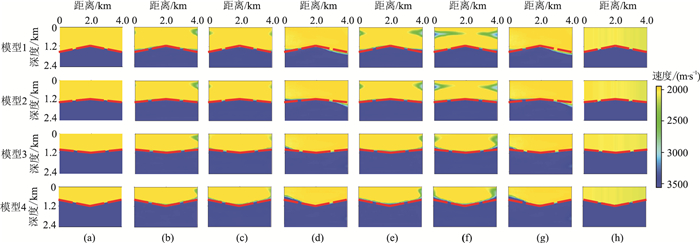
3.1 层状速度模型在层状模型的数值实验中,测试集速度模型是通过改变速度分界面倾角和位置而建立的,包含50个双层速度模型。图 5显示了4个典型的测试集速度模型。由图可以看出,利用未加噪声的测试集数据进行速度建模时,三种特征数据集都能较好地重构出双层地震速度模型的地层界面;但添加25%的高斯噪声后,只使用反射波形作为特征数据集的预测模型(图 5f)出现了明显的假象,而本文方法和只使用速度谱的方法都表现出较强的抗噪性能。
|
图 5 典型层状模型测试集建模结果 (a)真实速度模型;(b)~(d)分别为应用本文(联合)方法、反射波形、速度谱建模结果;(e)~(g)分别为加噪(25%的高斯噪声)后应用本文(联合)方法、反射波形、速度谱建模结果;(h)叠加速度分析计算的层速度模型。红色虚线为真实模型中地层界面的位置 |
由图 6可见,输入未加噪数据时,使用反射波形作为特征数据集的方法建模准确性最高,本文(联合)方法次之,只使用速度谱的方法最差。但用加噪数据进行速度建模时,只使用反射波形作为特征数据集的方法误差最大,抗噪性较差。综合来说,本文方法最好,在能保证较高的速度建模准确性的同时,还能具有较强的稳定性。

|
图 6 层状速度模型测试集预测模型与真实模型之间的eNRMS值 模型1~4与图 5相对应,最后一组柱状图表示50个测试模型的平均eNRMS值 |
叠加速度分析是一种常规的地震速度建模方法。该方法通过拾取速度谱中的能量团获得叠加速度场,然后利用Dix公式计算得到层速度。从图 5b、图 5h可以看到,深度学习方法和常规的叠加速度分析方法都可以有效构建层状速度模型。但叠加速度分析方法拾取速度谱耗时较长,速度建模的效率较低。而深度学习方法只需要对深度神经网络训练一次,就可以快速地对包含训练集速度模型特征的地下地质结构进行建模。在本文中,将准备好的数据输入训练好的深度神经网络,生成一个地震速度模型的用时不超过1s。这相对于常规方法而言,建模效率很高。因此在需要大量开展速度建模的地区,深度学习方法可以有效减少速度建模所需时间。
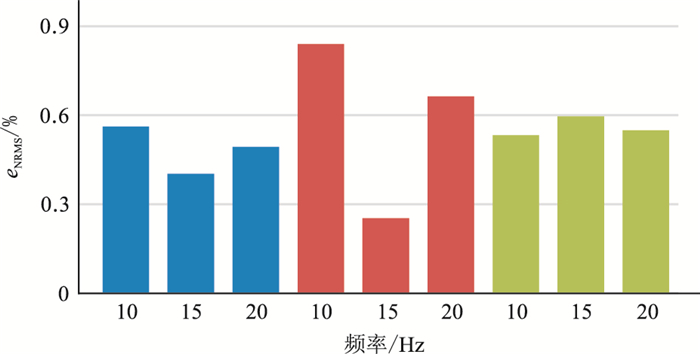
为了测试震源子波频带范围对本文方法速度建模结果的影响,分别应用主频为10、15和20Hz的雷克子波作为震源子波,正演得到50个测试集速度模型的反射波形和速度谱构成特征数据集。其中,15Hz主频的雷克子波是生成训练集数据的震源子波。用不同频率子波得到的特征数据集预测速度模型,预测模型与真实模型之间的eNRMS值如图 7所示。由图可见,震源子波主频率的改变仅导致eNRMS值的变化小于1%,因而对于本文所论及方法的速度建模结果影响不大;在这些方法中,子波主频变化对本文方法影响最小,对只用反射波形作为特征数据集的方法影响最大,这也反映了本文方法具有更高的稳定性。
|
图 7 子波主频改变时预测模型与真实模型之间的eNRMS值 蓝色、红色、绿色分别表示本文方法、反射波形、速度谱的建模结果的eNRMS值 |
孤立异常体模型测试集由5个速度模型构成。测试集模型与训练集模型的背景速度、异常体速度相同,但在异常体的大小和数量方面有所不同。测试集各个模型用于测试不同特征数据集对异常体形状、位置和异常体空间分布样式的重构能力。速度建模结果如图 8所示。前两个测试集速度模型中都只有一个异常体,异常体大小分别为1600m×400m和400m×1600m。中间两个测试集速度模型中各包含了2个大小均为400m×400m的高速异常体。最后一个测试集速度模型中包含了2个大小分别为400m×400m和1200m×1200m的高速异常体。

|
图 8 孤立异常体模型测试集建模结果 (a)真实速度模型;(b)单尺度异常体模型作为训练集,本文方法建模结果;(c)~(e) 分别为多尺度异常体模型作为训练集,本文方法、反射波形、速度谱建模结果。红色虚线为真实模型中异常体的位置 |
对比图 8b和图 8c可知,与单尺度训练集相比,使用多尺度训练集(由多个不同尺度的单尺度训练集构成)的速度模型重构结果更加接近真实模型;使用单尺度训练集的速度建模结果中,无论异常体数目增多与否,异常体的位置和速度都与真实模型较接近,但大小却都与单尺度训练集中400m×400m的异常体相近;这也从侧面说明了深度学习的方法以数据为驱动进行速度建模时,对训练集的依赖程度较大;而图 8c中的异常体形状都与真实模型较接近,既可以重构出长、宽差异大的异常体,也可以同时重构出两个不同大小的异常体,这说明多尺度异常体训练集缓解了深度学习速度建模对于训练集的依赖。
速度谱虽然在层状模型的重构中表现很好,但在重构异常体时,建模结果与真实模型差异很大(图 8e),这可能是受到速度分析过程中叠加的影响,导致网络模型的泛化能力降低。
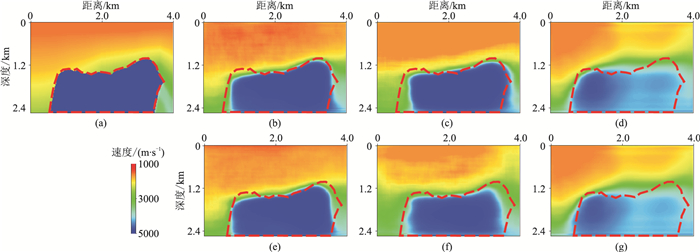
3.3 BP盐丘模型BP盐丘模型既具有沉积地层结构的层状速度特征,也具有孤立异常体的横向速度剧烈变化的特征,是测试本文方法的理想模型。测试集包含50个从图 4c中随机截取的速度模型,但截取窗口的位置、大小与训练集不同。图 9为其中一个测试集模型的速度建模结果。在未加噪声时,联合特征数据集的方法(本文方法)与只用反射波形的方法都可以较准确地确定速度模型中高速盐丘的位置、形状(图 9b、图 10c),而只用速度谱作为特征数据集时,异常体形状和速度的重构效果都不如前两种方法(图 9d)。加噪(5%高斯噪声)后,以反射波形为特征数据集的速度建模结果在盐丘异常体的附近出现了较明显的假象(图 9f)。
|
图 9 BP盐丘模型测试集建模结果 (a)真实速度模型;(b)~(d)分别为不同特征数据集本文方法、反射波形、速度谱速度建模结果;(e)~(g)分别为加λ5%高斯噪声后本文方法、反射波形、速度谱速度建模结果 |

|
图 10 BP盐丘模型测试集不同方法建模结果的速度曲线对比 水平距离分别为2km(a)、3km(b)处抽取的垂直方向和深度分别为1.2km(c)、1.8km(d)处抽取的水平方向速度变化曲线 |
图 10对比了图 9a~图 9d速度模型特定位置的速度剖面,抽取了水平距离为2km和3km以及深度为1.2km和1.8km共四个速度剖面进行对比。由图可以看出,本文方法的速度建模结果(红色实线)与真实模型最为接近。
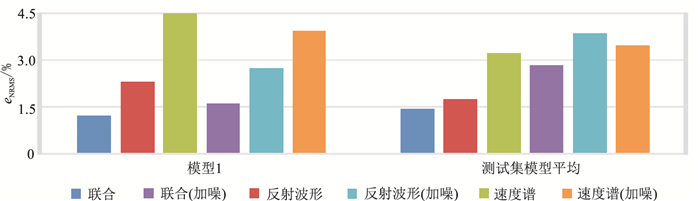
由图 11可见,只使用反射波形作为特征数据集时,相比于其他两种方法数据加噪后的预测模型与真实模型之间的误差有明显的增大,这说明只用反射波形作为深度学习的特征数据集时,速度建模受噪声的影响比其他两种方法大,抗噪能力较弱。而联合反射波形和速度谱作为数据集的方法(本文方法)不但误差较小,而且有较强的抗噪能力。
|
图 11 BP模型测试集预测模型与真实模型之间的eNRMS值 模型1是图 9中的模型 |
本文通过联合地震反射波形与速度谱作为特征数据集,采用多尺度速度模型构成训练集,并在FCN中加入Dropout层,构建了一种深度学习速度建模方法。对简单层状结构和孤立异常体以及复杂的BP盐丘模型的数值实验结果显示,结合地震反射资料和多尺度训练集的深度学习速度建模方法可以有效重构模型的主要特征。得到的认识和结论如下。
(1) 通过以加入Dropout层的FCN作为深度神经网络框架,深度学习方法能够重构层状结构和异常体结构,而且泛化能力较强。
(2) 相较于单独使用地震波形或速度谱,联合地震波形和速度谱作为深度学习的特征数据集能够兼顾两者作为特征数据集的优势,不仅可以提高速度模型重构的精度,而且还能够降低数据的冗余和计算难度,提高速度建模的稳定性。
(3) 多尺度训练集有助于提高深度学习速度建模的稳定性。多尺度训练集包含了不同尺度速度结构的信息,可提高深度学习速度建模刻画异常体形态的准确性。
| [1] |
潘宏勋, 方伍宝. 地震速度分析方法综述[J]. 勘探地球物理进展, 2006, 29(5): 305-311. PAN Hongxun, FANG Wubao. Review of seismic velocity analysis methods[J]. Progress in Exploration Geophysics, 2006, 29(5): 305-311. |
| [2] |
张敏, 李振春. 偏移速度分析与建模方法综述[J]. 勘探地球物理进展, 2007, 30(6): 421-427. ZHANG Min, LI Zhenchun. Review of migration velocity model building[J]. Progress in Exploration Geo-physics, 2007, 30(6): 421-427. |
| [3] |
雷栋, 胡祥云. 地震层析成像方法综述[J]. 地震研究, 2006, 29(4): 418-426. LEI Dong, HU Xiangyun. Review of seismic tomography methods[J]. Journal of Seismological Research, 2006, 29(4): 418-426. DOI:10.3969/j.issn.1000-0666.2006.04.018 |
| [4] |
李慧, 成德安, 金婧. 网格层析成像速度建模方法与应用[J]. 石油地球物理勘探, 2013, 48(增刊1): 12-16. LI Hui, CHENG Dean, JIN Jing. Velocity model building based on grid tomography[J]. Oil Geophy-sical Prospecting, 2013, 48(S1): 12-16. |
| [5] |
马彦彦, 李国发, 张星宇, 等. 叠前深度偏移速度建模方法分析[J]. 石油地球物理勘探, 2014, 49(4): 687-693. MA Yanyan, LI Guofa, ZHANG Xingyu, et al. Strategy of velocity model building in prestack depth migration[J]. Oil Geophysical Prospecting, 2014, 49(4): 687-693. |
| [6] |
韩明亮, 孙文亮, 邹志辉, 等. 基于地震节点和测线数据联合的含油气盆地层析速度建模[C]. 中国石油学会2019年物探技术研讨会论文集, 2019, 1351-1354. HAN Mingliang, SUN Wenliang, ZOU Zhihui, et al. Velocity model building of oil-gas bearing basin based on joint data of seismic nodes and lines[C]. CPS 2019 Geophysical Exploration Technology Conference, 2019, 1351-1354. |
| [7] |
Sun W L, Zou Z H, Zhou H W, et al. Velocity model building based on multiscale deformable-layer tomography using first-arrival and reflection traveltimes[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 5228-5232.
|
| [8] |
Wremez L, Lau K W H, Nedimovic M R, et al. Tra-veltime tomography of a dense wide-angle profile across Orphan Basin[J]. Geophysics, 2015, 80(3): B69-B82. DOI:10.1190/geo2014-0377.1 |
| [9] |
Zou Z H, Zhou H W, Gurrola H, et al. Impact and solutions of seawater heterogeneity on wide-angle tomographic inversion of crustal velocities in deep marine environments-numerical studies[J]. Journal of Earth Science, 2018, 29(6): 1380-1389. DOI:10.1007/s12583-017-0816-7 |
| [10] |
Tarantola A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [11] |
杨勤勇, 胡光辉, 王立歆. 全波形反演研究现状及发展趋势[J]. 石油物探, 2014, 53(1): 77-83. YANG Qinyong, HU Guanghui, WANG Lixin. Research status and development trend of full waveform inversion[J]. Geophysical Prospecting for Petroleum, 2014, 53(1): 77-83. DOI:10.3969/j.issn.1000-1441.2014.01.011 |
| [12] |
王庆, 张建中, 黄忠来. 时间域地震全波形反演方法进展[J]. 地球物理学进展, 2015, 30(6): 2797-2806. WANG Qing, ZHANG Jianzhong, Huang Zhonglai. Progress in the time-domain full waveform inversion[J]. Progress in Geophysics, 2015, 30(6): 2797-2806. |
| [13] |
卞爱飞, 於文辉, 周华伟. 频率域全波形反演方法研究进展[J]. 地球物理学进展, 2010, 25(3): 982-993. BIAN Aifei, YU Wenhui, ZHOU Huawei. Progress in the frequency-domain full waveform inversion method[J]. Progress in Geophysics, 2010, 25(3): 982-993. DOI:10.3969/j.issn.1004-2903.2010.03.037 |
| [14] |
杨午阳, 王西文, 雍学善, 等. 地震全波形反演方法研究综述[J]. 地球物理学进展, 2013, 28(2): 766-776. YANG Wuyang, WANG Xiwen, YONG Xueshan, et al. The review of seismic full waveform inversion method[J]. Progress in Geophysics, 2013, 28(2): 766-776. |
| [15] |
Araya-polo M, Jennings J, Adler A, et al. Deep-lear-ning tomography[J]. The Leading Edge, 2018, 37(1): 58-66. DOI:10.1190/tle37010058.1 |
| [16] |
Mosser L, Kimman W, Dramsch J, et al. Rapid seismic domain transfer: Seismic velocity inversion and mode-ling using deep generative neural networks[C]. Extended Abstracts of 80th EAGE Conference & Exhibition, 2018, PP1.
|
| [17] |
Li S, Liu B, Ren Y, et al. Deep learning inversion of seismic data[J]. IEEE Transactions on Image Processing, 2019, 58(3): 2135-2149. |
| [18] |
Zhang Z P, Yue W, Zheng Z, et al. VelocityGAN: subsurface velocity image estimation using conditio-nal adversarial networks[C]. IEEE Winter Conference on Applications of Computer Vision, 2019, 705-714.
|
| [19] |
Yuan C C, Zhang X, Jia X F, et al. Time-lapse velocity imaging via deep learning[J]. Geophysical Journal International, 2020, 220(2): 1228-1241. |
| [20] |
Yang F S, Ma J W. Deep-learning inversion: a next generation seismic velocity-model building method[J]. Geophysics, 2019, 84(4): R583-R599. DOI:10.1190/geo2018-0249.1 |
| [21] |
Park M J, Sacchi M D. Automatic velocity analysis using convolutional neural network and transfer lear-ning[J]. Geophysics, 2020, 85(1): V33-V43. DOI:10.1190/geo2018-0870.1 |
| [22] |
Fabien-ouellet G, Sarkar R. Seismic velocity estimation: A deep recurrent neural-network approach[J]. Geophysics, 2020, 85(1): U21-U29. DOI:10.1190/geo2018-0786.1 |
| [23] |
Wang W L, Ma J W. Velocity model building in a crosswell acquisition geometry with image-trained arti-ficial neural networks[J]. Geophysics, 2020, 85(2): U31-U46. DOI:10.1190/geo2018-0591.1 |
| [24] |
Chen Y Q, Schuster G T. Seismic inversion by newtonian machine learning[J]. Geophysics, 2020, 85(4): WA185-WA200. DOI:10.1190/geo2019-0434.1 |
| [25] |
孙宇航, 刘洋. 利用GRU神经网络预测横波速度[J]. 石油地球物理勘探, 2020, 55(3): 484-492, 503. SUN Yuhang, LIU Yang. Prediction of S-wave velocity based on GRU neural network[J]. Oil Geophysical Prospecting, 2020, 55(3): 484-492, 503. |
| [26] |
张昊, 朱培民, 顾元, 等. 基于深度学习的地震速度谱自动拾取方法[J]. 石油物探, 2019, 58(5): 724-733. ZHANG Hao, ZHU Peimin, GU Yuan, et al. Velocity auto-picking from velocity spectra based on deep learning[J]. Geophysical Prospecting for Petroleum, 2019, 58(5): 724-733. DOI:10.3969/j.issn.1000-1441.2019.05.011 |
| [27] |
张玉玺, 刘洋, 张浩然, 等. 基于深度学习的多属性盐丘自动识别方法[J]. 石油地球物理勘探, 2020, 55(3): 475-483. ZHANG Yuxi, LIU Yang, ZHANG Haoran, et al. Multi-attribute automatic interpretation of salt domes based on deep learning[J]. Oil Geophysical Prospecting, 2020, 55(3): 475-483. |
| [28] |
Zhou H W. Multiscale traveltime tomography[J]. Geo-physics, 2003, 68(5): 1639-1649. |
| [29] |
Long J, Shelhamer E, Darrel T. Fully convolutional networks for semantic segmentation[C]. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, 2015, 3431-3440.
|
| [30] |
Ronneberger O, Fischer P, Brox T. U-Net: Convolutional networks for biomedical image segmentation[C]. International Conference on Medical Image Computing and Computer-Assisted Intervention, 2015, 234-241.
|
| [31] |
高雪鹏, 丛爽. BP网络改进算法的性能对比研究[J]. 控制与决策, 2001, 16(2): 167-171. GAO Xuepeng, CONG Shuang. Comparative study on fast learning algorithms of BP networks[J]. Control and Decision, 2001, 16(2): 167-171. DOI:10.3321/j.issn:1001-0920.2001.02.009 |
| [32] |
Billette F J, Brandsberg-dhal S. The 2004 BP velocity benchmark[C]. Extended Abstracts of 67th EAGE Conference & Exhibition, 2005, B035.
|
| [33] |
Kosloff D D, Baysal E. Forward modeling by a Fourier method[J]. Geophysics, 1982, 47(10): 1402-1412. DOI:10.1190/1.1441288 |
| [34] |
马锐, 邹志辉, 芮拥军, 等. 基于SPML和海绵边界的伪谱法弹性波模拟复合吸收边界条件[J]. 石油物探, 2018, 57(1): 94-103. MA Rui, ZOU Zhihui, RUI Yongjun, et al. A compo-site absorbing boundary based on the SPML and sponge absorbing boundary for pseudo-spectral elastic wave modeling[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 94-103. DOI:10.3969/j.issn.1000-1441.2018.01.013 |



 邹志辉, 山东省青岛市崂山区松岭路238号中国海洋大学海洋地球科学学院, 266100。Email:
邹志辉, 山东省青岛市崂山区松岭路238号中国海洋大学海洋地球科学学院, 266100。Email: 