② 成都理工大学地球勘探与信息技术教育部重点实验室, 四川成都 610059;
③ 四川中成煤田物探工程院有限公司, 四川成都 610072
② Key Laboratory of Earth Exploration and Information Techniques (Chengdu University of Technology), Ministry of Education, Chengdu, Sichuan 610059, China;
③ Sichuan Zhongcheng Institute of Coalfield Geophysical Engineering, Chengdu, Sichuan 610072, China
众所周知,河道砂体往往是油气藏的重要载体,随着勘探开发不断深化,埋深更深、宽度更窄、厚度更薄的河道逐渐成为油气勘探领域的研究热点。针对河道空间展布特征识别的难题,业界广泛运用振幅、频率、相位等地震属性和速度、密度、阻抗等反演参数开展研究。然而,受河道埋藏深度大、纵横向分布复杂和地震资料主频偏低、频带窄、空间分辨率不足等因素的制约,传统方法对河道的识别精度往往不高,识别效果欠佳,不利于气藏空间分布预测、储量估算、水平井钻井等勘探开发和工程作业。
近几年来,时频分析技术在地震勘探领域发挥着越来越重要的作用[1],被广泛应用于主振幅和主频率等参数计算[2]、地震与测井信号的多分辨率分析[3]、储层预测[4]和吸收补偿[5]等。目前,地震信号时频分析技术也成为河道识别的重要手段,应用越来越广泛,针对地下河道沉积相的空间延展、厚度和宽度变化等特征,基于地震波在河道介质中的传播特性,利用地震信号开展时频分析,在时间域和频率域同时研究振幅、功率谱、能量、相位等地震属性。如,陈杰等[6]分析了短时傅里叶变换(STFT)的适用条件,并应用于河道砂体识别;杨道庆等[7]通过离散傅里叶变换,利用分频技术识别河道砂体;冯金义[8]应用时频分析技术提取了不同频率的瞬时振幅沿层切片,以检测河道砂体的空间分布。
1946年,Gabor[9]最早提出了利用声波信号频谱图等时频分析技术。根据核函数的不同,把时频分析法分为线性、双线性和非线性三大类[10]。其中,线性方法包括Gabor频谱图、STFT[11]、连续小波变换(CWT)[12]、S变换(ST)[13]和广义S变换(GST)[14-16]等,该类方法计算速度较快,但多具有窗口依赖性,因而无法同时提高时间分辨率与频率分辨率。双线性方法又称为二次型时频分布,包括WVD[17]、平滑伪Wigner-Ville分布(SPWVD)[18]和Choi-Williams分布(CWD)[19]等,以WVD为例,本质属于信号自相关系数的傅里叶变换,不受Heisenberg测不准原理[20]的制约,具有理论上优良的数学性质[21]。非线性方法包括基于数据驱动的自适应分解方法,如自适应STFT[22-23],相比STFT窗口长度灵活可变;Huang等[24]提出的经验模态分解(EMD)、集合经验模态分解(EEMD)以及完全集合经验模态分解(CEEMD)[25-26],时频分辨率高,但仍存在受信噪比影响大和计算效率低等问题;融合CWT与EMD的同步挤压小波变换[27],以及融合STFT、ST的同步挤压变换(SST)[28-29],分辨率和计算效率都很高,缺点是对低信噪比信号分析鲁棒性不足,且严格意义上同步挤压技术只是对时频变换结果的谱图重排处理。此外,还有基于信号稀疏表示的非线性方法,如基于Gabor原子的匹配追踪分解[30]等。
与非线性方法等其他时频分析方法相比,WVD具有极高的时频聚焦性,然而WVD存在交叉项干扰的缺陷。目前,最常用的消除交叉项的方法是核函数平滑法,如伪Wigner-Ville分布(PWVD)、SPWVD以及CWD等,然而这些方法均以牺牲时频分辨率为代价,且对交叉项干扰抑制不彻底。有学者也提出了许多消除交叉项的新方法,刘希康等[31]提出联合STFT和WVD消除交叉项,结合STFT不存在交叉项干扰和WVD时频聚焦性高的优点,既抑制了交叉项干扰,又保留了高分辨率特性,但仍存在依赖窗函数和地震信噪比等问题。孔慧芳等[32]提出基于分数阶傅里叶变换(FRFT)抑制WVD的交叉项,在有效抑制交叉项干扰的同时具有一定的抗噪性能,但仅限于线性调频信号。随后,纪永祯等[33]提出了结合贝叶斯学习算法和WVD消除交叉项,该方法在分辨率和保真性能方面具有一定优势,但依赖雷克子波库。与上述消除交叉项的方法相比,Zoukaneri等[34]提出的WVD-MEM具有极高的时频分辨率,计算简便、抗噪性能好,不依赖雷克子波等各种子波库,特别是对交叉项干扰有良好的抑制效果,且适用于包括地震信号在内的非平稳随机信号。
本文在前人研究基础上,利用非线性调频(FM)信号、合成地震信号和实际地震数据研究WVD-MEM消除交叉项干扰的方法。在对比分析目前广泛应用的STFT、CWT、GST、SPWVD、CWD等时频分析方法的基础上,针对调频信号、仿真信号、单道实测地震信号和楔状正演模型,开展WVD-MEM薄层分辨率定量分析和抗噪性能测试,并成功应用于四川盆地侏罗系沙溪庙组气藏的河道识别,基于WVD-MEM方法实现了对实测地震信号功率谱、瞬时振幅等高分辨地震属性的提取,获取了河道空间展布、宽度、厚度等重要信息,为气藏勘探开发提供了方法支撑。
1 方法原理 1.1 Wigner-Ville分布(WVD)Wigner-Ville给出的WVD定义为
| $ W(t, f)=\int_{-\infty}^{\infty} z\left(t+\frac{\tau}{2}\right) z^{*}\left(t-\frac{\tau}{2}\right) \mathrm{e}^{-2 \mathrm{j} {\rm{ \mathit{ π} }} f \tau} \mathrm{d} \tau $ | (1) |
式中:z(t)为信号x(t)的解析信号(解析信号包括原始信号和希尔伯特变换);上标“*”表示共轭转置;t是时间;f是频率;τ是时延;j为虚数单位。
在时间域进行离散处理,信号x(n)、z(n)的关系被定义为
| $ z(n)=x(n)+\mathrm{j} H[x(n)] $ | (2) |
式中:H[x(n)]为信号x(n)的希尔伯特变换;n为采样点整数,且n∈[0,N-1];N为最大采样点数。
利用解析信号z(n)可以生成信号自相关系数协方差矩阵C
| $ \boldsymbol{C}=z z^{\mathrm{T}} $ | (3) |
式中:C为N×N阶矩阵;上标“T”表示复共轭转置。
协方差矩阵C具有沿主对角线两端对称及复数实部相等、虚部相反的性质,求解C的一半即可完整求出矩阵。矩阵C沿每条交叉对角线的序列,构成了离散WVD的核函数,可以表示为
| $ K(n)=\left\{k_{n}(-l), \cdots, k_{n}(0), \cdots, k_{n}(l)\right\} $ | (4) |
式中:kn(0)表示矩阵C的主对角线元素;l∈[0,N-1]。定义kn(l)为
| $ k_{n}(l)=\left\{\begin{array}{cc} z(n-l) z^{*}(n+l) \quad l \leqslant \min (n, N-n) \\ 0 \quad l>\min (n, N-n) \end{array}\right. $ | (5) |
当l=0时,中心项kn(0)也是矩阵C的主对角线元素,有
| $ k_{n}(0)=z(n) z^{*}(n) \quad n=1, \cdots, N $ | (6) |
对核函数K(n)做快速傅里叶变换,即可得到离散WVD的瞬时功率谱(时频分布)
| $ \begin{aligned} W(n)=&\left\{W_{n}[-(N-1)], \cdots,\right.\\ &\left.W_{n}(0), \cdots, W_{n}(N-1)\right\} \end{aligned} $ | (7) |
最大熵(Maximum Entropy Method,MEM)原理指出,信号熵值最大的概率分布是最合理的分布。这样,基于最大熵原理的功率谱求解与自回归(autoregressive, AR)模型功率谱的求解是等价的[35],基本方程可以表示为
| $ P(f)=\frac{E_{p-1} \Delta t}{\left|\sum\limits_{m=0}^{p-1} c_{m} \mathrm{e}^{-\mathrm{j} 2 {\rm{ \mathit{ π} }} f m \Delta t}\right|^{2}} $ | (8) |
式中:P(f)为功率谱;p代表最大熵AR模型的阶数;m表示阶数p的序数,取值范围为[0,p-1];cm是序数为m阶时的自回归系数,当m=0时c=1;Ep-1对应p-1阶时的预测误差能量;Δt表示采样间隔。
在其他变量已知的前提下,方程求解的关键在于自回归系数c和预测误差能量E的求取。利用式(6)可得到E0,利用Burg算法[35]可直接从z(n)中求出自回归系数c
| $ c(m, m)=\frac{k_{z}(m)+\sum\limits_{i=1}^{m-1} k_{z}(m-i) c(m-1, i)}{E_{m-1}} $ | (9) |
| $ \begin{aligned} c(m, i)=&c(m-1, i)+c(m, m) c^{*}(m-1, m-i) \\ &i=1, \cdots, m-1 \end{aligned} $ | (10) |
| $ E_{m}=E_{m-1}\left[1-c(m, m) c^{*}(m, m)\right] $ | (11) |
式中kz (m)为输入信号自相关函数。联合式(9)~式(11),进入Levinson递归求解完整的自回归系数c和预测误差能量E,再由式(8)求得AR模型的最大熵功率谱。
1.3 基于WVD-MEM的高分辨时频属性计算方法离散WVD核函数的累计求和,是输入信号自相关函数的偶数项序列,表示为
| $ \begin{aligned} &\sum\limits_{n=0}^{N-1} K(n)=K_{z}(n)=\left\{k_{z}[-(N-1)], \cdots, k_{z}(-2),\right. \\ &\left.k_{z}(0), k_{z}(2), \cdots, k_{z}(N-1)\right\} \end{aligned} $ | (12) |
Burg在Levinson递归方程中推导出自相关函数的计算公式
| $ \begin{gathered} k_{z}(m)=-\sum\limits_{i=1}^{m-1} k_{z}(m-i) c(m-1, i)- \\ c(m, m) E_{m-1} \end{gathered} $ | (13) |
联合式(12)和式(13),得到WVD-MEN的核函数
| $ \begin{aligned} k_{n \mathrm{WM}}(m)=&-\sum\limits_{i=1}^{m-1} k_{n \mathrm{WM}} 1(m-i) c(m-1, i)-\\ & c(m, m) E_{m-1} \end{aligned} $ | (14) |
与WVD核函数求取方法类似,根据协方差矩阵的共轭性质,只需求取右半部分的值即可求出完整的WVD-MEM的核函数。之后对其进行快速傅里叶变换,可求出WVD的最大熵瞬时功率谱,即WVD-MEM时频分布。由于时频分布的峰值对应瞬时振幅的平方,且峰值在时频面的投影为瞬时频率,因而利用峰值检测法[36]可以获得瞬时频率和瞬时振幅等属性参数。
WVD-MEM高分辨时频属性的主要计算步骤如下:
(1) 由式(2)对原始输入数据x(n)做希尔伯特变换,获得解析信号z(n)。
(2) 为了抑制数据变换结果的端点效应(即时频表示平面上两端数据随窗口增大而消失的现象),需对z(n)进行加窗口扩展,在z(n)首尾各添一段数据,窗口长度均为L,设定值均为0。
| $ \begin{aligned} z_{L}(n)=&\left[z\left(n-\frac{L-1}{2}\right), \cdots,\right.\\ &\left.z(n), \cdots, z\left(n+\frac{L-1}{2}\right)\right] \end{aligned} $ | (15) |
式中:L为窗口长度,取奇数;zL(n)为解析信号z(n)扩展后的新数据,以z(n)为中心。
(3) 设定最大熵AR模型阶数。
(4) 由式(6)计算最大熵模型的预测误差初值(即WVD-MEM核函数的中心项)。
(5) 利用式(9)~式(11)求自回归系数c。
(6) 利用式(14)及自回归系数c,求WVD-MEM的核函数knWM(m)。
(7) 对knWM(m)做快速傅里叶变换,获得WVD-MEM高分辨时频属性。
需要说明的是,由于第(2)步扩展数据时首尾加上了窗口长度L的数据,因此需对求得的WVD-MEM时频属性结果矩阵边缘长度为L的数据做舍去处理。
采用上述步骤不仅可以求取地震信号的功率谱,还可以计算瞬时频率、瞬时振幅等地震属性。由于WVD-MEM时频属性计算方法结合了WVD的时频高聚焦特性和MEM的最大概率分布两项优势,因此获得的功率谱、瞬时频率、瞬时振幅等地震属性具有显著的高分辨特征,可为薄储层预测、窄河道识别及其他微型地质体研究提供方法支撑。
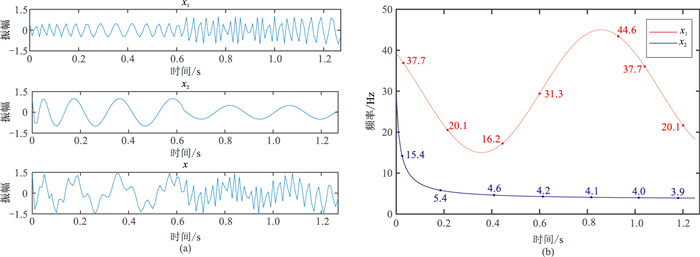
2 方法试验与分辨率定量分析 2.1 调频信号定量试验利用非线性调频(FM)信号研究WVD-MEM的时频分辨能力。图 1a显示了正弦调频信号x1、双曲线调频信号x2和二者线性叠加信号x的时间域波形特征。由图可见,x1的振幅随着时延增大, 曲线变密,x2的振幅随着时延减小,x的振幅随着时延变化并不明显,但曲线前半部分较为稀疏,后半段较密。图 1b显示x1和x2在频率域的变化特征,其中,x1的频率呈高低起伏的“波浪状”,x2的频率随着时延逐渐降低,且降低的幅度越来越小。
|
图 1 时间域和频率域的非线性调频信号 (a)时间域的非线性调频信号x1(上)、x2(中)及叠加信号x(下);(b)频率域的非线性调频信号x1和x2 |
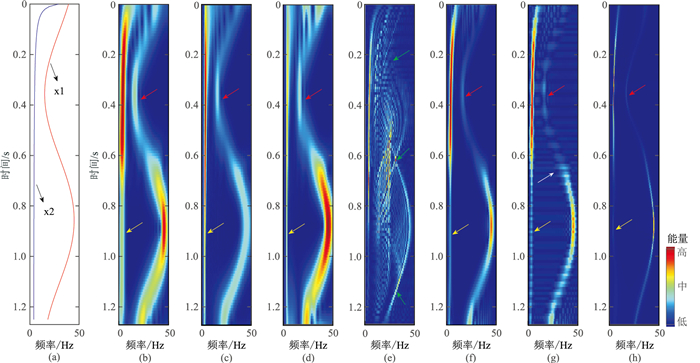
图 2是分别采用STFT、CWT、GST、WVD、SPWVD、CWD和WVD-MEM等7种时频分析方法获得的叠加信号x的时频谱。图 2a显示叠加信号x的实际时频谱是x1和x2两个分量的叠加,在时频域被分离成两部分,同时具有x1和x2的频谱特征。图 2b~图 2d为采用线性时频分析方法STFT、CWT和GST处理获得的时频谱,虽不存在交叉项干扰,对分量x2的频谱聚焦性也较好(黄色箭头所示),但对分量x1的频谱聚焦性相对较差(红色箭头所示)。WVD方法虽然时频聚焦性好,但存在严重的交叉项干扰(图 2e中绿色箭头所示)。SPWVD(图 2f)和CWD(图 2g)处理虽然消除了WVD产生的交叉项干扰,但降低了频率分辨率,尤其是CWD,存在时窗平滑效应产生的带状干扰(图 2g白色箭头所示)。相比之下,WVD-MEM方法(图 2h)不仅完整消除了WVD存在的交叉项干扰,而且保持了与实际频率基本一致的时频分布,清楚地显示出x1和x2频谱分别由低到高和由高向低的变化特征。
|
图 2 采用不同方法获得的叠加信号x时频分布特征 (a)叠加信号;(b)STFT;(c)CWT;(d)GST;(e)WVD;(f)SPWVD;(g)CWD;(h)WVD-MEM |
总之,试验表明这7种方法均能分辨叠加信号x中的x1、x2分量,且线性时频分析方法中,GST的聚焦性优于STFT和CWT;二次型时频分析方法中SPWVD、CWD和WVD-MEM的聚焦性整体优于线性时频分析法。其中WVD-MEM方法具有更显著的高分辨率优势。
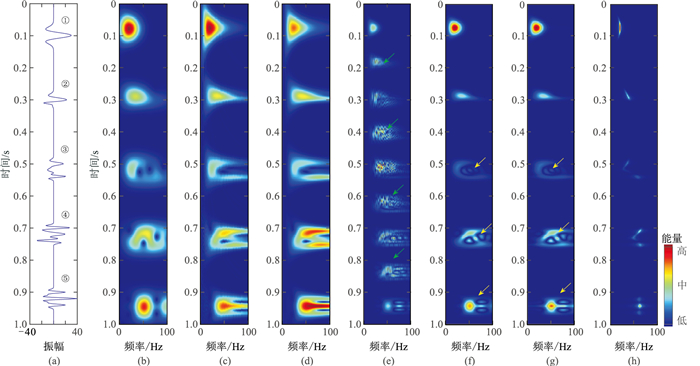
2.2 单道仿真地震信号——非平稳信号定量试验利用单道仿真地震信号定量检测WVD-MEM方法对非平稳信号的高分辨时频分析能力,并为实际地震信号功率谱、瞬时振幅等高分辨时频属性的提取和应用奠定基础。图 3a为使用5个雷克子波分量合成的单道仿真地震信号,子波分量的主频分别为:①20Hz;②30Hz和60Hz;③40Hz、30Hz和60Hz;④60Hz、40Hz和60Hz;⑤60Hz、60Hz和60Hz。最大振幅分别为:①30dB;②20dB和-10dB;③15dB、-10dB和20dB;④30dB、20dB和-30dB;⑤20dB、40dB和20dB。信号长度(采样总数)分别为①100;②100;③100;④100;⑤101。具体参数选取和计算方程如式(16)所示。
| $ \left\{\begin{array}{l} r(f, t)=\left[1-2({\rm{ \mathit{ π} }} f t)^{2}\right] \mathrm{e}^{-({\rm{ \mathit{ π} }} f t)^{2}} \\ f_{1}=20 ; f_{2}=30 ; f_{3}=40 ; f_{4}=60 ; f_{5}=60 \\ N_{1}=100 ; N_{2}=100 ; N_{3}=100 ; N_{4}=100 ; N_{5}=101 \\ t_{1}=\left(-\frac{N_{1}-1}{2}: \frac{N_{1}-1}{2}\right) \times T ; r_{1}=30 \times r\left(f_{1}, t_{1}\right) \\ t_{2}=\left(-\frac{N_{2}-1}{2}: \frac{N_{2}-1}{2}\right) \times T ; r_{2}=20 \times r\left(f_{2}, t_{2}\right)-10 \times r\left(f_{5}, t_{2}-0.01\right) \\ t_{3}=\left(-\frac{N_{3}-1}{2}: \frac{N_{3}-1}{2}\right) \times T ; r_{3}=15 \times r\left(f_{3}, t_{3}\right)-10 \times r\left(f_{2}, t_{3}-0.02\right)+20 \times r\left(f_{5}, t_{3}-0.04\right) \\ t_{4}=\left(-\frac{N_{4}-1}{2}: \frac{N_{4}-1}{2}\right) \times T ; r_{4}=30 \times r\left(f_{4}, t_{4}\right)+20 \times r\left(f_{3}, t_{4}-0.02\right)-30 \times r\left(f_{4}, t_{4}-0.04\right) \\ t_{5}=\left(-\frac{N_{5}-1}{2}: \frac{N_{5}-1}{2}\right) \times T ; r_{5}=20 \times r\left(f_{5}, t_{5}\right)+40 \times r\left(f_{5}, t_{5}-0.02\right)+20 \times r\left(f_{5}, t_{5}-0.04\right) \end{array}\right. $ | (16) |
|
图 3 单道仿真地震信号不同方法时频分析效果对比 (a)单道仿真地震信号;(b)STFT;(c)CWT;(d)GST;(e)WVD;(f)SPWVD;(g)CWD;(h)WVD-MEM |
式中:r(f, t)为雷克子波表达式;f1~f5为5个雷克子波分量频率。
图 3b~图 3h分别为采用STFT、CWT、GST、WVD、SPWVD、CWD和WVD-MEM等7种方法获得的仿真信号时频分布。由图可见,7种方法均在0.1、0.3、0.5、0.7及0.9s附近检测到相应的时频能量响应,但能量分布具有明显的差异。三种线性时频分析方法中,GST聚焦性和分辨率最好,CWT次之,STFT最差;相比之下,二次型时频分布的聚焦性均优于GST,但WVD法在0.2、0.4、0.6和0.8s附近出现了严重的干扰项(图 3e中绿色箭头所示);SPWVD和CWD虽然消除了图 3e中的交叉项干扰,但对于0.5、0.7和0.9s附近的交叉项干扰却无法完全抑制(黄色箭头所示)。而WVD-MEM则完全消除了WVD中存在的所有交叉项干扰,表现出最优的时频聚焦性和频率定位精度,清楚地显示了20、30、40、60Hz等频率位置的功率谱强弱变化。例如,在0.9s附近的仿真信号由3个60Hz主频、中间振幅较高(40dB)、两侧振幅较低且相同(20dB)的雷克子波合成,WVD-MEM时频分析方法不仅准确展示出子波能量变化特征,而且精确定位在60Hz频率位置,其他方法均未能达到如此高的分辨率。
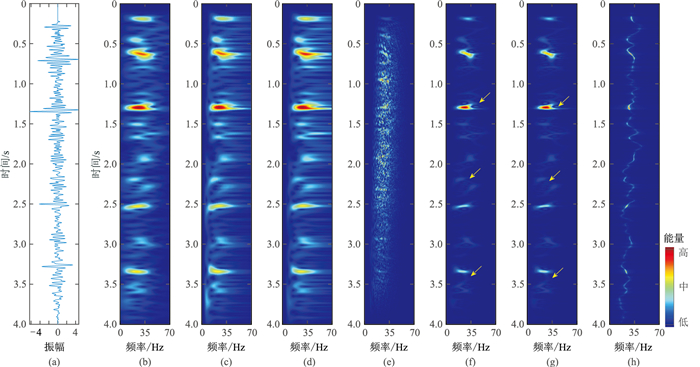
2.3 单道实测地震信号——非平稳信号试验上述仿真信号是由与实际地震信号近似的雷克子波组成,已知子波频率、相位、振幅等信息,而实测地震信号中这些信息是未知的,且更加复杂,二者存在明显差异。因此,有必要针对实测地震信号开展试验,进一步分析该方法对实际地震信号的适用性,为后续利用功率谱、瞬时频率、瞬时振幅等地震属性进行高分辨河道识别提供参考。图 4为单道实测地震信号及采用7种方法的时频分析结果对比。同样,在STFT、CWT和GST等3种线性时频分析方法中,GST的时频分辨率和聚焦性最优;WVD方法受到交叉项的干扰,有效的时频特征被完全淹没,无法进行信号分析;SPWVD和CWD方法的时频聚焦性优于线性时频分析方法,但交叉项干扰抑制不彻底(黄色箭头所指)。WVD-MEM则彻底消除了WVD存在的严重交叉项干扰,在保持高度时频聚焦性的同时,具有明显更高的时频分辨特性,对能量随频率和时间变化的细节刻画得更精确。可见,针对更复杂的实际地震信号,WVD-MEM方法仍然能获得高聚焦、高时频分辨率的处理效果。
|
图 4 单道实测地震信号时频分析效果对比 (a)单道实测信号;(b)STFT;(c)CWT;(d)GST;(e)WVD;(f)SPWVD;(g)CWD;(h)WVD-MEM |
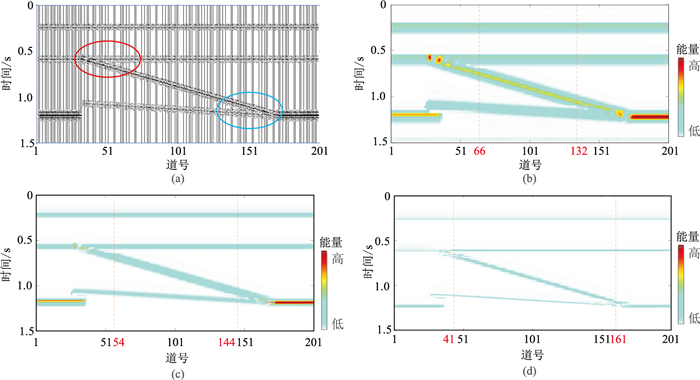
河道识别本质上是地震极限分辨率条件下的薄层识别问题。通过提高瞬时功率谱、瞬时频率、瞬时振幅等地震属性的分辨率,可以提高地震信号的薄层分辨率,从而实现河道识别。设计一个楔状模型正演数值模拟地震数据(图 5a),震源为主频35Hz的雷克子波,检波器的采样间距为5m,接收长度为1.5s,共201道。在地层变薄位置(红色与蓝色圈内),可以观察到薄层调谐效应产生的明显复合地震反射现象。
|
图 5 正演数值模拟记录及采用不同方法获得的35Hz单频剖面 (a)楔状模型正演地震记录;(b)GST;(c)SPWVD;(d)WVD-MEM |
图 5b~图 5d分别显示了利用GST、SPWVD和WVD-MEM三种方法提取的35Hz单频剖面。由图可见,在红色圈标识的薄层调谐位置,GST、SPWVD及WVD-MEM方法的最大识别位置分别为第66、54、41道;在蓝色圈标识的薄层调谐位置,GST、SPWVD及WVD-MEM方法的最大识别位置分别为第132、144、161道。显然,WVD-MEM表现出更高的能谱聚焦性,频谱被高度细化,增强了时频分辨能力,能更好地消除薄层调谐效应的影响,更有利于薄层识别。
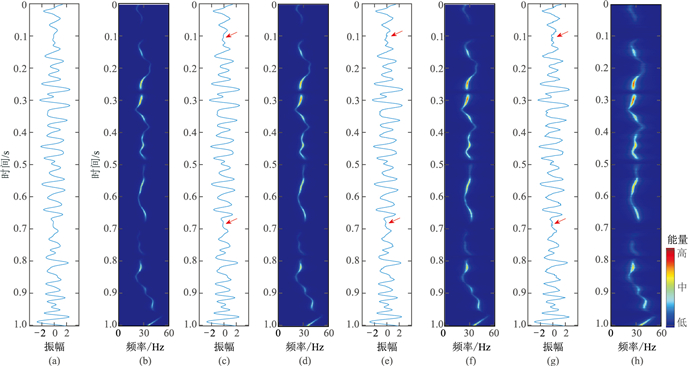
2.5 WVD-MEM的抗噪性能测试分析实际地震信号通常含有一定程度的噪声,因而,有必要在不同信噪比(SNR)条件下测试WVD-MEM方法的抗噪性能,以进一步明确其实用价值。图 6显示单道实测地震信号(图 6a)及SNR分别为30、20和10噪声条件下,应用WVD-MEM获得的瞬时振幅谱特征。可见,随着SNR由高向低转变,相应的WVD-MEM处理效果与原始地震信号处理结果相比较并未发生明显改变。由此可以证实,WVD-MEM具有良好的抗噪性能,能够适用于实测地震信号的时频处理。
|
图 6 不同SNR实测地震信号的WVD-MEM处理结果对比 (a)原始地震信号;(b)图a的WVD-MEM结果;(c)SNR=30;(d)图c的WVD-MEM结果;(e)SNR=20;(f)图e的WVD-MEM结果;(g)SNR=10;(h)图g的WVD-MEM结果 |
综上所述,在非线性调频信号、合成地震信号、单道实测地震信号及多波正演数值模拟地震记录的定量测试分析中,WVD-MEM时频分析方法都表现出较强的能谱聚焦和谱细化特性,时频分辨能力显著,且抗噪性能良好。因此,当地震波在地下介质中传播,遇到目标地质体时可能出现功率谱、瞬时振幅、瞬时频率等时频属性异常,借助WVD-MEM方法可以更精确地突出时频属性异常特征,进而有效识别薄储层、窄河道及其他微型地质体。
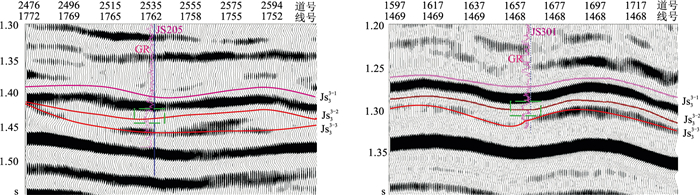
3 应用实例研究工区位于川西地区,目标层为侏罗系中统下沙溪庙组沙三段,沉积微相为分流河道,进一步细分为Js33-1、Js33-2和Js33-3三套地层[37]。地层中的河道砂体是重要的油气勘探开发目标,但河道砂体普遍相对较薄,与泥岩地层呈垂向交互叠置状态,识别难度较大。图 7显示过JS205井和JS301井河道的地震反射特征,其中,过JS205井的河道宽度约354m、厚度约35m,GR曲线表现为低值响应(绿色矩形框内),地震反射呈现“透镜状”特征;过JS301井的河道宽度约248m、厚度约30m,GR曲线表现为低值响应。相比之下,过JS301井的河道更窄、更薄,“透镜状”地震响应特征不明显,识别难度更大。
|
图 7 过JS205井(左)和JS301井(右)河道的地震反射特征 |
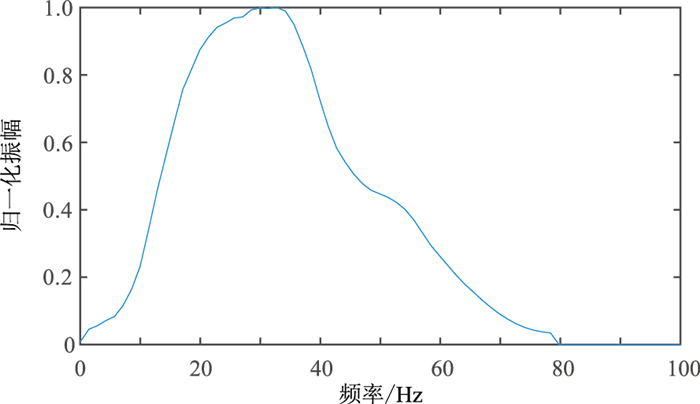
地震数据频谱分析对提取瞬时振幅及分频属性具有指导作用。首先对研究区地震数据进行频谱分析(图 8),可以看出,工区地震数据主频约为35Hz,频带范围为5~80Hz,优势频带范围为7~65Hz。结合前文方法与试验研究,采用WVD-MEM方法处理工区地震数据并提取瞬时频率、瞬时振幅和不同频率功率谱等地震属性,从中发现时频属性异常,以多视角分析出河道的异常响应特征,实现河道空间展布特征识别。
|
图 8 研究区频谱分析 |
由于单个频率对河道的刻画效果存在较大不足,依据工区优势频带范围,提取了7~65Hz的瞬时振幅及7~31(低)、23~49(中)和37~65Hz(高)三个不同频段的频谱特征进行分析和河道识别。图 9显示采用WVD-MEM方法(阶数p=7,汉宁窗,窗口长度L=31)提取的三个频段的频谱特征,可见明显的厚度响应差异常。以Js33-2层为例,当频率由低频段向中频段转变时,剖面上均能准确识别该地层河道(黑色箭头所示),且随着频率的升高,能谱的聚焦性及垂向分辨能力也相应提高。但对于河道而言,由中频段再提升到高频段时,对该层河道刻画能力反而下降。说明提高频率在一定程度上可以提高河道识别效果,但仅限于在工区地震数据主频范围内。

|
图 9 研究区WVD-MEM提取的不同频段频谱剖面 (a)7~31Hz;(b)23~49Hz;(c)37~65Hz |
结合WVD-MEM方法计算出优势频段的平均瞬时振幅及分频功率谱属性,通过沿层属性切片展现河道横向分布特征。图 10显示了Js33-2层原始振幅、7~65Hz瞬时振幅及7~31、23~49和37~65Hz三个频段功率谱属性沿层切片。可见,不同属性切片对工区河道展布均具有一定程度的识别效果。图 10a显示原始振幅沿层响应特征,主干河道表现为明显的负值响应(红色箭头所示),部分较窄河道则表现为不明显的负值异常(黄色箭头所示),且连续性刻画较差。在蓝色虚线框内,左、右两条窄河道(蓝色箭头所示)分别表现出不明显的正值和负值异常,红色虚线框内,河道特征表现出正、负值混叠的现象,较难识别。特别是绿色箭头所揭示的两条不明显河道,原始振幅切片基本上无法做到有效识别。总之,原始振幅仅能揭示工区的部分主干河道分布,对于窄河道、不明显河道展布特征、连续性等方面刻画效果不佳。
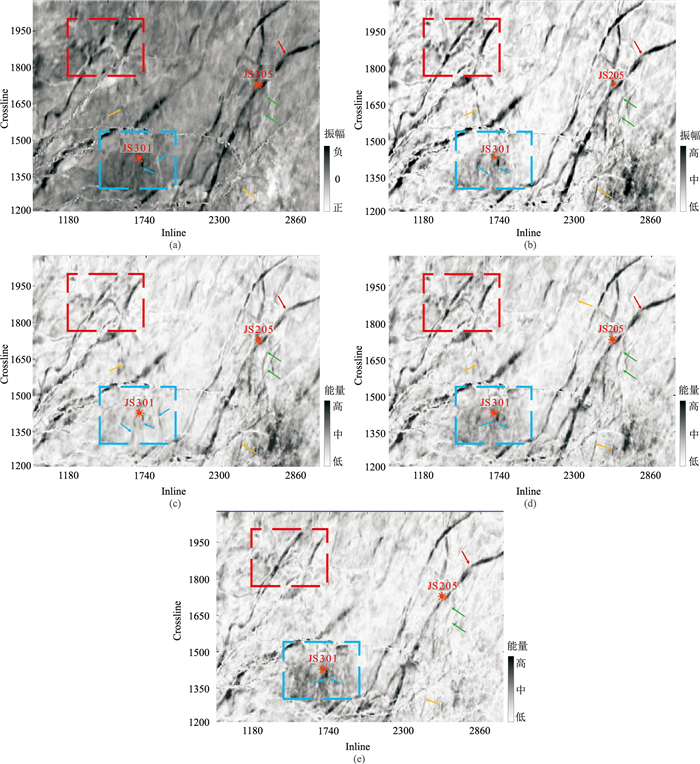
|
图 10 利用WVD-MEM方法提取的时频属性识别Js33-2层河道分布 (a)原始振幅;(b)7~65Hz瞬时振幅;(c)7~31Hz功率谱;(d)23~49Hz功率谱;(e)37~65Hz功率谱 |
图 10b~图 10e显示7~65Hz瞬时振幅及低、中、高不同频段功率谱切片对河道刻画能力较强,高值异常更清晰地显示不同宽度河道的沿层展布特征,除了主干河道(红色箭头所示)外,也能展示一些较窄的小河道(黄色箭头所示);对于红色虚线框内的河道,四图识别效果类似且均优于原始振幅切片;而对于蓝色虚线框内JS301井旁的细小河道(蓝色箭头所示),瞬时振幅及三个频段功率谱的揭示有所差异,但均能清晰刻画窄河道的展布。针对绿色箭头所示的两条不明显河道,瞬时振幅及不同频段功率谱也有不同的表现,其中,7~31Hz频谱刻画能力最佳,23~49Hz频谱稍逊,37~65Hz频谱及瞬时振幅较弱,这与不同频段剖面对河道的描述一致,在主频范围内,提高频率一定程度上可以提高河道描绘能力。整体而言,利用WVD-MEM方法提取的瞬时振幅和不同频段功率谱属性对不同宽度、尺度的河道均具有良好的分辨率优势,能够较好地刻画Js33-2层河道分布特征。
采用分频融合技术对WVD-MEM计算的低、中、高三个频段的功率谱特征开展多频融合增强显示,进一步增强河道识别效果。图 11a为RGB融合后识别效果,图 11b为CMY融合后的河道识别效果。由图可见,经过多频融合后,不同尺度、不同流向的河道得到进一步清晰展示,对一些较宽河道刻画效果更加明显(红色箭头所示),对于原始振幅切片上无法识别的两条不明显窄河道(绿色箭头所示)刻画效果明显改善。因此,利用WVD-MEM方法提取低、中、高三个频段的功率谱属性并融合显示,能够突出共性、弱化差异,有效改善单频段频谱在河道识别方面的不足,增强对工区河道的高分辨识别效果。

|
图 11 研究区WVD-MEM不同频率功率谱融合层位切片特征 (a)RGB融合;(b)CMY融合 |
这里需要进一步指出的是,基于时频分析方法进行河道识别,是将地震数据从时间域转换到时频域,即将地震数据从一个时间采样点对应一个原始振幅值转换到一个时间采样点对应不同频率下的多个值(无论振幅谱值还是功率谱值),本质上不同于从时间域的角度分析地震信号,属于在时频域对原始地震信号的直接应用,不会破坏原始振幅的连续性,因而识别结果具有可靠性。而影响河道高分辨识别效果的因素取决于时频分析方法的能谱聚焦性和分辨率。由于WVD-MEM方法结合了Wigner-Ville分布和最大熵原理的非平稳信号分析优势,不仅能够有效消除WVD信号分析中存在的交叉项,而且可以保持与瞬时频率基本一致的高度时频聚焦性,使计算的瞬时振幅、功率谱等地震属性具有高分辨率特性。
该方法在川西地区侏罗系沙溪庙组气藏河道识别的应用实例表明,WVD-MEM提取的功率谱、瞬时振幅等地震属性,能从垂向和横向较好地刻画河道的沉积厚度、延展宽度和流动方向等地质细节,可以在其他类似的油气探区开展推广应用。
4 结论与认识通过WVD-MEM方法研究和对非线性调频信号、仿真地震信号、单道实测地震(非平稳)信号、楔状模型正演模拟信号等定量试验,以及在川西侏罗系沙溪庙组气藏河道识别的实际应用,得到以下认识:
(1) 相比于STFT、CWT、GST、WVD、SPWVD、CWD等时频分析方法,WVD-MEM时频分析方法结合了WVD的高度时频聚焦性以及MEM的最大概率分布优势,不仅完整消除了WVD中存在的严重交叉项,且具有显著的频谱聚焦性和高分辨率优势,可以应用于薄储层、窄河道及其他地下微型地质体的识别研究;
(2) 针对埋藏较深、宽度较窄、厚度较薄、流向变化的河道高分辨识别难题,WVD-MEM方法能够在一定程度上解决地震资料主频不够高、频带不够宽等不利因素导致的空间分辨率不足的问题,利用WVD-MEM获得的瞬时振幅、分频功率谱等高分辨地震属性以及多频融合等手段,能够有效突出河道的厚度、宽度、流向等空间展布细节,进一步提高河道的识别精度;
(3) 在对WVD-MEM实测地震信号分析过程中,就整个工区而言,阶数p一般选择定值。如何在每道实测地震信号计算前自适应调整p的取值、优化WVD-MEM计算效率和程序设计以及方法的应用推广,将是下一步研究的方向。
感谢中国石化西南油气分公司为此研究提供实验数据。
| [1] |
庞锐, 刘百红, 孙成龙. 时频分析技术在地震勘探中的应用综述[J]. 岩性油气藏, 2013, 25(3): 92-96. PANG Rui, LIU Baihong, SUN Chenglong. Review on time-frequency analysis technique and its application in seismic exploration[J]. Lithologic Reservoirs, 2013, 25(3): 92-96. DOI:10.3969/j.issn.1673-8926.2013.03.016 |
| [2] |
黄德济, 赵宪生. 时频域中主参数剖面的计算及应用[J]. 物探化探计算技术, 1994, 16(3): 197-204. HUANG Deji, ZHAO Xiansheng. The calculation and applicatopn of seismic main characteristic sections in time frequency domain[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1994, 16(3): 197-204. |
| [3] |
余厚全, 刘益成, 黄载禄. 小波变换用于地震测井信号的多分辨率分析[J]. 石油地球物理勘探, 1994, 29(4): 441-448. YU Houquan, LIU Yicheng, HUANG Zailu. Application of wavelet transform to multiresolution analysis of seismic and log signals[J]. Oil Geophysical Prospecting, 1994, 29(4): 441-448. |
| [4] |
刘传虎, 刘福贵, 李卫忠. 时频分析方法及在储层预测中的应用[J]. 石油地球物理勘探, 1996, 31(S1): 11-20. |
| [5] |
白桦, 李鲲鹏. 基于时频分析的地层吸收补偿[J]. 石油地球物理勘探, 1999, 34(6): 642-648. BAI Hua, LI Kunpeng. Stratigraphic absorption compensation based on time-frequency analysis[J]. Oil Geophysical Prospecting, 1999, 34(6): 642-648. DOI:10.3321/j.issn:1000-7210.1999.06.005 |
| [6] |
陈杰, 王惠勇. 基于短时傅里叶变换时频分析技术的沉积旋回划分适应性研究[J]. 内江科技, 2014, 35(1): 125-126. |
| [7] |
杨道庆, 张永华, 罗家群, 等. 时频分析技术识别泌阳凹陷毕店地区河道砂体[J]. 特种油气藏, 2015, 22(1): 12-15. YANG Daoqing, ZHANG Yonghua, LUO Jiaqun, et al. Channel sandbodys identification by time-frequency analysis in Bidian of Biyang Sag[J]. Special Oil & Gas Reservoirs, 2015, 22(1): 12-15. DOI:10.3969/j.issn.1006-6535.2015.01.003 |
| [8] |
冯金义. 时频分析技术识别河道砂体在埕海一区明化镇组中的应用[J]. 中国石油和化工标准与质量, 2016, 36(6): 31-32. DOI:10.3969/j.issn.1673-4076.2016.06.016 |
| [9] |
Gabor D. Theory of communication[J]. Journal of the Institute of Electrical Engineers of Japan, 1946, 93: 429-457. |
| [10] |
黄昱丞, 郑晓东, 栾奕, 等. 地震信号线性与非线性时频分析方法对比[J]. 石油地球物理勘探, 2018, 53(5): 975-989. HUANG Yucheng, ZHENG Xiaodong, LUAN Yi, et al. Comparison of linear and nonlinear time-frequency analysis on seismic signals[J]. Oil Geophysical Prospecting, 2018, 53(5): 975-989. |
| [11] |
张贤达. 现代信号处理[M]. (第2版). 北京: 清华大学出版社, 2002.
|
| [12] |
QIAN Shi'e. Introduction to Time-Frequency and Wavelet Transforms[M]. Beijing: China Machine Press, 2005.
|
| [13] |
Stockwell R G, Mansinha L, Lowe R P. Localization of the complex spectrum: the S transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001. DOI:10.1109/78.492555 |
| [14] |
Pinnegar C R, Lalu M. The S-transform with windows of arbitrary and varying shape[J]. Geophysics, 2003, 68(1): 381-385. DOI:10.1190/1.1543223 |
| [15] |
高静怀, 陈文超, 李幼铭, 等. 广义S变换与薄互层地震响应分析[J]. 地球物理学报, 2003, 46(4): 526-532. GAO Jinghuai, CHEN Wenchao, LI Youming, et al. Generalized S transform and seismic response analysis of thin interbeds[J]. Chinese Journal of Geophysics, 2003, 46(4): 526-532. DOI:10.3321/j.issn:0001-5733.2003.04.015 |
| [16] |
陈学华, 贺振华, 黄德济. 基于广义S变换的地震资料高效时频谱分解[J]. 石油地球物理勘探, 2008, 43(5): 530-534. CHEN Xuehua, HE Zhenhua, HUANG Deji. High-efficient time-frequency spectrum decomposition of seismic data based on generalized S transform[J]. Oil Geophysical Prospecting, 2008, 43(5): 530-534. DOI:10.3321/j.issn:1000-7210.2008.05.008 |
| [17] |
Wigner E P. On the Quantum Correction For Thermodynamic Equilibrium[J]. Physical Review, 1932, 40(5): 749-759. DOI:10.1103/PhysRev.40.749 |
| [18] |
张贤达, 保铮. 非平稳信号分析与处理[M]. 北京: 国防工业出版社, 1998.
|
| [19] |
Choi H I, Williams W J. Improved time-frequency representation of multicomponent signals using exponential kernels[J]. IEEE Transactions on Acoustics Speech & Signal Processing, 2002, 37(6): 862-871. |
| [20] |
海森堡H9N——提出"测不准原理"[J]. 光谱实验室, 2008, 25(1): 112-113.
|
| [21] |
王见, 李金同, 卢华玲, 等. 采用STFT-Wigner变换抑制Wigner-Ville分布交叉项[J]. 重庆大学学报, 2013, 36(8): 16-18. WANG Jian, LI Jintong, LU Hualing, et al. Using STFT-Wigner transform to suppress the cross terms in Wigner-Ville distribution[J]. Journal of Chongqing University, 2013, 36(8): 16-18. |
| [22] |
Zhong J, Huang Y. Time-frequency representation based on an adaptive short-time Fourier transform[J]. IEEE Transactions on Signal Processing, 2010, 58(10): 5118-5128. DOI:10.1109/TSP.2010.2053028 |
| [23] |
Pei S C, Huang S G. STFT with adaptive window width based on the chirp rate[J]. IEEE Transactions on Signal Processing, 2012, 60(8): 4065-4080. DOI:10.1109/TSP.2012.2197204 |
| [24] |
Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings Mathematical Physical & Engineering Sciences, 1998, 454(1971): 903-995. |
| [25] |
Wu Z, Huang N E. Ensemble empirical mode decomposition: A noise assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. DOI:10.1142/S1793536909000047 |
| [26] |
Torres M E, Colominas M A, Schlotthauer G, et al. A complete ensemble empirical mode decomposition with adaptive noise[C]. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, 2011.
|
| [27] |
Daubechies I, Lu J, Wu H T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool[J]. Applied and Computational Harmonic Analysis, 2011, 30(2): 243-261. DOI:10.1016/j.acha.2010.08.002 |
| [28] |
Huang Z L, Zhang J, Zhao T H, et al. Synchrosquee-zing S-transform and its application in seismic spectral decomposition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(2): 817-825. DOI:10.1109/TGRS.2015.2466660 |
| [29] |
Thakur G, Wu H T. Synchrosqueezing-based reco-very of instantaneous frequency from nonuniform samples[J]. SIAM Journal on Mathematical Analysis, 2011, 43(5): 2078-2095. DOI:10.1137/100798818 |
| [30] |
Stéphane G. Mallat, Member, et al. Matching pursuits with time-frequency dictionaries[J]. IEEE Tran-sactions on Signal Processing, 1993, 41(12): 3397-3415. DOI:10.1109/78.258082 |
| [31] |
刘希康, 丁志峰, 李媛, 等. STFT与WVD在地震波时频分析中的应用[J]. 地震地磁观测与研究, 2016, 37(1): 15-21. LIU Xikang, DING Zhifeng, LI Yuan, et al. Application of short-time Fourier transform and Wigner-Ville distribution in time-frequency analysis of seismic wave[J]. Seismological and Geomagnetic Observation and Research, 2016, 37(1): 15-21. |
| [32] |
孔慧芳, 陶文益, 闫嘉鹏. 基于FRFT的Wigner-Ville分布交叉项抑制方法[J]. 测控技术, 2019, 38(10): 15-19. KONG Huifang, TAO Wenyi, YAN Jiapeng. Wigner-Ville distribution cross terms suppression method based on FRFT[J]. Measurement and control technology, 2019, 38(10): 15-19. |
| [33] |
纪永祯, 张渝悦, 朱立华, 等. 基于SBL-WVD的地震高分辨率时频分析[J]. 石油物探, 2020, 59(1): 80-86. JI Yongzhen, ZHANG Yuyue, ZHU Lihua, et al. High-resolution seismic time-frequency analysis based on sparse Bayesian learning combined with Wigner-Ville distribution[J]. Geophysical Prospecting for Petroleum, 2020, 59(1): 80-86. DOI:10.3969/j.issn.1000-1441.2020.01.009 |
| [34] |
Zoukaneri I, Porsani M J. A combined Wigner-Ville and maximum entropy method for high-resolution time-frequency analysis of seismic data[J]. Geophy-sics, 2015, 80(6): O1-O11. |
| [35] |
Burg J P. Maximum Entropy Spectrum Analysis [M]. 1975.
|
| [36] |
向道朴, 周东明, 何建国. 微多普勒瞬时频率估计算法对噪声的适应性能研究[J]. 电路与系统学报, 2010, 15(6): 90-101. XIANG Daopu, ZHOU Dongming, HE Jianguo. The adaptability study of micro-Doppler's instantaneous frequency estimation algorithm with noise[J]. Journal of Circuits and Systems, 2010, 15(6): 90-101. DOI:10.3969/j.issn.1007-0249.2010.06.016 |
| [37] |
王宽. 川西凹陷东坡沙溪庙组精细地震储层预测[D]. 北京: 中国石油大学, 2017. WANG Kuan. Fine seismic reservoir prediction in Shaximiao formation on east slope of western Sichuan Depression[D]. China University of Petroleum, Beijing, 2017. |



 程冰洁, 四川省成都市成华区二仙桥东三路一号成都理工大学地球物理学院, 610059。Email:
程冰洁, 四川省成都市成华区二仙桥东三路一号成都理工大学地球物理学院, 610059。Email: 