② 中国石油西南油气田分公司川西北气矿, 四川江油 621700
② Northwestern Sichuan Gas District, PetroChina Southwest Oil & Gas Field Company, Jiangyou, Sichuan 621700, China
裂缝发育受多种因素控制,分布复杂、规律性差,预测和识别难度大[1]。目前常规的裂缝预测技术主要有叠前和叠后两类。叠后裂缝预测理论完善、技术方法繁多,当前常用的有相干体、蚂蚁体追踪、曲率属性、边缘检测、构造不连续属性、衰减梯度属性、应力场数值模拟等[2-3]。与传统叠后裂缝预测相比,叠前方位各向异性裂缝检测不仅具有在空间上覆盖程度高的优势,同时包含方位角信息,可判定裂缝走向、裂缝密度[4-5]。
当前一种常用的叠前裂缝预测方法基于纵波各向异性速度椭圆拟合[6],但依赖于宽方位地震数据。对于海洋窄方位地震资料,方位各向异性裂缝检测方法受方位制约。当前应用窄方位叠前地震数据预测裂缝的方法还不太成熟。田立新等[1]综合应用叠前弹性参数反演与应力场模拟获取远、近炮检距间的属性差异预测裂缝储层。苏世龙等[7]采取限炮检距措施及五维插值技术或OVT域处理技术改善窄方位资料特性,进而开展叠前裂缝预测。Liu等[8]利用窄方位数据预测碳酸盐岩裂缝。熊晓军等[9]基于地震波在各向异性介质与各向同性介质中的AVO差异,提出标准差统计方法进行叠前裂缝预测,裂缝预测结果宏观趋势正确;但由于采用窄方位或单方位地震资料(覆盖次数低),预测的裂缝发育带连片性差。为此,本文改进文献[9]的裂缝预测流程,引入裂缝融合分析方法,有效克服了采用窄方位或单一方位数据预测裂缝的缺陷,可以准确表征高角度裂缝发育带的三维空间分布特征。
本文首先采用基于标准差统计的窄方位叠前裂缝预测方法,再引入基于网格聚类分析[10]的裂缝融合技术,最后得到纵横向连续性强的裂缝数据体。对中国N区的海洋窄方位叠前地震资料的应用结果表明,本文提出的裂缝预测技术可有效地表征高角度裂缝发育带的展布特征,与钻井数据符合度高,适用于发育高角度裂缝的地区。
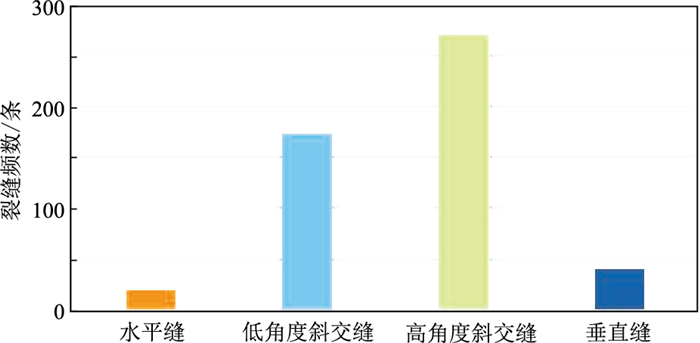
1 叠前裂缝预测的理论基础分析 1.1 N区的裂缝发育特征观察中国N区取心井的岩心发现,主要发育层理缝、构造缝两种裂缝,按产状将裂缝分为四种:倾角≤5°为水平缝(图 1a);5°<倾角<45°为低角度斜交缝(图 1b);45°≤倾角<85°为高角度斜交缝(图 1c);倾角≥85°为垂直缝(图 1d)。此外,在目的层岩心中共观察到502条裂缝(图 2)。因此,N区的目的层段普遍发育高角度裂缝。

|
图 1 岩心照片 (a)水平缝;(b)低角度斜交缝;(c)高角度斜交缝;(d)垂直缝 |
|
图 2 N区岩心裂缝产状分布图 |
N区目的层段普遍发育高角度裂缝,海上采集的三维叠前窄方位地震资料的叠前道集方位角主要分布于0°~30°,炮检距分布范围为200~6573m(图 3)。

|
图 3 N区叠前道集的方位角分析 (a)炮检距—方位角交会图;(b)面元方位,面元中的数字表示覆盖次数 |
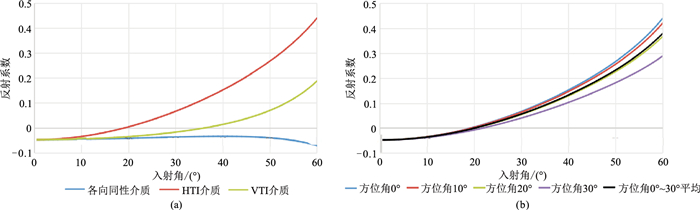
设计了三层模型(表 1),其中顶、底层为非储层(各向同性介质),中间层为储层(文中分别设定为各向同性、VTI、HTI介质)。为了有效地表征模型上界面的AVO特征,当中间层为各向同性介质时采用Aki近似式计算纵波在模型上界面反射系数,当中间层为各向异性(HTI和VTI)介质时采用Rüger近似式[11]计算纵波在模型上界面反射系数。可见:①方位角为0°时,当中间层分别为各向同性、HTI及VTI介质时,反射系数随入射角而变化,且中间层为HTI介质时反射系数随入射角的变化最显著(图 4a)。因此,对于零方位角的三维地震数据,当介质中高陡裂缝发育时,裂缝性质对叠前资料振幅特性的影响将不容忽略。②在窄方位情况下,当中间层为HTI介质时,相同的入射角、不同方位角的反射系数存在差异(图 4b)。
|
|
表 1 模型参数 |
|
图 4 三层模型AVO响应 (a)中间层分别为各向同性、HTI及VTI介质时的零方位角反射系数曲线;(b)中间层为HTI介质时的窄方位反射系数曲线 |
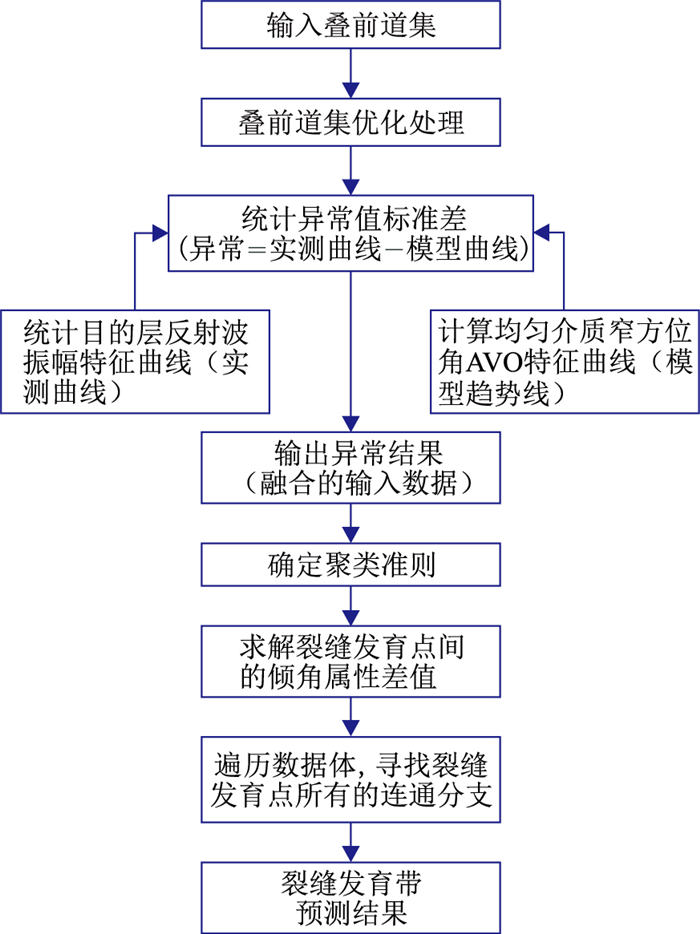
由图 4可见,纵波在不同介质中传播时存在AVO差异,基于标准差统计的窄方位叠前裂缝预测方法即通过提取该差异预测裂缝[9],但首先要对叠前道集优化处理[12-15]。图 5为基于裂缝融合分析的窄方位叠前裂缝预测技术流程。
|
图 5 基于裂缝融合分析的窄方位叠前裂缝预测技术的流程 |
聚类过程遵循“物以类聚”的原则,将本身相互孤立的一批现实或抽象的数据对象聚集成不同的数据样本集合,并描述每一个样本集合。其目的就是将数据集分成多个类簇,使同一个类簇的样本之间保持属性相近,而不同类簇的样本之间保持足够大的属性差异。
本文采用网格聚类分析法。基于网格的方法以独立的空间网格结构单元作为处理对象,整个数据样本空间首先被划分为若干空间网格单元,再对每一个网格单元单独进行聚类处理。聚类分析时,首先需要设定聚类准则判别最终的聚类结果是否符合要求。本文根据期望的破碎带融合效果,认为能够融合的裂缝发育点需同时满足两个条件:①需要融合的裂缝发育点必须彼此距离较小;②同一个裂缝融合带上的点必然具有相近的倾角属性。因此本文以空间距离和倾角属性作为聚类准则[10]。
基于空间网格距离的裂缝发育点聚类,通过裂缝发育点的空间网格距离寻找若干个连通分支,以达到对数据体拆分聚类的目的。但对于相距较近的裂缝发育点还不能直接融合,虽然离散的不同裂缝发育点可能彼此相近,但其所属地层的倾角属性并不一致,此时需要将这些点分类。因此还要判断各个散点的倾角属性,只有相近且倾角属性差别不大的裂缝发育点才能融合。
假定数据体中的所有裂缝发育点构成集合S,则对于每一个裂缝发育种子点p而言:
(1) 基于空间距离的聚类追踪,即寻找满足
| $ \mathit{\boldsymbol{D}}{\rm{(}}\mathit{p}{\rm{) = \{ }}\mathit{v|v} \in \mathit{\boldsymbol{O}}{\rm{(}}\mathit{p}{\rm{)}} \cap \mathit{\boldsymbol{S}}{\rm{\} }} $ | (1) |
的裂缝发育点子集。式中:O(p)为p点的连通邻域[16],一般为6连通邻域或者26连通邻域(图 6);v为连通域中的某点。6连通邻域指一个网格点x的6-邻近点中的任意网格点与x至少有一个公共面;26连通邻域指一个网格点x的26-邻近点中的网格点与x至少有一个公共点。本文选用6连通邻域进行裂缝融合处理。

|
图 6 6连通邻域(左)和26连通邻域(右)示意图 |
(2) 基于倾角属性的聚类追踪,即寻找满足
| $ \mathit{\boldsymbol{A}}(p) = \left\{ {v\mid \Delta \theta (v, p) < {\rm{Di}}{{\rm{p}}_{{\rm{threshold }}}}} \right\} $ | (2) |
的裂缝发育点子集。式中:Δθ(v, p)为点v与p间的倾角属性差值;Dipthreshold为裂缝的倾角属性阈值。
本文的裂缝发育点聚类算法基于种子点p,寻找同时满足式(1)和式(2)的裂缝发育子集
| $ \mathit{\boldsymbol{F}}(p) = \{ v\mid v \in \mathit{\boldsymbol{D}}(p) \cap \mathit{\boldsymbol{A}}(p)\} $ | (3) |
本文提出的窄方位叠前裂缝预测技术流程描述如下。
(1) 数据输入。将基于标准差统计的窄方位叠前裂缝预测方法得到的裂缝数据体作为输入数据;
(2) 确定聚类准则。根据实际工区期望的裂缝融合效果设定连通邻域及Dipthreshold。根据实际工区裂缝性质选择Dipthreshold为裂缝最大倾角与最小倾角之差,即Dipthreshold在裂缝最大倾角与最小倾角之间约束融合效果;
(3) 采用基于协方差矩阵法矢量估计的方法[17]求解裂缝发育点间的倾角属性差值Δθ(v, p)。
1) 基于(根据工区实际地层变化特征及裂缝长度)设定的搜索半径,求解裂缝发育点集合中每个裂缝发育点的若干邻近点x1, x2, …,xn,由这些邻近点得到局部微平面(离散点的局部小区域);
2) 求解局部微平面的质心,即
3) 基于微平面上散点与质心间的距离构建协方差矩阵[18];
4) 求解协方差矩阵最小特征值对应的特征向量,从而求得整个微平面的法向量,并以此作为单个裂缝发育散点的法向量;
5) 计算裂缝发育点间的倾角属性差值
| $ \Delta \theta (v, p) = \arccos \frac{{{\mathit{\boldsymbol{n}}_1} \cdot {\mathit{\boldsymbol{n}}_2}}}{{\left| {{\mathit{\boldsymbol{n}}_1}\parallel {\mathit{\boldsymbol{n}}_2}} \right|}} $ | (4) |
式中n1、n2分别为两个不同散点的法向量。
(4) 从第一个裂缝发育点开始遍历,寻找该种子点所有的连通分支,并计算种子点与连通分支中点之间的倾角属性差值,判断其是否小于事先给定的倾角属性阈值,对于满足条件的点纳入种子点队列中。同样地,将新加入到种子点队列中的点均标记为经处理过的点。如此循环扩充,直至队列中的所有种子点均无法再向外扩充为止。
(5) 一次遍历结束,认为此时种子队列中的裂缝发育点构成了裂缝发育带的点集(被融合)。寻找下一个没有被遍历标记过的种子点,循环操作步骤(4),直至遍历整个数据体,得到融合后的裂缝密度数据体。
(6) 采用RGB模型作为色标计算模型[19],色标颜色从紫色、红色、黄色到蓝色表征裂缝发育强度依次减弱。
3 实例分析N区海上采集的三维叠前窄方位地震资料的叠前道集方位角主要分布于0°~30°,炮检距分布范围为200~6573m。目的层为花港组七段(h7),主要发育高角度裂缝,已钻2口井。
本文利用N区窄方位叠前地震数据进行基于标准差统计的窄方位叠前裂缝预测,获得了叠前裂缝预测剖面(图 7a和图 8a),得到的井上裂缝预测结果与实钻结果一致,且裂缝发育的宏观趋势符合地质规律。但由于采用窄方位或单一方位地震资料(覆盖次数低),预测的裂缝发育带连片性差,不利于表征裂缝发育带的展布特征。为此,在图 7a和图 8a的基础上利用基于网格聚类分析的融合技术对裂缝发育点进行融合,分别得到裂缝发育带融合剖面(图 7b和图 8b),其中彩色区域为裂缝发育区,从紫色、红色、黄色到蓝色裂缝发育强度依次减弱,数据体纵、横向连续性更强。此外,在h7上方N1S井位裂缝不发育,在h7下方裂缝发育;在N12井裂缝发育。上述结果与该区钻井资料揭示的裂缝发育特征一致。

|
图 7 过N1S井的裂缝检测剖面
(a)基于标准差统计的窄方位角叠前裂缝预测剖面;(b)基于图a的裂缝发育带融合剖面 h11为渐新统花港组11段,p3为始新统平湖组3段,下同 |

|
图 8 过N12井的裂缝检测剖面 (a)基于标准差统计的窄方位角叠前裂缝预测剖面;(b)基于图a的裂缝发育带融合剖面 |
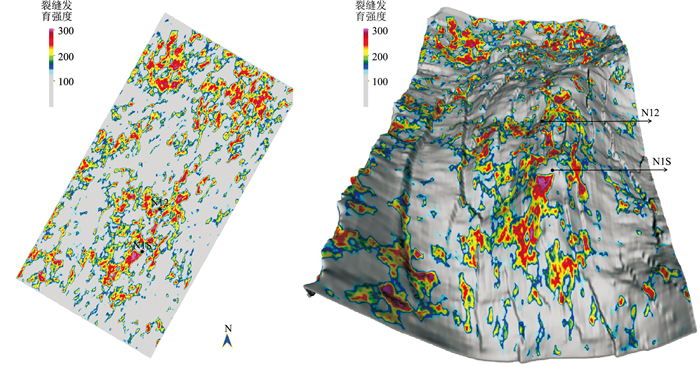
图 9为本文方法裂缝预测平面图及立体图。由图可见:N1S井位于灰色区域,表明裂缝不发育,N12井位于红、黄色区域,表明裂缝发育;从裂缝发育的整体分布来看,本区裂缝大多分布在构造高点和工区北部地层褶皱破碎处,总体沿南北向展布,后期井位可布控在构造高点裂缝带发育处。
|
图 9 本文方法裂缝预测平面图(左)及立体图(右) 时窗范围为h7上、下5ms,提取裂缝发育强度的平均值 |
基于标准差统计的窄方位叠前裂缝预测方法,通过提取各向异性与各向同性介质中的AVO特征差异效应进行叠前裂缝预测,适用于海上采集的窄方位地震资料,但预测的裂缝发育带连续性差。本文引入基于网格聚类分析的裂缝融合分析方法,有效克服了该缺陷,可以准确地表征高角度裂缝发育带的三维空间分布特征,在中国N区的实际应用效果较好。宽方位叠前裂缝预测方法可以更准确地获得地下信息,但对于只有窄方位叠前地震数据的区域,本文方法可作为“宽方位”技术的一个补充,为利用海洋窄方位数据预测裂缝提供一种备选技术。
| [1] |
田立新, 周东红, 明君, 等. 窄方位角地震资料在裂缝储层预测中的应用[J]. 成都理工大学学报(自然科学版), 2010, 37(5): 550-553. TIAN Lixin, ZHOU Donghong, MING Jun, et al. Application of narrow-azimuth seismic data to fractured reservoir prediction[J]. Journal of Chengdu University of Technology (Science & Technology Edition), 2010, 37(5): 550-553. DOI:10.3969/j.issn.1671-9727.2010.05.012 |
| [2] |
简世凯. 窄方位三维叠前地震资料裂缝预测技术研究及应用[D]. 四川成都: 成都理工大学, 2018.
|
| [3] |
姜晓宇, 张研, 甘利灯, 等. 花岗岩潜山裂缝地震预测技术[J]. 石油地球物理勘探, 2020, 55(3): 694-704. JIANG Xiaoyu, ZHANG Yan, GAN Lideng, et al. Seismic techniques for predicting fractures in granite buried hills[J]. Oil Geophysical Prospecting, 2020, 55(3): 694-704. |
| [4] |
王建花, 张金淼, 吴国忱. 宽方位杨氏模量反演和裂缝预测方法及应用——以渤中凹陷H构造潜山勘探为例[J]. 石油地球物理勘探, 2021, 56(3): 593-602. WANG Jianhua, ZHANG Jinmiao, and WU Guochen. Wide-azimuth Young's modulus inversion and fracture prediction: An example of H structure in Bozhong sag[J]. Oil Geophysical Prospecting, 2021, 56(3): 593-602. |
| [5] |
明君, 夏庆龙, 周东红, 等. 锦州南油田潜山裂缝储层地震预测技术研究[J]. 中国石油勘探, 2014, 19(1): 60-64. MING Jun, XIA Qinglong, ZHOU Donghong, et al. Study of seismic prediction technology for buried hill fractured reservoir of Jinzhounan Oilfield[J]. China Petroleum Exploration, 2014, 19(1): 60-64. DOI:10.3969/j.issn.1672-7703.2014.01.008 |
| [6] |
周晓越, 甘利灯, 杨昊, 等. 利用叠前振幅和速度各向异性的联合反演方法[J]. 石油地球物理勘探, 2020, 55(5): 1084-1091. ZHOU Xiaoyue, GAN Lideng, YANG Hao, et al. A joint inversion method using amplitude and velocity anisotropy[J]. Oil Geophysical Prospecting, 2020, 55(5): 1084-1091. |
| [7] |
苏世龙, 胡丹, 黄志, 等. 窄方位角地震数据预测裂缝储层方法[J]. 石油地球物理勘探, 2015, 50(3): 510-515. SU Shilong, HU Dan, HUANG Zhi, et al. Fractured reservoir prediction on narrow azimuthal seismic data[J]. Oil Geophysical Prospecting, 2015, 50(3): 510-515. |
| [8] |
Liu Z L, Zeng Y, Liu J J. The fractured prediction for narrow-azimuth seismic data of carbonate[J]. Applied Mechanics & Materials, 2014. DOI:10.4028/www.scientific.net/AMM.675-677.1336 |
| [9] |
熊晓军, 简世凯, 李翔, 等. 基于标准差统计的窄方位角叠前裂缝预测方法[J]. 石油地球物理勘探, 2017, 52(1): 114-120. XIONG Xiaojun, JIAN Shikai, LI Xiang, et al. Fracture prediction on prestack narrow azimuth data with standard deviation statistics[J]. Oil Geophysical Prospecting, 2017, 52(1): 114-120. |
| [10] |
陈文景. 三维地震数据体中的断层曲面自动提取方法[D]. 四川成都: 电子科技大学, 2014.
|
| [11] |
Rüger A. P-wave reflection coefficients for transversely isotropic models with vertical and horizontal axis of symmetry[J]. Geophysics, 1997, 62(3): 713-722. DOI:10.1190/1.1444181 |
| [12] |
张津海, 张远银, 孙赞东. 道集品质对叠前AVO/AVA同时反演的影响[J]. 石油地球物理勘探, 2012, 47(1): 68-73. ZHANG Jinhai, ZHANG Yuanyin, SUN Zandong. The effects of seismic data conditioning on pre-stack AVO/AVA simultaneous inversion[J]. Oil Geophysical Prospecting, 2012, 47(1): 68-73. |
| [13] |
周鹏, 刘志斌, 张益明, 等. 一种动态的道集拉平方法研究及应用[J]. 断块油气田, 2015, 22(1): 58-61. ZHOU Peng, LIU Zhibin, ZHANG Yiming, et al. Research and application of a dynamic gather flatten method[J]. Fault-Block Oil & Gas Field, 2015, 22(1): 58-61. |
| [14] |
赵洲. 地震叠前属性及流体识别因子研究[D]. 四川成都: 成都理工大学, 2011.
|
| [15] |
熊晓军, 简世凯, 李翔, 等. 叠前道集优化处理技术及其应用[J]. 西南石油大学学报(自然科学版), 2017, 39(6): 55-62. XIONG Xiaojun, JIAN Shikai, LI Xiang, et al. Pre-stack gather optimization technique and application[J]. Journal of Southwest Petroleum University(Na-tural Science Edition), 2017, 39(6): 55-62. |
| [16] |
袁小翠, 刘宝玲, 马永力. 基于空间邻域连通区域标记法的点云离群点检测[J]. 计算机应用研究, 2020, 37(增刊2): 380-382, 385. YUAN Xiaocui, LIU Baoling, MA Yongli. Outlier detection for point cloud based on spatial neighborhood connected region labeling[J]. Application Research of Computers, 2020, 37(S2): 380-382, 385. |
| [17] |
Lange C, Polthier K. Anisotropic smoothing of point sets[J]. Computer Aided Geometric Design, 2005, 22(7): 680-692. |
| [18] |
杜婷婷, 文国秋, 吴林, 等. 基于局部协方差矩阵的谱聚类算法[J]. 计算机工程与应用, 2019, 55(14): 148-154, 176. DU Tingting, WEN Guoqiu, WU Lin, et al. Spectral clustering algorithm based on local covariance matrix[J]. Computer Engineering and Applications, 2019, 55(14): 148-154, 176. |
| [19] |
王永涛, 杨战军, 王学慧, 等. 时频电磁多属性图像融合预测油气技术及应用[J]. 物探与化探, 2020, 44(5): 1221-1225. WANG Yongtao, YANG Zhanjun, WANG Xuehui, et al. TFEM multi-attribute image fusion hydrocarbon prediction technique and its application[J]. Geophysical and Geochemical Exploration, 2020, 44(5): 1221-1225. |



 张鑫, 四川省成都市成华区二仙桥成都理工大学地球勘探与信息技术教育部重点实验室, 610059。Email:
张鑫, 四川省成都市成华区二仙桥成都理工大学地球勘探与信息技术教育部重点实验室, 610059。Email: 