② 中国石化弹性波理论与探测技术重点实验室, 北京 100083;
③ 中国石化石油勘探开发研究院, 北京 102206
② Sinopec Key Laboratory of Seismic Elastic Wave Technology, Beijing 100083, China;
③ Sinopec Petroleum Exploration and Production Research Institute, Beijing 102206, China
高分辨率地震反演技术对于预测薄储层、薄互层油气藏具有至关重要的意义。确定性反演技术发展日趋成熟,其代表性方法包括递推反演、基于模型的反演、稀疏脉冲反演以及有色反演等。虽然确定性反演更忠实于地震资料本身,然而这也决定了反演结果难以突破地震资料的极限分辨率,方法本身受限于地震资料频带。随机地震反演结合随机模拟技术与地震反演理论,可以产生高分辨率反演结果。Joumel等[1]、Hass等[2]首先提出随机地震反演方法。Dubrule[3]利用地震数据约束地质建模。De-beye等[4]、Sams等[5]将模拟退火和蒙特卡洛—马尔科夫链(MCMC)算法引入随机反演,提高了计算效率。Mosegaard等[6]将贝叶斯理念引入地球物理反演问题,修正了MCMC算法系列的Metropolises—Hastings(M-H)算法,提出了更高效的扩展M-H算法,该算法只需评估概率转移前、后两个状态的似然函数值。Hansen等[7]结合序贯模拟和Gibbs采样提出了序贯Gibbs采样,根据地质统计学从复杂先验分布中抽样;实验证明,该方法配合扩展M-H算法可快速收敛于目标分布,提高了随机反演的计算效率。张繁昌等[8]将此随机反演思想用于叠后波阻抗反演,并在扩展M-H算法中引入退火因子,进一步提高了计算效率。张广智等[9]将经典M-H算法用于叠前地震反演,但未考虑子波效应,属于带限反演。王保丽等[10]引入快速傅里叶变换—滑动平均(FFT—MA)谱模拟与逐步变形算法(GDM),形成了一种快速叠后随机反演算法。刘兴业等[11]联合多点地质统计学反演与序贯高斯模拟随机反演岩相与物性参数。赵晨等[12]联合直接序贯协模拟与扩展M-H算法,构建了基于全局迭代反演策略的叠前随机反演,并进一步引入平滑约束和二阶差分横向约束,以提高反演结果的横向连续性。本文在前人的工作[6-8]基础上,提出了一种更适合实际资料的高分辨率叠后随机反演算法。该算法以序贯Gibbs扰动模拟、扩展M-H算法为核心,进一步引入层序地层网格,自适应融入地质统计学、构造以及沉积模式等信息,整个反演过程无需计算地层的局部倾角或进行复杂的坐标转换。针对随机地震反演结果的高频成分仍具有较大的不确定性,造成不同实现展示的储层特征差异较大,本文结合序贯Gibbs扰动模拟与同位协同克里金,通过引入确定性反演结果的协同约束,进一步限定随机反演候选解空间,从而降低随机地震反演高频成分的不确定性。本文首先结合地质统计学、贝叶斯原理以及反演理论严谨、详实地推导了算法;随后在实际资料试算中,通过对比确定性反演结果以及随机地震反演的四个不同实现,验证了算法的有效性。
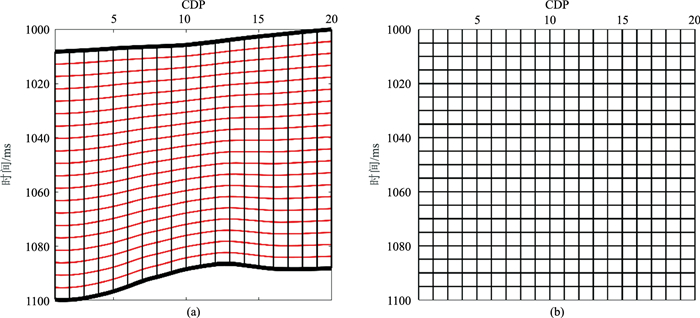
1 层序地层网格传统反演技术通常采用均匀地震网格计算(图 1b),网格的横向间距为CDP间距,垂向间距为地震采样率。本文的随机反演基于层序地层网格(图 1a),网格的横向间距为CDP间距,但是垂向间距并不等于地震采样率。
|
图 1 层序地层网格(平行顶、底沉积模式)(a)与均匀地震网格(b)示意图 图a中的粗黑线为构造解释层位,红线为层序地层,黑色竖线为CDP间隔线 |
基于构造解释层位和沉积模式建立层序地层网格,通过结合不同的沉积模式(平行顶、底或平行于顶及平行于底等)在层段中建立层序地层,每个层序地层与CDP间隔线相交便剖分出层序地层网格(图 1a)。利用层序地层网格进行随机反演,自适应融入了地层构造和沉积模式信息,因此只需沿着网格的水平方向利用水平变差约束随机反演结果的横向连续性;若采用均匀地震网格,则需要进一步计算地层的局部倾角或进行复杂的坐标变换,从而增加反演算法的难度以及降低计算效率。
2 先验分布模型参数的先验分布作为贝叶斯反演框架的重要组成部分,具有限定反演解空间以及减少反演过程的不确定性和多解性等作用。在确定性反演中,先验分布转化为反演目标函数的约束项,可有效改善反演的病态性和不适定性,根据先验分布是否服从“长尾分布”,决定反演结果是“块化”还是“光滑”[13];在随机地震反演中,先验分布还可有效限定解的搜索空间,如果利用先验分布产生候选解,则能有效加速反演的收敛过程[7]。
通过在先验分布中引入空间约束改善单道随机反演的横向不连续性问题。假设工区内待反演的地震道数为K,K道波阻抗的联合概率服从多变量高斯分布,记为
| $ p(\boldsymbol{m}) \propto \exp \left[-\frac{1}{2}\left(\boldsymbol{m}-\boldsymbol{\mu_{m}}\right)^{\mathrm{T}} \boldsymbol{C_{m}}^{-1}\left(\boldsymbol{m}-\boldsymbol{\mu_{m}}\right)\right] $ | (1) |
式中:m=[1m 2m…Km为由K道波阻抗组成的列向量,每道波阻抗jm=jm1jm2…jmN(j=1,2,…,K为道号)包含N个元素(N表示层序地层网格采样点数),因此m的维数为K×N;μm为期望,通过分层段统计工区内的测井数据或者建立反演低频模型得到;Cm为协方差矩阵,为K×N行、K×N列的对称矩阵,直接影响反演结果的垂向分辨率和横向连续性。
Cm的对角线元素表示波阻抗的方差,决定了反演结果的动态范围,通过分层段统计测井数据获取;Cm的非对角线元素表示同一道、不同采样点,不同道、相同采样点以及不同道、不同采样点之间的协方差。其中同一道、不同采样点之间的协方差与垂向变差有关,通过分层段统计测井数据获取,决定了反演结果的垂向分辨率;不同道、相同采样点之间的协方差与水平变差有关,通过统计地震数据沿层切片获取,决定了反演结果的横向连续性;根据变差函数的几何各向异性,计算水平变差和垂向变差得到不同道、不同采样点之间的协方差[14]。
3 似然函数在贝叶斯反演理论中,利用似然函数表征合成地震数据与实测地震数据之间的相似性,进而建立反演参数与地震数据之间的联系。
经过前期去除相干噪声(异常噪声、线性干扰、面波以及多次波等)处理,残留噪声仅剩随机噪声,因此利用高斯分布描述叠后地震反演的似然函数。由于不同采样点、不同道之间的随机噪声独立不相干,因此似然函数l(d|m)为
| $ \begin{aligned} &l(\boldsymbol{d} \mid \boldsymbol{m}) \propto \\ &\qquad \prod\limits_{j=1}^{K} \exp \left\{-\frac{\left[\boldsymbol{G}\left({ }^{j} \boldsymbol{m}\right)-{ }^{j} \boldsymbol{d}\right]^{\mathrm{T}}\left[\boldsymbol{G}\left({ }^{j} \boldsymbol{m}\right)-{ }^{j} \boldsymbol{d}\right]}{2 \sigma_{\mathrm{n}}^{2}}\right\} \end{aligned} $ | (2) |
式中:G(jm)表示叠后地震正演过程,即将jm转化为第j道合成地震记录js;jd为第j道地震数据;
由于反演波阻抗基于层序地层网格采样,地震数据基于均匀网格采样,因此须在G(jm)中引入重采样矩阵R(附录A),将波阻抗在均匀网格重采样,并结合近似公式计算反射系数r
| $ \boldsymbol{r} \approx \partial \ln (\boldsymbol{m}) / 2 $ | (3) |
最后将反射系数与子波褶积,便得到js,则
| $ \boldsymbol{G}\left({ }^{j} \boldsymbol{m}\right)=\frac{1}{2} \boldsymbol{W D}\left[\ln \left(\boldsymbol{R}^{j} \boldsymbol{m}\right)\right] $ | (4) |
式中:W为子波褶积矩阵;D为一阶差分矩阵;ln(·)表示对向量中每一个元素取自然对数;Rj为第j道重采样矩阵。可见,虽然反演波阻抗基于层序地层网格采样,但仍在地震网格进行褶积正演。
式(2)为无测井数据约束的似然函数,当有Kw口井的测井数据参与约束时,则似然函数为
| $ \begin{aligned} l(\boldsymbol{d}, & \left.\boldsymbol{m}_{\mathrm{w}} \mid \boldsymbol{m}\right) \propto \\ & \prod\limits_{j=1}^{K-K_{\mathrm{w}}} \exp \left\{-\frac{\left[\boldsymbol{G}\left({ }^{j} \boldsymbol{m}\right)-{ }^{j} \boldsymbol{d}\right]^{\mathrm{T}}\left[\boldsymbol{G}\left({ }^{j} \boldsymbol{m}\right)-{ }^{j} \boldsymbol{d}\right]}{2 \sigma_{\mathrm{n}}^{2}}\right\}\cdot \\ & \prod\limits_{j=1}^{K_{\mathrm{w}}} \exp \left[-\frac{\left({ }^{j} \boldsymbol{m}-{ }^{j} \boldsymbol{m}_{\mathrm{w}}\right)^{\mathrm{T}}\left({ }^{j} \boldsymbol{m}-{ }^{j} \boldsymbol{m}_{\mathrm{w}}\right)}{2 \sigma_{\mathrm{nw}}^{2}}\right] \end{aligned} $ | (5) |
式中:jmw为第j口井的波阻抗(须在层序地层网格重采样);σnw2为井旁道反演结果与实测波阻抗误差的方差,即
| $ \sigma_{\mathrm{nw}}^{2}=u_{\mathrm{w}} \cdot \sigma_\boldsymbol{m}^{2} $ | (6) |
式中:σm2为反演波阻抗的方差,由分层段统计测井数据获取;uw表示测井约束的不确定性,该值越小,则σnw2越小,表示测井数据对井旁道反演结果的约束越强,反之亦然。
4 后验分布的降维分解根据贝叶斯定理,整合反演参数的先验分布p(m)与似然函数l(d, mw|m),可以得到反演参数的后验分布
| $ p\left(\boldsymbol{m} \mid \boldsymbol{d}, \boldsymbol{m}_{\mathrm{w}}\right) \propto p(\boldsymbol{m}) \cdot l\left(\boldsymbol{d}, \boldsymbol{m}_{\mathrm{w}} \mid \boldsymbol{m}\right) $ | (7) |
将式(1)与式(5)代入式(7),得
| $ \begin{aligned} &p\left(\boldsymbol{m} \mid \boldsymbol{d}, \boldsymbol{m}_{\mathrm{w}}\right) \propto \exp \left[-\frac{1}{2}\left(\boldsymbol{m}-\boldsymbol{\mu_{m}}\right)^{\mathrm{T}} \boldsymbol{C_{m}}^{-1}\left(\boldsymbol{m}-\boldsymbol{\mu_{m}}\right)\right] \cdot \\ &\ \ \ \ \ \ \ \ \ \ \prod\limits_{j=1}^{K-K_{\mathrm{w}}} \exp \left\{-\frac{\left[\boldsymbol{G}\left({ }^{j} \boldsymbol{m}\right)-{ }^{j} \boldsymbol{d}\right]^{\mathrm{T}}\left[\boldsymbol{G}\left({ }^{j} \boldsymbol{m}\right)-{ }^{j} \boldsymbol{d}\right]}{2 \sigma_{n}^{2}}\right\} \\ &\ \ \ \ \ \ \ \ \ \ \prod\limits_{j=1}^{K_{\mathrm{w}}} \exp \left[-\frac{\left({ }^{j} \boldsymbol{m}-{ }^{j} \boldsymbol{m}_{\mathrm{w}}\right)^{\mathrm{T}}\left({ }^{j} \boldsymbol{m}-{ }^{j} \boldsymbol{m}_{\mathrm{w}}\right)}{2 \sigma_{\mathrm{nw}}^{2}}\right] \end{aligned} $ | (8) |
实际上,确定性反演结果等价于反演参数的最大后验概率解;随机反演结果则可以看作是对后验概率分布的一次随机抽样[15]。式(8)表明,后验分布是复杂的高维分布,无法采用直接抽样的方式从后验分布中获取一次随机反演实现。本文结合序贯模拟的思想,将后验分布降维分解
| $ \begin{aligned} p(\boldsymbol{m} \mid \boldsymbol{O})=& p\left({ }^{1} \boldsymbol{m} \mid \boldsymbol{O}\right) p\left({ }^{2} \boldsymbol{m} \mid{ }^{1} \boldsymbol{m}, \boldsymbol{O}\right) \cdots \\ & p\left({ }^{K} \boldsymbol{m} \mid{ }^{1} \boldsymbol{m},{ }^{2} \boldsymbol{m}, \cdots,{ }^{K-1} \boldsymbol{m}, \boldsymbol{O}\right) \end{aligned} $ | (9) |
式中O为观测数据的集合,包含地震数据和参与约束的测井数据,即O=d∪mw。因此jO代表第j道观测数据,如果第j道是井旁道,则jO=jd∪jmw,反之jO=jd。进一步,假设第j道的反演参数仅与第j道观测数据相关,而与第i道(i≠j)观测数据独立不相关,则式(9)简化为
| $ \begin{aligned} p(\boldsymbol{m} \mid \boldsymbol{O})=& p\left({ }^{1} \boldsymbol{m} \mid{ }^{1} \boldsymbol{O}\right) p\left({ }^{2} \boldsymbol{m} \mid{ }^{1} \boldsymbol{m},{ }^{2} \boldsymbol{O}\right) \cdots \\ & p\left({ }^{K} \boldsymbol{m} \mid{ }^{1} \boldsymbol{m},{ }^{2} \boldsymbol{m}, \cdots,{ }^{K-1} \boldsymbol{m},{ }^{K} \boldsymbol{O}\right) \end{aligned} $ | (10) |
由式(10)可见,对后验分布p(m|O)的抽样,可以借助序贯模拟的思想实现,即先对p(1m|1O)抽样,再将抽样结果1m作为条件数据,参与对p(2m|1m, 2O)的抽样,得到2m的抽样结果,以此类推,直到完成最后一道Km的抽样[17-21]。
利用序贯模拟的思想,将复杂的高维(维度为K×N)后验分布p(m|O)化简为K个低维(维度为N)后验分布p(jm|1m, 2m, …, j-1m, jO的乘积。然而p(jm|1m, 2m, …, j-1m, jO)仍然不便于直接抽样。为此,进一步结合贝叶斯定理,将p(jm|1m, 2m, …, j-1m, jO转化为
| $ \begin{aligned} &p\left({ }^{j} \boldsymbol{m} \mid{ }^{1} \boldsymbol{m},{ }^{2} \boldsymbol{m}, \cdots,{ }^{j-1} \boldsymbol{m},^{j} \boldsymbol{O}\right)=\\ &\ \ \ \ \ \ \ \ \ \ \frac{p\left({ }^{j} \boldsymbol{m} \mid{ }^{1} \boldsymbol{m},{ }^{2} \boldsymbol{m}, \cdots,^{j-1} \boldsymbol{m}\right) \cdot l\left({ }^{j} \boldsymbol{O} \mid{ }^{j} \boldsymbol{m}\right)}{p\left({ }^{j} \boldsymbol{O}\right)} \end{aligned} $ | (11) |
由于jO为已知,因此p(jO)为一个不影响后验概率分布形状的常数,则
| $ \begin{aligned} & p\left({ }^{j} \boldsymbol{m} \mid{ }^{1} \boldsymbol{m},{ }^{2} \boldsymbol{m}, \cdots,{ }^{j-1} \boldsymbol{m},^{j} \boldsymbol{O}\right) \propto \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ p\left({ }^{j} \boldsymbol{m} \mid{ }^{1} \boldsymbol{m},{ }^{2} \boldsymbol{m}, \cdots,{ }^{j-1} \boldsymbol{m}\right) \cdot l\left({ }^{j} \boldsymbol{O} \mid{ }^{j} \boldsymbol{m}\right) \end{aligned} $ | (12) |
式中l(jO|jm)为第j道的似然函数。结合式(2)和式(5)可知,当该道为非井旁道时
| $ \begin{aligned} &l\left({ }^{j} \boldsymbol{O} \mid{ }^{j} \boldsymbol{m}\right) \propto \\ &\qquad \exp \left\{-\frac{\left[\boldsymbol{G}\left({ }^{j} \boldsymbol{m}\right)-{ }^{j} \boldsymbol{d}\right]^{\mathrm{T}}\left[\boldsymbol{G}\left({ }^{j} \boldsymbol{m}\right)-{ }^{j} \boldsymbol{d}\right]}{2 \sigma_{\mathrm{n}}^{2}}\right\} \end{aligned} $ | (13) |
当该道为井旁道时
| $ \begin{aligned} l\left({ }^{j} \boldsymbol{O} \mid{ }^{j} \boldsymbol{m}\right) \propto & \exp \left\{-\frac{\left[\boldsymbol{G}\left({ }^{j} \boldsymbol{m}\right)-{ }^{j} \boldsymbol{d}\right]^{\mathrm{T}}\left[\boldsymbol{G}\left({ }^{j} \boldsymbol{m}\right)-{ }^{j} \boldsymbol{d}\right]}{2 \sigma_{\mathrm{n}}^{2}}-\right.\\ &\left.\frac{\left({ }^{j} \boldsymbol{m}-{ }^{j} \boldsymbol{m}_{\mathrm{w}}\right)^{\mathrm{T}}\left({ }^{j} \boldsymbol{m}-{ }^{j} \boldsymbol{m}_{\mathrm{w}}\right)}{2 \sigma_{\mathrm{nw}}^{2}}\right\} \end{aligned} $ | (14) |
针对式(12)的抽样,利用序贯Gibbs扰动模拟从先验分布p(jm|1m, 2m, …, j-1m)产生候选解,并配合扩展M-H算法进行概率转移,通过多次迭代,便可收敛于后验分布p(jm|1m, 2m,…,j-1m, jO)。
5 序贯Gibbs同位协同扰动模拟与扩展M-H概率转移序贯Gibbs扰动模拟结合序贯模拟的思想与Gibbs采样,从复杂先验分布中抽样。该算法配合扩展M-H算法形成一种改进的MCMC算法,进而可以从复杂的后验分布中抽样。Hansen等[7]指出,序贯Gibbs扰动模拟可以从更逼近真实情况的复杂先验分布中抽样,因此反演结果也更逼近真实解,并且可较大幅度地提高随机反演效率。
扩展M-H算法由经典M-H算法发展而来,属于MCMC算法的一个分支。MCMC算法利用建议分布产生候选解,并以一定概率接受候选解,经过多次迭代,便可以收敛于目标分布[6]。当建议分布为后验分布对应的全条件概率分布时,MCMC算法转化为Gibbs采样;当建议分布为均匀分布时,MCMC算法转化为经典M-H算法;当建议分布为先验分布对应的条件概率分布时,MCMC算法转化为扩展M-H算法。
相对于经典M-H算法,扩展M-H算法的候选解来自先验分布而非广泛的均匀分布,因此有效地限定了解空间的搜索范围,其反演结果也可以更快速地收敛于真实解[6]。另外,与经典M-H算法相比,扩展M-H算法在计算转移概率时,无需评估转移前、后两个状态的后验概率值,只需评估似然函数值,由于省略了评估先验分布概率值,因此提高了计算效率。
实际上,随机反演的高频成分(60Hz~Nyquist频率)仅受变差函数和测井数据约束,并不受地震数据约束。当工区内参与约束的测井数据较少时,反演结果的高频成分仍然有较大的不确定性,从而造成随机反演的不同实现展现的储层特征差异较大,因此对后续的储层精细预测带来一定困扰。为此,本文结合同位协同克里金修改式(12),提出确定性反演协同约束的随机反演算法,利用确定性反演结果约束随机反演的高频成分。通过在先验分布中引入确定性反演结果作为条件数据,则式(12)修正为
| $ \begin{aligned} p\left({ }^{j} \boldsymbol{m}\right.&|\left.{ }^{1} \boldsymbol{m},{ }^{2} \boldsymbol{m}, \cdots,{ }^{j-1} \boldsymbol{m},{ }^{j} \boldsymbol{O},{ }^{j} \boldsymbol{\xi}\right) \propto \\ & p\left({ }^{j} \boldsymbol{m} \mid{ }^{1} \boldsymbol{m},{ }^{2} \boldsymbol{m}, \cdots,^{j-1} \boldsymbol{m},{ }^{j} \boldsymbol{\xi}\right) \cdot l\left({ }^{j} \boldsymbol{O} \mid{ }^{j} \boldsymbol{m}\right) \end{aligned} $ | (15) |
式中:jξ为第j道波阻抗确定性反演结果;p(jm|1m, 2m, …, j-1m, jO, jξ)为修正后验分布;p(jm|1m, 2m, …, j-1m, jξ)为修正先验分布。
式(15)表明,当前道的波阻抗随机反演结果不仅与其他道的随机反演结果相关,还与当前道的确定性反演结果相关。
由于从先验分布p(jm|1m, 2m, …, j-1m, jξ)抽样产生候选解,需要结合序贯Gibbs扰动模拟和同位协同简单克里金(序贯Gibbs同位协同扰动模拟)。以后验分布p(jm|1m, 2m, …, j-1m, jO, jξ)为目标分布,结合序贯Gibbs同位协同扰动模拟与扩展M-H算法构建的MCMC算法流程如下。
(1) 以第j道的反演参数期望jμm作为扰动模拟的初始模型;并预设信噪比χ、测井数据约束不确定性uw以及最大迭代次数M;
(2) 从第j道N个采样点中随机选择一点i(i=1, 2, …, N);
(3) 利用同位协同简单克里金计算第i个采样点的条件均值和条件方差(附录B),进而构建第i个采样点的局部条件概率密度函数p(jmi|jm-i, 1mi, 2mi, …,j-1mi, jξi)
式中:jξi为第j道的第i个采样点的波阻抗确定性反演结果;jmi为第j道的第i个采样点的波阻抗,其他以此类推;jm-i为第j道的第i个采样点以外的波阻抗。
(4) 从p(jmi|jm-i, 1mi, 2mi, …,j-1mi, jξi)抽样,产生随机数jmiΔ,并保持其他采样点的波阻抗值不变,构建候选解jmΔ。
(5) 计算接受概率
| $ \alpha=\min \left[1, \frac{l\left({ }^{j} \boldsymbol{O} \mid{ }^{j} \boldsymbol{m}^{\varDelta}\right)}{l\left({ }^{j} \boldsymbol{O} \mid{ }^{j} \boldsymbol{m}\right)}\right] $ |
(6) 从均匀分布U(0, 1)产生一个随机数Б,如果Б≤α,则jm=jmΔ,反之则维持jm不变。
(7) 重复步骤(2)~步骤(6),完成第j道所有采样点的抽样,即完成一次迭代;计算当前迭代次数的信噪比χ*以及测井数据约束的不确定性uw*。
(8) 重复步骤(2)~步骤(7),当χ*≥χ、uw*≥uw或迭代次数达到M,则退出迭代。
为了降低克里金方程组的维度以提高计算效率,针对jmi的条件数据,只选取其他道的第i个采样点的波阻抗1mi, 2mi, …, j-1mi,而忽略其他道的第i个采样点以外的波阻抗。引入这种近似合乎地质认识,因为jm基于层序地层网格采样,同一采样点处于同一层序地层。由于不同道、同一层序地层之间的波阻抗的相关性较强,而不同道、不同层序地层之间的波阻抗相关性较弱,因此可以忽略。在实际地震数据反演时,还可以结合垂向变程和水平变程,进一步缩减jmi条件数据的有效个数。
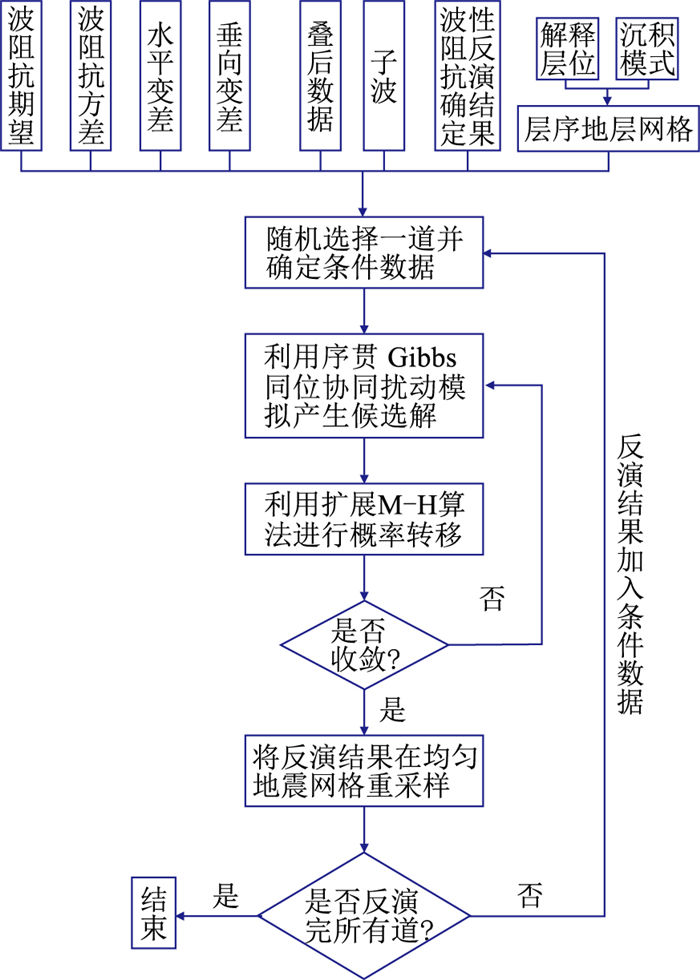
以上为某一道的算法流程。对于整个三维工区而言,须结合序贯模拟和改进的MCMC算法(图 2):
|
图 2 反演流程 |
(1) 从三维工区中随机选择一道j,结合水平变程,将当前道邻域内已反演道以及当前道的确定性反演结果作为条件数据;
(2) 利用序贯Gibbs同位协同扰动模拟与扩展M-H算法对目标分布p(jm|1m, 2m, …, j-1m, jO, jξ)抽样,获取当前道的随机反演结果jm;
(3) 将jm在地震网格重采样;
(4) 重复步骤(1)~(3),直到完成三维工区所有道的反演。
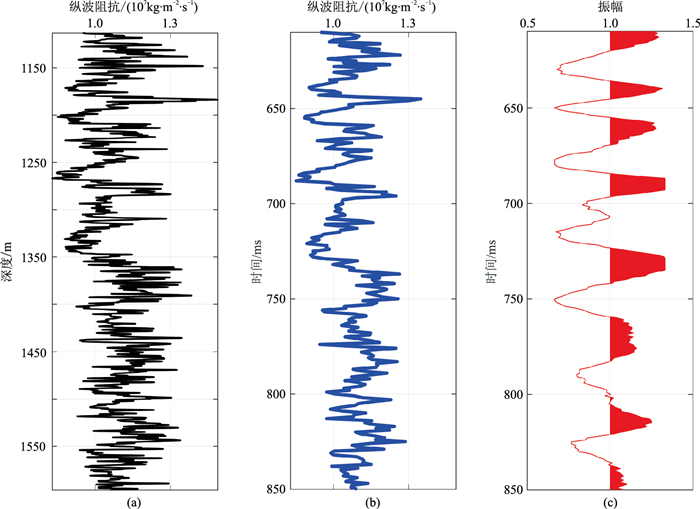
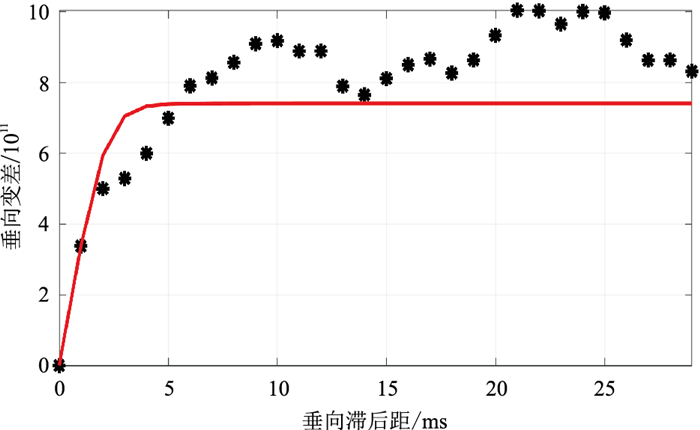
6 模型试算利用模型数据(图 3)验证所提随机反演算法的效果。由于该模型数据为一维数据,因此不用考虑横向变差,只需考虑波阻抗的期望、方差以及垂向变差。通过对时间域波阻抗曲线进行10Hz低通滤波获取波阻抗的期望,在此基础上计算波阻抗的方差。图 4为垂向实验变差与垂向拟合变差,其中变差函数模型由0.48倍的指数模型与0.52倍的高斯模型混合而成,两个模型的垂向变程均为3ms。
|
图 3 模型数据
(a)波阻抗深度域曲线;(b)波阻抗时间域曲线;(c)信噪比为10的合成记录 为了更逼近真实情况,图a选自一段实际测井曲线,经过Backus滤波(500Hz)再线性插值,得到图b(采样间隔为1ms);在此基础上计算法向反射系数,并与主频为30Hz的雷克子波褶积,并加入高斯随机噪声得到图c |
|
图 4 垂向实验变差(黑点)与垂向拟合变差(红线) |
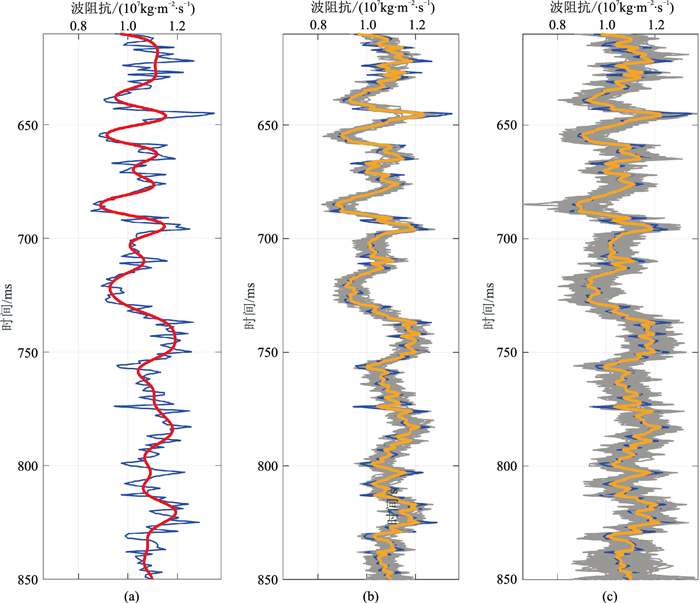
图 5为反演结果。由图可见:①确定性反演结果与实测曲线整体吻合度较高,但是垂向分辨率较低,仅为实测曲线的一种近似平滑(图 5a);②随机反演的高频细节与实测数据并不完全吻合(图 5b、图 5c);③基于确定性反演协同约束的随机反演(图 5b)的“灰色条带”宽度明显小于常规随机反演(图 5c),说明前者通过引入确定性反演协同约束,有效降低了随机反演高频成分的不确定性。造成以上现象的原因为:由于合成记录中含有随机噪声,且反演中无测井数据约束,合成记录的带限特性决定地震数据无法约束随机反演的高频成分(高频成分仅仅来自随机模拟的数学实现),因此高频成分具有不确定性。
|
图 5 反演结果
(a)确定性反演;(b)基于确定性反演协同约束的随机反演;(c)常规随机反演 蓝线代表实测曲线;红线代表确定性反演结果;100次随机反演实现的叠合形成的“灰色条带”宽度指示随机反演高频成分的不确定性,条带越宽表示不确定性越大,反之亦然;橘黄线代表100次实现的均值 |
为了进一步量化随机反演的不确定性,提出不确定性指示公式
| $ D=\frac{1}{N_{\mathrm{r}}} \sum\limits_{i=1}^{N_{\mathrm{r}}}\left\|_{i} \boldsymbol{m}-\boldsymbol{m}_{\mathrm{post}}\right\|_{2} $ | (16) |
式中:D表征随机反演的不确定性;Nr为随机反演次数;im为第i个波阻抗反演实现;mpost为波阻抗的后验期望,当实现次数足够多时,mpost近似等于多个实现的均值,即
式(16)的计算结果表明,确定性反演协同约束的随机反演的高频成分不确定性仅为244364.55,远小于常规随机反演的434247.63。
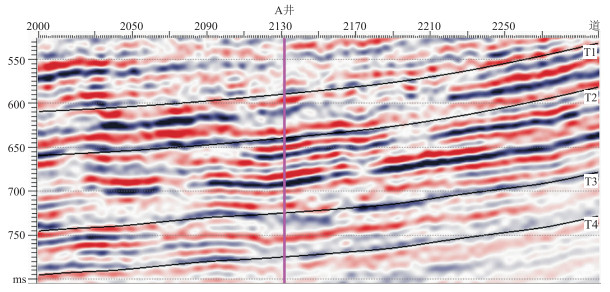
7 实际资料试算实际资料取自中国陆上M区块的过A井的地震剖面,目的层岩性主要为碎屑岩,反演时窗从层位T1到T4,共3个层段(图 6)。首先根据解释的4个层位构建层序地层网格,由于区内沉积相对平稳,地层厚度变化不大,因此3个层段的沉积模式均为平行顶、底。
|
图 6 过A井的地震剖面 |
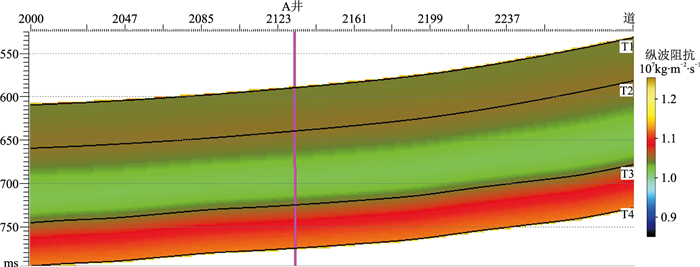
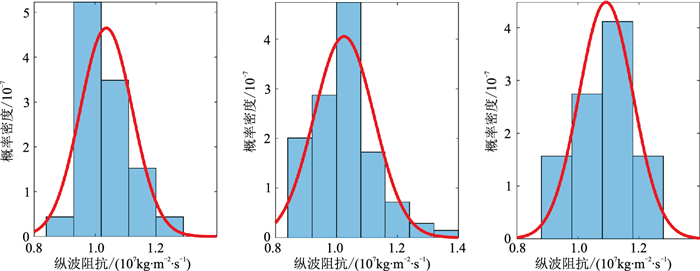
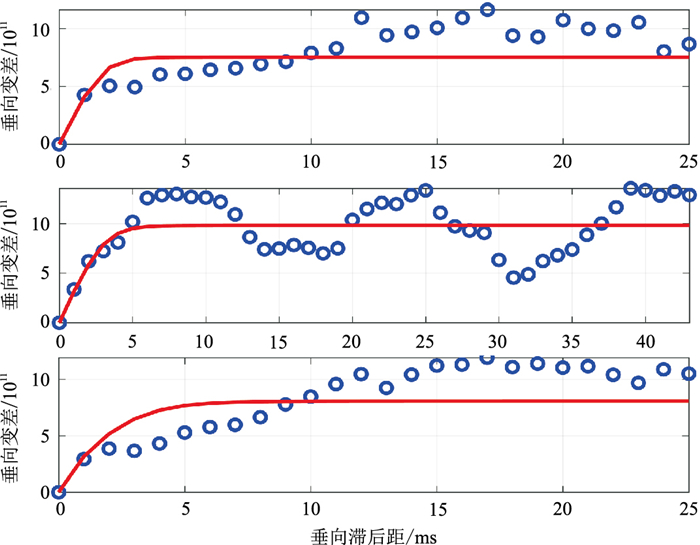
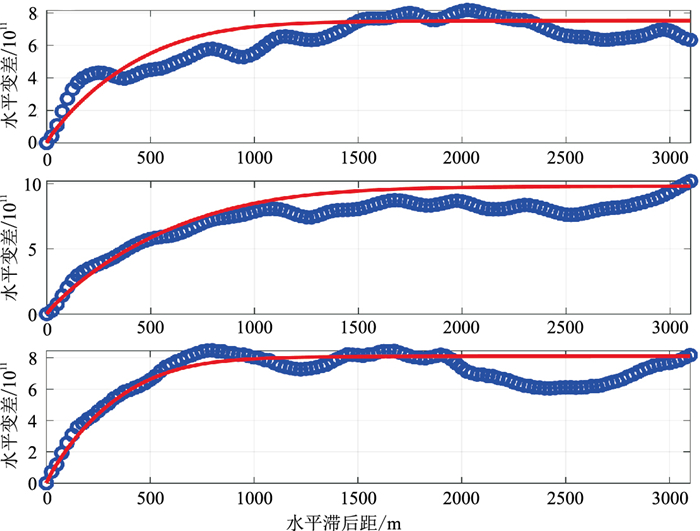
A井数据未参与约束,仅用于估算波阻抗的期望、方差和垂向变差。建立波阻抗期望的方法与建立确定性反演低频模型的方法一致,即对A井的波阻抗曲线沿层位横向插值并由0~10Hz的低通滤波获取(图 7)。根据拟合的高斯分布(图 8)求得T1-T2、T2-T3、T3-T4层段的波阻抗标准差,分别为867225、990082、898831kg·m-2·s-1。利用A井数据统计了T1-T2、T2-T3以及T3-T4层段的波阻抗垂向实验变差(图 9),变差函数模型由0.8倍的指数型变差函数与0.2倍的高斯型变差函数混合而成,得到T1-T2、T2-T3、T3-T4层段的垂向变程,分别为2.5、4.5、5.0ms。通过统计波阻抗确定性反演结果的层段计算均方根属性,得到水平实验变差(图 10),变差函数模型与垂向变差一致,得到T1-T2、T2-T3、T3-T4层段的水平变程,分别为1000、1400、800m。
|
图 7 确定性反演的低频模型 |
|
图 8 T1-T2(左)、T2-T3(中)、T3-T4(右)层段的波阻抗统计直方图及拟合的高斯分布(红线) |
|
图 9 T1-T2(上)、T2-T3(中)以及T3-T4(下)层段的波阻抗垂向实验变差(蓝圈)及垂向拟合变差(红线) |
|
图 10 T1-T2(上)、T2-T3(中)以及T3-T4(下)层段的波阻抗水平实验变差(蓝圈)及水平拟合变差(红线) |
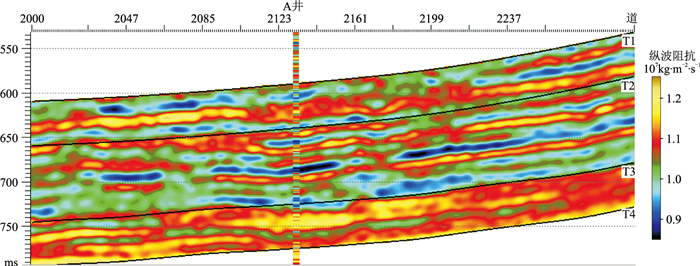
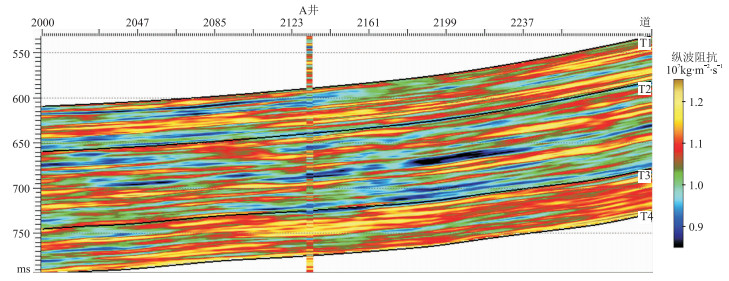
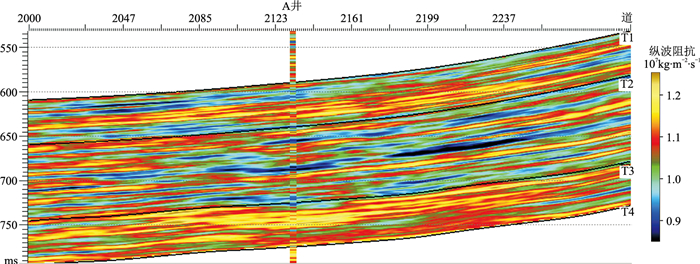
图 11为波阻抗确定性反演剖面,可见确定性反演结果更忠实于地震数据本身,其垂向分辨率与地震数据基本一致。图 12和图 13分别为随机地震反演的实现A和实现B。由图可见:①与确定性反演结果(图 11)相比,随机地震反演的垂向分辨率更高,在水平变差以及层序地层网格的双重约束下,横向连续且自然,井旁道反演结果与实测曲线吻合度较高(图 12、图 13)。但是由于随机地震反演结果的高频成分来自随机模拟和变差函数,当参与约束的测井数据较少时,其高频成分的不确定性较大。②虽然两次实现地震数据参与约束的程度一致,但是两者的储层整体特征差异较大(图 12、图 13),并且与图 11的整体特征也有较大差异。
|
图 11 波阻抗确定性反演剖面 |
|
图 12 波阻抗随机反演实现A 确定性反演结果未参与协同约束,预设地震信噪比为10,图 13同 |
|
图 13 波阻抗随机反演实现B |
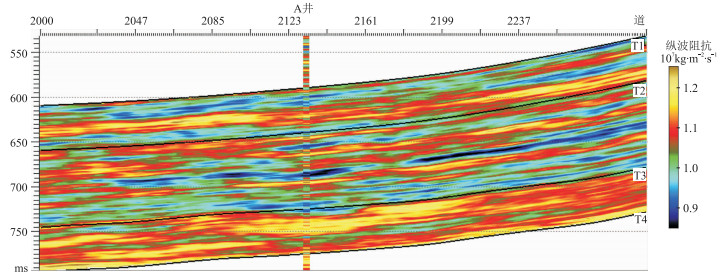
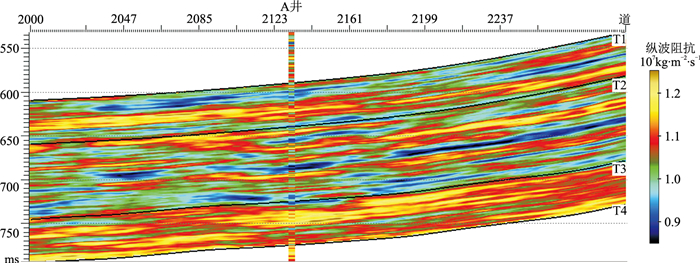
图 14和图 15分别为确定性反演协同约束的随机地震反演的实现C和实现D。由图可见:与图 12、图 13之间的差异相比,图 14和图 15的差异相对减小;图 14、图 15的整体特征更接近图 11,但前两者的垂向分辨率更高。这是由于序贯Gibbs同位协同扰动模拟是借助同位协同简单克里金而非简单克里金确定随机反演的先验解空间。相比常规随机反演,确定性反演协同约束的随机地震反演的某个采样点的波阻抗随机反演结果不仅与邻近采样点的波阻抗值相关,还与当前采样点的波阻抗确定性反演结果相关,在一定程度上增强了波阻抗随机反演结果与确定性反演结果之间的相关性,从而降低随机反演结果高频成分的不确定性。
|
图 14 确定性反演协同约束的随机地震反演实现C |
|
图 15 确定性反演协同约束的随机地震反演实现D |
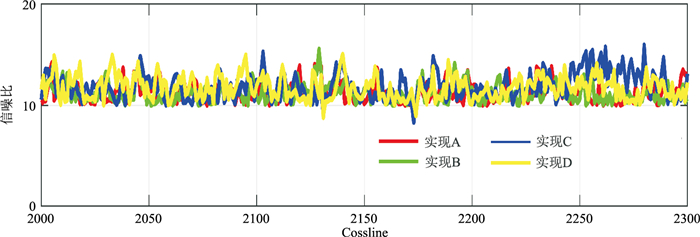
图 16为随机反演四个不同实现的信噪比,可见信噪比值约为10,说明地震数据对反演结果的约束程度基本相同,但这四个实现展现的储层细节存在一定差异,从而验证了地震反演具有多解性。
|
图 16 随机反演四个不同实现的信噪比 |
(1) 相比确定性反演,随机地震反演可以产生高分辨率的反演结果,其中垂向变差影响随机反演的垂向分辨率,横向变差影响随机反演的横向连续性。
(2) 与均匀地震网格相比,由于层序地层网格融入了构造和沉积模式等信息,因此更适合变差函数横向约束随机反演;借助重采样矩阵,在层序地层网格进行抽样模拟,在均匀地震网格进行褶积正演,整个反演过程既满足构造和沉积模式的约束,同时又符合地球物理原理。
(3) 常规随机反演的高频成分来自随机模拟、变差函数以及约束井数据等。当工区内参与约束的测井数据较少时,常规随机反演高频成分的不确定性较大。通过引入确定性反演的协同约束,可进一步限定候选解的解空间,增强波阻抗随机反演结果与确定性反演结果的相关性,进而降低随机反演高频成分不确定性。实际数据试算表明,通过对比随机反演的四个不同实现,验证了所提算法的有效性。
附录A 重采样矩阵重采样矩阵R借助矩阵相乘实现线性插值。假设jm代表第j道基于层序地层网格采样的波阻抗向量,sjm代表第j道基于地震网格采样的波阻抗向量,因此
| $ { }_{\mathrm{s}}^{j} \boldsymbol{m}=\boldsymbol{R} \cdot{ }^{j} \boldsymbol{m} $ | (A-1) |
假设待插值的节点为sjmk(k=1, 2, …, Ns),即第j道基于地震网格采样的第k个采样点的波阻抗(共Ns个采样点),对应的时间为sjTk;与sjmk相邻的两个已知节点为jmi和jmi+1(i=1, 2, …, N),即第j道基于层序地层网格采样的第i个和第i+1个采样点的波阻抗(共N个采样点),对应的时间分别为jTi和jTi+1。根据线性插值的定义,可得
| $ { }_{\mathrm{s}}^{j} m_{k}=\frac{{ }_{\mathrm{s}}^{j} T_{k}-{ }^{j} T_{i+1}}{{ }^{j}T_{i+1}-{ }^{j} T_{i}}{ }^{j} m_{i}+\frac{{ }_{\mathrm{s}}^{j} T_{k}-{ }^{j} T_{i}} {{ }^{j}T_{i+1}-{ }^{j} T_{i}}{ }^{j} m_{i+1} $ | (A-2) |
因此,重采样矩阵为Ns行、N列的稀疏矩阵
| $ \boldsymbol{R}=\left[\begin{array}{cccc} \ddots & \ddots & & 0 \\ & \frac{{ }^{j}_{\rm{s}} T_{k}-{ }^{j} T_{i+1}}{{ }^{j} T_{i+1}-{ }^{j} T_{i}} &\frac{{ }^{j}_{\rm{s}} T_{k}-{ }^{j} T_{i}}{{ }^{j} T_{i+1}-{ }^{j} T_{i}}& \\ {0} & &{\ddots} &{\ddots} \end{array}\right] $ | (A-3) |
同位协同简单克里金是同位协同克里金与简单克里金的结合[16],其克里金权重由线性方程组
| $ \left\{\begin{array}{l} \sum\limits_{\beta=1}^{n_{1}} \lambda_{\beta}^{(1)} \rho_{1}\left(u_{\beta}, u_{q}\right)+\lambda^{(2)} \rho_{12}(0) \rho_{1}\left(u, u_{q}\right)= \\ \rho_{1}\left(u, u_{q}\right) \quad q=1,2, \cdots, n_{1} \\ \sum\limits_{\beta=1}^{n_{1}} \lambda_{\beta}^{(1)} \rho_{12}(0) \rho_{1}\left(u_{\beta}, u\right)+\lambda^{(2)}=\rho_{12}(0) \end{array}\right. $ | (B-1) |
求解。式中:u表示待估点位置;ρ1(uβ, uq)为uβ(β=1, 2, …, n1)处的主变量z1与uq处的主变量的相关系数,该值可以通过变差函数得到,uq、uβ表示待估点邻域内的已知点;ρ12(0)表示同一位置的主变量z1与协变量z2之间的相关系数;λβ(1)和λ(2)为待求的克里金权重。克里金估值z1*(u)和克里金方差σSK2(u)分别由
| $ \begin{aligned} z_{1}^{*}(u)=& E_{1}+\sum\limits_{q=1}^{n_{1}} \lambda_{q}^{(1)}\left[z_{1}\left(u_{q}\right)-E_{1}\right]+\\ & \lambda^{(2)} \frac{\sigma_{1}\left[z_{2}(u)-E_{2}\right]}{\sigma_{2}} \end{aligned} $ | (B-2) |
和
| $ \sigma_{\mathrm{SK}}^{2}=\sigma_{1}^{2}\left[1-\sum\limits_{q=1}^{n_{1}} \lambda_{q}^{(1)} \rho_{1}\left(u, u_{q}\right)-\lambda^{(2)} \rho_{12}(0)\right] $ | (B-3) |
得到。式(B-2)和式(B-3)中:E1、E2分别为主变量z1、协变量z2的先验期望;σ1、σ2分别为主变量z1、协变量z2的先验标准差;λq(1)为待求克里金权重。通过调整ρ12(0),可以修正确定性反演协同约束的强度。ρ12(0)的值域为[0, 1],当ρ12(0)=0时,同位协同简单克里金退化为简单克里金,确定性反演对随机反演的协同约束强度为0;当ρ12(0)=1时,确定性反演对随机反演的协同约束强度最强,此时随机反演结果等同确定性反演结果。
| [1] |
Joumel A, Alabert F. New method for reservoir mapping[J]. Journal of Petroleum Technology, 1990, 42(2): 212-218. DOI:10.2118/18324-PA |
| [2] |
Hass A, Dubrule O. Geostatistical inversion: a sequential method for stochastic reservoir modeling constrained by seismic data[J]. First Break, 1994, 12(11): 561-569. |
| [3] |
Dubrule O. Geostatistical reservoir characterization constrained by 3D seismic data[J]. Petoleum Gesocience, 1998, 4(2): 121-128. DOI:10.1144/petgeo.4.2.121 |
| [4] |
Debeye H, Sabbah E. Stochastic inversion[C]. SEG Technical Program Expanded Abstracts, 1996, 15: 1212-1215.
|
| [5] |
Sams M S, Atkins D, Siad N, et al. Stochastic inversion for high resolution reservoir characterization in the Central Sumatra Basin[C]. SPE Asia Pacific Improved Oil Recovery Conference, 1999, SPE-57260-MS.
|
| [6] |
Mosegaard K, Tarantola A. Monte Carlo sampling of solutions to inverse problems[J]. Journal of Geophy-sical Research, 1995, 100(B7): 12431-12447. DOI:10.1029/94JB03097 |
| [7] |
Hansen T M, Cordua K S, Mosegaard K. Inverse problems with non-trivial priors: efficient solution through sequential Gibbs sampling[J]. Computational Geosciences, 2012, 16(3): 593-611. DOI:10.1007/s10596-011-9271-1 |
| [8] |
张繁昌, 肖张波, 印兴耀. 地震数据约束下的贝叶斯随机反演[J]. 石油地球物理勘探, 2014, 49(1): 176-182. ZHANG Fanchang, XIAO Zhangbo, YIN Xingyao. Bayesian stochastic inversion constrained by seismic data[J]. Oil Geophysical Prospecting, 2014, 49(1): 176-182. |
| [9] |
张广智, 王丹阳, 印兴耀, 等. 基于MCMC的叠前地震反演方法研究[J]. 地球物理学报, 2011, 54(11): 2926-2932. ZHANG Guangzhi, WANG Danyang, YIN Xingyao, et al. Study on prestack seismic inversion using Markov Chain Monte Carlo[J]. Chinese Journal of Geophy-sics, 2011, 54(11): 2926-2932. DOI:10.3969/j.issn.0001-5733.2011.11.022 |
| [10] |
王保丽, 印兴耀, 丁龙翔, 等. 基于FFT—MA谱模拟的快速随机反演方法研究[J]. 地球物理学报, 2015, 58(2): 664-673. WANG Baoli, YIN Xingyao, DING Longxiang, et al. Study of fast stochastic inversion based on FFT—MA spectrum simulation[J]. Chinese Journal of Geophy-sics, 2015, 58(2): 664-673. |
| [11] |
刘兴业, 李景叶, 陈小宏, 等. 联合多点地质统计学与序贯高斯模拟的随机反演方法[J]. 地球物理学报, 2018, 61(7): 2998-3007. LIU Xingye, LI Jingye, CHEN Xiaohong, et al. A stochastic inversion method integrating multi-point geostatistics and sequential Gaussian simulation[J]. Chinese Journal of Geophysics, 2018, 61(7): 2998-3007. |
| [12] |
赵晨, 张广智, 张佳佳, 等. 基于Metropolis优化的叠前全局迭代地质统计学反演方法[J]. 地球物理学报, 2020, 63(8): 3116-3130. ZHAO Chen, ZHANG Guangzhi, ZHANG Jiajia, et al. Prestack global iteration geostatistical inversion method based on metropolis sampling algorithm[J]. Chinese Journal of Geophysics, 2020, 63(8): 3116-3130. |
| [13] |
张丰麒, 金之钧, 盛秀杰, 等. 贝叶斯三参数低频软约束同步反演[J]. 石油地球物理勘探, 2016, 51(5): 965-975. ZHANG Fengqi, JIN Zhijun, SHENG Xiujie, et al. Bayesian prestack three-term inversion with soft low-frequency constraint[J]. Oil Geophysical Prospecting, 2016, 51(5): 965-975. |
| [14] |
姚凌青, 潘懋, 成秋明, 等. 三维Kriging方法中的变异函数套合[J]. 地球科学——中国地质大学学报, 2009, 34(2): 294-298. YAO Lingqing, PAN Mao, CHENG Qiuming, et al. Nested overlap of variograms in 3D Kriging[J]. Earth Science: Journal of China University of Geosciences, 2009, 34(2): 294-298. |
| [15] |
Buland A, Omre H. Bayesian linearized AVO inversion[J]. Geophysics, 2003, 68(1): 185-198. DOI:10.1190/1.1543206 |
| [16] |
Xu W, Tran T, Srivastava M, et al. Integrating seismic data in reservoir modelling: The collocated cokriging alternative[C]. The 67th Annual Technical Conference and Exhibition of the Society of Petroleum Engineers, 1992, SPE-24742-MS.
|
| [17] |
Soares A. Direct sequential simulation and cosimulation[J]. Mathematical Geology, 2001, 33(8): 911-926. DOI:10.1023/A:1012246006212 |
| [18] |
周爽爽, 印兴耀, 裴松, 等. 地震波形约束的蒙特卡洛—马尔科夫链随机反演方法[J]. 石油地球物理勘探, 2021, 56(3): 543-554, 592. ZHOU Shuangshuang, YIN Xingyao, PEI Song, et al. Monte Carlo-Markov Chain stochastic inversion constrained by seismic waveform[J]. Oil Geophysical Prospecting, 2021, 56(3): 543-554, 592. |
| [19] |
李祺鑫, 罗亚能, 张生, 等. 高分辨率波阻抗贝叶斯序贯随机反演[J]. 石油地球物理勘探, 2020, 55(2): 389-397. LI Qixin, LUO Ya'neng, ZHANG Sheng, et al. High-resolution Bayesian sequential stochastic inversion[J]. Oil Geophysical Prospecting, 2020, 55(2): 389-397. |
| [20] |
李坤, 印兴耀. 混合概率模型驱动的叠前地震反演方法[J]. 石油地球物理勘探, 2020, 55(4): 839-853. LI Kun, YIN Xingyao. Prestack seismic inversion driven by mixture probabilistic models[J]. Oil Geophysical Prospecting, 2020, 55(4): 839-853. |
| [21] |
陈文浩, 王志章, 刘月田, 等. 储层随机模拟中的多尺度变差函数估算方法[J]. 石油地球物理勘探, 2019, 54(1): 154-163, 174. CHEN Wenhao, WANG Zhizhang, LIU Yuetian, et al. Multi-scale horizontal variogram estimation in re-servoir stochastic simulation[J]. Oil Geophysical Prospecting, 2019, 54(1): 154-163, 174. |



 张丰麒, 北京市昌平区沙河镇百沙路5号中国石化科学技术研究中心, 102206。Email:
张丰麒, 北京市昌平区沙河镇百沙路5号中国石化科学技术研究中心, 102206。Email: 