② 青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071
② Laboratory for Marine Mineral Resources, National Laboratory for Marine Science and Techno-logy (Qingdao), Qingdao, Shandong 266071, China
经验模态分解(EMD)是由Huang等[1]提出的一种自适应处理非线性和非平稳信号的方法。EMD将随机信号分解为固有模式信号,赋予瞬时频率合理的物理含义和计算方法,创立了以瞬时频率表征信号变化的基本属性[2]。随着图像处理技术的发展,EMD在图像处理领域取得了巨大成功,如图像去噪、检测、增强等[3-5],但在地震勘探领域应用较少。
近年来,匹配追踪(Matching Pursuit,MP)算法广泛用于地震勘探领域,如检测低频阴影、提取瞬时谱、稀疏反演、去强反射等[6-10],其中谱分解技术可全频带扫描地震数据,获得特定频率下描述目标层地质特征的数据体,普遍用于岩性识别及烃类检测[11-12]。传统的谱分解技术(如短时傅里叶变换、小波变换和S变换等)可以有效地分析非平稳信号,但存在物理意义不明确、时频谱精度不高等问题。Mallat等[13]提出的MP算法根据信号的局部结构特征构造超完备字典原子库,并将信号扩展到一组适应不同时频特征的原子上,最后用有限个原子稀疏表示原始信号,实现信号的自适应分解。Liu等[14-15]推出了动态快速MP算法的概念,将信号的瞬时属性引入MP中,在每次迭代中,信号的瞬时属性变化引起参与内积的时频原子的变化,进而提高了信号的分解速率。张繁昌等[16-17]充分利用地震信号的瞬时属性确定时频原子动态参数的扫描范围,最终采用阻尼最小二乘法确定各个匹配小波的复振幅,进一步减少了扫描参数,计算效率提高了数百倍,但获得的瞬时频率稳定性较差且存在负值。为此,Boashash[18]、刘汉卿等[19]利用连续相位求取瞬时频率,但获得的瞬时频率易受噪声影响,并存在频率异常值。印兴耀等[20]引入局部频率约束时频原子的搜寻范围,但得到的局部频率与实际频率存在一定误差。
为此,本文针对瞬时频率存在负值的情况展开了一系列研究。瞬时频率是描述单分量信号的频率随时间变化的物理属性,一般的地震信号为多分量信号集合体,在某一个时刻具有诸多频率成分,该时刻的地震信号的瞬时频率实际上是该时刻所有频率的平均值。故对原始信号进行EMD得到单分量信号,引入连续相位,利用阻尼最小二乘法求出匹配原子的瞬时频率,由此得到匹配原子主频;采用改进的动态MP方法分解地震信号稳定性较好,得到的高分辨率单频谱剖面有助于确定含油气储层的范围。
1 EMD字典EMD将非平稳信号自适应地分解成一系列固有模式信号(IMF),IMF满足单分量信号的物理解释且含有不同的频率成分,这些IMF包括高频到低频成分,能够表征不同的地质、地层的信息。IMF需要满足两个条件[1]:①信号零值点与极值点的数量顶多相差一个;②在任意时刻,信号局部的极大值点和极小值点形成的上、下包络的平均值等于零。EMD依赖于“筛选”的过程提取IMF,从稀疏分解的角度看,EMD算法的结果非常稀疏,在分解过程中子成分分量只有若干个,远远少于其他稀疏时频分解方法(如MP)。因此,本文分解方法的时频字典(EMD字典)比其他时频字典(Morlet小波字典等)更具冗余性。根据EMD算法获得的所有可能的IMF的集合定义EMD字典,每一个IMF分量都是平稳的。根据IMF的定义,EMD字典中可以有无数个时频原子,Hou等[21]从子空间投影的角度给出了IMF的表达式
| $ \begin{gathered} D_{\mathrm{imf}}(t)=a(t) \cos \theta(t) \\ a(t), \theta^{\prime}(t) \in \boldsymbol{V}(\theta, \lambda) \quad \theta^{\prime}(t) \geqslant 0 \end{gathered} $ | (1) |
式中:Dimf(t)为经EMD的IMF函数;a(t)为瞬时振幅,t为时间;θ(t)为瞬时相位(递增函数),其导数θ′(t)可以表示瞬时频率。由于IMF的前提假设是平稳的,故信号的能量和瞬时频率不随时间发生剧烈变化,因此a(t)和θ′(t)属于由θ(t)定义的谐波列向量所组成的子空间V(θ, λ)
| $ \begin{aligned} \boldsymbol{V}(\theta, \lambda)=& \operatorname{span}\left\{1,\left[\cos \left(\frac{k \theta}{2 L_{\theta}}\right)\right]_{1 \leqslant k \leqslant 2 \lambda L_{\theta}},\right.\\ &\left.\left[\sin \left(\frac{k \theta}{2 L_{\theta}}\right)\right]_{1 \leqslant k \leqslant 2 \lambda L_{\theta}}\right\} \end{aligned} $ | (2) |
式中:参数λ控制IMF平滑度;参数k控制相位平滑度;span{·,·,·}表示空间函数,且
通过使用上述IMF作为超完备字典中的原子,即可定义EMD字典
| $ \boldsymbol{D}=\left\{\begin{array}{lll} a \cos \theta & \left.{a 、\theta^{\prime}} \in \boldsymbol{V}(\theta, \lambda) \quad \theta^{\prime} \geqslant 0\right\} \end{array}\right. $ | (3) |
一个二维地震信号s(t)经过EMD后,表示为
| $ s(t)=\sum\limits_{i=1}^{m} \operatorname{IMF}_{m}(t)+R_{m}(t) $ | (4) |
式中:IMFm(t)为第m个IMF;Rm(t)为残余量。
EMD过程是极具启发性的,虽然是基于经验的分解,不同于传统的稀疏时频分解方式,但仍可以视作基于EMD字典逐步搜索最优原子的过程。
2 基于EMD字典的自适应MP算法 2.1 快速MP基本原理Mallat等[13]提出的MP算法的核心是:根据信号的特性选定母函数创建一个冗余字典,将信号投影到原子库的所有原子上,选择与信号相关系数最大的原子作为最优匹配原子,并从原始信号中减去;对剩余信号继续上述操作,记录每次迭代产生的最优匹配子波,继续迭代下去,直到剩余信号的能量小于阈值或达到预先设置的最大迭代次数,则信号分解完成,原始信号可以由分解得到的一系列最优匹配原子表征。
假设要分解的信号为S,H表示Hilbert空间,定义H中的过完备原子库为D,即D∈H,D由l个列向量{gy1, gy2, ..., gyl}构成,字典库D中每一列叫做原子,用S的采样点数设置D中原子的长度,并且每一列原子都是归一化向量,即‖gy‖=1。故第一次匹配的最优原子gy1∈D满足
| $ \left|\left\langle\boldsymbol{S}, \boldsymbol{g}_{y_{1}}\right\rangle\right|=\sup _{i \in(1, \cdots, l)}\left|\left\langle\boldsymbol{S}, \boldsymbol{g}_{y_{i}}\right\rangle\right| $ | (5) |
式中:〈S, gyi〉为最优时频原子与信号的内积,yi是字典矩阵的列索引,i为D的列索引;sup表示取|〈S, gyi〉|的上确界。这样,S由第一次迭代搜寻获得的最优匹配原子gy1的投影分量及其信号残差R1S两部分组成,即
| $ \boldsymbol{S}=\left\langle{\boldsymbol{S}, \boldsymbol{g}_{y_{1}}}\right\rangle \boldsymbol{g}_{y_{1}}+\mathrm{R}_{1} \boldsymbol{S} $ | (6) |
将R1S作为新信号,重新搜索原子库寻找最优匹配原子,并从原始信号中减去,得到剩余信号,继续迭代下去。到第n+1次迭代时,经过匹配分解后残存信号为Rn+1S,搜索得到的最优匹配原子为gyn+1,则第n次迭代获得的残存信号RnS为
| $ \mathrm{R}_{n} \boldsymbol{S}=\left\langle{\mathrm{R}_{n} \boldsymbol{S}, \boldsymbol{g}_{y_{n+1}}}\right\rangle\boldsymbol{g}_{y_{n+1}}+\mathrm{R}_{n+1} \boldsymbol{S} $ | (7) |
其中gyn+1满足
| $ \left|\left\langle\mathrm{R}_{n} \boldsymbol{S}, \boldsymbol{g}_{y_{n+1}}\right\rangle\right|=\sup _{i \in(1,2, \cdots, l)}\left|\left\langle\mathrm{R}_{n} \boldsymbol{S}, \boldsymbol{g}_{y_{i}}\right\rangle\right| $ | (8) |
若经过K步迭代、分解后,匹配子波的次数达到预先设置的次数或迭代、分解后信号残存能量远低于能量阈值时,就完成对信号的分解。原始信号可以表示为K个最优匹配原子的线性组合与残差RK+1S之和
| $ \boldsymbol{S}=\sum\limits_{i=0}^{K}\left\langle\mathrm{R}_{i} \boldsymbol{S}, \boldsymbol{g}_{y_{i}}\right\rangle \boldsymbol{g}_{y_{i}}+\mathrm{R}_{K+1} \boldsymbol{S} $ | (9) |
传统的动态MP方法以信号的瞬时属性作为先验信息构建动态子波库,显著提高了每次迭代的内积计算速度,极大地加快了分解效率。传统MP的最优子波的搜索邻域由瞬时属性确定,瞬时频率计算结果存在“负频率”的问题,且受噪声干扰较大,得到的结果极不稳定。当获得的频率不合理时,只能全局搜寻时频原子的频率,这并不是真正意义上的动态搜寻。为此,引入连续相位概念计算瞬时频率[22-23]。根据正则化理论,利用正则化算子得到的局部域值求取数据点处的频率信息,进而求得准确的信号瞬时频率属性信息,并且计算结果稳定,抗噪声能力强。因此,本文提出的瞬时相位计算方法可以直接找到最优时频原子。
自Taner等[24]初次将瞬时频率引入地震勘探领域之后,瞬时频率成为基本地震属性之一。人们又提出了求取瞬时频率的优化算法。高静怀等[25]提出基于小波变换域的瞬时频率计算方式;尹继尧等[26]基于TK能量的最大幅值计算瞬时频率;刘汉卿等[19]采用连续相位求取瞬时频率;印兴耀等[20]利用局部频率替代瞬时频率去除强反射,获得了较好效果。
针对传统MP方法计算瞬时频率出现负值及计算过程鲁棒性差的问题,本文引入连续相位,借助阻尼最小二乘法,加入整形正则化算子[27]对数据平滑处理,得到了稳定的瞬时频率,并获得匹配原子主频。采用改进的动态MP算法对地震信号谱分解,具有良好的稳定性,获得的高分辨率单频谱剖面有助于确定含油气储层的范围。
连续信号x(t)的复地震道为
| $ Z(t)=x(t)+\mathrm{j} h(t)=A(t) \mathrm{e}^{\mathrm{j} \theta(t)} $ | (10) |
式中:h(t)为x(t)的Hilbert变换;A(t)为地震道包络;θ(t)为信号的瞬时相位。
设θ和φ分别为连续相位和主值相位,P、Q分别为计算θ、φ的算子,则连续相位定义为
| $ \theta=P(\varphi)=\varphi+r {\rm{ \mathit{ π} }} $ | (11) |
式中r为正整数。由式(11)可得
| $ \Delta \theta(t)=\theta(t+1)-\theta(t) \in(0, {\rm{ \mathit{ π} }}] $ | (12) |
Q为求主值相位的算子,即P是Q的逆运算
| $ \varphi=Q(\theta)=P^{-1}(\theta) $ | (13) |
Q(θ)位于区间(-π,π],则
| $ \Delta \theta(j)=P\{Q[\Delta \varphi(j)]\} $ | (14) |
将式(14)代入式(12)可得连续相位的计算公式
| $ \theta(t+1)=P\{Q[\Delta \varphi(t)]\}+\theta(t) $ | (15) |
传统的瞬时频率f(t)是θ(t)的变化率,即
| $ \begin{aligned} f(t)=& \theta^{\prime}(t)=\operatorname{Im}\left[\frac{Z^{\prime}(t)}{Z(t)}\right]=\\ & \frac{x(t) h^{\prime}(t)-x^{\prime}(t) h(t)}{x^{2}(t)+h^{2}(t)}=\frac{l(t)}{b(t)} \end{aligned} $ | (16) |
用连续相位替代瞬时相位φ(t),引入阻尼最小二乘法,并加入整形正则化算子求取瞬时频率
| $ f(t)=\left[e^{2} \boldsymbol{I}+(\boldsymbol{M} \boldsymbol{B})^{\mathrm{T}}(\boldsymbol{M} \boldsymbol{B})\right]^{-1}(\boldsymbol{M B})^{\mathrm{T}} \boldsymbol{l} $ | (17) |
式中:e为权系数,一般取B中元素最大值的1%~5%;M为整形正则化算子;l和B分别为l(t)和b(t)组成的向量(矩阵);I为单位阵。
本文基于连续相位求解的瞬时频率有效避免了“负频率”现象,相较于直接求逆过程,利用整形正则化平滑算子的阻尼最小二乘法不会出现频率异常值,得到的瞬时频率曲线更平滑、真实,且更突显高频成分。
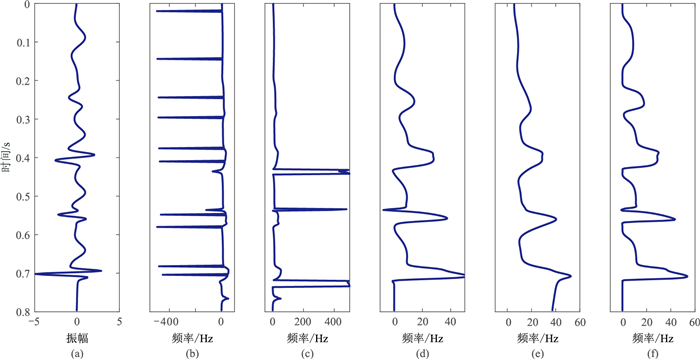
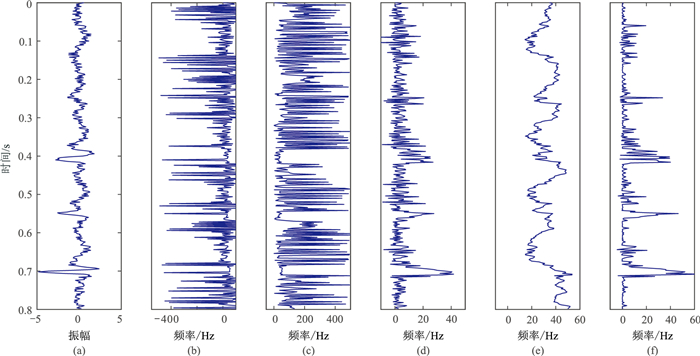
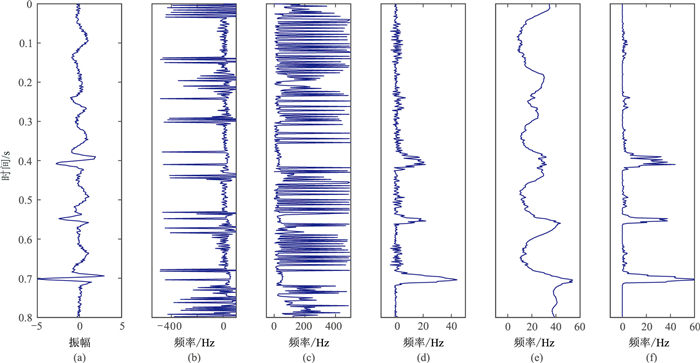
为了验证瞬时频率计算结果的合理性,设计了合成信号(图 1a)及加噪合成信号(图 2a、图 3a、图 4a),并由不同方法计算瞬时频率(图 1~图 4)。由图 1可见:①瞬时频率求导计算结果出现很多“负频率”现象(图 1b),连续相位求导计算结果虽然避免了“负频率”现象,但在0.4~0.5s出现瞬时频率异常(图 1c)。②连续相位常规阻尼最小二乘法(图 1d)、连续相位改进阻尼最小二乘法(图 1f)计算结果没有出现瞬时频率异常,且后者的计算结果更平滑,并且突显了频率异常点。③局部频率(图 1e)与连续相位改进阻尼最小二乘法(图 1f)计算结果接近真实频率,并且突显了高频成分,但后者更接近真实频率。由图 2~图 4可见,基于连续相位改进阻尼最小二乘法(图 2f、图 3f、图 4f)能很好地处理加噪地震数据,计算结果相对于局部频率曲线(图 2e、图 3e、图 4e)更光滑,且突显了频率异常点,证明本文方法具有很好的抗噪性。
|
图 1 由不同方法获得的合成信号瞬时频率 (a)合成信号;(b)瞬时频率求导;(c)连续相位求导;(d)连续相位常规阻尼最小二乘法;(e)局部频率;(f)连续相位改进阻尼最小二乘法 |

|
图 2 由不同方法获得的加噪合成信号(信噪比为1)瞬时频率 (a)加噪合成信号;(b)瞬时频率求导;(c)连续相位求导;(d)连续相位常规阻尼最小二乘法;(e)局部频率;(f)连续相位改进阻尼最小二乘法 |
|
图 3 由不同方法获得的加噪合成信号(信噪比为2)瞬时频率 (a)加噪合成信号;(b)瞬时频率求导;(c)连续相位求导;(d)连续相位常规阻尼最小二乘法;(e)局部频率;(f)连续相位改进阻尼最小二乘法 |
|
图 4 由不同方法获得的加噪合成信号(信噪比为5)瞬时频率 (a)加噪合成信号;(b)瞬时频率求导;(c)连续相位求导;(d)连续相位常规阻尼最小二乘法;(e)局部频率;(f)连续相位改进阻尼最小二乘法 |
传统动态MP方法将信号转换到Hilbert空间,并在信号包络幅值最大值处展开、分解信号。首先对信号在先验信息确定的搜寻邻域内的所有原子进行匹配,找出相关系数最大的时频原子作为最优原子,这种分解策略造成每一次迭代历经搜寻范围内所有的原子,仅获得一个最优匹配的时频原子,影响了信号的收敛速度[28-29]。为了加快MP算法的收敛速度,采用多原子分解方法,即不仅仅在包络幅值最大值处进行,而是找到所有的信号能量极大值位置,并设置特定的搜索条件,在满足搜索条件的时间点处进行匹配[30],通过一次迭代得到多个最优匹配子波,并利用最小二乘法求出每个子波的幅值参数。
多原子分解的动态MP算法需要在每一次迭代过程中搜索满足一定条件的极大值附近的所有原子,从而获得最优匹配的时频原子,搜索条件的限制严重降低了信号的分解速度。故本文引入EMD思想,将每个地震波形自适应地分解为多个不同波形的组合,每一次迭代只在所有信号包络幅值极大值处分解,当信号的残存能量与原始信号总能量的比值非常小时停止分解。在实际的地震信号分析中,当残存能量远小于原始信号总能量时,可以忽略残存量。故当残留能量小于原始信号总能量的千分之一时,文中MP停止迭代,能在一次迭代中快速生成多个匹配子波,极大提高了分解效率和分解精度。
本文搜索方法的每次迭代过程可简单表示为
| $ \begin{gathered} \boldsymbol{g}_{y_{i}}=\left\{T_{0}, f \in \boldsymbol{U}\left[f\left(T_{0}\right)\right], \theta \in \boldsymbol{U}\left[\theta\left(T_{0}\right)\right]\right\} \\ i=1,2, \cdots, M \end{gathered} $ | (18) |
式中:M表示每一次迭代搜寻确定的最优匹配子波的个数;T0为每个最优匹配子波在搜索位置处的时间;U[f(T0)]和U[θ(T0)]分别为在搜索位置处的频率与相位的搜索邻域集合,f(T0)和θ(T0)分别为搜索位置处信号的瞬时频率信息和相位信息。
经过n次、n+1次匹配分解后,分别得到信号的残差RnS、Rn+1S,假定第n+1次迭代搜索到M个符合条件的匹配原子gyi(i=1,2,…,M),则
| $ \mathrm{R}_{n} \boldsymbol{S}=\mathrm{R}_{n+1} \boldsymbol{S}+\sum\limits_{i=1}^{M} \boldsymbol{a}_{i} \cdot \boldsymbol{g}_{y_{i}}(t) $ | (19) |
式中ai(i=1,2,…,M)为第n+1次迭代搜索获得的每个匹配子波的幅值,即
| $ \boldsymbol{a}=\left[\boldsymbol{G}^{\mathrm{T}} \boldsymbol{G}+\varepsilon \boldsymbol{I}\right]^{-1} \boldsymbol{g}^{\mathrm{T}} \boldsymbol{c} $ | (20) |
式中:a=(a1, a2, …, aM)T为采用多原子搜寻策略通过一次迭代确定的M个时频原子的振幅构成的列向量;c代表第n+1次迭代后的Rn+1S构成的N维列向量,N≥M为信号列向量的元素个数;G=[gy1, gy2, …, gyM]为最优原子组成的N×M阶原子库矩阵,其中每个元素表征一个最优时频原子;I为M阶单位矩阵;ε为阻尼因子。
利用11个Morlet小波合成理论信号,采用基于EMD字典的改进MP算法分解理论信号。图 5为无噪声条件下理论信号的迭代分解过程。由图可见,每一次迭代都筛选出信号的所有极大值点,并逐个匹配原子,经过11次迭代后,重构信号与理论信号波形基本吻合,重构残差几乎为零。

|
图 5 无噪声条件下理论信号的迭代分解过程 (1)为重构信号(蓝色)与理论信号(红色)叠后显示,(2)~(12)为第1次~第11次迭代匹配出的原子,(13)为重构残差(实际地震信号与重构地震信号的差值,下同) |
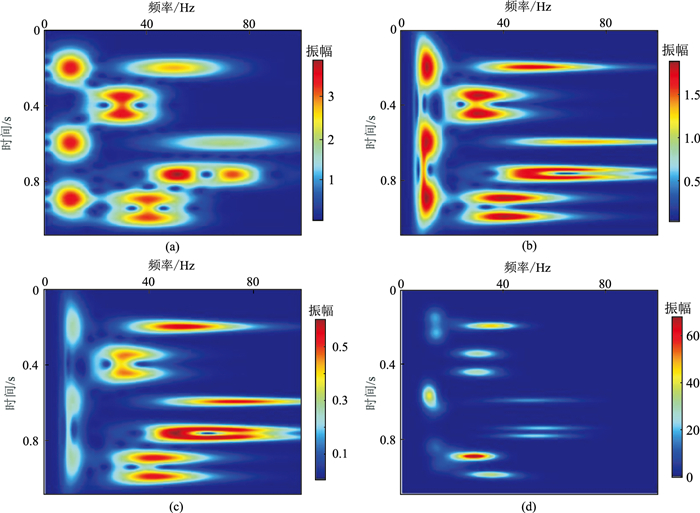
为进一步验证联合EMD与连续相位求解瞬时频率方法的实用性和稳定性,对图 5的合成理论信号利用基于EMD字典的匹配追踪Wigner-Ville分布(EMP-WVD)进行时频表征,并对比、分析短时傅里叶变换(STFT)、连续小波变换(CWT)、S变换(ST)以及EMP-WVD的时频谱计算结果(图 6)。可见,EMP-WVD时频谱(图 6d)的时频分辨率远高于常规时频分析方法(图 6a~图 6c),时频能量聚集能力更强,能清晰定位原子时频信息,为储层预测奠定了基础。
|
图 6 不同时频分析方法得到的时频谱 (a)STFT;(b)CWT;(c)ST;(d)EMP-WVD |
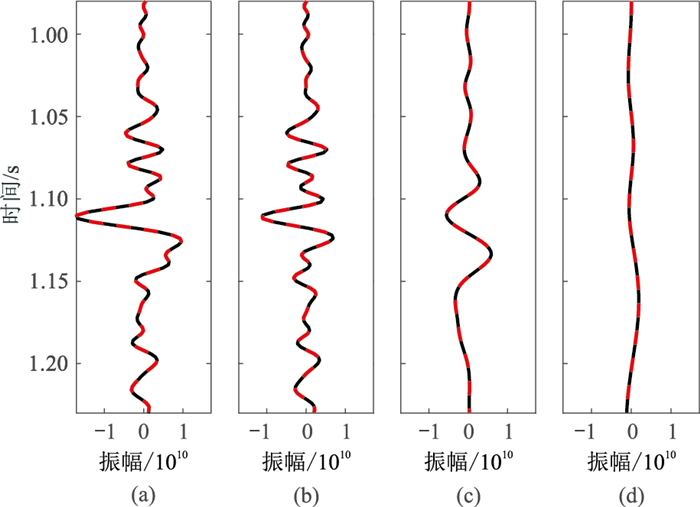
为验证基于EMD和连续相位求取瞬时频率方法的抗噪性,利用M区A井的测井资料建立了一维模型。图 7为多尺度地震信号,图 8为实际信号与重构信号的残差。由图可见:EMD从地震信号最高频率分量开始,依次分解出频率范围逐渐降低的IMF成分,可以有效获得低频和高频成分(图 7);残差基本为0(图 8)。图 9~图 14分别为多尺度加噪地震信号及其重构信号残差。由图可见,残差基本为0(图 10、图 12、图 14),表明本文方法能够完全重构原始地震信号,具有良好的抗噪性。
|
图 7 多尺度地震信号
(a)原始地震信号;(b)大尺度地震信号;(c)中尺度地震信号;(d)小尺度地震信号 黑色代表实际地震信号,红色代表重构地震信号,下同 |
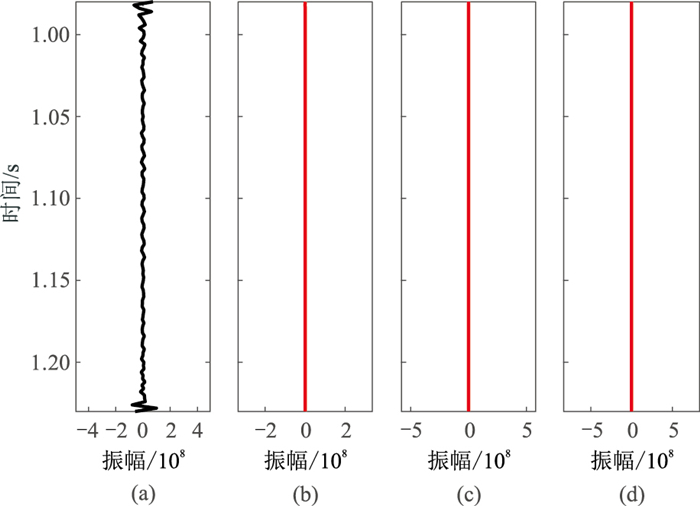
|
图 8 图 7的重构信号残差 (a)原始地震信号;(b)大尺度地震信号;(c)中尺度地震信号;(d)小尺度地震信号 |
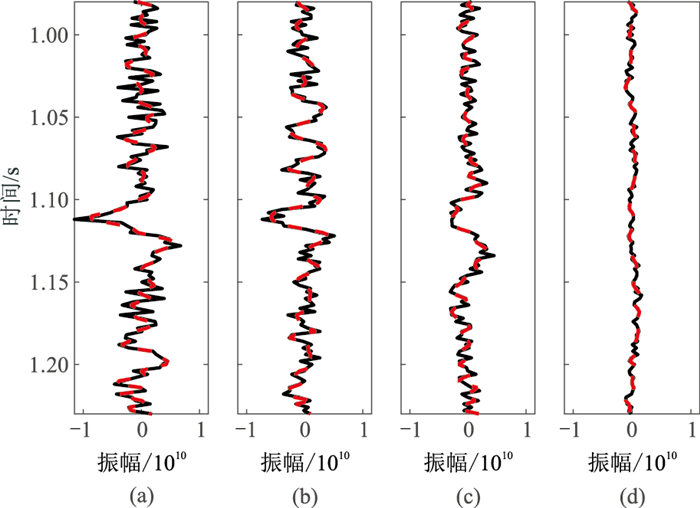
|
图 9 多尺度加噪地震信号(信噪比为1) (a)原始地震信号;(b)大尺度地震信号;(c)中尺度地震信号;(d)小尺度地震信号 |
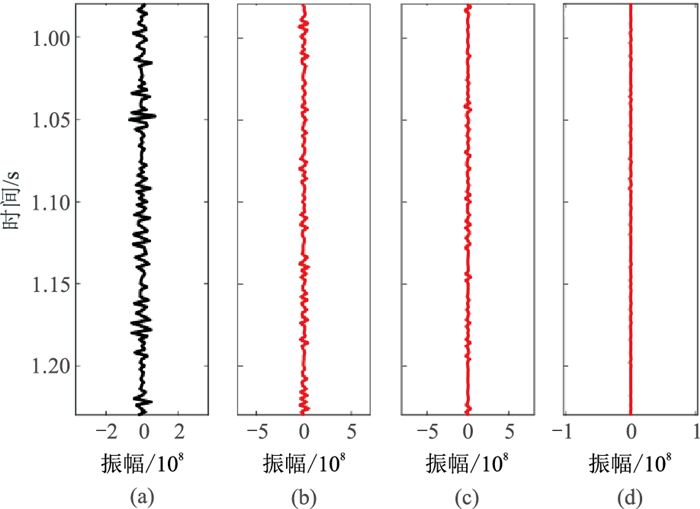
|
图 10 图 9的重构信号残差 (a)原始地震信号;(b)大尺度地震信号;(c)中尺度地震信号;(d)小尺度地震信号 |
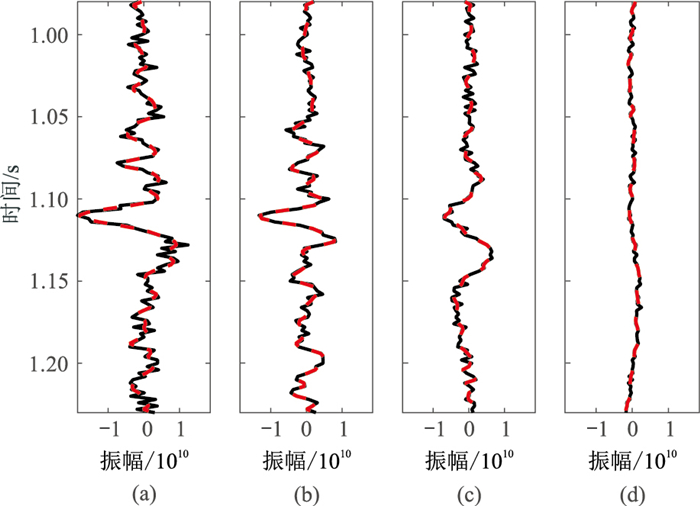
|
图 11 多尺度加噪地震信号(信噪比为2) (a)原始地震信号;(b)大尺度地震信号;(c)中尺度地震信号;(d)小尺度地震信号 |
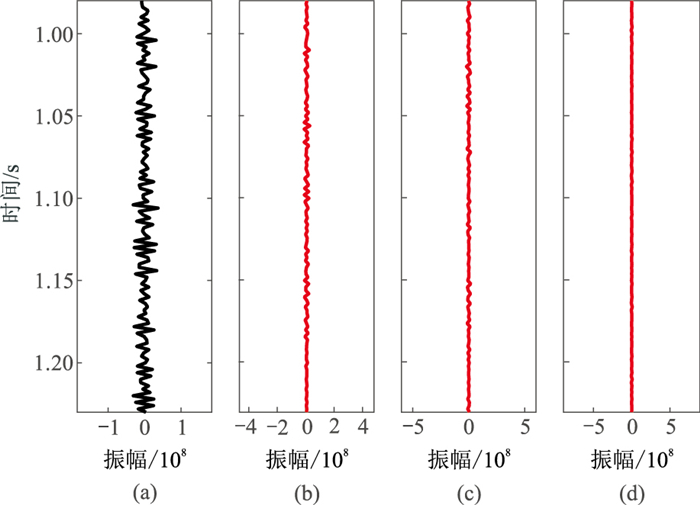
|
图 12 图 11的重构信号残差 (a)原始地震信号;(b)大尺度地震信号;(c)中尺度地震信号;(d)小尺度地震信号 |
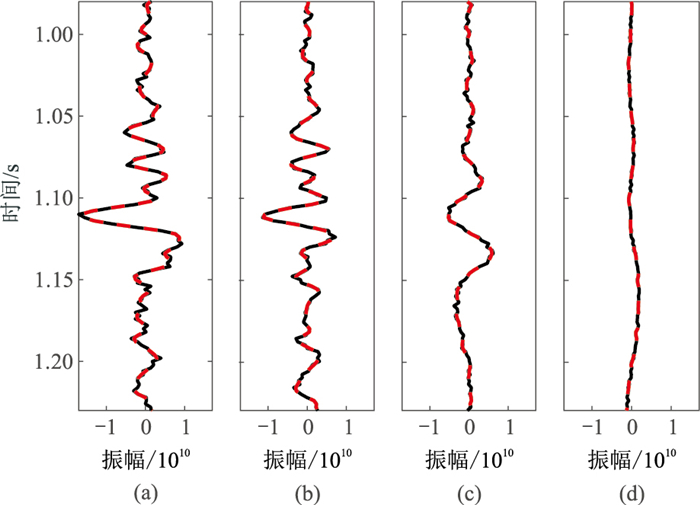
|
图 13 多尺度加噪地震信号(信噪比为5) (a)原始地震信号;(b)大尺度地震信号;(c)中尺度地震信号;(d)小尺度地震信号 |
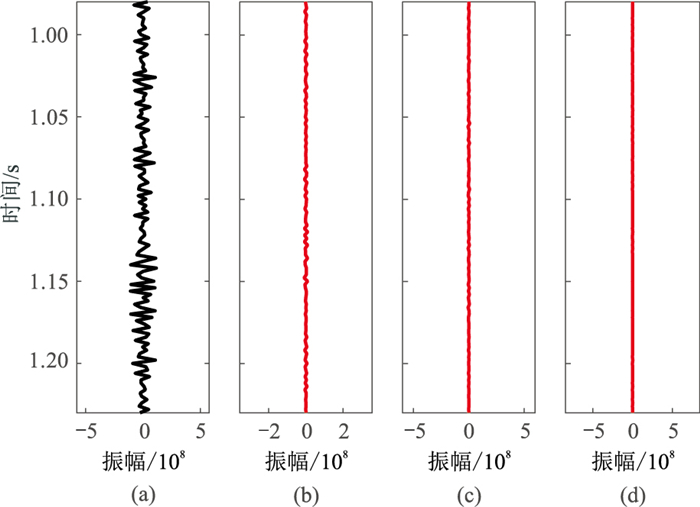
|
图 14 图 13的重构信号残差 (a)原始地震信号;(b)大尺度地震信号;(c)中尺度地震信号;(d)小尺度地震信号 |
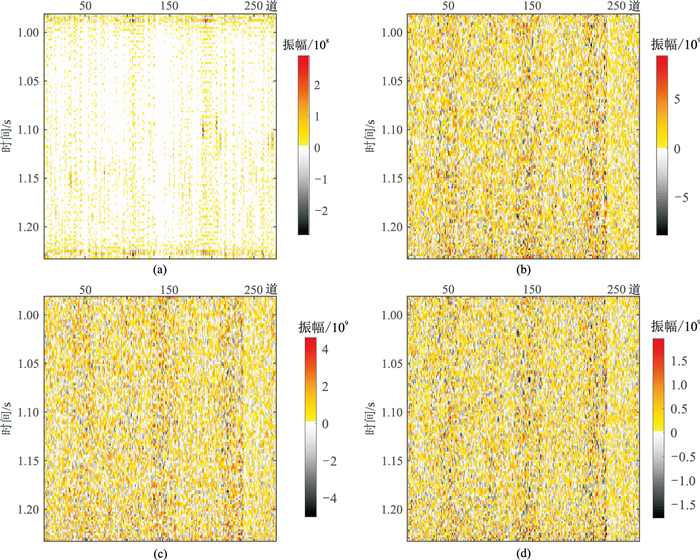
针对复杂薄互层二维模型开展基于EMD改进MP算法抗噪性测试。图 15为由改进MP算法重构的M区地震剖面,图 16为图 15的重构剖面残差。由图可见:基于EMD字典的改进MP方法的重构剖面(图 15b)与实际地震剖面(图 15a)极相似,但前者分辨率得较高,残差(图 16a)只剩随机噪声;对地震记录加噪后,残差基本为随机噪声(图 16b~图 16d),且重构剖面的分辨率均有提升(图 15d、图 15f、图 15h),进一步验证了本文方法的可行性。
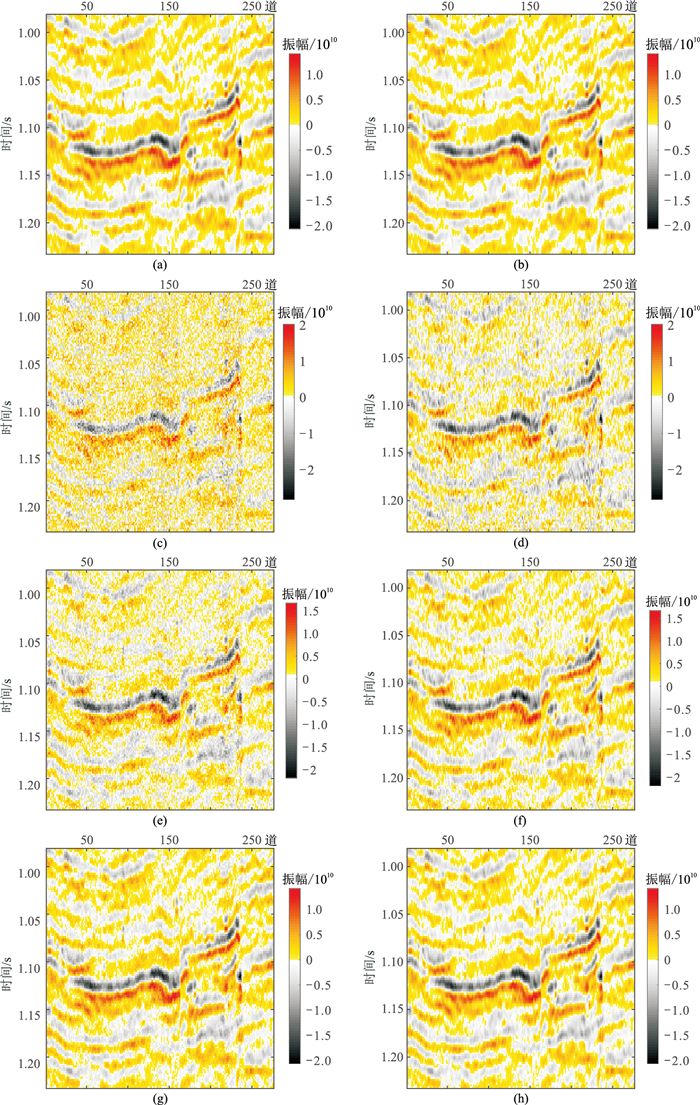
|
图 15 由改进MP算法重构的M区地震剖面 (a)实际地震剖面;(b)重构图a;(c)加噪地震剖面(信噪比为1);(d)重构图c;(e)加噪地震剖面(信噪比为2);(f)重构图e;(g)加噪地震剖面(信噪比为5);(h)重构图g |
4 实际资料处理
在对一维及二维模型测试的基础上,为进一步验证文中方法对实际资料的应用效果,利用中国N区地震资料进行测试。图 17为N区多尺度瞬时谱剖面。由图可见:①EMD是从信号最高频率成分开始,依次分解出频率范围逐渐降低的IMF分量(图 17b~图 17d),因此可以有效获得地震信号的低频和高频成分。②当频率较低时,储层底部能量很强,当频率较高时,储层底部出现能量减弱现象,当频率再次增大时,储层下方能量基本消失,能够观测到明显的低频阴影现象。因此,联合EMD和改进MP谱分解技术检测低频阴影的效果更好,结合测井资料可更好地指示油气储层。
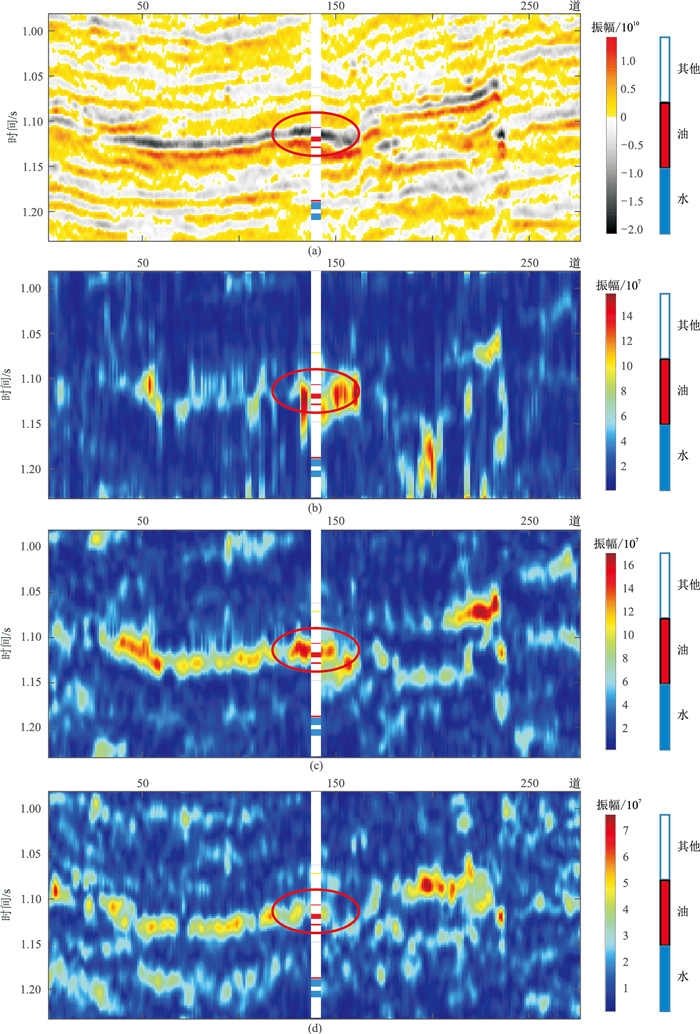
|
图 17 N区多尺度瞬时谱剖面
(a)实际地震剖面;(b)小尺度IMF1瞬时谱剖面;(c)中尺度IMF2瞬时谱剖面;(d)大尺度IMF3瞬时谱剖面 红色线框处为含油气储层,瞬时谱剖面由基于EMD得到的IMF通过EMP-WVD获得 |
图 18为基于EMD改进MP追踪与传统三参数的动态快速MP方法计算时间对比。由图可见,本文提出的基于EMD的自适应MP方法显著提升了MP分解效率。
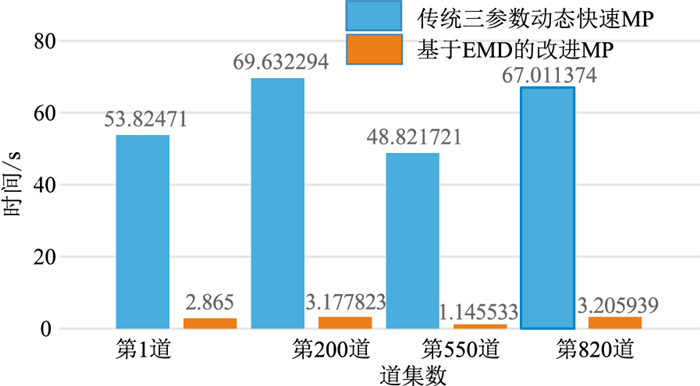
|
图 18 基于EMD改进MP追踪与传统三参数的动态快速MP方法计算时间对比 设定相同的迭代终止条件,对N区的多道不同地震记录进行分解 |
本文结合EMD稀疏分解与MP算法,提出了一种基于EMD字典的稀疏时频分解算法。此外,在连续相位的阻尼最小二乘反演求解瞬时频率的方法中加入整形平滑算子约束,有效地避免了奇异值,同时进一步提高了MP计算效率。经过理论分析与实验测试得到以下认识:
(1) 基于整形平滑算子约束的连续相位求解瞬时频率方法的计算过程并不依赖于每个数据点的瞬时值,而是基于数据点的局部邻域值求取的。因此即使在部分信号微弱或缺失的情况下,该方法也能从相邻时窗中提取有效信息,从而得到合理的频率值,有效降低了噪声敏感度。
(2) 基于EMD字典的MP算法,在确定动态快速MP先验信息的搜索范围时,以连续相位替换瞬时相位求解瞬时频率,提高了运算效率,但继承了EMD的端点效应,在重构地震数据时,未能较好地重构端点数据。
(3) 本文将基于EMD字典的快速MP方法应用于储层含油气性预测,对比不同尺度瞬时谱剖面可以清楚地看到明显的低频阴影现象,且提高了分解效率,从而进一步验证了方法可行性。
| [1] |
Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings Mathematical Physical & Engineering Sciences, 1998, 454(1971): 903-995. |
| [2] |
杨培杰, 印兴耀, 张广智. 希尔伯特—黄变换地震信号时频分析与属性提取[J]. 地球物理学进展, 2007, 22(5): 1585-1590. YANG Peijie, YIN Xingyao, ZHANG Guangzhi. Seismic signals time-frequency analysis and attribute extraction based on HHT[J]. Progress in Geophysics, 2007, 22(5): 1585-1590. DOI:10.3969/j.issn.1004-2903.2007.05.037 |
| [3] |
Liu D, Chen X. Image denoising based on improved bidimensional empirical mode decomposition thresholding technology[J]. Multimedia Tools and Applications, 2018, 78(6): 1-37. |
| [4] |
Huang H, He Y, Yang S, et al. Chaotic image encryption based on bidimensional empirical mode decomposition and double random phase encoding[J]. Multimedia Tools and Applications, 2020, 79(37): 28065-28078. DOI:10.1007/s11042-020-09378-4 |
| [5] |
赵谦, 钱渠, 任志奇. BEMD分解的矿下图像增强算法[J]. 西安科技大学学报, 2020, 40(3): 484-491. ZHAO Qian, QIAN Qu, REN Zhiqi. Undermine image enhancement algorithm based on BEMD decomposition[J]. Journal of Xi'an University of Science and Technology, 2020, 40(3): 484-491. |
| [6] |
Castagna J P, Sun S, Siegfried R W. Instantaneous spectral analysis: Detection of low frequency shadows associated with hydrocarbons[J]. The Leading Edge, 2003, 22(2): 120-127. DOI:10.1190/1.1559038 |
| [7] |
Wang Y H. Seismic time-frequency spectral decomposition by matching pursuit[J]. Geophysics, 2007, 72(1): V13-V20. DOI:10.1190/1.2387109 |
| [8] |
李坤, 印兴耀, 宗兆云. 基于匹配追踪谱分解的时频域FAVO流体识别方法[J]. 石油学报, 2016, 37(6): 777-786. LI Kun, YIN Xingyao, ZONG Zhaoyun. Time-frequency-domain FAVO fluid discrimination method based on matching pursuit spectrum decomposition[J]. Acta Petrolei Sinica, 2016, 37(6): 777-786. |
| [9] |
李坤, 印兴耀, 宗兆云, 等. 基于快速匹配追踪的混合域地震稀疏反演方法[J]. 中国石油大学学报(自然科学版), 2018, 42(1): 50-59. LI Kun, YIN Xingyao, ZONG Zhaoyun, et al. Seismic sparse inversion in mixed-domain utilizing fast match-ing pursuit algorithm[J]. Journal of China University of Petroleum(Edition of Natural Seismic), 2018, 42(1): 50-59. DOI:10.3969/j.issn.1673-5005.2018.01.006 |
| [10] |
许璐, 吴笑荷, 张明振, 等. 基于局部频率约束的动态匹配追踪强反射识别与分离方法[J]. 石油地球物理勘探, 2019, 54(3): 587-593. XU Lu, WU Xiaohe, ZHANG Mingzhen, et al. Strong reflection identification and separation based on the local-frequency-constrained dynamic matching pursuit[J]. Oil Geophysical Prospecting, 2019, 54(3): 587-593. |
| [11] |
张繁昌, 李传辉. 三角洲砂岩尖灭线的地震匹配追踪瞬时谱识别方法[J]. 石油地球物理勘探, 2012, 47(1): 82-88. ZHANG Fanchang, LI Chuanhui. Detla fringe line recognition based on seismic matching pursuit instantaneous spectral characteristic[J]. Oil Geophysical Prospecting, 2012, 47(1): 82-88. |
| [12] |
Partyka G, Gridley J, Lopez J. Interpretational applications of spectral decomposition in reservoir characterization[J]. The Leading Edge, 1999, 18(3): 173-184. |
| [13] |
Mallat S G, Zhang Z. Matching-pursuit with time frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415. DOI:10.1109/78.258082 |
| [14] |
Liu J, Wu Y, Han D, et al. Time-frequency decomposition based on Ricker wavelet[C]. SEG Technical Program Expanded Abstracts, 2004, 23: 1937-1940.
|
| [15] |
Liu J, Marfurt K J. Matching pursuit decomposition using Morlet wavelets[C]. SEG Technical Program Expanded Abstracts, 2005, 24: 786-789.
|
| [16] |
张繁昌, 李传辉, 印兴耀. 基于动态匹配子波库的地震数据快速匹配追踪[J]. 石油地球物理勘探, 2010, 45(5): 667-673. ZHANG Fanchang, LI Chuanghui, YIN Xingyao. Seismic data fast matching pursuit based on dynamic matching wavelet library[J]. Oil Geophysical Prospecting, 2010, 45(5): 667-673. |
| [17] |
张繁昌, 李传辉. 地震信号复数域高效匹配追踪分解[J]. 石油地球物理勘探, 2013, 48(2): 171-175. ZHANG Fanchang, LI Chuanghui. Complex domain efficient matching pursuit decomposition of seicmic siganls[J]. Oil Geophysical Prospecting, 2013, 48(2): 171-175. |
| [18] |
Boashash B. Estimating and interpreting the instantaneous frequency of a signal. Ⅱ. Algorithms and Applications[J]. IEEE Proceedings, 1992, 80(4): 540-568. DOI:10.1109/5.135378 |
| [19] |
刘汉卿, 张繁昌, 代荣获, 等. 动态匹配追踪中利用连续相位求取瞬时频率[J]. 物探与化探, 2015, 39(1): 211-216. LIU Hanqing, ZHANG Fanchang, DAI Ronghuo, et al. The calculation of the instantaneous frequency using the continuous phase in dynamic matching pursuit algorithm[J]. Geophysicial and Geochemical Exploration, 2015, 39(1): 211-216. |
| [20] |
印兴耀, 许璐, 宗兆云, 等. 基于局部频率约束的动态快速匹配追踪方法[J]. 中国石油大学学报(自然科学版), 2018, 42(6): 64-71. YIN Xingyao, XU Lu, ZONG Zhaoyun, et al. Dynamic and fast matching pursuit method based on local frequency constraint[J]. Journal of China University of Petroleum(Natural Science Edition), 2018, 42(6): 64-71. |
| [21] |
Hou T Y, Shi Z. Data-driven time-frequency analysis[J]. Applied and Computational Harmonic Analysis, 2013, 35(2): 284-308. |
| [22] |
Shatilo A P. Seismic phase unwrapping: methods, results, problems 1[J]. Geophysical Prospecting, 2010, 40(2): 211-225. |
| [23] |
Mcgowan R, Kuc R. A direct relation between a signal time series and its unwrapped phase[J]. IEEE Transactions on Acoustics Speech & Signal Processing, 2003, 30(5): 719-726. |
| [24] |
Taner M T, Koehler F, Sheriff R E. Complex seismic trace analysis[J]. Geophysics, 1979, 44(6): 1041-1063. DOI:10.1190/1.1440994 |
| [25] |
高静怀, 吴茜, 陈文超, 等. 小波变换域地震资料瞬时频率分析方法[J]. 石油物探, 2007, 46(6): 534-540. GAO Jinghuai, WU Qian, CHEN Wenchao, et al. Instantaneous frequency analysis of seismic data in wavelet transform domain[J]. Geophysical Prospecting for Petroleum, 2007, 46(6): 534-540. DOI:10.3969/j.issn.1000-1441.2007.06.002 |
| [26] |
尹继尧, 吴宝成, 王维, 等. 基于TK能量的峰值瞬时频率在薄互层预测中的应用[J]. 石油地球物理勘探, 2015, 50(3): 516-522. YIN Jiyao, WU Baocheng, WANG Wei, et al. Thin interbed thickness prediction using peak instantaneous frequency of time-frequency Teager-Kaiser energy[J]. Oil Geophysical Prospecting, 2015, 50(3): 516-522. |
| [27] |
Fomel S. Shaping regularization in geophysical-estimation problems[J]. Geophysics, 2007, 72(2): R29-R36. |
| [28] |
Vincent P, Bengio Y. Kernel matching pursuit[J]. Machine Learning, 2002, 48(1-3): 165-187. DOI:10.1023/A:1013955821559 |
| [29] |
Durka P J, Matysiak A, Eduardo M M, et al. Multichannel matching pursuit and EEG inverse solutions[J]. Journal of Neuroence Methods, 2005, 148(1): 49-59. |
| [30] |
Gribonval R. Fast matching pursuit with a multiscale dictionary of Gaussian chirps[J]. IEEE Transactions on Signal Processing, 2011, 49(5): 994-1001. |



 印兴耀, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
印兴耀, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: