滚动背斜是出现在正断层下降盘的一种背斜构造[1-2],在拉张型断陷盆地中广泛发育。该类构造成藏条件较好,在世界不同地区均有油气田发现[3-7],是有利的油气勘探目标,人们深入研究了其构造特征及成因机理[8-11]。
南海东部广泛发育滚动背斜,并发现多个商业油田。在油田开发的不同阶段储量规模发生成倍变化,表明该类构造速度变化较快,构造高点、范围不确定性较大。目前对上述速度变化的机理还未形成量化认识。为此,在梳理、统计研究区开发井较多的同类油田的相关数据的基础上,借鉴大数据分析技术中的数字思维[12-14],以期通过数据驱动的方式获得滚动背斜速度变化的规律性认识,并进一步提出定量构造评价方法,以指导滚动背斜含油构造的勘探和开发。另外,通过定性分析构造局部应变、应力特征,探讨了速度变化机理,以期形成该类构造速度问题的理论认识。
1 滚动背斜构造变化特征南海东部滚动背斜地震资料信噪比较高、成像效果好、易于层位追踪(图 1),并且构造解释的继承性好,因此构造解释成果可信度较高。

|
图 1 南海东部典型滚动背斜构造垂直断层走向地震剖面 (a)HZ-A油田;(b)XJ-B油田;(c)LF-C油田;(d)HZ-D油田 |
然而在油田开发过程中出现构造变化较大的问题,主要表现为时、深域高点位置不同及钻井误差大。以下分别以HZ-A油田和XJ-B油田为例进行说明。
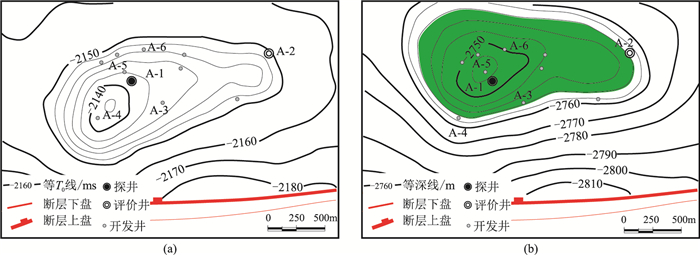
HZ-A油田地震解释构造“时间高点”距断层约600m,探井A-1及评价井A-2相对“时间高点”远离主断层。开发阶段,前2口开发井(A-3、A-4)位于“时间高点”附近(图 2a),实钻构造大幅度加深,最大深度预测误差达40m。随着油田的进一步钻探,基本确定了“深度高点”的实际位置(距断层约1km),“时间高点”相对于“深度高点”向断层方向移动了约400m(图 2b)。根据底水油藏H1界面深度一致的认识,可判断“深度高点”位于井A-1、A-5附近(图 3)。在构造变化的影响下,各油藏含油范围及储量规模均有较大变化,如对于H1,井A-3钻前预测储量规模为x万方,开发井钻后储量规模约为x/2万方。
|
图 2 HZ-A油田构造变化 (a)H1等T0图;(b)H1深度构造图,绿色区域为含油范围,图 4同 |
|
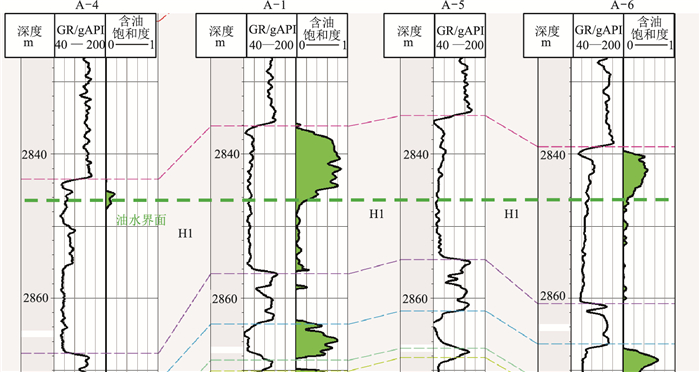
图 3 HZ-A油田测井曲线 对于底水油藏H1,井A-1油柱最高,井A-5测深最小(未测量密度,无含油饱和度解释成果)。绿色指示含油层位 |
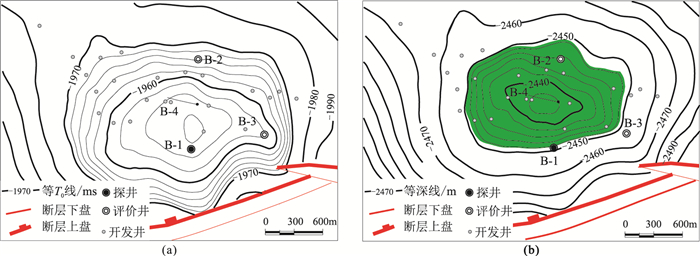
XJ-B油田探井B-1位于“时间高点”,评价井B-2远离断层,且处于“低部位”,实钻深度高于井B-1(图 4a)。开发井井网完善后更新构造图,证实“深度高点”位于井B-1、B-2之间的井B-4,深度高点远离断层,距“时间高点”约500m(图 4b)。评价井和开发井在“深度高点”发现了多个新油藏(如J1油藏),储量规模相对于初期增加了1倍。
|
图 4 XJ-B油田构造变化 (a)J1等T0图;(b)J1深度构造图 |
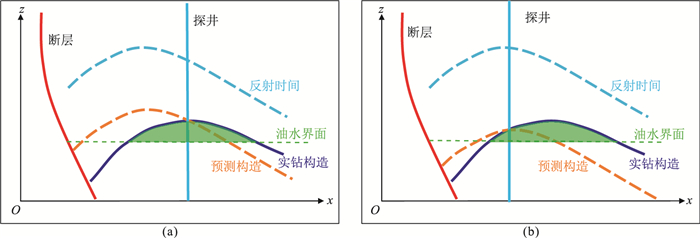
图 5为HZ-A、XJ-B油田构造变化示意图。由图可见,虽然构造变化对储量评估的影响不同,但构造变化规律基本一致,即:近断层位置构造加深、远离断层位置构造抬升及深度高点相对于时间高点远离断层。
|
图 5 HZ-A(a)、XJ-B(b)油田构造变化示意图 |
HZ-A油田和XJ-B油田的构造变化表明,远离主断层速度快速减小。针对地震解释层位,利用实钻分层深度D和井点等T0值获得井点沿层平均速度
| ${V_{\rm{a}}} = 2D/{T_0} $ | (1) |
实际工作中,等T0解释一般选用稳定相位,与实际分层点标定相位并非完全一致,因此Va与真实平均速度可能存在系统差,但趋势一致,即两者随位置的变化率一致。基于速度点勾绘沿层平均速度分布图(图 6)。
|
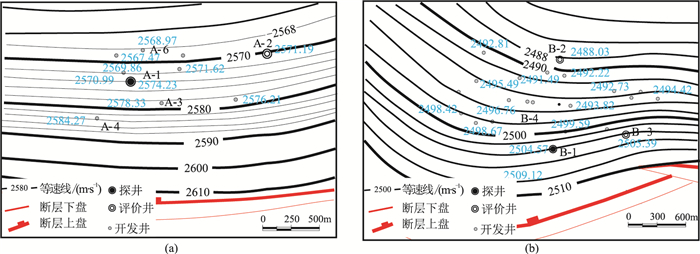
图 6 HZ-A油田和XJ-B油田沿层平均速度分布图 (a)HZ-A油田H1;(b)XJ-B油田J1蓝色数值表示井点速度(m·s-1) |
为了定量表征速度的变化规律,将特定方向单位距离内的速度变化定义为速度梯度。根据图 6初步估算,HZ-A和XJ-B油田含油范围内速度梯度分布于14~42m·s-1·km-1。
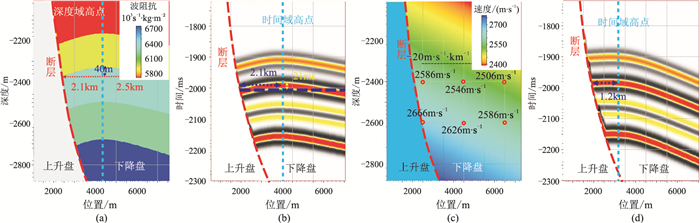
2.2 速度梯度影响分析上述分析表明,研究区存在远离断层位置速度快速减小的特征。基于地震解释的构造研究中,这种沿特定方向的速度变化对刻画构造的影响较大。为此,设计二维褶积模型分析速度梯度对时间域地震剖面的影响。图 7为速度梯度对滚动背斜时间域地震剖面的影响分析。由图可见,波阻抗模型(图 7a)的褶积模型(图 7b)与横向变速模型(图 7c)的褶积模型(图 7d)的差异较大:图 7b的时间域圈闭幅度约20ms,“时间高点”位置与“深度高点”(图 7a)一致;图 7d的“时间高点”距断层1.2km,相对“深度高点”漂移了近900m,圈闭幅度较小(约1~2ms)。
|
图 7 速度梯度对滚动背斜时间域地震剖面的影响分析 (a)波阻抗模型;(b)图a的褶积模型;(c)横向变速模型(远离断层方向速度梯度为-20m·s-1·km-1);(d)图c的褶积模型波阻抗模型的长度和高度分别为8、3km,其中第2个界面埋深约为2.4km,幅度约为40m,高点距断层约为2.1km |
一般情况下探井位于“时间高点”附近,而在速度梯度的影响下,这种构造变化特征对油藏储量规模评估的影响非常明显,这里以一组二维数值模型为例讨论其影响程度。
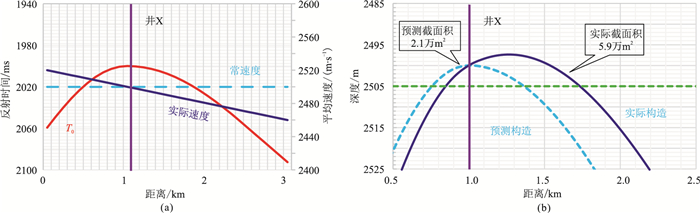
(1) 在时间域剖面存在一个圈闭幅度约40ms(2km范围内)的滚动背斜构造(图 8a)。
|
图 8 速度梯度对构造预测影响的数值模型 (a)M1层反射时间及速度分布; (b)实际构造与常速预测构造 |
(2) 探井X位于距断层1km的“时间高点”,并在M1层钻遇5m油柱,平均速度为2500m·s-1。
(3) 利用常速度预测深度构造,最大油柱为5m,则含油截面积约为2.1万m2;假定存在速度梯度(20m·s-1·km-1),利用实际速度预测深度构造,最大油柱约11m,则含油截面积约为5.9万m2,即预测结果与实际结果相差约1.8倍(图 8b)。
(4) 固定井点速度(2500m·s-1)、调整速度梯度(0~60m·s-1·km-1),可定量评价速度梯度对含油截面积的影响(图 9a);固定速度梯度(20m·s-1·km-1)、调整井点速度(2000~3000m·s-1),可定量评价速度对含油截面积的影响(图 9b)。可见:

|
图 9 速度梯度、速度与含油截面积交会图 (a)速度梯度—含油截面积; (b)速度—含油截面积 |
1) 速度梯度对油藏构造评估的影响较大,单井、常速度对构造的控制作用有限;
2) 速度梯度变化时,油藏规模呈指数变化。对于所设计模型,当速度梯度为60m·s-1·km-1时,常速度预测油藏规模约为实际油藏规模的1/50(图 9a);
3) 相对而言,井点平均速度对构造评价影响较小(图 9b)。
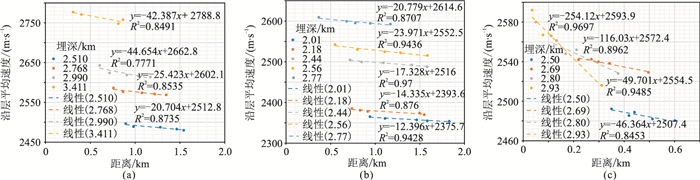
3 滚动背斜速度分布规律 3.1 速度变化特征通过统计南海东部HZ-A、XJ-B、LF-C油田不同层段、不同井点的钻井速度数据,并与井点距断层的距离进行回归分析(图 10),可见:①在远离断层的位置速度减小;②速度变化与埋深有关,即埋深越大速度变化越快;③井区距断层较近时,速度变化更快。因此,研究区同类构造速度变化与埋深、断层位置有关。
|
图 10 井点沿层平均速度y—井点距断层距离x交会图 (a)HZ-A油田;(b)XJ-B油田;(c)LF-C油田。R2为拟合系数,下同 |
图 10中线性拟合关系可反映油田范围速度梯度平均值(线性关系的斜率),并且具有一定代表性:①地层埋深为2.0~3.5km,涵盖南海东部大部分含油目的层;②井点距断层距离为0~2km,是滚动背斜的发育位置;③速度梯度的数值分布范围较广(10~254m·s-1·km-1),可降低无关因素影响。
基于上述数据分析速度梯度分布规律,包括以下步骤:
(1) 收集不同类型数据,包括各油田不同层段速度梯度、埋深、高点距断层距离(下文简称距离)、最大断距(下文简称断距)等。
(2) 将速度梯度与其他数据进行交会分析(图 11),可见:①速度梯度与距离相关性好,采用幂函数拟合(指数接近-1),表明速度梯度与距离近似呈反比(图 11a);②速度梯度与埋深(图 11b)、断距(图 11c)相关性较差,但存在一定正相关关系,说明速度梯度同时受埋深和断距影响。

|
图 11 滚动背斜沿层速度梯度y与不同参数x的交会图 (a)速度梯度—距离;(b)速度梯度—埋深;(c)速度梯度—断距 |
(3) 分别将梯度与距离倒数、埋深/距离、断距/距离、埋深×断距/距离等不同数据进行相关性分析(图 12),线性拟合系数均大于0.95,而常数项绝对值分别约为8.8(图 12a)、5.6(图 12b)、2.3(图 12c)、0.2(图 12d)。因此,加入埋深、断距数据有效减小了常数项,当略去常数项后,拟合关系式的地质意义更明确,即局部范围内速度梯度与断距、埋深呈正比、与距离呈反比。

|
图 12 滚动背斜沿层速度梯度y与组合数据x的相关性分析 (a)速度梯度—距离倒数;(b)速度梯度—埋深/距离;(c)速度梯度—断距/距离;(d)速度梯度—埋深×(断距/距离) |
(4) 基于上述分析,得到合并项(埋深×断距/距离)沿层速度梯度KVL数据(表 1),并将常数项设为0重新进行线性拟合(图 13a),得到经验公式
| ${K_{{\rm{VL}}}} \approx 46.35H{D_{\rm{F}}}/L $ | (2) |
|
|
表 1 南海东部滚动背斜沿层速度梯度数据 |

|
图 13 滚动背斜油田合并项x与沿层速度梯度y(a)、水平速度梯度y(b)交会图 |
式中:H为目的层埋深;DF为断距;L为构造距断层平均距离。
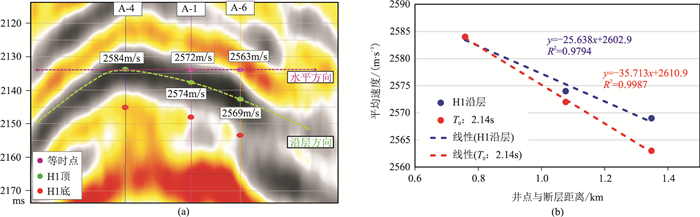
(5) 沿层平均速度受构造幅度影响,为降低该影响,进一步统计了水平切片的平均速度变化(图 14),对比了HZ-A油田某水平切片平均速度与H1沿层平均速度,沿层平均速度是在井点校正速度模型的基础上提取的井点等时速度(表 2)。
|
图 14 HZ-A油田H1沿层平均速度与邻近水平平均速度 (a)沿层速度与水平速度示意图;(b)H1沿层速度与水平速度数据分布(x为距离,y为平均速度) |
|
|
表 2 南海东部滚动背斜水平速度梯度数据 |
(6) 参考步骤(1)~(4),将水平速度梯度KVH与合并项进行相关性分析,得到经验公式
| ${K_{{\rm{VH}}}} \approx 63.83H{D_{\rm{F}}}/L $ | (3) |
式(3)表明,在上述油田局部范围内,水平平均速度横向变化率影响因素与沿层速度一致,但变化更快。油田范围内水平平均速度线性拟合系数(0.999)高于沿层平均速度拟合系数(0.98)(图 13b),表明利用KVH表征速度变化时构造变化的影响更小。
假设式(2)、式(3)中的系数为K,已知某井点(参考井)的平均速度为V0,距断层距离为L0,且局部研究范围内速度梯度不变,可求解深度H、下降盘平面位置(x, y)处的平均速度Vx, y
| ${V_{x,y}} \approx {V_0} - ({L_{x,y}} - {L_0})KH{D_{\rm{F}}}/{L_0} $ | (4) |
式中Lx, y为点(x, y)距断层距离,则Lx, y-L0表示点(x, y)与已知点在垂直断层方向的视距离。
当研究范围较大时,速度梯度随距离而变化,此时速度估算表达式为
| ${V_{x, y}} \approx {V_0} - KH{D_{\rm{F}}}\int_{{L_0}}^{{L_{x, y}}} {\frac{1}{l}{\rm{d}}l} $ | (5) |
求解定积分,得
| ${V_{x, y}} \approx {V_0} - KH{D_{\rm{F}}}\ln \frac{{{L_{x, y}}}}{{{L_0}}} $ | (6) |
相对于式(4),在远离断层位置式(6)的预测速度略大,因此构造预测风险相对较小。
4 构造评价方法及应用 4.1 梯度约束的平均速度预测基于式(2)、式(3),推荐两种针对滚动背斜构造的平均速度定量评价方法:①根据实钻井点(钻井较多), 结合式(2)勾绘目的层沿层平均速度趋势图,然后对等T0图时深转换获得深度构造图;②基于井点数据建立水平层状平均速度模型,然后利用式(3)计算速度梯度并校正该速度模型。方法①易于操作、效率较高。方法②实现过程相对复杂,但更适用于少井情况,这里详细介绍其实现流程:
(1) 对研究区钻井数据进行井震标定获得单井时深关系,若无钻井则利用周边区域时深关系在“时间高点”建立虚拟井;
(2) 从评价目的层段以上开始以较小的间隔(如50ms或100ms)建立一系列切片,利用式(6),取K=63.83,求解下降盘切片不同位置速度并勾绘速度趋势图;
(3) 利用井点速度、深度切片、速度趋势图建立梯度约束的水平层状平均速度模型;
(4) 利用上述速度模型将等T0图转换为等深度图。
4.2 LF-C油田应用K1是LF-C油田的一个高渗透的小型滚动背斜型油藏,处于特高含水期,采出程度60%以上,剩余油挖潜空间较小。研究前上钻的井C-6、C-7、C-8均加深,最大达11m(图 15a、图 15b),加剧了油田开发的被动局面。

|
图 15 LF-C油田K1时深关系及速度分布 (a)等T0图;(b)井C-6、C-7、C-8钻井前、后深度构造图;(c)原速度趋势图;(d)重新认识的速度趋势图 |
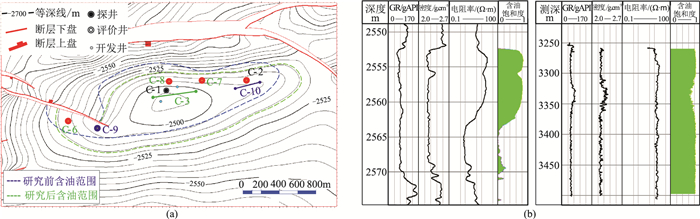
基于本次研究成果,利用方法①重新评价K1,与原速度趋势图(图 15c)相比,重新认识的速度趋势图(图 15d)在近似垂直断层方向,随着与断层距离变大,速度快速减小。由重新评价的深度构造图(图 16a)可见,井C-6东南侧约200m处出现局部高点,井C-2南侧也有抬升。在该认识指导下,在井C-6东南布设开发井C-9、在井C-2南侧布设水平开发井C-10,并成功投产(图 16b)。井C-9、C-10构造较原认识分别抬升约6、4m,其中井C-9由低部位抬升为高点,证实了方法的合理性。
|
图 16 重新评价的K1深度构造图(a)及井C-9(左)、C-10(右)测井解释曲线(b)绿色指示含油层位 |
HZ-D油田为一个小型滚动背斜油田(图 1d),仅有1口探井D-1位于“时间高点”(图 17a)。采用常规方法(单井时深关系)进行评价,含油面积仅为0.23km2,规模非常有限(图 17b)。

|
图 17 HZ-D滚动背斜含油构造潜力评价 (a)M1层等T0图; (b)M1层单井时深转换(对应切片速度为2746m·s-1); (c)M1层附近切片平均速度趋势图; (d)M1层深度构造图。主断层断距为0.25km, M1层埋深为0.33km, D-1井距断层0.46km |
利用本文研究成果,根据式(3)得到水平速度梯度约为112.5m·s-1·km-1,基于方法②获得M1层附近切片平均速度趋势图(图 17c)。基于一系列切片速度趋势建立速度模型,并对M1层进行时深转换,得到M1层深度构造图(图 17d)。对比研究前(图 17d蓝色虚线)、后(图 17d中红色虚线)含油范围可见,后者的高点向远离断层方向移动约200m,对应含油面积增至0.76km2。该油田其他油藏含油面积变化规律与M1层类似。因此,HZ-D油田在远离断层位置还有较大的挖潜空间。
5 成因机理探讨研究区小型滚动背斜构造速度变化的统计结果表明,速度在局部范围内具有远离断层方向快速减小的特征,且速度变化方向与断层走向有关,显然速度分布受断层影响。
根据滚动背斜的地质认识,该类构造主要发育在上陡下缓的“犁式”(或“椅式”)正断层的下降盘,其成因有多种解释,其中被广泛认可的有两种:①形成于后生断层,断层两盘地层分离,下降盘(上盘)在重力作用下发生扭曲形成背斜;②形成于同生断层,上盘构造位置低,近断层地层厚度较大,可压实空间及上覆地层重力大,地层向下变形形成背斜。根据地层的相对形态,滚动背斜近断层位置地层变形更大,反映该位置承受的挤压应力更大,地层压实作用增强(图 18a);如果在同生断层附近,显然近断层位置地层厚度变化更大、压实程度更高(图 18b)。另外,从应力的角度来看,如果把正断层的断面看作一种相对光滑的界面,那么上覆地层对下部地层的垂向应力会因断面的存在重新分布,下降盘近断层位置的应力会更大,同样导致下降盘近断层位置存在较强的压实作用(图 19b)。

|
图 18 滚动背斜地层变形示意图 (a)后生断层附近滚动背斜地层变形;(b)同生断层附近滚动背斜地层厚度变化 |

|
图 19 地层应力分布变化示意图 (a)无断层;(b)正断层参与F为上覆地层重力,箭头表示垂向应力分布 |
基于上述分析可知,在应力、应变作用下,下降盘近断层位置压实作用更强,地层速度直接受压实作用影响呈近断层位置速度相对增大、远离断层位置速度相对减小的特征。因此,本文认为远离断层位置速度快速减小的特征可能并不局限于南海东部,而是广泛存在于不同区域滚动背斜构造中,应引起业界重视。
另外,其他因素可能导致速度发生横向变化:①地层岩性会影响地层的差异压实作用[15-16],不同岩性的地层组合可能引起略有差异的速度梯度;②某些滚动背斜速度变化的方向与断层并不完全垂直(如LF-C油田),也就是说还存在平行断层方向的速度变化,反映了在断层走向上存在形态或力学性质的变化对速度的影响[17-19]。本文的实例有限,无法通过统计的方法逐一量化上述因素,但是在特定地质条件下这些因素可能对利用所提方法预测速度产生较大影响。
6 结论与认识本文基于南海东部开发阶段滚动背斜的钻探数据,分析该类构造速度变化特征,发现存在特征一致且可量化的速度变化。基于此研究构造影响特征及定量评价方法,并用于老油田的剩余油挖潜和新油田的滚动评价。获得以下结论与认识:
(1) 小型滚动背斜可能普遍存在速度在局部范围内具有远离断层方向快速减小的特征,出现近断层位置构造加深、远离断层位置构造抬升、深度高点相对时间高点远离断层的现象,影响油气勘探和开发。
(2) 地震资料高点往往是探井优选的位置,实钻及模拟分析结果显示,对于滚动背斜构造,若仅钻探“时间高点”,可能会误判含油气构造,有必要进一步评价。
(3) 研究区滚动背斜圈闭范围内速度梯度近似与埋深、断距呈正比,与距断层的距离呈反比,所获得的经验公式可定量评价该区同类构造。
(4) 根据油田的实钻结果,认为滚动背斜速度存在特定方向变化,但对问题的讨论仅限于少数油田数据以及现象的总结,还缺乏深层次的机理研究,认识和方法难免存在疏漏;本文目的在于对滚动背斜速度变化问题起到抛砖引玉的作用,以就教于业界专家。
| [1] |
李德生. 滚动背斜油气田[J]. 石油实验地质, 1980. DOI:10.11781/sysydz198002001 |
| [2] |
李晓清, 程有义, 熊保贤, 等. 正断层断面样式与上盘伴生褶皱及其油气勘探意义[J]. 石油地球物理勘探, 2001, 36(2): 205-212. LI Xiaoqing, CHENG Youyi, XIONG Baoxian, et al. Normal fault plane pattern and associated fold in upside and their meaning in oil-gas exploration[J]. Oil Geophysical Prospecting, 2001, 36(2): 205-212. DOI:10.3321/j.issn:1000-7210.2001.02.010 |
| [3] |
鲍倩倩, 吴智平, 李伟, 等. 济阳坳陷东营组沉积末期正反转构造研究[J]. 特种油气藏, 2009, 16(3): 31-34. BAO Qianqian, WU Zhiping, LI Wei, et al. Study on positive inversion structure in the end of Dongying sedimentation in Jiyang Depression[J]. Special Oil and Gas Reservoirs, 2009, 16(3): 31-34. DOI:10.3969/j.issn.1006-6535.2009.03.008 |
| [4] |
祁鹏, 任建业, 艾能平, 等. 歧口凹陷后裂陷期构造特征与浅层油气成藏[J]. 石油地球物理勘探, 2010, 46(6): 970-977. QI Peng, REN Jianye, AI Nengping, et al. Post-rifting structure characteristics and shallow hydrocarbon accumulations in Qikou sag[J]. Oil Geophysical Prospecting, 2010, 46(6): 970-977. |
| [5] |
曹彤, 王延斌. 辽河断陷盆地西部凹陷西斜坡齐欢地区同生断层发育特征及其控制作用[J]. 科技导报, 2016, 34(2): 116-120. CAO Tong, WANG Yanbin. Reservoir control of contemporaneous faults in Qihuan Area of Western Slope in the western depression of Liaohe River Rifted Basin[J]. Science & Technology Review, 2016, 34(2): 116-120. |
| [6] |
赵江, 王秋良, 卢圣力, 等. 尼日尔三角洲东部深水区构造特征及其形成机理[J]. 大地测量与地球动力学, 2019, 39(7): 691-695. ZHAO Jiang, WANG Qiuliang, LU Shengli, et al. Structural characteristics and formation mechanism of deep water in Eastern Niger Delta[J]. Journal of Geo-desy and Geodynamics, 2019, 39(7): 691-695. |
| [7] |
李爱山, 蔡文杰, 卢景美, 等. 墨西哥北部博格斯盆地石油地质条件与勘探潜力分析[J]. 海洋地质前沿, 2020, 36(7): 31-39. LI Aishan, CAI Wenjie, LU Jingmei, et al. Analysis on petroleum conditions and exploration potential in Burgos Basin, North of Mexico[J]. Marine Geology Frontiers, 2020, 36(7): 31-39. |
| [8] |
陈发景. 逆牵引背斜构造特征和成因[J]. 现代地质, 2008, 22(4): 664-668. CHEN Fajing. Structural characteristics and origin of reverse drag anticlines[J]. Geoscience, 2008, 22(4): 664-668. DOI:10.3969/j.issn.1000-8527.2008.04.026 |
| [9] |
张玮, 李明杰, 孙增玖, 等. 辽河油田大民屯凹陷东部陡坡带的构造演化特征[J]. 现代地质, 2008, 22(4): 489-494. ZHANG Wei, LI Mingjie, SUN Zengjiu, et al. The characteristics of structural evolution of the steep slope zone of the Eastern Part of the Damintun Depression, Liaohe Oilfield[J]. Geoscience, 2008, 22(4): 489-494. DOI:10.3969/j.issn.1000-8527.2008.04.001 |
| [10] |
黄晶. 滚动背斜形成演化机制——基于构造物理模拟分析[J]. 世界有色金属, 2017, 32(15): 264-266. HUANG Jing. Formation and evolution mechanism of rolling anticline: Based on structural physics simulation analysis[J]. World Nonferrous Metals, 2017, 32(15): 264-266. |
| [11] |
孟祥超, 韦学锐, 韩维哲. 差异压实作用中的同沉积小断层成因探讨——以高台子地区扶杨油层为例[J]. 大庆石油地质与开发, 2007, 26(6): 20-23. MENG Xiangchao, WEI Xuerui, HAN Weizhe. Origin of small-scaled syndepositional faults during differential compaction: Taking Fuyang reservoir in Gaotaizi area as an example[J]. Petroleum Geology and Oilfiled Development in Daqing, 2007, 26(6): 20-23. DOI:10.3969/j.issn.1000-3754.2007.06.005 |
| [12] |
卿勇. 大数据研究综述[J]. 软件导刊, 2016, 15(12): 175-177. |
| [13] |
张云志. 油田大数据分析模式研究[J]. 信息与电脑, 2020, 32(19): 4-6. ZHANG Yunzhi. Research on big data analysis of di-gital oilfield[J]. China Computer & Communication, 2020, 32(19): 4-6. DOI:10.3969/j.issn.1003-9767.2020.19.002 |
| [14] |
王奭. 基于大数据的高效数据挖掘算法及应用[J]. 信息与电脑, 2020, 32(19): 48-49. WANG Shi. Efficient data mining algorithm and application based on big data[J]. China Computer & Communication, 2020, 32(19): 48-49. |
| [15] |
董树政, 卢刚臣, 马军, 等. 对地震剖面中正断层几种特殊表现形式的认识[J]. 石油地球物理勘探, 2003, 38(1): 72-76. DONG Shuzheng, LU Gangchen, MA Jun, et al. Knowledge of several special representative features of normal fault on seismic section[J]. Oil Geophysical Prospecting, 2003, 38(1): 72-76. |
| [16] |
杨满平, 王翠姣, 王倩, 等. 鄂尔多斯盆地差异压实作用及其石油地质意义[J]. 河北工程大学学报(自然科学版), 2017, 34(2): 74-79. YANG Manping, WANG Cuijiao, WANG Qian, et al. Differential compaction in Ordos Basin and its petroleum geological significance[J]. Journal of Hebei University of Engineering (Natural Science Edition), 2017, 34(2): 74-79. |
| [17] |
海洋. 瓜什则盆地的地应力场分析与模拟[J]. 华南地震, 2019, 39(3): 101-108. HAI Yang. Analysis and simulation of in-situ stress field of Guashize Basin[J]. South China Journal of Seismology, 2019, 39(3): 101-108. |
| [18] |
刘佳庚, 李静, 苏玉亮, 等. 塔河油田奥陶系储层构造应力场研究[J]. 地质力学学报, 2020, 26(1): 48-54. LIU Jiageng, LI Jing, SU Yuliang, et al. Tectonic stress field research on the Ordovician reservoirs in the Tahe Oilfield[J]. Journal of Geomechanics, 2020, 26(1): 48-54. |
| [19] |
马妮, 印兴耀, 宗兆云, 等. 基于曲率属性的构造应力预测方法[J]. 石油地球物理勘探, 2020, 55(3): 643-650. MA Ni, YIN Xingyao, ZONG Zhaoyun, et al. Tectonic stress prediction method based on curvature attribute[J]. Oil Geophysical Prospecting, 2020, 55(3): 643-650. |



 刘振, 广东省深圳市南山区后海滨路(深圳湾段)3168号中海油大厦A座南海东部石油研究院, 518041。Email:
刘振, 广东省深圳市南山区后海滨路(深圳湾段)3168号中海油大厦A座南海东部石油研究院, 518041。Email: 