2 中国石化石油物探技术研究院, 江苏南京 211103;
3 北京大学地球与空间科学学院石油与天然气研究中心, 北京 100871
2 SINOPEC Geophysical Research Institute, Nanjing, Jiangsu 211103, China;
3 Institute of Oil & Gas, School of Earth and Space Sciences, Peking University, Beijing 100871, China
水力压裂储层改造技术可以在低孔、低渗地层中创造新的油气连接通道,从而达到压裂增产目的,是目前国内外页岩、低渗透等非常规油气藏开采中的重要技术手段[1-3]。微地震监测资料不仅包含震源位置、发震时刻以及震级大小等信息,还有震源机理信息,震源机理有助于了解压裂目标区的裂缝破裂状态、破裂面几何参数及储层区域应力分布状态等[4],对压裂效果评价及后续压裂方案制定具有重要意义。早期微地震震源机制研究参考天然地震,认为其震源机理以剪切(DC)成分为主,多使用剪切位错模型[5-6]。随着后续研究的深入,发现水力压裂引起的微震也通常含有较为明显的非DC成分[7-8],因此Vavryčuk[9]在剪切位错模型基础上通过引入张裂角参数增加震源的非DC成分。Aki等[10]系统描述了震源矩张量理论并将其应用于天然地震震源的研究。Vavryčuk[11]的理论研究表明,在无先验约束条件下各向同性介质中单井观测记录的纵波辐射模式不依赖震源矩张量M的M12、M22、M23元素,横波辐射模式不依赖M22元素,且对矩张量迹不敏感;P、S波联合反演时仍对M22元素不敏感,无法实现全矩张量反演。因此单井观测系统下的微地震震源机制反演通常需要对震源模型加以约束。
近年来,随着中国页岩气勘探的发展,微地震震源机制反演技术也得到了相当的发展。杨心超等[12-13]参考天然地震的研究成果,在地面观测系统下通过纵波初至极性进行了微地震事件的震源机制求解;翟鸿宇等[14]将震源正则化分解,讨论了地层吸收衰减因子的变化对微地震震源机制反演分辨率的影响;赵炜等[15]通过将震源假定为纯剪切型,利用波形能量特征进行了全空间网格搜索下的震源机制反演;李晗等[16-17]将震源约束为“剪切+张裂”一般位错模型,在频率域进行了地面和井中微震震源机制求解;唐杰等[18-19]的理论研究表明在剪张源约束下的单井、三井震源机制反演具有可行性,且比矩张量反演有更好的反演效果;谭玉阳等[20]用全波形匹配方法确定震源机制,并在此基础上发展了一种基于邻域算法、分级优化确定震源机制的方法。
以上研究表明,单井观测系统下的有效微地震震源机制反演及其处理流程仍不成熟,需要做更为深入的研究。
本文首先介绍了“剪切—张裂”震源(剪张源)模型及矩张量加载下的微地震波场正演方法;然后,在前人研究基础上提出了一种基于波形能量和极性的反演方法;最后,将该方法应用于模型数据和实际资料,并对结果进行了分析和讨论。
1 方法原理 1.1 矩张量与剪张源张量为了描述不同类型的地震震源,Gilbert[21]首先提出将不同方向的力矩整合到一个张量
| $ \boldsymbol{M}=M_{0}\left[\begin{array}{lll} M_{11} & M_{12} & M_{13} \\ M_{21} & M_{22} & M_{23} \\ M_{31} & M_{32} & M_{33} \end{array}\right] $ | (1) |
式中:M0为标量地震矩;Mij=Mji,表示矩张量M具有对称性,实际只需要求解6个元素。
同矩张量相比,剪张源将震源模型限定为断层错位产生,其张量既包含剪切成分也包含涨缩部分。与剪切源相比,剪张源位错矢量v一般与断面斜交,斜交角度定义为张裂角α,取值范围为[-90°,90°]。用断层面走向角φ、倾角δ、滑动角ψ和张裂角α表示的断面法向矢量n、位错矢量v、剪张源张量D分别为
| $ \left\{\begin{array}{l} n_{1}=-\sin \delta \sin \varphi \\ n_{2}=\sin \delta \cos \varphi \\ n_{3}=-\cos \delta \end{array}\right. $ | (2) |
| $ \left\{\begin{aligned} v_{1}=&(\cos \psi \cos \varphi+\cos \delta \sin \psi \sin \varphi) \cos \alpha-\\ & \sin \delta \sin \varphi \sin \alpha \\ v_{2}=&(\cos \psi \sin \varphi-\cos \delta \sin \psi \cos \varphi) \cos \alpha+\\ & \sin \delta \cos \varphi \sin \alpha \\ v_{3}=&-\sin \psi \sin \delta \cos \alpha-\cos \delta \sin \alpha \end{aligned}\right. $ | (3) |
| $ \begin{aligned} &\boldsymbol{D}=\frac{T}{2}\left(\boldsymbol{n}^{\mathrm{T}} \boldsymbol{v}+\boldsymbol{v}^{\mathrm{T}} \boldsymbol{n}\right) \\ &=\frac{T}{2}\left[\begin{array}{ccc} 2 n_{1} v_{1} & n_{1} v_{2}+n_{2} v_{1} & n_{1} v_{3}+n_{3} v_{1} \\ n_{1} v_{2}+n_{2} v_{1} & 2 n_{2} v_{2} & n_{2} v_{3}+n_{3} v_{2} \\ n_{1} v_{3}+n_{3} v_{1} & n_{2} v_{3}+n_{3} v_{2} & 2 n_{3} v_{3} \end{array}\right] \end{aligned} $ | (4) |
式中T为震源强度。
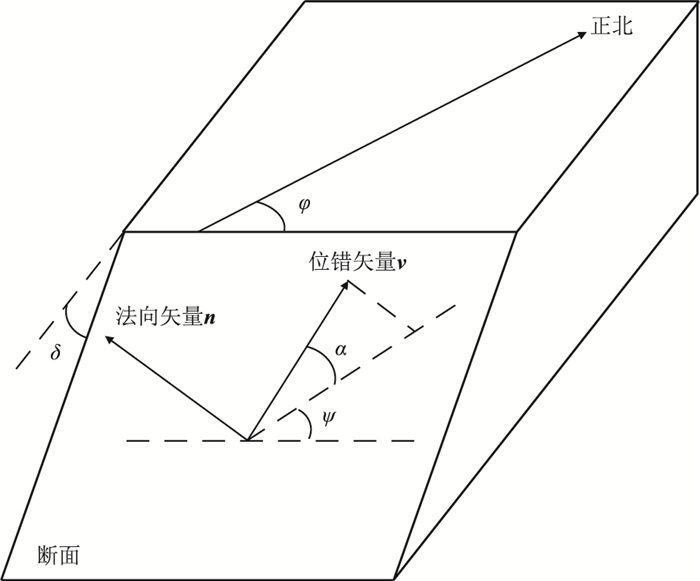
|
图 1 剪切—张裂源模型示意图 |
各向异性介质中矩张量M与剪张源张量D的关系[22]为
| $ M_{i j}=c_{i j k l} D_{k l} $ | (5) |
各向同性介质中可以简化为
| $ M_{i j}=\lambda D_{k k} \delta_{i j}+2 \mu D_{i j} $ | (6) |
式中:cijkl为介质弹性参数;λ、μ为介质的拉梅系数;δij为克罗内克函数。
1.2 矩张量微地震波场记录正演Aki等[10]将各向同性介质中矩张量震源下的远波场表示为
| $ \begin{aligned} u_{i}(\boldsymbol{x}, t)=& \frac{R_{i}^{\mathrm{P}} f\left(t-\tau^{\mathrm{P}}\right)}{4 {\rm{ \mathsf{ π} }} \rho r A^{3}}+\frac{R_{i}^{\mathrm{SH}} f\left(t-\tau^{\mathrm{SH}}\right)}{4 {\rm{ \mathsf{ π} }} \rho r B_{\mathrm{SH}}^{3}}+\\ & \frac{R_{i}^{\mathrm{SV}} f\left(t-\tau^{\mathrm{SV}}\right)}{4 {\rm{ \mathsf{ π} }} \rho r B_{\mathrm{SV}}^{3}} \end{aligned} $ | (7) |
式中:ui(x, t)表示x处t时刻i方向的波场;ρ为介质密度;r为震源与检波器间的距离;A、BSV和BSH分别为P波、SV波和SH波速度;f为震源函数对时间的偏导;τP、τSV、τSH为三种波震源到检波器的旅行时;RiP、RiSH和RiSV为三种波的辐射模式函数,经过数学推导和Einstein求和约定可以简写为
| $ R_{i}^{\mathrm{P}}=m_{i} m_{j} m_{k} M_{j k} $ | (8) |
| $ R_{i}^{\mathrm{S}}=\delta_{i j} m_{k} M_{i j}-R_{i}^{\mathrm{P}} $ | (9) |
| $ R_{i}^{\mathrm{SV}} =q_{i} q_{j} R_{i}^{\mathrm{S}} $ | (10) |
| $ R_{i}^{\mathrm{SH}} =o_{i} o_{j} R_{j}^{\mathrm{S}} $ | (11) |
式中m、q、o分别为P波、SV波和SH波从震源点到检波点波的初始振动方向单位向量,且相互正交,可表示为
| $ \left\{\begin{array}{l} \boldsymbol{m}=(\sin \beta \cos \theta, \sin \beta \sin \theta, \cos \beta) \\ \boldsymbol{q}=(\cos \beta \cos \theta, \cos \beta \sin \theta,-\sin \beta) \\ \boldsymbol{o}=(-\sin \theta, \cos \theta, 0) \end{array}\right. $ | (12) |
其中β和θ分别表示射线方向与垂直方向和正北方向的夹角。各向同性介质中,SV波和SH波传播速度一致且相互耦合,S波可直接由RiS计算。
1.3 基于波形能量和极性的震源机制反演方法由于震源机制与微地震事件记录的初至极性和波形能量之间存在很强的关联性,本文设计了一种基于微地震事件记录初至极性和波形能量的震源机制反演方法。该方法的具体流程如下。
(1) 通过微地震监测资料、测井资料和射孔资料等获得微地震事件波形记录,及其对应的震源位置、观测点位置、地层速度模型等信息。
(2) 井中微地震资料偏振归位处理。根据射孔资料,震源和检波器相对位置信息进行偏振角的计算,并进行偏振处理实现三分量记录中水平分量波形记录旋转为观测坐标系统下的x和y分量。
(3) 利用微地震事件P、S波初至选取有效时窗长度k。实际微地震事件能量大小不一导致振幅数据不一致,为消除震级大小影响,需要对事件进行振幅归一化。计算振幅归一化后波形窗口内P、S波能量EIP和EIS
| $ \left\{\begin{array}{l} E_{I}^{\mathrm{P}}=\sum\limits_{t=t_{\mathrm{P}}}^{t_{\mathrm{P}}+k_{\mathrm{P}}} W_{I}^{2}(t) \\ E_{I}^{\mathrm{S}}=\sum\limits_{t=t_{\mathrm{S}}}^{t_{\mathrm{S}}+k_{\mathrm{S}}} W_{I}^{2}(t) \end{array}\right. $ | (13) |
式中:WI为第I个检波器的振幅归一化后微地震数据;P、S波时窗长度kP、kS一般选取一致;tP、tS分别为P、S波初至时间。
(4) 实际微地震事件波形初至极性PI识别和主频分析。初至极性为正极性记为1,负极性记为-1,正演时子波采用雷克子波对时间的偏导数,该函数的初至为负值,因此实测资料中初至为负值时表现为正极性,初至为正值时表现为负极性;主频会影响子波的“胖瘦”程度,从而影响能量计算,而且实际井中观测的微地震事件P、S波主频不完全一致,有时会有较大差别而造成反演误差。
(5) 在不同走向角φ、倾角δ、滑动角ψ和张裂角α网格剖分下正演的波场记录后,根据步骤(3)、步骤(4)求取该网格点模型正演的P、S波波场能量eIP和eIS以及初动极性pn,设计目标函数
| $ \begin{aligned} F=& \sum\limits_{I=1}^{N} \sum\limits_{i=1}^{3}\left(a_{1}\left|E_{i, I}^{\mathrm{P}}-e_{i, I}^{\mathrm{P}}\right|+\right.\\ &\left.a_{2}\left|E_{i, I}^{\mathrm{S}}-e_{i, I}^{\mathrm{S}}\right|+a_{3}\left|P_{i, I}-p_{i, I}\right|\right) \end{aligned} $ | (14) |
以计算实际监测记录和理论波形的匹配程度。式中:N表示井下监测检波器的个数;a1、a2、a3为权重系数。
(6) 选取一定量极小目标函数网格点对应解,并继续向下剖分,重复步骤(5),直至满足求解精度要求。
2 模型测试 2.1 模型正、反演模型为三层均匀各向同性介质,参数如表 1所示。震源位于(200m,200m,2500m),三分量井中检波器位于(375m,375m,2300~2700m),共21级,间隔为20m,时间采样间隔为0.5ms,观测系统如图 2所示。
|
|
表 1 速度模型参数 |

|
图 2 模型及观测系统 |
加载的φ=60°、δ=45°、ψ=60°和α=10°的“剪张型”震源在泊松比为0.25介质中的震源机制参数如表 2所示,该源的Hudson投影[23]及沙滩球表示如图 3所示。在确定震源位置、各级检波器位置以及速度模型后,利用射线追踪方法确定透射波在各层中的传播路径和旅行时。结合波在震源层传播路径和式(7)取得波在震源层的传播波场,之后计算各层透射系数得到波从震源位置出发到检波器位置的波场振幅系数,最后在时间域与雷克子波对时间的偏导函数褶积合成三分量微地震事件透射波记录,如图 4所示。三分量波形记录中可以明显观察到直达P和S波,且横波能量强于纵波。
|
|
表 2 剪张型模拟震源的参数 |
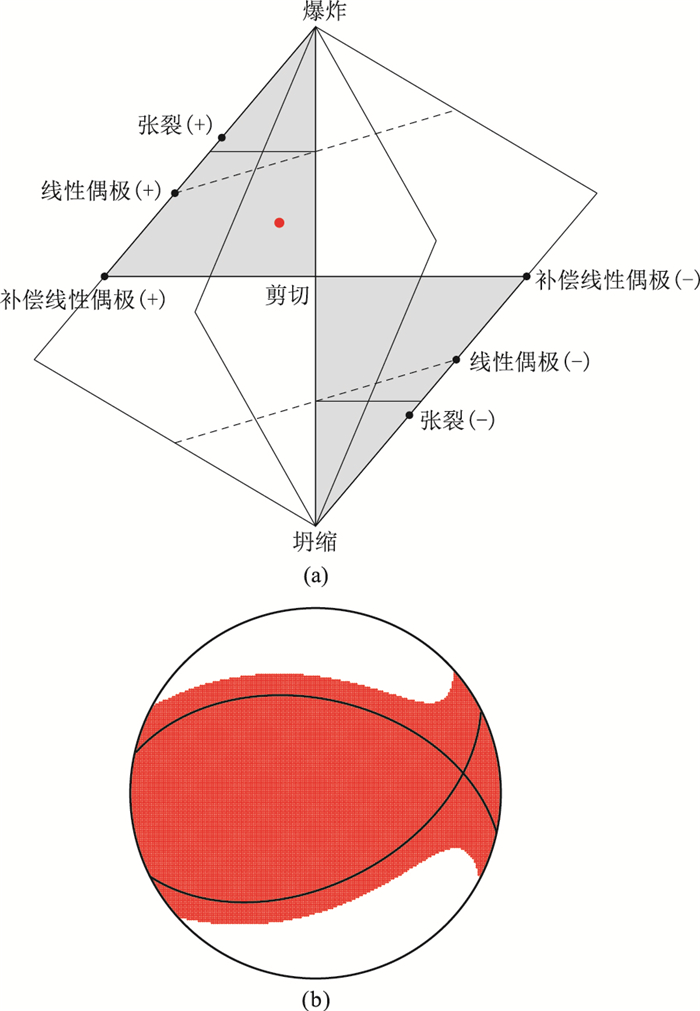
|
图 3 剪张型震源机制的Hudson投影(a)及沙滩球表示(b) |

|
图 4 三层水平层状介质正演三分量微地震事件透射波波形记录 |
针对合成的井中三分量微地震波形记录,按照上述方法进行反演,反演结果的φ=60°、δ=45°、ψ=60°和α=10°,与正演参数一致,验证了本文反演方法的可行性。固定α=10°时,φ、δ和ψ参数的全空间网格搜索下目标函数残差如图 5所示。值得注意的是目标函数残差在φ=300°、δ=45°、ψ=120°处存在另一个“蓝色”收敛区域。经分析,该区域为所设震源的共轭断面解,但其目标函数残差仍略大于真实解。针对震源机制反演目标函数的多个局部收敛域,在实际资料反演时,前期较大间隔网格搜索时选取继续向下剖分网格点的数量可依据目标函数的极值设置为3~4个,以保证收敛到全局最优解。
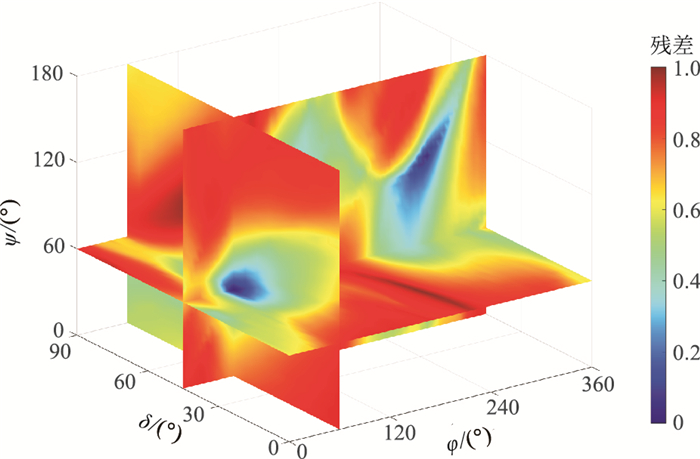
|
图 5 模拟数据反演目标函数残差在走向角、倾向角和滑动角三参数的全网格分布 |
理论上φ、δ、ψ和α的取值范围分别为[0°,360°]、[0°,90°]、[0°,180°]和[-90°,90°]。本文设计的初始网格剖分间隔为10°,则会形成129960(36×10×19×19)种不同的“剪张型”震源三分量观测记录。首先对无噪声条件下的微地震合成记录进行“剪张型”震源机制反演,反演过程中采用式(14)作为目标函数,反演的φ、δ、ψ和α的误差统计如图 6所示。将0°误差区间的样本占比等效为反演准确率。由图可以看出,在无噪声情况下,φ和ψ反演准确率超过81%,δ和α反演准确率超过98%。在全空间下的反演准确率可以说明“剪张源”模型参数对矩张量大小影响程度依次为:张裂角>倾角>走向角>滑动角。
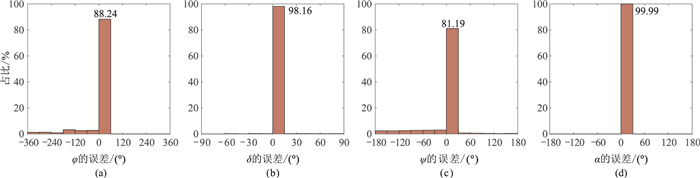
|
图 6 无噪声情况下走向角(a)、倾向角(b)、滑动角(c)和张裂角(d)的反演误差统计 |
由图 6可见,误差主要集中在φ和ψ,δ存在小部分误差。由于模型参数已固定,影响反演误差只包含矩张量因素,在某些情况下不同“剪张源”参数表示的矩张量相同。经过对误差分析认为造成δ误判的规律并不明显,发现当φ超过90°后存在小部分解与走向相差90°和180°所表示的矩张量相同造成δ的误判,是真解的共轭断面解,例如(230°,90°,10°,0°)与(140°,80°,180°,0°)、(230°,10°,90°,10°)与(50°,70°,90°,10°),误判的数量约为整体样本数的1.84%。φ误判的原因有两类,一类与造成δ误判的原因类似,该类误判约占φ误判样本的17.93%;其二是当δ为0°、α固定不变时,φ和ψ改变相同大小度数时矩张量不发生变化,例如(0°,0°,0°,30°)与(10°,0°,10°,30°)和(20°,0°,20°,30°)所表示的矩张量相同,该类误判约占φ误判样本的82.07%。而造成ψ误判的原因除与φ误判的两类外,当α为-90°或90°时,固定走向和倾向后,矩张量将不随ψ改变而改变,例如(30°,50°,30°,-90°)与(30°,50°,80°,-90°)表示矩张量相同,该类误判约占ψ误判样本的55.96%。
由上述误差原因分析可见,除造成δ误判的原因不规律外,其余都是由于δ和α在其极值处的某些特定情况,而实际资料震源机制反演中该类特殊极值情况极少,因此认为本文方法对实际资料的震源机制反演具有可行性。
2.3 含噪声数据及扰动速度模型反演本文应用合成数据加噪及扰动速度模型测试反演算法的稳定性。扰动速度模型参数如表 3所示,其中P波速度进行10%扰动,并保持纵横波速度比不变。合成信号的信噪比通过下式计算
| $ \mathrm{SNR}=20 \lg \frac{\|S\|_{F}}{\|\xi\|_{F}} $ | (15) |
|
|
表 3 扰动速度模型参数 |
式中:‖●‖F表示信号的F范数,通常选取1或2范数;S为有效微地震信号;ξ为随机噪声。
采用本文提出的基于微地震事件波形能量和极性反演方法,不同信噪比及速度模型扰动10%情况下的129960个“剪张型”震源机制的走向角、倾向角、滑动角和张裂角反演误差分布如图 7所示。在40dB信噪比时,各参数反演误差分布情况同无噪声数据类似,都保持较高准确率。随着信噪比的降低,各参数反演误差逐渐增大,在10dB信噪比下, ψ作为最低准确率参数仍能超过51%,表明该方法有较强的抗噪性。在10%速度模型的扰动下,δ和α参数准确率超过84%,但φ和ψ参数准确率降低较为明显,其中ψ参数准确率最低,为58%。为了保证实测资料震源机制反演的有效性,应当选取尽可能准确的速度模型和高信噪比微地震事件反演震源机制。

|
图 7 不同信噪比及扰动速度模型情况下“剪张型”震源机制的四个参数反演误差统计 (a)40dB信噪比;(b)10dB信噪比;(c)速度模型扰动10% |
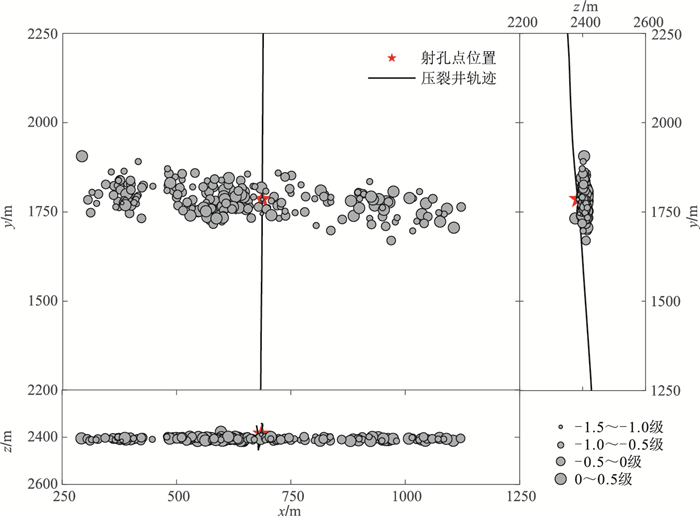
实际资料来源于中国M页岩区一口水平油气井第11压裂段的微地震监测,压裂深度约为2385m。观测系统为一组22级井中检波器,级间距为20m,时间采样间隔为0.5ms。通过声波测井数据获得的P、S波速度模型如图 8所示。该次压裂时长为3.1小时,通过长、短时窗比(STA/LTA)法共识别出216个有效微地震事件,压裂微地震震源定位结果如图 9所示,经过筛选216个有效微地震事件,选取出123个信噪比较高、有效信号明显的微地震事件作为目标事件进行“剪张源”约束下的震源机制反演。

|
图 8 工区速度模型 |
|
图 9 水力压裂微地震震源定位结果 |
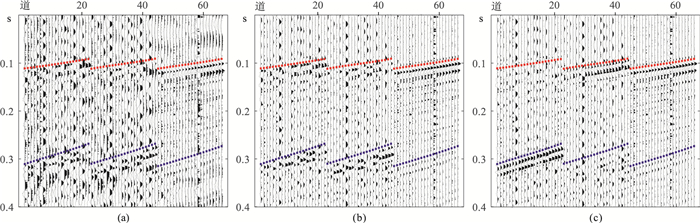
在识别出有效微地震事件之后,首先要对原始三分量数据(图 10a)进行30~300Hz的带通滤波以提高信噪比(图 10b);再根据射孔资料信息和震源定位结果进行偏振分析和水平分量旋转(图 10c)。
|
图 10 实际三分量监测资料及预处理结果 (a)原始记录;(b)带通滤波记录;(c)水平分量旋转记录。1~22道为x分量;23~44道为y分量;45~66道为z分量 红色和蓝色虚线分别表示手动拾取的P和S波初至 |
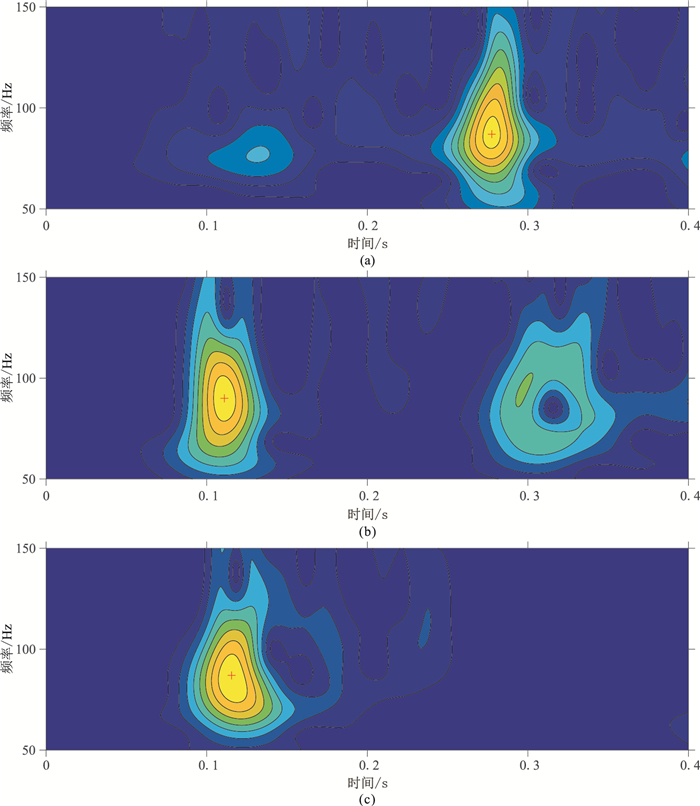
单井观测系统下的微地震实际资料,由于震动方式不同,地层对P、S波的吸收衰减程度不完全相同,特别是在页岩这类各向异性性质较为明显的地层当中差别会更大。因此,实际监测到的微地震事件中P、S波主频不会完全一致。显然,主频会直接影响到子波的“胖瘦”程度,也就是信号的能量大小。因此,事件的纵、横波主频分析十分必要。为了减小微地震事件主频对能量计算的影响,提高反演精度,本文采用S变换进行微地震信号时频分析[24-26]。第一个目标事件的微地震事件时频分析结果如图 11所示,P、S波主频大致分别约为90Hz(y、z分量的红色“+”所示)和87Hz(x分量的红色“+”所示)。本文在图 10c水平分量旋转后采用能量比法从x分量拾取S波初至(蓝色虚线),从y和z分量拾取P波初至(红色虚线)。
|
图 11 三分量微地震记录时频率分析结果 (a)x分量;(b)y分量;(c)z分量。红色“+”标示初至主频位置 |
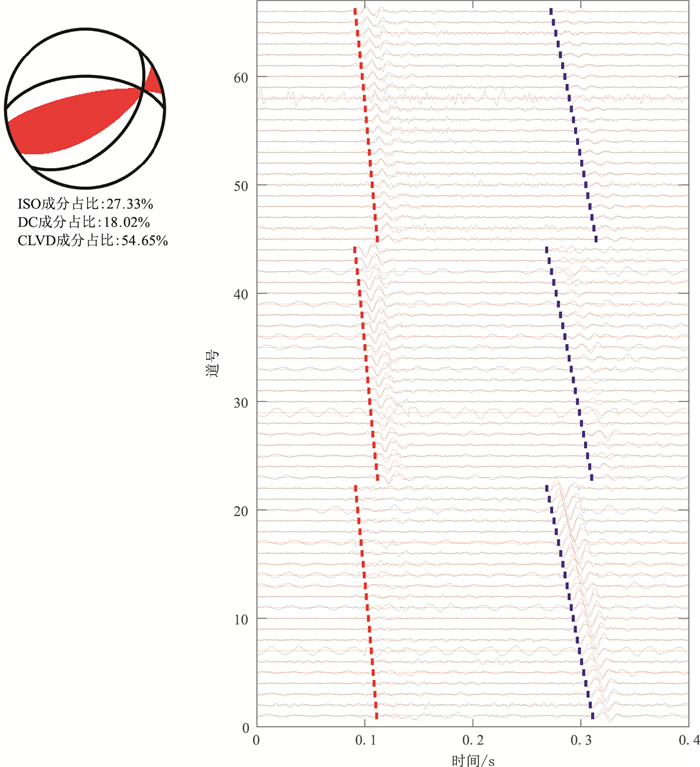
经过资料的预处理后,应用本文提出的基于波形能量和极性的“剪张型”震源机制反演方法,对第一个目标微地震事件反演结果如图 12所示。最终该事件反演结果φ=258.40°、δ=76.80°、ψ=116.00°、α=-44.00°。对比实际数据波形和震源机制反演结果的理论正演波形可以看出,大部分波形数据匹配较好,除去资料处理和部分道资料监测质量较差的影响,在不考虑地层各向异性条件下,可以认为本文方法的震源机制反演结果可靠。
|
图 12 井中观测第一个目标微地震事件震源机制反演结果和对应波形拟合 黑色实线表示实际数据波形,红色实线曲线表示反演结果的理论正演记录;红色和蓝色虚线分别表示手动拾取的纵波和横波初至。1~22道为x分量;23~44道为y分量;45~66道为z分量 |
图 13和图 14分别是反演出的震源机理沙滩球显示和各反演参数的分布。图 13中不同颜色表示不同成分占优的震源类型,从中可以看出该页岩压裂段的震源类型主要为DC型(DC成分占优)和CLVD型(CLVD成分占优),且CLVD型多于DC型。从震源机制反演结果可见,裂缝走向主要集中在南偏西85°附近,与压裂产生的东西向主裂缝一致;裂缝破裂面主要是倾角约为75°的高角度缝,其次是倾角约为40°的中倾角缝;裂缝滑动角集中在120°及其正交方向30°附近,裂缝张裂角主要分布在-10°附近,表明该段页岩压裂大部分岩石破裂时的受力状态是向内的挤压力大于向外的扩张力。

|
图 13 123个目标微地震事件震源机制反演结果的沙滩球显示 |
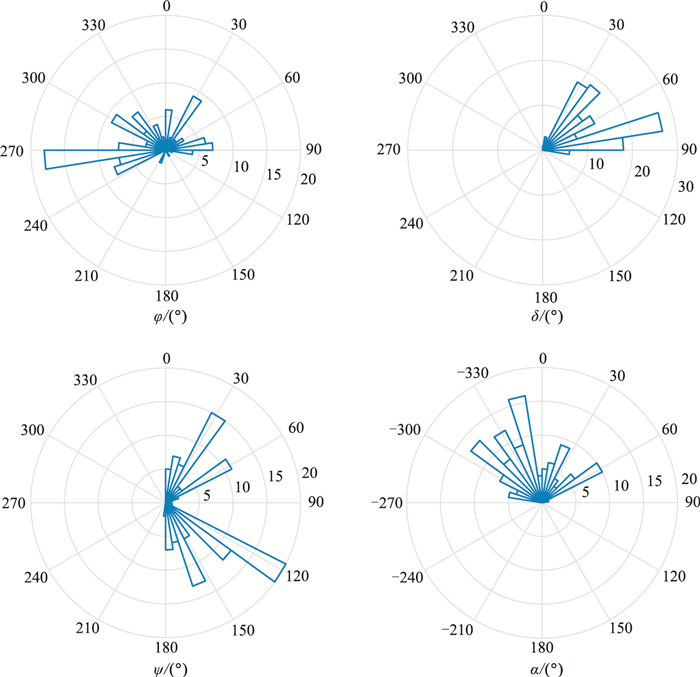
|
图 14 微地震事件破裂面走向角、倾向角、滑动角及张裂角分布 扇形的长度表示事件个数 |
图 15是微地震事件震源三种成分的占比统计结果。其中ISO成分的占比一般不超过45%且集中分布在30%左右;CLVD成分占比一般不超过75%,其中60%附近分布最广;DC成分的占比与震源类型密切相关,在非DC型震源中DC占比一般不超过20%,而在DC型震源中占比可达30%~100%。图 16为微地震事件反演的震源机制Hudson映射图,左上和右下分别表示岩石受由内向外扩张力的作用导致岩石破裂形成的张开型裂缝和岩石受由外向内挤压力的作用导致岩石破裂形成的闭合(内塌)型裂缝。从图中可以看出该段页岩水力压裂过程中, 随着压裂的进行,岩石主要受一对或者双对不同大小力偶造成岩石的破裂和滑移,并且岩石受挤压破裂形成的闭合型裂缝多于受扩张破裂形成的张开型裂缝,但无论是张开型还是闭合型裂缝,都应是在地层原生裂缝或原有小型断层的基础上形成的新裂缝。

|
图 15 微地震事件震源三种成分的占比统计直方图 |

|
图 16 实际微地震事件震源机制Hudson投影 |
本文在将水力压裂的震源约束为“剪—张”类型基础上,提出了一种基于微地震监测资料的波形能量和初至极性结合的单井微地震震源机制反演方法。合成数据测试结果表明该反演方法具有较高的准确性和较强的抗噪性,其中各参数的抗噪能力依次为:张裂角>倾角>走向角>滑动角。将本文方法用于国内M区页岩压裂信噪比较高的微地震事件,震源机制反演结果表明,该段压裂的微地震事件主要由岩体受一对力偶或两对大小不同力偶的破裂和滑移形成,且岩石受挤压破裂形成的闭合型裂缝要多于受扩张破裂形成的张开型裂缝。在单井观测系统条件下,该方法对合成数据和实际资料均取得了较好的反演效果,反演的破裂断面各参数稳定、可靠。
本文反演过程中暂未考虑地层各向异性的影响,若在资料处理过程中能够获得可靠的地层各向异性信息,将会使得反演结果更为准确。
| [1] |
Maxwell S C, Urbancic T I. The role of passive microseismic monitoring in the instrumented oil field[J]. The Leading Edge, 2001, 20(6): 636-639. DOI:10.1190/1.1439012 |
| [2] |
邹才能, 张国生, 杨智, 等. 非常规油气概念、特征、潜力及技术——兼论非常规油气地质学[J]. 石油勘探与开发, 2013, 40(4): 385-399. ZOU Caineng, ZHANG Guosheng, YANG Zhi, et al. Geological concepts, characteristics, resource potential and key techniques of unconventional hydrocarbon: On unconventional petroleum geology[J]. Petroleum Exploration and Development, 2013, 40(4): 385-399. |
| [3] |
刘振武, 撒利明, 杨晓, 等. 页岩气勘探开发对地球物理技术的需求[J]. 石油地球物理勘探, 2011, 46(5): 810-818. LIU Zhenwu, SA Liming, YANG Xiao, et al. Needs of geophysical technologies for shale gas exploration[J]. Oil Geophysical Prospecting, 2011, 46(5): 810-818. |
| [4] |
唐杰, 温雷, 王浩, 等. 正交各向异性介质中的剪张源震源机制与矩张量特征[J]. 石油地球物理勘探, 2018, 53(6): 1247-1255. TANG Jie, WEN Lei, WANG Hao, et al. Focal me-chanisms and moment tensor in orthorhombic anisotropic media[J]. Oil Geophysical Prospecting, 2018, 53(6): 1247-1255. |
| [5] |
Pearson C. The relationship between microseismicity and high pore pressures during hydraulic stimulation experiments in low permeability granitic rocks[J]. Journal of Geophysical Research: Solid Earth, 1981, 86(B9): 7855-7864. DOI:10.1029/JB086iB09p07855 |
| [6] |
Phillips W S, Fairbanks T D, Rutledge J T, et al. Induced microearthquake patterns and oil-producing fracture systems in the Austin Chalk[J]. Tectonophysics, 1998, 289(1-3): 153-169. DOI:10.1016/S0040-1951(97)00313-2 |
| [7] |
Foulger G, Julian B, Hill D, et al. Non-double-couple microearthquakes at long valley caldera, California, provide evidence for hydraulic fracturing[J]. Journal of Volcanology Geothermal Research, 2004, 132(1): 45-71. DOI:10.1016/S0377-0273(03)00420-7 |
| [8] |
Šílenỳ J, Hill D P, Eisner L, et al. Non-double-couple mechanisms of microearthquakes induced by hydraulic fracturing[J]. Journal of Geophysical Research: Solid Earth, 2009, 114(B8): 1621-1643. |
| [9] |
Vavryčuk V. Inversion for parameters of tensile earthquakes[J]. Journal of Geophysical Research: Solid Earth, 2001, 106(B8): 16339-16355. DOI:10.1029/2001JB000372 |
| [10] |
Aki K, Richards P G. Quantitative Seismology (Se-cond Edition)[M]. Sau-salito, California: University Science Books, 2002.
|
| [11] |
Vavryčuk V. On the retrieval of moment tensors from borehole data[J]. Geophysical Prospecting, 2007, 55(3): 381-391. DOI:10.1111/j.1365-2478.2007.00624.x |
| [12] |
杨心超, 朱海波, 崔树果, 等. 纵波初动震源机制解在水力压裂微地震监测中的应用[J]. 石油物探, 2015, 54(1): 43-50. YANG Xinchao, ZHU Haibo, Cui Shuguo, et al. Application of P-wave first-motion focal mechanism solutions in microseismic monitoring for hydraulic fracturing[J]. Geophysical Prospecting for Petroleum, 2015, 54(1): 43-50. DOI:10.3969/j.issn.1000-1441.2015.01.006 |
| [13] |
杨心超, 朱海波, 李宏, 等. 基于纵波辐射花样的压裂微地震震源机制反演方法研究及应用[J]. 石油物探, 2016, 55(5): 640-648. YANG Xinchao, ZHU Haibo, LI Hong, et al. Microseismic focal mechanism inversion based on P-wave radiation pattern and its application[J]. Geophysical Prospecting for Petroleum, 2016, 55(5): 640-648. DOI:10.3969/j.issn.1000-1441.2016.05.002 |
| [14] |
翟鸿宇, 常旭, 王一博. 含衰减地层微地震震源机制反演及其反演分辨率[J]. 地球物理学报, 2016, 59(8): 3025-3036. ZHAI Hongyu, CHANG Xu, WANG Yibo, et al. Inversion for microseismic focal mechanisms in attenuated strata and its resolution[J]. Chinese Journal of Geophysics, 2016, 59(8): 3025-3036. |
| [15] |
赵炜, 辛维, 毛中华, 等. 利用单井微地震波形能量反演震源机制[J]. 石油地球物理勘探, 2018, 53(5): 945-953. ZHAO Wei, XIN Wei, MAO Zhonghua, et al. Focal mechanism inversion with single-well microseismic wave energy[J]. Oil Geophysical Prospecting, 2018, 53(5): 945-953. |
| [16] |
李晗, 姚振兴. 基于"剪切+张裂"一般位错模型频率域求解微震震源机制[J]. 地球物理学报, 2018, 61(3): 905-916. LI Han, YAO Zhenxing. Microseismic focal mechanism inversion in frequency domain based on general dislocation point model[J]. Chinese Journal of Geophysics, 2018, 61(3): 905-916. |
| [17] |
李晗, 常旭. 微地震震源机制研究进展[J]. 中国科学: 地球科学, 2021, 51(3): 325-338. LI Han, CHANG Xun. A review of the microseismic focal mechanism research[J]. Science China: Earth Sciences, 2021, 51(3): 325-338. |
| [18] |
唐杰, 温雷, 李聪, 等. 水力压裂诱发的剪张型微地震震源机制矩张量反演方法[J]. 石油地球物理勘探, 2019, 54(4): 826-835. TANG Jie, WEN Lei, LI Cong, et al. Hydraulic-fracturing shear-tensile microseismic focal mechanism moment tensor inversion[J]. Oil Geophysical Prospecting, 2019, 54(4): 826-835. |
| [19] |
唐杰, 李聪, 刘英昌, 等. 剪张源约束的井中微地震震源机制反演方法[J]. 石油地球物理勘探, 2020, 55(1): 126-135. TANG Jie, LI Cong, LIU Yingchang, et al. Moment tensor inversion method from borehole data constrained by shear-tensile source model[J]. Oil Geophysical Prospecting, 2020, 55(1): 126-135. |
| [20] |
谭玉阳, 胡隽, 张海江, 等. 利用全波形匹配方法确定水力压裂诱发地震震源机制[J]. 地球物理学报, 2019, 62(11): 4417-4436. TAN Yuyang, HU Jun, ZHANG Haijiang, et al. Source mechanism determination for hydraulic fracturing induced seismicity using full-waveform matching[J]. Chinese Journal of Geophysics, 2019, 62(11): 4417-4436. DOI:10.6038/cjg2019M0516 |
| [21] |
Gilbert F. Excitation of the normal modes of the Earth by earthquake sources[J]. Geophysical Journal International, 1971, 22(2): 223-226. DOI:10.1111/j.1365-246X.1971.tb03593.x |
| [22] |
Vavryčuk V. Focal mechanisms in anisotropic media[J]. Geophysical Journal International, 2005, 161(2): 334-346. DOI:10.1111/j.1365-246X.2005.02585.x |
| [23] |
Hudson J, Pearce R, Rogers R. Source type plot for inversion of the moment tensor[J]. Journal of Geophysical Research, 1989, 94(1): 765-774. |
| [24] |
Stockwell R G, Mansinha L, Lowe R P. Localization of the complex spectrum: the S transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001. DOI:10.1109/78.492555 |
| [25] |
王小杰, 印兴耀, 吴国忱. 基于S变换的吸收衰减技术在含气储层预测中的应用研究[J]. 石油物探, 2012, 51(1): 37-42. WANG Xiaojie, YIN Xingyao, WU Guochen. The application of an S transform based absorption and attenuation technique for prediction of gas-bearing re-servoir[J]. Geophysical Prospecting for Petroleum, 2012, 51(1): 37-42. |
| [26] |
李波, 文晓涛, 张懿疆, 等. 基于Lucy-Richardson算法和广义S变换的Q值提取[J]. 石油物探, 2019, 58(5): 689-699. LI Bo, WEN Xiaotao, ZHANG Yijiang, et al. Combined generalized S transform and Lucy-Richardson algorithm for Q-value extraction[J]. Geophysical Prospecting for Petroleum, 2019, 58(5): 689-699. DOI:10.3969/j.issn.1000-1441.2019.05.007 |



 宋维琪, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
宋维琪, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: 