地震层析成像是了解地下地质结构和岩层物理性质的主要方法,根据理论不同可分为射线类和波形类。射线类层析成像由于理论简单和计算效率高,已广泛应用于实际的资料处理[1-3];而波形类反演需依赖于初始的速度模型和观测数据的低频信息[4]。
1992年,Stork[5]利用最小化时间残差实现层析成像,奠定了层析反演的理论基础。一般来说,偏移与层析成像交替进行,分别恢复速度场的高波数信息(速度界面)以及低波数信息(速度)[6]。在偏移速度分析中主要有基于共成像点道集(CIG)的曲率分析[7]和深度聚焦分析[8]两种方法。由于聚焦深度很难拾取,所以深度聚焦分析方法使用较少。当CIG包含多路径波场传播信息,曲率分析易造成假象,甚至速度准确时CIG也不能完全拉平。同时,在求解过程中需要拾取剩余曲率以获得旅行时残差。总的来说,层析成像是一个迭代求解模型参数的过程,在每次迭代中都需要进行偏移,计算量较大。同时在射线追踪的过程中,需要模拟复杂地质结构的反射,增加了正演的难度[9]。
为了解决这些问题,Kabir等[10]提出了一种基于共聚焦点(CFP)技术[11]的速度反演方法。该方法利用差分时移(DTS)面板拾取时移来对速度模型进行扰动与判定。利用CFP技术进行速度反演主要有同步和异步两种方法[12]。同步反演是聚焦算子与速度模型相结合,同步更新聚焦算子与速度模型。异步反演是将聚焦算子的计算与速度模型反演分离,在不更新速度模型的情况下,从反射数据中获得聚焦算子。然后通过逆时聚焦算子的单向旅行时进行速度反演,更新算子的位置和速度模型。
在异步反演中,算子更新与速度模型扰动分离。首先利用CFP技术求取逆时聚焦算子,在求取的过程中需要拾取DTS面板上的时移。一般只需要迭代四次就可获得逆时聚焦算子,当初始模型接近实际模型时,迭代两次就可以求解出逆时聚焦算子。在之后的速度反演阶段,不再需要拾取时移。所以较传统层析中每次迭代都需要拾取残差相比,异步反演大大减少了工作量。在速度反演阶段,不需要重复偏移计算,只在初始阶段对逆时聚焦算子进行单炮偏移选取初始的CFP。并且,逆时聚焦算子代表了一组从CFP到地表的单向旅行时,在速度反演阶段没有复杂界面的反射问题,降低了正演计算的难度。
在速度反演中,需要进行大量的射线追踪,同时需要求解一个大型矩阵的逆,因而基于CFP技术的反演方法计算量极大。为此,本文分别从网格划分、扰动方法和模型更新方法三个方面进行改进。在网格划分方面可以减少运算时间的方法有二,一是Santos等[13]提出的分层网格化,第二个是Cox[14]提出的不规则网格化。结合CFP技术的特性,本文采用分层网格化。将同一反射界面上的聚焦算子分为一组,并相互连接起来。这样的划分方法不用显式地划分层位与定义断层,在计算的过程中利用这些分层进行约束,加速收敛。并且在计算中,算子的互不干扰特性让并行计算非常容易实现。在扰动方法方面,利用旅行时残差的分布确定扰动方向,利用旅行时残差的大小确定扰动量。同时,在扰动后射线旅行时的计算中,利用射线的出射角度和扰动量估计旅行时的变化量,避免大量重复的射线追踪计算,大幅提升了计算效率。为了避免扰动过大,难以收敛,本文采取了分步扰动策略,先进行深度扰动再进行水平扰动。最后,利用收敛速度快、收敛性能较好的代数迭代法(Algebraic Reconstruction Technique,ART)[15]进行速度模型的更新。
1 共聚焦技术原理与反演方法 1.1 CFP理论Berkhout[11]根据地震观测的几何关系提出了WRW模型,该模型将地震波的传播过程分为震源的激发响应、下行波场传播算子、反射算子、上行波场传播算子、检波器的接收响应,即
| $ \begin{aligned} \boldsymbol{P}&\left(z_{0}\right)=\boldsymbol{D}\left(z_{0}\right) \times \\ &\sum\limits_{m}\left[\boldsymbol{W}\left(z_{0}, z_{m}\right) \boldsymbol{R}\left(z_{m}\right) \boldsymbol{W}\left(z_{m}, z_{0}\right)\right] \boldsymbol{S}\left(z_{0}\right) \end{aligned} $ | (1) |
式中:z0为激发、接收点深度;zm为第m个反射界面深度;P(z0)表示地震记录;S(z0)和D(z0)分别为激发响应和接受响应;W(z0,zm)和W(zm,z0)分别是上行和下行波传播效应算子;R(zm)为反射算子。
共聚焦理论的聚焦过程分为两步,激发聚焦与接收聚焦,聚焦过程通过逆时聚焦算子实现。逆时聚焦算子可以看作地下反射点激发、地表接收的单程旅行时数据。逆时聚焦算子表达式为
| $ \boldsymbol{F}_{j}^{*}\left(z_{0}, z_{m}\right)=\boldsymbol{A}^{*}\left(z_{0}\right) \boldsymbol{W}\left(z_{0}, z_{m}\right) \boldsymbol{I}_{j}\left(z_{m}\right) $ | (2) |
式中:Fj*(z0, zm)为深度为zm、横向位置j处的聚焦算子;Ij(zm)为单位矩阵;A*(z0)为振幅保持算子。
根据上述理论,CFP道集求取方法如下:首先,利用聚焦算子与共炮点道集对应的道进行卷积,这就是第一步聚焦。其中,聚焦算子为逆时聚焦算子的按时间轴倒置。然后,将该道集中所有的响应结果进行叠加,叠加结果为CFP道集的一道。对所有共炮点道集进行相同的过程,就生成了CFP道集。CFP道集Pj(z0,zm)(j=1,2,…,J,J为道数)反映了地下反射点激发、地表接收的地震响应,其表达式为[5]
| $ \boldsymbol{P}_{j}\left(z_{0}, z_{m}\right)=\boldsymbol{D}\left(z_{0}\right) \boldsymbol{W}\left(z_{0}, z_{m}\right) \boldsymbol{R}_{j}^{*}\left(z_{m}\right) $ | (3) |
式中Rj*(zm)为反射矩阵。
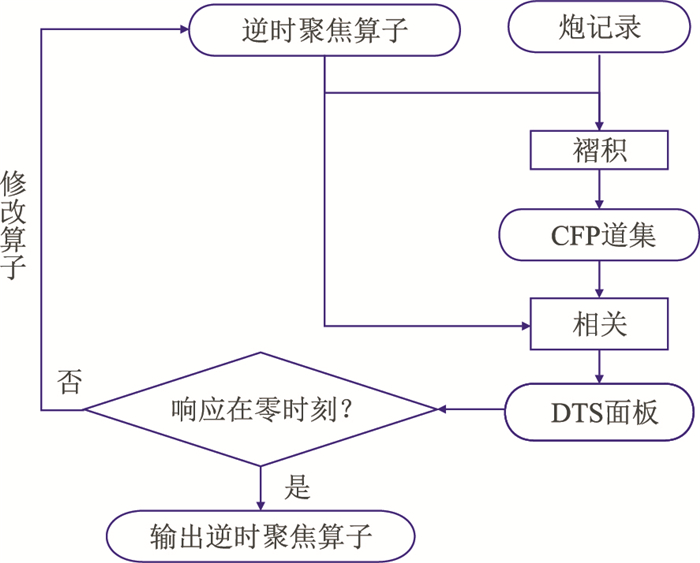
比较CFP道集与逆时聚焦算子可以看出,速度模型隐含在传播矩阵中,如果速度模型正确,那么逆时聚焦算子与CFP道集有相同的旅行时,即等时原理。用聚焦算子对CFP道集进行互相关运算,就可以得到DTS面板,这是第二步聚焦。在两步聚焦过程中,消除了下行波与上行波的传播效应,所以差分时移面板就相当于在聚焦点处激发、聚焦点处接收所产生的响应。因此在DTS面板中,所有的响应都在零时刻发生,若偏离了零时刻,则表示逆时聚焦算子不准。逆时聚焦算子的求取主要利用了上述性质,具体方法是从DTS面板上拾取偏离零时刻的响应时间,将这个时间的一半作用在聚焦算子上,完成一次迭代,直到DTS面板位于零线为止。具体流程如图 1所示。
|
图 1 逆时聚焦算子求取流程 |
逆时聚焦算子是在不知道具体速度模型的情况下,通过数据驱动更新的方法从一组共炮点道集中获得[16]。在本文的速度反演方法中,逆时聚焦算子是重要的输入数据。
1.2 速度反演方法 1.2.1 速度模型更新方法本文采用代数迭代法更新速度模型。首先将模型离散为网格,每个网格有一个对应的参数值,然后用大型的线性方程组描述速度模型与旅行时的关系
| $ \left\{\begin{array}{l} l_{1,1} s_{1}+l_{1,2} s_{2}+\cdots+l_{1, N} s_{N}=t_{1} \\ l_{2,1} s_{1}+l_{2,2} s_{2}+\cdots+l_{2, N} s_{N}=t_{2} \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots \\ l_{M, 1} s_{1}+l_{M, 2} s_{2}+\cdots+l_{M, N} s_{N}=t_{M} \end{array}\right. $ | (4) |
将上式归纳可写为
| $ t_{i}=\sum\limits_{j=1}^{N} t_{i, j}=\sum\limits_{j=1}^{N} l_{i, j} s_{j} \quad i=1,2, \cdots, M $ | (5) |
式中:sj为第j个网格的慢度;ti为第i条射线的旅行时;li, j表示第i条射线在第j个网格内的长度;M为射线条数;N为网格总数。利用代数迭代法求解上述方程组。对于第i条射线,第j个网格的ART迭代公式为
| $ s_{j}^{(k+1)}=s_{j}^{(k)}+\lambda \frac{t_{i}-\sum\limits_{n=1}^{N} l_{i, n} s_{n}^{(k)}}{\sum\limits_{n=1}^{N} l_{i, n}^{2}} l_{i, j} $ | (6) |
式中:k为迭代次数;λ是松弛系数,取值区间为(0,2)。在计算完所有的焦点与射线后,即为完成一次迭代,每次迭代都以上次迭代的结果作为初值,直到达到收敛条件。具体迭代步骤如下:
(1) 给定初始速度模型;
(2) 正演计算模拟数据ti*;
(3) 计算逆时聚焦算子的旅行时ti与模拟数据ti*的差
| $ \Delta \tau_{i}=t_{i}-t_{i}^{*} $ | (7) |
(4) 计算第j个网格的慢度修正量,并转化为速度修正量
| $ \Delta s_{j}=\frac{l_{i, j} \Delta \tau_{i}}{\sum\limits_{n=1}^{N} l_{i, n}^{2}} $ | (8) |
| $ \Delta v_{j}=-\left[v_{j}^{(k)}\right]^{2} \Delta s_{j} $ | (9) |
(5) 修正第j个网格的速度
| $ v_{j}^{(k+1)}=v_{j}^{(k)}+\lambda \Delta v_{j} $ | (10) |
(6) 将上一轮的结果作为初值,重复步骤(2)~步骤(5),直到达到收敛条件。
1.2.2 聚焦点位置估计除了速度模型,聚焦算子的空间位置也是反演重要的一部分。若焦点位置不正确,由代数迭代算法反演出的速度模型也会不准确。为了找到最正确的聚焦算子的空间分布,需要分析模拟旅行时与逆时聚焦算子的旅行时的残差分布,确定扰动量和扰动方向。
首先需要选取初始的共聚焦点位置,共聚焦点初始位置的选取决定着下一步反演的参数选取以及约束策略,所以相对科学的选取办法可以减少反演的计算量,提高反演的质量。本文利用逆时聚焦算子做单炮偏移,根据偏移后的能量分布选取初始的共聚焦点位置,即用初始速度模型对逆时聚焦算子进行偏移,能量会汇聚到一个区域,然后求取该区域的能量重心
| $ \left\{\begin{array}{l} x_{\mathrm{g}}=\frac{\sum\limits_{K=1}^{L} x_{K} E_{K}}{\sum\limits_{K=1}^{L} E_{K}} \\ z_{\mathrm{g}}=\frac{\sum\limits_{K=1}^{L} z_{K} E_{K}}{\sum\limits_{K=1}^{L} E_{K}} \end{array}\right. $ | (11) |
式中:L为能量区样点数;EK为样点(xK,zK)的能量。
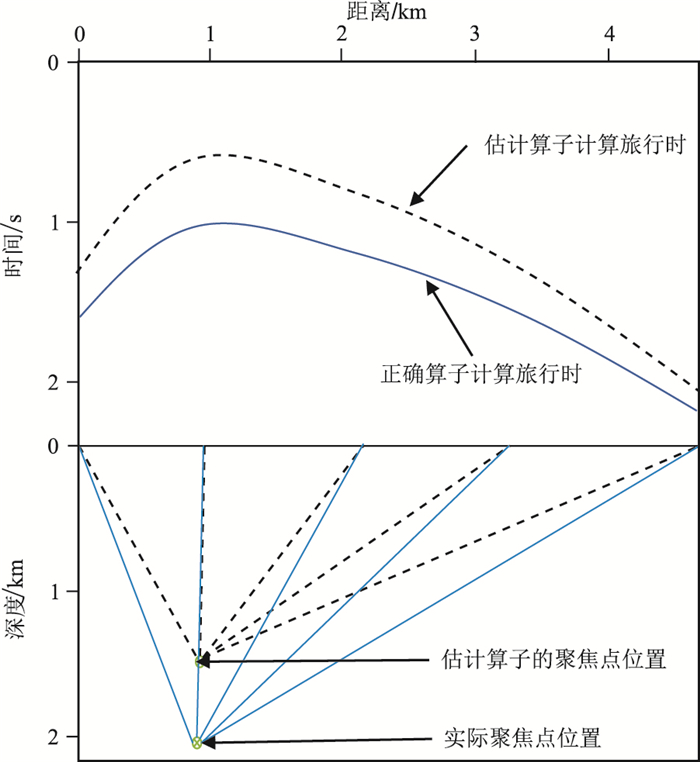
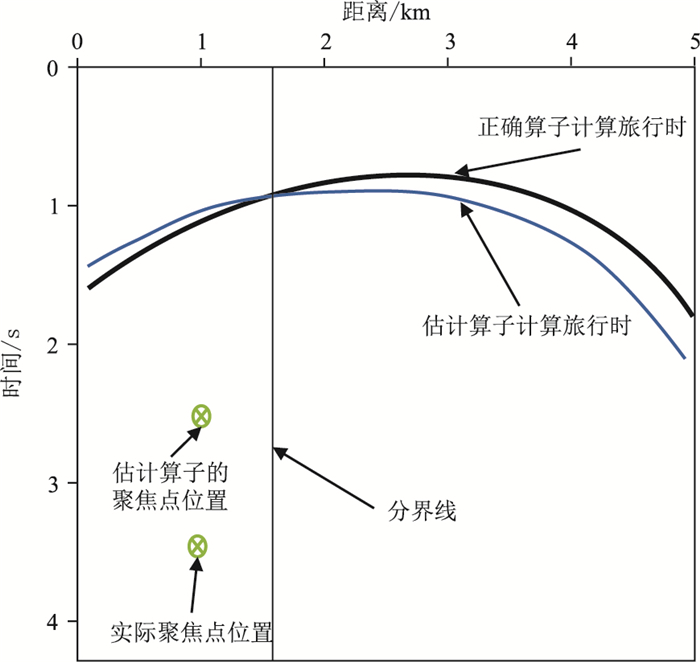
提取初始共聚焦点后,需要对其位置进行分析。图 2为当聚焦点有深度误差时正确算子与估计算子计算的旅行时信息对比,可以看出,当聚焦点的深度比实际深度小时,整体射线路径变短,计算旅行时比实际旅行时小。在进行代数迭代时,旅行时残差数变大。在利用旅行时残差进行多次代数迭代后,模型速度与焦点位置会达到一个耦合关系,反映的是与当前焦点位置最匹配的模型速度。在图 2例子中,因为估计算子的聚焦点深度比准确聚焦点的深度小,所以与估计算子相匹配的模型速度值也比准确的模型速度值小,从而才能达到耦合关系。图 3为在达到这种耦合关系时正确聚焦点与估计算子的聚焦点计算旅行时的相对关系。在图 3中,在分界线以左,残差为正,在迭代过程中使模型速度变小;在分界线以右,残差为负,反映在迭代过程中使速度变大。当左右的残差对速度的效应达到平衡时,速度就会收敛。同时,因为整体的射线路径变短,导致最终模型速度比实际更小。相反,当聚焦点深度比实际深度大时,整体的射线路径变长,导致最终模型速度比实际更大。
|
图 2 聚焦点深度误差示意图 |
|
图 3 残差与速度耦合示意图 |
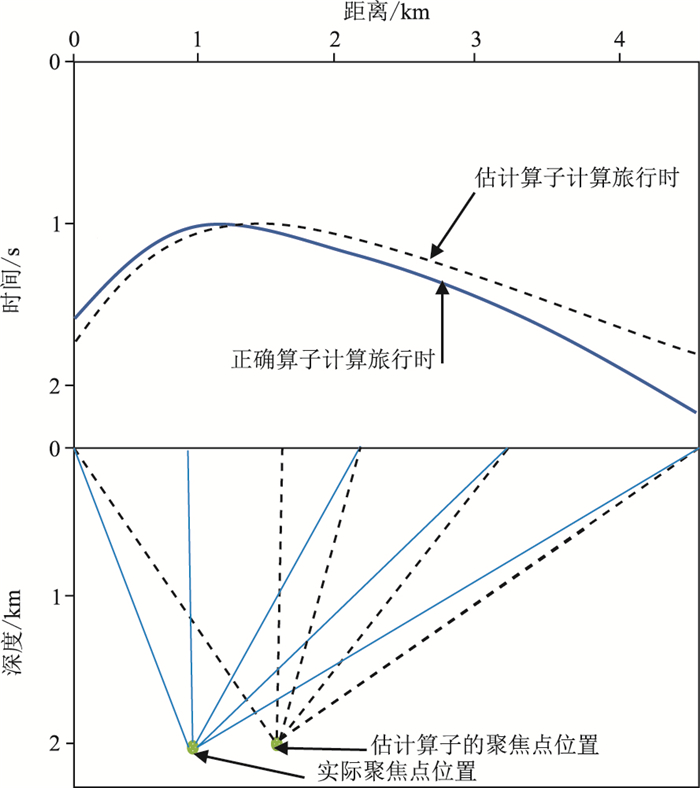
图 4是当聚焦点有水平位置误差时,正确算子与估计算子计算的旅行时信息对比。因为每次的扰动量很小,旅行时的变化量也较小。在算子只有水平误差时,若估计算子在正确算子的右边,左边的射线路径变长,右边的射线路径变短。估计算子计算的左边旅行时变大,右边旅行时变小,两条旅行时曲线会相交。相反的情况下,若估计算子在正确算子的左边,右边的射线路径变长,左边的射线路径变短,则算子左边的旅行时变小,右边的旅行时变大。
|
图 4 聚焦点水平误差示意图 |
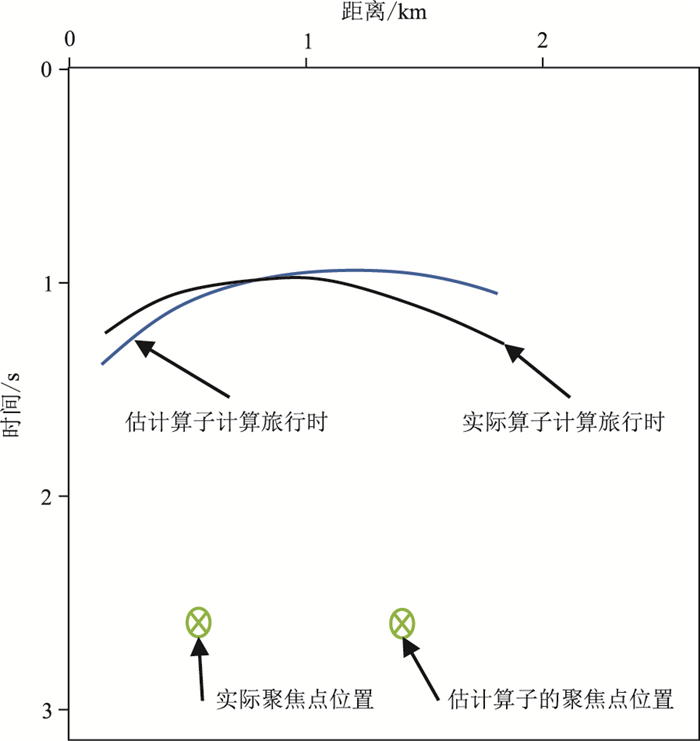
当聚焦点只有水平误差时,垂直向上的射线路径与正确的算子路径是相当的(假设地面水平)。同时,在层状模型中,算子上方的速度横向变化较小,竖直向上的射线的旅行时与准确算子的旅行时基本相等,所以二者旅行时信息的交点在估计算子的横向位置附近(图 5),即在只有水平误差时,估计算子横向位置的旅行时残差约等于零。
|
图 5 算子横向误差放大示意图 |
根据以上分析,算子的扰动方法如下。
(1) 因为深度的误差对速度影响更大,为了避免速度不准确对横向位置的影响,所以先扰动深度位置与速度模型。深度的扰动量由焦点上方的旅行时残差决定,即
| $ \Delta z=\Delta t \times v $ | (12) |
式中:Δz为深度扰动量;Δt为焦点位置上方的旅行时残差;v为焦点附近的速度值。
(2) 深度与速度模型扰动后,进行水平位置的扰动。因为水平位置的误差与旅行时残差的关系不明显,所以将横向位置的扰动给定一个范围,在这个范围内寻找最匹配逆时聚焦算子的坐标。
(3) 利用更新后的速度模型与扰动后的焦点进行正演,得到估计旅行时。利用估计旅行时与准确旅行时做差得到旅行时残差,进行下一次迭代。
在迭代过程中,需要在一定范围内寻找最佳匹配逆时聚焦算子的坐标,本文利用叠加振幅进行判定。根据射线追踪得到的旅行时,沿着旅行时曲线轨迹对逆时聚焦算子做曲线积分,就可以得到叠加振幅。叠加振幅越大,说明估计旅行时与逆时聚焦算子更匹配。
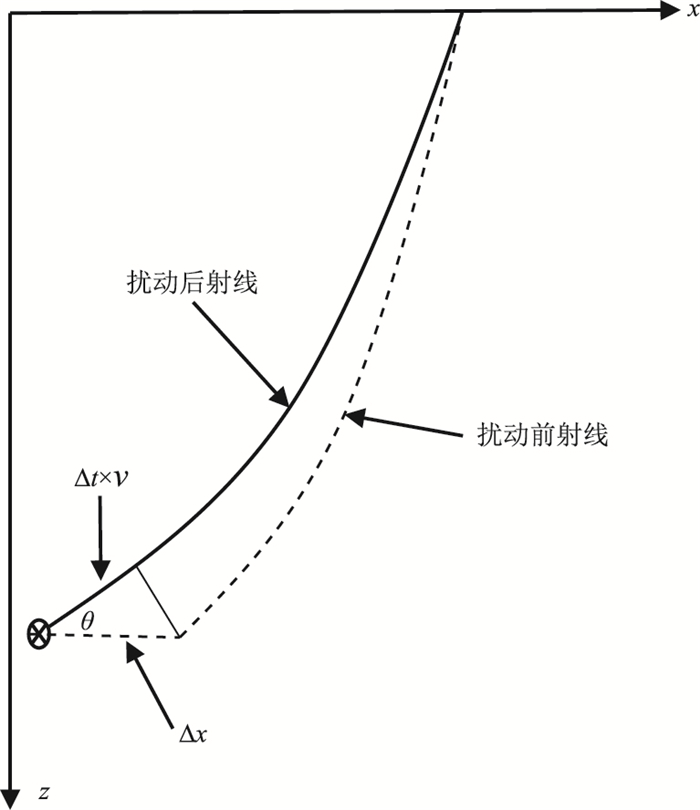
在横向位置的扰动中,需要知道聚焦点在扰动范围内的所有旅行时,需要反复进行正演计算,计算量很大。本文采用近似的方法求取每次扰动后的旅行时(图 6),近似公式为
| $ \varDelta t=\frac{\varDelta x \cdot \cos \theta}{v} $ | (13) |
|
图 6 水平扰动量计算示意图 |
式中θ为射线出射角度。
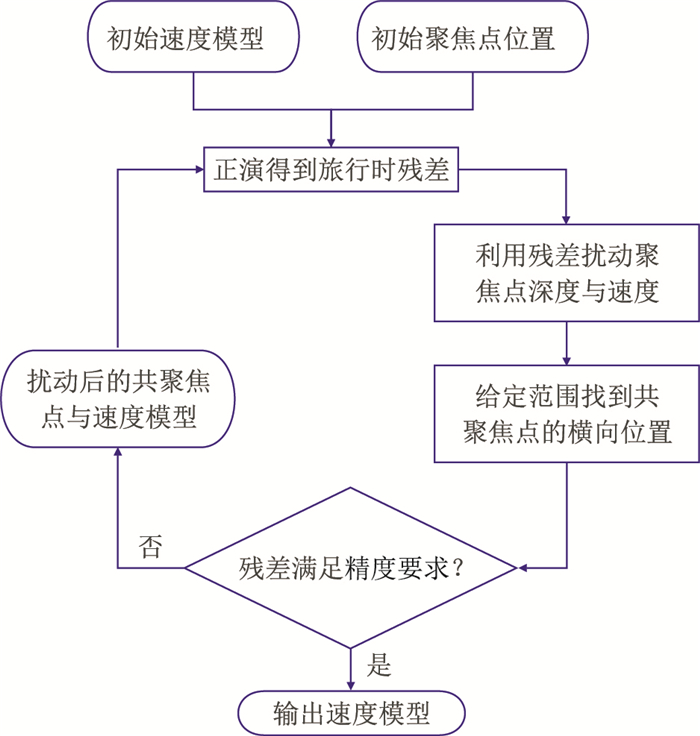
在没有约束的情况下,由于代数迭代算法的特性,旅行时残差的分配对速度变化非常敏感,会陷入局部极值,并且在新一轮的残差分配中会加剧这种状况。由于算子反映的是反射波的单向旅行时,所以可以将同一反射面的算子分为一组,在同一组反射算子中利用插值,构成一个反射面。这样则不用显式划分层位或者断层,只需要利用几个具有几何关系的算子,就可以划分一个反射界面。通过反射界面定义的地质体内的速度是不变的,数值为层中所有网格速度的均值。在模型复杂的情况下,在分层约束达到收敛后,可以取消约束,以求得模型的细节特征。这种方法给定了算子的扰动方向与扰动大小,比一般的遍历寻找更高效。图 7为速度反演的具体实施流程。
|
图 7 共聚焦点技术速度反演流程 |
在利用代数迭代反演速度模型的过程中,需要给定一个松弛因子。松弛因子如果太大,反演算法可能出现不收敛情况;如果太小,反演算法的收敛会变慢。同时,在扰动共聚焦点位置之前,需要利用残差与代数迭代法更新一次速度模型。目的是避免初始速度模型与正确速度模型的差值过大,引起算子位置的过量扰动。并且,在每次更新速度模型后,都需对速度模型进行约束。
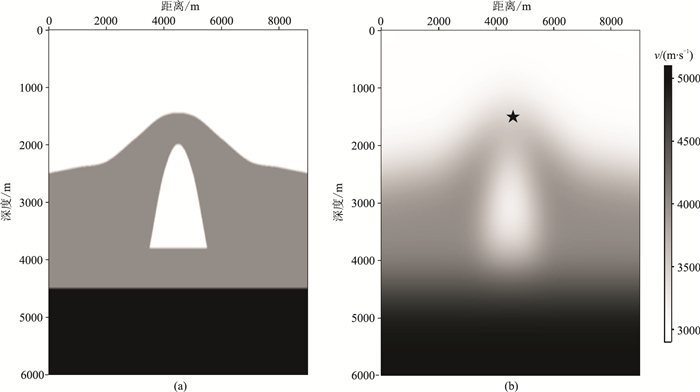
2 模型试验应用图 8a所示低速体速度模型验证本文方法。图 8b为初始速度模型,由准确速度模型平滑之后获得。
|
图 8 低速体速度模型 (a)真实速度;(b)初始速度 |
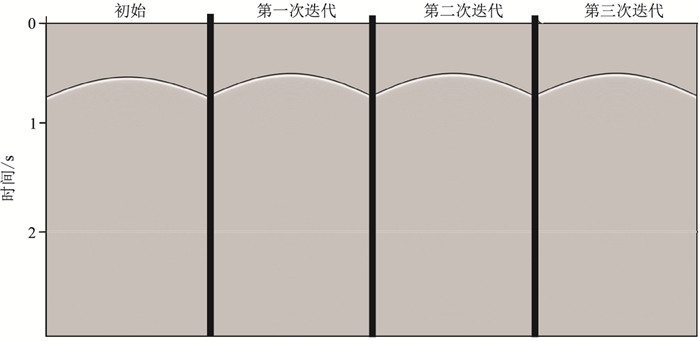
首先利用共聚焦点技术求取逆时聚焦算子。以横向位置为4500m处的逆时聚焦算子为例,初始的共聚焦点如图 8b星号所示,坐标为(4500m,1600m),初始逆时聚焦算子为在初始模型上以初始共聚焦点为震源进行正演得到。首先利用初始的逆时聚焦算子求取第一个反射界面的逆时聚焦算子,迭代过程如图 9所示,DTS面板的迭代过程如图 10所示图。因为第一个反射界面的同相轴在DTS面板上与零时很近,迭代三次就收敛了。
|
图 9 低速体模型第一个界面的聚焦算子迭代过程 |

|
图 10 低速体模型第一个界面的DTS面板迭代过程 |
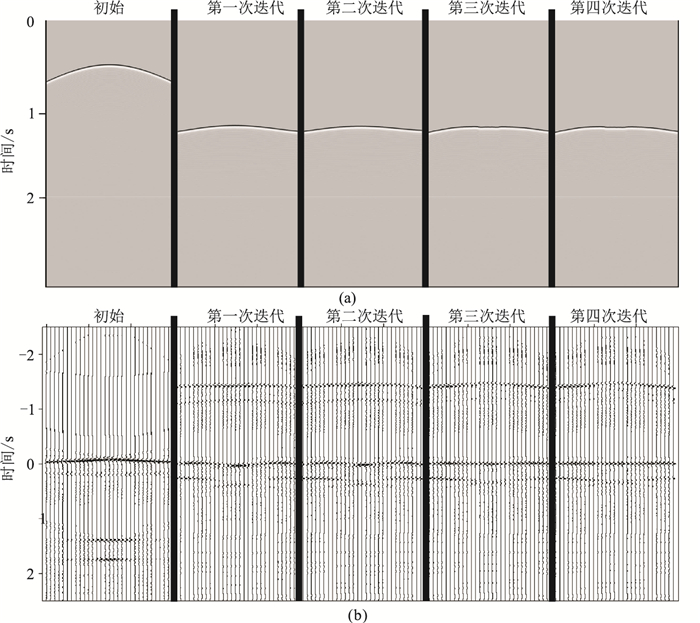
第三个反射界面的迭代过程如图 11所示,可以看出,迭代四次后DTS面板上的响应基本拉平,算子形态基本固定。考虑到初始算子与第三个反射界面的距离太远,速度模型的误差较大,这种计算效率完全可以接受。
|
图 11 低速体模型第三个反射界面迭代过程 (a)聚焦算子;(b)DTS面板 |
在计算第四层的逆时聚焦算子前,可以充分利用已知信息。第三个反射界面与第四个反射界面距离很近,可以利用第三层的逆时聚焦算子作为第四层的初始逆时聚焦算子,计算结果如图 12所示。由图 12可以看出,因为初始聚焦算子选取十分接近正确的算子,所以收敛很快,并且在DTS面板上拾取时移也更加方便。

|
图 12 低速体模型第四个反射界面迭代过程 (a)聚焦算子;(b)DTS面板 |
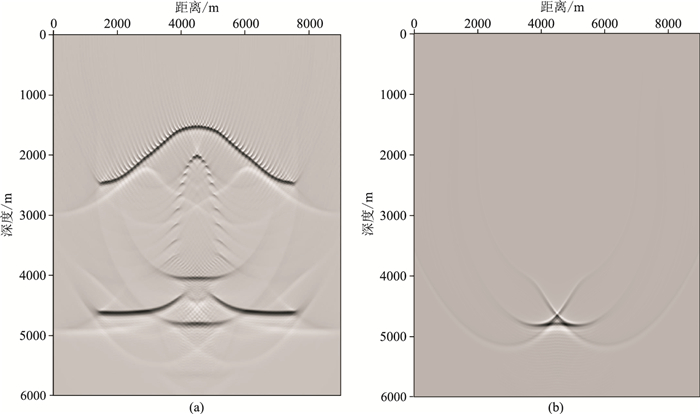
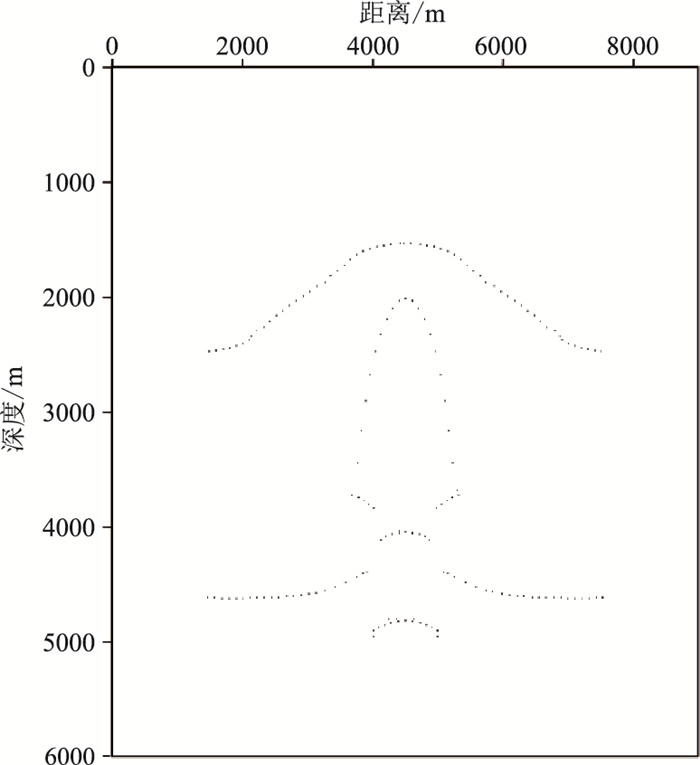
将求得的聚焦算子作为输入数据,反演速度模型。首先,应用初始速度模型对逆时聚焦算子进行单炮偏移,结果如图 13a所示。横向位置为4500m处第四个反射界面的逆时聚集算子偏移结果如图 13b所示,可以看出偏移能量较为发散。在能量区利用式(11)提取初始的共聚焦点,如图 14所示。
|
图 13 低速体模型初始速度逆时聚焦算子偏移结果 (a)所有算子偏移结果的叠加;(b)单个算子偏移结果 |
|
图 14 低速体模型初始共聚焦点分布 |
利用上述初始共聚焦点进行迭代反演,速度反演的松弛因子设置为0.5,迭代20次后的结果如图 15所示,可见焦点位置基本归位,低速体形状基本还原,速度与层位反演效果较好。

|
图 15 低速体模型迭代20次后反演结果 (a)焦点分布;(b)速度模型 |
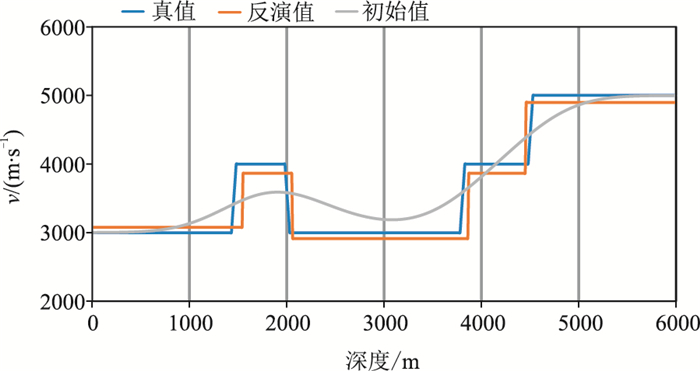
图 16为横向4500m处的反演速度曲线与真值的对比,可见低速体的边界和速度值反演结果较准确,同时低速体下方的层位与速度已基本复原。
|
图 16 低速体模型x=4500m处反演与真实速度曲线的对比 |
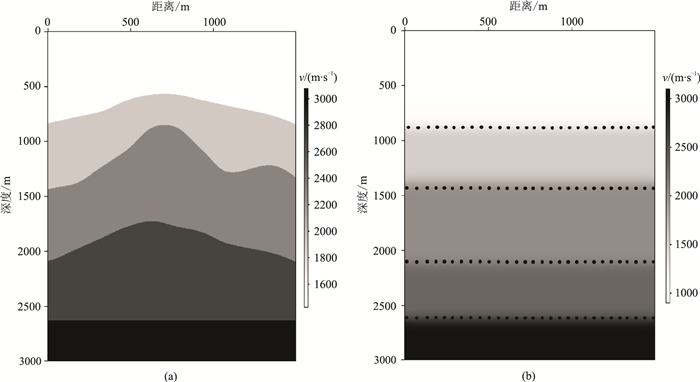
在上述模型试验中,初始的聚焦算子选取较精确,扰动量较小,为了验证反演算法的适用性,选取较复杂的起伏界面速度模型(图 17a)进行试验。模型共有五层,第二层底面起伏较大,速度分别为3500、3900、4300、4700、5000m/s,模型网格数为300×600,网格间距为5m。图 17b为初始的速度模型,初始速度模型为水平层状速度模型平滑后产生。初始的共聚焦点每层设置29个焦点(图 17中的黑点所示),均匀分布在界面上,共116个。
|
图 17 界面起伏速度模型 (a)真实速度;(b)初始速度 |
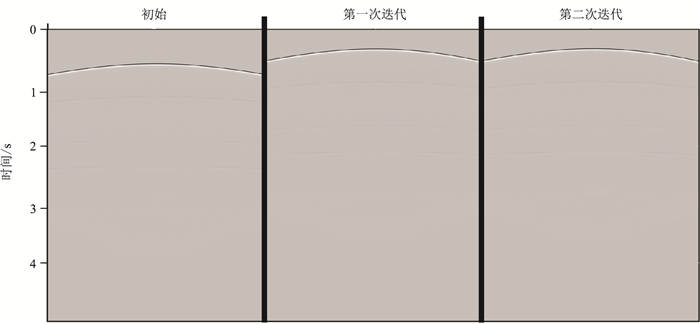
在求取逆时聚焦算子时,利用横向位置(750m,800m)处的初始共聚焦点,在初始速度模型上做正演得到初始的逆时聚焦算子。利用初始聚焦算子求取横向位置为750m处第一个反射界面的逆时聚焦算子,迭代过程如图 18、图 19所示。由于第一个界面反射界面较浅、同相轴清晰,迭代两次后DTS面板的响应被拉平,完成第一界面逆时聚焦算子的求取。
|
图 18 界面起伏速度模型第一个界面聚焦算子迭代过程 |

|
图 19 界面起伏速度模型第一个界面DTS面板迭代过程 |
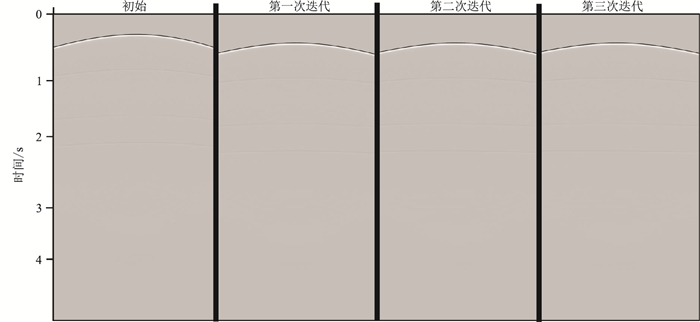
利用求取的第一个界面的逆时聚焦算子作为第二界面的初始值,求取第二个界面的逆时聚焦算子,迭代过程如图 20、图 21所示。
|
图 20 界面起伏速度模型第二个界面聚焦算子迭代过程 |

|
图 21 界面起伏速度模型第二个界面DTS面板迭代过程 |
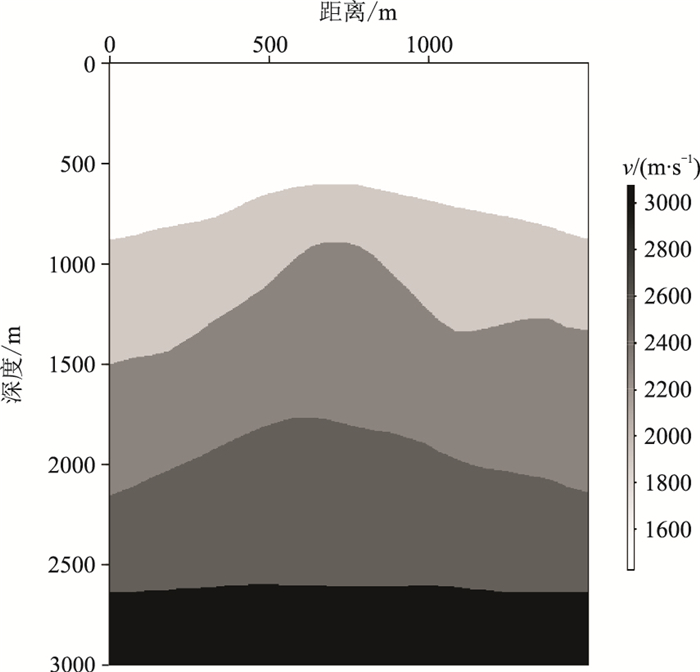
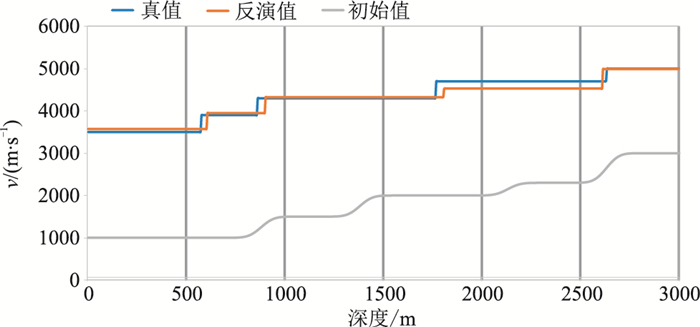
在求取所有的逆时聚焦算子后,利用初始速度模型与初始共聚焦点,进行反演计算,松弛因子设为0.5。图 22为迭代35次后的反演速度模型,图 23为横向750m处的反演与真实速度曲线对比。
|
图 22 界面起伏速度模型反演结果 |
|
图 23 界面起伏模型x=750m处反演与真实速度曲线对比 |
可以看出,速度和层位基本还原,最大速度误差约为10m/s,考虑到初始速度模型与真实模型差距较大,该误差在可接受范围内。
总之,由上述模型试验可知,即使在初始速度模型与真实模型差距较大情况下,本文方法求取的逆时聚焦算子稳定性高、效率高,利用逆时聚焦算子反演的速度也较精确。
3 结论总结上述成果,可以得出以下结论:
(1) 利用共聚焦点技术,拾取DTS面板时移求取逆时聚焦算子的方法是可行的。即使初始的逆时聚焦算子与准确的算子相差较大的情况下,也能准确地求取逆时聚焦算子。但是在每次迭代中,需要人工拾取时移,有较大的工作量。
(2) 利用逆时聚焦算子与ART反演方法能够反演出一个可靠的速度模型,并且即使初始速度模型较差的情况下,也能得到较好的结果。
(3) 通过ART的方法反演速度,不需要重复的偏移计算,并且在反演过程中只考虑反射界面上的多个几何点,计算量大大降低。
(4) 与其他反射层析成像方法相同,本文方法同样要求反射波信号具有较高的信噪比,可准确拾取共反射点。
| [1] |
徐夷鹏, 任志明, 李振春, 等. 一阶近似瞬时频率时间域声波全波形反演[J]. 石油地球物理勘探, 2020, 55(5): 1029-1038. XU Yipeng, REN Zhiming, LI Zhenchun, et al. Full waveform inversion of time-domain acoustic wave based on first-order approximate instantaneous frequency[J]. Oil Geophysical Prospecting, 2020, 55(5): 1029-1038. |
| [2] |
杨雪霖, 李振春, 尹正, 等. 多频组合胖射线旅行时层析成像方法[J]. 石油地球物理勘探, 2014, 49(5): 911-915. YANG Xuelin, LI Zhenchun, YIN Zheng, et al. Fat ray traveltime tomographic imaging based on multiple frequencies' combination[J]. Oil Geophysical Prospecting, 2014, 49(5): 911-915. |
| [3] |
黄光南, 刘洋, Ari Tryggvason, 等. 变网格间距速度层析成像方法[J]. 石油地球物理勘探, 2013, 48(3): 379-389. HUANG Guangnan, LIU Yang, TRYGGVASON Ari, et al. Variable grid spacing velocity tomography[J]. Oil Geophysical Prospecting, 2013, 48(3): 379-389. |
| [4] |
刘定进, 胡光辉, 蔡杰雄, 等. 高斯束层析与全波形反演联合速度建模[J]. 石油地球物理勘探, 2019, 54(5): 1046-1056. LIU Dingjin, HU Guanghui, CAI Jiexiong, et al. A joint velocity model building method with Gaussian beam tomography and full waveform inversion for land seismic data[J]. Oil Geophysical Prospecting, 2019, 54(5): 1046-1056. |
| [5] |
Stork C. Reflection tomography in the post migrated domain[J]. Geophysics, 1992, 57(5): 680-692. DOI:10.1190/1.1443282 |
| [6] |
李振春. 地震偏移成像技术研究现状与发展趋势[J]. 石油地球物理勘探, 2014, 49(1): 1-21. LI Zhenchun. Research status and development trends for seismic migration technology[J]. Oil Geophysical Prospecting, 2014, 49(1): 1-21. |
| [7] |
Liu Z Y. An analytical approach to migration velocity analysis[J]. Geophysics, 1997, 62(4): 1238-1249. DOI:10.1190/1.1444225 |
| [8] |
MacKay S, Abma R. Imaging and velocity estimation with depth focusing analysis[J]. Geophysics, 1992, 57(12): 1608-1622. DOI:10.1190/1.1443228 |
| [9] |
戴海涛, 成剑冰, 王红博, 等. 复杂地表浅层速度建模技术研究及应用[J]. 石油物探, 2020, 59(3): 336-343. DAI Haitao, CHENG Jianbing, WANG Hongbo, et al. A shallow velocity modeling technique for complex surface[J]. Geophysical Prosoecting for Petro-leum, 2020, 59(3): 336-343. DOI:10.3969/j.issn.1000-1441.2020.03.002 |
| [10] |
Kabir M M N, Verschuur D J. Velocity estimation of the complex subsurface using the common focus point technology[C]. SEG Technical Program Expanded Abstracts, 1997, 16: 1822-1825.
|
| [11] |
Berkhout A J. Pushing the limits of seismic imaging, Part I: Prestack migration in terms of double dynamic focusing[J]. Geophysics, 1997, 62(3): 937-953. DOI:10.1190/1.1444201 |
| [12] |
王成祥, 张关泉, 刘超颖, 等. 速度模型反演的CFP方法[J]. 石油地球物理勘探, 2003, 38(2): 139-146. WANG Chengxiang, ZHANG Guanquan, LIU Chao-ying, et al. CFP method for velocity model inversion[J]. Oil Geophysical Prospecting, 2003, 38(2): 139-146. DOI:10.3321/j.issn:1000-7210.2003.02.008 |
| [13] |
Santos L A, Mansur W J, McMechan G A. Tomography of diffraction-based focusing operators[J]. Geophysics, 2012, 77(5): R217-R225. DOI:10.1190/geo2011-0392.1 |
| [14] |
Cox B. Tomographic Inversion of Focusing Operators[D]. Delft University of Technology, Delft, Colorado, 2004.
|
| [15] |
钱伟婷. 图像复原问题的正则化迭代算法研究[D]. 四川成都: 成都理工大学, 2017.
|
| [16] |
van der Rijzen M J. Estimation of Focussing Operators[D]. Delft University of Technology, Delft, Colorado, 2007.
|



 胡叶正, 四川省成都市新都区新都大道8号西南石油大学地球科学与技术学院, 610000。Email:
胡叶正, 四川省成都市新都区新都大道8号西南石油大学地球科学与技术学院, 610000。Email: 