2 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071;
3 中国石化胜利油田物探研究院, 山东东营 257022
2 Laboratory for Marine Mineral Resources, Pilot National Laboratory for Marine Science and Technology(Qingdao), Qingdao, Shandong 266071, China;
3 Geophysical Research Institute of Shengli Oilfield, SINOPEC, Dongying, Shandong 257022, China
全波形反演(FWI)是一种将模拟和观测数据之间的残差最小化以获得高分辨率介质参数的方法[1]。Tarantola[2]从波动方程出发,通过波场残差逆时传播计算梯度方向,建立了基于最小二乘理论的时间域声波波形反演(AFWI)。在声波波形反演理论基础上,Tarantola[3]进一步提出了基于二阶位移形式的弹性波动方程的波形反演(EFWI)理论,从此奠定了弹性波形反演理论的坚实基础。
在弹性波反演领域,Mora[4]应用模型数据对Tarantola的弹性波波形反演理论[3]进行了测试并指出FWI对低频信息依赖性强、计算量大且效率低。Köhn等[5]分析了不同参数化对弹性波反演结果串扰现象的影响。Jeong等[6]在频率域利用超低频信号实现了密度和速度的准确反演。Ren等[7]利用弹性波波动方程解耦压制参数之间的串扰。Wang等[8]提出P/S模式解耦梯度预条件方法,借助海森与分辨率矩阵“模式”分解建立了波模式解耦的EFWI方法,有效降低纵、横波速度串扰效应,改善了反演的收敛性。Raknes等[9]在Sleipner区域利用纵、横波速度和密度间的经验公式实施了弹性参数反演。相比纵、横波速度参数,密度变化主要影响地震波场的振幅信息,而对诸如传播时间和相位之类的波扩散参数影响很小,因此密度很难准确反演,由于其与速度的高度耦合性,通常反演中被设定为某个常数。李青阳等[10]利用速度和密度的高度耦合性进行了密度建模和反演。
自20世纪90年代以来,海底电缆(OBC)系统的出现促进了海洋地震勘探技术[11-13]取得了巨大的进展。2000年后,陆上多波多分量勘探逐渐发展起来。对于多分量地震数据,EFWI比AFWI更适合于地下弹性参数的高精度重构[14]。在复杂区域,AFWI无法描述弹性波的传播过程[15],例如P/S转换波和振幅AVO效应。弹性波多参数全波形反演还存在诸多问题,在工程方面主要面临四方面困难。①计算量巨大。EFWI中弹性波数值模拟涉及弹性变量是常规标量波数值模拟的五倍以上,巨大的内存需求对设备提出极高要求,同时计算效率严重限制了其在实际中的应用。②多分量采集数据不规则化。由于弹性波方程是矢量方程,高精度、准确的弹性参数反演势必需要高信噪比、高保真的多分量地震数据。③初始速度建模和低频缺失问题。④地震子波的求取问题[16]。
目前大多数陆上勘探所采集的地震数据均是单分量资料,即从垂直地震检波器接收到的粒子运动响应。当实际工区地表存在低降速带时,根据斯奈尔定理,这会导致传播至检波器的反射波波路径几乎与地表垂直,根据纵横波传播方向与偏振方向的关系,垂直检波器接收的数据集可以称为纯纵波数据[17]。在此情况下,经典的假设是将地下视为流体[9],并使用声波方程来匹配纵波数据,因此AFWI是目前陆上全波形反演应用中最常用的方法。但AFWI无法反演横波速度。尽管单分量采集的地震数据只包含纵波,不直接包含横波,但包含了大量转换纵波信息,例如P-S-P波,同时地下介质是弹性的,纵波振幅也满足弹性AVO特征。因此,用纵波资料反演弹性介质中的弹性参数是可能的,Li等[17]利用标量波信号实现了单分量资料的弹性参数反演。
FWI是强非线性反演过程[18],局部极值问题一直困扰着该方法的发展。目标函数的设计对FWI至关重要,采用不同目标函数进行反演能够改变反演对初始速度和数据低频的依赖程度,有可能解决周期性跳跃问题[19]。最小二乘L2范数由于其简便性和高分辨率特性而被广泛使用,但存在明显的周期性跳跃现象。当背景速度不准确导致观测记录的波形与模拟记录波形相位差超过半个周期时,FWI通常会收敛到局部最小值[20]。因此在FWI实现过程中,通常选取保证运动学信息准确的初始速度,或者是从相对较低的频率开始反演。
全局优化策略是解决FWI周期性跳跃问题的一种解决方案,例如引入蒙特卡洛算法、遗传算法和模拟退火等方法。但全局优化算法计算量巨大,与之相比,局部优化策略的优势更加明显。局部优化策略中,多尺度反演[21]、包络反演[22]、反射波全波形反演[23]、波动方程旅行时反演[20]、基于自适应滤波器的波形反演[24]均一定程度上解决了FWI周期性跳跃问题。
近年来,最优输运理论在地球物理界得到广泛的关注,并成功应用于FWI,解决局部极值问题有很好的效果。当前有两类基于最优输运原理的目标函数。第一类是二次Wasserstein距离(W2距离)[25]。另一类与Kantorovich-Rubinstein(KR)规范[26]有关。KR规范的优点是它不需要数据满足非负性或质量守恒条件。
本文首先分析了地震勘探中单分量数据存在的AVO特征和转换波信息,由此可知单分量数据具备指示地下介质弹性参数(纵、横波速度和密度)变化的潜力。再从弹性动力学理论出发,通过分解本构方程为球张量和旋转张量的形式,推导出弹性介质中的伪压力弹性波方程。然后介绍了基于L2范数构建目标函数的伪压力弹性波波形反演方法(L2反演),并将最优输运理论下的W2范数引入反演,提出一种基于最优输运原理的陆上单分量资料弹性波全波形反演方法(W2反演),基于W2范数构建的目标函数具有更强的凸性。将基于W2范数的反演结果作为初始模型,再进行L2反演(W2+L2反演),克服了对初始模型的依赖性。最后应用Marmousi模型模拟数据和实际资料验证了本文方法的正确性和实用性。
1 理论 1.1 弹性介质中的伪压力弹性波方程 1.1.1 单分量地震勘探AVO特征与转换波针对陆上单分量地震勘探,通常会用声波方程为基础的全波形反演预测地下的纵波速度参数,并结合测井得到的经验关系计算横波速度、密度参数[9],进而进行储层预测和流体识别[27]。该策略将地下介质假设为流体,即纵波速度和密度参数化模式。采用这种处理方式主要有两个原因,第一是传统的地震信号处理技术聚焦于纵波的运动学信息,通过声波方程模拟结果可以完好地吻合其运动学信息;第二是多分量地震资料进行弹性波FWI存在较多的问题,例如带宽不一致、子波不统一等问题亟待解决。目前陆上勘探采集仍以垂直检波器为主,所采集地震信号为粒子在垂直地面方向的振动速度或者位移。
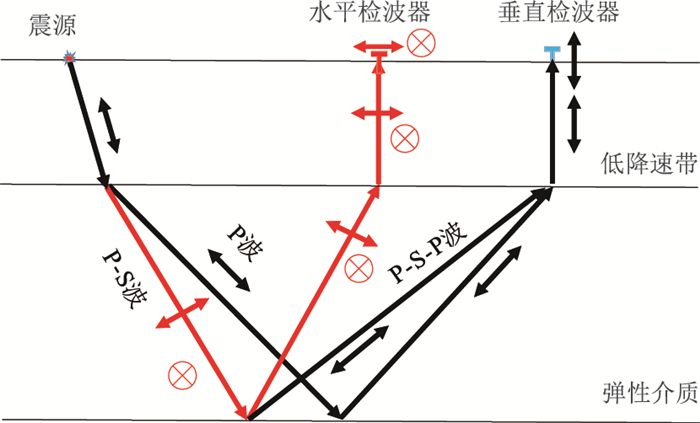
实际上地下介质是弹性介质,参数化除纵波速度和密度外,还应包括横波速度,因此采用弹性波方程模拟得到的数值解比声波方程更加可靠[1]。真实的单分量地震数据包含大量转换纵波,会对声波FWI的结果产生较强的影响。幸运的是近地表往往存在一个低降速带,由斯奈尔定理可知,低降速带会导致从地下波阻抗界面反射的地震波传播到检测器的角度几乎垂直于地表(图 1)。纵波偏振方向与传播方向相同,从垂直检波器接收到的地震波可以视为纯纵波,而偏振方向为水平方向的横波信号则不能被接收。因此可以假定纵波和横波在陆上地震数据中是自然解耦的(基岩裸露和地表为强各向异性介质除外)。针对该类介质,本文提出应用伪压力弹性波方程模拟地震数据,通过伪压力弹性波方程模拟结果与弹性波方程、声波方程的模拟结果进行对比,分析在单分量地震勘探中数据的AVO特征与转换波信息。
|
图 1 近地表低降速带弹性介质模型地震波路径示意图 |
以一个四层弹性模型(图 2)为例,模型尺寸为2400m×1500m,常密度设置为1420kg/m3。震源是峰值频率为20Hz的Ricker子波,位于(1200m,8m),网格间距8m,时间采用间隔为0.5ms。

|
图 2 层状弹性介质模型示意图 |
图 3a和图 3b分别为弹性波总位移波场和解耦后的弹性纵波位移波场的垂直分量波场快照。与声波波场(图 3c)相比,弹性波总位移波场(图 3a)包含转换纵波和横波,它们在陆地地震数据中被天然解耦,即垂直检波器接收到的波场(图 3b)为纵波位移波场的垂直分量。反射界面产生转换波[28],在第二界面处存在上行的转换P-S-P波(图 3b黑框所示),该转换纵波伪压力弹性波方程建模的伪压力场(图 3d)中同样存在,而在声波方程建模的纯压力场(图 3c)中并不存在。

|
图 3 层状模型不同方法正演的0.5s时刻波场快照 (a)弹性介质总波场的垂直分量;(b)弹性介质纵波波场的垂直分量;(c)声介质声波波场;(d)弹性介质伪压力波场 |
由于地表低降速带对纵波和横波的天然解耦作用,反射波垂直于地表射出,因此解耦弹性波方程的纵波位移分量与伪压力弹性波方程的伪压力都可以用于陆上弹性FWI中地震数据的匹配,但伪压力数据是匹配观测数据的更好选择。因为使用纵横波解耦弹性波方程的建模方法,计算成本比伪压力弹性波方程高;而且常规的地震数据处理聚焦于纵波的运动学信息,更适合采用标量波波动方程建模。
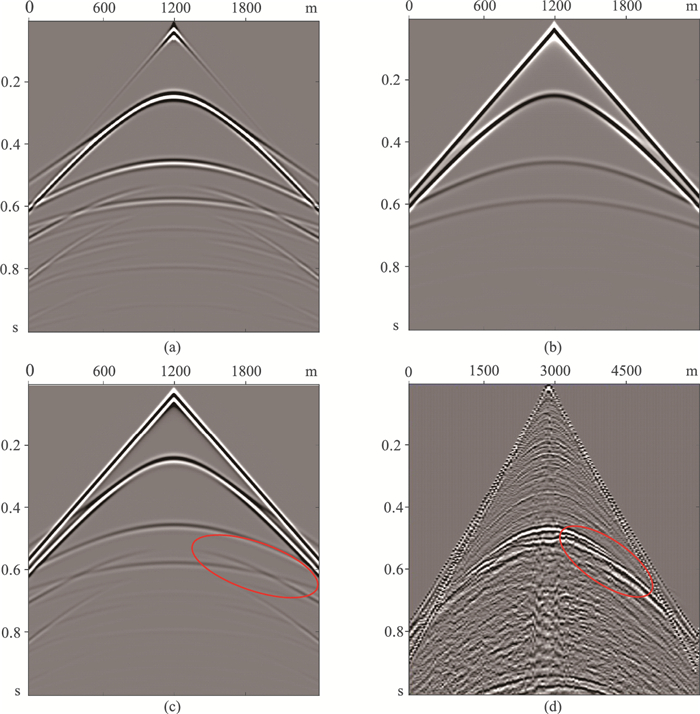
图 4a和图 4c是弹性纵波垂直分量地震记录和伪压力地震记录,对比可知在弹性介质中二者反射波类型是一致的,其转换纵波在声波地震记录(图 4b)中无法被模拟,这也表明了横波速度反演的可能性。图 4c中红圈中存在纵波的同相轴交叉,对比可知二者分别是浅中层转换反射S-P波和深层反射P波。图 4d为中国东部M区采集的单分量地震数据,对比红圈部分,该资料同样存在同相轴交叉现象,验证了实际资料存在转换纵波。
|
图 4 层状模型不同方法正演记录与实际地震记录的对比 (a)弹性介质纵波记录的垂直分量; (b)声介质声波记录; (c)弹性介质伪压力记录; (d)实际单分量地震数据 |
由上述分析可见,伪压力弹性波方程建模不仅考虑了弹性AVO效应,同时也包含转换纵波,相比于声波方程只能反演纵波速度和密度,伪压力弹性波方程更加贴合实际介质是弹性介质的情况,同时还具备了反演横波速度模型的潜能。关于压力与速度数据存在的振幅及相位不匹配问题,在实际资料应用中,通过处理(振幅补偿、去噪、去面波处理)可用标量波方程模拟去匹配实际数据;而子波相位的不匹配问题则可以通过提取实际数据的子波加以解决。
1.1.2 伪压力弹性波方程的建立经典的弹性波方程是从弹性动力学中的几何方程、本构方程和牛顿运动微分方程三个基本方程导出。表示弹性应变和位移关系的几何方程又称柯西方程,为
| $ e_{i j}=\frac{1}{2}\left(u_{i j}+u_{j i}\right) $ | (1) |
式中:e表示应变;u表示位移;下标i、j的范围均为1~3,并且满足爱因斯坦求和约定。
各向同性介质的本构方程又称广义虎克定律,为
| $ \tau_{i j}=C_{i j k l} e_{k l}=\lambda \theta \delta_{i j}+2 \mu e_{i j} $ | (2) |
式中:Cijkl=λδijδkl+μδikδjl+δilδjk表示刚度矩阵,其中λ和μ表示拉梅常数;θ为体应变;δij为Kronecker符号;τ表示应力。
牛顿运动微分方程又称纳维尔方程,为
| $ \rho \ddot{u}_{i}=\frac{\partial}{\partial x_{j}} \tau_{i j}+f_{i} $ | (3) |
式中:ρ为密度;
式(2)可以写为等价胀缩与剪切张量形式的本构方程[29]
| $ \left\{\begin{array}{l} P=3 K \theta_{\mathrm{P}} \\ S_{i j}=2 \mu T_{i j} \end{array}\right. $ | (4) |
式中:K为体积模量;P=τkk/3和θP=ekk/3分别为应力和应变张量的第一不变量;Pδij和Sij分别为应力张量的球张量和偏斜张量,S可表示为
| $ \boldsymbol{S}=\left[\begin{array}{ccc} \tau_{11}-P & \tau_{12} & \tau_{13} \\ \tau_{21} & \tau_{22}-P & \tau_{23} \\ \tau_{31} & \tau_{y z} & \tau_{33}-P \end{array}\right] $ | (5) |
θPδij和Tij分别为应变张量的球张量和偏斜张量,T可表示为
| $ \boldsymbol{T}=\left[\begin{array}{ccc} e_{11}-\theta_{\mathrm{P}} & e_{12} & e_{13} \\ e_{21} & e_{22}-\theta_{\mathrm{P}} & e_{23} \\ e_{31} & e_{32} & e_{33}-\theta_{\mathrm{P}} \end{array}\right] $ | (6) |
由此可得弹性介质中不解耦的伪压力弹性波方程(详细推导见附录A)
| $ \frac{1}{K} \frac{\partial^{2} P}{\partial t^{2}}-\frac{\partial}{\partial x_{i}}\left[\frac{1}{\rho} \frac{\partial}{\partial x_{j}}\left(\frac{1}{2} C_{i j k l}^{\mathrm{T}} \frac{\partial u_{k}}{\partial x_{l}}+P \delta_{i j}\right)\right]=f_{\mathrm{P}} $ | (7) |
式中:CijklT=λδijδkl+μ(δikδjl+δilδjk)-Kδijδkl表示刚度矩阵的偏斜分量;fP表示纵波震源项。
在声学/流体介质中,剪切模量等于零(μ=0),因此λ=K,即CijklT=0,则式(7)退化为传统声波方程
| $ \frac{1}{K} \frac{\partial^{2} P}{\partial t^{2}}-\frac{\partial}{\partial x_{i}}\left(\frac{1}{\rho} \frac{\partial P}{\partial x_{j}}\right) \delta_{i j}=f_{\mathrm{P}} $ | (8) |
经典全波形反演的目标函数E通常由模拟记录与观测记录之间的差异构建
| $ E(\boldsymbol{m})=\sum\limits_{r=1}^{R}\left\|\boldsymbol{d}_{\mathrm{cal}}\left(\boldsymbol{x}_{r}, t ; \boldsymbol{m}\right)-\boldsymbol{d}_{\mathrm{obs}}\left(\boldsymbol{x}_{r}, t\right)\right\|^{p} $ | (9) |
式中:dcal为模拟数据;dobs为观测数据;xr表示第r个检波点坐标;R为检波点个数;m为模型的弹性参数;||●||p表示p范数。
本文反演采用梯度类算法,其迭代格式为
| $ \boldsymbol{m}^{(n+1)}=\boldsymbol{m}^{(n)}-\alpha \boldsymbol{H}^{-1} \nabla_{\boldsymbol{m}} E^{(n)} $ | (10) |
式中:n为迭代次数;α为迭代步长;H为海森矩阵;▽mE为目标函数对模型参数的梯度。
为了避免直接计算海森矩阵,可以使用正向和反向传播波场能量对梯度进行加权。本文直接选取伪压力波场互相关构建海森矩阵
| $ H\left(\boldsymbol{x}_{s}, \boldsymbol{x}\right) \approx \sum\limits_{s} \int_{0}^{t_{\max }} P\left(\boldsymbol{x}_{s}, \boldsymbol{x}, t\right) \cdot P\left(\boldsymbol{x}_{s}, \boldsymbol{x}, t\right) \mathrm{d} t $ | (11) |
式中:xs为第s个炮点坐标;tmax为记录长度。
迭代步长计算一般采用线性搜索方法,在模型测试中常用的有非精确线搜索或者抛物线搜索方法。为降低计算空间复杂度,本文采用实际模型与梯度的最大值之比计算,即
| $ \alpha=\beta \frac{\max (\boldsymbol{m})}{\max (\Delta \boldsymbol{m})} $ | (12) |
式中:max(m)为模型参数m的最大值;max(Δm) 为模型参数的最大变化量;β=0.02,对应于2%的最大模型变化量。这种可变步长计算方法可以有效降低计算量。
1.2.1 基于L2范数伪压力弹性波波形反演Tarantola[2]应用模拟记录dcal与观测记录dobs之间的差异最小的L2范数为目标函数
| $ E(\boldsymbol{m})=\frac{1}{2} \sum\limits_{r=1}^{R} \int_{0}^{t_{\max }}\left[\boldsymbol{d}_{\mathrm{cal}}\left(\boldsymbol{x}_{r}, t ; \boldsymbol{m}\right)-\boldsymbol{d}_{\mathrm{obs}}\left(\boldsymbol{x}_{r}, t\right)\right]^{2} \mathrm{~d} t $ | (13) |
根据Plessix[30]的伴随状态法可得到目标函数对拉梅参数和密度的梯度表达式(详见附录B)
| $ \left\{\begin{aligned} \nabla_{\lambda} E=& \int_{0}^{t_{\max }} \frac{\partial K}{\partial \lambda} P^{*} u_{k k} \mathrm{~d} t \\ \nabla_{\mu} E=& \int_{0}^{t_{\max }}\left[S_{i j}^{*}\left(\delta_{i k} \delta_{j l}+\delta_{i l} \delta_{j k}-\frac{\partial K}{\partial \mu} \delta_{i j} \delta_{k l}\right) e_{k l}+\right.\\ &\left.\frac{\partial K}{\partial \mu} P^{*} u_{k k}\right] \mathrm{d} t \\ \nabla_{\rho} E=& \int_{0}^{t_{\max }} \ddot{u}_{i}^{*} \ddot{u}_{i} \mathrm{~d} t \end{aligned}\right. $ | (14) |
式中上标“*”表示反传波场。
通过链式法可得目标函数对纵、横波速度的梯度
| $ \left\{\begin{aligned} \nabla_{v_{\mathrm{P}}} E &=\frac{\partial \lambda}{\partial v_{\mathrm{P}}} \nabla_{\lambda} E+\frac{\partial \mu}{\partial v_{\mathrm{P}}} \nabla_{\mu} E \\ &=2 \rho v_{\mathrm{P}} \nabla_{\lambda} E \\ \nabla_{v_{\mathrm{S}}} E &=\frac{\partial \lambda}{\partial v_{\mathrm{S}}} \nabla_{\lambda} E+\frac{\partial \mu}{\partial v_{\mathrm{S}}} \nabla_{\mu} E \\ &=-4 \rho v_{\mathrm{S}} \nabla_{\lambda} E+2 \rho v_{\mathrm{S}} \nabla_{\mu} E \end{aligned}\right. $ | (15) |
常规L2范数的FWI是一个非线性反演问题,易发生周期性跳跃现象,进而陷入局部极小值。因此对于初始模型精度有很高的要求,在实际应用中往往难以满足。为解决常规L2范数FWI局部极值问题,基于最优输运理论,本文构建模拟记录与观测记录之间的Wasserstein距离的平方作为新的目标函数,以提高目标函数的凸性,从而提高反演结果的精度。
1.2.2 基于W2范数伪压力弹性波波形反演最优输运理论是用于分析概率分布之间的关系,找寻一种最优化的运输方案。Wasserstein距离表示两种概率分布之间的差异,其衡量标准是将一种分布重新排列为另一种分布的最优输运成本。将模拟和观测地震数据集视为两个概率密度函数的概率分布,可以将其想象为总体质量相等(同时等于单位1)的两堆沙子的分布。给定特定的成本函数,将一堆沙运送到另一堆沙的不同方案会导致不同的运输成本,成本最低的方案就是最优方案,而Wasserstein距离就是这一最低成本。本文采用二次Wasserstein范数(W2距离),定义为
| $ W_2^2(b,q) = \mathop {\inf }\limits_{{Q_{b,q}} \in \mathit{\boldsymbol{M}}} \int_X {{{\left| {x - {A_{b,q}}(x)} \right|}^2}} b(x){\rm{d}}x $ | (16) |
式中:b和q为概率密度函数,其对应的概率分布函数分别被定义在X和Y空间;M为将b重新排列或搬运为q的所有映射的集合;inf表示集合M的下确界;A表示运输方案。
推广到地球物理问题,本文采用一维W2目标函数
| $ E^{\mathrm{OT}}=W_{2}^{2}(b, q)=\int_{0}^{1}\left|x-Q^{-1}[B(x)]\right|^{2} b(x) \mathrm{d} x $ | (17) |
式中:Q-1与Q互为逆函数,为表示方便,后文用Q-1ºB(x)代替Q-1B(x);B和Q分别对应于模拟数据和观测数据的概率分布函数。地震数据不是严格的概率密度函数,因此本文采用Yang等[25]的地震数据预处理方案。
根据伴随状态法原理可知,梯度形式只和状态方程(伪压力弹性波方程)有关,因此梯度仍然是式(14)和式(15),唯一不同的是反传虚震源项,Yang等[25]给出了一维虚震源δη的表达形式
| $ \begin{aligned} \delta \eta(t)=& \frac{-2 b(t) \cdot\left[t-Q^{-1} \circ B(t)\right] \cdot(\mathrm{d} t)^{2}}{q\left[Q^{-1} \circ B(t)\right]}+\\ &\left[t-Q^{-1} \circ B(t)\right]^{2} \mathrm{~d} t \end{aligned} $ | (18) |
式中dt表示地震数据的时间采样间隔。
2 数值模拟结果及分析 2.1 目标函数的凸性分析选取完全满足概率密度函数特征的Gauss子波(不含负极性)和Ricker子波(含负极性)测试L2范数和W2范数目标函数的凸性。图 5a为Gauss子波模拟数据及观测数据,图 5b为Gauss子波的模拟数据和观测数据的基于L2范数与基于W2范数误差量随时移量变化的形态对比。图 5c为Ricker子波模拟数据及观测数据,图 5d模拟数据和观测数据的基于L2范数与基于W2范数误差量随时移量变化的形态对比。对于高斯子波数据,W2范数构建了一个全局凸的目标函数,而L2范数目标函数虽然也是一个凸函数,但是在数据相位差超过一个波长的情况下,L2范数不能指示误差下降。对于Ricker子波数据,两种目标函数曲线均存在局部极小值,但是W2范数的凸性比L2范数更好,在一定程度上降低了基于L2范数FWI的周期性跳跃问题的影响。可见,理论上W2范数比L2范数的凸性更好。

|
图 5 L2范数和W2范数目标函数的凸性分析 (a)Gauss子波模拟数据及观测数据;(b)Gauss子波的L2范数和W2范数目标函数;(c)Ricker子波模拟数据及观测数据;(d)Ricker子波的L2范数和W2范数目标函数 |
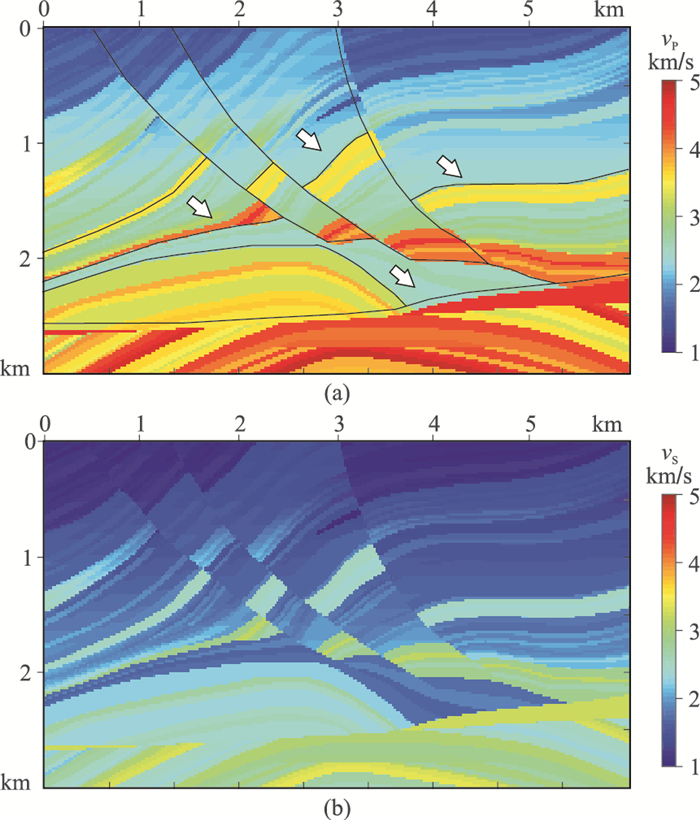
利用重采样后Marmousi纵、横波速度模型(图 6)测试本文反演方法效果。模型网格数为300×150,网格间距均为20m。正演采用主频为8Hz的Ricker子波作为震源,时间采样间隔为2ms。共设置42炮,炮检点均匀分布于地表,起始炮点位于0,炮间距为140m;每一炮的检波点数均为300,起始检波点位于0,检波点距为20m。
|
图 6 Marmousi真实模型 (a)纵波速度; (b)横波速度 |
本文采取两种策略实现Marmousi模型弹性参数反演:一是基于L2范数的伪压力弹性波方程纵、横波速度参数反演;二是首先用基于W2范数进行弹性参数反演得到修正的低波数纵、横波速度模型,然后再用经典L2范数进行高波数扰动纵横波速度模型反演。测试中,均不考虑密度参数的影响,密度参数设置为常值1500kg/m3。
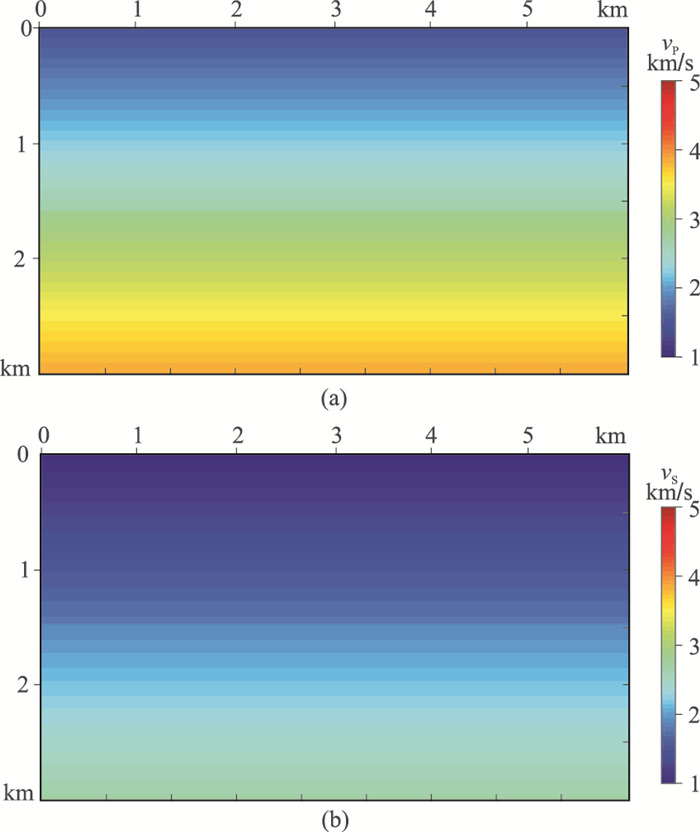
为保证本文提出的方法能够仅利用纵波资料准确反演弹性参数模型,采用纵、横波速度横向不变、垂向线性增加的初始模型(图 7)。误差大的初始速度会引起波形反演的周期性跳跃问题,进而导致非线性反演落入局部极值。图 8为真实模型和初始模型采用伪压力弹性波方程正演模拟得到的第21炮记录(观测记录和模拟记录),可以看出模拟记录不存在反射波信息。
|
图 7 Marmousi初始模型 (a)纵波速度;(b)横波速度 |

|
图 8 Marmousi模型模拟地震记录 左为观测记录;中为初始模型模拟记录;右为水平翻转观测记录 |
图 9和图 10展示了在L2范数和W2范数目标函数下的伪压力弹性波波形反演的第21炮虚震源记录。L2反演结果以中高波数为主,因此其虚震源记录频带中的高低频信息分布与观测记录频带特征基本吻合。由于线性初始速度无法提供可靠的运动学信息,很容易导致FWI落入局部极值。W2的虚震源主要集中在低频带,记录中分布了大量“竖直线条状”的低频能量,这些能量主要更新梯度中的低波数更新量,它对于残差模型(真实模型和初始模型的残差)中的低波数分量恢复具有重要的贡献,解决了波形反演由于初始速度精度低导致周期性跳跃和局部极值问题。

|
图 9 L2范数目标函数的虚拟震源记录 |

|
图 10 W2范数目标函数的虚拟震源记录 |
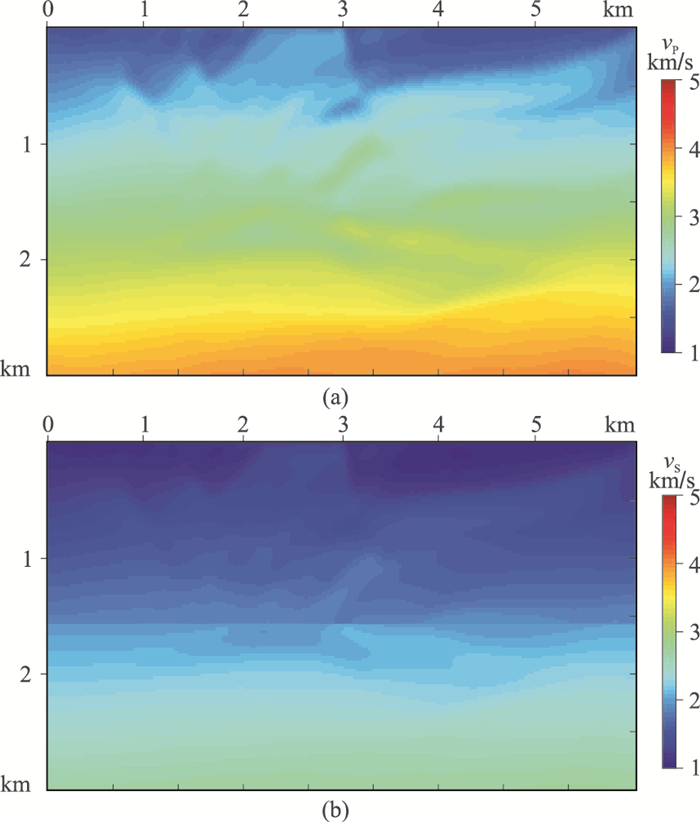
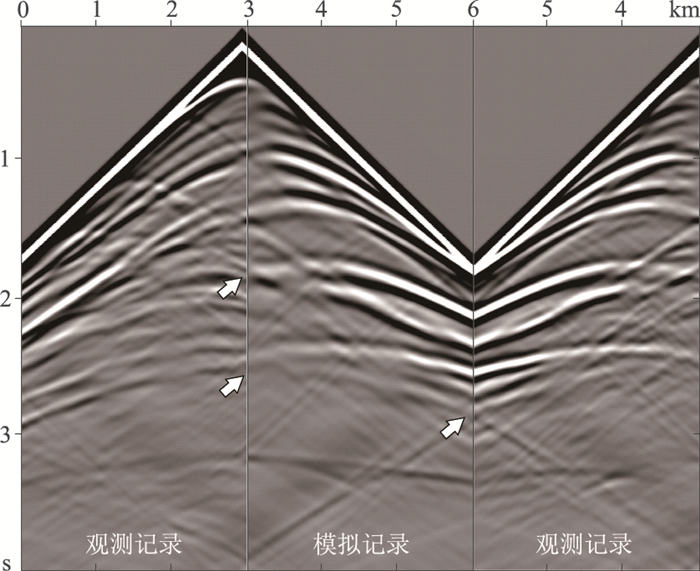
图 11为基于W2范数的纵、横波速度第21次迭代反演结果。第22次迭代误差上升,反演终止。反演模型的浅、中、深层的背景模型均得到修正,间断面没有被准确刻画,说明反演过程中主要以低波数模型的修正为主,验证了图 10的分析。图 12为用W2反演结果进行伪压力弹性波正演的模拟记录和真实模型模拟的观测记录的对比,模拟记录中强反射界面产生的反射波非常清晰,对比两侧的观测记录,衔接处的反射波位置基本一致,但是W2反演结果的模拟记录缺失了高频信息,箭头处明显与右边观测记录不一致,缺失了一些细小的反射轴信息(高频信息)。
|
图 11 Marmousi模型W2反演结果 (a)纵波速度;(b)横波速度 |
|
图 12 Marmousi模型W2反演结果模拟记录与观测记录的对比 左为观测记录;中为W2反演结果的模拟记录;右为水平翻转观测记录 |
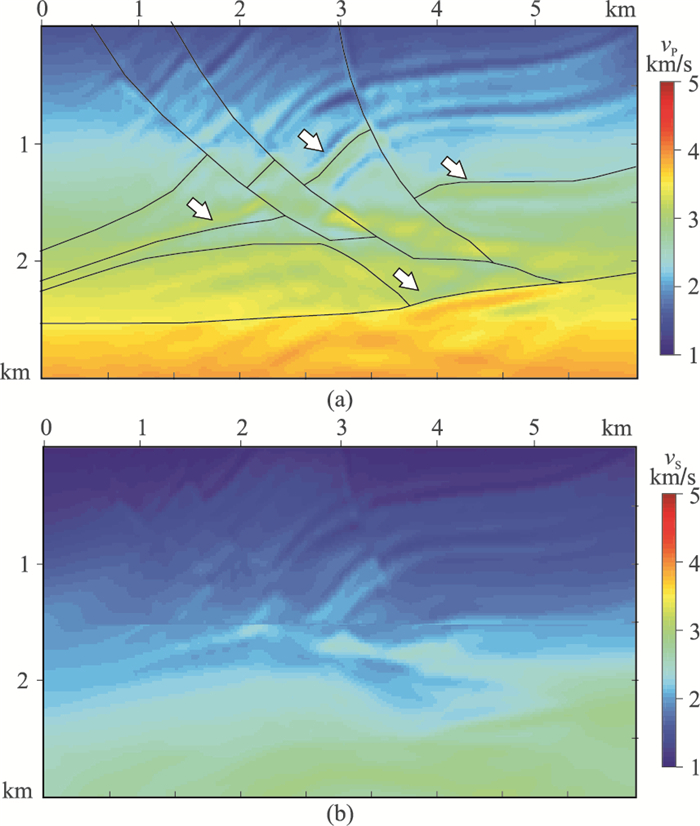
基于L2范数的纵、横波速度反演误差在迭代57次后上升,反演终止,结果如图 13所示。由图可见,基于L2范数的反演陷入局部极值且反演结果严重偏离了真实模型。为了更直观的展示该结果,将真实纵波速度模型(图 6a)主要构造界面映射到L2范数的纵波速度反演结果(图 13a黑线所示),可见,基于L2范数的反演结果的地质构造整体上移,箭头所指的四处弹性间断面均与反演速度不一致,因此以线性初始速度模型为驱动的基于L2范数的反演失败。
|
图 13 Marmousi模型L2反演结果 (a)纵波速度;(b)横波速度 |
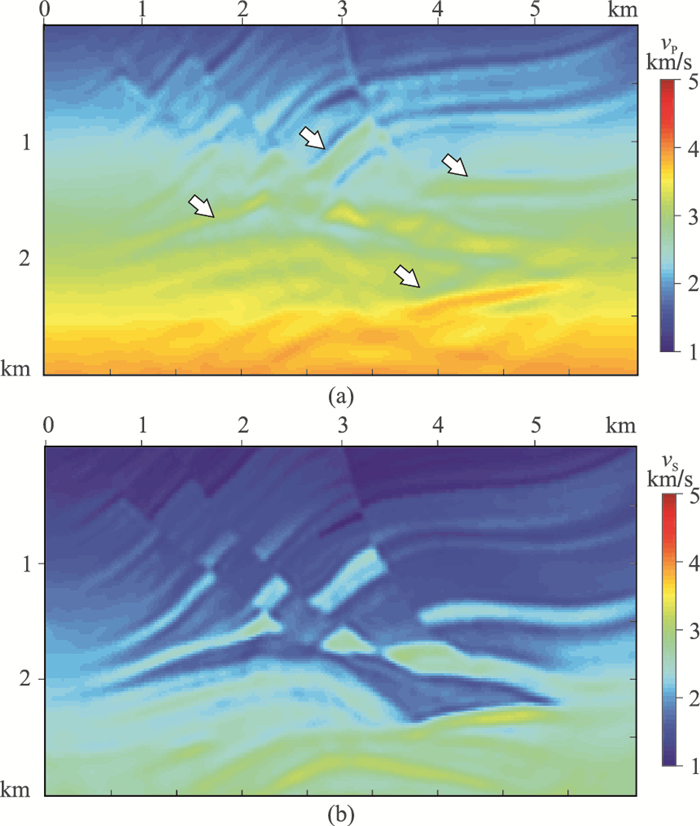
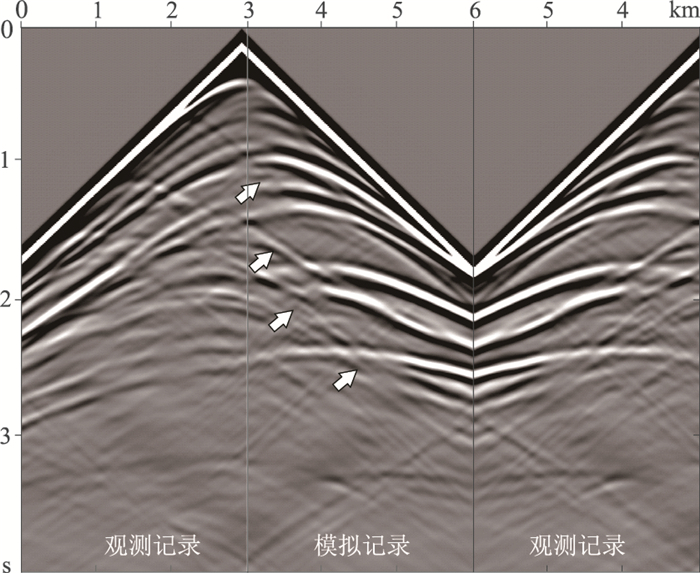
以W2反演结果作为初始模型,进一步实施L2反演,W2+L2反演共迭代了78次,结果如图 14所示。对比图 6a、图 13a、图 14a可见,W2+L2反演结果的构造界面与真实模型基本吻合,比L2反演结果更精确,说明W2反演的纵横波速度模型准确修正了模型中、低波数信息。图 15为用W2+L2最终反演结果进行伪压力弹性波正演的模拟记录与真实模型模拟的观测记录的对比,可见,模拟记录丰富了图 12数据的高频信息,并且与观测记录吻合良好。
|
图 14 Marmousi模型W2+L2反演结果 (a)纵波速度;(b)横波速度 |
|
图 15 Marmousi模型W2+L2反演结果模拟记录与观测记录的对比 左为观测记录;中为W2+L2反演结果的模拟记录;右为水平翻转观测记录 |
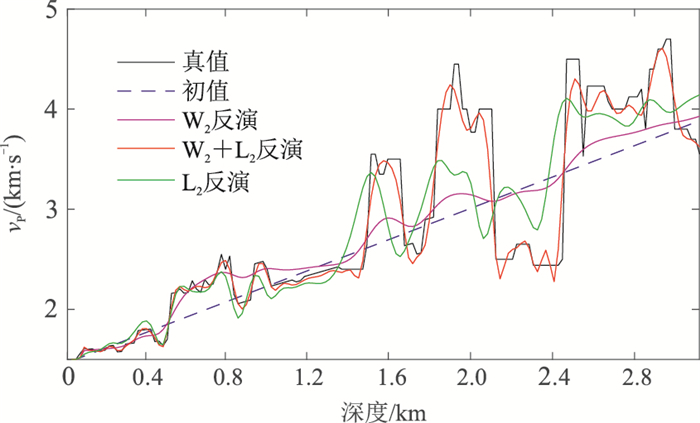
图 16为两种反演过程中纵波速度模型梯度,可见,在W2反演过程中,速度更新量从浅层开始,逐步递进到中深层,并且更新量主要以低波数信息为主,尤其是图 16b的梯度剖面上中深层的低波数的更新量能量均衡,界面位置基本准确。对比L2反演的第1次迭代与W2+L2反演的第21+1次迭代的梯度剖面(图 16c与16d),L2反演梯度主要界面完全偏离了真实构造位置(实线所示);由于W2反演提供的准确背景速度,W2+L2反演梯度主要界面与真实构造位置(实线所示)一致。图 17和图 18分别为Marmousi模型反演结果与初始、真实模型的抽道对比(横向4km处),可见,W2+L2反演策略能够准确地恢复模型的低—中—高波数(在现有数据频带范围内)成分。图 19为L2和W2+L2两种反演策略的归一化误差曲线,W2+L2反演收敛速度更快,且误差更小,结果更接近真值。

|
图 16 Marmousi模型反演过程中梯度剖面 (a)W2反演第1次迭代;(b)W2反演第18次迭代;(c)L2反演第1次迭代;(d)W2+L2第21+1次迭代 |
|
图 17 Marmousi纵波速度反演结果与初值、真值的单道对比 |

|
图 18 Marmousi横波速度反演结果与初值、真值的单道对比 |

|
图 19 Marmousi模型W2+L2和L2反演收敛曲线 |
采用中国东部M工区的二维地震数据验证本文的基于伪压力弹性波方程的陆上单分量资料弹性波波形反演方法的实用性。该工区在近地表存在明显的低降速带,反射波路径几乎垂直于地面并被垂直检波器接收,数据集可以视为纵波数据,符合本文方法的适用条件。
图 20为通过偏移速度分析得到的初始纵波速度模型,横波速度模型是根据测井数据和岩石物理建模分析拟合出的经验关系(vS=-728.168+0.748×vP)计算得到,密度参数设为常数。速度模型网格数为3151×500,水平和垂直方向的网格间距均为10m。地震数据采样间隔为2ms,长度为4s。为满足稳定性条件,使用傅立叶变换方法进行数据插值,重采样间隔为0.8ms。震源和检波器均在地面,总炮数为233炮,单炮最大炮检距为4km,检波器间距为10m。震源子波是由地震记录提取,主频约为20Hz。

|
图 20 纵波速度初始模型 |
由于横波速度与纵波速度满足经验关系,因此在W2反演过程中,采用以下纵横波速度梯度作为更新量
| $ \left\{\begin{array}{l} \delta v_{\mathrm{P}}=0.02 \times \frac{2 \rho v_{\mathrm{P}} \int_{0}^{t_{\max }} P^{*} u_{k, k} \mathrm{~d} t}{\int_{0}^{t_{\max }} P\left(\boldsymbol{x}_{\mathrm{s}}, \boldsymbol{x}, t\right) \cdot P\left(\boldsymbol{x}_{\mathrm{s}}, \boldsymbol{x}, t\right) \mathrm{d} t} \\ \delta v_{\mathrm{S}}=-728.168+0.748 \times \delta v_{\mathrm{P}} \end{array}\right. $ | (19) |
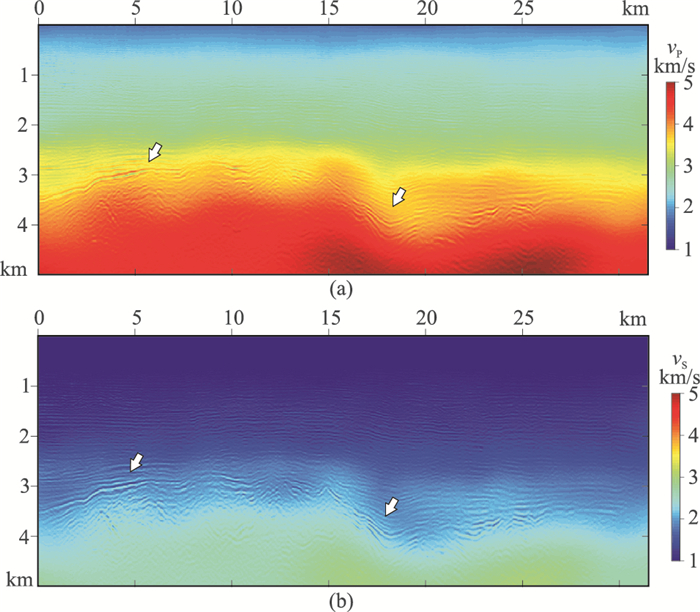
图 21为W2反演迭代5次的纵波速度模型,箭头所指处更新较为明显,横波速度与其满足经验关系,因此没有展示。然后将W2反演结果作为初始模型进行L2反演,并采用式(16)的弹性波双参数反演梯度进行纵、横波速度迭代更新。图 22为经过11次L2反演迭代后纵、横波速度模型,从图中箭头处可以看出反演速度的构造细节,并且有较高的分辨率。

|
图 21 W2反演迭代5次的纵波速度模型 |
|
图 22 W2+L2反演迭代5+11次后的速度模型 (a)纵波速度;(b)横波速度 |
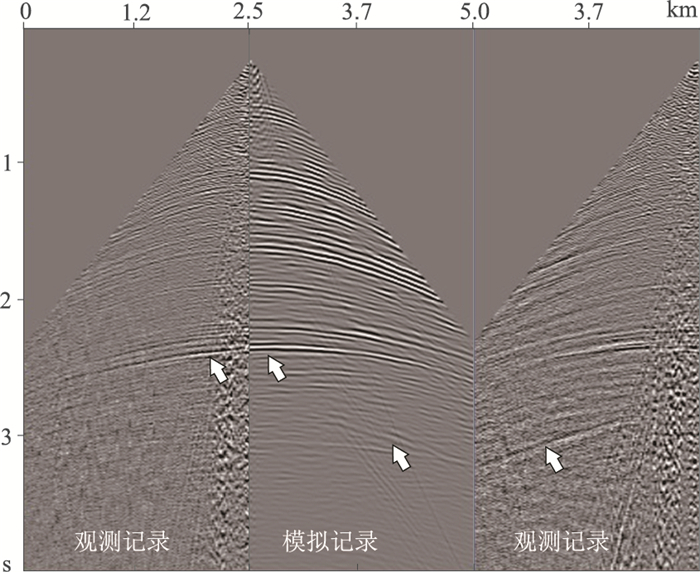
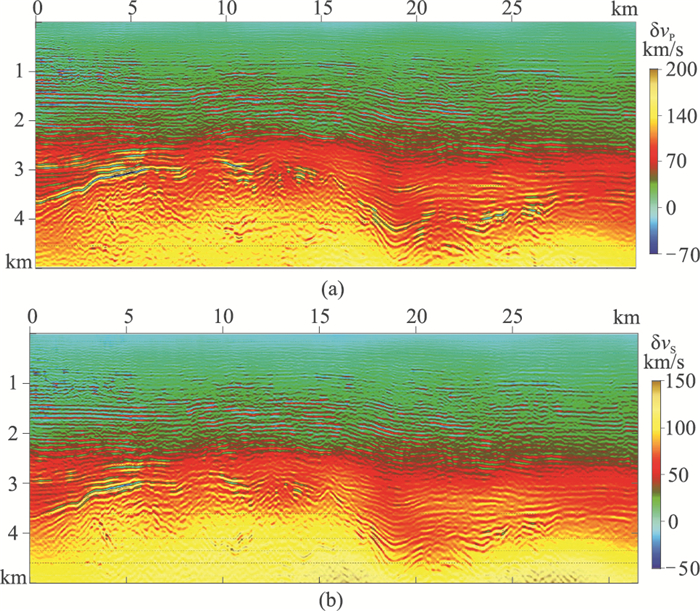
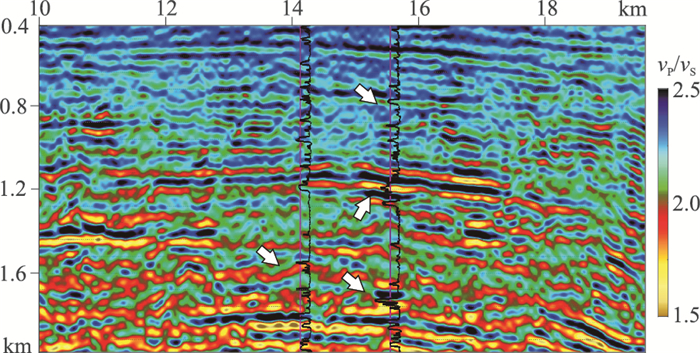
图 23为观测与用最终反演速度模型模拟的单炮记录的对比,二者均主要包含纵波信息,由图中箭头处可见,模拟记录与观测记录对应关系良好。为验证反演结果的可靠性,应用JASON软件去除纵、横波速度低波数背景信息,得到纵、横波速度扰动模型,如图 24所示。然后计算纵横波速度比(vP/vS)模型,如图 25所示。根据式(12)可知模型反演更新量与该模型的数值成比例,因此纵横波速度的扰动量模型计算得到的vP/vS数值仍然稳定,而去除背景干扰后,模型高频细节更加突出。图 25白色方框部分的放大如图 26所示,其中两条黑线为自然电位测井曲线。当砂岩含量较高时,泊松比较低,对应的vP/vS在测井曲线上表现为低值(图中白色箭头所指),说明反演结果与测井解释较吻合。
|
图 23 W2+L2反演迭代5+11次后速度模型模拟记录与观测记录的对比 左为观测记录,中为模拟记录,右为水平翻转观测记录 |
|
图 24 去除低波数背景的纵(a)、横(b)波速度扰动模型 |

|
图 25 去除低波数背景的纵横波速度比模型 |
|
图 26 去除低波数背景的纵横波速度比模型局部放大显示 黑线为自然电位测井曲线 |
综上所述,基于伪压力弹性波方程的波形反演方法能够适用于陆上单分量地震数据的纵、横波速度弹性反演,有利于含油气储层的预测。
3 结论本文针对陆上地震单分量勘探提出了一种高效、稳定的弹性参数波形反演方法,并通过模型数据和实际数据验证了方法的正确性和实用性。
(1) 由于地表低降速带影响,地震反射波路径几乎与地表垂直,垂直分量检波器采集接收的地震资料可视为纵波数据,这类数据包含大量转换纵波信号和弹性AVO信息。伪压力弹性波方程可以适应陆上地震单分量勘探的需求,同时满足转换纵波和弹性AVO特征,具备在弹性介质中用标量波数据实现弹性参数反演的能力。
(2) W2范数相比于L2范数具有更优的凸性。Marmousi模型数值实例说明L2范数目标函数在波形反演应用中存在周期性跳跃问题,W2范数避免了周期性跳跃现象,W2+L2反演策略减弱了波形反演对初始模型的依赖性。就收敛速度而言,W2反演更快。
(3) 中国东部M工区二维实际资料反演应用结果说明伪压力弹性波方程反演方法能够适用于实际工区的弹性参数求取,有利于含油气储层的预测。
本文方法介于纵波勘探和多分量勘探之间,在多分量勘探技术尚未成熟之前,为弹性参数反演提供了一个折中的思路。
附录A 伪压力弹性波方程将牛顿运动微分方程(式(3))中应力项替换为球张量和偏斜张量之和的形式,即将式(5)代入式(3),可得
| $ \rho \ddot{u}_{i}=\frac{\partial}{\partial x_{j}}\left(S_{i j}+P\delta_{ i j}\right)+f_{i} $ | (A-1) |
对该式两边同时求散度,有
| $ \frac{\partial^{2}\left(u_{i, i}\right)}{\partial t^{2}}=\nabla \cdot\left[\frac{1}{\rho} \frac{\partial}{\partial x_{j}}\left(S_{i j}+P \delta_{i j}\right)\right]+\underbrace{\nabla \cdot\left(\frac{\boldsymbol{f}}{\rho}\right)}_{f_{\mathrm{P}}} $ | (A-2) |
由于P⇔Kuk, k,调整位移的时间导数项,有
| $ \frac{1}{K} \frac{\partial^{2}\left(K u_{i, i}\right)}{\partial t^{2}}=\nabla \cdot\left[\frac{1}{\rho} \frac{\partial}{\partial x_{j}}\left(S_{i j}+P \delta_{i j}\right)\right]+f_{\mathrm{P}} $ | (A-3) |
可得张量表示的伪压力弹性波方程
| $ \frac{1}{K} \frac{\partial^{2} P}{\partial t^{2}}=\frac{\partial}{\partial x_{i}}\left[\frac{1}{\rho} \frac{\partial}{\partial x_{j}}\left(S_{i j}+P \delta_{i j}\right)\right]+f_{P} $ | (A-4) |
在各向同性完全弹性介质条件下,刚度矩阵Cijkl可以分解为胀缩CijklP和旋转CijklT形式
| $ \left\{\begin{array}{l} C_{i j k l}=C_{i j k l}^{\mathrm{P}}+C_{i j k l}^{\mathrm{T}} \\ C_{i j k l}^{\mathrm{P}}=K \delta_{i j} \delta_{k l} \\ C_{i j k l}^{\mathrm{T}}=\lambda \delta_{i j} \delta_{k l}+\mu\left(\delta_{i k} \delta_{j l}+\delta_{i l} \delta_{j k}\right)-C_{i j k l}^{\mathrm{P}} \end{array}\right. $ | (A-5) |
根据胡克定律,球应力分量和偏斜应力分量与应变的关系为
| $ \left\{\begin{array}{l} P=C_{i j k l}^{\mathrm{P}} e_{k l}=K \delta_{i j} \delta_{k l} e_{k l} \\ S_{i j}=C_{i j k l}^{\mathrm{T}} e_{k l}=\left[\lambda \delta_{i j} \delta_{k l}-K \delta_{i j} \delta_{k l}+\right. \\ \ \ \ \ \ \ \ \ \ \ \left.\mu\left(\delta_{i k} \delta_{j l}+\delta_{i l} \delta_{j k}\right)\right] e_{k l} \end{array}\right. $ | (A-6) |
将式(A-6)代入式(A-4)中,可得
| $ \frac{\partial^{2} P}{\partial t^{2}}=\frac{\partial}{\partial x_{i}}\left[\frac{1}{\rho} \frac{\partial}{\partial x_{j}}\left(C_{i j k l}^{\mathrm{T}} e_{k l}+P \delta_{i j}\right)\right]+f_{\mathrm{P}} $ | (A-7) |
代入位移与应变关系
| $ \frac{1}{K} \frac{\partial^{2} P}{\partial t^{2}}-\frac{\partial}{\partial x_{i}}\left[\frac{1}{\rho} \frac{\partial}{\partial x_{j}}\left(\frac{1}{2} C_{i j k l}^{\mathrm{T}} \frac{\partial u_{k}}{\partial x_{l}}+P \delta_{i j}\right)\right]=f_{\mathrm{P}} $ | (A-8) |
Plessix[30]在非线性反演中提出伴随状态法,大大减化了非线性反演中梯度的计算难度。目标函数E用泛函h定义为
| $ E(\boldsymbol{m})=h[u(\boldsymbol{m}), \boldsymbol{m}] $ | (B-1) |
其伴随状态方程为
| $ G[u(\boldsymbol{m}), \boldsymbol{m}]=0 $ | (B-2) |
因此目标函数/伴随状态方程的梯度由正传波场(波动方程和状态方程对模型参数的导数)和反传波场互相关计算得到,即
| $ \nabla_{m} E=-\left\langle u^{*}, \frac{\partial G(u, \boldsymbol{m})}{\partial \boldsymbol{m}}\right\rangle $ | (B-3) |
式中u*表示反传波场,由伴随状态方程对模型参数的导数作为虚震源反传计算
| $ \frac{\partial G(u, \boldsymbol{m})}{\partial u} u^{*}=\frac{\partial h(u, \boldsymbol{m})}{\partial u} $ | (B-4) |
结合式(A-1)和式(A-6)可得伪压力弹性波方程的状态方程F(φ, m),其中φ=(P, ux, uy, uz)。下面给出伪压力弹性波方程
| $ \left\{\begin{array}{l} \rho \ddot{u}_{i}-\frac{\partial}{\partial x_{j}}\left(S_{i j}+P \delta_{i j}\right)-f_{i}=0 \\ P=K \delta_{i j} \delta_{k l} e_{k l} \\ S_{i j}=\left[\lambda \delta_{i j} \delta_{k l}-K \delta_{i j} \delta_{k l}+\mu\left(\delta_{i k} \delta_{j l}+\delta_{i l} \delta_{j k}\right)\right] e_{k l} \end{array}\right. $ | (B-5) |
根据伴随状态法可得目标函数对拉梅常数的梯度
| $ \left\{\begin{array}{l} \begin{aligned} \nabla_{\lambda} E=&\int_{0}^{t_{\max }}\left[\ddot{u}_{i}^{*} \frac{\partial \rho}{\partial \lambda} \ddot{u}_{i}+\frac{\partial K}{\partial \lambda} P^{*} \delta_{i j} \delta_{k l} e_{k l}+\right. \\ &S_{i j}^{*} \delta_{i j} \delta_{k l} e_{k l}-S_{i j}^{*} \frac{\partial K}{\partial \lambda} \delta_{i j} \delta_{k l} e_{k l}+ \\ & \left.S_{i j}^{*} \frac{\partial \mu}{\partial \lambda}\left(\delta_{i k} \delta_{j l}+\delta_{i l} \delta_{j k}\right) e_{k l}\right] \mathrm{d} t \end{aligned}\\ \begin{aligned} \nabla_{\mu} E=&\int_{0}^{t_{\max }}\left[\ddot{u}_{i}^{*} \frac{\partial \rho}{\partial \mu}{\ddot{u}}_{i}+\frac{\partial K}{\partial \mu} P^{*} \delta_{i j} \delta_{k l} e_{k l}+\right. \\ &S_{i j}^{*} \frac{\partial \lambda}{\partial \mu} \delta_{i j} \delta_{k l} e_{k l}-S_{i j}^{*} \frac{\partial K}{\partial \mu} \delta_{i j} \delta_{k l} e_{k l}+ \\ &\left.S_{i j}^{*}\left(\delta_{i k} \delta_{j l}+\delta_{i l} \delta_{j k}\right) e_{k l}\right] \mathrm{d} t \end{aligned}\\ \begin{aligned} \nabla_{\rho} E=& \int_{0}^{t_{\max }}\left[\ddot{u}_{i}^{*} \ddot{u}_{i}+\frac{\partial K}{\partial \rho} P^{*} \delta_{i j} \delta_{k l} e_{k l}+\right.\\ & S_{i j}^{*} \frac{\partial \lambda}{\partial \rho} \delta_{i j} \delta_{k l} e_{k l}-S_{i j}^{*} \frac{\partial K}{\partial \rho} \delta_{i j} \delta_{k l} e_{k l}+\\ &\left.S_{i j}^{*} \frac{\partial \mu}{\partial \rho}\left(\delta_{i k} \delta_{j l}+\delta_{i l} \delta_{j k}\right) e_{k l}\right] \mathrm{d} t \end{aligned} \end{array}\right. $ | (B-6) |
化简可得
| $ \left\{\begin{aligned} \nabla_{\lambda} E=& \int_{0}^{t_{\max }} \frac{\partial K}{\partial \lambda} P^{*} u_{k k} \mathrm{~d} t \\ \nabla_{\mu} E=& \int_{0}^{t_{\max }}\left[S_{i j}^{*}\left(\delta_{i k} \delta_{j l}+\delta_{i l} \delta_{j k}-\frac{\partial K}{\partial \mu} \delta_{i j} \delta_{k l}\right) e_{k l}+\right.\\ &\left.+\frac{\partial K}{\partial \mu} P^{*} u_{k k}\right] \mathrm{d} t \\ \nabla_{\rho} E=& \int_{0}^{t_{\max }} \ddot{u}_{i}^{*} \ddot{u}_{i} \mathrm{~d} t \end{aligned}\right. $ | (B-7) |
式中
感谢中国石化胜利油田物探研究院提供了数据支持,以及纽约大学Yunan YANG老师提供了有益的建议和帮助。
| [1] |
Virieux J, Operto S. An overview of full-waveform inversion in exploration geophysics[J]. Geophysics, 2009, 74(6): WCC1-WCC26. DOI:10.1190/1.3238367 |
| [2] |
Tarantola A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [3] |
Tarantola A. A strategy for nonlinear elastic inversion of seismic reflection data[J]. Geophysics, 1986, 51(10): 1893-1903. DOI:10.1190/1.1442046 |
| [4] |
Mora P. Elastic wave-field inversion of reflection and transmission data[J]. Geophysics, 1988, 53(6): 750-759. DOI:10.1190/1.1442510 |
| [5] |
Köhn D, De Nil D, Kurzmann A, et al. On the influence of model parametrization in elastic full waveform tomography[J]. Geophysical Journal International, 2012, 191(1): 325-345. DOI:10.1111/j.1365-246X.2012.05633.x |
| [6] |
Jeong W, Lee H, Min D J. Full waveform inversion strategy for density in the frequency domain[J]. Geophysical Journal International, 2012, 188(3): 1221-1242. DOI:10.1111/j.1365-246X.2011.05314.x |
| [7] |
Ren Z, Liu Y. A hierarchical elastic full-waveform inversion scheme based on wavefield separation and the multistep-length approach[J]. Geophysics, 2016, 81(3): R99-R123. DOI:10.1190/geo2015-0431.1 |
| [8] |
Wang T, Cheng J. Elastic full waveform inversion based on mode decomposition: the approach and mechanism[J]. Geophysical Journal International, 2017, 209(2): 606-622. DOI:10.1093/gji/ggx038 |
| [9] |
Raknes E, Arntsen B, Weibull W. Three-dimensional elastic full waveform inversion using seismic data from the Sleipner area[J]. Geophysical Journal International, 2015, 202(3): 1877-1894. DOI:10.1093/gji/ggv258 |
| [10] |
李青阳, 吴国忱, 吴建鲁. 基于互相关目标函数的反射波波形反演[J]. 石油地球物理勘探, 2020, 55(4): 754-765. LI Qingyang, WU Guochen, WU Jianlu. Reflection waveform inversion based on cross-correlation misfit function[J]. Oil Geophysical Prospecting, 2020, 55(4): 754-765. |
| [11] |
Sears T J, Singh S C, Barton P J. Elastic full waveform inversion of multi-component OBC seismic data[J]. Geophysical Prospecting, 2008, 56(6): 843-862. DOI:10.1111/j.1365-2478.2008.00692.x |
| [12] |
Li Q, Wu G, Wu J, et al. Finite difference seismic forward modeling method for fluid-solid coupled media with irregular seabed interface[J]. Journal of Geophysics and Engineering, 2019, 16(1): 198-214. DOI:10.1093/jge/gxy017 |
| [13] |
李青阳, 吴国忱, 吴建鲁. 非均匀流-固边界耦合介质多参数全波形反演方法[J]. 地球物理学报, 2019, 62(9): 3557-3570. LI Qingyang, WU Guochen, WU Jianlu. A multi-parameter full waveform inversion method for a heterogeneous medium with a fluid-solid coupled boundary[J]. Chinese Journal of Geophysics, 2019, 62(9): 3557-3570. |
| [14] |
Brossier R, Operto S, Virieux J. Seismic imaging of complex onshore structures by 2D elastic frequency-domain full-waveform inversion[J]. Geophysics, 2009, 74(6): WCC105-WCC118. DOI:10.1190/1.3215771 |
| [15] |
Barnes C, Charara M. The domain of applicability of acoustic full-waveform inversion for marine seismic data[J]. Geophysics, 2009, 74(6): WCC91-WCC103. DOI:10.1190/1.3250269 |
| [16] |
刘立彬, 李振春, 张云银, 等. 一种时间域全波形反演中的地震子波估计方法[J]. 地球物理学进展, 2019, 35(3): 987-994. LIU Libing, LI Zhenchun, ZHANG Yunyin. Seismic wavelet estimation for full-waveform inversion in time domain[J]. Progress in Geophysics, 2019, 35(3): 987-994. |
| [17] |
Li Q, Wu G. 2D multi-parameter waveform inversion of land reflection seismic data obtained from the particle-motion response from the vertical geophone[J]. Acta Geophysica, 2020, 68(2): 377-388. DOI:10.1007/s11600-020-00403-6 |
| [18] |
王毓玮, 董良国, 黄超, 等. 降低弹性波全波形反演强烈非线性的分步反演策略[J]. 石油地球物理勘探, 2016, 51(2): 288-294. WANG Yuwei, DONG Liangguo, HUANG Chao, et al. A multi-step strategy for mitigating severe nonli-nearity in elastic full-waveform inversion[J]. Oil Geo-physical Prospecting, 2016, 51(2): 288-294. |
| [19] |
Wu Z, Alkhalifah T. Selective data extension for full-waveform inversion: An efficient solution for cycle skipping[J]. Geophysics, 2018, 83(3): R201-R211. DOI:10.1190/geo2016-0649.1 |
| [20] |
吴彦, 马玥, 刘玉金, 等. 全走时反演及其应用[J]. 石油物探, 2017, 56(1): 50-56. WU Yan, MA Yue, LIU Yujin, et al. Full-traveltime inversion and its application[J]. Geophysical Prospecting for Petroleum, 2017, 56(1): 50-56. |
| [21] |
Bunks C, Saleck F, Zaleski S, et al. Multiscale seismic waveform inversion[J]. Geophysics, 1995, 60(5): 1457-1473. DOI:10.1190/1.1443880 |
| [22] |
Wu R, Luo J, Wu B. Seismic envelope inversion and modulation signal model[J]. Geophysics, 2014, 79(3): WA13-WA24. DOI:10.1190/geo2013-0294.1 |
| [23] |
Xu S, Wang S, Chen F, et al. Full waveform inversion for reflected seismic data[C]. Extended Abstracts of 74th EAGE Conference & Exhibition, 2012, W024.
|
| [24] |
Warner M, Guasch L. Adaptive waveform inversion[J]. Geophysics, 2016, 81(6): R429-R445. DOI:10.1190/geo2015-0387.1 |
| [25] |
Yang Y, Engquist B, Sun J. Application of optimal transport and the quadratic Wasserstein metric to full-waveform inversion[J]. Geophysics, 2018, 83(1): R43-R62. DOI:10.1190/geo2016-0663.1 |
| [26] |
Métivier L, Brossier R, Mérigot Q, et al. Measuring the misfit between seismograms using an optimal transport distance: Application to full waveform inversion[J]. Geophysical Journal International, 2016, 205(1): 345-377. DOI:10.1093/gji/ggw014 |
| [27] |
石玉梅, 张研, 姚逢昌, 等. 基于声学全波形反演的油气藏地震成像方法[J]. 地球物理学报, 2014, 57(2): 607-617. SHI Yumei, ZHANG Yan, YAO Fengchang, et al. Methodology of seismic imaging for hydrocarbon re-servoirs based on acoustic full waveform inversion[J]. Chinese Journal of Geophysics, 2014, 57(2): 607-617. |
| [28] |
Tang C, McMechan G. Multidirectional-vector-based elastic reverse time migration and angle-domain common-image gathers with approximate wavefield decomposition of P- and S-waves[J]. Geophysics, 2017, 83(1): S57-S79. |
| [29] |
牛滨华, 孙春岩. 半空间介质与地震波传播[M]. 北京: 石油工业出版社, 2002.
|
| [30] |
Plessix R. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications[J]. Geophysical Journal Internatio-nal, 2006, 167(2): 495-503. DOI:10.1111/j.1365-246X.2006.02978.x |



 吴国忱, 山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
吴国忱, 山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: 