2 成都理工大学地球勘探与信息技术教育部重点实验室, 四川成都 610059
2 Key Laboratory of Earth Exploration and Information Techniques of Ministry of Education(Chengdu University of Technology), Chengdu, Sichuan 610059, China
波动方程正演模拟是研究全波形反演及逆时偏移技术的基础。目前常用的波动方程数值模拟方法主要有伪谱法[1-2]、有限元法[3-4]、有限差分法[5-9]等。其中有限差分法具有内存占用小、易于实现和计算效率高的优点,因此它在波动方程数值模拟领域中广受欢迎。但是由于差分网格离散引起的数值频散无法避免,直接影响数值模拟的精度。
时域有限差分方法求解波动方程在时间域和空间域同时进行,按照数值相速度和真实传播速度的相对大小,其固有的频散误差可分为时间频散和空间频散[10]。Koene等[11]提出的时间频散变换,在远远超过稳定性极限所允许的时间步长条件下,能很好地去除时间频散。因此,本文主要针对空间频散问题开展研究。通常用于压制空间数值频散的方法有以下几种:其一,采用较小的空间步长[12],但这会大大增加计算量和所需计算内存;其二,空间方向采用高阶差分格式[13];其三,利用FCT(Flux-Corrected Transport)技术[14-15]削弱数值频散影响;其四,利用优化算法求取新的差分系数[16-20]进行波动方程数值模拟。在相同阶数下,相对于传统泰勒级数展开(TE)方法,利用优化算法求取新的差分系数在较大波数域区间精度更高,因此能取得更好的数值频散压制效果。Holberg[16]首次提出通过最小化给定空间频带内群速度的峰值相对误差优化空间有限差分(FD)算子,但是对群速度的最大相对误差没有严格的限制,导致模拟结果与精确解有较大偏差。Liu[17]基于L2范数建立目标函数,采用最小二乘法(LS)优化近似求取差分系数。此外,Zhang等[18]、Yang等[19]、He等[20]基于L∞范数建立目标函数求解有限差分系数,用于波动方程数值模拟。Zhang等[18]用模拟退火算法求得了声波方程空间导数的有限差分系数,并且给出了0.0001的误差容限。Yang等[19]采用Remez迭代算法求解空间一阶偏导数交错网格差分系数。He等[20]在Yang等[19]的基础上引入新的约束条件,得到“等波纹”解,获得理论上最宽有效频带。
现有的L2范数和L∞范数方法只考虑峰值误差,缺乏对中低波数的误差约束,因此实际数值测试中的误差积累较大。虽然上述方法都能有效减少数值频散,但是应该更加关注有限差分方法在波场传播中的误差积累,而不是一味地追求给定误差容限下的最大覆盖带宽[20-21]。Miao等[21]基于L1范数建立新的目标函数,然后通过交替方向乘子法算法(ADMM)[22]获得了空间二阶偏导数的规则网格有限差分系数。数值实验表明,在不改变误差容限的情况下,此方法尽管略微降低了有效带宽的覆盖范围,但是能加强对中低波数的误差约束,减小有效带宽内的总误差。
本文首先将ADMM优化方法推广到空间一阶偏导数交错网格有限差分系数的求解,将其用于一阶应力—速度声波方程的交错网格有限差分数值模拟。然后对基于三种不同范数优化方法进行频散曲线误差分析。最后利用均匀介质模型和复杂模型的长时程数值实验,证明本文L1范数优化方法在减小误差积累方面的优越性。
1 方法原理 1.1 交错网格有限差分格式非均匀介质的二维一阶应力—速度声波方程组可表示为
| $ \left\{\begin{array}{l} \frac{\partial V_{x}}{\partial t}=\frac{1}{\rho} \frac{\partial P}{\partial x} \\ \frac{\partial V_{z}}{\partial t}=\frac{1}{\rho} \frac{\partial P}{\partial z} \\ \frac{\partial P}{\partial t}=\rho v^{2}\left(\frac{\partial V_{x}}{\partial x}+\frac{\partial V_{z}}{\partial z}\right) \end{array}\right. $ | (1) |
式中:P为应力(标量);Vx和Vz分别表示x和z方向上质点振动速度分量;ρ为介质密度;v为地震波速度。
交错网格有限差分格式在同等条件下比规则网格有限差分格式精度更高。通常,使用高阶有限差分系数可以提高空间导数的精度[7],空间一阶导数的2M阶有限差分交错网格定义为
| $ \begin{gathered} \frac{\partial u}{\partial x} \approx \frac{1}{h} \sum\limits_{m=1}^{M} c_{m}\left[u\left(x+m h-\frac{1}{2} h\right)-\right. \\ \left.u\left(x-m h+\frac{1}{2} h\right)\right] \end{gathered} $ | (2) |
式中:cm是有限差分系数;h是空间网格间距。根据平面波理论有
| $ u(x)=u_{0} \mathrm{e}^{\mathrm{j} k x} $ | (3) |
式中:u0是常数;j为虚数单位;k为波数。令β=kh/2,代入式(2)得到
| $ \beta \approx \sum\limits_{m=1}^{M} c_{m} \sin [(2 m-1) \beta] $ | (4) |
本文的目的是通过在给定范围内最小化绝对误差的总和计算优化的差分系数。绝对误差的总和可以表示为
| $ E=\int_{0}^{k_{\max } h}\left|\sum\limits_{m=1}^{M} c_{m} \sin [(2 m-1) \beta]-\beta\right| \mathrm{d} \beta $ | (5) |
将上式中β离散为β(i)=ikmaxh/N, 其中N为离散度,kmax为最大波数。在忽略常数项kmaxh/N后,目标函数E可写成
| $ E=\sum\limits_{i=1}^{N}\left|\sum\limits_{m=1}^{M} c_{m} \sin \left[(2 m-1) \frac{i k_{\max } h}{N}\right]-\frac{i k_{\max } h}{N}\right| $ | (6) |
将式(6)改写成线性方程组的形式
| $ F(\boldsymbol{c})=\|\boldsymbol{A} \boldsymbol{c}+\boldsymbol{b}\|_{1} $ | (7) |
式中:||●||1为L1范数;A为N×M阶系数矩阵;b为N阶系数向量;c为优化的M阶有限差分常系数矩阵。具体形式为
| $ \left\{\begin{array}{l} \boldsymbol{A}_{i, j}=\sin \left[(2 j-1) \frac{i k_{\max } h}{N}\right] \\ \boldsymbol{b}_{i}=-\frac{i k_{\max } h}{N} \\ \boldsymbol{c}=\left[c_{1}, c_{2}, \cdots, c_{M}\right]^{\mathrm{T}} \end{array}\right. $ | (8) |
Wang等[23]证明了直接优化目标函数F(c)的常系数矩阵c可能导致数值振荡。因此,使用正则化技术[24]克服不稳定解。建立正则化目标函数为
| $ \psi(\boldsymbol{c})=F(\boldsymbol{c})+J(\boldsymbol{c}) $ | (9) |
| $ \mathrm{J}(\boldsymbol{c})=\alpha\|\boldsymbol{D c}\|_{2}^{2} $ | (10) |
式中:α=0.0001为正则化参数;D为单位矩阵。本文的目的是通过求解正则化的问题来找到最优解,即
| $ \boldsymbol{c}=\underset{\boldsymbol{c}}{\arg \min }\left(\|\boldsymbol{A} \boldsymbol{c}+\boldsymbol{b}\|_{1}+\alpha\|\boldsymbol{D} \boldsymbol{c}\|_{2}^{2}\right) $ | (11) |
式(11)为非线性问题,目前可以运用多种方法求解。但是为了高效和精确地求得常系数,采用交替方向乘子法[22]将原始问题转换为约束问题
| $ (\boldsymbol{c}, \boldsymbol{d})=\underset{\boldsymbol{c}, \boldsymbol{d}} {\arg \min } \left(\|\boldsymbol{d}\|_{1}+\alpha\|\boldsymbol{D} \boldsymbol{c}\|_{2}^{2}\right) $ | (12) |
式中d=Ac+b,对应的增广拉格朗日函数可以写成
| $ \begin{aligned} l(\boldsymbol{c}, \boldsymbol{d})=&\|\boldsymbol{d}\|_{1}+\alpha\|\boldsymbol{D} \boldsymbol{c}\|_{2}+\\ & \frac{\eta}{2}\|\boldsymbol{A} \boldsymbol{c}+\boldsymbol{b}-\boldsymbol{d}+\boldsymbol{u}\|_{2}^{2} \end{aligned} $ | (13) |
式中:u为拉格朗日变量;η为软阈值。后面的模型测试中取η=40。
ADMM求解最小化模型主要分为三步:更新c、更新d、更新u。
第一步:更新c
| $ \left\{\begin{array}{l} \boldsymbol{c}=\underset{\boldsymbol{c}}{\arg \min } f^{(k+1)}(\boldsymbol{c}) \\ f^{(k+1)}(\boldsymbol{c})=\alpha\|\boldsymbol{D} \boldsymbol{c}\|_{2}^{2}+\frac{\eta}{2}\left\|\boldsymbol{A} \boldsymbol{c}+\boldsymbol{b}-\boldsymbol{d}^{(k)}+\boldsymbol{u}^{(k)}\right\|_{2}^{2} \end{array}\right. $ | (14) |
这是一个标准的最小二乘问题,c(k+1)可通过
| $ \left(\alpha \boldsymbol{D}^{\mathrm{T}} \boldsymbol{D}+\frac{\eta}{2} \boldsymbol{A}^{\mathrm{T}} \boldsymbol{A}\right) \boldsymbol{c}^{(k+1)}=\frac{\eta}{2} \boldsymbol{A}^{\mathrm{T}}\left(-\boldsymbol{b}+\boldsymbol{d}^{(k)}-\boldsymbol{u}^{(k)}\right) $ | (15) |
第二步:更新d
| $ \left\{\begin{array}{l} \boldsymbol{d}^{(k+1)}=\underset{\boldsymbol{d}}{\arg \min } g^{(k+1)}(\boldsymbol{d}) \\ g^{(k+1)}(\boldsymbol{d})=\|\boldsymbol{d}\|_{1}^{2}+\frac{\eta}{2}\left\|\boldsymbol{A} \boldsymbol{c}^{(k+1)}+\boldsymbol{b}-\boldsymbol{d}+\boldsymbol{u}^{(k)}\right\|_{2}^{2} \end{array}\right. $ | (16) |
上式为一个套索问题[26],可以用次微分学的封闭形式解决。上式的解可以表达成
| $ \boldsymbol{d}^{(k+1)}=S_{1 / \eta}\left(\boldsymbol{A} \boldsymbol{c}^{(k+1)}+\boldsymbol{b}+\boldsymbol{u}^{(k)}\right) $ | (17) |
式中软阈值算子S定义为
| $ S_{k}(a)=\left\{\begin{array}{lc} a-k & a>k \\ 0 & |a| \leqslant k \\ a+k & a<-k \end{array}\right. $ | (18) |
第三步:更新u
| $ \boldsymbol{u}^{(k+1)}=\boldsymbol{u}^{(k)}+\left(\boldsymbol{A} \boldsymbol{c}^{(k+1)}+\boldsymbol{b}-\boldsymbol{d}^{(k+1)}\right) $ | (19) |
为了得到带宽的上限kmax,本文计算不同kmax和M条件下的最大误差
| $ \varepsilon_{\max }=\max \limits_{\beta \in\left[0, k_{\max } h\right]} \varepsilon(\beta) $ | (20) |
| $ \varepsilon(\beta)=\sum\limits_{m=1}^{M} c_{m} \sin [(2 m-1) \beta]-\beta $ | (21) |
为了寻找最优解,从一个小的kmax开始,它产生一个最大误差εmax。当εmax小于给定的容错允差时,稍微增大kmax并重复上述过程,直到εmax等于(或小于)给定的容错允差。表 1为M=8时不同范数优化后求解的差分系数。L1范数优化后求解的差分系数如表 2所示。
|
|
表 1 不同优化方法的差分系数(M=8) |
|
|
表 2 一阶导数交错网格有限差分系数 |
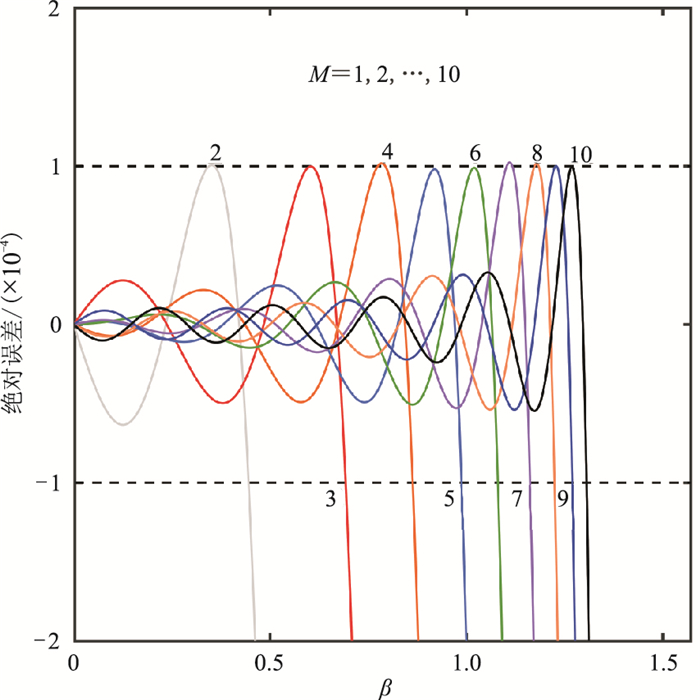
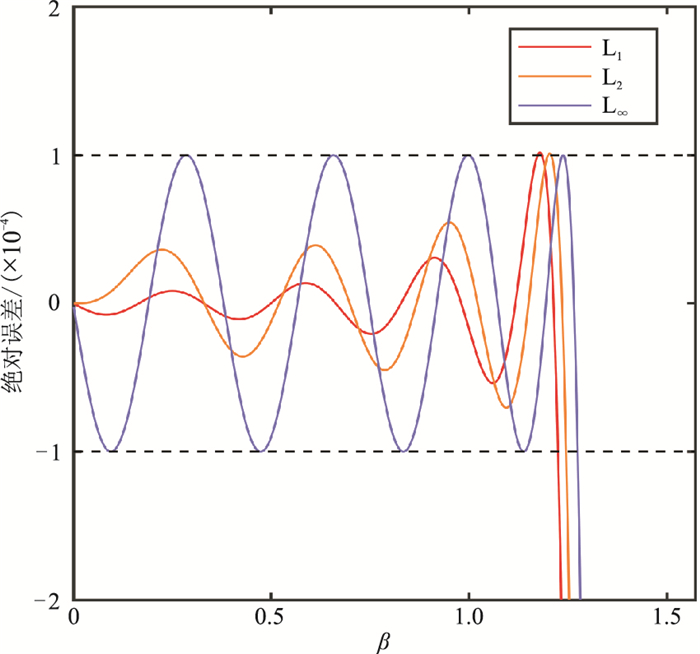
从图 1中不同差分阶数的频散曲线可以看出,采用增大差分阶数可以获得更广的频带覆盖范围,且随着差分阶数的增加,低波数区间的频散误差逐渐减小。为了对各种方法进行比较,分别基于L1范数、L2范数[12]和L∞范数[20]求解声波方程的交错网格有限差分系数,并对其进行频散分析。图 2中,在M=8(16阶)时,在误差阀值为0.0001的条件下,相对于L2范数和L∞范数来说,尽管基于L1范数优化方法频带覆盖范围略微变窄,但能更好地约束在中低波数区间的频散误差。
|
图 1 L1范数优化后的频散曲线 |
|
图 2 三种范数约束下的频散曲线(M=8) |
二维一阶应力—速度声波方程交错网格有限差
分离散格式的稳定性条件[26]为
| $ r \leqslant s $ | (22) |
式中:r为库郎数;s为稳定性因子[27]
| $ s=\frac{1}{\sqrt{2}}\left(\sum\limits_{m=1}^{M}\left|c_{m}\right|\right)^{-1} $ | (23) |
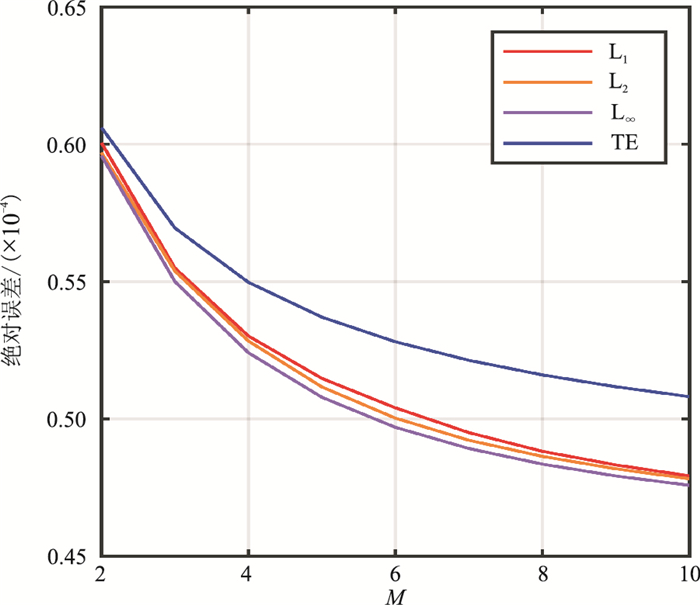
泰勒展开与L1、L2、L∞约束下的稳定性因子曲线如图 3所示。
|
图 3 不同方法的稳定性因子随差分阶数(2M)的变化 |
总体来看,无论是传统TE方法还是各种范数的优化方法,稳定性因子s都会随着差分阶数的增大而减小。此外,在相同差分阶数时,TE方法稳定性因子的值大于其他优化方法。值得注意的是,本文利用L1范数约束优化求得差分系数的稳定性因子比另外两种范数大,证明其稳定性限制条件比另外两种方法宽松。
2 理论模型试算在本次正演模拟实验中,分别对均匀介质模型和Marmousi Ⅱ模型进行正演数值模拟。
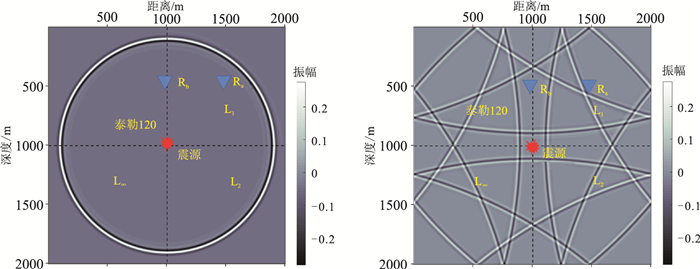
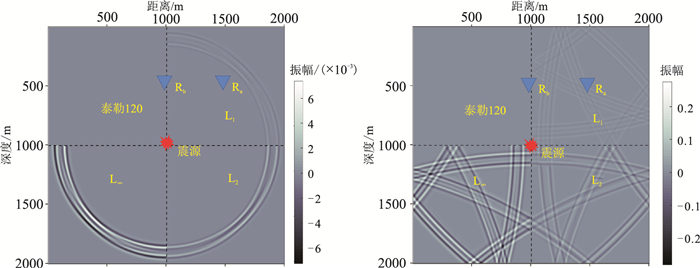
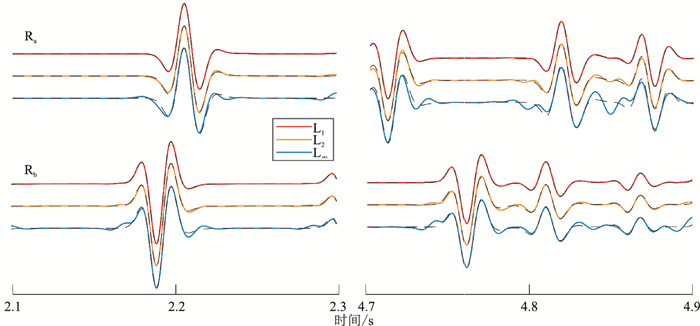
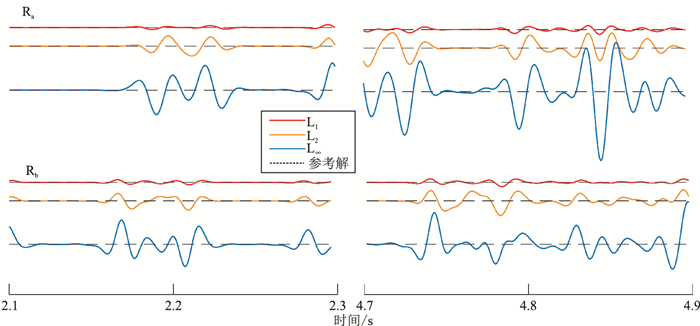
2.1 均匀介质模型均匀介质模型中,纵波速度为2000m/s,网格大小为401×401,网格间距h=5m,时间步长为0.2ms,使用主频为30Hz的雷克子波,震源放在模型的中心位置(1005m,1005m)。为获得声波长时长的传播记录,在未加边界条件下,总采样时间设为2s。不同优化方法得到二维交错网格有限差分声波方程数值模拟的波场快照如图 4所示;图 5为基于三种不同范数优化方法与采用传统泰勒120阶展开算法的模拟结果(参考解)的差值。在接收点Ra(1500m,500m)和Rb(1000m,500m)的单点部分接收记录如图 6所示;图 7为基于三种不同范数优化方法结果与参考解的差值。
|
图 4 均匀介质模型波场快照(左图:t=0.5s;右图t=2.0s) |
|
图 5 均匀介质模型波场快照与参考解的差值(左图:t=0.5s;右图t=2.0s) |
|
图 6 均匀介质模型Ra和Rb单点部分时段接收记录 |
|
图 7 均匀介质模型Ra和Rb单点部分接收时段记录与参考解的差值 |
从图 5中波场快照的差值对比可看出,三种不同范数优化算法的模拟结果中,对误差控制最好的为L1范数,其次是L2范数,最差的是L∞范数,这与频散关系(图 2)分析结果是一致的。图 5中t=2.0s时刻的差值比t=0.5s时刻更大,说明随着波场传播时间的增加,误差积累更严重。L1范数对误差积累的控制较好,从Ra点和Rb点接收记录分析(图 6、图 7)也可得出这一结论。
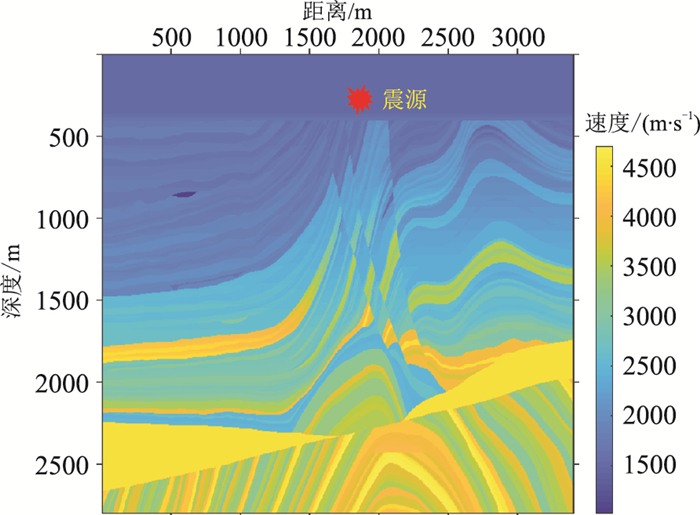
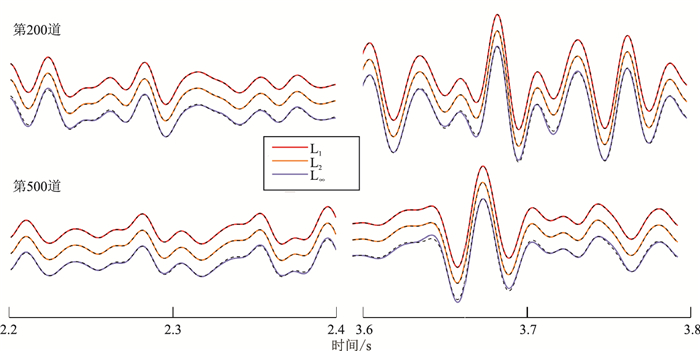
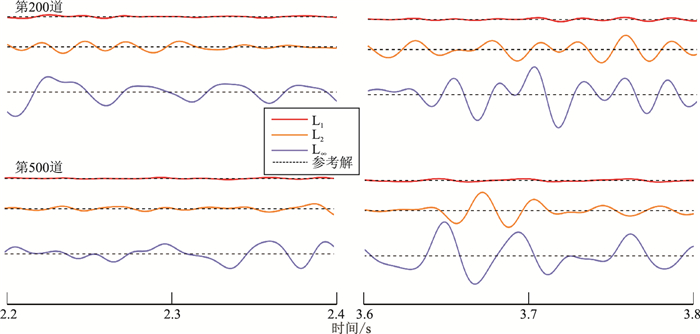
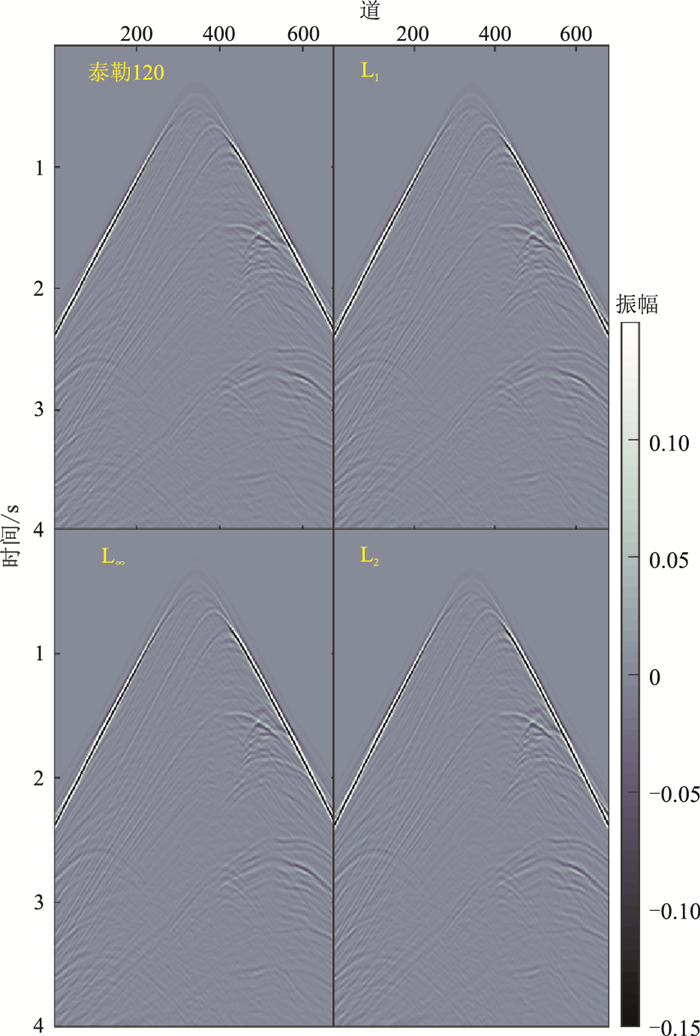
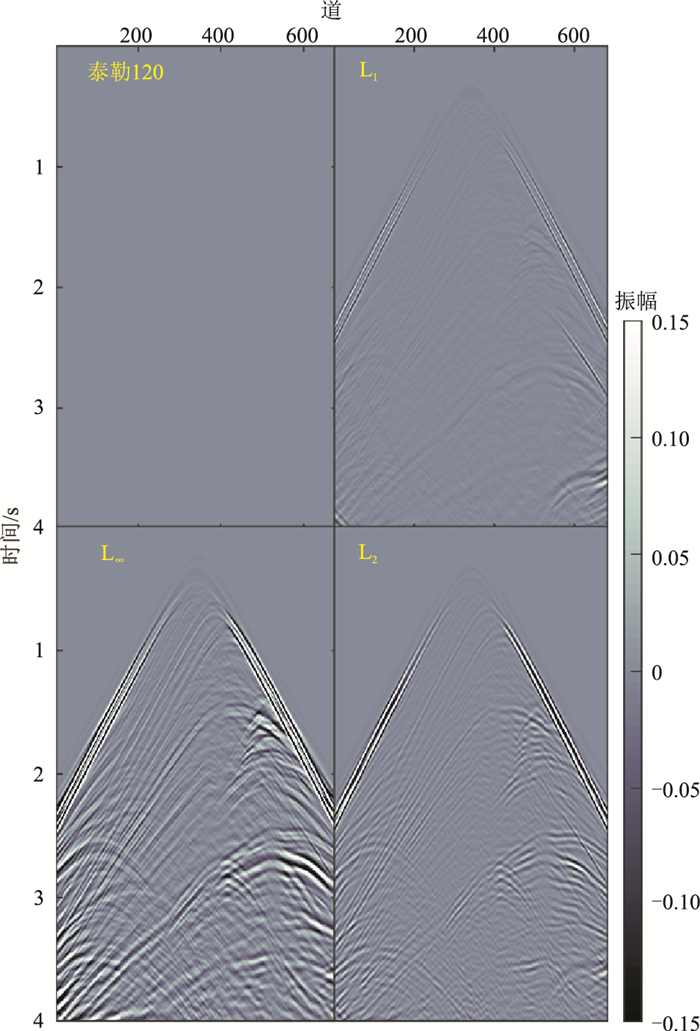
2.2 复杂模型复杂模型Marmousi Ⅱ速度模型如图 8所示,纵波速度范围为1500m/s~4800m/s。震源函数使用主频为25Hz的雷克子波,震源在(1800m,250m)处,接收线与炮点同深度且水平排列。空间步长5m,时间采样间隔0.2ms,总采样时长4s。用不同优化方法得到二维交错网格有限差分声波方程数值模拟的单炮记录,提取第200道和第500道的部分时段地震记录如图 9所示,图 10为基于三种不同范数优化方法模拟结果与参考解的差值。不同优化方法得到的单炮炮集如图 11所示,与参考解的炮集差如图 12所示。
|
图 8 MarmousiⅡ模型(网格681×561) |
|
图 9 MarmousiⅡ模型第200道(上)和第500道(下)部分时段地震记录 |
|
图 10 MarmousiⅡ模型第200道(上)和第500道(下)部分时段地震记录与参考解的差值 |
|
图 11 不同方法模拟的MarmousiⅡ模型单炮炮集 |
在第200道和第500道的地震记录上(图 9),从波形上看,三种范数都与参考解比较吻合。但从单道误差(图 10)分析来看,L1范数对误差积累的控制效果更好;从炮集误差对比(图 12)可得出,L1范数对误差积累的控制效果最好,特别是对深层目标模拟误差控制更为明显。
|
图 12 不同方法模拟的MarmousiⅡ模型单炮炮集与参考解(泰勒120阶模拟)炮集的差值 |
本文基于L1范数建立了求取空间域一阶偏导交错网格有限差分系数的目标函数,采用ADMM算法计算了差分系数,进行了一阶应力—速度声波方程的均匀介质模型和复杂模型的正演模拟。主要结论如下:
(1) 建立了空间一阶偏导数交错网格有限差分系数基于L1范数的目标函数,并通过ADMM算法求解,与L2范数、L∞范数优化后的差分系数频散关系进行了对比,在0.0001容许误差条件下,L1范数以牺牲很小的频带覆盖范围使较小波数范围的误差得到更好的控制;
(2) 通过对均匀介质模型和复杂模型的数值模拟得知,在对深层目标进行数值模拟时,随着波场的延拓,误差积累现象会更加严重,这时对误差的控制就显得尤为重要。本文基于L1范数建立的目标函数优化差分系数,更有利于降低在对深层目标的数值模拟中的误差积累。
| [1] |
Gazdag M, Szepesi G. Separation of large polypeptides by high-performance liquid chromatography[J]. Journal of Chromatography A, 1981, 218: 603-612. DOI:10.1016/S0021-9673(00)82085-3 |
| [2] |
刘财, 兰慧田, 郭智奇, 等. 基于改进BISQ机制的双相HTI介质波传播伪谱法模拟与特征分析[J]. 地球物理学报, 2013, 56(10): 3461-3473. LIU Cai, LAN Huitian, GUO Zhiqi, et al. Simulation and characteristic analysis of two-phase HTI media wave propagation based on improved BISQ mechanism by pseudo-spectral method[J]. Chinese Journal of Geophysics, 2013, 56(10): 3461-3473. DOI:10.6038/cjg20131021 |
| [3] |
Marfurt K J. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations[J]. Geophysics, 1984, 49(4): 533-549. |
| [4] |
张金波, 杨顶辉, 贺茜君, 等. 求解双相和黏弹性介质波传播方程的间断有限元方法及其波场模拟[J]. 地球物理学报, 2018, 61(3): 926-937. ZHANG Jinbo, YANG Dinghui, HE Xijun, et al. Discontinuous finite element method and wave field simu-lation for wave propagation equations in two-phase and viscoelastic media[J]. Chinese Journal of Geophysics, 2018, 61(3): 926-937. |
| [5] |
Alterman Z S, Karal F C J. Propagation of elastic waves in layered media by finite difference methods[J]. Bulletin of the Seismological Society of America, 1968, 58(1): 367-398. |
| [6] |
Virieux J. SH-wave propagation in heterogeneous media: velocity-stress finite-difference method[J]. Exploration Geophysics, 1984, 49(11): 1933-1942. |
| [7] |
董良国, 马在田, 曹景忠, 等. 一阶弹性波方程交错网格高阶差分解法[J]. 地球物理学报, 2000, 43(3): 411-419. DONG Liangguo, MA Zaitian, CAO Jingzhong, et al. Staggered mesh high-order difference solution for first-order elastic wave equation[J]. Chinese Journal of Geophysics, 2000, 43(3): 411-419. DOI:10.3321/j.issn:0001-5733.2000.03.015 |
| [8] |
王秀明, 张海澜, 王东. 利用高阶交错网格有限差分法模拟地震波在非均匀孔隙介质中的传播[J]. 地球物理学报, 2003, 46(6): 842-849. WANG Xiuming, ZHANG Hailan, WANG Dong. The propagation of seismic waves in nonuniform porous media is simulated by using a high-order staggered grid finite difference method[J]. Chinese Journal of Geophysics, 2003, 46(6): 842-849. DOI:10.3321/j.issn:0001-5733.2003.06.018 |
| [9] |
Zhang Y, Gao J, Peng J. Variable-order finite difference scheme for numerical simulation in 3-D poroelastic media[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(5): 2991-3001. DOI:10.1109/TGRS.2017.2789159 |
| [10] |
Dablain M A. The application of high-order differencing to the scalar wave equation[J]. Geophysics, 1986, 51(1): 54-66. DOI:10.1190/1.1442040 |
| [11] |
Koene E F M, Robertsson Johan O A, Filippo B, et al. Eliminating time dispersion from seismic wave modeling[J]. Geophysical Journal International, 2018, 13(1): 169-180. |
| [12] |
Liu Y. Optimal staggered-grid finite-difference schemes based on least-squares for wave equation modelling[J]. Geophysical Journal International, 2014, 197(2): 1033-1047. DOI:10.1093/gji/ggu032 |
| [13] |
裴正林. 三维各向同性介质弹性波方程交错网格高阶有限差分法模拟[J]. 石油物探, 2005, 44(4): 308-315. PEI Zhenglin. 3D isotropic medium elastic wave equation is simulated by staggered mesh high-order finite difference method[J]. Geophysical Prospecting for Petroleum, 2005, 44(4): 308-315. DOI:10.3969/j.issn.1000-1441.2005.04.002 |
| [14] |
丰赟. 基于FCT有限差分方法的瑞雷波数值模拟[D]. 湖南长沙: 中南大学, 2010. FENG Bin. Numerical Simulation of Rayleigh Wave Based on FCT Finite Difference Method[D]. Central South University, Changsha, Huanan, 2010. |
| [15] |
黄明曦, 薛霆虓, 王有学. 基于辛算法及FCT的地震波场模拟[J]. 地球物理学进展, 2015, 30(2): 565-570. HUANG Mingxi, XUE Tingxiao, WANG Youxue. Seismic wave field simulation based on symplectic algorithm and FCT[J]. Progress in Geophysics, 2015, 30(2): 565-570. |
| [16] |
Holberg O. Computational aspects of the choice of opera-tor and sampling interval for numerical differentiation in large-scale simulation of wave phenomena[J]. Geophysical Prospecting, 2010, 35(6): 629-655. |
| [17] |
Liu Y. Globally optimal finite-difference schemes based on least squares[J]. Geophysics, 2013, 78(4): T113-T132. DOI:10.1190/geo2012-0480.1 |
| [18] |
Zhang J H, Yao Z X. Optimized explicit finite-difference schemes for spatial derivatives using maximum norm[J]. Journal of Computational Physics, 2013, 250: 511-526. DOI:10.1016/j.jcp.2013.04.029 |
| [19] |
Yang L, Yan H, Liu H. Optimal staggered-grid finite-difference schemes based on the minimax approximation method with the Remez algorithm[J]. Geophy-sics, 2017, 82(1): T27-T42. |
| [20] |
He Z, Zhang J, Yao Z. Determining the optimal coefficients of the finite difference method using the Remez exchange algorithm[J]. Geophysics, 2019, 84(3): S137-S147. DOI:10.1190/geo2018-0446.1 |
| [21] |
Miao Z, Zhang J. Reducing error accumulation of optimized finite-difference scheme using minimum norm[J]. Geophysics, 2020, 85(5): T275-T291. DOI:10.1190/geo2019-0758.1 |
| [22] |
Boyd S, Parikh N, Chu E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations & Trends in Machine Learning, 2010, 3(1): 1-122. |
| [23] |
Wang Y, Liang W, Nashed Z, et al. Determination of finite difference coefficients for the acoustic wave equation using regularized least-squares inversion[J]. Journal of Inverse & Ill-Posed Problems, 2016, 24(6): 743-760. |
| [24] |
Tikhonov A N, Goncharsky A, Stepanov V V, et al. Numerical Methods for the Solution of Ill-posed Problems[M]. Springer Science & Business Media, 2013.
|
| [25] |
Bau D. Numerical Linear Algebra[M]. Society for Industrial and Applied Mathematics, 1997.
|
| [26] |
Tibshirani R. Regression shrinkage and selection via the lasso: a retrospective[J]. Journal of the Royal Statal Society, 1996, 58(1): 267-288. |
| [27] |
Liu Y, Sen M K. Scalar wave equation modeling with time-space domain dispersion-relation-based staggered-grid finite-difference schemes[J]. Bulletin of the Seismological Society of America, 2011, 101(1): 141-159. DOI:10.1785/0120100041 |



 文晓涛, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院5405室, 610059。Email:
文晓涛, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院5405室, 610059。Email: 