2 中国石油大学(北京) CNPC物探重点实验室, 北京 102249;
3 中国科学院地质与地球物理研究所, 北京 100029;
4 中国科学院地球科学研究院, 北京 100029;
5 中国科学院油气资源研究重点实验室, 北京 100029;
6 北京航天控制仪器研究所, 北京 100094;
7 北京市光纤传感系统工程技术研究中心, 北京 100094
2 CNPC Key Laboratory of Geophysical Exploration, China University of Petroleum(Beijing), Beijing 102249, China;
3 Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
4 Innovation Academy for Earth Science, Chinese Academy of Sciences, Beijing 100029, China;
5 Key Laboratory of Petroleum Resources Research, Chinese Academy of Sciences, Beijing 100029, China;
6 Beijing Institute of Aerospace Control Devices, Beijing 100094, China;
7 Beijing Engineering Research Center of Optical Fiber Sensing System, Beijing 100094, China
地震波场模拟在地震勘探中占有举足轻重的地位,既是人们了解地震波在地下介质中传播规律的主要手段,也是地震反演、偏移成像和地质解释等[1-3]的基础。传统地震波场模拟一般是基于声波方程或弹性波方程[4]。而实际地下介质是非均匀、多相、非弹性甚至各向异性的,为了能更准确地描述地震波的传播规律,相继发展了黏弹性、多相以及各向异性波动方程模拟方法。时间域有限差分法和波数域伪谱法因为计算效率高、易于实现等优点而备受人们青睐。但这两种方法面对速度低且变化剧烈的复杂构造时,往往需要更小的时空采样步长,以解决数值频散和稳定性问题。除此之外,波动方程是一种宏观方程,因而必须要作介质连续性假设,对包含多相强间断面、多孔、多尺度介质,应用往往受限,模拟结果可信度降低。因此,很有必要发展一种更灵活、更适用于复杂介质的波场模拟技术。
格子Boltzmann方法(LBM),是一种基于Boltzmann方程,以当代统计物理学为理论依据,求解Navier-Stokes方程的简单流体数值模拟方法[5]。它通过追踪介观尺度上离散粒子的相互作用,试图模拟宏观层面的复杂物理现象。鉴于该方法稳定性好、计算精度高、物理意义明确、不考虑非线性项、算法简单易实现且扩展迁移性强、天然的并行特性以及内部边界条件处理灵活等优势,且对复杂非线性问题和复杂边界适用性强,在计算流体力学、气动声学、热力学、电磁学以及地震学等领域[6-8]都有一定的应用。LBM自诞生以来,主要经历了细胞自动机(CA)、格子气自动机(LGA)、声格固体模型(PLS)和LBM模型等[9]几个发展过程。
在地震学领域,姚姚[10]及李幼铭等[11]使用CA模型进行地震模拟,刘舒考等[12]将LGA模型用于地震数据正演。针对CA模型在地震正演中的计算量大的问题,王真理等[13]提出了相应的并行算法。刘劲松等[14]利用CA模型进行地震模拟、偏移试验,取得了一定效果。贺艳晓[15]实现了PLS和LBM模型在简单非均匀介质中的波场模拟。针对黏弹介质波场模拟,Xia等[8]根据松弛时间与品质因子之间的定量关系,建立了LBM模型和地震波衰减参数的联系。Jiang等[16]用数值实验进一步探索了LBM在地震波场正演时的稳定性条件。凭借对微观力学模型研究成果,夏木明[17]结合格子Boltzmann模型和弹簧网络模型实现了流—固耦合复杂介质波场的正演模拟。
众所周知,在数值模拟过程中,由于计算区域有限,不可避免地会引入人工截断边界,如何施加吸收效果好的边界条件一直是一个热点问题[18]。目前关于LBM的无反射边界条件(NRBC)的研究主要集中在计算流体力学和气动声学领域[19-20]。在地震学领域,刘劲松等[21]提出在一定范围内的网格点上的准粒子数乘以一个衰减系数以实现边界反射的压制;Jiang等[22]引入了基于松弛时间的海绵层吸收边界,通过改变衰减系数及函数类型,在LBM波场数值模拟时取得了较好的边界反射压制效果。
以上关于LBM的吸收边界大多是基于单松弛时间格子Boltzmann模型(SRT-LBM),依赖Bhatnagar-Gross-Krook (BGK)碰撞算子,且只考虑一个松弛时间。精度更高、物理意义更明确、能实现各物理模式解耦、稳定性更好,但碰撞过程更加复杂的多松弛时间格子Boltzmann模型(MRT-LBM),用于地震模拟的吸收边界研究还未见到。相对于SRT-LBM,MRT-LBM的碰撞更加灵活,控制方程更复杂,吸收边界的加载就更困难。
为采用MRT-LBM进行地震波场模拟,本文提出一种基于多松弛参数的黏滞吸收边界。通过数值模拟实验优化衰减参数组合,利用均匀模型和非均质模型检验了该黏滞吸收边界的效果和适用性。
1 多松弛时间格子Boltzmann方法 1.1 离散速度模型LBM是一种基于介观领域的数值求解方法,它描述了每个格子点上的粒子速度分布函数的演化过程。与传统宏观方程的离散方法不同,LBM不仅在物理空间和时间上进行离散,同时也需要在速度空间上进行离散。
LBM主要包含两个要素:离散速度模型和演化方程。根据维度不同,最常用的离散速度模型依次为D1Q3、D2Q9和D3Q19,其中D后的数字表示空间维度,Q后的数字表示离散速度对的个数,本文研究是基于D2Q9模型。
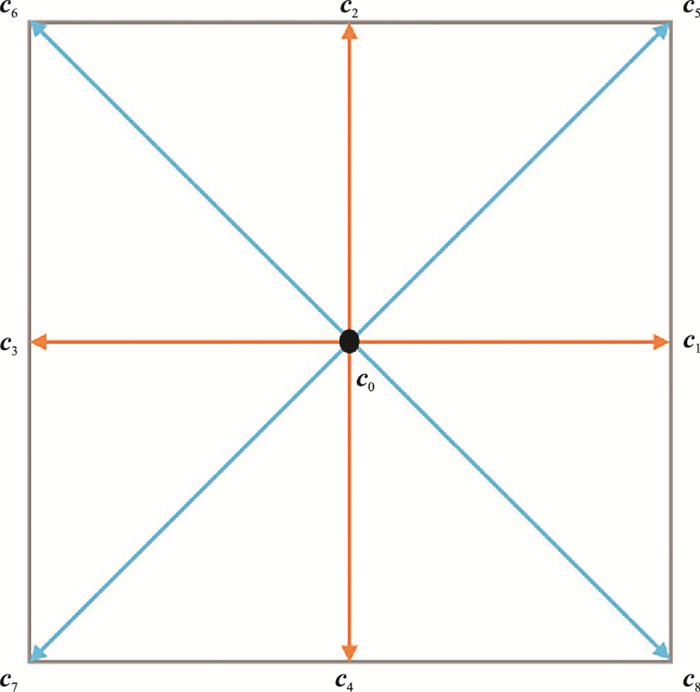
图 1为D2Q9离散速度模型的基本结构,表示在中心点处的粒子每一时刻有9种不同的迁徙方向。图 1的离散速度对为
| $ \begin{aligned} &{\left[\begin{array}{llllllll} \boldsymbol{c}_{0} & \boldsymbol{c}_{1} & \boldsymbol{c}_{2} & \boldsymbol{c}_{3} & \boldsymbol{c}_{4} & \boldsymbol{c}_{5} & \boldsymbol{c}_{6} & \boldsymbol{c}_{7} & \boldsymbol{c}_{8} \end{array}\right]} \\ &\ \ \ \ =\left[\begin{array}{ccccccccc} 0 & 1 & 0 & -1 & 0 & 1 & -1 & -1 & 1 \\ 0 & 0 & 1 & 0 & -1 & 1 & 1 & -1 & -1 \end{array}\right] \end{aligned} $ | (1) |
|
图 1 D2Q9离散速度模型 |
MRT-LBM的演化方程[5]为
| $ \begin{aligned} &\boldsymbol{f}\left(\boldsymbol{x}+\boldsymbol{c}_{i} \Delta t, t+\Delta t\right)-\boldsymbol{f}(\boldsymbol{x}, t)=\\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -\boldsymbol{M}^{-1} \boldsymbol{S}\left[\boldsymbol{m}(\boldsymbol{x}, t)-\boldsymbol{m}^{\mathrm{eq}}(\boldsymbol{x}, t)\right] \end{aligned} $ | (2) |
该式左边表示粒子在速度空间中的迁徙过程,右边表示粒子在速度矩空间中的碰撞过程。式中:Δt为时间采样间隔;M是转换矩阵
| $ \begin{aligned} &\boldsymbol{M}= \\ &{\left[\begin{array}{rrrrrrrrr} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ -4 & -1 & -1 & -1 & -1 & 2 & 2 & 2 & 2 \\ 4 & -2 & -2 & -2 & -2 & 1 & 1 & 1 & 1 \\ 0 & 1 & 0 & -1 & 0 & 1 & -1 & -1 & 1 \\ 0 & -2 & 0 & 2 & 0 & 1 & -1 & -1 & 1 \\ 0 & 0 & 1 & 0 & -1 & 1 & 1 & -1 & -1 \\ 0 & 0 & -2 & 0 & 2 & 1 & 1 & -1 & -1 \\ 0 & 1 & -1 & 1 & -1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & -1 & 1 & -1 \end{array}\right]} \end{aligned} $ | (3) |
其逆为
| $ \begin{aligned} &\boldsymbol{M}^{-1}=\frac{1}{36} \times \\ &{\left[\begin{array}{rrrrrrrr} 4 & -4 & 4 & 0 & 0 & 0 & 0 & 0 & 0 \\ 4 & -1 & -2 & 6 & -6 & 0 & 0 & 9 & 0 \\ 4 & -1 & -2 & 0 & 0 & 6 & -6 & -9 & 0 \\ 4 & -1 & -2 & -6 & 6 & 0 & 0 & 9 & 0 \\ 4 & -1 & -2 & 0 & 0 & -6 & 6 & -9 & 0 \\ 4 & 2 & 1 & 6 & 3 & 6 & 3 & 0 & 9 \\ 4 & 2 & 1 & -6 & -3 & 6 & 3 & 0 & -9 \\ 4 & 2 & 1 & -6 & -3 & -6 & -3 & 0 & 9 \\ 4 & 2 & 1 & 6 & 3 & -6 & -3 & 0 & -9 \end{array}\right]} \end{aligned} $ | (4) |
S是一个对角矩阵
| $ \boldsymbol{S}=\operatorname{diag}\left[s_{0}, s_{1}, s_{2}, s_{3}, s_{4}, s_{5}, s_{6}, s_{7}, s_{8}\right] $ | (5) |
其元素是松弛参数;f(x, t)和feq(x, t)分别表示在t时刻、x处的粒子速度分布函数向量和相应的平衡态分布函数向量
| $ \left\{\begin{array}{l} \boldsymbol{f}=\left[f_{0}, f_{1}, f_{2}, f_{3}, f_{4}, f_{5}, f_{6}, f_{7}, f_{8}\right]^{\mathrm{T}} \\ \boldsymbol{f}^{\mathrm{eq}}=\left[f_{0}^{\mathrm{eq}}, f_{1}^{\mathrm{eq}}, f_{2}^{\mathrm{eq}}, f_{3}^{\mathrm{eq}}, f_{4}^{\mathrm{eq}}, f_{5}^{\mathrm{eq}}, f_{6}^{\mathrm{eq}}, f_{7}^{\mathrm{eq}}, f_{8}^{\mathrm{eq}}\right]^{\mathrm{T}} \end{array}\right. $ | (6) |
m和meq分别为速度矩向量和平衡态速度矩向量,与f和feq的转换关系为
| $ \left\{\begin{array}{l} \boldsymbol{m}=\boldsymbol{M} \boldsymbol{f} \\ \boldsymbol{m}^{\mathrm{eq}}=\boldsymbol{M} \boldsymbol{f}^{\mathrm{eq}} \end{array}\right. $ | (7) |
m的每个元素对应于宏观物理量[5],可表示为
| $ \boldsymbol{m}=\left[\rho, e, \varepsilon, j_{x}, q_{x}, j_{y}, q_{y}, p_{x x}, p_{x y}\right]^{\mathrm{T}} $ | (8) |
式中:ρ为介质密度;e为能量;ε为能量的平方;jx和jy是动量的x和y方向分量;qx和qy是能量通量的x和y方向分量;pxx和pxy是压力张量的对角线和非对角线成分。meq可以通过式(7)求得,即
| $ \begin{array}{c} \boldsymbol{m}^{\mathrm{eq}}=\left[\rho,-2 \rho+3\left(j_{x}^{2}+j_{y}^{2}\right) / \rho, \rho-3\left(j_{x}^{2}+j_{y}^{2}\right) / \rho,\right. \\ \left.j_{x},-j_{x}, j_{y},-j_{y},\left(j_{x}^{2}-j_{y}^{2}\right) / \rho, j_{x} j_{y} / \rho\right]^{\mathrm{T}} \end{array} $ | (9) |
式(6)中的平衡态分布函数[8]为
| $ f_{i}^{\mathrm{eq}}=w_{i} \rho\left[1+\frac{\boldsymbol{c}_{i} \cdot \boldsymbol{u}}{c_{\mathrm{s}}^{2}}+\frac{\left(\boldsymbol{c}_{i} \cdot \boldsymbol{u}\right)^{2}}{2 c_{\mathrm{s}}^{4}}-\frac{\boldsymbol{u}^{2}}{2 c_{\mathrm{s}}^{2}}\right] $ | (10) |
式中:u为介质速度;cs和wi分别为D2Q9模型对应的格子声速和权系数
| $ \left\{\begin{array}{l} c_{\mathrm{s}}=\frac{1}{\sqrt{3}} \\ w_{i}= \begin{cases}\frac{4}{9} & i=0 \\ \frac{1}{9} & i=1,2,3,4 \\ \frac{1}{36} & i=5,6,7,8\end{cases} \end{array}\right. $ | (11) |
LBM通过下式建立了微观量fi与宏观量ρ和u的关系[8]
| $ \left\{\begin{array}{l} \rho=\sum\limits_{i=0}^{8} f_{i} \\ \rho \boldsymbol{u}=\sum\limits_{i=0}^{8} \boldsymbol{c}_{i} f_{i} \end{array}\right. $ | (12) |
使用MRT-LBM进行波场数值模拟主要分为以下五个步骤:
① 初始化密度、速度、松弛参数、粒子数密度等物理量;
② 计算平衡态分布函数;
③ 在速度矩空间进行碰撞过程以及外部吸收层区域的数值计算;
④ 在速度空间进行迁徙过程以及应用周期、镜面、外推等内部边界条件;
⑤ 根据粒子数密度计算宏观量密度、速度。
1.3 LBM与常规波动方程对比有限差分法(FDM)与LBM在实现算法、数值离散方式和震源加载这三方面的对比如下。
(1) 实现算法:LBM是一种介观尺度的数值算法,求解的是Navier-Stokes方程,其关键步骤是平衡态分布函数的求取、执行碰撞过程和迁徙过程、宏观量的求取。而FDM是一种宏观尺度的数值算法,可以求解常规的波动方程,其实现算法的关键步骤是将波动方程的时间或者空间偏导数用差分代替,迭代求取压力项或振动速度项。
(2) 数值离散方式:LBM除了离散空间和时间外,还离散速度;FDM只离散空间和时间。
(3) 震源加载:LBM震源一般加载在介观量粒子数密度上;FDM通常加载在宏观量压力或质点速度上。
2 基于多松弛参数的黏滞吸收边界式(5)中的9个松弛参数对MRT-LBM的数值计算尤为重要,它们直接影响模拟波场的频散性、衰减性、各向异性、准确性、稳定性等[5]。松弛参数的大小表明了相应的速度矩向其平衡态矩线性松弛的速率
| $ m_{i}^{*}=m_{i}-s_{i}\left(m_{i}-m_{i}^{\mathrm{eq}}\right) $ | (13) |
松弛参数s1、s7、s8与介质的运动剪切黏度ν和运动体积黏度μ有关[8]
| $ \left\{\begin{array}{l} \mu=\frac{1}{3}\left(\frac{1}{s_{1}}-\frac{1}{2}\right) \\ \nu=\frac{1}{3}\left(\frac{1}{s_{7}}-\frac{1}{2}\right)=\frac{1}{3}\left(\frac{1}{s_{8}}-\frac{1}{2}\right) \end{array}\right. $ | (14) |
该式表明,s1越小,μ越大,衰减越严重;同样地,s7越小,ν越大,衰减越严重。
鉴于此,为了实现MRT-LBM地震波场模拟时截断反射的压制,可以考虑在模拟区域外加一定厚度的吸收层,通过同时改变吸收层松弛参数s1以及s7和s8的取值,以改变黏滞性,从而实现边界反射波的“黏滞”吸收。
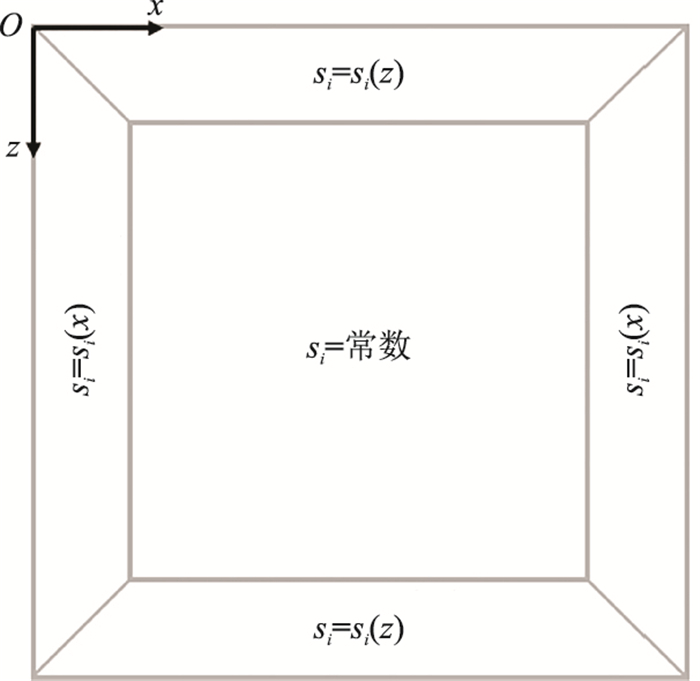
模拟区域设计如图 2所示,分为内部区域和上、下、左、右四个梯形吸收区域。内部区域的松弛参数保持不变,吸收区域的松弛参数会随坐标x或者z而变化。以左边吸收区域(0≤x≤L-1)为例,松弛参数为
| $ \left\{\begin{array}{l} s_{1}(x)=\frac{1}{1 / s_{1}^{0}+a_{1}(L-1-x)^{n_{1}}} \\ s_{7}(x)=\frac{1}{1 / s_{7}^{0}+a_{2}(L-1-x)^{n_{2}}} \\ s_{8}(x)=\frac{1}{1 / s_{8}^{0}+a_{3}(L-1-x)^{n_{3}}} \end{array}\right. $ | (15) |
|
图 2 模拟区域示意图 |
式中:L为吸收层的厚度网格数;s10、s70、s80为内部区域的“黏滞”松弛参数;n1、n2、n3为选取的幂函数的指数;a1、a2、a3为相应的衰减系数。
为简单起见,本文假设
| $ \left\{\begin{array}{l} n=n_{1}=n_{2}=n_{3} \\ a=a_{1}=a_{2}=a_{3} \end{array}\right. $ | (16) |
很明显,参数L、n、a的选择对吸收效果影响很大。不失一般性,L越大,对边界反射压制更好,但是会增加计算负担;当L一定时,如何选取n和a的参数组合则显得尤为重要。
3 衰减参数组合优化衰减系数a可以看作是吸收层厚度L和幂函数指数n的函数。对于MRT-LBM的黏滞吸收边界,由于没有经验公式可参考,因而首先需要进行参数优化。策略是通过选取不同的L、n、a参数组合在均匀模型中进行波场正演,记录直达波和截断边界反射的能量,进而计算信噪比[22]
| $ \mathrm{SNR}=10 \lg \left(E_{\mathrm{d}} / E_{\mathrm{r}}\right) $ | (17) |
式中:Ed是直达波能量;Er是截断边界反射能量。参数组合的取值如下
| $ \left\{\begin{array}{l} L \in\{10,15,20,25,30,35\} \\ n \in\{0.5,1.0,1.5,2.0,2.5,3.0,3.5,4.0\} \\ -\lg a \in\{8,7,6,5,4,3,2,1,0,-1,-2\} \end{array}\right. $ | (18) |
均匀模型的参数设置如下:模拟网格数为401×401,空间步长为1m×1m;记录时长为0.4s,时间采样间隔为0.5ms;纵波速度为1500m/s,密度为1000kg/m3;35Hz主频的Ricker子波放在模型中心作为震源;设置四个检波点记录信号,坐标分别为(xs-160,zs-130)、(xs+100,zs+100)、(xs-120,zs+130)和(xs+30,zs-150),其中(xs,zs)为源点的离散坐标;区域外部加上厚度为L的吸收层;内部区域的松弛参数设置为
| $ \left\{\begin{array}{l} s_{0}^{0}=s_{3}^{0}=s_{5}^{0}=0 \\ s_{2}^{0}=s_{4}^{0}=s_{6}^{0}=1.8 \\ s_{1}^{0}=s_{7}^{0}=s_{8}^{0}=1.9 \end{array}\right. $ | (19) |
为了保持模拟的稳定,各个松弛参数始终需满足
| $ 0<s_{i}<2 \quad i=1,2,4,6,7,8 $ | (20) |
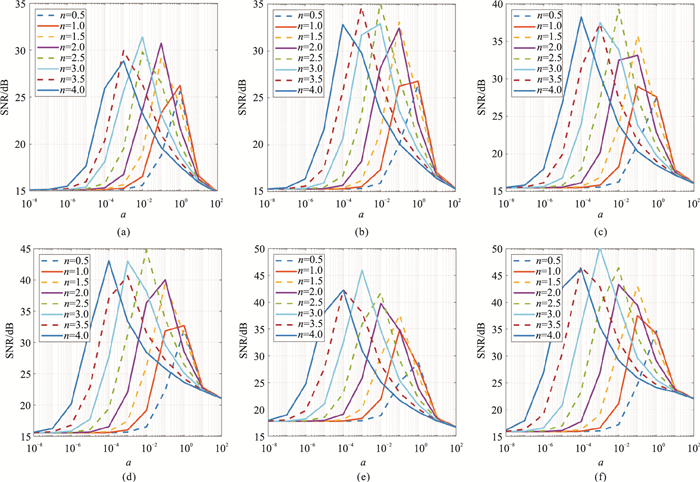
MRT-LBM在式(18)的L、n、a参数组合下进行若干次波场正演并通过四个检波点记录直达波和边界反射的能量。图 3展示了不同参数组合时上述四个检波点信噪比的算术平均,很容易发现衰减系数的选取对边界的吸收效果影响很明显。实际参数优化的过程如下:
|
图 3 不同参数组合下信噪比曲线 (a)~(f)分别对应于L=10、15、20、25、30、35 |
(1) 先选择L。通过对比图 3的6个子图,人为定义信噪比大于45dB且L在可接受的范围内,最终选择L=30。
(2) 其次选择n和a。通过对比图 3e的六条曲线的最大值,发现指数为3.0时信噪比最大,因此选择n=3.0;然后找到该曲线最大信噪比对应的衰减系数,可得a=0.001。
理论上,MRT-LBM的黏滞吸收边界采用30层厚度的计算量会大于常规PML厚度10~20层的计算量,然而此吸收边界形式简单,兼容性强,同样的层数不会带来过多的计算量。
进一步地,将该均匀模型扩大到801×801的网格数,时间记录1001个采样点,比较LBM与求解一阶压力—速度形式的二维波动方程的FDM在计算复杂度和计算效率方面的差异。计算复杂度可以分为时间复杂度和空间复杂度,一般地,这可分别由程序的实际运行时间(Time)与占用的最大物理内存百分比(Mem)表示。所有的模拟均在3.0GHz的英特尔处理器、内存为15.980GB的电脑上实施,采用C语言编程,结果如表 1所示。从表 1可以看出,LBM的计算效率比FDM低,其所需计算时间大约是FDM的两倍;LBM所需的计算内存大约是FDM的2~3倍。这主要是因为LBM在速度模型上进行了9个方向的离散,开辟的动态数组以及实际需要计算的物理量会相应地增加。
|
|
表 1 FDM与LBM计算复杂度及计算效率对比 |
将上面优化后的衰减参数组合的黏滞吸收边界应用到基于MRT-LBM的均匀介质的波场模拟,模型参数设置同上。
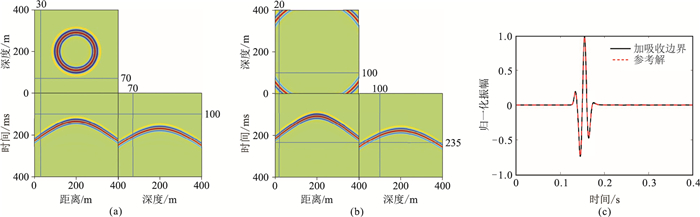
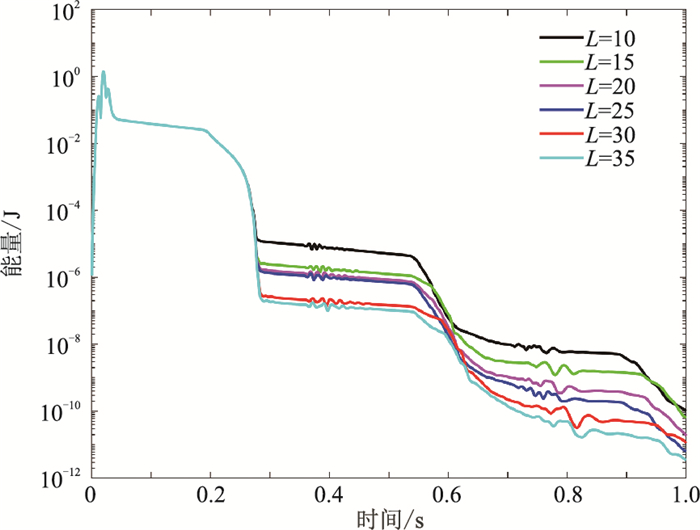
模拟的波场切片及地震记录如图 4a和图 4b所示,未见明显的截断边界反射。第4个检波点记录的振动曲线如图 4c所示,并将扩大的模型的相应记录作为参考解(边界反射出现在考察的时间之外)进行对比。由图 4c可见,施加吸收边界的振幅曲线与参考解只有微小的差异,说明边界反射吸收得比较好。图 5为不同吸收层厚度的地震波场总能量(某一时刻波场所有点的振幅的平方和)随时间的动态变化,模拟总时长为1s。由图 5可见,选取优化后的衰减参数组合,波场能量在通过吸收层时迅速衰减(大约5个数量级),且当剩余反射重新到达边界时会继续得到大幅度的压制。
|
图 4 均匀模型的波场切片及地震记录和单道波形 (a)t=100ms的波场切片以及x=30m和z=70m的地震记录;(b)t=235ms时的波场切片以及x=20m和z=100m的地震记录;(c)第4个接收点记录的波形 |
|
图 5 波场总能量随时间衰减曲线 |
进一步通过测试非均质模型的波场模拟检验本文的黏滞吸收边界优化参数的有效性。若无特殊说明,黏滞吸收边界采用的衰减参数组合均为L=30、n=3、a=0.001。
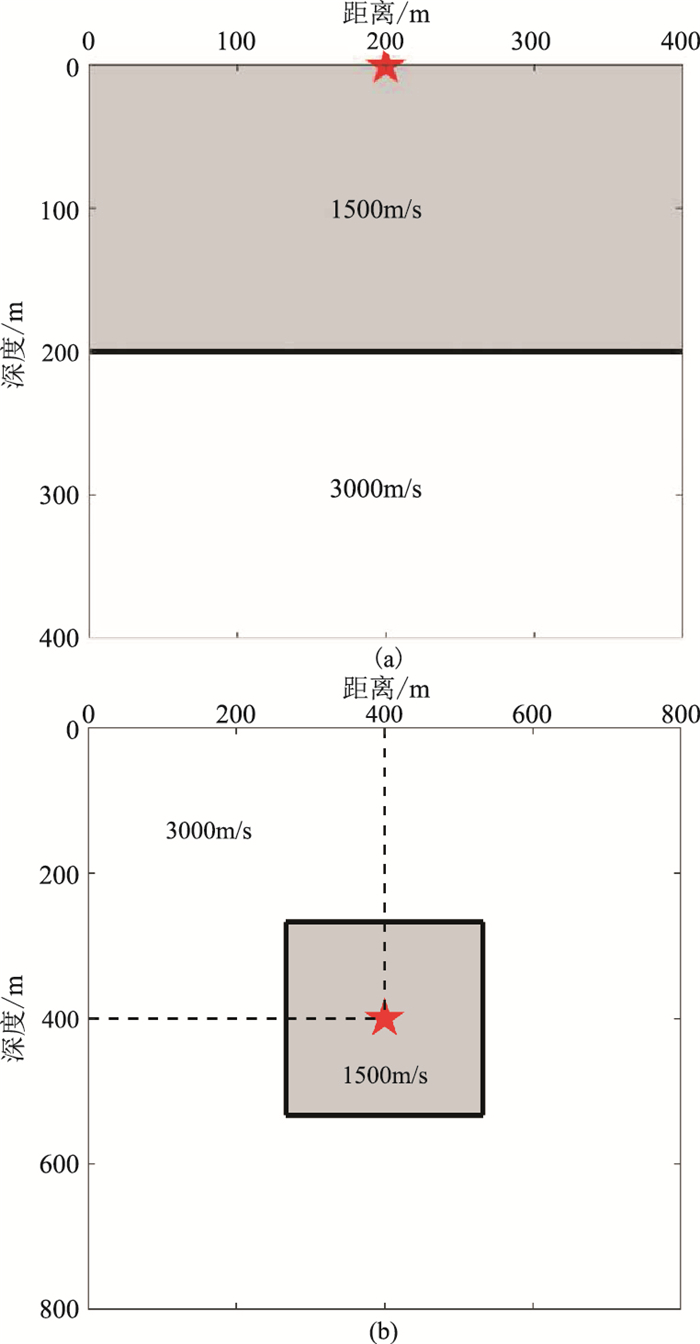
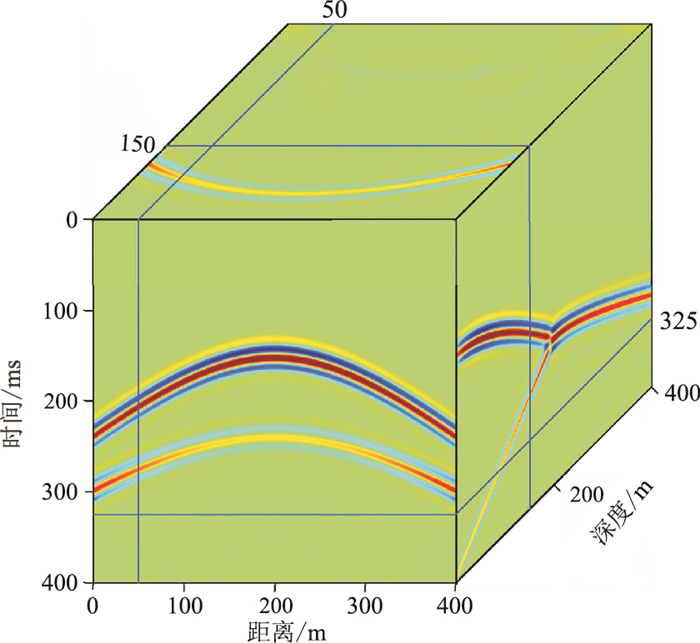
首先考察两个简单的非均质模型:层状模型(图 6a)和孔洞模型(图 6b)的波场模拟结果。层状模型的速度为1500、3000m/s,以20 Hz的雷克子波作为震源放在地表中心(五星所示),其他参数设置同均质模型。图 7为t=325ms的波场切片以及x=50m和z=150m的地震记录。可以发现,相对于直达波和反射波,截断边界反射波并不明显,证实了本文的黏滞吸收边界对MRT-LBM波场模拟时产生的截断边界反射波有较好的衰减效果。
|
图 6 简单非均质模型 (a)层状模型;(b)孔洞模型。五角星表示震源位置 |
|
图 7 层状模型的波场切片及地震记录 |
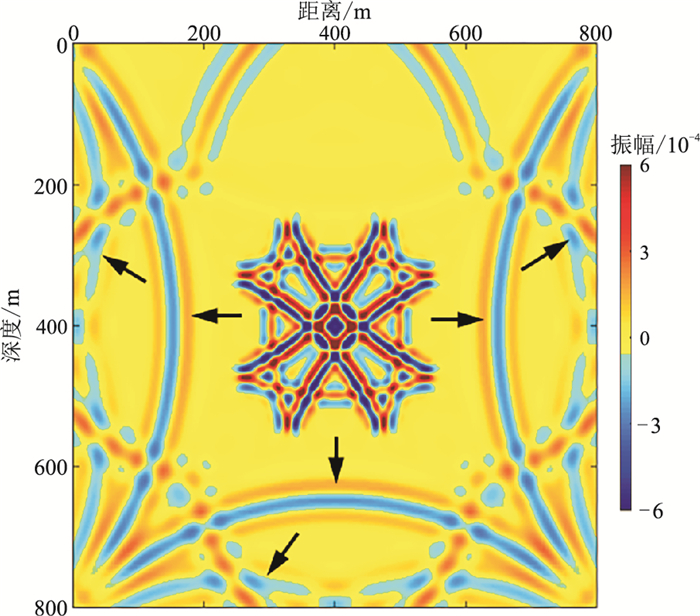
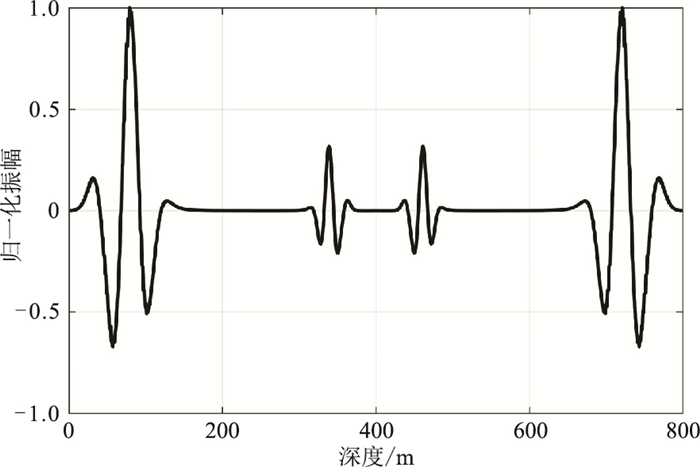
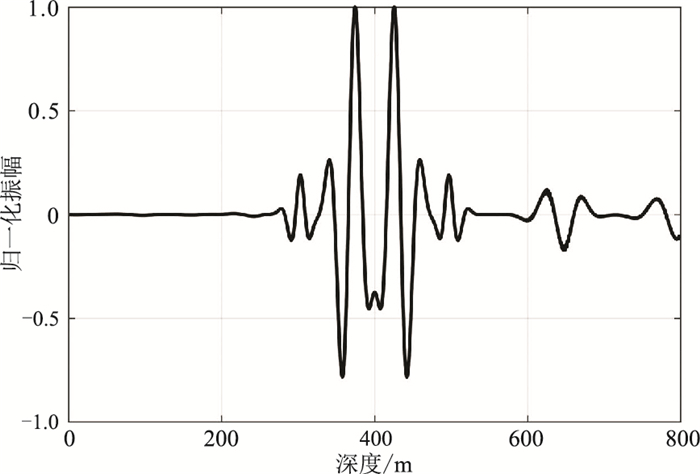
孔洞模型的网格数为801×801,中间异常体的尺寸为267m×267m,速度为1500m/s,围岩的速度为3000m/s,模拟时长为0.5s,只在模型的上表面加载了黏滞吸收边界,其他设置同均匀模型。图 8为t=362.5ms的波场切片,由图可知,左、右、下三个边界的反射(黑色箭头处)很明显,而加载吸收边界的上部边界的截断边界反射显著衰减。为了更清楚地展示上边界的吸收效果,抽取了x=400m,t=225.0ms和362.5ms的波形曲线。当t=225.0ms时(图 9)直达波并未到达模型边界,因而未产生截断边界反射,波形曲线关于z=400m对称;当t=362.5ms时(图 10),在z=600~800m之间的下边界反射很严重,已经干扰了有效层间反射波的识别,而z=0~200m的上边界反射被吸收得比较彻底。
|
图 8 孔洞模型t=362.5ms时的波场切片 |
|
图 9 孔洞模型x=400m、t=225.0ms的波形曲线 |
|
图 10 孔洞模型x=400m、t=362.5ms的波形曲线 |
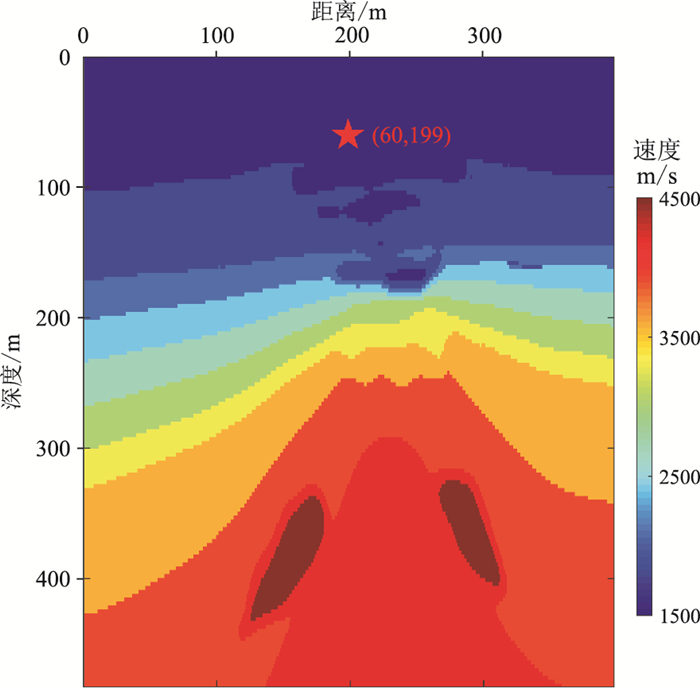
最后,用沿深度方向拉伸的BP模型(图 11)验证本文的黏滞吸收边界对复杂模型的适用性。模型网格数为483×398,最大速度为4500m/s,最小速度为1500m/s,25Hz主频的雷克子波作为震源加在地表中心向下60个网格处(红五星位置),其他参数设置同均匀模型。
|
图 11 沿深度拉伸的BP速度模型 |
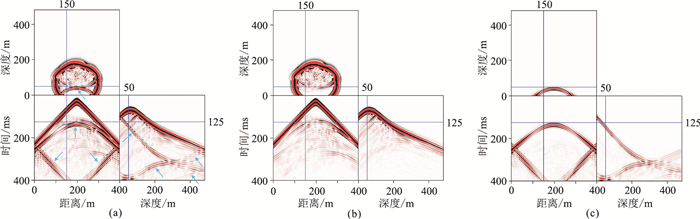
图 12为MRT-LBM模拟的BP模型t=125ms的波场切片及x=150m和z=50m的地震记录。其中图 12a未作吸收边界处理,可以看出,直达波产生的反射(青色箭头处)极其严重,明显覆盖了有效信号;对比而言,四周加载黏滞吸收边界后的波场(图 12b)中的截断边界反射得以明显压制,有效信号更加清楚;图 12c为图 12a和图 12b的差,可以清晰地看到,除了直达波导致的边界反射外,还有很多反射波引起的边界噪声。图 12证实了本文的吸收边界条件适用于复杂模型的MRT-LBM地震波场模拟。
|
图 12 BP模型计算的波场切片及地震记录 (a)未施加吸收边界;(b)施加吸收边界;(c)图a和图b的差 |
考虑到MRT-LBM地震波动正演模拟的特性,本文提出了一种基于多松弛参数的黏滞吸收边界,该边界算法简单,易实现且可扩展性强。考虑到衰减参数组合对边界反射吸收效果影响显著,因而通过数值实验对其进行了优化。
用均均匀模型、层状模型、孔洞模型和复杂的BP模型进行了测试,结果表明本文的黏滞吸收边界条件较好地压制了边界反射,且适用复杂模型地震波场模拟。
需要注意的是,本文衰减参数组合只尝试了几种幂函数,衰减系数以10的整数倍为间隔,因而得到的未必是最优的参数组合。还可以通过尝试新的衰减函数,比如Sigmoid函数、正弦函数、反正切函数等[23],以及二次加密衰减系数的采样间隔等方式进一步优化。另外,为了简单起见,本文实现边界衰减的三个松弛参数采用的是同一套衰减体系,为了使边界吸收效果更好,各个松弛参数可以尝试不同的衰减过程,但是要注意在松弛参数变化的过程中要满足MRT-LBM的稳定性条件。最后,可以采用并行方式处理MRT-LBM计算量大的问题。
| [1] |
撒利明, 杨午阳, 姚逢昌, 等. 地震反演技术回顾与展望[J]. 石油地球物理勘探, 2015, 50(1): 184-202. SA Liming, YANG Wuyang, YAO Fengchang, et al. Review and prospect of seismic inversion technology[J]. Oil Geophysical Prospecting, 2015, 50(1): 184-202. |
| [2] |
刘张聚, 童思友, 方云峰, 等. 基于时域加权的拉普拉斯-频率域弹性波全波形反演[J]. 石油地球物理勘探, 2021, 56(2): 302-312. LIU Zhangju, TONG Siyou, FANG Yunfeng, et al. Full elastic waveform inversion in Laplace-Fourier domain based on time domain weighting[J]. Oil Geophysical Prospecting, 2021, 56(2): 302-312. |
| [3] |
王华忠. "两宽一高"油气地震勘探中的关键问题分析[J]. 石油物探, 2019, 58(3): 313-324. WANG Huazhong. Key problem analysis in seismic exploration based on wide-azimuth, high-density, and broadband seismic data[J]. Geophysical Prospecting for Petroleum, 2019, 58(3): 313-324. DOI:10.3969/j.issn.1000-1441.2019.03.001 |
| [4] |
陈汉明, 汪燚林, 周辉. 一阶速度-压力常分数阶黏滞声波方程及其数值模拟[J]. 石油地球物理勘探, 2020, 55(2): 302-310. CHEN Hanming, WANG Yilin, ZHOU Hui. A novel constant fractional-order Laplacians viscoacoustic wave equation and its numerical simulation method[J]. Oil Geophysical Prospecting, 2020, 55(2): 302-310. |
| [5] |
Krüger T, Kusumaatmaja H, Kuzmin A, et al. The lattice Boltzmann method[J]. Springer International Publishing, 2017, 10(978-3): 4-15. |
| [6] |
Xu H, Sagaut P. Optimal low-dispersion low-dissipation LBM schemes for computational aeroacoustics[J]. Journal of Computational Physics, 2011, 230(13): 5353-5382. DOI:10.1016/j.jcp.2011.03.040 |
| [7] |
He X, Doolen G D. Thermodynamic foundations of kinetic theory and lattice Boltzmann models for multiphase flows[J]. Journal of Statistical Physics, 2002, 107(1-2): 309-328. |
| [8] |
Xia M, Wang S, Zhou H, et al. Modelling viscoacoustic wave propagation with the lattice Boltzmann me-thod[J]. Scientific Reports, 2017, 7(1): 1-9. DOI:10.1038/s41598-016-0028-x |
| [9] |
McNamara G R, Zanetti G. Use of the Boltzmann equation to simulate lattice-gas automata[J]. Physical Review Letters, 1988, 61(20): 2332. DOI:10.1103/PhysRevLett.61.2332 |
| [10] |
姚姚. 细胞自动机方法地震正演模拟[J]. 石油地球物理勘探, 1995, 30(2): 216-222. YAO Yao. Forward seismic modeling by cellular automaton method[J]. Oil Geophysical Prospecting, 1995, 30(2): 216-222. |
| [11] |
李幼铭, 胡健行. 细胞自动机在地震波传播研究中的应用[J]. 地球物理学报, 1995, 38(5): 651-661. LI Youming, HU Jianxing. Application of cellular automata approach to the study of seismic wave propagation[J]. Chinese Journal of Geophysics, 1995, 38(5): 651-661. DOI:10.3321/j.issn:0001-5733.1995.05.012 |
| [12] |
刘舒考, 刘雯林. 格子气自动机模型——一种地震数据正演研究的新方法[J]. 石油地球物理勘探, 1998, 33(5): 658-662. LIU Shukao, LIU Wenlin. Lattice gas automata mo-del: A new method for seismic data forward simulation[J]. Oil Geophysical Prospecting, 1998, 33(5): 658-662. |
| [13] |
王真理, 李幼铭. 细胞自动机地震波模拟的并行化算法[J]. 地球物理学报, 1999, 42(3): 410-415. WANG Zhenli, LI Youming. Parallel algorithm for simulating seismic wave propagation by cellular automata[J]. Chinese Journal of Geophysics, 1999, 42(3): 410-415. DOI:10.3321/j.issn:0001-5733.1999.03.014 |
| [14] |
刘劲松, 许云, 刘福田, 等. 细胞自动机用于地震偏移: 数值模拟试验[J]. 地球物理学进展, 2004, 19(3): 621-624. LIU Jinsong, XU Yun, LIU Futian, et al. Numerical experiment of seismic migration using cellular auto-mata[J]. Progress in Geophysics, 2004, 19(3): 621-624. DOI:10.3969/j.issn.1004-2903.2004.03.021 |
| [15] |
贺艳晓. 基于细胞自动机方法的地震波场模拟研究[D]. 北京: 中国石油大学(北京), 2011.
|
| [16] |
Jiang C, Zhou H, Xia M, et al. Stability analysis of multiple-relaxation-time lattice Boltzmann model for wave simulation[C]. SEG Technical Program Expanded Abstracts, 2020, 39: 2699-2703.
|
| [17] |
夏木明. 格子玻尔兹曼模型-弹簧网络模型流固耦合复杂介质波场模拟研究[D]. 北京: 中国石油大学(北京), 2019.
|
| [18] |
Berenger J P. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 1994, 114(2): 185-200. DOI:10.1006/jcph.1994.1159 |
| [19] |
Vergnault E, Malaspinas O, Sagaut P. A lattice Boltzmann method for nonlinear disturbances around an arbitrary base flow[J]. Journal of Computational Phy-sics, 2012, 231(24): 8070-8082. DOI:10.1016/j.jcp.2012.07.021 |
| [20] |
Najafi-Yazdi A, Mongeau L. An absorbing boundary condition for the lattice Boltzmann method based on the perfectly matched layer[J]. Computers & Fluids, 2012, 68: 203-218. |
| [21] |
刘劲松, 许云. 声格固体模型地震波场模拟[J]. 石油地球物理勘探, 1997, 32(3): 370-375. LIU Jinsong, XU Yun. Seismic wave field simulation using phononic lattice solid model[J]. Oil Geophysical Prospecting, 1997, 32(3): 370-375. |
| [22] |
Jiang C, Zhou H, Xia M, et al. Study on absorbing boundary conditions of viscous sponge layers based on lattice Boltzmann method[C]. Extended Abstracts of 82nd EAGE Conference & Exhibition, 2020, 1-5.
|
| [23] |
陈可洋. 完全匹配层吸收边界条件研究[J]. 石油物探, 2010, 49(5): 472-477. CHEN Keyang. Study on perfectly matched layer absorbing boundary condition[J]. Geophysical Prospecting for Petroleum, 2010, 49(5): 472-477. DOI:10.3969/j.issn.1000-1441.2010.05.006 |



 周辉, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院, 102249。Email:
周辉, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院, 102249。Email: 