2 陕西省油气井测控技术重点实验室, 陕西西安 710065
2 The Key Laboratory of Oil and Gas Well Mea-surement and Control Technology in Shaanxi, Xi'an, Shaanxi 710065, China
实际地震勘探中采集的数据包含多种干扰波,有效信号受其影响而被扭曲、畸变甚至湮没。多年来,为了消除干扰噪声以突出有效信号,人们展开一系列探究并提出许多行之有效的方法。
随机噪声是地震数据中最常见的背景噪声,呈高斯性、平稳性[1-3]分布。随机噪声压制方法的研究从未停滞,从20世纪小波滤波、F-X预测滤波、K-L(Karhunen-Loeve)变换等方法的兴起,到21世纪被广泛应用于地震数据处理领域,并被不断改进,同时又推出许多新方法,且大多取得较显著成效。
这些方法常用的有:通过估计信号特征设计的滤波方法,如F-X预测滤波[4-6]。该方法能很好地提取有效信号特征,但由于在实际应用中需假设一些条件并存在不可预测的因素,因此该方法所能达到的滤波效果很有限。对于同相轴为直线型或近似直线型,且相邻两地震道的间距不变的地震记录,该方法具有较好的预测效果,但对于含有曲线型同相轴的记录,其去噪效果较差。
有利用相关性增强有效信号的滤波方法,如K-L变换法[7-8]、SVD(Singular value decomposition)滤波[9]等。K-L变换是基于统计特性的一种变换,其突出优点是去相关性好,在均方误差意义下具有最佳性能。但使用该方法需首先知道信源的协方差矩阵并求出其特征值,而这些在维数较高时不易获知和求解。然后,通过保留相关性较强的信号特征值,舍弃相关性较小的噪声特征值,再进行重构以实现信噪分离。实际应用中,该方法对水平或倾角较小的同相轴增强效果明显,而对于倾角较大的同相轴跟踪能力不足,因此增强效果很有限。SVD滤波通过对含噪信号分解后所得特征值矩阵中奇异值的合理划分,将表征有效信号的奇异值保留用以重构,得到去噪后的信号。由于奇异值矩阵中的元素值是从大到小排列的,且奇异值减小得很快,一般选取前10%甚至1%的元素即可捕捉有效信号的特征。但该方法分解出的矩阵解释性不够强,奇异值取值个数对计算精度有较大影响。因此,单纯采用SVD滤波往往难以得到理想去噪效果。
有基于时频变换的滤波方法,如基于WVD (Wigner-Ville分布)和PWVD(Pseudo Wigner-Ville分布)的时频峰值滤波[10-11]。PWVD是WVD的加窗形式,更适用于非线性、非平稳信号的处理。在实际应用中,时频峰值滤波法多采用PWVD,以尽可能满足信号局部线性化的无偏估计条件。因此,也使该方法存在窗长选择与噪声压制之间的矛盾[12-16]。
还有基于多尺度分析的滤波方法,如小波滤波[17-20]、曲波滤波[21-23]、Shearlet滤波[24-25]等。该类方法通过对含噪数据进行多尺度分解,根据有效信号和噪声分布在不同尺度系数上的特点,采用阈值划分等手段实现信噪分离。但这些方法存在无方向性,或不能达到最优的稀疏逼近,或对阈值函数的选择较苛刻等不足,其滤波效果仍有较大提升空间。
波原子变换是由Demanet等[26]提出的一种新型多尺度几何分析工具,可看成是二维小波包变换的变体。该变换具有良好的方向特性,每个波包的振动周期和支撑尺寸满足抛物尺度关系,即波长约等于支撑尺寸的平方[26-29],在此意义下,可简单地将波原子理解为方向小波与Gabor原子的插值。
波原子变换对于纹理模型具有最优的稀疏表示。一条地震记录可看作为一幅纹理图像,利用波原子变换可以更好地捕捉其特征[27, 29]。在此基础上,需采用适宜的划分方法使波原子分解系数中的信号成分与噪声成分有效分离,舍弃噪声系数,然后通过波原子重构得到去噪后的地震记录。
本文采用对波原子分解所得系数进行自适应Wiener滤波[30-36]的方案,设计出性能更优且易于实现的滤波方法压制地震勘探随机噪声以突出有效信号。通过实验验证,该方法较之于阈值分离方法可达到更优的效果。
1 方法原理 1.1 波原子变换原理相比于小波变换、曲波变换等,波原子变换对具有振荡性的函数或具有丰富方向纹理特征的信号能呈现最优稀疏表示[26, 28]。定义波原子为φμ(x),μ=(j, m, n),其中m=(m1, m2),n=(n1, n2)。五个参量j、m1、m2、n1、n2是整数,且有j≥0,m≥0, n∈Z。定义相空间中一点(xμ, ωμ)为
| $ \begin{aligned} &\boldsymbol{x_{\mu}}=2^{-j} \boldsymbol{n} \quad \boldsymbol{\omega_{\mu}}={\rm{ \mathit{ π} }} 2^{j} \boldsymbol{m} \\ &C_{1} 2^{j} \leqslant \max \limits_{i=1,2}\left|m_{i}\right| \leqslant C_{2} 2^{j} \end{aligned} $ | (1) |
式中:C1、C2是两个正常数,根据实际应用情况进行合理选择,可都取为1;位置向量xμ和波向量ωμ分别表征φμ(x)的空域和频域中心。
波包{φμ}的框架元称为波原子,波原子围绕相空间点(xμ, ωμ)遵循局部化条件。即对于任意M>0,有
| $ \left|\boldsymbol{\varphi_{\mu}}(x)\right| \leqslant C_{M} \cdot 2^{j}\left(1+2^{j}\left|\boldsymbol{x}-\boldsymbol{x_{\mu}}\right|\right)^{-M} $ | (2) |
| $ C_{M} \cdot 2^{-j}\left(1+2^{-j}\left|\boldsymbol{\omega}+\boldsymbol{\omega_{\mu}}\right|\right)^{-M} $ | (3) |
对于任意f(x)∈L2R2,在2-j尺度上的空间域一维波原子系数为
| $ {C_{j,\mathit{\boldsymbol{m}},\mathit{\boldsymbol{n}}}} = \int {\mathit{\boldsymbol{\psi }}_\mathit{\boldsymbol{m}}^j} \left( {\mathit{\boldsymbol{x}} - {2^{ - j}}\mathit{\boldsymbol{n}}} \right)f(\mathit{\boldsymbol{x}}){\rm{d}}\mathit{\boldsymbol{x}} $ | (4) |
式中ψmj(x-2-jn)是实值波包ψm,nj(x)在2-j上的抽样卷积。根据Plancherel关系,得到频域一维波原子系数为
| $ {C_{j,\mathit{\boldsymbol{m}},\mathit{\boldsymbol{n}}}} = \frac{1}{{2{\rm{ \mathit{ π} }} }}\int {\exp } \left( {{\rm{i}}{2^{ - j\mathit{\boldsymbol{n\omega }}}}} \right)\overline {\mathit{\boldsymbol{\hat \psi }}_\mathit{\boldsymbol{m}}^j(\mathit{\boldsymbol{\omega }})} \hat f(\mathit{\boldsymbol{\omega }}){\rm{d}}\mathit{\boldsymbol{\omega }} $ | (5) |
式中频域
Hilbert变换记为H,在二维情形下,定义正交基及对偶正交基分别为
| $ \mathit{\boldsymbol{\varphi }}_\mathit{\boldsymbol{\mu }}^ + \left( {{x_1},{x_2}} \right) = \mathit{\boldsymbol{\psi }}_{{m_1}}^j\left( {{x_1} - {2^{ - j}}{n_1}} \right)\mathit{\boldsymbol{\psi }}_{{m_2}}^j\left( {{x_2} - {2^{ - j}}{n_2}} \right) $ | (6) |
| $ \mathit{\boldsymbol{\varphi }}_\mathit{\boldsymbol{\mu }}^ - \left( {{x_1},{x_2}} \right) \equiv {\rm{H}}\mathit{\boldsymbol{\psi }}_{{m_1}}^j\left( {{x_1} - {2^{ - j}}{n_1}} \right){\rm{H}}\mathit{\boldsymbol{\psi }}_{{m_2}}^j\left( {{x_2} - {2^{ - j}}{n_2}} \right) $ | (7) |
若记
| $ \sum\limits_\mathit{\boldsymbol{\mu }} {{{\left| {\left\langle {\mathit{\boldsymbol{\varphi }}_\mathit{\boldsymbol{\mu }}^{(1)},f} \right\rangle } \right|}^2}} + \sum\limits_\mathit{\boldsymbol{\mu }} {{{\left| {\left\langle {\mathit{\boldsymbol{\varphi }}_\mathit{\boldsymbol{\mu }}^{(2)},f} \right\rangle } \right|}^2}} = {\left\| f \right\|^2} $ | (8) |
那么,二维波原子变换系数为
| $ {C_\mathit{\boldsymbol{\mu }}} = \left\langle {f,\mathit{\boldsymbol{\varphi }}_\mathit{\boldsymbol{\mu }}^{(1)}} \right\rangle + \left\langle {f,\mathit{\boldsymbol{\varphi }}_\mathit{\boldsymbol{\mu }}^{(2)}} \right\rangle $ | (9) |
该系数参量是一个关于j、m、n三参数的三维矩阵。j为该矩阵包含的系数矩阵组数,这里j分别取1和2,得到两组系数矩阵,每组系数矩阵都是二维矩阵,其维度分别为m1×n1、m2×n2。在后续滤波中,需对这两组系数分别进行处理;在最后的重构过程中,还需将处理过的两组系数进行组合。
对多道地震信号做二维滤波能很好地保持有效信号之间的相关性,这也是其优于一维滤波之处。本文选择二维波原子变换正是充分考虑地震记录中各道有效信号之间的相关性,使有效信号得到更大程度的凸显。
1.2 自适应Wiener滤波维纳滤波器[30-31]是Wiener在二十世纪四十年代提出的一种基于最小均方误差准则的自适应最佳线性滤波器。该方法被应用于众多领域,如地震勘探[32-33]、生物医学[34]、遥感图像[35]以及语音信号处理[36]等。
方法中需处理二维波原子分解系数,因此需采用二维自适应Wiener滤波。假设一个不含噪信号为ξ(l, k),加性随机噪声为η(l, k),那么含噪信号为
| $ s(l, k)=\xi(l, k)+\eta(l, k) $ | (10) |
式中l、k分别为二维信号的行、列元素序号。
滤波的目的是从含噪信号中去除随机噪声,得到有效信号的估计值
| $ \operatorname{MSE}(\hat{\xi})=\sum\limits_{l=1}^{L} \sum\limits_{k=1}^{K}[\hat{\xi}(l, k)-\xi(l, k)]^{2} $ | (11) |
式中L、K分别为二维信号的行、列元素个数。二维滤波时,需选取滤波局域窗(掩模)。那么,在局域窗中采样点的局部均值和方差可分别表示为
| $ \lambda=\frac{1}{P Q} \sum\limits_{p=l-r_{1} / 2}^{l+r_{1} / 2} \sum\limits_{q=k-r_{2} / 2}^{k+r_{2} / 2} s(p, q) $ | (12) |
| $ \sigma^{2}=\frac{1}{P Q} \sum\limits_{p=l-r_{1} / 2}^{l+r_{1} / 2} \sum\limits_{q=k-r_{2} / 2}^{k+r_{2} / 2} s^{2}(p, q)-\lambda^{2} $ | (13) |
式中:r1×r2为局域窗维度;P、Q分别为局部区域内行、列元素个数,p、q为相应元素序号。对于该区域内的采样点,其二维自适应Wiener滤波可表示为
| $ y(p, q)=\lambda+\frac{\sigma^{2}-\nu^{2}}{\sigma^{2}}[s(p, q)-\lambda] $ | (14) |
式中ν2为噪声方差。
如果噪声方差未知,则可用所有局部估计方差的均值代替。根据式(14)求出各局部区域的信号估计值,再将这些估计值合并为一个整体矩阵即为最终估计值。Wiener滤波的此种实现方法有别于其他传统实现方法。传统实现方法中,需求解Wiener滤波器的响应函数,然后用输入信号卷积(时域实现)或乘积(频域实现)此响应函数而得到输出信号。以最小均方误差准则(式(11))为滤波误差约束条件。
但是,该误差公式用到信号的期望值,而该期望值在实际中很难得到。式(14)所示的Wiener滤波实现过程不依赖于期望信号,主要是利用局部均值与方差得到有效信号的估计值,是一种更实用的自适应滤波方法。
2 在地震数据处理中的应用 2.1 处理过程概述前文述及,对波原子分解系数进行滤波处理,需去除不必要的系数,即表征噪声的系数,保留表征有效信号的系数,然后对这些有效信号系数进行波原子重构即可得到滤波后的信号。本文采用自适应Wiener滤波对分解系数进行处理,是利用其在最小均方误差意义下可达到最佳线性滤波的特点。
对地震记录进行处理时,一般采样点数与道数不是2的整数次幂,因此首先要将地震数据通过补零得到行、列元素个数均为2的整数次幂的矩阵。在分解过程中,得到如式(9)中的φμ(1)和φμ(2),依照式(12)~式(14)分别对这两组系数进行二维自适应Wiener滤波。滤波时,需根据记录中的同相轴形态与分布特征,合理选择局域窗,即对于同相轴不对称分布的记录一般选用矩形窗,而对于同相轴呈近似对称分布的记录一般选用正方形局域窗。对于双曲同相轴记录与线性同相轴记录选取的窗函数的维度也有所区别,同等噪声条件下,前者滤波窗的r2一般小于后者。最后将滤波后的波原子系数进行重构,即可得到能量增强后的地震记录。
2.2 模拟地震记录处理首先针对含有线性同相轴的模拟地震记录进行实验。该记录为2ms采样,道间距为10m,共有50道。其中包含四个线性同相轴,每个同相轴由主频为30Hz的Ricker子波构成。对该不含噪模拟地震记录(图 1a)加入高斯白噪声,使其信噪比约为-5dB(图 1b)。

|
图 1 含有线性同相轴的模拟地震记录及其处理结果 (a)不含噪记录;(b)含噪记录;(c)方法1滤波后重构记录;(d)方法2滤波后重构记录;(e)方法3滤波后重构记录;(f)本文方法滤波后重构记录 |
SVD阈值(方法1)、二维多尺度小波分解阈值(方法2)和二维波原子分解阈值(方法3)三种滤波方法中,阈值的选取须综合考虑随机噪声压制与有效信号保幅,并历经多次实验测试。三种方法滤波后重构的地震记录依次如图 1c~图 1e所示。
对含噪记录进行二维波原子分解系数自适应Wiener滤波(本文方法)时,考虑记录中有效同相轴分布情况,选取的局域窗为长宽不等的矩形窗,即r1=5、r2=187。当噪声强度改变时,可适当调整r1和r2值。由此,本文方法滤波后重构的地震记录如图 1f所示。
从滤波结果可见:方法1对背景噪声的去除及对有效信号的保留效果均较差(图 1c中矩形框);方法2对有效同相轴的损伤较严重且在同相轴边缘产生阴影和模糊现象(图 1d中椭圆和矩形框);方法3滤波效果较前二者有所提高,但模拟记录两边地震道有效信号损失较严重(图 1e中矩形框);本文方法处理效果最好,在随机噪声压制和有效信号保持方面均表现较优(图 1f)。据图中右侧能量值色标也能看出图 1f中有效信号能量显著强于图 1c~图 1e。经定量计算,得到四种方法滤波后记录的信噪比分别为0.1686、7.6282、7.8338和8.7075dB。
对上述纯净记录加入不同强度随机噪声,得到不同信噪比含噪记录,分别采用四种方法做滤波实验,滤波前后地震记录信噪比数据如表 1所示。
|
|
表 1 含噪的线性同相轴记录滤波前、后信噪比(单位:dB) |
从表 1可见:方法1所能达到的信噪比很低,对原含噪记录信噪比的提高较少;方法2、方法3的滤波后记录能达到较高信噪比,其中方法3信噪比提升幅度稍高于方法2,但二者都存在同相轴局部损失较多的问题,且方法2还会导致有效同相轴边缘不清晰;本文方法相对于其他三种方法优势更明显,对有效同相轴的增强及边缘保留效果最好,对含噪记录信噪比的提升能力最强。
本次实验采用一台高性能便携式工作站。在相同计算机条件下,上述四种滤波方法处理图 1b所示含噪记录的时间依次为:0.0071、0.7044、3.4747、3.9913s。可见方法1虽用时最短,但效果不佳;方法2用时次短,但效果也欠理想;方法3和本文方法的用时虽较前二者长,但本文方法处理效果更好。
再对含有双曲同相轴的地震记录(图 2)做滤波实验。该数据采样间隔为1ms,道间距为20m,采用主频为35Hz的Ricker子波,共有76道。层速度分别为2300、2500、2900m/s。对不含噪记录(图 2a)加入高斯白噪声使其信噪比为-5dB(图 2b),三种方处理后的地震记录分别如图 2c~图 2e所示。
|
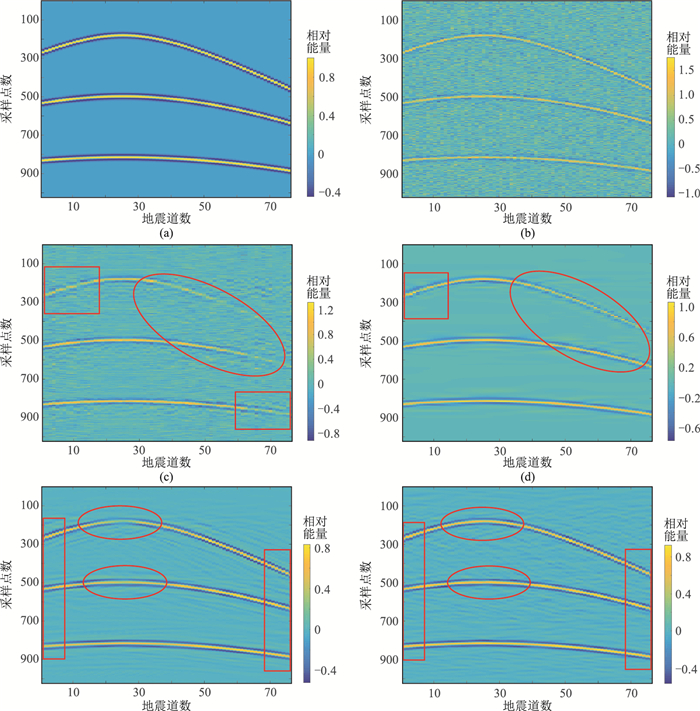
图 2 含有双曲同相轴的模拟地震记录及其处理结果 (a)不含噪记录;(b)含噪记录;(c)方法1滤波后重构记录;(d)方法2滤波后重构记录;(e)方法3滤波后重构记录;(f)本文方法滤波后重构记录 |
由于图 2a同相轴的形态和分布与图 1a不同,因此需调整Wiener滤波窗函数。调整时须兼顾随机噪声压制与有效信号保持。此时,选取r1=5、r2=117,即可得到本文方法处理后的地震记录(图 2f)。
观察四种滤波方法所得滤波记录(图 2)可知:方法1对背景噪声的消除能力很有限且对有效同相轴损失较多(图 2c中矩形和椭圆框);方法2和方法3能较有效地压制随机噪声,但对有效信号的损失不容忽视,前者会造成同相轴边缘模糊(图 2d中矩形和椭圆框),后者会使双曲同相轴拱起部分损失较严重(图 2e中椭圆框);而本文方法能在随机噪声压制和有效信号保持方面做到很好权衡(图 2f)。四种方法处理后记录的信噪比分别为0.3301、7.1616、7.4222、9.1073dB。
同样,对上述纯净记录加入不同强度随机噪声,得到不同信噪比含噪记录,分别采用四种方法进行滤波实验,滤波前、后的信噪比数据如表 2所示。分析对比该表数据,也能得到与表 1相似的结论。
|
|
表 2 含噪的双曲同相轴记录滤波前、后信噪比(单位:dB) |
选取实际共炮点记录做滤波对比测试。该共炮点记录共有168道,采样间隔为1ms,仅截取记录的上部(0~2048ms)。首先分别采用方法2、方法3和本文方法进行滤波处理(图 3)。此次处理选取的Wiener滤波窗为正方形,即r1=r2=95。

|
图 3 实际地震记录滤波效果对比(一) (a)原始记录;(b)方法2滤波记录;(c)方法3滤波记录;(d)本文方法滤波记录 |
从滤波结果(图 3)可见:方法2(图 3b)和方法3(图 3c)滤波效果明显不理想,对有效同相轴造成较大程度的损失及畸变;而本文方法使有效同相轴更清晰、连续,能量得到显著增强(图 3d中梯形和矩形框)。
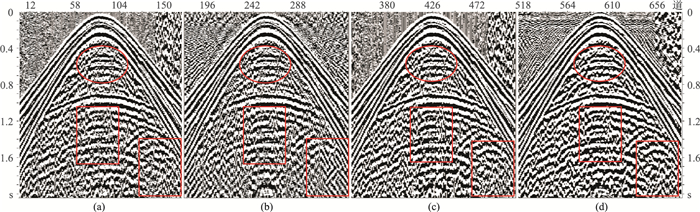
对该实际记录还应用方法1和一维时频峰值滤波法进行处理。方法1处理时,若选取过少特征值,就会导致有效同相轴损失太多;若选取较多特征值,就几乎没有去噪效果。对于此次实际记录,选取分解后奇异值矩阵中的前60个特征值进行重构较适宜(图 4b)。但该方法对背景噪声的压制效果非常有限,且对有效同相轴造成了一定程度的畸变。
|
图 4 实际地震记录滤波效果对比(二) (a)原始记录;(b)方法1滤波记录;(c)时频峰值滤波记录;(d)本文方法滤波记录 |
进行时频峰值滤波时,滤波窗长不宜太大或太小,若太大虽能较好地压制随机噪声,但有效信号损失较大;若太小则不能很好地压制随机噪声。对于该实际记录,选取滤波窗长为13点(图 4c)。与本文方法所得结果(图 4d)对比,可见一维时频峰值滤波处理结果虽然背景噪声有所压制,但同相轴的清晰度和连续性提升效果欠理想,而本文方法处理后的记录中同相轴的清晰度更高、连续性更好。
3 结论本文提出二维波原子分解系数自适应Wiener滤波方法,对地震资料进行随机噪声消减处理以增强有效同相轴。其实现过程是,先对地震记录进行二维波原子分解,再对所得系数进行二维自适应Wiener滤波,最后对滤波后的系数进行波原子重构得到同相轴增强的记录。通过对人工合成记录与实际记录的滤波处理,得到以下认识和结论:
(1) 通过对模拟地震记录的滤波实验,并与SVD阈值滤波、二维多尺度小波分解阈值滤波及二维波原子分解阈值滤波结果作比较,验证本文所提滤波方法在地震随机噪声压制及有效信号保持方面具有优越性。
(2) 采用二维多尺度小波分解阈值滤波、二维波原子分解阈值滤波、SVD阈值滤波、一维时频峰值滤波及二维波原子分解系数自适应Wiener滤波五种方法对实际共炮点记录进行滤波处理,并将处理后的结果作对比,发现本文本文方法能够较彻底地压制记录中的随机噪声,同时使有效同相轴更清晰、连续性更好。
因此,应用本文方法对地震数据进行处理,可为后续的地震成像及综合解释提供可靠资料,对提高地震资料解释的准确性具有重要意义。
| [1] |
陆基孟. 地震勘探原理及资料解释[M]. 北京: 石油工业出版社, 1991.
|
| [2] |
李庆忠. 走向精确勘探的道路[M]. 北京: 石油工业出版社, 1993.
|
| [3] |
钟铁, 李月, 杨宝俊, 等. 陆地地震勘探随机噪声统计特性[J]. 地球物理学报, 2017, 60(2): 655-664. ZHONG Tie, LI Yue, YANG Baojun, et al. Statistical features of the random noise in land seismic prospecting[J]. Chinese Journal of Geophysics, 2017, 60(2): 655-664. |
| [4] |
康冶, 于承业, 贾卧, 等. f-x域去噪方法研究[J]. 石油地球物理勘探, 2003, 38(2): 136-138. KANG Ye, YU Chengye, JIA Wo, et al. A study on noise-suppression method in f-x domain[J]. Oil Geophysical Prospecting, 2003, 38(2): 136-138. DOI:10.3321/j.issn:1000-7210.2003.02.007 |
| [5] |
魏海涛, 陆文凯, 郑晓东. 基于F-X域预测和全变分的串行滤波器[J]. 石油地球物理勘探, 2011, 46(5): 700-704. WEI Haitao, LU Wenkai, ZHENG Xiaodong. Cascaded filter based on F-X prediction and total variation filter[J]. Oil Geophysical Prospecting, 2011, 46(5): 700-704. |
| [6] |
Ma Y Y, Li G F, Wang Y J, et al. Random noise attenuation by f-x spatial projection-based complex empi-rical mode decomposition predictive filtering[J]. Applied Geophysics, 2015, 12(1): 47-54. DOI:10.1007/s11770-015-0467-3 |
| [7] |
周洁玲. 利用K-L变换提高地震记录的信噪比[J]. 西南石油学院学报, 2003, 25(3): 5-7. ZHOU Jieling. Improving the signal-noise rate of seismic record with K-L transform[J]. Journal of Southwest Petroleum Institute, 2003, 25(3): 5-7. DOI:10.3863/j.issn.1674-5086.2003.03.002 |
| [8] |
彭才, 朱仕军, 孙建库, 等. 小波变换域K-L变换及其去噪效果分析[J]. 石油物探, 2007, 46(2): 112-114. PENF Cai, ZHU Shijun, SUN Jianku, et al. K-L transformation in wavelet conversion domain and the analysis of de-noise effect[J]. Geophysical Prospecting for Petroleum, 2007, 46(2): 112-114. |
| [9] |
陆文凯, 李衍达. SVD分解提高地震资料的信噪比和分辨率[J]. 石油地球物理勘探, 1998, 33(增刊1): 145-149. LU Wenkai, LI Yanda. A SVD method to improve SNR and resolution[J]. Oil Geophysical Prospecting, 1998, 33(S1): 145-149. |
| [10] |
Mesbah M and Boashash B. Reduced bias time-frequency peak filtering[C]. International Symposium on Signal Processing and Its Applications (ISSPA), Kuala Lumpur, Malaysia, 2001, 327-330.
|
| [11] |
Boashash B and Mesbah M. Signal enhancement by time-frequency peak filtering[J]. IEEE Transactions on Signal Processing, 2004, 52(4): 929-937. DOI:10.1109/TSP.2004.823510 |
| [12] |
金雷, 李月, 杨宝俊. 用时频峰值滤波方法消减地震勘探资料中随机噪声的初步研究[J]. 地球物理学进展, 2005, 20(3): 724-728. JIN Lei, LI Yue, YANG Baojun. Reduction of random noise for seismic data by time-frequency peak filtering[J]. Progress in Geophysics, 2005, 20(3): 724-728. DOI:10.3969/j.issn.1004-2903.2005.03.024 |
| [13] |
林红波, 李月, 叶文海, 等. 时频峰值滤波去噪技术及其应用[J]. 地球物理学进展, 2008, 23(6): 1953-1957. LIN Hongbo, LI Yue, YE Wenhai, et al. Denoising technique based on Time-Frequency Peak Filtering and its application[J]. Progress in Geophysics, 2008, 23(6): 1953-1957. |
| [14] |
李月, 林红波, 杨宝俊, 等. 强随机噪声条件下时窗类型局部线性化对TFPF技术的影响[J]. 地球物理学报, 2009, 52(7): 1899-1906. LI Yue, LIN Hongbo, YANG Baojun, et al. The in-fluence of limited linearization of time window on TFPT under the strong noise background[J]. Chinese Journal of Geophysics, 2009, 52(7): 1899-1906. DOI:10.3969/j.issn.0001-5733.2009.07.025 |
| [15] |
Tian Y and Li Y. Parabolic-trace time-frequency peak filtering for seismic random noise attenuation[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(1): 158-162. DOI:10.1109/LGRS.2013.2250906 |
| [16] |
Zhang C, Li Y, Lin H B, et al. Signal preserving and seismic random noiseattenuation by Hurst exponent based time-frequency peak filtering[J]. Geophysical Journal International, 2015, 203(2): 901-909. DOI:10.1093/gji/ggv340 |
| [17] |
傅燕, 赵荣椿, 王刚. 小波变换在地震信号噪声处理中的应用[J]. 西北工业大学学报, 2004, 22(6): 774-777. FU Yan, ZHAO Rongchun, WANG Gang. Seismic data denoising based on wavelet transform[J]. Journal of Northwestern Polytechnical University, 2004, 22(6): 774-777. DOI:10.3969/j.issn.1000-2758.2004.06.021 |
| [18] |
Droujinine A. Theory and seismic applications of the eigenimage discrete wavelet transform[J]. Geophysical Prospecting, 2006, 54(4): 441-461. DOI:10.1111/j.1365-2478.2006.00546.x |
| [19] |
吴招才, 刘天佑. 地震数据去噪中的小波方法[J]. 地球物理学进展, 2008, 23(2): 493-499. WU Zhaocai, LIU Tianyou. Wavelet transform me-thods in seismic data noise attenuation[J]. Progress in Geophysics, 2008, 23(2): 493-499. |
| [20] |
郭思, 郭科, 陈聆, 等. 基于小波变换新阈值函数的地震资料去噪方法[J]. 成都理工大学学报(自然科学版), 2014, 41(3): 378-381. GUO Si, GUO Ke, CHEN Ling, et al. Seismic data de-noising method based on a new threshold function of wavelet transformation[J]. Journal of Chengdu University of Technology(Science & Technology Edition), 2014, 41(3): 378-381. DOI:10.3969/j.issn.1671-9727.2014.03.14 |
| [21] |
吴爱弟, 赵秀玲. 基于曲波变换的地震信号去噪方法[J]. 中国石油大学学报(自然科学版), 2010, 34(3): 30-33. WU Aidi, ZHAO Xiuling. Seismic signal denoising method based on curvelet transform[J]. Journal of China University of Petroleum(Edition of Natural Science), 2010, 34(3): 30-33. DOI:10.3969/j.issn.1673-5005.2010.03.006 |
| [22] |
Wang D L, Tong Z F, Tang C, et al. An iterative curvelet thresholding algorithm for seismic random noise attenuation[J]. Applied Geophysics, 2010, 7(4): 315-324. DOI:10.1007/s11770-010-0259-8 |
| [23] |
刘磊, 刘振, 张军华. 曲波阈值法地震弱信号识别及去噪方法研究[J]. 地球物理学进展, 2011, 26(4): 1415-1422. LIU Lei, LIU Zhen, ZHANG Junhua. Denoising and detecting seismic weak signal based on curvelet thresholding method[J]. Progress in Geophysics, 2011, 26(4): 1415-1422. DOI:10.3969/j.issn.1004-2903.2011.04.037 |
| [24] |
童思友, 高航, 刘锐, 等. 基于Shearlet变换的自适应地震资料随机噪声压制[J]. 石油地球物理勘探, 2019, 54(4): 744-750. TONG Siyou, GAO Hang, LIU Rui, et al. Seismic random noise adaptive suppression based on the Shearlet transform[J]. Oil Geophysical Prospecting, 2019, 54(4): 744-750. |
| [25] |
薛林, 程浩, 巩恩普, 等. Shearlet域自适应阈值地震数据随机噪声压制[J]. 石油地球物理勘探, 2020, 55(2): 282-291. XUE Lin, CHENG Hao, GONG Enpu, et al. Random noise suppression using adaptive threshold in Shearlet domain[J]. Oil Geophysical Prospecting, 2020, 55(2): 282-291. |
| [26] |
Demanet L, Ying L. Wave atoms and sparsity of oscillatory patterns[J]. Applied and Computational Harmonic Analysis, 2007, 23(3): 368-387. DOI:10.1016/j.acha.2007.03.003 |
| [27] |
杨宁, 贺振华, 黄德济. 基于系数相关性阈值的波原子域叠前地震资料信噪分离方法[J]. 石油地球物理勘探, 2011, 46(1): 53-57. YANG Ning, HE Zhenhua, HUANG Deji. Signal and noise separation method for pre-stack seismic data in wave atomic domain based on coefficient correlation threshold[J]. Oil Geophysical Prospecting, 2011, 46(1): 53-57. |
| [28] |
Liu F, Cheng L M, Leung H Y, et al. Wave atom transform generated strong image hashing scheme[J]. Optics Communications, 2012, 285(24): 5008-5018. DOI:10.1016/j.optcom.2012.08.007 |
| [29] |
何峰, 周亚同, 赵翔宇, 等. 基于波原子变换的三维地震信号盲去噪[J]. 振动与冲击, 2019, 38(8): 88-95. HE Feng, ZHOU Yatong, ZHAO Xiangyu, et al. Blind denoising of 3D seismic signals based on the wave atom transform[J]. Journal of Vibration and Shock, 2019, 38(8): 88-95. |
| [30] |
Kutay A, Ozaktas H M, Ankan O, et al. Optimal filtering in fractional Fourier domains[J]. IEEE Transactions on Signal Processing, 1997, 45(5): 1129-1143. DOI:10.1109/78.575688 |
| [31] |
Kao T S. Wiener filter as an optimal MMSE interpolator[J]. International Journal of Electrical, Compu-ter, Energetic, Electronics and Communication Engineering, 2007, 1(6): 942-944. |
| [32] |
聂鹏飞, 曾谦, 马海涛, 等. 消减地震勘探随机噪声: 导数算子约束下的维纳滤波[J]. 吉林大学学报(地球科学版), 2010, 40(6): 1471-1478. NIE Pengfei, ZENG Qian, MA Haitao, et al. Reducing Seismic Random Noise: Derivative Operator Constrainted Wiener Filtering[J]. Journal of Jilin University(Earth Science Edition), 2010, 40(6): 1471-1478. |
| [33] |
张力起, 张猛, 王华忠, 等. 高维地震数据Wiener中心滤波方法[J]. 石油物探, 2019, 58(3): 325-334. ZHANG Liqi, ZHANG Meng, WANG Huazhong, et al. Centralized Wiener filtering for high-dimensional seismic data[J]. Geophysical Prospecting for Petro-leum, 2019, 58(3): 325-334. DOI:10.3969/j.issn.1000-1441.2019.03.002 |
| [34] |
Mohan J, Krishnaveni V, Guo Y H. A New neutrosophic approach of Wiener filtering for MRI denoising[J]. Measurement Science Review, 2013, 13(4): 177-186. DOI:10.2478/msr-2013-0027 |
| [35] |
Tang C H. Noise reduction method of adaptive Wiener filtering for ocean remote sensing image[J]. Journal of Coastal Research, 2018, 83(S1): 651-655. |
| [36] |
Garg A, Sahu O P. Enhancement of speech signal using diminished empirical mean curve decomposition-based adaptive Wiener filtering[J]. Pattern Analysis and Applications, 2020, 23(1): 179-198. DOI:10.1007/s10044-018-00768-x |



 刘彦萍, 陕西省西安市雁塔区电子二路东段18号西安石油大学电子工程学院, 710065。Email:
刘彦萍, 陕西省西安市雁塔区电子二路东段18号西安石油大学电子工程学院, 710065。Email: 