② 河北省地震灾害监测仪器与监测技术重点实验室, 河北三河 065201
② Hebei Key Laboratory of Seismic Disaster Ins-trument and Monitoring Technology, Sanhe, Hebei 065201, China
地震勘探是油气勘探开发的重要手段,且依赖于高质量的处理成果数据。受人类活动、环境、天气、仪器等多方面因素影响,实际采集的地震数据中往往存在各种噪声干扰,这无疑会影响地震资料处理和解释的准确性。为了提高地震勘探精度,使地震资料能更真实地反映地下地质情况,压制噪声干扰在地震数据处理中就显得极为重要了。
地震资料噪声包括规则噪声和随机噪声两大类。面波是其中一种能量较强且广泛存在的规则干扰,其频率低、衰减慢,大大降低了地震资料信噪比;而随机噪声则显得杂乱无规律,频率分布宽泛,空间上无确定的视速度。因此,可根据面波和随机噪声各自的特点探寻相应的适用去噪方法。
在面波压制领域,S变换[1]、广义S变换[2-3]、Curvelet变换[4-5]、小波变换[6-7]和f-x域滤波[8]等方法广泛使用,利用面波与有效波在变换域上的特征差异实施分离。这些方法有一定效果但也有局限性,且会不同程度地损害有效信号。
在随机噪声去除方面,经验模态分解(Empirical mode decomposition,EMD)[9]、小波阈值去噪[10]、深度学习[11]等方法被引入,但这些方法同样有各自优缺点。如EMD存在模态混叠、伪模态等问题,难以兼顾增强去噪效果与降低有效信号损伤;小波阈值去噪效果依赖于小波基的选取;深度学习需大量训练数据,计算量大。这些算法一般只针对单一类型噪声,难以同时处理面波和随机噪声这两种最普遍存在的干扰。
作为一种自适应的信号处理方法,EWT(经验小波变换)[12]结合小波变换和EMD技术优势,通过分割信号的傅里叶谱,并在每个分割区间构造正交小波基,将信号分解为若干分量,从而准确提取信号中固有模态分量,适用于非线性非平稳信号。
EWT推出后被广泛应用于噪声压制及故障诊断等方面[13-15],在地震数据处理与分析领域,也倍受青睐。Liu等[16]基于EWT对多通道地震资料进行时频分析,分解出不同频率分量,并根据计算边界提取地震信号分量,分辨率明显高于传统连续小波变换。基于油气藏导致地震波衰减增大的原理,Hui等[17]利用EWT分析地震波衰减时频特性,圏定衰减异常位置,以厘清含气层厚度变化,实现油气检测。在地震数据去噪方面,覃发兵等[18]利用EWT将地震信号分解为若干分量,并计算各分量主频,剔除阈值外分量后重构实现随机噪声压制。Chen等[19]利用EWT将地震信号分解为若干IMF,再利用聚类算法对含噪分量做阈值化处理。
以上应用表明利用EWT可有效分析地震信号,但传统EWT根据信号频谱幅值进行频带划分和信号分解,易受噪声影响,因此有必要根据地震信号特点改进EWT频谱分割方法,使之更适用于地震信号。Liu等[20]基于尺度空间表示提取信号傅里叶谱的慢变分量,再根据尺度参数获取地震信号中包含的频率分量和边界,自适应分割频谱,但尺度参数通常依据经验获取,使频谱分割的准确性受限。孟娟等[21]对地震信号连续小波变换后计算各频率点能量,得到小波谱能量曲线(WSEC),以该曲线局部极大值点的频率及ε邻域法确定频谱分割边界进行改进EWT,实现依地震信号频率和能量的自适应分解,取得良好效果,但连续小波变换中基小波函数的选取影响变换结果精度,且通过尺度参数调整小波函数形状,获得的并不是真实的时频谱。
为同时分离地震资料中的面波和随机噪声,针对传统EWT根据频谱极值分割频带抗干扰性差的不足,本文提出基于S谱能量曲线的改进EWT地震资料噪声压制算法,实现面波和随机噪声同步压制。通过对地震信号S变换后计算各频点能量得到S谱能量曲线(SSEC),根据曲线极大值点分布进行频带分割,将原信号自适应分解为若干按频率和能量分布的IMF,并根据SSEC确定面波IMF;为保护面波IMF中的低频有效信号,对其进行带通滤波,以实现精准的面波剔除;最后根据有效波频率阈值和各IMF主频去除随机噪声,完成面波和随机噪声的压制,有效提高地震资料信噪比。
1 EWT基本原理EWT通过计算信号的傅里叶频谱,并基于频谱幅值的极值点进行频谱分割,在每个分割区间内构建正交的小波滤波器组,提取不同频带内的调幅、调频分量,实现信号分解。其原理详述如下:
(1) 获取原信号f(t)的傅里叶频谱F(ω),ω∈[0,π]。
(2) 获取F(ω)的M个按频率升序排列的局部极大值点ω1,…,ωM,将[0,π]频带划分成N(N≤M)个子频带,设以ωn为中心的分量子频带为[Ωn-1, Ωn]。获取边界Ω的常用方法有两种:一是根据频谱的M个极大值点,将相邻两个极大值中点定义为边界,Ωn-1=(ωn-1+ωn)/2,n=2,…, N,Ω0=0, ΩN=π;或先找到信号频谱的极大值点,再寻找两相邻极大值间的极小值点,以该极小值点为边界。这样将原信号频谱划分为N个连续、不重叠的子频带。
(3构造正交小波滤波器组分解信号,针对子频带[Ωn-1, Ωn]设定尺度函数
| $ \hat{\phi}_{n}(\omega)=\left\{\begin{array}{cc} 1 & |\omega|<(1-\gamma) \varOmega_{n} \\ \cos \left\{\frac{{\rm{ \mathsf{ π} }} \beta}{2}\left[\frac{|\omega|-(1-\gamma) \varOmega_{n}}{2 \gamma \varOmega_{n}}\right]\right\} & (1-\gamma) \varOmega_{n} \leqslant|\omega| \leqslant(1+\gamma) \varOmega_{n} \\ 0&其他 \end{array}\right\} $ | (1) |
| $ \hat{\psi}_{n}(\omega)=\left\{\begin{array}{ll} 1 & (1+\gamma) \varOmega_{n}<|\omega|<(1-\gamma) \varOmega_{n+1} \\ \cos \left\{\frac{{\rm{ \mathsf{ π} }} \beta}{2}\left[\frac{|\omega|-(1-\gamma) \varOmega_{n+1}}{2 \gamma \varOmega_{n+1}}\right]\right\} & (1-\gamma) \varOmega_{n+1} \leqslant|\omega| \leqslant(1+\gamma) \varOmega_{n+1} \\ \sin \left\{\frac{{\rm{ \mathsf{ π} }} \beta}{2}\left[\frac{|\omega|-(1-\gamma) \varOmega_{n}}{2 \gamma \varOmega_{n}}\right]\right\} & (1-\gamma) \varOmega_{n} \leqslant|\omega| \leqslant(1+\gamma) \varOmega_{n} \\ 0 & \text { 其他 } \end{array}\right\} $ | (2) |
式中:过渡函数β(x)=x4(35-84x+70x2-20x3);0 < γ < 1,且
在[Ωn-1, Ωn]频段,EWT近似系数wfε(0, t)和细节系数wfε(n, t)为
| $ w_{f}^{\varepsilon}(0, t)=\int f(\tau) \hat{\phi}{}_{1}^{*}(\tau-t) \mathrm{d} \tau=\mathrm{F}^{-1}\left[F(\omega) \hat{\phi}{}_{1}^{*}(\omega)\right] $ | (3) |
| $ w_{f}^{\varepsilon}(n, t)=\int f(\tau) \hat{\psi}{}_{n}^{*}(\tau-t) \mathrm{d} \tau=\mathrm{F}^{-1}\left[F(\omega) \hat{\psi}{}_{n}^{*}(\omega)\right] $ | (4) |
则得到的低频分量和高频分量分别为
| $ f_{0}(t)=w_{f}^{\varepsilon}(0, t) * \hat{\phi}_{1}(t) $ | (5) |
| $ f_{k}(t)=w_{f}^{\varepsilon}(n, t) * \hat{\psi}_{k}(t) $ | (6) |
式(3)~式(6)中:F-1为傅里叶逆变换;
须注意的是,传统EWT分解信号需预先设定经验模态分解阶数N,该参数选取会影响信号分解精度,过大或过小都不能较好表征原信号。
2 基于S谱能量曲线的改进EWT 2.1 S谱能量曲线SSEC作为短时傅里叶变换和以Morlet小波为小波基的连续小波变换的发展,S变换采用带有频率变量的高斯窗函数截取信号,从而实现信号的局部分析。S变换免去了窗函数选择,且其窗函数可随频率需求自适应地变化,具有多分辨率的特点。与连续小波变换相比,S变换分辨率依赖于频率而不是尺度,因此更直观;且每一频率的绝对相位不变,与傅里叶谱直接关联,能精确描述信号各时刻的频谱,较好适应非平稳信号频率不规律变化的特点,因此在地震数据处理领域应用较广。其原理如下:
根据短时傅里叶变换,定义高斯窗函数为
| $ g(t, \sigma, \tau)=\frac{1}{\sigma \sqrt{2 {\rm{ \mathsf{ π} }}}} \mathrm{e}^{-\frac{(\tau-t)^{2}}{2 \sigma^{2}}} $ | (7) |
式中σ为尺度因子,可控制窗函数宽度。它与频率直接联系,从而改变时频分辨率
| $ \sigma(f)=\frac{1}{|f|} $ | (8) |
代入短时傅里叶变换公式,即有
| $ \begin{array}{r} \operatorname{STFT}(f, \sigma, \tau)=\int_{-\infty}^{\infty} h(t) g(\tau-t) \mathrm{e}^{-\mathrm{i}{\omega} t} \mathrm{~d} t \\ =\int_{-\infty}^{\infty} h(t) \frac{1}{\sigma \sqrt{2 {\rm{ \mathsf{ π} }}}} \mathrm{e}^{-\frac{(\tau- t)^{2}}{2 \sigma^{2}}} \mathrm{e}^{-\mathrm{i} 2 {\rm{ \mathsf{ π} }} f t} \mathrm{~d} t \end{array} $ | (9) |
可得到其S变换
| $ S(f, \tau)=\int_{-\infty}^{\infty} h(t) \frac{|f|}{\sqrt{2 {\rm{ \mathsf{ π} }}}} \mathrm{e}^{-\frac{f^{2}(\tau-t)^{2}}{2}} \mathrm{e}^{-\mathrm{i} 2 {\rm{ \mathsf{ π} }} f t} \mathrm{~d} t $ | (10) |
对信号进行S变换得到信号时频分布的S谱后,根据式(11)对频点i定义S谱能量,实现信号时频域到频率—能量域的转换。表示为
| $ E_{i}^{S}=\frac{\int_{-\infty}^{\infty}\left|S\left(f_{i}, \tau\right)\right|^{2} \mathrm{~d} \tau}{\int_{-\infty}^{\infty} \int_{-\infty}^{\infty}|S(f, \tau)|^{2} \mathrm{~d} f \mathrm{d} \tau} $ | (11) |
式中:fi为S变换后频点i的频率;S(fi, τ)为该频点对应的S变换值,即S谱。
对某信号按式(11)获取所有频点能量值,从而得到依频率分布的SSEC,该曲线能清晰描绘不同频率处信号的能量分布及不同频率成分的能量强弱。
2.2 基于SSEC的改进EWT对含面波的地震信号进行S变换并获取SSEC,SSEC能直接反映不同频率成分的能量大小。由于面波的频率低且能量强,因此通过SSEC能区分面波与有效地震波。不同于传统EWT根据傅里叶频谱的局部极大值分割频谱,本文根据SSEC的极大值点自适应地分割频谱,即以SSEC极大值点对应的频率为初始边界,通过ε邻域法搜索重新确定边界,以进行改进EWT,根据信号不同频率分量的能量大小自适应分解。算法如下:
(1) 对地震信号s(t)进行傅里叶变换和S变换,得到傅里叶频谱F(ω), ω∈[0, π]和S谱S(f, τ)。
(2) 根据式(11)获取各频率点能量,绘制SSEC。
(3) 求取S谱能量曲线的N-1个局部极大值点Eiloc(i=1,…,N-1),将N-1个极大值点对应的频率ωi(i=1,…,N-1)作为频谱分割的初始边界集
(4)ε邻域法搜索确定边界集。对于第k个边界点ωk(k=1,…,N-1),它将第k-1与第k个子频带分开,长度分别为Lk-1=ωk-ωk-1, Lk=ωk+1-ωk。为确定边界点,且保证边界点不重叠,以两子频带长度的1/2为半径,即在区间[ωk-Lk-1/2, ωk+Lk/2]内重新寻找两个局部极大值和一个最小值,以该最小值为新边界点ωk'。依次获取初始边界集{ωn}对应的新边界集
(5) 构造正交小波滤波器组分解信号:对子频带[ωn-1', ωn'],确定尺度函数
改进EWT可将原地震信号分解为一系列具有紧支撑频谱的IMF分量,对各IMF解调可得到其瞬时频率、幅度、相位等属性,从而获取原信号特征。
3 基于SSEC-EWT的噪声压制方法与地震信号相比,面波频率范围低,频带一般为4~18Hz[2],且能量较强。本文改进EWT是根据S变换后各频点能量大小进行频谱分割,各IMF是根据原信号不同频率成分的能量大小分解的,从而可将低频、高能量面波成分从原信号中分离出来。
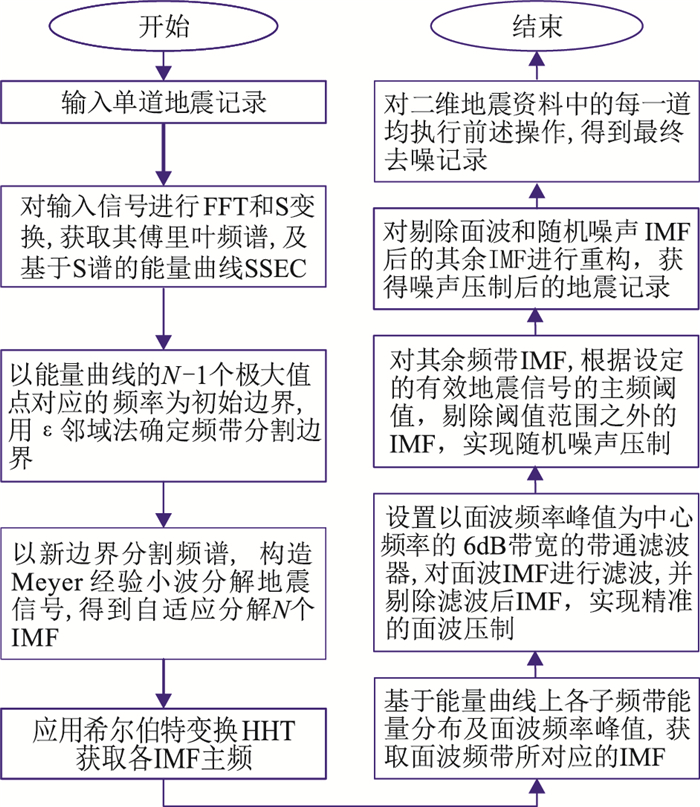
而随机噪声在时域内广泛存在,且一般为高频率,可根据有效地震信号频率范围设定阈值,剔除阈值范围外的噪声IMF,实现随机噪声压制。基于此思路,本文提出基于SSEC-EWT的面波和随机噪声压制方法,其流程如图 1所示。
|
图 1 基于SSEC-EWT的面波和随机噪声压制方法流程 |
根据有效波与面波在频率和能量上的不同,本文利用改进EWT进行地震信号分解,提取面波IMF后进行面波压制,流程如下:
(1) 计算地震信号SSEC,以能量曲线极值点及ε邻域法分割频谱,进行改进的EWT,自适应得到依频率和能量分解的各模态分量IMF1,…,IMFN。
(2) 对各IMF进行希尔伯特变换,得到瞬时频率、瞬时振幅,并据下式计算各IMF主频
| $ f_{\mathrm{m}}=\frac{\int_{0}^{\infty} f s(f) \mathrm{d} f}{\int_{0}^{\infty} s(f) \mathrm{d} f} $ | (12) |
式中:fm为IMF主频;f为瞬时频率;s(f)为瞬时振幅谱。
(3) 结合SSEC,找到频率在4~18Hz范围内,且能量强于其他邻近子频带的子频段位置,确定面波所在的IMF。
(4) 根据SSEC中面波频率峰值,对该IMF进行带通滤波。滤波器截止频率为面波IMF频谱峰值的6dB带宽频率,即以频谱功率下降为功率峰值25%、幅度下降为峰值50%时的频率为截止频率,对面波IMF进行带通滤波,以最大限度地保护面波IMF中的低频有效波不被破坏。
(5) 从原记录剔除滤波后面波IMF,实现面波压制。
3.2 随机噪声压制随机噪声一般以高频率广泛存在于地震资料中,常规地震勘探中检波器接收的有效地震波频率范围一般在150Hz以内[22]。因此,根据地震波与随机噪声的频率范围差异,可实现随机噪声衰减。本文基于改进EWT的随机噪声压制具体算法如下:
(1) 设定有效地震波最高频率阈值为150Hz;
(2) 计算完成面波压制后的其余IMF主频,剔除阈值范围外IMF,进行随机噪声压制;
(3) 对剔除面波后IMF和随机噪声IMF信号进行重构,得到噪声压制后的地震信号。
至此,完成面波和随机噪声的同时压制。对二维资料中所有道进行以上相同操作,即可得到最终去噪记录。
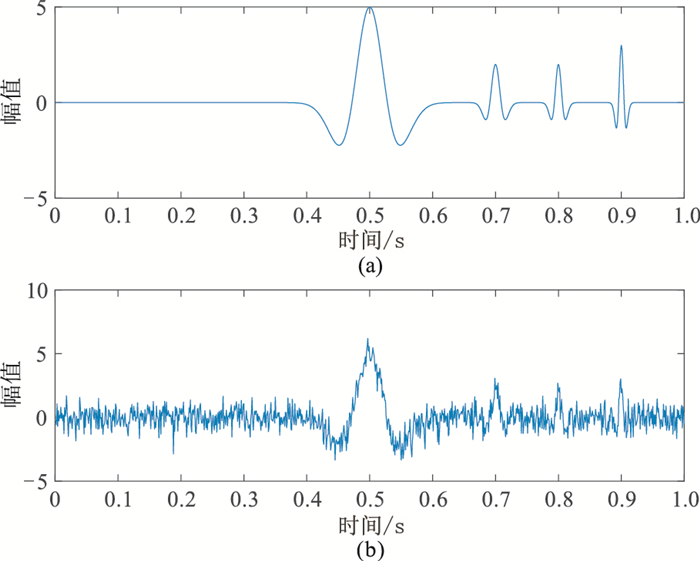
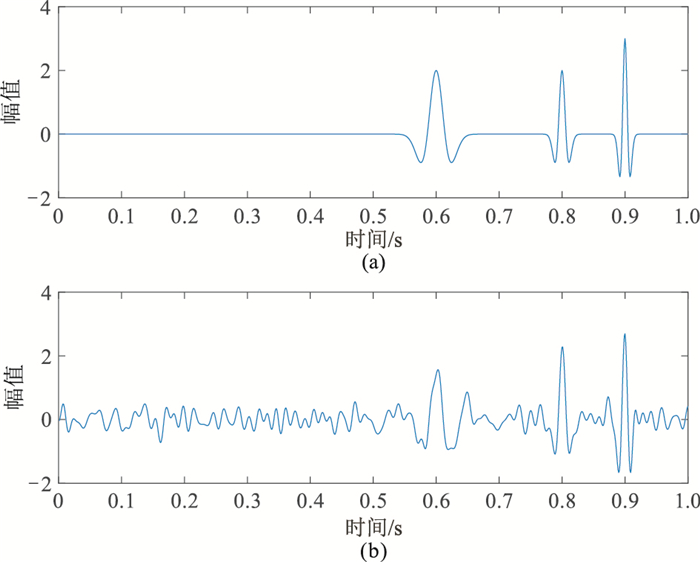
4 实验与分析 4.1 SSEC-EWT地震信号分解先对模拟地震记录进行SSEC-EWT分解,并与传统的EWT及文献[21]中的小波谱能量曲线EWT(WSEC-EWT)进行地震信号分解对比。利用Ricker子波模拟单道地震信号,设0.5s处的面波是主频为10Hz的Ricker子波,幅值为5,能量较强,0.7、0.8、0.9s处为有效波,频率分别为20、35、50Hz,幅值分别为2、2、3,其合成波及SNR=3dB的含噪合成记录如图 2所示。
|
图 2 合成单道地震波(a)及含噪地震波(b) |
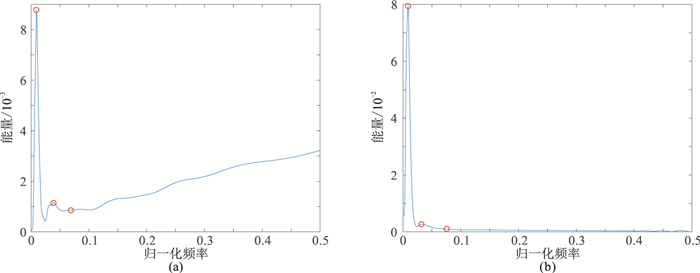
对该含噪记录(图 2b)进行S变换,根据S谱对每个频点按式(11)计算能量得到SSEC(图 3a)。可见SSEC和WSEC(图 3b)都能较好体现原信号不同频率处的能量大小。但因CWT是通过尺度参数改变小波函数形状,变换结果并不是真正的时频谱,从而导致信号特征精度受影响,而S变换反映的是信号最真实的频率构成,得到的是真实时频谱。因此,相比于WSEC,本文SSEC能更真实地体现原信号低频和高频部分各频率成分的能量分布。
|
图 3 图 2b数据的SSEC(a)和WSEC(b) |
基于SSEC极大值点及ε邻域法进行子频带划分结果如图 4a所示,可见较好地将面波频谱与邻近频率有效波频谱分割开;WSEC-EWT分割结果(图 4b)中面波与有效波频谱有少许混叠;而传统EWT划分的子带(图 4c)更不能很好地反映面波与有效波的差异,故不能直接应用于面波压制。相比WSEC,本文SSEC极大值点能更直接、准确地表示有效信号和面波的频率和能量大小,因此本文频谱分割方法能更显著体现地震信号中面波与有效波的能量、频率的不同,具有更好的频谱分割性能。

|
图 4 SSEC-EWT(a)、WSEC-EWT(b)、传统EWT(c)三种方法的频谱分割结果 |
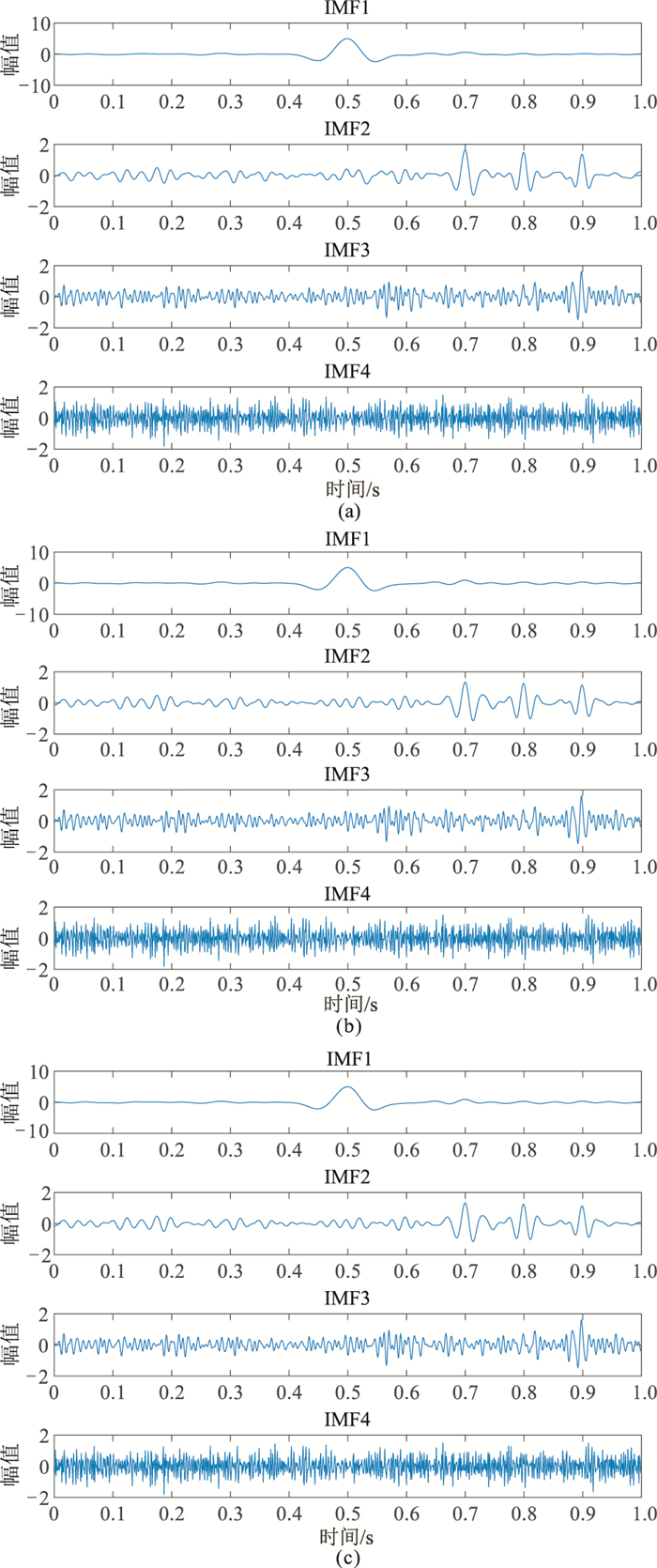
本文方法得到的IMF如图 5a所示,可见SSEC-EWT和WSEC-EWT(图 5b)都能较好地根据信号的频率和能量进行模态分解。图 5a中IMF1主要为0.5s处的面波分量(含有微量有效波),IMF2主要为0.7、0.8、0.9s处的有效波分量,而IMF4主要为高频随机噪声,有利于实现面波与随机噪声的有效分离;图 5b中IMF1主要为面波,但其中包含部分有效波;而传统EWT分解结果(图 5c)中,有效波与面波混叠不清,难以实现面波提取。因此,本文SSEC能完整描述原信号各频率点的能量特征,其曲线极大值点能更直接、更真实地表示有效信号和面波的频率和能量值,从而更好地进行频谱分割和信号分解,实现面波与有效波的精确分离。
|
图 5 SSEC-EWT(a)、WSEC-EWT(b)、传统EWT(c)三种分解方法所得的IMF |
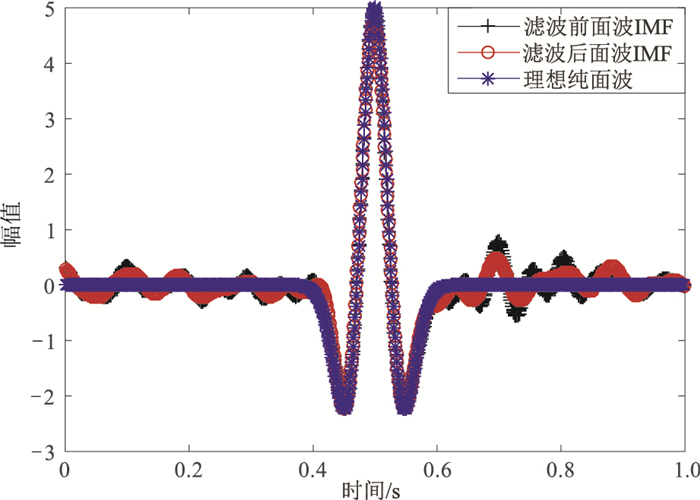
为防止面波IMF中有效波被同时压制,根据SSEC面波频率峰值,对频段做带通滤波,保留面波频率附近的有效波。图 6中滤波前的面波IMF中含有少量有效波,滤波后大部分有效波被保留,二者与理想纯面波的标准差分别为0.0225、0.0209,方差分别为0.1310、0.1154,可见能最大限度减少对有效波的损伤。从经面波和随机噪声提取后重构所得的最终去噪结果(图 7)可见,面波压制较彻底,随机噪声也得到有效抑制,去噪后的SNR=8.5dB。
|
图 6 滤波前、后的面波IMF |
|
图 7 理想合成波(a)及本文方法去噪结果(b) |
为测试SSEC-EWT的抗噪性,定义
| $ \mathrm{SNR}=10 \lg \left[\frac{\sum\limits_{i=1}^{N} \hat{s}(t)^{2}}{\sum\limits_{i=1}^{N}[\hat{s}(t)-s(t)]^{2}}\right] $ | (13) |
式中:
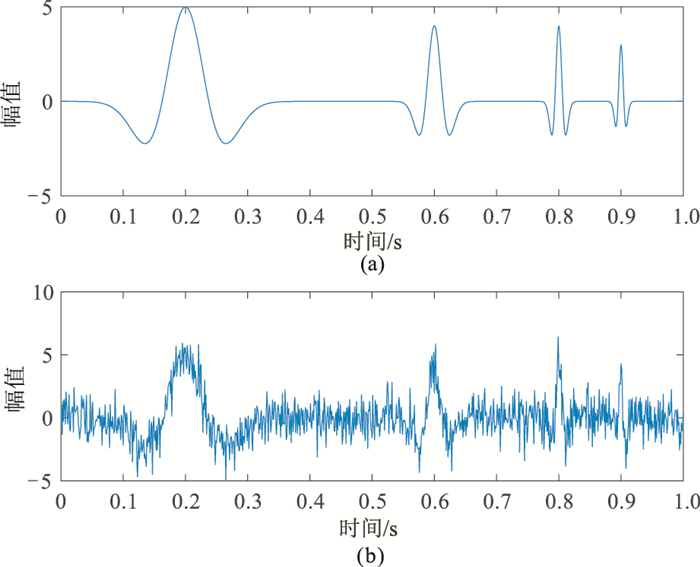
首先测试在SNR较低(图 8)情况下SSEC-EWT分解的准确性。选取有效波频率分别为16、35、48Hz,面波频率为6Hz,添加随机噪声后SNR=-8.8dB,有效波淹没于噪声中难以分辨。
|
图 8 模拟合成波(a)及其加噪信号(SNR=-8.8dB)(b) |
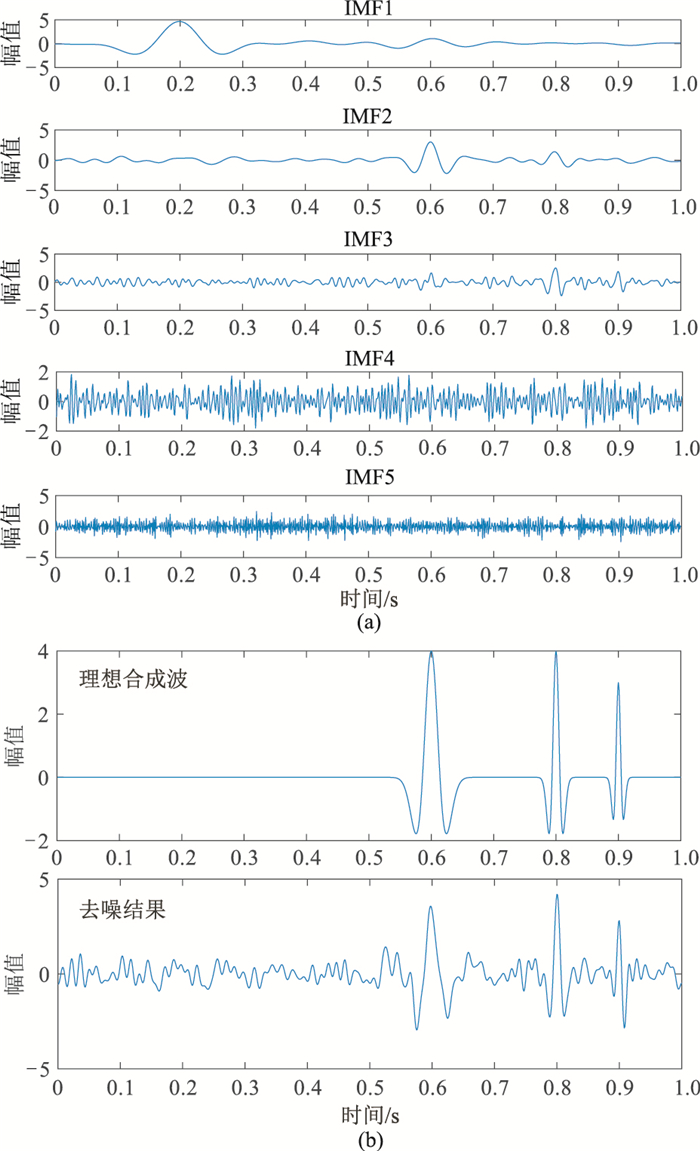
从本文SSEC-EWT分解结果(图 9a)可见,IMF1是面波IMF,其中含有很少量有效波,IMF2、IMF3主要为有效波,IMF4、IMF5主要为高频噪声。显然SSEC-EWT根据原信号的频率成分和能量大小进行信号分解,在SNR较低时仍具有较好的信号分解能力,具有较好的抗噪性。面波和随机噪声压制后所得结果(图 9b)中,SNR=9.3dB,面波压制较彻底,随机噪声也得到有效压制,且有效波得到较好保护。可见在较低SNR下,本文算法仍具有较好性能。
|
图 9 SNR较低时SSEC-EWT分解所得IMF(a)及去噪结果(b) |
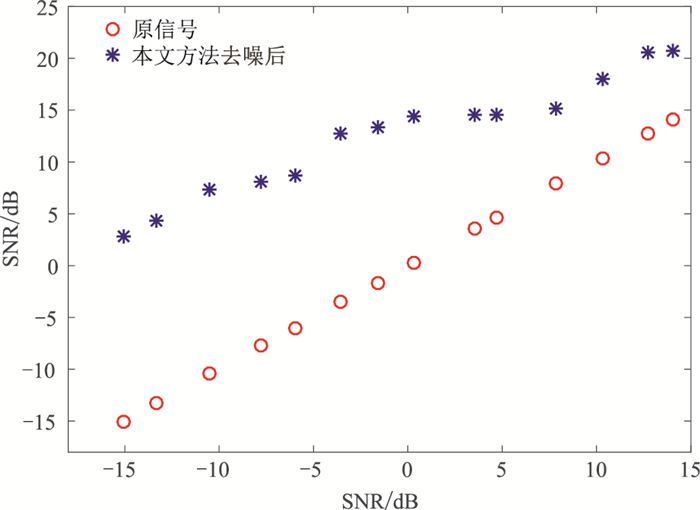
再针对不同SNR(-15~15dB)模拟信号,用本文算法进行处理(图 10)并做对比,可见经本文算法处理后,SNR明显提高(幅度高达17.9dB),尤其是在低SNR时,本文算法也能较好压制面波和随机噪声,具有较好抗噪性能。
|
图 10 相同SNR条件下本文去噪效果 |
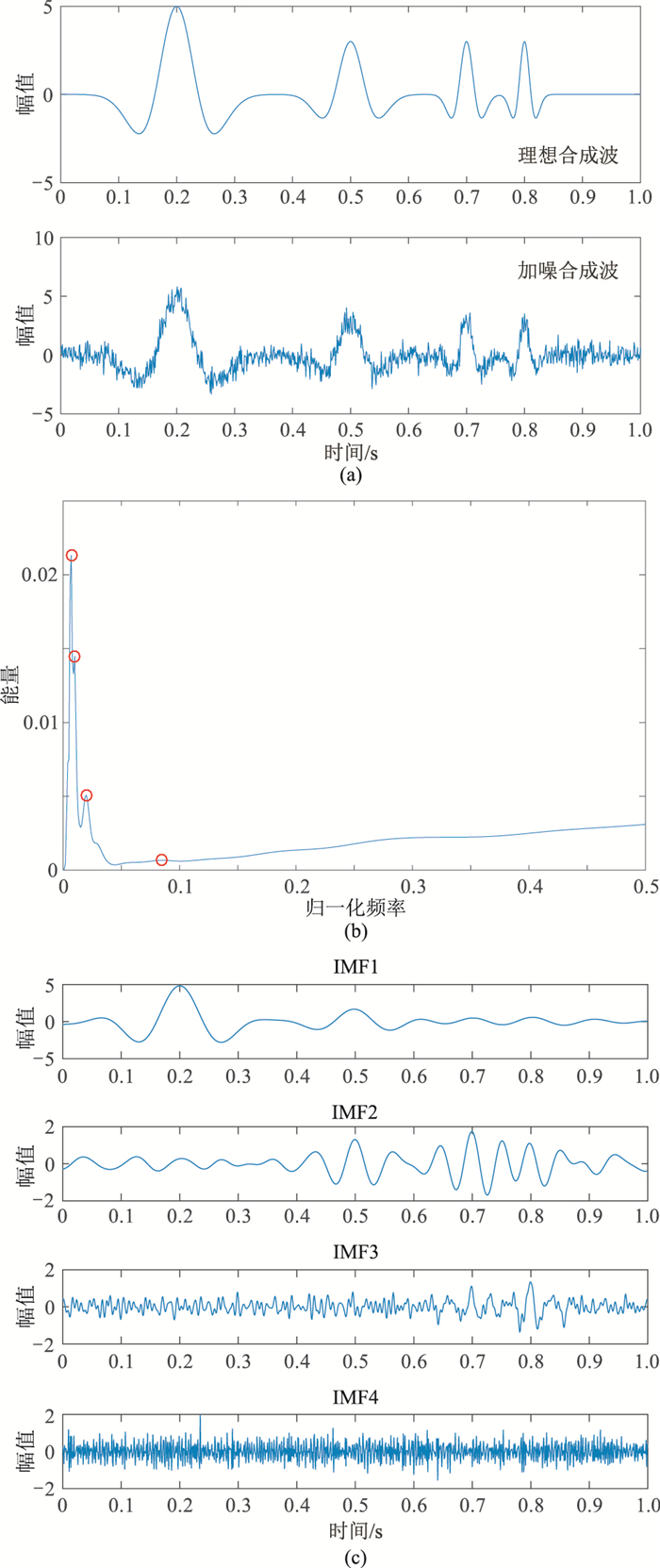
进一步测试有效波与面波的频率有重叠时,改进EWT的分解效果。图 11a中面波主频设为6Hz(图 11a上),最大峰值为5,有效波主频为7、15、20Hz,最大峰值均为3,并添加随机噪声,面波与有效波的频率几近重叠(图 11a下)。按式(11)得到的SSEC如图 11b所示,该曲线较清晰地体现了不同频率地震波成分的能量大小,有助于区分有效波与面波。从基于该SSEC曲线进行频谱分割后所得IMF(图 11c)可见,IMF1主要为面波,IMF4为随机噪声,由于面波与有效波频率非常接近,故面波IMF中尚含有少量的有效波。
|
图 11 面波和有效波几近重叠的模拟地震波(a)及其SSEC(b)与分解所得IMF(c) |
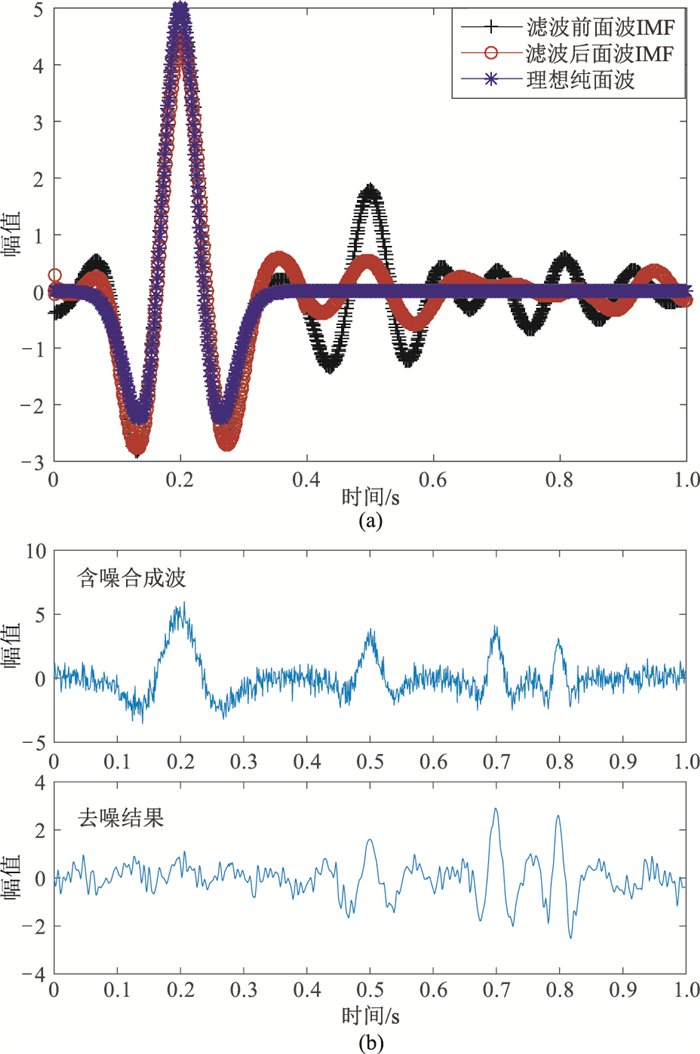
对IMF1进行带通滤波(图 12a)后,除了极少部分有效波被损伤,绝大部分有效波得到有效保护。从最终去噪结果(图 12b下)也可见,面波得到充分压制,有效波得到尽可能保护,显著提高了资料的SNR。
|
图 12 面波IMF滤波前、后对比(a)及最终去噪结果(b) |
对同时含有面波和随机噪声的二维地震道集进行噪声压制测试。根据层状速度模型和波场模拟得到图 13a所示地震道集。面波速度为200m/s,直达波速度为2000m/s,合成地震记录采样间隔为1ms,共计10道、1000个采样点,面波主频为8Hz,反射波频率为40Hz。添加信噪比为15dB的随机噪声(图 13b),面波与有效反射波叠加,导致同相轴模糊。

|
图 13 含面波(a)、且含随机噪声(b)地震道集、本文方法去噪结果(c)及去噪残差(d) |
从应用本文算法压制面波和随机噪声后结果道集(图 13c)可见,面波和随机噪声同时得到有效压制,有效地震信号更光滑、更平稳,且有效反射波与面波混叠的同相轴变得清晰。观察最终被去除的噪声残差(图 13d)可知,其上基本为面波和随机噪声,仅损失极少量的有效波,且面波压制彻底。
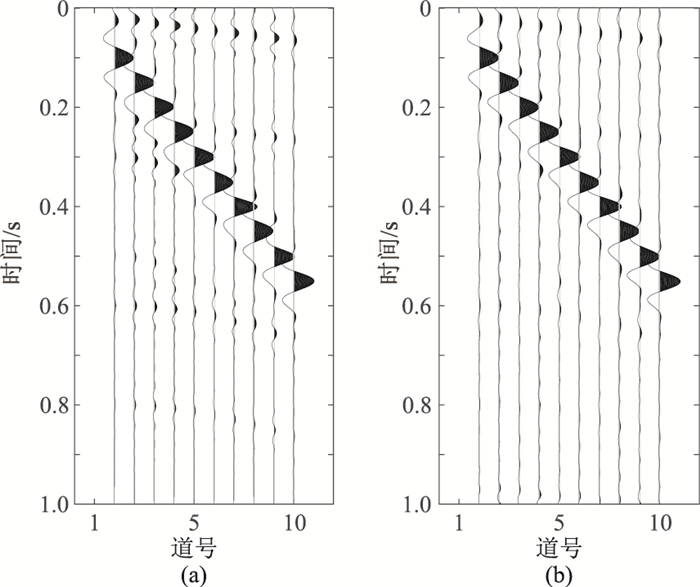
对经SSEC-EWT分解后所得面波IMF记录(图 14a)进行滤波处理,可见滤波后记录(图 14b)上大部分有效波被保留,仅极少部分有用信息被滤除。
|
图 14 本文方法滤波前(a)、后(b)的面波IMF记录 |
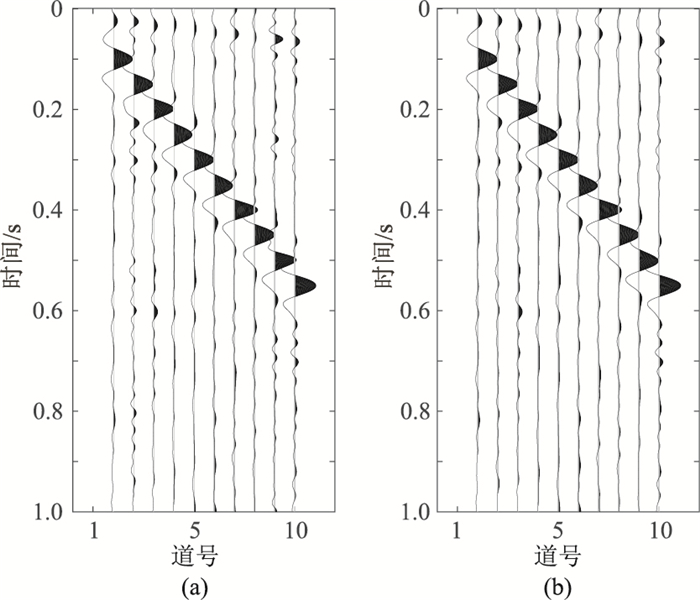
将WSEC-EWT与本文SSEC-EWT提取面波的结果(图 15)进行对比,可见二者都能较好地提取面波,但相比WSEC-EWT中面波IMF会包含“少量”有效波,而本文方法提取面波则只含有“微量”有效波,面波提取更精准。这是因为相比连续小波变换,S变换的时频分析精确度更高,而基于频率和能量进行频谱分割后能更好分解信号。
|
图 15 WSEC-EWT(a)与本文算法(b)提取面波对比 |
为对比随机噪声压制效果,对图 13b地震道集应用文献[18]算法去噪(图 16a),可见虽然随机噪声被压制,但面波未被压制;而本文算法去噪后(图 13c)不仅能去除面波,还能有效压制随机噪声,而且能最大限度保护有效波。从文献[18]算法去噪残差(图 16a)可知,部分有效波被损害;而本文算法去噪残差(图 13d)中基本不含有效波。

|
图 16 文献[18]去噪结果(a)及随机噪声残差(b) |
不同于传统EWT按傅里叶频谱极值点分割频谱,本文算法是根据频点能量进行频谱分割,故可使面波、有效波、随机噪声根据各自能量大小自适应分割,进而能同时分离面波和随机噪声。
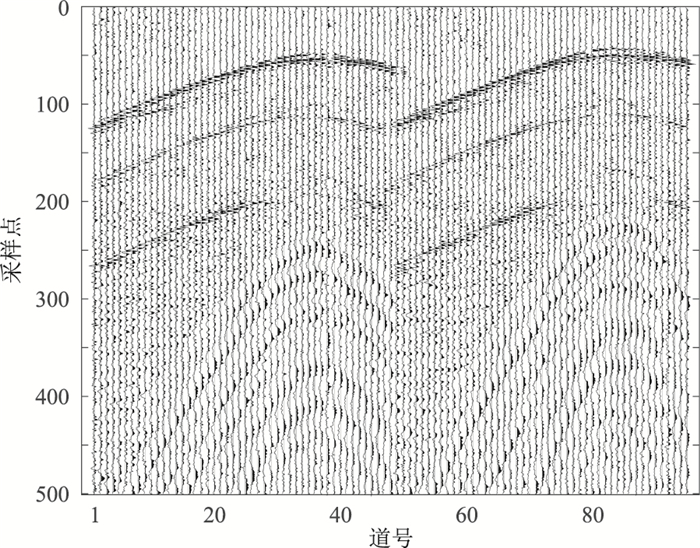
4.4 实际地震资料处理图 17所示实际地震数据共有95道,每道采样点数为500,采样间隔为2ms,图上可见典型的扫帚状面波,降低了地震资料的SNR。
|
图 17 实际地震资料 |
观察从该记录抽取第17道信号进行S变换后根据SSEC所得子频带分割(图 18a)情况,可见低频有效波和面波的频谱被分割为不同子频带。在根据频谱分割得到的IMF(图 18b)中,IMF2为面波,IMF1为低频有效波,IMF3~IMF4为有效波,IMF5为随机噪声。对该记录中每道都进行改进EWT,并根据各IMF的频率和能量确定面波IMF,再做带通滤波,分离出记录中的面波。

|
图 18 第17道地震信号的子频带分割结果(a)与所得IMF(b) |
对比本文方法与WSEC-EWT算法分离出的面波记录,可见二者都能够较好地分离出面波,但与WSEC-EWT(图 19b)相比,本文算法提取的面波记录(图 19a)中仅含更少量的有效波成分。这是因为本文方法能更好地根据地震信号中各频率成分的能量大小做信号分解,从而能更精准地提取面波记录。

|
图 19 本文(a)与WSEC-EWT(b)算法分离出的面波记录 |
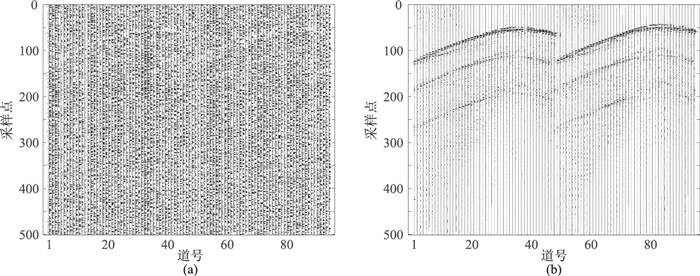
本文方法提取的随机噪声记录(图 20a)基本为杂乱无章的随机噪声,未见有效波残留。从最终去除面波和随机噪声后的结果(图 20b)可见,有效波充分保留,面波和随机噪声被分离,提高了SNR。
|
图 20 本文分离出的随机噪声(a)与最终去噪结果(b) |
实际地震资料处理结果表明,SSEC-EWT能根据地震信号的频率、能量准确地分解信号,从而实现有效波、面波、随机噪声的分离,并最大限度地保护有效波,提高资料的SNR。
5 结论(1) 基于S变换的S谱能量曲线,能根据面波、有效波和随机噪声的频率和能量进行频谱分割和自适应分解,从而实现面波和随机噪声的同步压制。
(2) 为减少面波压制过程中对低频有效波的损伤,根据SSEC中的面波频谱峰值频率进行带通滤波,从而达到有效提取面波的同时,最大限度地保留有效反射波。
(3) 仿真实验表明,SSEC能真实、完整地反映信号的能量、频率特征,完成信号分解,相比WSEC-EWT,本文SSEC-EWT能更精准提取面波。
(4) 对模拟地震道集的处理表明,本文方法对面波的压制效果优于WSEC-EWT面波压制算法,能更充分保护有效波;对随机噪声压制效果也优于文献[18],表明所提算法的良好性能。
(5) 实际地震资料处理结果表明,该算法不仅能有效抑制高频随机噪声,而且能准确有效地分离面波,提高地震资料的信噪比,是一种能同时去除面波和随机噪声的可靠、实用方法。
| [1] |
Ma J, Li Q. Ground roll suppression with joint S transform and TT transform[J]. Procedia Earth & Planetary Science, 2011, 33(3): 246-252. |
| [2] |
徐阳, 罗明璋, 王智, 等. 广义S变换与二维离散小波变换联合压制面波[J]. 石油物探, 2018, 57(3): 395-403. XU Yang, LUO Mingzhang, WANG Zhi, et al. Surface wave suppression using generalized S-transform and 2D discrete wavelet transform[J]. Geophysical Prospecting for Petroleum, 2018, 57(3): 395-403. DOI:10.3969/j.issn.1000-1441.2018.03.009 |
| [3] |
Li J H, Ma J Q. Seismic ground roll suppression based on the generalized S transform[J]. International Journal of Digital Content Technology and Its Applications, 2013, 7(7): 554-560. DOI:10.4156/jdcta.vol7.issue7.65 |
| [4] |
董烈乾, 李振春, 王德营, 等. 第二代Curvelet变换压制面波方法[J]. 石油地球物理勘探, 2011, 46(6): 897-904. DONG Lieqian, LI Zhenchun, WANG Deying, et al. Ground-roll suppression based on second generation Curvelet transform[J]. Oil Geophysical Prospecting, 2011, 46(6): 897-904. |
| [5] |
李继伟, 刘晓兵, 周俊骅, 等. 基于能量比的Curvelet阈值迭代面波压制[J]. 石油地球物理勘探, 2019, 54(5): 997-1004. LI Jiwei, LIU Xiaobing, ZHOU Junhua, et al. A curvelet threshold iteration method based on energy ratio for surface-wave suppression[J]. Oil Geophysical Prospecting, 2019, 54(5): 997-1004. |
| [6] |
Liu Z, Chen Y K, Ma J W. Ground roll attenuation by synchrosqueezed curvelet transform[J]. Journal of Applied Geophysics, 2018, 151: 246-262. DOI:10.1016/j.jappgeo.2018.02.016 |
| [7] |
曾祥堃, 乔宝平, 刘依谋, 等. 基于小波变换的自适应面波压制方法[J]. 北京大学学报(自然科学版), 2015, 51(5): 837-842. ZENG Xiangkun, QIAO Baoping, LIU Yimou, et al. Adaptive ground roll attenuation based on the wavelet transform[J]. Acta Scientiarum Naturalium Universitatis Pekinensis (Natural Science Edition), 2015, 51(5): 837-842. |
| [8] |
董烈乾, 李振春, 杨少春, 等. 基于经验模态分解的f-x域面波压制方法[J]. 石油地球物理勘探, 2013, 48(1): 42-48. DONG Lieqian, LI Zhenchun, YANG Shaochun, et al. Ground roll suppression in f-x domain based on empirical mode decomposition[J]. Oil Geophysical Prospecting, 2013, 48(1): 42-48. |
| [9] |
Chen W, Xie J, Zu S, et al. Multiple-reflection noise attenuation using adaptive randomized-order empirical mode decomposition[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 1(14): 18-22. |
| [10] |
Golestani A, Kolbadi S S, Heshmati A A. Localization and de-noising seismic signals on SASW measurement by wavelet transform[J]. Journal of Applied Geophysics, 2013, 98: 124-133. DOI:10.1016/j.jappgeo.2013.08.010 |
| [11] |
李海山, 陈德武, 吴杰, 等. 叠前随机噪声深度残差网络压制方法[J]. 石油地球物理勘探, 2020, 55(3): 493-503. LI Haishan, CHEN Dewu, WU Jie, et al. Pre-stack random noise suppression with deep residual network[J]. Oil Geophysical Prospecting, 2020, 55(3): 493-503. |
| [12] |
Gilles J. Empirical wavelet transform[J]. IEEE Transactions on Signal Processing, 2013, 61(16): 3999-4010. DOI:10.1109/TSP.2013.2265222 |
| [13] |
王秋生, 陈璐, 袁海文, 等. 基于经验小波变换的电晕电流降噪方法[J]. 电网技术, 2017, 41(2): 670-676. WANG Qiusheng, CHEN Lu, YUAN Haiwen, et al. Corona current de-noising method based on empirical wavelet transform[J]. Power System Technology, 2017, 41(2): 670-676. |
| [14] |
吕跃刚, 何洋洋. EWT和ICA联合降噪在轴承故障诊断中的应用[J]. 振动与冲击, 2019, 38(16): 42-48. LYU Yuegang, HE Yangyang. Application of an EWT-ICA combined method in fault diagnosis of rolling bearings[J]. Journal of Vibration and Shock, 2019, 38(16): 42-48. |
| [15] |
Chegini S N, Bagheri A, Najafi F. Application of a new EWT-based de-noising technique in bearing fault diagnosis[J]. Measurement, 2019, 144(5): 275-297. |
| [16] |
Liu W, Cao Y. Seismic Time-Frequency Analysis via Empirical Wavelet Transform[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 1(13): 28-32. |
| [17] |
Hui C, Kang J, Chen Y, et al. An improved time-frequency analysis method for hydrocarbon detection based on EWT and SET[J]. Energies, 2017, 10(8): 1090. DOI:10.3390/en10081090 |
| [18] |
覃发兵, 徐振旺, 啜晓宇, 等. 基于经验小波变换的地震资料噪声压制方法[J]. 中国石油勘探, 2018, 23(5): 100-110. QIN Fabing, XU Zhenwang, CHUAN Xiaoyu, et al. Seismic noise suppression based on empirical wavelet transformation[J]. China Petroleum Exploration, 2018, 23(5): 100-110. DOI:10.3969/j.issn.1672-7703.2018.05.013 |
| [19] |
Chen W, Song H. Automatic noise attenuation based on clustering and empirical wavelet transform[J]. Journal of Applied Geophysics, 2018, 159: 649-665. DOI:10.1016/j.jappgeo.2018.09.025 |
| [20] |
Liu N, Li Z, Sun F, et al. The improved empirical wavelet transform and applications to seismic reflection data[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(6): 1103-1103. DOI:10.1109/LGRS.2020.2991604 |
| [21] |
孟娟, 韩智明, 高琴, 等. 基于小波谱能量曲线EWT的面波压制算法[J]. 地球物理学进展, 2021, 36(4): 1581-1589. MENG Juan, HAN Zhiming, GAO Qin, et al. An seismic surface wave suppression algorithm based on wavelet spectrum energy curve EWT[J]. Progress in Geophysics, 2021, 36(4): 1581-1589. |
| [22] |
Liu Z D, Lu Q T, Dong S X, et al. Research on velocity and acceleration geophones and their acquired information[J]. Applied Geophysics, 2012, 9(2): 149-158. DOI:10.1007/s11770-012-0324-6 |



 孟娟, 河北省三河市燕郊开发区学院街防灾科技学院, 065201。Email:
孟娟, 河北省三河市燕郊开发区学院街防灾科技学院, 065201。Email: 