② 中国石油大学(北京)地球物理学院, 北京 102249;
③ 中国石油大港油田公司, 天津 300280
② Institute of Geophysics, China University of Petroleum, Beijing 102249, China;
③ Dagang Oilfield Company, PetroChina, Tianjin 300280, China
反射系数反演是提高地震资料分辨率的重要手段之一。传统反演方法大多基于稳态褶积模型,即假设地震子波已知,且其振幅谱和相位谱在地震波传播过程中是时不变的。由于实际地层介质的非完全弹性,地震子波在传播过程中具有动态衰减性且是未知的。因此,根据地震数据估计反射系数不仅是非稳态的,更是一个全盲的过程[1-2]。
针对这一问题,人们提出了多种方法估计时变子波[3],进而实现从非稳态地震数据中反演反射系数。冯晅等[4]提出了分时窗提取子波并将其用于合成地震记录。Van der Baan[5]利用旋转相位和峰值最大化准则成功提取了非最小相位时变子波。
上述方法大多采用分段处理,并假设每一段内地震子波是时不变的,进而从每一段内提取一个时不变子波[6-7]。这类方法的精度易受时窗长度选择的影响,且所提取的具有平均意义的子波并不能充分反映子波的时变特征[8-10]。近年来,为了消除时窗长度对提取子波的影响,戴永寿等[11]和王蓉蓉等[12]相继提出了基于时频谱模拟估计时变混合相位子波的方法。在此基础上,Zhang等[13]利用局部谱提取技术求取时变子波并应用于地震反演中。李婧等[14]和姚振岸等[15]分别利用广义S变换和基追踪谱分解改进了该方法,实现从非稳态地震数据中反演反射系数。这类方法的核心理论是通过对非稳态地震数据进行时频分析处理,利用每一采样点的频谱提取时变子波,这是现今逐点提取子波的常用有效方法。
时频分析技术是刻画非稳态信号频谱变化特征的重要工具[16],它通过时间频率的联合函数准确描述信号在不同时间和频率的能量密度和强度。短时傅里叶变换是最常用的时频分析方法之一[17],通过对时域信号进行加窗处理得到时频谱图。但由于受海森堡不确定原理的约束[18],其分辨率精度不能达到非稳态地震信号的要求。为了解决短时傅里叶变换窗口形状固定不变的问题,Sinha等[19]提出连续小波变换方法。S变换巧妙地将短时傅里叶变换与小波变换相结合,兼具两者的优势,且其窗口宽度直接与频率相联系[20]。为了提高S变换的适用性和准确性,Moukadem等[21]通过增加控制高斯窗函数的参数而提出了广义S变换,使其在高频段具有较高时间分辨率和相对低的频率分辨率,能更好地识别信号的高频信息,此性质符合非稳态地震数据的动态衰减特性。因此,利用广义S变换对地震记录进行时频分析,能获得具有更高时频分辨率和更好聚焦性的时频分析结果[22-23],从而准确刻画地震数据频谱随时间轴的变化,实现逐点提取时变子波。
考虑到地震数据的非稳态特征,本文提出一种新的时变子波提取方法。该方法利用广义S变换的优势,将非稳态地震数据变换到时频域,并基于自相关理论实现子波的逐点提取,克服了分段提取时变子波方法的局限性。同时,考虑到地震数据处理过程是全盲的,即子波通常是未知的,本文利用每一时刻提取的子波重构时变子波矩阵,而不是整道地震记录仅提取一个时不变子波矩阵,并将其应用于反演模型中,最终实现非稳态地震记录反射系数的盲反演。此外,该方法是由数据本身驱动的,对实际地震资料具有更强自适应性,有利于更精细地刻画地层结构,提高地震资料反映薄层的能力。
1 方法原理 1.1 基于广义S变换的时变子波提取根据传统褶积模型[24],地震记录s(t)可表示为
| $ s(t)=w(t) * r(t)+n(t) $ | (1) |
式中:w(t)为地震子波;r(t)为反射系数序列;n(t)为噪声;t为时间;“*”为褶积算符。
基于反射系数白噪的假设条件,可认为反射系数的自相关函数为脉冲函数,即地震子波频谱可从地震记录的频谱中获取。因此,对式(1)等号两边同时取自相关,建立地震记录自相关与子波自相关的关系式
| $ \left.\begin{array}{r} s \otimes s=r \otimes r * w \otimes w \\ r \otimes r=\delta \end{array}\right\} \Rightarrow s \otimes s=w \otimes w $ | (2) |
式中“⊗”代表自相关算符。
根据Wiener-Khintchine定理[13, 24],自相关函数的傅里叶变换等于信号的能量谱,则式(2)变形为
| $ F(s \otimes s)=F(w \otimes w) \Rightarrow F(s)^{2}=F(w)^{2} $ | (3) |
式中F(·)表示傅里叶变换。
根据式(3),基于稳态假设条件的子波估计方法通过对每一道地震记录的能量谱取算术平方根后,再利用逆傅里叶变换得到一个时不变地震子波。由于时不变子波的假设条件忽略了地震资料的非稳态特征,将其用于地震资料反演时限制了反演结果的精度。而事实上,地震数据的频谱是随时间变化的,为了更好地表征非稳态地震数据的时变特点,利用广义S变换对地震记录进行分析,准确定位每一时刻的频率信息,得到每一点的频谱,再根据式(3)提取每一时刻的子波,最后沿地震记录的时间轴得到每一采样点的子波,而不是一整条地震道仅提取一个子波。
信号s(t)的传统S变换数学表达式为
| $ \mathrm{ST}(t, f)=\int s(\tau) w(\tau-t, f) \mathrm{e}^{-\mathrm{i} 2 \pi f_{\tau}} \mathrm{d} \tau $ | (4) |
式中:t和f分别是时间和频率;w(τ-t,f)是高斯窗函数,控制了窗口的位置。
传统S变换虽然实现了多尺度分辨率表达,但仍受窗口本身形状的影响。由于基本窗函数的固定形态限制了S变换的使用范围,Moukadem等[21]提出引入控制参数重新定义高斯窗函数变化,则改进的S变换的数学表达式为
| $ \mathrm{ST}^{*}(t, f)= \\ \int s(\tau) \frac{|f|^{r}}{\left(m f^{p}+k\right) \sqrt{2 \pi}}\text{e} ^\frac{-(\tau-t)^{2} f^{2 r}}{2\left(m f^{p}+k\right)^{2}}\text{e}^{-\mathrm{i} 2 \pi f \tau} \mathrm{d} \tau $ | (5) |
式中m、p、k、r均为控制参数,由信号本身决定最佳参数组合。
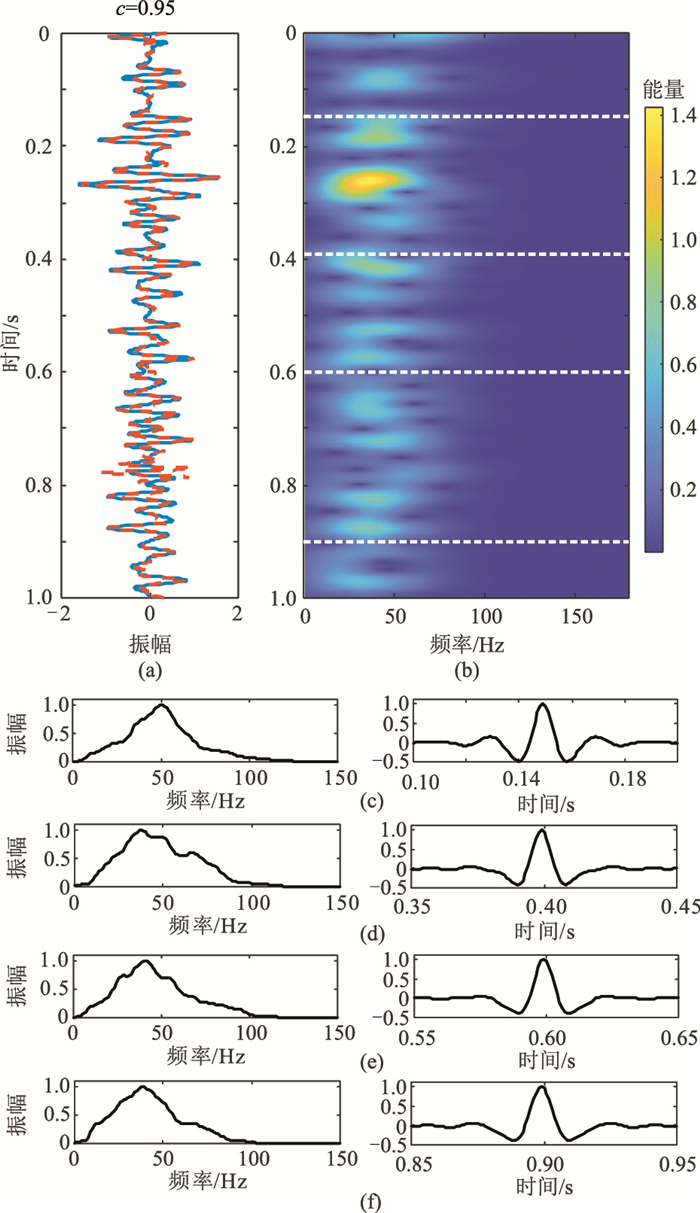
广义S变换根据地震数据自身特点通过调节参数控制时窗,适应频率的变化,使得时频分析结果具有较好的聚焦性,有利于准确提取子波局部谱。图 1a和图 1b分别为一道合成地震记录及广义S变化后的时频分析结果,可明显地看出频谱随时间变化,再根据每一时刻的子波局部谱,利用逆傅里叶变换得到其对应采样点的时变子波。
|
图 1 基于广义S变换提取时变子波 (a)合成地震记录;(b)广义S变换结果;(c)~(f)分别对应150、400、600、900ms处提取的局部谱(左)和时变子波(右) |
为简化反演模型,将式(1)中的褶积模型改写为子波矩阵与反射系数向量乘积的形式
| $ \boldsymbol{s}=\boldsymbol{W} \boldsymbol{r}+\boldsymbol{n} $ | (6) |
式中:s、r和n分别代表地震记录、反射系数和噪声的向量;W是由地震子波w(t)沿对角线平移组成的托普利兹矩阵,因此是时不变的。
该模型是基于稳态子波的假设条件,即认为子波在传播过程中不会随传播距离的增加而变化。实际上,由于地层存在吸收衰减效应,地震子波会随传播时间不断变化,因此,式(6)基于时不变子波矩阵的模型已不能准确描述实际地震资料。
为了表征子波在地层传播的非稳态物理过程,将上述方法提取的时变子波沿对角线元素排列,进而得到重构的子波矩阵W*。值得注意的是,W*为时变子波矩阵,其中每一列代表通过该列传播时间的子波,逐列取代W中的时不变子波。虽然该矩阵不再是托普利兹形式,但它具有代表地震子波非稳态特性的物理意义,允许子波随时间而变化。
根据地层构造特点,假设反射系数序列具有稀疏性,基于稀疏约束策略利用式(6)反演反射系数存在不确定性和多解性[25]。为了得到稀疏的反射系数,在目标函数中加入L1范数约束目标函数[26],考虑噪声通常是随机的且大多是非稀疏的,因此对噪声向量施加L2范数约束,最终反演目标函数为
| $ \min \left\|\boldsymbol{s}-\boldsymbol{W}^{*} \boldsymbol{r}\right\|_{2}^{2}+\lambda\|\boldsymbol{r}\|_{1} $ | (7) |
式中:W*是W的转置;λ为正则化参数。
针对式(7)中稀疏正则化目标函数的求解问题,近年来研究人员提出了许多实用的算法。本文选取固定点迭代(FPC_AS)算法进行求解[27],其优势在于运算效率和稳定性方面都有明显提高,并且针对大规模数据反问题也具有良好表现。
2 模型测试通过一组非稳态模型测试,验证本文所述方法的有效性和优越性。分别在无噪声和含噪声条件下与传统基于时不变子波的反演方法进行对比,同时讨论式(7)中参数的选择对结果的影响。
2.1 时变子波估计首先,考虑地层吸收衰减因素的影响,建立无噪声条件下非稳态地震记录模型(图 1a实线)。子波初始主频为40Hz,且随着时间增加主频线性减小,传播1s后子波主频为30Hz。从利用广义S变换得到的时频分析结果(图 1b)可见,地震记录的频谱是随传播时间变化的,体现了非稳态地震数据的时变特性。因此,该时频分析结果有利于提取每一时刻地震记录的频谱,从而实现逐点子波的提取。
图 1c左~图 1f左分别显示沿图 1b中四条白色虚线在150、400、600和900ms处提取的地震记录频谱,再利用逆傅里叶变换得到其对应的时域子波(图 1c右~图 1f右的波形)。可明显看出,随着传播时间增加,提取的子波主频逐渐减小,此现象反映了子波在传播过程中的动态衰减特性。沿着整道地震记录做相同处理,即可得到每一时刻的频谱及其时域子波。图 1a中虚线为利用提取的时变子波与已知反射系数重构的地震记录结果,可见重构地震记录与理论地震记录模型十分吻合,表明利用本文方法提取时变子波的准确性。为了更全面评价该方法的准确性,还计算了重构地震记录与理论地震记录模型的相关系数c(c=0.95)。
为了进一步说明本文方法的优越性,利用S变换对该模型进行处理,得到图 2b所示的时频分析结果。对比图 1b与图 2b时频谱图可知,基于广义S变换的时频分析结果具有更好的能量聚焦性,这将有利于时变子波的精确提取。同样,图 2c~图 2f分别显示沿图 2b中四条白色虚线在150、400、600和900ms处提取的地震记录频谱及其对应的时域子波。对比图 1与图 2中的波形图,可看出时频分析的精确度会直接影响提取时变子波的效果。图 2a中虚线为利用基于S变换提取的时变子波与已知反射系数重构的地震记录结果,可见虽然基于广义S变换方法的重构地震记录与理论地震记录模型基本吻合,但在振幅能量的恢复上有一定误差,其重构地震记录与理论模型的相关系数为0.88。因此,通过定性和定量的比较分析,本文所提方法都具有更好的可行性和更高精确性。

|
图 2 基于S变换提取时变子波 (a)合成地震记录;(b)S变换的结果;(c)~(f)分别对应150、400、600、900ms处提取的局部谱(左)和时变子波(右) |
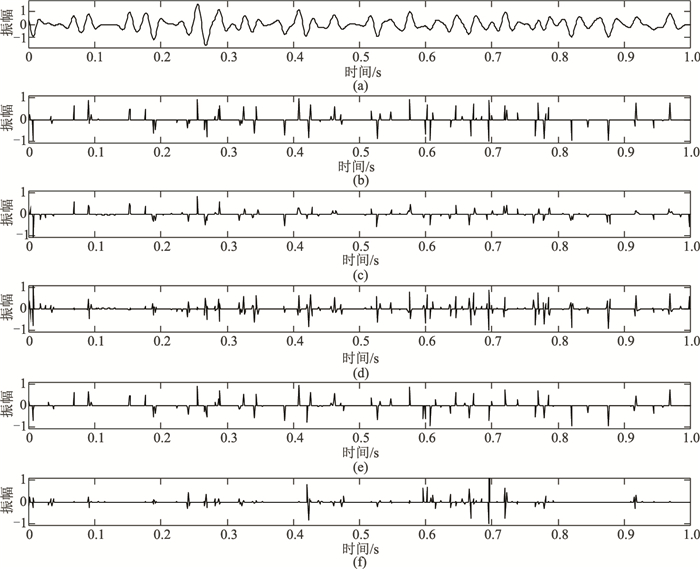
基于上述模型,分别在无噪声和含噪声两种情况下,对比测试本文方法与传统基于时不变子波假设条件的反射系数反演方法。通过不含噪声非稳态地震记录(图 3a)和理论反射系数模型(图 3b),得到基于时不变子波反演反射系数结果(图 3c)及其误差(图 3d)、本文方法反演反射系数结果(图 3e)及其误差(图 3f)。可见基于时变子波的反演结果与理论反射系数吻合程度明显优于基于时不变子波的反演结果,通过误差对比分析,利用本文方法得到的结果不仅改善了反射系数位置错位的情况,并且最大程度地恢复了反射系数的相对振幅,因此其计算结果误差更小,所得反射系数更精确。
|
图 3 无噪声时反射系数反演结果 (a)无噪合成记录;(b)理论反射系数;(c)、(d)基于时不变子波的反演结果及误差;(e)、(f)本文方法的反演结果及误差 |
在上述非稳态地震记录模型中加入信噪比为15dB的随机噪声,分别基于时变子波和时不变子波进行反射系数反演实验(图 4)。利用含噪声非稳态地震记录(图 4a)和理论反射系数模型(图 4b),得到基于时不变子波反演反射系数的结果(图 4c)及其误差(图 4d)、本文方法反演反射系数的结果(图 4e)及其误差(图 4f)。对比图 3可见,由于噪声的加入,会给反演结果带来一定误差,但基于时变子波反演得到的反射系数与理论模型仍具有较好一致性。分析、对比图 4c与图 4e,可知含噪情况下基于时不变子波的反演结果较差,图 4c中存在许多小脉冲,这些假反射系数会直接降低反演结果的分辨率,该现象也说明精确时变子波的提取对反演结果的重要性,同时展示了本文方法的有效性和稳定性。

|
图 4 含噪声时反射系数反演结果(信噪比为15dB) (a)含噪合成记录;(b)理论反射系数;(c)、(d)基于时不变子波的反演结果及误差;(e)、(f)本文方法的反演结果及误差 |
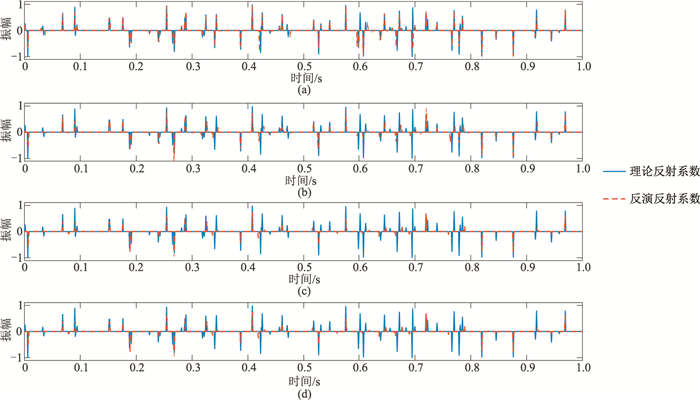
根据式(7)进行反演时,需合理设置正则化参数λ,以有利于反演结果。针对上述模型在无噪声情况下进行测试,所得结果如图 5所示。其中,实线为理论的反射系数模型,虚线为λ分别取0.001λmax、0.01λmax、0.05λmax和0.1λmax时的反演结果(λmax=‖2W*Ts‖∞)。当λ取值在0.001λmax~0.005λmax时,其结果大致相同;当λ取值较大时,反射系数的恢复效果较差,其振幅值不能被很好地保护,导致较大反演误差,降低反演结果的分辨率。
|
图 5 λ分别取0.001λmax、0.01λmax、0.05λmax和0.1λmax时的反演结果 |
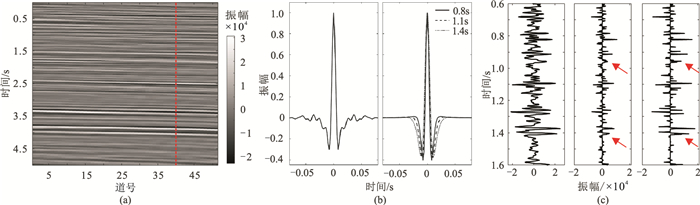
选取图 6a所示实际地震资料,道数为50,截取时窗范围是0.6~1.6s,采样间隔为2ms。图 6b左侧为提取的时不变子波,右侧为基于广义S变换分别在0.8、1.1和1.4s三个时刻提取的时变子波。由图可见,因地震记录高频成分吸收衰减得更快,故地震子波主频逐渐降低,波形随传播时间增大而变宽,该现象符合子波在地层传播时的动态衰减特征,也反映了实际地震资料的非稳态特性。利用传统时不变子波进行反演时,因子波欠精确,使得反演结果有较大误差,降低了反演剖面的分辨率。
|
图 6 实际地震资料处理效果 (a)地震剖面;(b)时不变子波(左)与时变子波(右);(c)单道地震记录(左)、时不变子波(中)与时变子波(右)反褶积结果 |
图 6c的左侧为第40道(图 6a红色虚线)地震记录,中间和右侧分别为基于图 6b中时不变子波与时变子波的反褶积结果,可见基于时不变子波的反褶积结果中存在较强噪声,并且不能较好地保护反射系数的相对振幅值(箭头所指)。
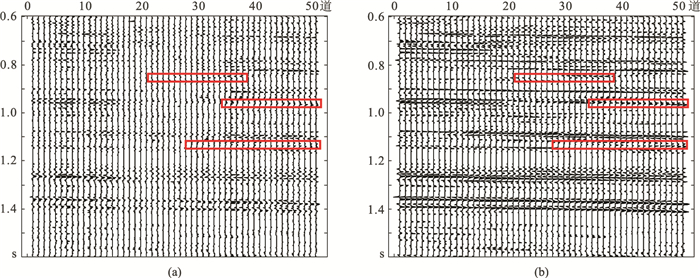
对比基于以上两种方法得到的完整反射系数剖面(图 7),可见基于时变子波所得剖面(图 7a)能更清晰地反映同相轴形态;相较于时不变子波的反演结果(图 7b),本文方法反褶积结果横向更稳定,分辨率也得到明显提高(表现为同相轴增加,矩形框所示),可更好地恢复地下地层特征。
|
图 7 基于时不变子波(a)和时变子波(b)反演的反射系数剖面 |
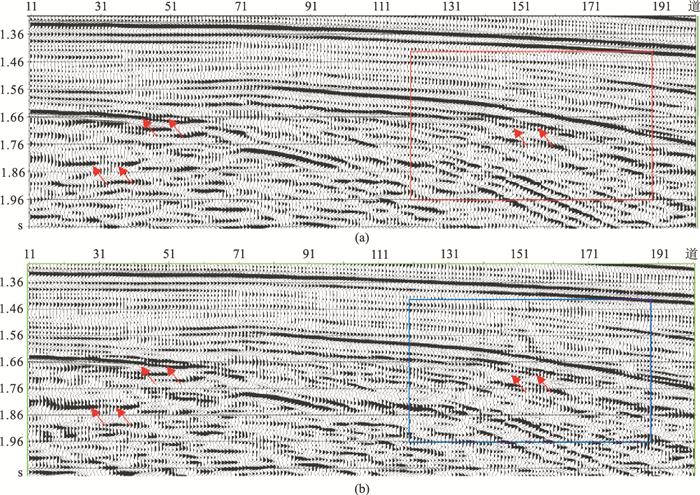
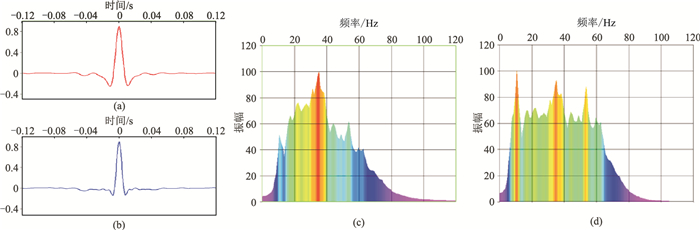
考察分别利用时不变子波(图 8a)和时变子波(图 8b)对二维地震资料处理实例、从图 8中矩形框提取的子波(图 9),发现用本文方法提取的子波旁瓣能量小,频带更宽,高频部分能量抬升,具有更高分辨率,使处理后剖面构造更清晰(箭头所指),进一步提高地震资料表征薄层真实细节的能力。
|
图 8 基于时不变子波(a)与时变子波(b)反演的剖面实例 |
|
图 9 时不变子波(a)及其频谱(c)与时变子波(b)及其频谱(d)的对比 |
将基于广义S变换提取的时变子波用于子波矩阵重构,通过求解L1范数稀疏约束问题,实现从非稳态地震数据中盲反演反射系数,数值模拟和实际资料处理结果均表明:
(1) 基于广义S变换的时频分析结果可更好地表征地震数据的局部属性,有利于更精细地分析地层结构。
(2) 由于本文方法数据驱动的自适应性与实现的便捷性,逐点提取的时变子波精度较高,符合地震数据的时变特征,且具有一定的容噪能力,为后续反射系数反演提供了保证。
(3) 相较于采用时不变子波的常规反演方法,基于广义S变换的时变子波的盲反射系数反演方法可以获得更高精度、更高分辨率的反射系数剖面,提高地震资料表征薄层的能力。
本文方法基于一维褶积模型,理论上旨在处理叠后地震数据,目前需逐道进行处理,如何充分考虑地震数据的横向连续性是下一步的研究方向。
| [1] |
Chai X T, Wang S X, Yuan S Y, et al. Sparse reflectivity inversion for nonstationary seismic data[J]. Geophysics, 2014, 79(3): V93-V105. DOI:10.1190/geo2013-0313.1 |
| [2] |
Hojjat H L, Gholami A. Nonstationary blind deconvolution of seismic records[J]. Geophysics, 2019, 84(1): V1-V9. DOI:10.1190/geo2018-0225.1 |
| [3] |
戴永寿, 张彧豪, 张鹏, 等. 时变地震子波提取研究方法综述[J]. 石油物探, 2020, 59(2): 169-176. DAI Yongshou, ZHANG Yuhao, ZHANG Peng, et al. A review on time-varying seismic wavelet extraction[J]. Geophysical Prospecting for Petroleum, 2020, 59(2): 169-176. DOI:10.3969/j.issn.1000-1441.2020.02.002 |
| [4] |
冯晅, 刘财, 杨宝俊, 等. 分时窗提取地震子波及在合成地震记录中的应用[J]. 地球物理学进展, 2002, 17(1): 71-77. FENG Xuan, LIU Cai, YANG Baojun, et al. The extractive method of seismic wavelet in different time window and the application in synthetic seismogram[J]. Progress in Geophysics, 2002, 17(1): 71-77. DOI:10.3969/j.issn.1004-2903.2002.01.008 |
| [5] |
Van der Baan M. Time-varying wavelet estimation and deconvolution by kurtosis maximization[J]. Geophy-sics, 2008, 73(2): V11-V18. |
| [6] |
高静怀, 汪玲玲, 赵伟. 基于反射地震记录变子波模型提高地震记录分辨率[J]. 地球物理学报, 2009, 52(5): 1289-1300. GAO Jinghuai, WANG Lingling, ZHAO Wei. Enhancing resolution of seismic traces based on the changing wavelet model of the seismogram[J]. Chinese Journal of Geophysics, 2009, 52(5): 1289-1300. DOI:10.3969/j.issn.0001-5733.2009.05.018 |
| [7] |
Wang L L, Gao J H, Zhao W, et al. Enhancing resolution of nonstationary seismic data by molecular-Gabor transform[J]. Geophysics, 2013, 78(1): V31-V41. DOI:10.1190/geo2011-0450.1 |
| [8] |
孔德辉, 彭真明. 利用改进的在线字典学习估计时变子波[J]. 石油地球物理勘探, 2016, 51(5): 901-908. KONG Dehui, PENG Zhenming. Time-varying wavelet estimation based on improved online dictionary learning[J]. Oil Geophysical Prospecting, 2016, 51(5): 901-908. |
| [9] |
李福元, 韦成龙, 邓桂林, 等. 从海洋地震资料直达波提取震源子波[J]. 石油地球物理勘探, 2019, 54(3): 512-521. LI Fuyuan, WEI Chenglong, DENG Guilin, et al. Source signature extraction from marine seismic direct waves[J]. Oil Geophysical Prospecting, 2019, 54(3): 512-521. |
| [10] |
赵宝银, 陈思远, 陶钰, 等. 应用宽带Ricker子波的期望目标频谱整形[J]. 石油地球物理勘探, 2020, 55(3): 541-547. ZHAO Baoyin, CHEN Siyuan, TAO Yu, et al. Spectrum shaping of desired targets based on broadband Ricker wavelets[J]. Oil Geophysical Prospecting, 2020, 55(3): 541-547. |
| [11] |
戴永寿, 张漫漫, 张亚南, 等. 基于时频谱模拟的时变混合相位子波提取[J]. 石油地球物理勘探, 2015, 50(5): 830-838. DAI Yongshou, ZHANG Manman, ZHANG Yanan, et al. Time-variant mixed-phase seismic wavelet estimation based on spectral modeling in the time-frequency domain[J]. Oil Geophysical Prospecting, 2015, 50(5): 830-838. |
| [12] |
王蓉蓉, 戴永寿, 李闯, 等. 时频分析与自适应分段相结合的时变子波提取方法[J]. 石油地球物理勘探, 2016, 51(5): 850-862. WANG Rongrong, DAI Yongshou, LI Chuang, et al. Time-varying wavelet extraction based on time-frequency analysis and adaptive segmentation[J]. Oil Geophysical Prospecting, 2016, 51(5): 850-862. |
| [13] |
Zhang R, Fomel S. Time-variant wavelet extraction with a local-attribute-based time-frequency decomposition for seismic inversion[J]. Interpretation, 2017, 5(1): SC9-SC16. DOI:10.1190/INT-2016-0060.1 |
| [14] |
李婧, 王修田, 宋鹏, 等. 基于改进广义S变换的时变反射系数反演[J]. 中国海洋大学学报(自然科学版), 2020, 50(6): 109-118. LI Jing, WANG Xiutian, SONG Peng, et al. Time-varying reflectivity inversion based on modified gene-ralized S transform[J]. Periodical of Ocean University of China, 2020, 50(6): 109-118. |
| [15] |
姚振岸, 孙成禹, 李红星, 等. 基于基追踪的时变子波提取与地震反射率反演[J]. 石油地球物理勘探, 2019, 54(1): 137-144. YAO Zhen'an, SUN Chengyu, LI Hongxing, et al. Time-variant wavelet extraction and seismic reflecti-vity inversion based on basis pursuit[J]. Oil Geophy-sical Prospecting, 2019, 54(1): 137-144. |
| [16] |
曹思远, 邴萍萍, 路交通, 等. 利用改进希尔伯特-黄变换进行地震资料时频分析[J]. 石油地球物理勘探, 2013, 48(2): 246-254. CAO Siyuan, BING Pingping, LU Jiaotong, et al. Seismic data time-frequency analysis by the improved Hilbert-Huang transform[J]. Oil Geophysical Prospecting, 2013, 48(2): 246-254. |
| [17] |
Allen J. Short term spectral analysis, synthesis, and modification by discrete Fourier transform[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1977, 25(3): 235-238. DOI:10.1109/TASSP.1977.1162950 |
| [18] |
Stephane M. A Wavelet Tour of Signal Processing (Second Edition)[M]. Academic Press, 1999.
|
| [19] |
Sinha S, Routh P S, Anno P D, et al. Spectral decomposition of seismic data with continuous-wavelet transform[J]. Geophysics, 2005, 70(6): P19-P25. DOI:10.1190/1.2127113 |
| [20] |
Stockwell R G, Mansinha L, Lowe R P. Localization of the complex spectrum: The S transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001. DOI:10.1109/78.492555 |
| [21] |
Moukadem A, Bouguila Z, Ould Abdeslam D, et al. A new optimized Stockwell transform applied on synthetic and real non-stationary signals[J]. Digital Signal Processing, 2015, 46(1): 226-238. |
| [22] |
杨子鹏, 宋维琪, 刘军, 等. 联合广义S变换和压缩感知提高地震资料分辨率[J/OL]. 地球物理学进展(网络首发), 2020: 1-11. http://kns.cnki.net/kcms/detail/11.2982.P.20200608.1427.130.html. YANG Zipeng, SONG Weiqi, LIU Jun, et al. Combine generalized S transform with compressed sensing to improve the resolution of seismic data[J/OL]. Process in Geophysics, 2020: 1-11. http://kns.cnki.net/kcms/detail/11.2982.P.20200608.1427.130.html. |
| [23] |
朱晓刚, 郑鹏飞, 王海萍, 等. 广义S变换在地震信号处理中的应用研究[J]. 西安文理学院学报(自然科学版), 2019, 22(3): 109-112. ZHU Xiaogang, ZHENG Pengfei, WANG Haiping, et al. Research on application of generalized S-transform in seismic signal processing[J]. Journal of Xi'an University (Natural Science Edition), 2019, 22(3): 109-112. DOI:10.3969/j.issn.1008-5564.2019.03.025 |
| [24] |
Margrave G F, Lamoureux M P, Henley D C. Gabor deconvolution: Estimation reflectivity by nonstatio-nary deconvolution of seismic data[J]. Geophysics, 2011, 76(3): W15-W30. DOI:10.1190/1.3560167 |
| [25] |
Oliveira S A M, Lupinacci W M. L1 norm inversion method for deconvolution in attenuating media[J]. Geophysical Prospecting, 2013, 61(4): 771-777. DOI:10.1111/1365-2478.12002 |
| [26] |
Sui Y H, Ma J W. A nonstationary sparse spike deconvolution with anelastic attenuation[J]. Geophy-sics, 2019, 84(2): R221-R234. |
| [27] |
Wen Z, Yin W, Goldfarb D. A fast algorithm for sparse reconstruction based on shrinkage, subspace optimization, and continuation[J]. SIAM Journal on Scientific Computing, 2010, 32(4): 1832-1857. DOI:10.1137/090747695 |



 曹思远, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院, 102249。Email:
曹思远, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院, 102249。Email: 