② 中国地质大学(武汉)地球物理与空间信息学院, 湖北武汉 430074
② Institute of Geophysics & Geomatics, China University of Geosciences(Wuhan), Wuhan, Hubei 430074, China
大地电磁测深(magnetotelluric,MT)作为发展较早的地球物理勘探方法之一,广泛应用于地球固体矿产和石油天然气的勘探等领域。当前大地电磁反演已经发展到三维成像阶段,然而三维反演的计算量较大,对硬件要求高,因此二维反演在实际应用中仍然具有很大优势[1]。典型的二维反演有OCCAM反演[2-3]、快速松弛反演(RRI)[4]、简化基OCCAM反演(REBOCC)[5]及非线性共轭梯度反演(NLGG)[6]等。尽管这些反演方法都可以得到很好的反演效果,但分别是以最小模型约束、最平缓模型约束或最光滑模型约束作为稳定泛函,因此只能得到平滑的反演效果,而不能得到清晰的地质体分界面。针对这个问题,Last等[7]首先提出用最小支撑泛函(minimum support,MS)作为稳定泛函,提高了块状结构的分辨率。随后,Portniaguine等[8]在此基础上提出使用最小梯度支撑(minimum gradient support,MGS)作为稳定泛函进行地球物理反演,得到了清晰的地质体分界面。Zhang等[9]和Zhdanov[10]针对MGS做了进一步研究,取得了较好的聚焦反演效果;张罗磊等[11]结合MGS稳定泛函和OCCAM方法,反演结果突出了对尖锐电性边界的刻画。随着反演理论的发展,一些新的稳定泛函被引入,如Sun等[12]提出的反正切稳定泛函、Hu等[13]提出的反余切稳定泛函、Zhao等[14]和Hu等[15]提出的指数型稳定泛函,以及Xiang等[16]提出的最小支撑梯度稳定泛函(minimum support gradient,MSG)。尽管基于这些稳定泛函可以得到清晰的地质体分界面,但是聚焦反演可能会使构造形态发生畸变,反演结果不准确。
采用高斯—牛顿法求解反演目标泛函时,由于正则化因子是数据拟合泛函和模型稳定泛函的折中参数,正则化因子过大会过于强调模型稳定泛函,导致数据总体欠拟合;反之,则容易产生虚假的反演构造。因此,正则化因子的选取对反演结果影响很大。关于正则化因子选取的典型方法,主要有Hansen等[17]提出的L曲线法、吴小平等[18]提出的自适应递减方法及陈小斌等[19]提出的完全自适应正则化方法(CMD方案)。此外,也有一些改进的正则化因子方案,如张罗磊等[11]、朴英哲等[20]及向阳等[21]都对正则化因子的选取提出了改进策略,这在一定程度上提高了反演效率。
本文对光滑反演和聚焦反演的缺陷进行分析,进而提出一种新的反演目标泛函。该目标泛函将最光滑约束与MSG稳定泛函进行加权结合,利用高斯—牛顿法对目标泛函进行求解,不仅可以得到稳定的反演结果,还可以使地质体分界面变得更加清晰。同时,在进行反演迭代时,本文提出利用Nelder-Mead优化算法优化Morozov偏差原理选取正则化因子的方法,不仅弥补了Morozov偏差原理后期收敛速度慢的不足,还加快了反演算法的收敛速度。同时,本文采用自适应衰减的聚焦因子。文中对典型模型进行反演,通过对比不同反演策略的反演结果,验证了本文算法的优势。最后,针对山西阳高县的一条实测数据进行反演,结果验证了光滑聚焦反演的有效性和可靠性。
1 理论分析 1.1 反演理论根据正则化理论,大地电磁反演目标泛函表达式为
| $ P({\boldsymbol{m}}, {\boldsymbol{d}}) = f({\boldsymbol{m}}, {\boldsymbol{d}}) + \alpha s({\boldsymbol{m}}) $ | (1) |
式中:P(m, d)是参数目标泛函,m=[m1, m2, …, mM]T为模型参数向量,其中M是模型参数的数量,d=[d1, d2, …, dN]T是观测数据向量,N是观测数据的数量; α是正则化参数;f(m, d)和s(m)分别是数据目标泛函和模型目标泛函。f(m, d)的表达式为
| $ f({\boldsymbol{m}}, {\boldsymbol{d}}) = \left\| {{{\boldsymbol{W}}_{\rm{d}}}[F({\boldsymbol{m}}) - {\boldsymbol{d}}]} \right\|_2^2 $ | (2) |
式中:Wd是数据加权矩阵;F是正演算子。
采用不同的模型目标泛函进行约束,会得到不同的反演结果。目前常用的三种稳定泛函是最小模型约束、最平缓模型约束和最光滑模型约束,这三种约束泛函尽管可以得到较好的反演结果,却不能得到清晰的地质体分界面。聚焦反演的引入很好地解决了这一难题。另一方面,采用聚焦反演很可能导致反演结果严重聚焦。为了避免这一缺陷,本文采用最光滑约束和MSG同时对模型目标泛函进行约束,具体表达式为
| $ s({\boldsymbol{m}}) = {\gamma _{{s_1}}}({\boldsymbol{m}}) + (1 - \gamma ){s_2}({\boldsymbol{m}}) $ | (3) |
| $ {s_1}({\boldsymbol{m}}) = \sum\limits_{i = 1}^M {{{\left[ {\nabla \frac{{\left( {{m^i} - m_{{\rm{apr}}}^i} \right)}}{{\sqrt {{{\left( {{m^i} - m_{{\rm{apr}}}^i} \right)}^2} + {\beta ^2}} }}} \right]}^2}} $ | (4) |
| $ {s_2}({\boldsymbol{m}}) = \sum\limits_{i = 1}^M {{{\left[ {\nabla \left( {{m^i} - m_{{\rm{apr}}}^i} \right)} \right]}^2}} $ | (5) |
式中:s1(m)是MSG稳定泛函;γ是平衡MGS泛函与最光滑约束的权重系数;s2(m)是最光滑约束泛函;mi是模型m的第i个参数;mapri是先验模型mapr的第i个参数;β为聚焦参数,是一个较小的值,可以避免式(4)中(mi-mapri)→0,保证函数的稳定性。
式(4)中的MSG稳定泛函s1(m)是在Last等[7]提出的MS泛函的基础上进一步求空间梯度得到的,Zhdanov[22]已证明MS满足正则稳定器的Tikhonov准则,可以作为稳定泛函对模型进行约束。因此,MSG同样也可以作为模型稳定泛函,Zhao等[14]对此作了相关描述。
式(4)中,聚焦参数β过大会导致聚焦效果不明显,过小则可能使泛函产生奇异,所以选择合适的聚焦因子对反演结果同样重要。针对β的选取,Zhdanov等[23]提出了L曲线法,但每次迭代都要进行曲率计算。为此,本文提出下列自适应衰减因子
| $ \beta = {{\rm{e}}^{ - \omega k}} $ | (6) |
式中:ω为控制系数,本文取1;k为当前的迭代次数,k=1, 2, …,K,K表示停止迭代次数。
空间梯度算子▽可用相邻模型单元之间的有限差分得到,尽管并不精确,但差别不大,后面用W▽表示▽。例如,对于一维的情况,其表达式为
| $ {{\boldsymbol{W}}_\nabla } = \left( {\begin{array}{*{20}{c}} 0&0&0& \cdots &0&0\\ { - 1}&1&0& \cdots &0&0\\ 0&{ - 1}&1& \cdots &0&0\\ 0&0&{ - 1}& \ddots & \vdots &0\\ \vdots & \vdots & \vdots & \ddots &1& \vdots \\ 0&0&0& \cdots &{ - 1}&1 \end{array}} \right) $ |
因此式(3)和式(4)可写成泛函形式
| $ {{s_1}({\boldsymbol{m}}) = \left\| {{{\boldsymbol{W}}_{\rm{e}}}\left( {{\boldsymbol{m}} - {{\boldsymbol{m}}_{{\rm{apr}}}}} \right)} \right\|_2^2} $ | (7) |
| $ {{s_2}({\boldsymbol{m}}) = \left\| {{{\boldsymbol{W}}_\nabla }\left( {{\boldsymbol{m}} - {{\boldsymbol{m}}_{{\rm{apr}}}}} \right)} \right\|_2^2} $ | (8) |
式中We=W▽W,W的表达式为
| $ {\boldsymbol{W}} = \left( {\begin{array}{*{20}{c}} {\frac{1}{{\sqrt {\left( {{m^1} - m_{{\rm{apr}}}^1} \right) + {\beta ^2}} }}}&{}&{}\\ {}& \ddots &{}\\ {}&{}&{}\\ {}&{}&{\frac{1}{{\sqrt {\left( {{m^M} - m_{{\rm{apr}}}^M} \right) + {\beta ^2}} }}} \end{array}} \right) $ |
则式(1)中的参数目标泛函可以转化为
| $ \begin{array}{l} P({\boldsymbol{m}}, {\boldsymbol{d}}) = \left\| {{{\boldsymbol{W}}_{\rm{d}}}[F({\boldsymbol{m}}) - {\boldsymbol{d}}]} \right\|_2^2 + \alpha \left[ {\gamma \left\| {{{\boldsymbol{W}}_{\rm{e}}}\left( {{\boldsymbol{m}} - {{\boldsymbol{m}}_{{\rm{apr}}}}} \right)} \right\|_2^2 + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {(1 - \gamma )\left\| {{{\boldsymbol{W}}_\nabla }\left( {{\boldsymbol{m}} - {{\boldsymbol{m}}_{{\rm{apr}}}}} \right)} \right\|_2^2} \right] \end{array} $ | (9) |
对于模型加权矩阵We,本文采用Portniaguine等[8]提出的方法进行处理。假设第k次迭代时,当前模型参数为mk, 则令We=We(mk),这样在每次迭代过程中,模型加权矩阵We就可当做一个常数矩阵。
对式(9)进行一阶泰勒展开,并令目标泛函的一阶变分等于零。为保证迭代的稳定性,对反演迭代公式先取对数后再反演,则可得到高斯—牛顿法的更新迭代公式
| $ \begin{array}{l} \ln {{\boldsymbol{m}}_{k + 1}} - \ln {{\boldsymbol{m}}_{{\rm{apr}}}} = \left\{ {{{\left( {{{\boldsymbol{W}}_{\rm{d}}}{{\boldsymbol{J}}_k}} \right)}^{\rm{H}}}{{\boldsymbol{W}}_{\rm{d}}}{{\boldsymbol{J}}_k} + } \right.\\ {\left. {\;\;\;\;\;\;\;\;\;\;\alpha \left[ {\gamma {\boldsymbol{W}}_{\rm{e}}^{\rm{T}}{{\boldsymbol{W}}_{\rm{e}}} + (1 - \gamma ){\boldsymbol{W}}_\nabla ^{\rm{T}}{{\boldsymbol{W}}_\nabla }} \right]} \right\}^{ - 1}}{\widehat {\boldsymbol{d}}_k} \end{array} $ | (10) |
| $ \begin{array}{l} {\widehat {\boldsymbol{d}}_k} = {\left( {{{\boldsymbol{W}}_{\rm{d}}}{{\boldsymbol{J}}_k}} \right)^{\rm{H}}}{{\boldsymbol{W}}_{\rm{d}}}\left[ {\ln {\boldsymbol{d}} - \ln F\left( {{{\boldsymbol{m}}_k}} \right) + } \right.\\ \;\;\;\;\;\;\;\left. {{{\boldsymbol{J}}_k}\left( {\ln {{\boldsymbol{m}}_k} - \ln {{\boldsymbol{m}}_{{\rm{apr}}}}} \right)} \right] \end{array} $ | (11) |
式中:J为雅克比矩阵;H表示共轭转置。
由式(10)可知,正则化因子α对反演是否收敛至关重要。下文将阐述如何基于Nelder-Mead优化算法的Morozov偏差原理确定正则化因子。
1.2 Morozov偏差原理利用Morozov偏差原理确定正则因子的应用详见文献[24]。该原理决定了正则因子存在反演后期收敛速度变慢甚至不收敛的缺陷。Morozov偏差原理是根据后验策略选择最优的正则化参数,而且可以自动选择唯一的正则化参数。假设数据采集时误差水平已知,则需要满足以下偏差方程
| $ \phi (\alpha ) = {\left\| {{\boldsymbol{Am}} - {\boldsymbol{d}}} \right\|^2} - {\delta ^2} $ | (12) |
式中:||Am-d||2是α的偏差函数,反演中A=WdJ;δ2表示误差。式(12)采用具有二次收敛速率的牛顿迭代法求解α,可得当前迭代点αk的线性逼近公式
| $ \phi (\alpha ) \approx \phi \left( {{\alpha _k}} \right) + {\phi ^\prime }\left( {{\alpha _k}} \right)\left( {\alpha - {\alpha _k}} \right) $ | (13) |
令ϕ(α)=0,可以得到牛顿法的迭代格式
| $ {\alpha _{k + 1}} = {\alpha _k} - \frac{{\phi \left( {{\alpha _k}} \right)}}{{{\phi ^\prime }\left( {{\alpha _k}} \right)}} $ | (14) |
采用Morozov偏差原理决定了正则化因子尽管能使反演结果收敛,但是算法后期的收敛速度很慢,反演效率低,因此需要对Morozov偏差原理的结果做进一步优化处理。
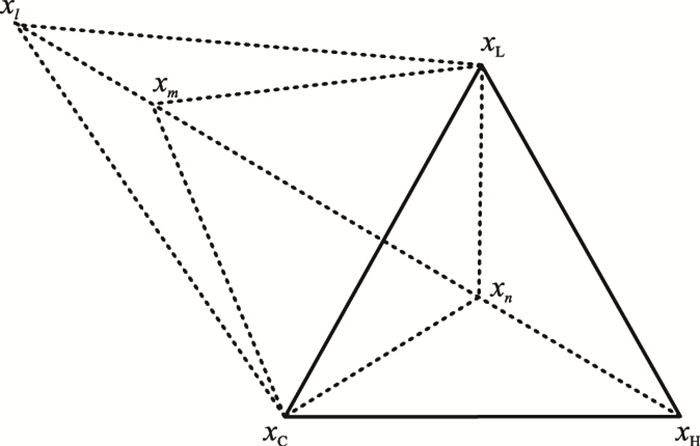
1.3 Nelder-Mead优化算法Nelder-Mead优化算法又称为可变的多面体搜索法,是一种无约束的直接搜索方法。该算法的基本思想是首先利用起始点x0构建一个具有n+1个顶点的线性多面体(x0, x1, …,xn),通过对比各个顶点的目标函数值确定各顶点的优劣。假设计算可得xL为最差点,xH为最优点,xC为次优点,可通过启发式的反射、扩张、压缩等运算得到新的顶点(xl,xm,xn),然后用较好的顶点替换最差的顶点xL组成新的多面体。Nelder-Mead优化算法如图 1所示,Yildiz等[25]对Nelder-Mead优化算法的具体过程进行了描述。最后,对该流程反复进行迭代运算,最终逼近目标函数的最优解。Nelder-Mead优化算法收敛速度快,对局部的搜索能力强,可用极小的时间成本搜寻局部最优值。
|
图 1 Nelder-Mead优化算法示意图 |
反演的均方根误差RMS的计算公式为
| $ {\rm{RMS}} = \sqrt {\frac{{\sum\limits_{i = 1}^N {\left[ {\left( {d_i^{{\rm{obs}}} - d_i^{{\rm{fwd}}}} \right)/d_i^{{\rm{obs}}}} \right]} }}{N}} $ | (15) |
式中:diobs和difwd分别表示第i个观察数据和第i个正演数据;N表示最大迭代次数。
本文基于优化策略的光滑聚焦反演的具体步骤如下。
(1) 给出初始模型m0、先验模型mapr、初始正则化因子α1、权重因子γ、反演迭代次数K、目标拟合差及采用Nelder-Mead优化算法寻优的最大迭代次数N。
(2) 计算数据的RMS,判断是否满足给定的停止条件。若满足,则停止迭代;若不满足,则转步骤(3)。
(3) 计算当前模型的雅克比矩阵Jk、F(mk)、W▽和We(mk)。利用Nelder-Mead优化算法对正则化因子αk进一步优化,得到新的正则化因子α'k。利用式(10)更新模型。
(4) 采用Morozov偏差原理决定下一次迭代的正则化因子αk+1,然后令k=k+1,转至步骤(2)。
1.4 矢量化与并行进行大地电磁二维反演时需要反复调用正演子程序和雅可比矩阵的计算子程序,考虑到反演效率,反演时本文采用矢量化思想和Matlab的并行策略进行编程。矢量化编程是利用单元网格局部编码和整体编码的策略,将整体的刚度矩阵中的非零行和非零列直接写成了矩阵形式,通过一次性赋值即可得到整体的刚度矩阵,这样可避免使用多次循环进行赋值,提高了赋值效率,减少了正演的时间。Matlab并行计算是利用正演时各个频率间的正演过程相互独立,调用CPU多核进行并行计算,大大提高了正演速度。以上两种策略可保证较快的反演过程。
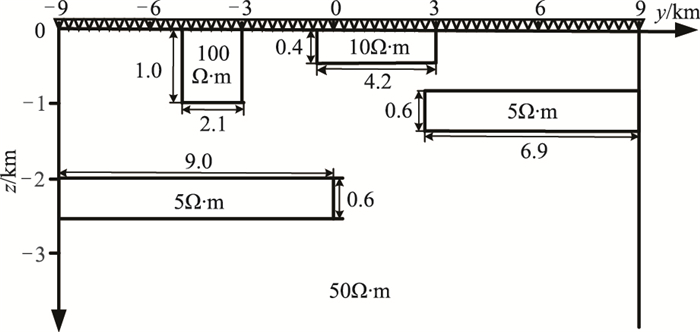
2 模型试验 2.1 Sasaki模型为了验证算法的优势和可靠性,选用典型的Sasaki模型[26]进行反演,见图 1。背景模型是电阻率为50Ω·m的均匀半空间,包含不同的高阻和低阻异常体。测点位于地面,间距为0.3km,沿y轴分布,分布区域为-9~9km,频点数为25,频率范围是0.1~100Hz,按对数等间距分布。
反演过程中,对于初始模型m0选取50Ω·m的均匀半空间,设mapr=m0,目标拟合差设定为0.01,反演迭代次数为10,对正则化因子进行优化时,Nelder-Mead优化算法的迭代次数N取10。
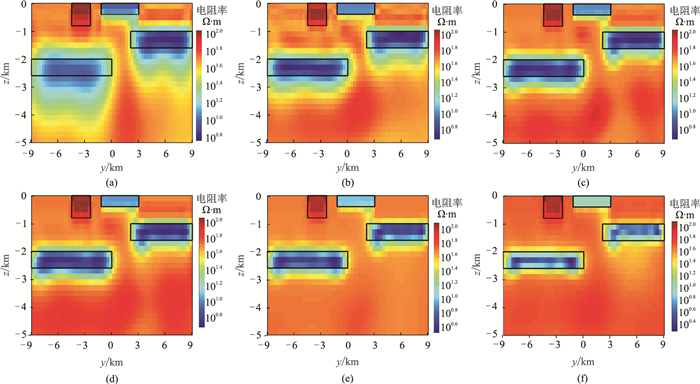
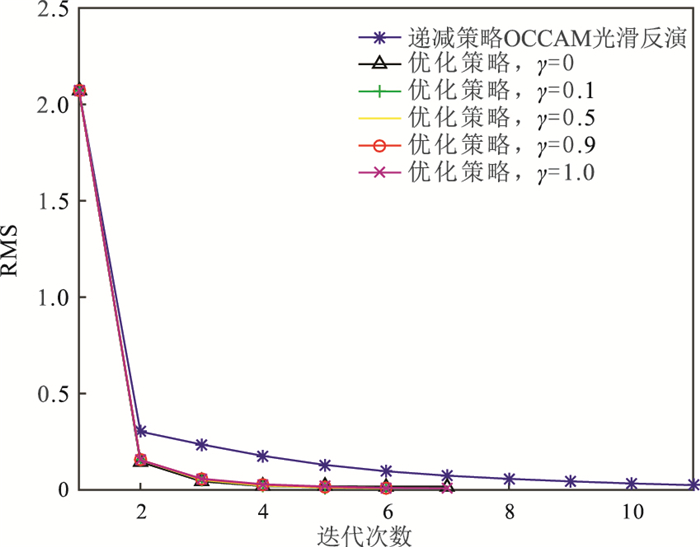
为了对比分析,采用递减策略选取正则化因子的OCCAM进行反演,结果见图 3a;图 3b为优化策略的OCCAM反演结果,即式(3)中γ=0时的反演结果;图 3c~图 3f为γ分别取0.1、0.5、0.9和1.0的反演结果,其中γ=1.0即对应MSG反演。图 4为对应图 3的不同方法拟合差迭代曲线。由图 3和图 4可见,优化策略的反演收敛速度更快,所需时间更少。对比图 3a、图 3b与图 3c~图 3f可知,目标函数含有MSG项的稳定泛函可反演得到更清晰的地质体界面。从图 3c~图 3f还可见,随着γ的增加,地质体的分界面越来越清晰,聚焦效果也越来越明显,但低阻体电阻率偏离真值的程度也越来越高。图 5是对应图 3a~图 3f的反演结果与真实模型的绝对误差剖面。对比图 3与图 5可知,γ=0.9时的反演效果相对最好。
|
图 2 Sasaki模型示意图 |
|
图 3 不同策略的OCCAM电阻率反演结果 (a)递减策略;(b)~(f)优化策略, γ分别取0, 0.1, 0.5, 0.9, 1.0 |
|
图 4 对应图 3的不同策略反演收敛曲线对比 |
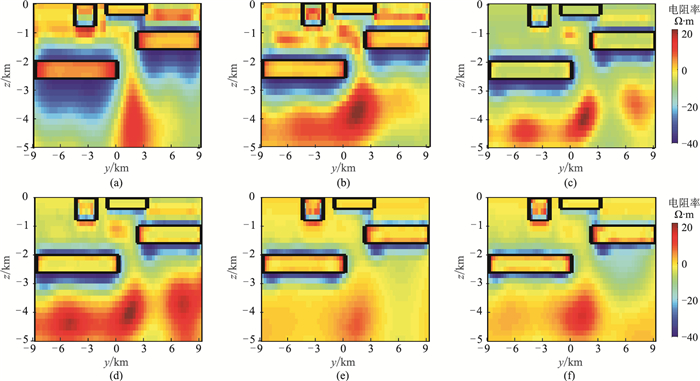
|
图 5 对应图 3的不同反演策略反演结果与真实值的绝对误差 (a)递减策略;(b)~(f)优化策略, γ分别取0, 0.1, 0.5, 0.9, 1.0 |
进行光滑聚焦联合反演时,模型泛函s1(m)中聚焦因子β的选取对聚焦效果有很大影响。因此,计算γ=0.9时,β分别取1.0、0.5和0.1的反演结果见图 6。由图可见,随着β值的降低,聚焦效果越来越明显,因此进行聚焦反演时需分析选取合适的聚焦因子。而式(6)因采用了自适应递减的聚焦因子,故不必考虑这一问题。
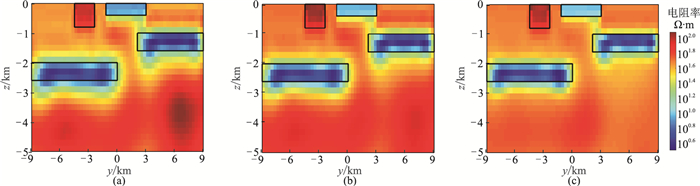
|
图 6 优化策略聚焦反演时不同β值的反演结果对比(γ=0.9) (a)1.0;(b)0.5;(c)0.1 |
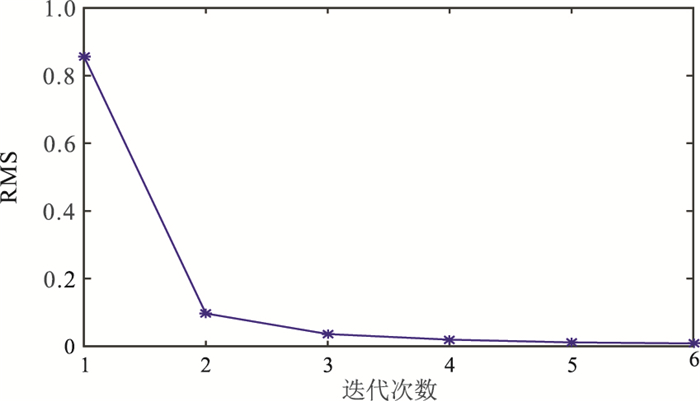
构建一个二维楔形模型,验证本文方法反演结果的可靠性和精度性,模型参数见图 7。设置测点间距为0.2km。图 8是γ=0、0.9时的反演结果及其与模型真实电阻率的误差分布,图 9是γ=0.9时的迭代收敛曲线。从图 8电阻率反演结果可以看出,光滑聚焦反演结果中地质体界面更加清晰;从图 9收敛曲线可以看出,对于楔形模型,采用Nelder-Mead优化算法的Morozov偏差原理确定正则化因子仍有很好的收敛效果。
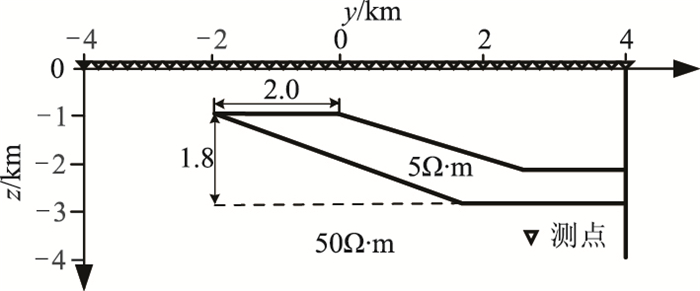
|
图 7 二维楔形模型示意图 |
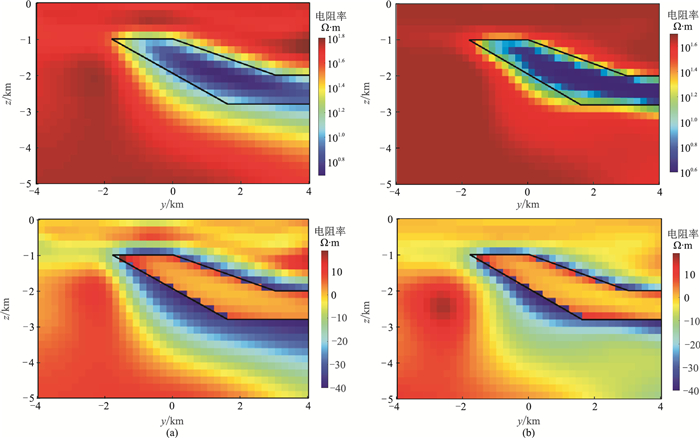
|
图 8 二维楔形模型优化策略聚焦反演结果(上)及其与模型真实电阻率的差值(下) (a)γ=0;(b)γ=0.9 |
|
图 9 二维楔形模型优化策略(γ=0.9)聚焦反演收敛曲线 |
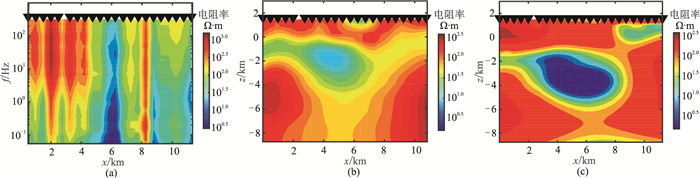
为了进一步检验算法的有效性和可靠性,对山西省阳高县某地热勘探测线的实测数据进行了反演。该测线位于阳高县城北侧大同盆地北缘,测线经过一个断裂,该断裂是在燕山期"阳高破碎带"的基础上继承形成的。测点点距为500m,共22个测点,所测数据为MT。图 10a是该测线实测数据的拟断面图,图 10b是采用有限差分正演和非线性共轭梯度(商业软件Winglink)的反演结果,图 10c是本文光滑聚焦的电阻率反演结果。从图 10b和图 10c可以看出,在深度2~6km范围内都有一个明显的低阻体,根据已有的实际资料推断,低阻区域为断裂含水带,是断裂构造作用造成岩石破碎,导致透水性增大形成的。对比图 10b与图 10c可见,光滑聚焦反演的结果与Winglink软件反演的结果大致相同,验证了本文算法的有效性和可靠性。由图 10c还可以看到,光滑聚焦反演的低阻区域较为明显,并且对低阻体边界的刻画较Winglink软件反演结果更清晰,因此光滑聚焦反演算法对于实际大地电磁资料的反演也是有效的。
|
图 10 实测数据及电阻率反演结果 (a)实测MT数据剖面;(b)Winglink软件反演结果;(c)光滑聚焦反演结果 |
(1) 本文提出了一种新的目标泛函,利用高斯—牛顿法求解反演目标函数,实现了二维大地电磁数据的稳定聚焦反演,可以得到清晰的地质界面。
(2) 针对反演迭代过程,提出了利用Nelder-Mead优化算法优化Morozov偏差原理确定正则化因子的优化策略,减少了反演迭代次数,加快了反演收敛速度。
(3) 通过对典型模型和实测数据的反演分析,验证了光滑聚焦反演的可靠性和有效性,为三维MT反演奠定了应用基础。
| [1] |
Zhang R, Li T, Deng X, et al. Two-dimensional data-space joint inversion of magnetotelluric, gravity, magnetic and seismic data with cross-gradient constraints[J]. Geophysical Prospecting, 2020, 68(2): 721-731. DOI:10.1111/1365-2478.12858 |
| [2] |
韩波, 胡祥云, 何展翔, 等. 大地电磁反演方法的数学分类[J]. 石油地球物理勘探, 2012, 47(1): 177-188. HAN Bo, HU Xiangyun, HE Zhanxiang, et al. Mathe-matical classification of magnetotelluric inversion methods[J]. Oil Geophysical Prospecting, 2012, 47(1): 177-187. |
| [3] |
Degroot-Hedlin C, Constable S. Occam's inversion to generate smooth, two-dimensional models from magnetotelluric data[J]. Geophysics, 1990, 55(12): 1613-1624. DOI:10.1190/1.1442813 |
| [4] |
Smith J T, Booker J R. Rapid inversion of two-and three-dimensional magnetotelluric data[J]. Journal of Geophysical Research: Solid Earth, 1991, 96(B3): 3905-3922. DOI:10.1029/90JB02416 |
| [5] |
Siripunvaraporn W, Egbert G. An efficient data-subspace inversion method for 2-D magnetotelluric data[J]. Geophysics, 2000, 65(3): 791-803. DOI:10.1190/1.1444778 |
| [6] |
Rodi W, Mackie R L. Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion[J]. Geophysics, 2001, 66(1): 174-187. DOI:10.1190/1.1444893 |
| [7] |
Last B J, Kubik K. Compact gravity inversion[J]. Geophysics, 1983, 48(6): 713-721. DOI:10.1190/1.1441501 |
| [8] |
Portniaguine O, Zhdanov M S. Focusing geophysical inversion images[J]. Geophysics, 1999, 64(3): 874-887. DOI:10.1190/1.1444596 |
| [9] |
Zhang L, Koyama T, Utada H, et al. A regularized three-dimensional magnetotelluric inversion with a minimum gradient support constraint[J]. Geophysical Journal International, 2012, 189(1): 296-316. DOI:10.1111/j.1365-246X.2012.05379.x |
| [10] |
Zhdanov M S. New advances in regularized inversion of gravity and electromagnetic data[J]. Geophysical Prospecting, 2009, 57(4): 463-478. DOI:10.1111/j.1365-2478.2008.00763.x |
| [11] |
张罗磊, 于鹏, 王家林, 等. 光滑模型与尖锐边界结合的MT二维反演方法[J]. 地球物理学报, 2009, 52(6): 1625-1632. ZHANG Luolei, YU Peng, WANG Jialin, et al. Smoothest model and sharp boundary based two-dimensional magnetotelluric inversion[J]. Chinese Journal of Geophysics, 2009, 52(6): 1625-1632. DOI:10.3969/j.issn.0001-5733.2009.06.025 |
| [12] |
Sun S, Yin C, Liu Y, et al. 3D regularized focusing inversion of gravity data with a new stabilizing functional[C]. International Workshop and Gravity & Magnetic Methods and Their Applications, Chengdu, China, 2015, 322-325.
|
| [13] |
Hu S, Zhao Y, Qin T, et al. Travel time tomography of cross hole ground-penetrating radar based on an arctangent functional with compactness constraints[J]. Geophysics, 2017, 82(3): H1-H14. DOI:10.1190/geo2016-0249.1 |
| [14] |
Zhao C, Yu P, Zhang L. A new stabilizing functional to enhance the sharp boundary in potential field regularized inversion[J]. Journal of Applied Geophysics, 2016, 135: 356-366. DOI:10.1016/j.jappgeo.2016.10.033 |
| [15] |
Hu M, Yu P, Rao C, et al. 3D sharp-boundary inversion of potential-field data with an adjustable exponential stabilizing functional[J]. Geophysics, 2019, 84(4): J1-J15. DOI:10.1190/geo2018-0132.1 |
| [16] |
Xiang Y, Yu P, Zhang L, et al. Regularized magnetotelluric inversion based on a minimum support gradient stabilizing functional[J]. Earth, Planets and Space, 2017, 69(1): 1-18. DOI:10.1186/s40623-016-0587-x |
| [17] |
Hansen P C, Leary D P O. The use of the L-curve in the regularization of discrete ill-posed problems[J]. SIAM Journal on Scientific Computing, 1993, 14(6): 1487-1503. DOI:10.1137/0914086 |
| [18] |
吴小平, 徐果明. 大地电磁数据的Occam反演改进[J]. 地球物理学报, 1998, 41(4): 547-554. WU Xiaoping, XU Guoming. Improvement of Occam's inversion for MT data[J]. Chinese Journal of Geophysics, 1998, 41(4): 547-554. DOI:10.3321/j.issn:0001-5733.1998.04.013 |
| [19] |
陈小斌, 赵国泽, 汤吉, 等. 大地电磁自适应正则化反演算法[J]. 地球物理学报, 2005, 48(4): 937-946. CHEN Xiaobin, ZHAO Guoze, TANG Ji, et al. An adaptive regularized inversion algorithm for magnetotelluric data[J]. Chinese Journal of Geophysics, 2005, 48(4): 937-946. DOI:10.3321/j.issn:0001-5733.2005.04.029 |
| [20] |
朴英哲, 李桐林, 刘永亮. 在大地电磁二维Occam反演中求取拉格朗日乘子方法改进[J]. 吉林大学学报(地球科学版), 2014, 44(2): 660-667. PAK Yongchol, LI Tonglin, LIU Yongliang. Improvement of choosing Lagrange Multiplier on MT 2D Occam inversion[J]. Journal of Jilin University(Earth Science Edition), 2014, 44(2): 660-667. |
| [21] |
向阳, 于鹏, 陈晓, 等. 大地电磁反演中改进的自适应正则化因子选取[J]. 同济大学学报(自然科学版), 2013, 41(9): 1429-1434. XIANG Yang, YU Peng, CHEN Xiao, et al. An improve adaptive regularized parameter selection in magnetotelluric inversion[J]. Journal of Tongji University (Natural Science), 2013, 41(9): 1429-1434. DOI:10.3969/j.issn.0253-374x.2013.09.024 |
| [22] |
Zhdanov M S. Geophysical Inverse Theory and Regularization Problems[M]. Elsevier, 2002.
|
| [23] |
Zhdanov M S, Tolstaya E. Minimum support nonlinear parametrization in the solution of a 3D magnetotelluric inverse problem[J]. Inverse Problems, 2004, 20(3): 937-952. DOI:10.1088/0266-5611/20/3/017 |
| [24] |
Zhang Y M S, Li Q H, Wang L P, et al. Regularization particle size inversion of PCS based on fast algorithm[C]. IEEE World Congress on Intelligent Control and Automation(WCIA), 2014, 5641-5645.
|
| [25] |
Yildiz A R, Yildiz B S, Sait S M, et al. A new hybrid Harris Hawks-Nelder-Mead optimization algorithm for solving design and manufacturing problems[J]. Materials Testing, 2019, 61(8): 735-743. DOI:10.3139/120.111378 |
| [26] |
Sasaki Y. Two-dimensional joint inversion of magnetotelluric and dipole-dipole resistivity data[J]. Geophysics, 1989, 54(2): 254-262. DOI:10.1190/1.1442649 |



 胡祥云, 湖北省武汉市鲁磨路388号中国地质大学(武汉)地球物理与空间信息学院, 430074。Email:
胡祥云, 湖北省武汉市鲁磨路388号中国地质大学(武汉)地球物理与空间信息学院, 430074。Email: 