② 东华理工大学核资源与环境国家重点实验室, 江西南昌 330013
② State Key Laboratory of Nuclear Resources and Environment, East China University of Technology, Nanchang, Jiangxi 330013, China
电磁勘探方法分支众多,在矿产资源勘查、油气勘探、地质环境调查等方面得到广泛应用[1-3]。可控源电磁法(CSEM)作为其中很重要的一个分支,其应用效果一定程度上依赖于高精度的三维正反演解释技术,而三维正演效率和求解精度的提高可为三维高效反演奠定基础[4]。目前,用于三维电磁正演的主流数值模拟方法包括积分方程法[5-7]、有限差分法[8-11]、有限体积法[12-14]和有限单元法[15-16]。
有限单元法因其模拟网格的多样性,可精确模拟地形起伏、不规则异常体形态而备受关注。国内外诸多学者采用非结构网格开展了三维电磁有限元正演模拟:Puzyrev等[17]基于二次耦合势和非结构化四面体网格开展了三维电磁正演模拟研究,通过引入一种TAI(刚度矩阵的近似截断逆矩阵)预条件矩阵加速了迭代求解过程;Ansari等[18]基于二次耦合势的双旋度方程开展了非结构化四面体网格的三维电磁正演,通过ILUT预条件的QMR(Quasi-Minimum Residual)方法求解线性方程组;Cai等[19]基于总场和非结构化网格开展了三维电磁矢量有限元正演,通过直接求解器MUMPS对线性方程组进行求解,这种方法适用于多源电磁问题;刘长生等[20]、杨军等[21]、殷长春等[22]、刘颖等[23]、叶益信等[24]及赵宁等[25]也开展了基于非结构化网格的三维电磁正演研究。
基于非结构化网格对电场直接求解时,其有限元正演方程的求解绝大多数是基于直接法。究其原因,一方面是非结构化网格相比结构化网格得到的线性方程组条件数更大,另一方面对于较低频率,基于电场方程迭代求解时电流密度散度不严格为零。因此,利用迭代法求解存在收敛慢甚至不收敛的问题;而基于直接法求解时,对内存需求大,在个人PC上不易实现大规模正演计算。当采用结构化网格进行正演时,往往可通过散度校正改善低频正演的迭代收敛速度[26-29], 但目前未见散度校正技术在非结构化网格正演中的应用。秦策等[30]利用分块对角预条件并结合辅助空间预条件实现了高效率迭代解法,可将迭代求解次数降低到几十以内,提高了正演计算效率。但该方法实现较复杂,需借助开源程序库实现辅助空间预条件算法。
本文结合非结构化四面体网格和散度校正技术开展三维CSEM正演模拟研究,为非结构三维正演的迭代求解提供一条路径。首先介绍基于二次电场的正演模拟方法及散度校正技术,之后分别通过一个层状介质模型和两个三维地电模型的数值模拟验证算法的有效性及高精度。
1 方法原理 1.1 三维电磁正演边值问题对于频率小于1×105 Hz的电磁问题,从麦克斯韦方程出发(准静态极限),在频率域采用负谐变形式(e-iωt),则电磁场满足
| $ \nabla \times {\boldsymbol{E}} = - \frac{{\partial {\boldsymbol{B}}}}{{\partial t}} = {{\rm{i}}_{\omega \mu }}_0{\boldsymbol{H}} $ | (1) |
| $ \nabla \times {\boldsymbol{H}} = \sigma {\boldsymbol{E}} + {{\boldsymbol{J}}_外} $ | (2) |
式中:E表示电场矢量; H为磁场矢量;B表示磁场强度矢量; ω表示角频率;μ0表示真空中的磁导率;σ表示电导率参数;J外表示外电流密度。对式(1)两边求旋度,得到
| $ \nabla \times \nabla \times {\boldsymbol{E}} = {\rm{i}}\omega {\mu _0}\nabla \times {\boldsymbol{H}} $ | (3) |
将式(2)代入式(3),整理即可得到关于电场E的双旋度方程
| $ \nabla \times \nabla \times {\boldsymbol{E}} - {\rm{i}}\omega {\mu _0}\sigma {\boldsymbol{E}} = {{\rm{i}}_\omega }{\mu _0}{{\boldsymbol{J}}_外} $ | (4) |
为了避免场源的奇异性,兼顾网格划分的便利性,采用一次场与二次场分离办法,即总场E分解为一次场Ep及二次场Es
| $ {\boldsymbol{E}} = {{\boldsymbol{E}}_{\rm{p}}} + {{\boldsymbol{E}}_{\rm{s}}} $ | (5) |
对于基于参考模型电导率分布σp的一次场Ep,其双旋度方程为
| $ \nabla \times \nabla \times {{\boldsymbol{E}}_{\rm{p}}} - {\rm{i}}\omega {\mu _0}{\sigma _{\rm{p}}}{{\boldsymbol{E}}_{\rm{p}}} = {\rm{i}}\omega {\mu _0}{{\boldsymbol{J}}_外} $ | (6) |
参考模型一般选为均匀半空间或水平层状介质模型,Ep可预先通过快速汉克尔变换计算得到。用式(4)减去式(6),并结合式(5),整理可得关于二次电场的双旋度方程
| $ \nabla \times \nabla \times {{\boldsymbol{E}}_{\rm{s}}} - {\rm{i}}\omega {\mu _0}\sigma {{\boldsymbol{E}}_{\rm{s}}} = {\rm{i}}\omega {\mu _0}\Delta \sigma {{\boldsymbol{E}}_{\rm{p}}} $ | (7) |
式中Δσ=σ-σp,表示异常电导率的分布。当研究区域足够大,以至于边界上的二次场可忽略时,可采用狄利克雷边界条件,得到边值问题[31]
| $ \left\{ {\begin{array}{*{20}{l}} {\nabla \times \nabla \times {{\boldsymbol{E}}_s} - {\mathop{\rm i}\nolimits} \omega {\mu _0}\sigma {{\boldsymbol{E}}_s} = {\mathop{\rm i}\nolimits} \omega {\mu _0}\Delta \sigma {{\boldsymbol{E}}_{\rm{p}}}\;\;\;\;\; \in \mathit{\Omega }}\\ {{\boldsymbol{n}} \times {{\boldsymbol{E}}_{\rm{s}}} = 0\;\;\;\;\;\; \in \mathit{\Gamma }} \end{array}} \right. $ | (8) |
式中:Ω表示包含地下介质和空气层的长方体研究区域;Γ表示其外边界;n为两个相邻单元界面的法向单位向量。
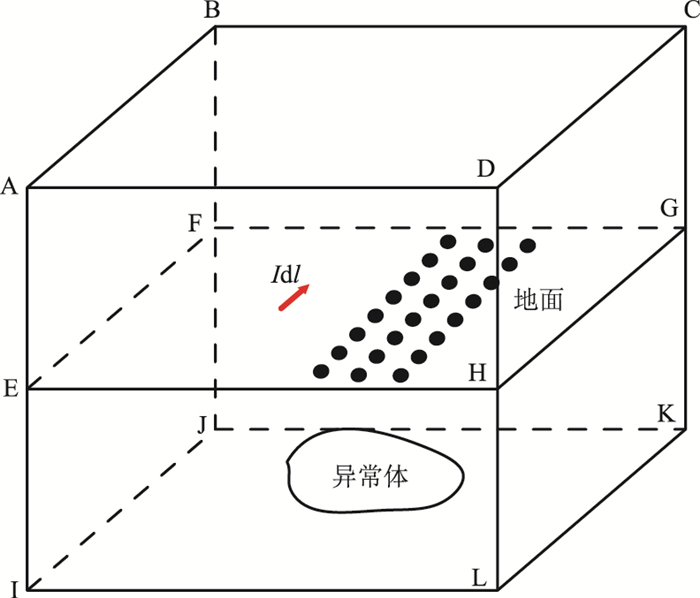
1.2 基于伽辽金有限元法的边值问题求解为了适应任意地形起伏及复杂地质目标模拟的需要,采用伽辽金有限元法对式(8)边值问题进行求解。图 1所示为研究区域示意图,研究区域包含空气层及地下介质层。同时,为了在电导率分界面上满足电场法向分量不连续的边界条件,采用基于棱边的矢量有限元,并采用四面体网格对研究区域进行剖分(图 2)。
|
图 1 研究区域示意图 Idl代表接地电流源,黑点代表测点 |
|
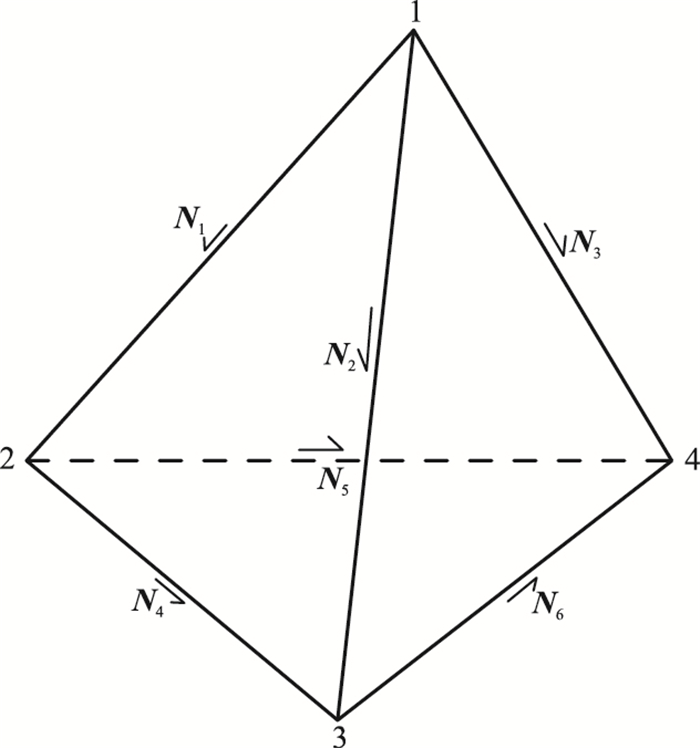
图 2 四面体剖分单元示意图 数字1~4表示节点编号,N1~N6表示对应各条棱边的矢量形函数 |
设对应各条棱边的形函数为Ni,那么一次电场及二次电场可分别表示为
| $ {{\boldsymbol{E}}_{\rm{p}}} = \sum\limits_{i = 1}^6 {{{\boldsymbol{N}}_i}} {E_{{\rm{p}}i}} $ | (9) |
| $ {{\boldsymbol{E}}_{\rm{s}}} = \sum\limits_{i = 1}^6 {{{\boldsymbol{N}}_i}} {E_{{\rm{s}}i}} $ | (10) |
式中Epi和Esi分别代表第i条棱边上的一次场和二次场值,i=1~6。本文选用矢量基函数
| $ {{\boldsymbol{N}}_i} = \left( {{{\boldsymbol{L}}_{{i_1}}}\nabla {{\boldsymbol{L}}_{{i_2}}} - {{\boldsymbol{L}}_{{i_2}}}\nabla {{\boldsymbol{L}}_{{i_1}}}} \right){l_i} $ | (11) |
式中:i1和i2分别表示第i条棱边的两个节点编号;li代表该棱边的长度;L为对应于各节点的形函数,▽L为L的梯度[32]。根据伽辽金有限元方法,可在式(8)两边同时乘以形函数Ni并对整个研究区域Ω积分
| $ \begin{array}{l} \int_\mathit{\Omega} {\left( {\nabla \times \nabla \times {{\boldsymbol{E}}_{\rm{s}}} - {\rm{i}}\omega {\mu _0}\sigma {{\boldsymbol{E}}_{\rm{s}}}} \right)} \cdot {{\boldsymbol{N}}_i}{\rm{d}}\mathit{\Omega }\\ \;\;\;\;\;\;\;\; = \int_\mathit{\Omega} {\rm{i}} \omega {\mu _0}\Delta \sigma {{\boldsymbol{E}}_{\rm{p}}} \cdot {{\boldsymbol{N}}_i}{\rm{d}}\mathit{\Omega } \end{array} $ | (12) |
用LHS表示上式左端项,可分解为两项,即
| $ \begin{array}{l} {\rm{LHS}} = \int_\mathit{\Omega} {{{\boldsymbol{N}}_i}} \cdot \left( {\nabla \times \nabla \times {{\boldsymbol{E}}_{\rm{s}}}} \right){\rm{d}}\mathit{\Omega } - \\ \;\;\;\;\;\;\;\;\;\;\;\sum\limits_{j = 1}^6 {\int_\mathit{\Omega} {\rm{i}} } \omega {\mu _0}\sigma {{\boldsymbol{N}}_i} \cdot {{\boldsymbol{N}}_j}{{\boldsymbol{E}}_{{\rm{s}}j}}{\rm{d}}\mathit{\Omega } \end{array} $ | (13) |
根据矢量恒等式
| $ - {\boldsymbol{A}} \cdot (\nabla \times {\boldsymbol{B}}) + {\boldsymbol{B}} \cdot (\nabla \times {\boldsymbol{A}}) = \nabla \cdot ({\boldsymbol{A}} \times {\boldsymbol{B}}) $ |
式(13)右边的第一项可作如下变换

|
(14) |
式中S表示面积矢量。根据二次电场和二次磁场的关系,当边界离异常区域足够远时,满足
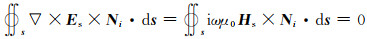
|
(15) |
结合式(13)~式(15),式(12)可表示为
| $ \begin{array}{l} \sum\limits_{j = 1}^6 {\left[ {\int_\mathit{\Omega} {\left( {\nabla \times {{\boldsymbol{N}}_i}} \right)} \cdot \left( {\nabla \times {{\boldsymbol{N}}_j}} \right){\rm{d}}\mathit{\Omega} - } \right.} \\ \;\;\;\;\left. {\int_\mathit{\Omega} {\rm{i}} \omega {\mu _0}\sigma {{\boldsymbol{N}}_i} \times {{\boldsymbol{N}}_j}{\rm{d}}\mathit{\Omega} } \right]{E_{{\rm{s}}j}}\\ \;\;\;\; = {E_{{\rm{p}}j}}\left( {\sum\limits_{j = 1}^6 {\rm{i}} \omega {\mu _0}\int_\mathit{\Omega} \Delta \sigma {{\boldsymbol{N}}_i} \cdot {{\boldsymbol{N}}_j}{\rm{d}}\mathit{\Omega} } \right) \end{array} $ | (16) |
式(16)可表示为线性方程组
| $ {\boldsymbol{K}}{{\boldsymbol{E}}_{\rm{s}}} = {\boldsymbol{M}}{{\boldsymbol{E}}_{\rm{p}}} $ | (17) |
式中:K代表式(17)左边作用于Es的刚度矩阵;M代表作用于Ep的矩阵。K和M的矩阵元素分别为
| $ \left\{ {\begin{array}{*{20}{l}} {{K_{ij}} = \int_\mathit{\Omega} {\left[ {\left( {\nabla \times {{\boldsymbol{N}}_i}} \right) \cdot \left( {\nabla \times {{\boldsymbol{N}}_j}} \right) - {\mathop{\rm i}\nolimits} \omega {\mu _0}\sigma {{\boldsymbol{N}}_i} \cdot {{\boldsymbol{N}}_j}} \right]} {\rm{d}}\mathit{\Omega} }\\ {{M_{ij}} = {\rm{i}}\omega {\mu _0}\Delta \sigma \int_\mathit{\Omega} {{{\boldsymbol{N}}_i}} \cdot {{\boldsymbol{N}}_j}{\rm{d}}\mathit{\Omega} } \end{array}} \right. $ | (18) |
式(17)中的刚度矩阵K为大型、稀疏、复对称矩阵。为了降低三维正演模拟的内存需求,采用Krylov子空间迭代方法QMR对式(17)中的线性方程组进行求解,并基于不完全Cholesky分解得到预条件矩阵[33]。
1.3 散度校正技术在迭代求解正演线性方程组时,尽管采用了基于不完全Cholesky分解的预条件矩阵以加速迭代求解,但对于频率较低或非结构化网格质量较差时,迭代过程无法经较少迭代次数收敛到预期残差,甚至可能不收敛。常用的改善措施是在迭代求解过程中对电流密度的散度进行校正。散度校正最早由Smith[26]在三维大地电磁有限差分正演中提出,尔后普遍应用于结构化网格三维电磁正演迭代求解[26-29],但在非结构化网格正演中的应用尚未见报道。以下将以非结构化网格正演为例探讨散度校正方法。
对式(8)中的第1个方程两边求散度并略去常系数项,可得
| $ \nabla \cdot \left( {\sigma {{\boldsymbol{E}}_{\rm{s}}} + \Delta \sigma {{\boldsymbol{E}}_{\rm{p}}}} \right) = 0 $ | (19) |
上式即为二次电场需满足的散度条件。在剖分单元内,由于矢量元插值函数的散度为零,式(19)自动满足。但由于矢量元插值函数定义在棱边上,其方向是棱边切向方向,故仅可保证切向分量的连续性,无法保证法向分量的跃变数值,法向跃变数值需要依靠电导率项约束。因此,对于低频正演,由于双旋度方程中的电导率项比重很小,故迭代初期在不同剖分单元的界面上有可能不满足散度条件。当在界面上的散度条件不满足时,通过这些过电荷计算对应的静态电势,再对迭代得到的近似电场进行校正,则校正之后的电场满足散度条件。在迭代求解有限元方程时,交替施加散度校正,与未进行散度校正的场相比,近似电场会更快地收敛到真实解,从而达到加快迭代求解的目的。
通过求解偏微分方程
| $ \nabla \cdot (\sigma \nabla \phi ) = 0\;\;\;\; \in \Omega $ | (20) |
得到静态电势ϕ。图 3为电导率分界面上的散度校正示意图,结合该分界面上的内边界条件
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;{\boldsymbol{n}} \cdot \left( {{\sigma _i}\nabla {\phi _i} - {\sigma _j}\nabla {\phi _j}} \right)\left| {{s_{ij}} = } \right.\\ {\boldsymbol{n}} \cdot \left( {{\sigma _i}{{\boldsymbol{E}}_{si}} - {\sigma _j}{{\boldsymbol{E}}_{sj}} + \Delta {\sigma _i}{{\boldsymbol{E}}_{pi}} - \Delta {\sigma _j}{{\boldsymbol{E}}_{pj}}} \right)\;\;\; \in \Gamma \end{array} $ | (21) |

|
图 3 电导率分界面上的散度校正示意图 |
式中:Sij为单元i与单元j的界面;ϕj表示单元j的静态电势。同时,界面两边的一次场及二次场必须同时取在棱边上,保持一致性。取外边界条件为势函数在边界上为零。式(20)可通过传统的节点有限单元法求解。设剖分区域内有M个节点,则电势可表示为
| $ \phi = \sum\limits_{k = 1}^M {{\phi _k}} {v_k} $ | (22) |
式中:vk为节点k的插值函数;ϕk为节点k的电势。一次场及二次场可通过各条棱边上的电场表示为
| $ {{\boldsymbol{E}}_{\rm{p}}} = \sum\limits_{j = 1}^N {{E_{{\rm{p}}j}}} {{\boldsymbol{\omega }}_j} $ | (23) |
| $ {{\boldsymbol{E}}_{\rm{s}}} = \sum\limits_{j = 1}^N {{E_{{\rm{s}}j}}} {{\boldsymbol{\omega }}_j} $ | (24) |
式中:ωj为矢量插值函数;N为剖分区域内总的棱边数。求解偏微分方程(式(20)、式(21))可等效于求解线性方程组
| $ {\boldsymbol{Dp}} = {\boldsymbol{t}} $ | (25) |
式中:
| $ \left\{ \begin{array}{l} {D_{hk}} = \int_\mathit{\Omega} \sigma \nabla {v_h} \cdot \nabla {v_k}{\rm{d}}\mathit{\Omega} \\ {P_k} = {\phi _k}\\ {t_h} = \sum\limits_{j = 1}^N {\left( {{E_{sj}}\int_S {{\sigma _h}} {{\boldsymbol{\omega }}_j} \cdot {\boldsymbol{n}}{\rm{d}}{\boldsymbol{S}} + } \right.} \\ \;\;\;\;\;\;\left. {{E_{{\rm{p}}j}}\int_S \sigma {v_h}{{\boldsymbol{\omega }}_j} \cdot {\boldsymbol{n}}{\rm{d}}{\boldsymbol{S}}} \right)\;\;\;\;\;h, k = 1, \cdots , M \end{array} \right. $ |
将复线性方程组(式(24))的实部及虚部分开,可得到两组实线性方程组,可分别应用预处理双共轭梯度法求解。然后,通过下式进行散度校正
| $ {\boldsymbol{E}}_{\rm{s}}^{\rm{c}} = {{\boldsymbol{E}}_{\rm{s}}} - \nabla \phi $ | (26) |
式中Esc代表经散度校正的二次电场。
以上所述的散度校正过程可以在迭代法求解过程中交替进行,这样可加快迭代法的收敛速度,以更短的计算时间求得满足所需精度的解。
2 数值模拟实验为了验证所提算法的有效性,设计了三个地电模型。首先通过水平层状介质模型验证散度校正的有效性及其对正演精度的影响。在此基础上,对一个三维低阻体模型进行模拟,并对比基于二次耦合势的正演结果,进一步验证所提算法的有效性。最后,通过一个油气模型证实该算法在油气勘探数值模拟中的适用性。
2.1 水平层状介质模型图 4为一个水平层状介质模型的yOz面示意图,该模型为三层介质模型。采用右手坐标系统,z轴垂直向下,x、y方向在水平面内正交。将沿x方向的单位电偶极置于原点激发谐变电磁场信号。

|
图 4 水平三层介质模型yOz面示意图 |
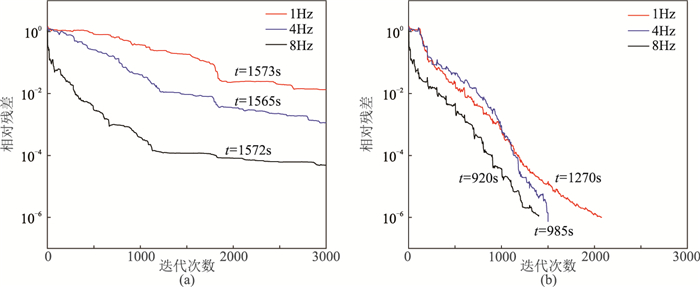
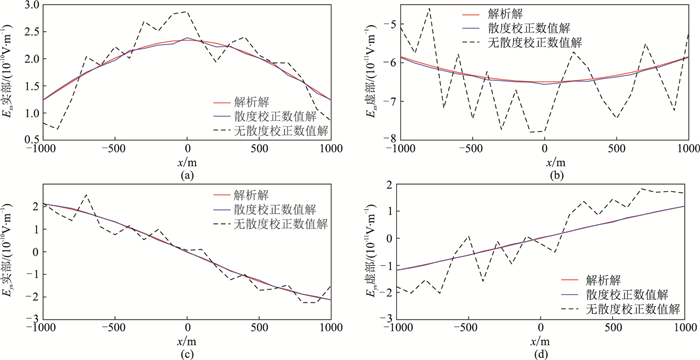
为了验证本文算法的有效性,采用同样的迭代求解方法对未施加散度校正与施加了散度校正后的迭代收敛情况及数值解进行对比。利用开源的TetGen工具[34]对该模型进行剖分, 采用统一的剖分网格,分别计算1、4、8Hz下的电磁场。图 5为正演线性方程组的迭代收敛曲线图。其中图 5b为迭代过程中每迭代100次施加一次散度校正得到的结果。由图可知,当不施加散度校正时,在3000次迭代后各个频率下的正演线性方程组无法收敛到预期残差(1×10-6);而施加散度校正后,尽管在初期迭代残差有所上升,但之后残差迅速下降,总体上使得各个频率下的正演线性方程组迭代过程明显得到加速,且成功收敛到预期残差。图中还给出了各个频率下的正演计算时间t,正演计算时间基本与迭代次数成线性关系,说明散度校正过程几乎不会额外增加正演计算时间。总体而言,施加了散度校正后,由于迭代收敛加快,正演计算时间也有所减少,且计算频率越高,加速越快。图 6展示了频率为1Hz时本文方法计算得到的二次电场数值解与解析解的对比。由图可知,未施加散度校正时正演得到的数值解与解析解差别很大,无法满足精度要求,而施加散度校正之后得到的数值解与解析解吻合较好,精度明显提高。该数值实验表明散度校正可加速非结构化有限元正演,且相比未施加散度校正时数值解精度更高。
|
图 5 水平层状介质模型线性方程组迭代求解收敛曲线对比 (a)无散度校正;(b)施加散度校正 |
|
图 6 水平层状介质模型二次电场分量数值解与解析解对比(1Hz) (a)Exs实部;(b)Exs虚部;(c)Eys实部;(d)Eys虚部 |
为了进一步验证本文算法对三维地电模型模拟的有效性,设计了一个低阻体埋藏于均匀半空间的三维地电模型(图 7)。模型采用右手坐标系,Idl为中心点位于坐标原点、沿x方向的单位电偶源。低阻体体积为800m(x)×800m(y)×200m(z),关于x轴对称。由于三维模型不存在解析解,以下将本文算法的数值解与经过精度验证的基于二次耦合势正演计算结果[35]对比。

|
图 7 三维地电模型示意图 |
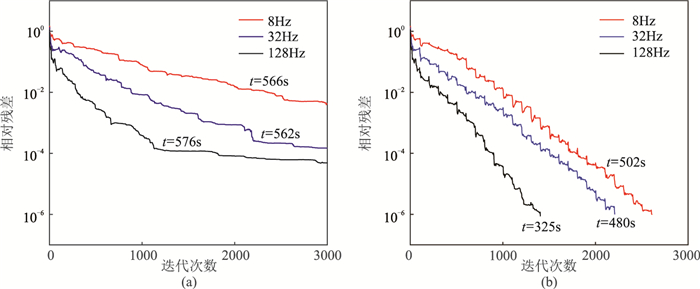
采用四面体网格对该模型进行离散,分别计算8、32、128Hz时的电磁场。图 8所示为该模型的部分网格剖分切面图。蓝色区域代表良导体所在区域,采用较密的网格,四面体网格棱边长不大于40m。白色线条代表位于地面长为2km的沿x方向的测线,点距为100m,坐标范围为-1000~1000m。对测线附近区域采用最密的网格,网格棱边长不大于20m。从观测区域往外网格逐步加大。图 9所示为各频率下正演线性方程组迭代收敛曲线,迭代过程中每100次迭代施加1次散度校正。由图可知,未施加散度校正时线性方程组的相对残差降至1×10-4后无法继续下降;而施加散度校正后各个频率下都能在3000次内收敛到预期残差,且总体正演计算时间有所减少,尤其是频率为128Hz时,正演加速比达1.77。

|
图 8 三维地电模型网格剖分切面图
(a)全区域yOz切面;(b)全区域xOy切面;(c)图a中蓝色方框区域放大图;(d)图b中蓝色方框区域放大图 紫红色区域代表空气,绿色区域代表地下围岩,蓝色区域代表低阻体,白色线条代表地面测线位置 |
|
图 9 三维地电模型不同频率时的迭代收敛曲线 (a)无散度校正;(b)施加散度校正。图中标注的时间t为模拟耗时 |
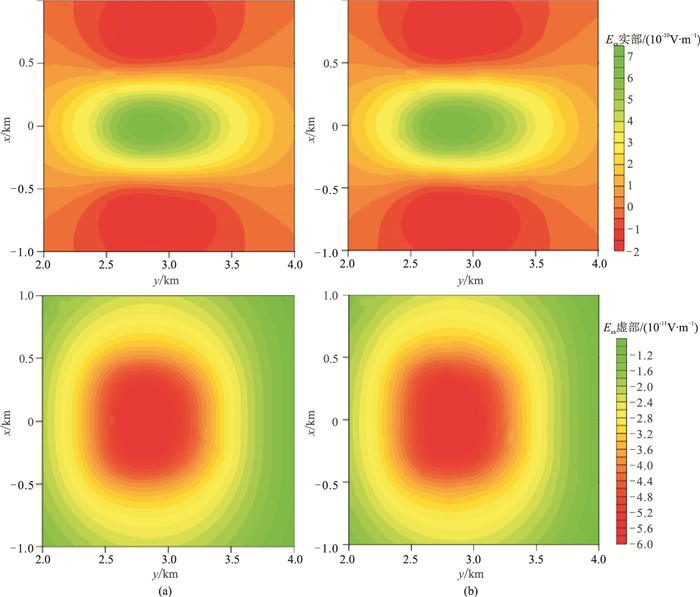
图 10是计算得到的8Hz时x方向的二次电场Exs在地面位置的平面图。由图可知,本文算法(基于二次电场)与基于二次耦合势得到的电场分布形态保持一致,具有很高的吻合度。
|
图 10 基于二次耦合势(a)及二次电场(b)计算的8Hz时Exs数值解实部(上)及虚部(下) |
进一步地,对基于二次电场和基于二次耦合势计算得到的Exs和Eys进行对比,以证实本文方法的可靠性。
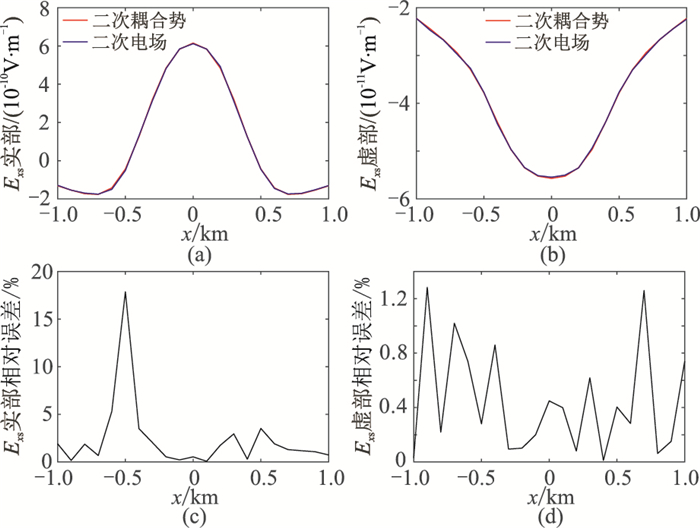
图 11和图 12分别为8Hz和32Hz时y=3km测线上二次电场分量Exs对比,其中图 11给出了相对误差曲线。由图可见,总体上基于二次电场与基于二次耦合势计算得到的Exs数值解吻合较好。另外,从图 11可知,除了在x=-500m处相对误差偏大(达17%)之外,实部分量相对误差都小于5.0%,虚部分量相对误差都小于1.4%。进一步分析图 11a可知,在x=-500m附近实部分量刚好在零值附近变换符号,场值非常小,因此其绝对误差足够小,但相对误差偏大,这是符合预期的。
|
图 11 8Hz时y=3km剖面分别基于二次电场和二次耦合势计算得到的Exs数值解对比 (a)实部分量;(b)虚部分量;(c)实部分量相对误差;(d)虚部分量相对误差 |
|
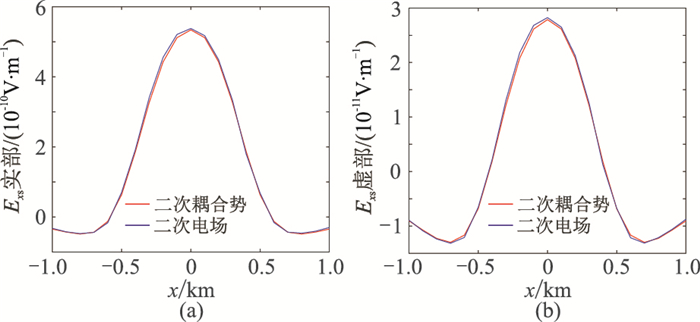
图 12 32Hz时y=3km剖面分别基于二次电场和二次耦合势计算得到的Exs数值解对比 (a)实部分量;(b)虚部分量 |
图 13为y=5km测线上基于二次电场和基于二次耦合势计算得到的二次电场Exs电场分布。由图可知,电场实部和虚部分量在2km长的测线范围内未改变符号,此时基于二次电场与基于二次耦合势的数值解实部和虚部吻合很好,相对误差都在5%以下。

|
图 13 16Hz时y=5km剖面分别基于二次电场和二次耦合势计算得到的Exs数值解对比 (a)实部分量;(b)虚部分量;(c)实部分量相对误差;(d)虚部分量相对误差 |
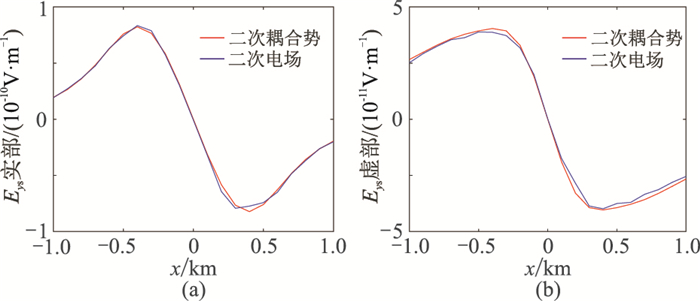
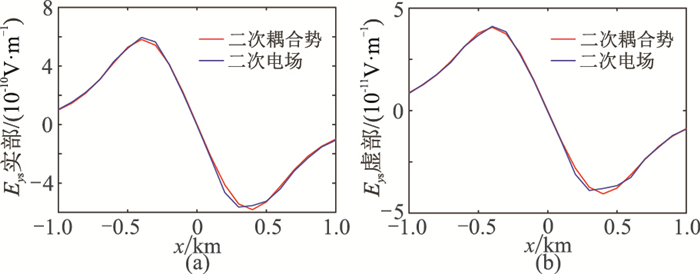
图 14和图 15分别为8Hz、32Hz时二次电场Eys数值解对比。总体而言,除了在峰值位置差异稍大外,基于二次电场和基于二次耦合势计算得到的Eys数值解吻合较好。因此,该三维地电模型的数值解对比进一步说明了本文算法的可靠性。
|
图 14 8Hz时y=3km剖面分别基于二次电场和二次耦合势计算得到的Eys数值解对比 (a)实部分量;(b)虚部分量 |
|
图 15 32Hz时y=3km剖面分别基于二次电场和二次耦合势计算得到的Eys数值解对比 (a)实部分量;(b)虚部分量 |
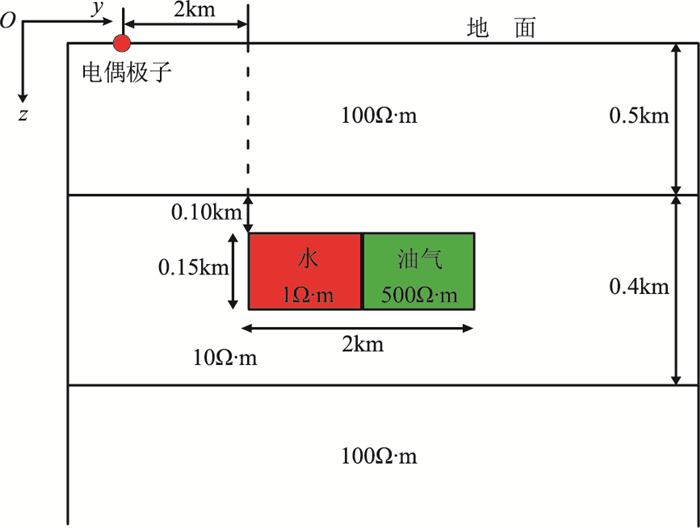
为了分析可控源电磁法在油气监测方面应用的可能性,设计了一个水驱油气监测模型(图 16)。单位电偶源置于坐标原点。该水平三层介质模型包含一个2000m×2000m×150m规模的长方体异常区域,一边是低阻的水,另一边是高阻油气,异常区域关于x轴对称。该模型可模拟从左边注入水驱动油气的过程。通过设置不同的水/油气的体积占比,分析油气占比分别为100%、50%及0时电场分量Ex和Ey分布,计算频率为1Hz,结果如图 17所示。由图可知,电场分量是关于x轴对称的,这与模型本身关于x轴对称是一致的,同时,在远离电偶源区域,场的变化较为明显。为了更清晰展示电场振幅随偏移距的变化特征,绘制了图 18。由图可知,油气含量从100%降至50%时,电场振幅变化较大,基本在偏移距y>1km时异常明显。当油气含量从50%降至0时,电场振幅的变化相对弱一些,直至偏移距y>3km时异常才变得明显。这说明当水驱动油气发生变化时,地面的电场分量变化是可探测的,有规律的。该模型实例说明本文算法可用于可控源油气监测模型的模拟。
|
图 16 三维水驱油气监测模型yOz断面图 |

|
图 17 三维油气监测模型电场水平分量Ex(上)和Ey(下)振幅 (a)油气占比100%;(b)油气占比50%;(c)无油气 |

|
图 18 三维油气监测模型x=-1.75km(上)和x=-1.00km(下)剖面电场分量Ex(a)和Ey(b)振幅曲线 |
本文开展了基于二次电场的三维可控源电磁有限元正演研究,通过结合非结构化网格和散度校正技术,为基于非结构网格的三维电磁正演线性方程组的迭代求解提供了技术支撑。层状介质模型和两个三维地电模型的数值模拟实验表明,散度校正技术适用于非结构化网格的三维正演,可加速复杂三维模型电磁响应的正演计算。通过在迭代过程中交替施加散度校正,可加快迭代求解收敛速度,在较少的迭代次数收敛到预期残差,从而达到减少正演计算时间和节约内存需求的目的。相比未施加散度校正的计算方法,本文算法能进一步提高正演精度。
| [1] |
Nabighian M, Corbett J. Electromagnetic Methods in Applied Geophysics: Theory[M]. SEG, 1988.
|
| [2] |
He Z, Liu X, Qiu W, et al. Mapping reservoir boundary by borehole-surface TFEM: Two case studies[J]. The Leading Edge, 2005, 24(9): 896-900. DOI:10.1190/1.2056379 |
| [3] |
邓居智, 陈辉, 殷长春, 等. 九瑞矿集区三维电性结构研究及找矿意义[J]. 地球物理学报, 2015, 58(12): 4465-4477. DENG Juzhi, CHEN Hui, YIN Changchun, et al. Three-dimensional electrical structures and significance for mineral exploration in the Jiujiang-Ruichang District[J]. Chinese Journal of Geophysics, 2015, 58(12): 4465-4477. DOI:10.6038/cjg20151211 |
| [4] |
汤井田, 何继善. 可控源音频大地电磁法及其应用[M]. 湖南长沙: 中南大学出版社, 2005.
|
| [5] |
Wannamaker P E, Hohmann G W, and San Filipo W A. Electromagnetic modeling of three-dimensional bodies in layered earths using integral equations[J]. Geophysics, 1984, 49(1): 60-74. DOI:10.1190/1.1441562 |
| [6] |
Wannamaker P E. Advances in three-dimensional magnetotelluric modeling using integral equations[J]. Geophysics, 1991, 56(11): 1716-1728. DOI:10.1190/1.1442984 |
| [7] |
李静和, 何展翔, 孟淑君, 等. 三维地形频率域井筒电磁场区域积分方程法模拟[J]. 物理学报, 2019, 68(14): 202-211. LI Jinghe, HE Zhanxiang, MENG Shujun, et al. Domain decomposition based integral equation modeling of 3D topography in frequency domain for well electromagnetic[J]. Acta Physica Sinica, 2019, 68(14): 202-211. |
| [8] |
Newman G A, Alumbaugh D L. Frequency-domain modelling of airborne electromagnetic responses using staggered finite differences[J]. Geophysical Prospecting, 1995, 43(8): 1021-1042. DOI:10.1111/j.1365-2478.1995.tb00294.x |
| [9] |
沈金松. 用交错网格有限差分法计算三维频率域电磁响应[J]. 地球物理学报, 2003, 46(2): 281-288. SHEN Jinsong. Modeling of 3D electromagnetic responses in frequency domain by using staggered-grid finite difference method[J]. Chinese Journal of Geophysics, 2003, 46(2): 281-288. DOI:10.3321/j.issn:0001-5733.2003.02.024 |
| [10] |
Streich R. 3D finite-difference frequency-domain mode-ling of controlled-source electromagnetic data: Direct solution and optimization for high accuracy[J]. Geophysics, 2009, 74(5): F95-F105. DOI:10.1190/1.3196241 |
| [11] |
邓居智, 谭捍东, 陈辉, 等. CSAMT三维交错采样有限差分数值模拟[J]. 地球物理学进展, 2011, 26(6): 2026-2032. DENG Juzhi, TAN Handong, CHEN Hui, et al. CSAMT 3D modeling using staggered grid finite difference method[J]. Progress in Geophysics, 2011, 26(6): 2026-2032. DOI:10.3969/j.issn.1004-2903.2011.06.017 |
| [12] |
Haber E, Ascher U, Aruliah D, et al. Fast simulation of 3D electromagnetics problems using potentials[J]. Journal of Computational Physics, 2000, 163: 150-171. DOI:10.1006/jcph.2000.6545 |
| [13] |
Jahandari H and Farquharson C. Finite-volume model-ling of geophysical electromagnetic data on unstructured grids using potentials[J]. Geophysical Journal International, 2015, 202: 1859-1876. DOI:10.1093/gji/ggv257 |
| [14] |
陈辉, 殷长春, 邓居智. 基于Lorenz规范条件下磁矢势和标势耦合方程的频率域电磁法三维正演[J]. 地球物理学报, 2016, 59(8): 3087-3097. CHEN Hui, YIN Changchun, DENG Juzhi. A finite volume solution to 3D frequency-domain electromagnetic modelling using Lorenz-gauged magnetic vector and scalar potentials[J]. Chinese Journal of Geophy-sics, 2016, 59(8): 3087-3097. |
| [15] |
Badea E A, Everett M E, Newman G A, et al. Finite-element analysis of controlled-source electromagnetic induction using Coulomb-gauged potentials[J]. Geophysics, 2001, 66(3): 786-799. DOI:10.1190/1.1444968 |
| [16] |
徐志锋, 吴小平. 可控源电磁三维频率域有限元模拟[J]. 地球物理学报, 2010, 53(8): 1931-1939. XU Zhifeng, WU Xiaoping. Controlled source electromagnetic 3-D modeling in frequency domain for finite element method[J]. Chinese Journal of Geophysics, 2010, 53(8): 1931-1939. DOI:10.3969/j.issn.0001-5733.2010.08.019 |
| [17] |
Puzyrev V, Koldan J, Puente J, et al. A parallel finite-element method for three-dimensional controlled-source electromagnetic forward modelling[J]. Geophysical Journal International, 2013, 193(2): 678-693. DOI:10.1093/gji/ggt027 |
| [18] |
Ansari S, Farquharson C G. 3D finite-element forward modeling of electromagnetic data using vector and scalar potentials and unstructured grids[J]. Geophy-sics, 2014, 79(4): E149-E165. |
| [19] |
Cai H, Hu X, Li J, et al. Parallelized 3D CSEM mode-ling using edge-based finite element with total field formulation and unstructured mesh[J]. Computers & Geosciences, 2017, 99: 125-134. |
| [20] |
刘长生, 汤井田, 任政勇, 等. 基于非结构化网格的三维大地电磁自适应矢量有限元模拟[J]. 中南大学学报(自然科学版), 2010, 41(5): 1855-1859. LIU Changsheng, TANG Jingtian, REN Zhengyong, et al. Three-dimension magnetotellurics modeling by adaptive edge finite-element using unstructured meshes[J]. Journal of Central South University (Science and Technology), 2010, 41(5): 1855-1859. |
| [21] |
杨军, 刘颖, 吴小平. 海洋可控源电磁三维非结构矢量有限元数值模拟[J]. 地球物理学报, 2015, 58(8): 2827-2838. YANG Jun, LIU Ying, WU Xiaoping. 3D simulation of marine CSEM using vector finite element method on unstructured grids[J]. Chinese Journal of Geophysics, 2015, 58(8): 2827-2838. |
| [22] |
殷长春, 张博, 刘云鹤, 等. 面向目标自适应三维大地电磁正演模拟[J]. 地球物理学报, 2017, 60(1): 327-336. YIN Changchun, ZHANG Bo, LIU Yunhe, et al. A goal-oriented adaptive algorithm for 3D magnetotelluric forward modeling[J]. Chinese Journal of Geophy-sics, 2017, 60(1): 327-336. |
| [23] |
刘颖, 李予国, 韩波. 可控源电磁场三维自适应矢量有限元正演模拟[J]. 地球物理学报, 2017, 60(12): 4874-4886. LIU Ying, LI Yuguo, HAN Bo. Adaptive edge finite element modeling of the CSEM field on unstructured grids[J]. Chinese Journal of Geophysics, 2017, 60(12): 4874-4886. DOI:10.6038/cjg20171227 |
| [24] |
叶益信, 李予国, 刘颖, 等. 基于局部加密非结构网格的海洋可控源电磁法三维有限元正演[J]. 地球物理学报, 2016, 59(12): 4747-4758. YE Yixin, LI Yuguo, LIU Ying, et al. 3D finite element modeling of marine controlled-source electromagnetic fields using locally refined unstructured meshes[J]. Chinese Journal of Geophysics, 2016, 59(12): 4747-4758. DOI:10.6038/cjg20161233 |
| [25] |
赵宁, 王绪本, 余刚, 等. 面向目标自适应海洋可控源电磁三维矢量有限元正演[J]. 地球物理学报, 2019, 62(2): 779-788. ZHAO Ning, WANG Xuben, YU Gang, et al. 3D MCSEM parallel goal-oriented adaptive vector finite element modeling[J]. Chinese Journal of Geophysics, 2019, 62(2): 779-788. |
| [26] |
Smith J T. Conservative modeling of 3D electromagnetic fields, part Ⅱ: Biconjugate gradient solution and an accelerator[J]. Geophysics, 1996, 61(5): 1319-1324. DOI:10.1190/1.1444055 |
| [27] |
陈辉, 邓居智, 谭捍东, 等. 大地电磁三维交错网格有限差分数值模拟中的散度校正方法研究[J]. 地球物理学报, 2011, 54(6): 1649-1659. CHEN Hui, DENG Juzhi, TAN Handong, et al. Study on divergence correction method in three dimensional magnetotelluric modeling with staggered-grid finite difference method[J]. Chinese Journal of Geophysics, 2011, 54(6): 1649-1659. DOI:10.3969/j.issn.0001-5733.2011.06.025 |
| [28] |
Farquharson C G, Miensopust M P. Three-dimensional finite-element modelling of magnetotelluric data with a divergence correction[J]. Journal of Applied Geophysics, 2011, 75: 699-710. DOI:10.1016/j.jappgeo.2011.09.025 |
| [29] |
Liu Y H, Yin C C. Electromagnetic divergence correction for 3D anisotropic EM modeling[J]. Journal of Applied Geophysics, 2013, 77: 19-27. |
| [30] |
秦策, 王绪本, 赵宁, 等. 频率域电磁法三维有限元正演线性方程组迭代算法[J]. 地球物理学报, 2020, 63(8): 3180-3190. QIN Ce, WANG Xuben, ZHAO Ning, et al. Research on the iterative solver of linear equations in three-dimensional finite element forward modeling for frequency domain electromagnetic method[J]. Chinese Journal of Geophysics, 2020, 63(8): 3180-3190. |
| [31] |
汤文武, 李耀国, 柳建新, 等. 基于二次电场的可控源电磁法三维矢量有限元正演模拟[J]. 石油物探, 2015, 54(6): 665-673. TANG Wenwu, LI Yaoguo, LIU Jianxin, et al. Three-dimensional controlled-source electromagnetic forward modeling by edge-based finite element using secondary electrical field[J]. Geophysical Prospecting for Petroleum, 2015, 54(6): 665-673. |
| [32] |
Jin J. The Finite Element Method in Electromagne-tics[M]. Wiley Interscience, 2002.
|
| [33] |
Saad Y. Iterative Methods for Sparse Linear Systems[M]. SIAM, 2003.
|
| [34] |
Hang Si. TetGen: a delaunay-based quality tetrahedral mesh generator[J]. ACM Transactions on Mathematical Software, 2015, 41(2): 1-36. |
| [35] |
Tang W W, Li Y G, Swidinsky A, et al. Three-dimensional controlled-source electromagnetic modelling with a well casing as a grounded source: a hybrid method of moments and finite element scheme[J]. Geo-physical Prospecting, 2015, 63(4): 1491-1507. |



 汤文武, 江西省南昌市经开区广兰大道418号东华理工大学, 330013。Email:
汤文武, 江西省南昌市经开区广兰大道418号东华理工大学, 330013。Email: 