② 中南大学地球科学与信息物理学院, 湖南长沙 410083;
③ 中国能源建设集团湖南省电力设计院有限公司, 湖南长沙 410083;
④ 东华理工大学地球物理与测控技术学院, 江西南昌 330013;
⑤ 湖南城市学院信息与电子工程学院, 湖南益阳 413002
② School of Geosciences and Info-Physics, Central South University, Changsha, Hunan 410083, China;
③ China Energy Engineering Group Hunan Electric Power Design Institute Co., Ltd., Changsha, Hunan 410083, China;
④ School of Geophysics and Measurement-control Technology, East China University of Technology, Nanchang, Jiangxi 330013, China;
⑤ College of Information and Electronic Engineering, Hunan City University, Yiyang, Hunan 413002, China
在地球物理电磁法中,正演是反演的基础。正演方法主要包括边界单元法、有限差分法、积分方程法、有限元法等,其中有限元法因其对任意复杂地形及复杂地质构造的适应能力强、计算精度较高等优点被广泛应用[1]。无论是关于位的还是关于场的方程,都需要对有限元的数值解进行数值微分后处理才能进行阻抗计算,进而获得视电阻率和相位响应。直接从有限元解计算的梯度值在单元边界上不连续且整体精度不高,虽然加密剖分网格或者增加单元形函数插值次数一定程度上可以提高精度,然而随着网格的加密和插值次数的提高,有限元方法产生的线性方程组的未知数将按几何级数急剧增加,这极大地增加了对计算机内存的需求,计算时间急剧增加。因此,对有限元数值解进行恰当的后处理以提高有限元解梯度值的精度,是有限元数值模拟中的一项重要内容。
对于有限单元法的后处理,最早是直接对单元形函数微分(Shape-function differentiation,SFD)求取辅助场,这种方法在单元边界上误差较大[2];Rodi[3]针对大地电磁法(Magnetotellurics,MT)矩形单元双线性插值的二维正演使用矩量法(the Method of Moment,MOM),其实质是将辅助场的计算函数定义为与主场形函数相同的形式,用主场值重新定义函数中的列矢量,目的是让辅助场自动满足MT的边界条件,但实现过程非常复杂且繁琐;陈乐寿等[4]进行MT二维正演时,为了适应倾斜界面,整体采用矩形网格剖分,而在分界面上将矩形单元按对角线分为两个直角三角形,求主场时直接在三角形单元上采用二次插值,然后基于形函数微分提高辅助场的精度,取得了不错的效果,但这种方法依然存在计算量和对内存需求过大的问题;陈小斌等[5-7]提出利用有限元直接迭代法实现MT二维正演模拟及线源频率电磁响应的计算,由有限元直接迭代格式得到地表三角形单元上各边中点的主场值,从而在单元上构造二次插值的形函数,然后基于形函数微分计算辅助场,该方法得到的辅助场精度有所提高,但并不适于以有限元数值模拟为前提的后处理。
对于结构化网格的节点有限元正演,拉格朗日插值(LI)法是常用的后处理方法。基于该方法,徐世浙[8]实现了MT的正演模拟,张继峰[9]实现了可控源电磁法(Controlled Source Electromagnetic Method,CSEM)的三维有限元正演,张林成等[10]实现了CSEM的三维有限元—无限元耦合正演。LI法尽管理论简单且计算量非常小,但其精度严重依赖网格大小,且要求测点附近的网格被等距剖分。在非结构化网格有限元的后处理中,移动最小二乘插值法(Moving least-square interpolation,MLSI)应用最为广泛。Badea等[11]在开展基于Coulomb位的有限元井中电磁正演模拟时,采用该算法进行后处理;Vladimir等[12]、蔡红柱等[13]及陈汉波等[14]在开展基于Coulomb位的完全非结构化网格有限元正演时,都沿用了MLSI算法,仅在权函数的使用上有所差别。尽管MLSI法可以恢复任意点的梯度值,但精度依然不高。
为获得高精度且稳定的后处理数值结果,本文引入一种基于超收敛单元片梯度值恢复(Super-convergence Patch Recovery,SPR)的后处理技术,并以可控源电磁法节点有限元正演作为应用基础,对该算法进行了详细的说明和验证。
Zienkiewicz等[15-20]发现有限元解的导数在某些特殊点上具有特别高的精度,并将这种有限元的超收敛性质用于渐进准确的Z-Z后验误差估计方法,系统地提出了SPR技术。由于SPR技术具有计算简洁、容易理解、效果显著及现有的有限元接口方便等优势,在计算流体力学、结构力学等领域已经得到广泛应用。在地球物理领域,Ren等[21]基于该方法实现了直流电阻率法的三维非结构化网格自适应有限元正演。
本文以可控源电磁法为应用基础,基于电场二次场的双旋度方程,采用结构化六面体单元的伽辽金有限元法对电场双旋度方程进行离散化;然后以单元片上高斯点的电场分量梯度值进行最小二乘曲面拟合,恢复单元片上地表测线节点上的电场梯度;最后根据电场分量的旋度方程计算地表测线上的磁场分量。地电模型分析表明,在保证主场有限元数值模拟程序可靠的前提下,与SFD、LI和MLSI方法相比,SPR后处理技术能够以极小的计算量显著提高磁场分量的计算精度,且相对误差较稳定。
1 SPR方法原理 1.1 CSEM满足的边值问题对CSEM的电场二次场的双旋度方程引入散度校正项[9]
| $ \begin{array}{l} \nabla \times \nabla \times {{\boldsymbol{E}}^{\rm{s}}} - {\rm{i}}\omega {\mu _0}\left( {\sigma - {\rm{i}}\omega {{\boldsymbol{\varepsilon }}_0}} \right){{\boldsymbol{E}}^{\rm{s}}} + \nabla \left( {\nabla \cdot \sigma {{\boldsymbol{E}}^{\rm{s}}}} \right)\\ \;\;\;\;\;\;\;\; = {\rm{i}}\omega {\mu _0}\left( {\sigma - {\sigma _{\rm{p}}}} \right){{\boldsymbol{E}}^{\rm{p}}} \end{array} $ | (1) |
式中:ω为角频率;μ0为真空中磁导率;ε0为真空中介电常数;σ为电导率;σp为背景电导率;Ep和Es分别是电场一次场和二次场。
可控源电磁法数值模拟中,为保证控制微分方程(式(1))解的唯一性,常加入无穷远边界条件,令外边界Γ上的二次场Es衰减为零
| $ {{\boldsymbol{E}}^{\rm{s}}} = 0\;\;\;\;\;\;\;\;\; \in \Gamma $ | (2) |
本文采用伽辽金节点有限元法求解边值问题(式(1)和式(2)),剖分网格采用结构化六面体单元,单元形函数采用三线性插值。整个研究区域划分为目标区域和网格边界区域:测线和源所在的区域是目标区域,采用均匀网格剖分;向外延伸区域是网格边界区域,采用逐渐向外扩大的网格剖分, 以降低边界的影响,提高数值模拟的精度。关于有限元求解的细节参考文献[9]。
1.2 有限元后处理算法本文节点有限元数值模拟的解仅针对电场。为了获得卡尼亚视电阻率、阻抗和相位等电磁响应,还需要利用有效的数值微分后处理算法,由电场的旋度方程恢复出高精度的磁场,其计算公式为
| $ {\boldsymbol{H}} = \frac{1}{{{\rm{i}}\omega {\mu _0}}}(\nabla \times {\boldsymbol{E}}) $ | (3) |
下面首先阐述本文引入SPR技术的原理。为了与常规的有限元后处理算法进行对比,分别介绍、对比SFD、LI和MLSI三种有限元后处理算法。
1.2.1 SPR后处理技术根据Herrmann理论,有限元解及其梯度在某些特殊的点上具有至少高1阶的精度,这种现象称为超收敛,这些特殊点称为超收敛点[15]。有限元解的超收敛点在节点上,而有限元解梯度的超收敛点一般与高斯点对应。
SPR技术的原理简述如下:由围绕任一公共节点的所有相关单元组成一单元片,一般将单元片上高斯点的有限元解梯度作为采样对象,设近似多项式进行最小二乘曲面拟合,以恢复单元片上节点或其他特定点的梯度值,恢复的梯度值同样具有超收敛性。
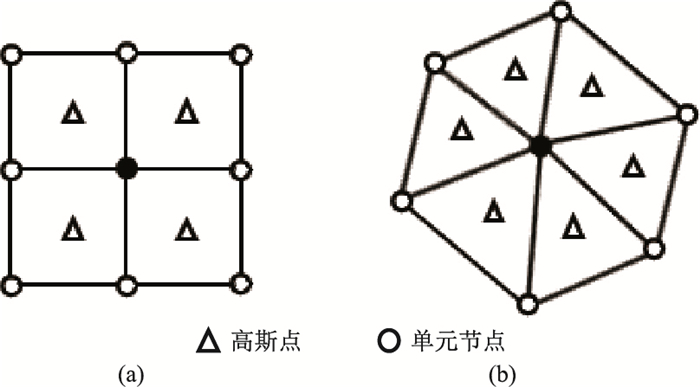
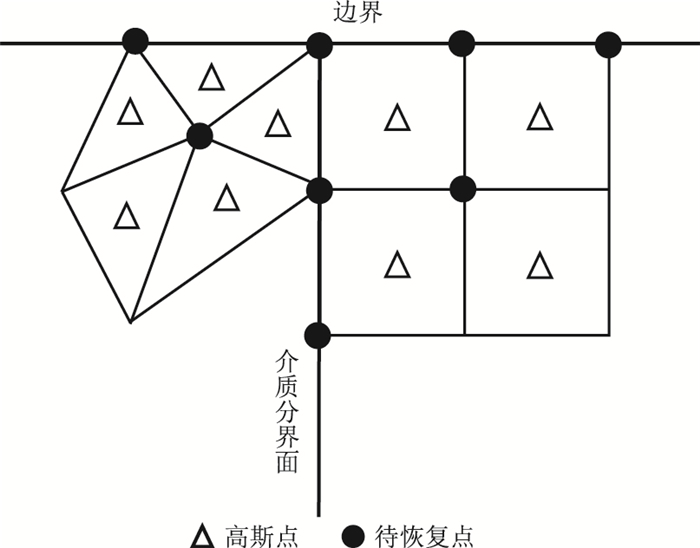
单元片一般是由以待恢复点作为公共节点的所有单元组合而成,如图 1所示。若待恢复点位于介质分界面或者介质边界时,选择界面任意一侧的邻近节点作为中心组成单元片,如图 2所示。
|
图 1 二维线性插值单元片 (a)矩形单元片;(b)三角形单元片 |
|
图 2 介质边界及分界面上的二维单元片 |
不是所有单元高斯点上梯度的收敛阶都与最佳收敛阶相对应,如二次插值的三角形单元,由于高斯点上的梯度值仍然具有很高的精度,对于梯度恢复仍然具有重要意义。单元形状和有限元插值阶次的不同都会造成高斯点上梯度的收敛阶的差异,因而恢复结果的精度也存在差异。在近似多项式的设置上,一般与有限元单元形函数的形式保持一致,可以达到最佳恢复效果。在这一过程中,若待恢复点位于介质边界或者不同介质分界面时,则该点可同时隶属于两侧不同介质的单元片,因而根据其所属的单元片恢复结果取均值。
本文有限元正演采用六面体单元及三线性插值的形函数。由于测线一般都位于地空分界面(即地面)上,以地下一侧的单元合成单元片,则测点位于单元片的边界上,如图 3所示。具体后处理过程如下。

|
图 3 六面体单元组成的单元片(三线性插值)示意图 |
首先,由单元形函数计算单元片上各采样点上的电场的梯度值∂Ei,其中i表示采样点编号。如图 3所示六面体单元,以位于单元几何中心的高斯点作为采样点,每个单元片上共计n=8个采样点。
在单元片上一般以单元片集中点作为原点建立坐标系(图 3)。在单元片上设拟合多项式的形式与三线性插值保持一致
| $ \partial {{\boldsymbol{E}}^*} = {\boldsymbol{Pm}} $ | (4) |
式中:∂E*表示电场梯度拟合式;多项式P=[1,x, y, z, xy, xz, yz, xyz];系数向量m=[m1, m2, m3, m4, m5, m6, m7, m8]T。
在每个单元片上,对于n个采样点的电场梯度值,极小化最小二乘泛函
| $ \mathit{\Pi }({\boldsymbol{m}}) = \sum\limits_{i = 1}^n {{{\left( {\partial {{\boldsymbol{E}}_i} - \partial {\boldsymbol{E}}_i^*} \right)}^2}} $ | (5) |
然后,分别对系数向量m的各分量求偏导,整理后得到
| $ {\boldsymbol{m}} = {{\boldsymbol{A}}^{ - 1}}{\boldsymbol{k}} $ | (6) |
式中:方程组系数矩阵
由上述方程组求解得到多项式的系数向量m后,便可根据式(4)恢复单元片上的地表测线上节点的电场分量梯度,并由式(3)计算磁场分量。
1.2.2 单元形函数微分法(SFD)在剖分区域内采用矩形六面体网格进行离散,母单元与子单元坐标对应关系为
| $ \left\{ {\begin{array}{*{20}{l}} {x = {x_0} + \frac{a}{2}\xi }\\ {y = {y_0} + \frac{b}{2}\eta }\\ {z = {z_0} + \frac{c}{2}\gamma } \end{array}} \right. $ | (7) |
式中:(ξ,η,γ)是母单元坐标;(x, y, z)是子单元坐标;(x0, y0, z0)是子单元的中心坐标;a、b、c分别是子单元x、y、z三个方向的棱长。
三线性插值的单元形函数统一表示为
| $ {N_i} = \frac{1}{8}\left( {1 + {\xi _i}\xi } \right)\left( {1 + {\eta _i}\eta } \right)\left( {1 + {\gamma _i}\gamma } \right) $ | (8) |
式中(ξi,ηi,γi)表示母单元上第i个节点的坐标。
六面体单元上任意点的电场分量可表示为
| $ {E_p} = \sum\limits_{i = 1}^n {{N_i}} {E_{p, i}}\;\;\;\;p = x, y, z $ | (9) |
根据上式可得空间各方向上的电场分量梯度为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial {E_p}}}{{\partial x}} = \frac{1}{{4a}}\sum\limits_{i = 1}^n {{\xi _i}} \left( {1 + {\eta _i}\eta } \right)\left( {1 + {\gamma _i}\gamma } \right){E_{p, i}}}\\ {\frac{{\partial {E_p}}}{{\partial y}} = \frac{1}{{4b}}\sum\limits_{i = 1}^n {{\eta _i}} \left( {1 + {\xi _i}\xi } \right)\left( {1 + {\gamma _i}\gamma } \right){E_{p, i}}}\\ {\frac{{\partial {E_p}}}{{\partial z}} = \frac{1}{{4c}}\sum\limits_{i = 1}^n {{\zeta _i}} \left( {1 + {\xi _i}\xi } \right)\left( {1 + {\eta _i}\eta } \right){E_{p, i}}}\\ {p = x, y, z} \end{array}} \right. $ | (10) |
最后,根据式(3)可计算磁场分量。
1.2.3 拉格朗日插值(LI)法LI法是已知节点的电场分量,令插值基函数lj(x)在点xj处取值为1,在其他点xi(i≠j)处取值为0。
所选测线处于均匀剖分的网格区域,在x和y方向采用三点中心差分、在z方向地表以下采用四点向前差分求电场梯度,可避免高阶插值出现振荡现象。计算公式为
| $ \left\{ {\begin{array}{*{20}{l}} {{{\left. {\frac{{\partial {E_p}}}{{\partial x}}} \right|}_{{x_1}}} = \frac{{E_p^{{x_2}} - E_p^{{x_0}}}}{{2a}}}\\ {{{\left. {\frac{{\partial {E_p}}}{{\partial y}}} \right|}_{{y_1}}} = \frac{{E_p^{{y_2}} - E_{{p^0}}^{{y_0}}}}{{2b}}}\\ {{{\left. {\frac{{\partial {E_p}}}{{\partial z}}} \right|}_{{z_0}}} = \frac{{ - 11E_p^{{z_0}} + 18E_p^{{z_1}} - 9E_p^{{z_2}} + 2E_p^{{z_3}}}}{{6c}}} \end{array}} \right. $ | (11) |
式中:p=x, y, z;Epx0、Epx1、Exp2和Epy0、Epy1、Epy2分别表示x和y方向上相邻节点的电场p分量值;Epz0、Epz1、Epz2、Epz3表示z方向上地表及其以下相邻节点的电场p分量值。最后,根据式(3)可计算磁场分量。
1.2.4 移动最小二乘(MLSI)法MLSI法被广泛应用于非结构化网格有限元正演的后处理。与SPR后处理技术不同,它的采样对象是节点上的电场分量,同时引入权函数,使距离中心点越远的点被赋予越小的权重,恢复局部域中任意位置的电场梯度[22]。
对于任意点K恢复其梯度值,以该点为原点、以半径R确定一个球体范围局部域,以域中节点上的电场分量f*作为采样对象。
设局部域上电场分量的线性插值函数为
| $ f = {\boldsymbol{U\alpha }} $ | (12) |
式中:多项式U=[1, x, y, z];系数向量α=[α1, α2, α3, α4]T。
设加权函数随与点K的距离增大而单调降低
| $ \omega (j) = {{\rm{e}}^{ - {\beta ^2}\left[ {{{\left( {{x_j}/{x_{\rm{m}}}} \right)}^2} + {{\left( {{y_j}/{y_{\rm{m}}}} \right)}^2} + {{\left( {{z_j}/{z_{\rm{m}}}} \right)}^2}} \right]}} $ | (13) |
式中:j表示采样点编号;xm=Max(|xj|);ym=Max(|yj|);系数β控制权函数逐渐递减到零的速度,本文取β=2。
对于局部域上的N个采样点求极小化问题
| $ F({\boldsymbol{\alpha }}) = \sum\limits_{j = 1}^N \omega (j){\left( {f_j^* - {f_j}} \right)^2} $ | (14) |
与前文泛函求极值同理,对系数向量α求偏导,可得简化的方程组
| $ {\boldsymbol{\alpha }} = {{\boldsymbol{B}}^{ - 1}}{\boldsymbol{v}} $ | (15) |
式中:系数矩阵
通过式(15)求解出方程组中的系数向量α后,便可获得点K处电场分量在x、y和z三个方向上的梯度值
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial f}}{{{\partial _{{x_K}}}}} = {\alpha _2}}\\ {\frac{{\partial f}}{{{\partial _{{y_K}}}}} = {\alpha _3}}\\ {\frac{{\partial f}}{{{\partial _{{z_K}}}}} = {\alpha _4}} \end{array}} \right. $ | (16) |
最后,结合式(16)和式(3)便可计算出点K处磁场的各个分量。
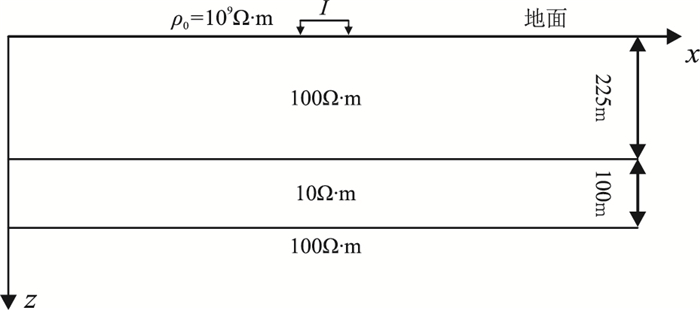
2 数值对比与分析 2.1 主程序验证为了确保后处理算法对比的可靠性,首先需要验证有限元数值模拟主程序的可靠性。设计如图 4所示的含一低阻(10Ω·m)薄层异常体的层状模型。水平电偶极源的中心位于坐标轴原点,沿x轴布设,长度为1m;供电电流I=1A,计算时考虑位移电流;发射频率为128Hz。将二次场的解析解作为参考解。
|
图 4 一维低阻层状模型 |
采用矩形六面体网格对计算区域进行剖分;对目标区域进行均匀剖分,边界区域剖分网格逐渐变大。剖分的具体方案为:x方向[-20000m, 20000m],剖分为105层;y方向[-10000m, 10000m],剖分为42层;z方向[-10000m, 5000m],剖分为34层,其中空气部分被划分为11层。
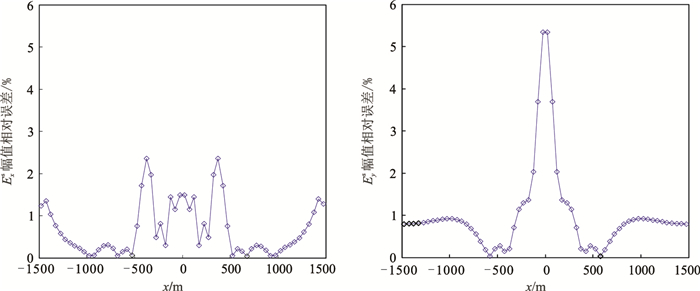
测线为y=1500m,测点沿x方向-1475~1475m均匀分布。图 5为基于节点有限元法计算的128Hz时二次电场分量的幅值相对误差曲线。由图可见,二次电场分量Exs幅值的平均相对误差为0.688%,最大相对误差为2.4%;二次电场分量Eys幅值的平均相对误差为1.00%,最大相对误差为5.3%,在x=0附近相对误差较大,这是由于Eys的解析解在这个位置非常小,趋于零。总体而言,二次电场分量幅值的相对误差基本都在2%以下,平均误差均低于1%,验证了主程序的正确性与可靠性。
|
图 5 二次电场分量128Hz时Exs(左)和Eys(右)的幅值相对误差 |
为了对比不同后处理算法的处理效果,本文选取了多个层状模型及均匀半空间模型进行测试。对于层状模型,其主场为电场二次场有限元解;对于均匀半空间模型,其主场为电场总场有限元解。本文后处理分析涉及磁场二次场Hxs、Hys及磁场总场Hx、Hy。
2.2.1 低阻层状异常体模型的二次场分析采用图 4所示低阻层状异常体模型,发射频率取128Hz,测线为y=1500m。
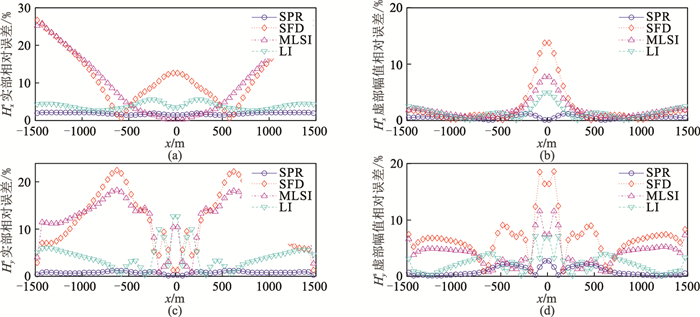
针对此低阻层状模型分别利用四种后处理算法,对二次磁场分量实部与虚部的相对误差进行分析,结果见图 6。表 1为单条测线的精度、计算时间和计算内存对比。由图 6和表 1可知,SFD法和MLSI法的相对误差较大,最高达26%,整体相对误差波动非常大。相对这两种方法,LI法的相对误差较小,但是在中垂线附近较大,最大相对误差约为14%。经SPR处理的计算结果相对误差非常小且很稳定,最大相对误差仅为2.67%,各项平均相对误差均在1.8%以内,基本没有放大二次电场的误差,恢复所得二次磁场在中垂线附近效果良好。从平均相对误差来看,二次磁场的结果优于二次电场。从表 1可知,SPR法在计算时间和计算内存的需求上都高于其他三种方法,但是对于几分钟的计算时间和几十GB内存消耗的有限元正演模拟,这样的代价是可接受的。
|
图 6 低阻层状模型不同后处理算法二次磁场分量相对误差曲线(y=1500m,f=128Hz) (a)Hxs实部;(b)Hxs虚部;(c)Hys实部;(d)Hys虚部 |
|
|
表 1 低阻层状模型四种后处理方法单测线相关参数统计 |
另外,SFD法是直接由单元形函数求取节点上的电场梯度,而SPR后处理技术是对单元形函数在高斯点上的电场梯度进行最小二乘拟合,恢复所得节点电场梯度与高斯点上具有相同的精度级别,因而SPR后处理技术恢复所得磁场的精度远高于SFD方法,说明高斯点上的电场梯度值的确比节点上值精度高,从这个角度也印证超收敛现象。
2.2.2 高阻层状异常体模型二次场分析本节采用的高阻层状异常体模型与图 4模型类似,区别是异常层的电阻率为高阻(1000Ω·m),发射频率为256Hz,测线仍取y=1500m。
图 7为高阻层状模型分别经四种后处理算法得到的二次磁场分量实部与虚部相对误差曲线,表 2为平均相对误差统计。由图 7和表 2可知,SFD法和MLSI法计算结果的平均相对误差较大,SFD法的Hxs实部和虚部、Hys实部和虚部的相对误差分别为17.90%、8.82%、18.85%和10.60%,MLSI法的Hxs实部和虚部、Hys实部和虚部的相对误差分别为8.30%、15.50%、20.60%、8.62%,整体相对误差的波动也非常大。LI法计算的Hxs和Hys实部相对误差也明显变大,相对来说对应的虚部曲线更稳定。相对前述三种方法,经SPR处理后,各项平均相对误差均低于2.4%,最大相对误差约为5%。可见经SPR后处理的数据不仅相对误差非常小,且稳定性良好。

|
图 7 高阻层状模型不同后处理算法二次磁场分量相对误差(y=1500m,f=256Hz) (a)Hxs实部;(b)Hxs虚部;(c)Hys实部;(d)Hys虚部 |
|
|
表 2 高阻层状模型四种后处理方法二次磁场分量平均相对误差统计 |
本节采用与图 4类似的均匀半空间模型,发射频率f=256Hz,测线取y=1300m。
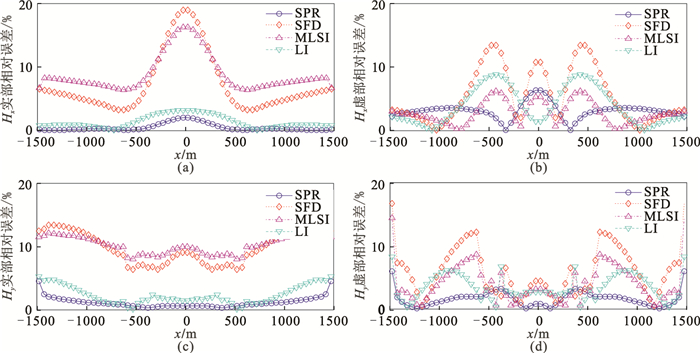
图 8为均匀半空间模型四种后处理算法得到的磁场总场分量的实部与虚部相对误差,表 3为单条测线对应参数的统计数据。由图 8和表 3可知,经SFD法处理后的Hx和Hy实部的相对误差分别为7.25%和9.90%,对应的虚部相对误差小于3%,单点的最大相对误差达到19%。经MLSI后处理的各项平均相对误差均在10%以内,最大相对误差约为16%。经LI法处理的数据相对误差较小,各项相对误差均低于2.3%。与LI法相比,经SPR处理的数据相对误差更小,平均相对误差最大值为1.55%,且误差非常稳定。
|
图 8 高阻层状模型不同后处理算法磁场总场分量相对误差图(y=1500m,f=256Hz) (a)Hx实部;(b)Hx虚部;(c)Hy实部;(d)Hy虚部 |
|
|
表 3 均匀半空间模型四种后处理方法磁场总场分量平均相对误差统计 |
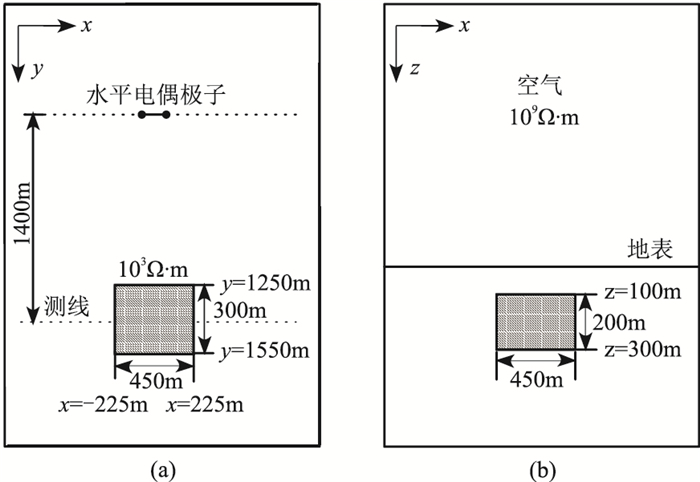
为了说明本文引入的SPR后处理对三维模型模拟的有效性,建立了图 9所示高阻体(1000Ω·m)三维模型。背景模型参数同图 4所示模型。测线为y=1400m,发射频率f=256Hz。
|
图 9 三维高阻体模型 (a)俯视图;(b)侧视图 |
对三维体空间网格进行加密,使得到的数值解无限趋近于真实解,将收敛的数值解作为近似解析解(AAS)。这里仅分析磁场,以LI法计算所得磁场数据作为磁场的近似解析解。本文在网格相对稀疏的情况下进行后处理方法的对比分析。
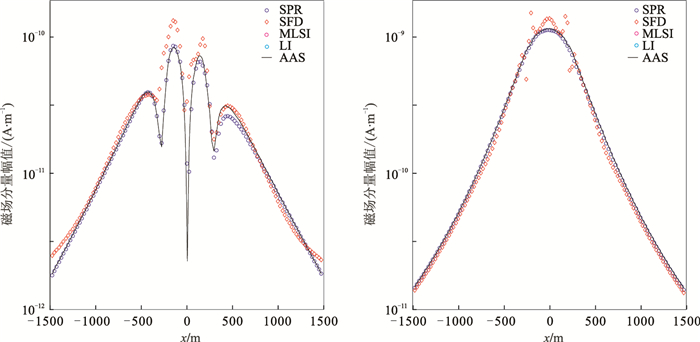
将异常体剖分为312×202×186个网格单元,以LI法计算的磁场二次场作为近似解析解。对于稀疏的剖分网格(196×156×59),不同方法后处理结果如图 10所示。可以看出,与其他三种后处理方法结果相比,SPR后处理所得磁场二次场曲线光滑性更好,不存在任何突变点,且总体上与近似解析解一致性更高。
|
图 10 三维高阻体模型不同后处理方法磁场二次场分量Hxs(左)和Hys(右)幅值曲线(y=1400m,f=256Hz) |
本文引入基于超收敛单元片梯度值恢复(SPR)的后处理技术,该算法充分利用有限元解的梯度值在高斯点上具有至少高一阶精度的超收敛现象,使用高斯点上的有限元解的梯度值进行最小二乘曲面拟合,恢复得到高精度的磁场。以结构化网格的三维可控源电磁法节点有限元正演为应用基础,与SFD、MLSI法和LI法相比,SPR后处理技术在几乎不增加正演数值模拟时间和内存的情况下,显著提高了辅助场的精度,且稳定性强。
超收敛现象同样存在于非结构化网格节点有限元,因而SPR后处理技术可进一步推广应用到非结构化网格节点有限元正演,恢复结果的精度与采样点上有限元解梯度值的收敛阶数、网格形状和形函数阶数等有关。由于超收敛性是基于节点有限元的,因而理论上SPR技术不适用于矢量有限元正演后处理。
| [1] |
吴桂桔, 胡祥云, 刘慧. CSAMT三维正演数值模拟研究进展[J]. 地球物理学进展, 2010, 25(5): 1795-1801. WU Guiju, HU Xiangyun, LIU Hui. Progress in CSAMT three-dimensional forward numerical simulation[J]. Progress in Geophysics, 2010, 25(5): 1795-1801. |
| [2] |
陈乐寿, 王光锷. 大地电磁测深法[M]. 北京: 地质出版社, 1990.
|
| [3] |
Rodi W L. A technique for improving the accuracy of finite element solutions for magnetotelluric data[J]. Geophysical Journal International, 1976, 44(2): 483-506. DOI:10.1111/j.1365-246X.1976.tb03669.x |
| [4] |
陈乐寿, 孙必俊. 有限元法在大地电磁场二维正演中的改进[J]. 石油地球物理勘探, 1982, 17(3): 69-76. CHEN Leshou, SUN Bijun. Improvement on the application of finite element method to 2-D forward solution of magnetotelluric field[J]. Oil Geophysical Prospecting, 1982, 17(3): 69-76. |
| [5] |
陈小斌. 有限元直接迭代算法[J]. 物探化探计算技术, 1999, 21(2): 165-171. CHEN Xiaobin. Direct iterative algorithm of the finite element[J]. Computing Techniques for Geophy-sical and Geochemical Exploration, 1999, 21(2): 165-171. DOI:10.3969/j.issn.1001-1749.1999.02.010 |
| [6] |
陈小斌, 胡文宝. 有限元直接迭代算法及其在线源频率域电磁响应计算中的应用[J]. 地球物理学报, 2002, 45(1): 119-130. CHEN Xiaobin, HU Wenbao. Directly iterative finite element algorithm and its application in line current source electromagnetic response modeling[J]. Chinese Journal of Geophysics, 2002, 45(1): 119-130. DOI:10.3321/j.issn:0001-5733.2002.01.015 |
| [7] |
陈小斌, 张翔, 胡文宝. 有限元直接迭代算法在MT二维正演计算中的应用[J]. 石油地球物理勘探, 2000, 35(4): 487-496. CHEN Xiaobin, ZHANG Xiang, HU Wenbao. Application of finite-element direct iteration algorithm to MT 2-D forward computation[J]. Oil Geophysical Prospecting, 2000, 35(4): 487-496. DOI:10.3321/j.issn:1000-7210.2000.04.011 |
| [8] |
徐世浙. 地球物理中的有限单元法[M]. 北京: 科学出版社, 1994.
|
| [9] |
张继锋. 基于电场双旋度方程的三维可控源电磁法有限单元法数值模拟[D]. 湖南长沙: 中南大学, 2008.
|
| [10] |
张林成, 汤井田, 任政勇, 等. 基于二次场的可控源电磁法三维有限元-无限元数值模拟[J]. 地球物理学报, 2017, 60(9): 3655-3666. ZHANG Lincheng, TANG Jingtian, REN Zhengyong, et al. Forward modeling of 3D CSEM with the coupled finite-infinite element method based on the se-cond field[J]. Chinese Journal of Geophysics, 2017, 60(9): 3655-3666. |
| [11] |
Badea E A, Everett M E, Newman G A, et al. Finite-element analysis of controlled-source electromagnetic induction using Coulomb-gauged potentials[J]. Geophysics, 2001, 66(3): 786-799. DOI:10.1190/1.1444968 |
| [12] |
Vladimir P, Jelena K, Josep D L P, et al. A parallel finite-element method for three-dimensional controlled-source electromagnetic forward modelling[J]. Geophysical Journal International, 2013, 56(2): 678-693. |
| [13] |
蔡红柱, 熊彬, Michael Zhdanov. 电导率各向异性的海洋电磁三维有限单元法正演[J]. 地球物理学报, 2015, 58(6): 2839-2850. CAI Hongzhu, XIONG Bin, MICHAEL Zhdanov. Three-dimensional marine controlled-source electromagnetic modelling in anisotropic medium using finite element method[J]. Chinese Journal of Geophysics, 2015, 58(6): 2839-2850. |
| [14] |
陈汉波, 李桐林, 熊彬, 等. 基于Coulomb规范势的电导率呈任意各向异性海洋可控源电磁三维非结构化有限元数值模拟[J]. 地球物理学报, 2017, 60(8): 3254-3263. CHEN Hanbo, LI Tonglin, XIONG Bin, et al. Finite-element modeling of 3D MCSEM in arbitrarily anisotropic medium using potentials on unstructured grids[J]. Chinese Journal of Geophysics, 2017, 60(8): 3254-3263. |
| [15] |
Zienkiewicz O C, Cheung Y K. The Finite Element Method in Structural and Continuum Mechanics: Numerical Solution of Problems in Structural and Continuum Mechanics[M]. McGraw-Hill Publishing Company Limited, 1967.
|
| [16] |
Zienkiewicz O C, Zhu J Z. A simple error estimator and adaptive procedure for practical engineering analy-sis[J]. International Journal for Numerical Methods in Engineering, 1987, 24(2): 337-357. DOI:10.1002/nme.1620240206 |
| [17] |
Zienkiewicz O C, Zhu J Z. The superconvergent patch recovery and a posteriori error estimates, Part Ⅰ: The recovery technique[J]. International Journal for Numerical Methods in Engineering, 1992, 33(7): 1331-1364. DOI:10.1002/nme.1620330702 |
| [18] |
Zienkiewicz O C, Zhu J Z. The superconvergent patch recovery and a posteriori error estimates, Part Ⅱ: Error estimates and adaptivity[J]. International Journal for Numerical Methods in Engineering, 1992, 33(7): 1365-1382. DOI:10.1002/nme.1620330703 |
| [19] |
Zienkiewicz O C, Zhu J Z. The superconvergent patch recovery(SPR) and adaptive finite element refinement[J]. Computer Methods in Applied Mechanics & Engineering, 1992, 101(1): 207-224. |
| [20] |
Zienkiewicz O C, Zhu J Z. Superconvergence and the superconvergent patch recovery[J]. Finite Elements in Analysis & Design, 1995, 19(1-2): 11-23. |
| [21] |
Ren Z, Tang J. 3D direct current resistivity modeling with unstructured mesh by adaptive finite-element method[J]. Geophysics, 2010, 75(1): H7-H17. DOI:10.1190/1.3298690 |
| [22] |
Tabbara M, Blacker T, Belytschko T. Finite element derivative recovery by moving least square interpolants[J]. Computer Methods in Applied Mechanics & Engineering, 1994, 117(1-2): 211-223. |



 陈煌, 湖南省长沙市麓山南路932号中南大学校本部地学楼, 410083。Email:
陈煌, 湖南省长沙市麓山南路932号中南大学校本部地学楼, 410083。Email: 