如何高效、准确地识别断裂系统、解释断层一直是石油地球物理勘探研究的热点与难点[1-4],断层解释成果数据是三维地质建模的重要数据来源,可为复杂断块油藏定量描述与开发提供论证基础[5-8]。在地震资料解释过程中逐一命名断层是一项繁琐而艰巨的工作,解释人员为了提高工作效率往往只命名一些重要断层,或者将断层分组,每组有几条甚至几百条断层。地质建模时依据不同的断层名区分不同断面,若不同断层的断层名相同,会造成虚假断面的现象。因此,在断层建模之前需要拆分断层。
手工拆分断层工作繁琐且十分耗时,而且断层拆分精度受主观因素制约,特别是在复杂断块区域,可能会造成错误的拆分结果。由于不同工区的地质问题不同,解释精度要求也不一致,致使自动拆分断层难度极大。因此,前人针对自动拆分断层技术的研究较少。田静[9]利用深探软件,提出基于聚类分析的自动拆分断层技术,在萨尔图油田取得了较好效果。本文提出了基于张量投票的自动拆分断层方法,详细介绍了方法原理与实现过程。渤海F工区实例证实该方法的精度在90%以上,并极大地提高了工作效率。
1 基本原理断层解释成果(断棱数据)通常包含坐标(x、y、z)、线号(Inline number)、道号(Crossline number)和断棱编号等信息,在三维空间可以视为表示位置信息的点、线数据,但拆分断层仅仅依靠位置信息是不够的。受构造运动影响,断层之间往往存在复杂的交切关系,在断层拆分时不仅需要断层的空间位置信息,还需要断层的产状(走向、倾向、倾角等)信息进行约束。因此,需要计算断层点集方向信息。计算点集数据方向信息的方法包括主成分分析法(PCA)[10-11]、最小二乘拟合法[12-13]、随机采样一致性(RANSAC)[14-15]和张量投票法[16-18]等。张量投票法具有较强的鲁棒性,因此本文选择张量投票法计算断层点集的方向属性。
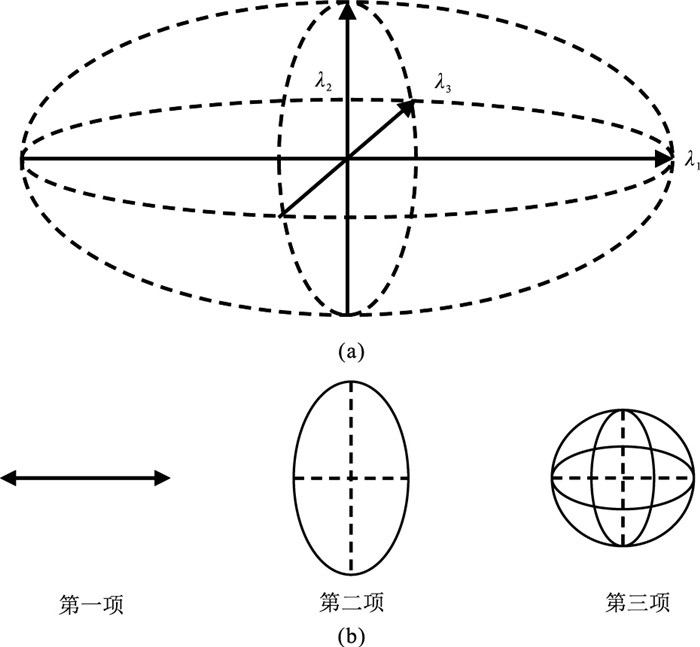
三维张量投票中的张量为一个非负定三维对称方阵,其特征值表示一个点位于某种几何结构的可能性(即显著性),对应的特征向量则代表该几何结构的方向。三维张量T在几何上描述为一个椭球体(图 1a),对其特征值分解可了解几何意义
| $ \begin{gathered} \boldsymbol{T}= {\lambda _1}{{\boldsymbol{e}}_1}{\boldsymbol{e}}_1^{\text{T}} + {\lambda _2}{{\boldsymbol{e}}_2}{\boldsymbol{e}}_2^{\text{T}} + {\lambda _3}{{\boldsymbol{e}}_3}{\boldsymbol{e}}_3^{\text{T}} = \hfill \\ \;\;\;\left( {{\lambda _1} - {\lambda _2}} \right){{\boldsymbol{e}}_1}{\boldsymbol{e}}_1^{\text{T}} + \left( {{\lambda _2} - {\lambda _3}} \right)\left( {{{\boldsymbol{e}}_1}{\boldsymbol{e}}_1^{\text{T}} + {{\boldsymbol{e}}_2}{\boldsymbol{e}}_2^{\text{T}}} \right) + \hfill \\ \;\;\;{\lambda _3}\left( {{{\boldsymbol{e}}_1}{\boldsymbol{e}}_1^{\text{T}} + {{\boldsymbol{e}}_2}{\boldsymbol{e}}_2^{\text{T}} + {{\boldsymbol{e}}_3}{\boldsymbol{e}}_3^{\text{T}}} \right) \hfill \\ \end{gathered} $ | (1) |
|
图 1 T的几何表示(a)及其分解(b) |
式中λ1>λ2>λ3为特征向量e1、e2、e3对应的特征值。式中第一项对应三维棒张量,代表一个法向量为e1的平面。第二项对应一个圆盘状椭圆体,被命名为板张量。第三项对应一个三维球张量,代表一个没有主方向的结构(图 1b)。
在构造点的初始张量表示后,每一个点将在邻域范围内产生张量场。从实现层面上看,“投票”过程就是空间邻近点产生的张量场互相叠加的过程。所谓张量场叠加,表示投票点在邻域产生的张量乘以投票点的显著性并与接收点张量矩阵直接相加。通过张量投票,接收点的张量经叠加,使特征值和特征向量方向发生变化,意味着接收点的方向和显著性不同于初始值。这一过程实现了邻域内结构信息的传递。
由于存在不同形式的张量,计算张量投票的张量场也分为不同形式。Wu等[19]将棒张量场、板张量场和球张量场统一,推导了闭合形式的张量解。在空间数据中,在点xj的张量Kj投票到点xi的张量为
| $ {{\boldsymbol{S}}_{ij}} = {c_{ij}}{{\rm{\boldsymbol{R}}}_{ij}}{{\boldsymbol{K}}_j}{\rm{\boldsymbol{R}}}{{\rm{'}}_{ij}} $ | (2) |
式中:Kj为二阶对称张量,由张量类型决定;Rij=I-2rijrijT,I为单位矩阵,rij为从点xj指向点xi的单位向量;
| $ {c_{ij}} = \exp \left( { - \frac{{{{\left\| {{{\boldsymbol{x}}_i} - {{\boldsymbol{x}}_j}} \right\|}_2}}}{{{\sigma _{\rm{d}}}}}} \right) $ | (3) |
式中σd为尺度参数。经过张量投票后,在点xi的张量通过叠加所有投票到该点的张量场得到
| $ {{\boldsymbol{K}}_i} = \sum\limits_{{{\boldsymbol{x}}_j}} {{{\boldsymbol{S}}_{ij}}} $ | (4) |
式中xj为在点xi邻域范围内的点。
由于原始断层点集没有方向信息,在张量表示时所有点的初始张量都被定义为单位矩阵,即Kj=I。然后利用式(2)、式(4)计算、更新张量场。当所有点完成张量计算、更新之后,对Ki使用特征值分解,得到按降序排列的特征值λi1、λi2和λi3以及对应的特征向量ei1、ei2和ei3。其中ei1=(e1x, e1y, e1z)为xi点所在断层面的法矢量。根据ei1可以计算断层点集中每个点对应的瞬时倾角θ和瞬时倾向Ψ
| $ \left\{ {\begin{array}{*{20}{l}} {\theta = \arccos {e_{1z}}}\\ {{\mathit{\Psi}} = {\rm{arctan}}\frac{{{e_{1x}}}}{{{e_{1y}}}}} \end{array}} \right. $ | (5) |
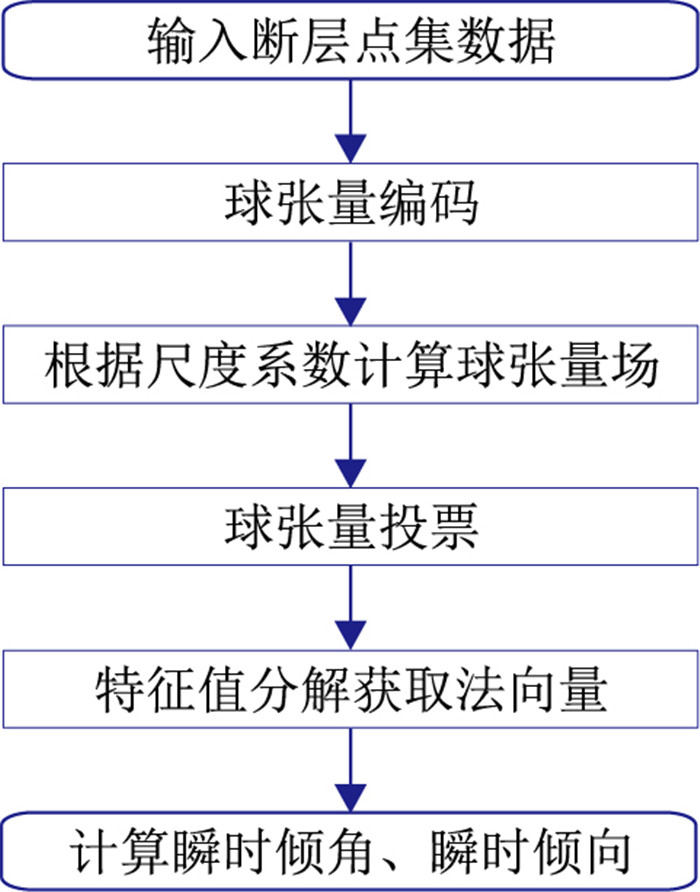
利用张量投票法计算断层点集方向的流程(图 2)为:①将所有散点编码,并以球张量的形式表现;②根据σd计算所有散点的球张量场;③球张量投票;④对投票后的张量场进行特征值分解,得到所有散点的法向量;⑤根据法向量计算所有散点的θ和Ψ。在利用张量投票法计算断层点集方向属性时,唯一需要控制的参数为σd。
|
图 2 断层点集方向信息计算流程 |
为了验证方法的效果,并分析σd对方向属性计算的影响,运用模拟交叉断层数据和实际工区数据分别测试。
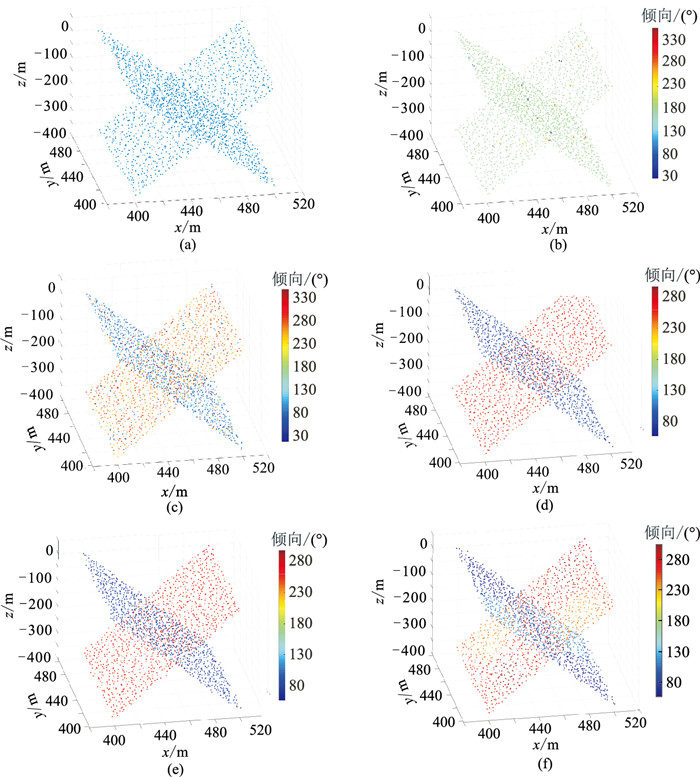
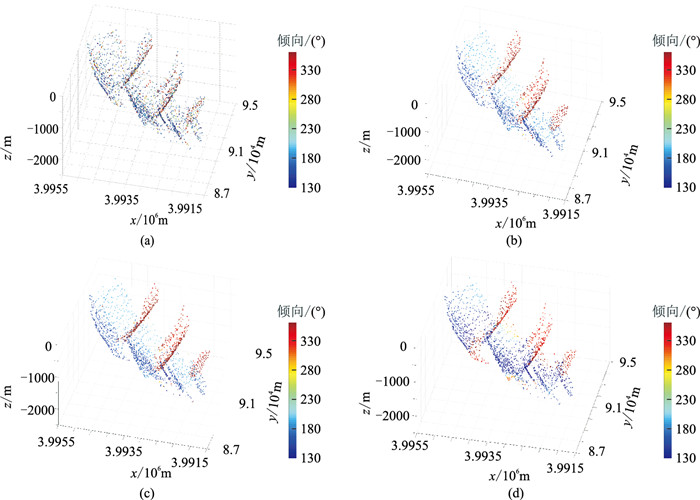
首先,根据存在交切关系的断层,模拟生成了相交断层点集模型(图 3a),分别设定不同的σd得到张量投票法计算结果(图 3b~图 3f)。分析计算结果可知:当σd取值过小时(1、5m),离散点之间无法建立投票通道,因此无法计算方向信息(图 3b、图 3c);当σd取值合适时(10、20m),主要由同一个平面的离散点相互建立投票和通信通道,因此较准确地计算了方向信息(图 3d、图 3e);当σd取值过大时(100m),同一个平面和不同平面之间的离散点均能相互建立投票和通信通道,导致计算的方向信息偏差较大(图 3f)。此外,实际断层点集的三维空间分布与模拟数据不同,纵向分布往往比横向稀疏很多,同一断棱上相邻点的纵向距离可达600m以上,而同一断层的相邻断棱的水平距离与解释的线间隔有关,一般为125~250m。测试工区相邻断棱的平均水平距离为125m,为了保证断层点集的纵向距离、水平距离的均匀性,首先对断层点集纵向插值,之后抽取部分断层点集按照不同的σd计算方向信息(图 4)。可见:当σd为50m(图 4a)时,利用同一断层相邻线的断棱无法建立投票和通信通道,此时计算误差较大;当σd为300m和500m时计算结果较准确(图 4b、图 4c);当σd为2000m(图 4d)时,部分断层的边界点受其他断层的影响,导致较大角度误差。理论数据和实际数据测试结果表明,当σd设定为横向断层点平均距离的2~4倍时,能较好地计算断点产状,为后续断层拆分提供依据。
|
图 3 不同σd计算的断层点集模型产状 (a)相交断层点集模型;(b)σd=1m;(c)σd=5m;(d)σd=10m;(e)σd=20m;(f)σd=100m图a中存在两条倾角和走向一致(倾角为75°)、倾向相对(分别为90°和270°)的断层,相邻点之间的平均空间距离为5m |
|
图 4 不同σd计算的断层点集产状 (a)50m;(b)300m;(c) 500m;(d)2000m |
通过计算得到断点的方向信息后,可以利用的信息包括空间坐标(x,y,z)、断棱编号(Segment ID,可判断断点是否属于同一条断棱)、Inline号和Crossline号、断层方向信息(瞬时倾角、瞬时倾向和走向)。根据这些信息,首先初步拆分断层,具体拆分流程为:①从断层点集中随机选取同一条断棱的点集作为初始断面模型;②从余集选取小于预设的距离阈值(同一断层相邻断棱距离的2~4倍)、倾角阈值和倾向阈值的点,构成新的断面模型;③修正新的断面模型的平均法矢量,重复步骤②,直至找不到新的样本点为止;④对找到的断层模型标号,并从断层点集删除该断棱数据,然后重复步骤①;⑤算法结束。
3.2 精细拆分在初步拆分过程中将具有相近空间位置和相似断层产状的数据分为一类,形成一条断层。这种方法在构造相对简单的工区可以有效拆分断层。但是遇到空间上非常接近且具有相近产状的多条断层时,使用正常的距离和方向阈值不能初步拆分断层(图 5a);如果调整距离和方向阈值,则可能造成过度拆分。因此需要结合地质认识对初步拆分结果质控,若不满足需求,则对所有初步拆分结果精细拆分。
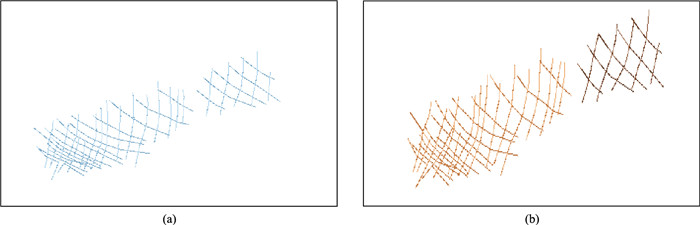
|
图 5 空间接近、产状相近的两条断层初步拆分(a)与精细拆分(b)结果 蓝色代表未拆分的同一断层,红色和黑色断棱表示精细拆分后的两条断层 |
在初步拆分的基础上,融合地震、地质解释的先验知识:①同一断面在每条Inline测线通常只有一条断棱;②同一断层的局部产状变化不大,即相邻线的断棱应具有相近的倾角,并且局部走向与断层总体走向相差不大;③同一断层在Inline和Crossline方向的断棱闭合差较小。经过精细拆分(图 5b),将相邻且产状相近的断层(图 5a)成功拆分成为两条断层。
4 实际数据测试在实际断层拆分时,相邻断层距离越小、产状越相近,拆分难度越大。因此,对于同一工区,先对一部分断层分组命名可大大减小拆分难度,后期可以依次人工拆分(只是耗时较长)。否则,当构造复杂时,手工拆分断层的难度非常大。本文选取构造十分复杂的F区,测试在近似极限情况下的断层自动拆分效果。F区位于渤海湾盆地西部,面积约为800km2。受多期次构造运动影响[20],发育三组左阶排列走滑断层(NE向、NWW向和近EW),断层之间距离很近且产状相近,存在“Y”字型相交断层,剖面上呈花状构造[21-25]。为了测试效果,将所有原始断层数据命名为一个名字(图 6a中所有断棱颜色相同),在此基础上拆分断层。可见:①与原始数据(图 6a)相比,初步拆分结果(图 6b)删除了部分小规模孤立断棱,能准确拆分大部分断层,但部分断层拆分不彻底(图 7上左、图 7下左)。主要原因是这些断层空间接近、产状相近,甚至出现部分相连的情况,因此在相同参数情况下,仅利用初步拆分算法很难一次性完成准确拆分。②精细拆分结果基于初步拆分结果,将初步拆分不彻底的断层进一步拆分(图 6c,图 7上右、图 7下右),断层位置更准确、合理,更有利于建模,精细拆分结果的准确率大于90%。
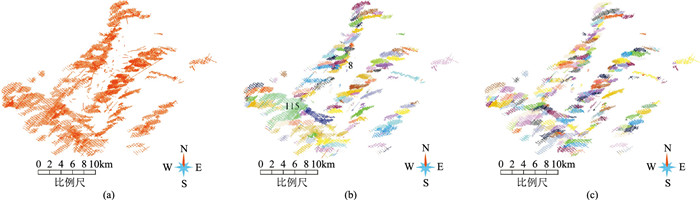
|
图 6 F区原始断层数据(a)的初步(b)、精细(c)拆分结果 在初步拆分时,原始数据相邻Inline解释间距为100m,因此选择σd=300m,距离阈值为400,角度差阈值为35°。精细合并拆分时,走向差阈值为40°,闭合差阈值(Inline和Crossline交点之间的距离)为50m |

|
图 7 8号断层(上)、115号断层(下)初步拆分(左)和精细拆分(右)结果 断层拆分时,断层颜色呈随机分布,通常不同颜色代表不同断层,若紧邻断层的颜色相同,则可能不能拆分(8号和115号断层) |
本文提出了一种自动拆分断层方法,该方法的核心是利用张量投票算法计算原始断层点集的方向信息,然后结合断层文件中的空间位置和断棱编号信息,融合现有地质认识,实现断层的自动拆分。精细拆分融合了地震、地质解释的先验知识,通过走向差阈值和闭合差阈值的约束,进一步拆分初步拆分结果。对于走向差阈值和闭合差阈值的选取,则需要建模人员以工区地质背景为参考。断层自动拆分可以极大地提高建模效率,以F区为例,传统的手动拆分耗时在1周以上,而本文提出的自动拆分算法在准确率大于90%的前提下,可在30分钟内完成拆分,因此可以作为一种有效的建模辅助手段,使建模人员摆脱繁琐的手动拆分工作,同时为地震资料解释人员提供一种高效、快速拆分、命名断层的方法。下一步的研究方向是减少阈值的硬约束,进一步提高自动拆分算法的智能性。
| [1] |
常德宽, 雍学善, 王一惠, 等. 基于深度卷积神经网络的地震数据断层识别方法[J]. 石油地球物理勘探, 2021, 56(1): 1-8. CHANG Dekuan, YONG Xueshan, WANG Yihui, et al. Seismic fault interpretation based on deep convolutional neural networks[J]. Oil Geophysical Prospecting, 2021, 56(1): 1-8. |
| [2] |
张政, 严哲, 顾汉明. 基于残差网络与迁移学习的断层自动识别[J]. 石油地球物理勘探, 2020, 55(5): 950-956. ZHANG Zheng, YAN Zhe, GU Hanming. Automatic fault recognition with residual network and transfer learning[J]. Oil Geophysical Prospecting, 2020, 55(5): 950-956. |
| [3] |
王静, 张军华, 冯德永, 等. 利用不连续性的各向异性扩散滤波方法识别断层[J]. 石油地球物理勘探, 2020, 55(6): 1349-1357. WANG Jing, ZHANG Junhua, FENG Deyong, et al. Fault identification based on a discontinuous anisotropic diffusion filter[J]. Oil Geophysical Prospecting, 2020, 55(6): 1349-1357. |
| [4] |
黄瑞婕, 刘红欣. 基于三维地质建模的断裂构造识别技术[J]. 石油天然气学报, 2010, 32(2): 217-220. |
| [5] |
徐芳, 张文旗, 李菊红, 等. "地质网格"技术在复杂断块油藏地质建模中的应用[J]. 石油地球物理勘探, 2013, 48(增刊1): 75-81. XU Fang, ZHANG Wenqi, LI Juhong, et al. Geological grid technology for 3D geology modeling in complex fault-block reservoirs[J]. Oil Geophysical Prospecting, 2013, 48(S1): 75-81. |
| [6] |
崔廷主, 马学萍. 三维构造建模在复杂断块油藏中的应用——以东濮凹陷马寨油田卫95块油藏为例[J]. 石油与天然气地质, 2010, 31(2): 198-205. CUI Tingzhu, MA Xueping. An application of 3D structural modeling to complex fault-block reservoirs: a case of the lower unit reservoir of Sha-3 Member in Block Wei-95, Mazhai Oilfield, Dongpu Depression[J]. Oil & Gas Geology, 2010, 31(2): 198-205. |
| [7] |
谭学群, 刘云燕, 周晓舟, 等. 复杂断块油藏三维地质模型多参数定量评价[J]. 石油勘探与开发, 2019, 46(1): 185-194. TAN Xuequn, LIU Yunyan, ZHOU Xiaozhou, et al. Multi-parameter quantitative assessment of 3D geological models for complex fault-block oil reservoirs[J]. Petroleum Exploration and Development, 2019, 46(1): 185-194. |
| [8] |
李兆亮, 潘懋, 韩大匡, 等. 三维构造建模技术[J]. 地球科学, 2016, 41(12): 2136-2146. LI Zhaoliang, PAN Mao, HAN Dakuang, et al. Three-dimensional structural modeling technique[J]. Earth Science, 2016, 41(12): 2136-2146. DOI:10.11764/j.issn.1672-1926.2016.12.2136 |
| [9] |
田静. 基于聚类分析的断层自动拆分技术及应用[J]. 国外测井技术, 2019, 40(6): 38-41. TIAN Jing. Fault automatic splitting technology and application based on cluster analysis[J]. World Well Logging Technology, 2019, 40(6): 38-41. |
| [10] |
Barnes A E. A filter to improve seismic discontinuity data for fault interpretation[J]. Geophysics, 2006, 71(3): P1-P4. DOI:10.1190/1.2195988 |
| [11] |
史皓良, 吴禄慎, 余喆琦, 等. 散乱点云数据特征信息提取算法[J]. 计算机工程, 2017, 43(8): 279-283. SHI Haoliang, WU Lushen, YU Zheqi, et al. Algorithm for feature information extraction from scattered point cloud data[J]. Computer Engineering, 2017, 43(8): 279-283. DOI:10.3969/j.issn.1000-3428.2017.08.047 |
| [12] |
陈俊吉, 皮大伟, 谢伯元, 等. 基于几何特征与三维点云特征的道路边沿识别算法[J]. 河北科技大学学报, 2019, 40(6): 461-468. CHEN Junji, PI Dawei, XIE Boyuan, et al. Curb re-cognition algorithm based on geometric characters and 3D point cloud features[J]. Journal of Hebei University of Science and Technology, 2019, 40(6): 461-468. |
| [13] |
LIU X P, ZHANG J, CAO J J, et al. Quality point cloud normal estimation by guided least squares representation[J]. Computers & Graphics, 2015, 51(5): 106-116. |
| [14] |
Li L, Yang F, Zhu H, et al. An improved RANSAC for 3D point cloud plane segmentation based on normal distribution transformation cells[J]. Remote Sensing, 2017. DOI:10.3390/rs9050433 |
| [15] |
Li B, Schnabel R, Klein R, et al. Robust normal estimation for point clouds with sharp features[J]. Computers & Graphics, 2010, 34(2): 94-106. |
| [16] |
Park M K, Lee S J, Lee K H. Multi-scale tensor vo-ting for feature extraction from unstructured point clouds[J]. Graphical Models, 2012, 74(4): 197-208. DOI:10.1016/j.gmod.2012.04.008 |
| [17] |
Liu M, Pomerleau F, Colas F, et al. Normal estimation for pointcloud using GPU based sparse tensor voting[C]. IEEE International Conference on Robotics and Biomimetics, 2012, doi: 10.1109/ROBIO.2012.6490949.
|
| [18] |
林洪彬, 王伟, 邵艳川, 等. 基于解析张量投票的散乱点云特征提取[J]. 图学学报, 2017, 38(2): 137-143. LIN Hongbin, WANG Wei, SHAO Yanchuan, et al. Feature extraction from unorganized point cloud based on analytical tensor voting[J]. Journal of Graphics, 2017, 38(2): 137-143. |
| [19] |
Wu T P, Yeung S K, Jia J, et al. A closed-form solution to tensor voting: Theory and applications[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 34(8): 1482-1495. |
| [20] |
张正涛, 林畅松, 李慧勇, 等. 渤海湾盆地沙垒田地区新近纪走滑断裂发育特征及其对油气富集的控制作用[J]. 石油与天然气地质, 2019, 40(4): 778-788. ZHANG Zhengtao, LIN Changsong, LI Huiyong, et al. Characteristics of the Neogene strike-slip faults and their controls on hydrocarbon accumulation in Shaleitian uplift, Bohai Bay Basin[J]. Oil & Gas Geo-logy, 2019, 40(4): 778-788. |
| [21] |
石文龙, 张志强, 彭文绪, 等. 渤海西部沙垒田凸起东段构造演化特征与油气成藏[J]. 石油与天然气地质, 2013, 34(2): 242-247. SHI Wenlong, ZHANG Zhiqiang, PENG Wenxu, et al. Tectonic evolution and hydrocarbon accumulation in the east part of Shaleitian Sailent, western Bohai Sea[J]. Oil & Gas Geology, 2013, 34(2): 242-247. |
| [22] |
谈明轩, 朱筱敏, 刘强虎, 等. 渤海沙垒田地区新近系明下段多河型地震地貌学特征[J]. 石油实验地质, 2019, 41(3): 411-419. TAN Mingxuan, ZHU Xiaomin, LIU Qianghu, et al. Seismic geomorphological characteristics of multiple fluvial patterns in the Neogene Lower Minghuazhen Member in the Shaleitian area, Bohai Sea[J]. Petroleum Geology & Experiment, 2019, 41(3): 411-419. |
| [23] |
彭文绪, 张如才, 樊建华, 等. 渤海海域西部凸起区大型雁列断层特征[J]. 石油地球物理勘探, 2011, 46(5): 795-801. PENG Wenxu, ZHANG Rucai, FAN Jianhua, et al. Large scale en echelon faults on the west uplift in Bohai Gulf, China[J]. Oil Geophysical Prospecting, 2011, 46(5): 795-801. |
| [24] |
时梦临, 张成, 解习农. 渤海沙垒田凸起带地层流体特征及其形成机制[J]. 特种油气藏, 2020, 27(2): 78-86. SHI Menglin, ZHANG Cheng, XIE Xinong. Formation fluid properties and mechanism of Shaleitian uplift zone in Bohai Sea[J]. Special Oil and Gas Reservoirs, 2020, 27(2): 78-86. DOI:10.3969/j.issn.1006-6535.2020.02.012 |
| [25] |
彭文绪, 张志强, 姜利群, 等. 渤海西部沙垒田凸起区走滑断层演化及其对油气的控制作用[J]. 石油学报, 2012, 33(2): 204-212. PENG Wenxu, ZHANG Zhiqiang, JIANG Liqun, et al. Evolution of strike-slip faults in the Shaleitian bulge of the western Bohai offshore and their control on hydrocarbons[J]. Acta Petrolei Sinica, 2012, 33(2): 204-212. |



 刘旭明, 天津市滨海新区中心北路1889号中海油田服务股份有限公司, 300451。Email:
刘旭明, 天津市滨海新区中心北路1889号中海油田服务股份有限公司, 300451。Email: 