② 成都理工大学地球勘探与信息技术教育部重点实验室, 四川成都 610059
② Key Lab of Earth Exploration & Information Techniques of Ministry of Education, Chengdu University of Technology, Chengdu, Sichuan 610059, China
时频分析方法[1]是一种时变非平稳信号处理方法,它对信号进行时频分析处理,得到时频域信号的能量分布,是地震资料精细构造解释和储层预测的有力工具。
基于傅里叶变换的时频分析方法发展很快,如:Gabor[1]提出的短时傅里叶变换;Morlet等[2]提出的小波变换;Stockwell等[3]结合前两种方法的优点提出的S变换。但上述方法受到自身固有的测不准原则所限,时频分辨率无法达到很好的效果,为了达到最佳效果,研究人员又提出了各种改进的时频分析方法。陈学华等[4]提出广义S变换,引入了λ和p两个参数共同控制窗函数,相比S变换具有更好的适应性和更高的时频分辨率;Lu等[5]基于零相位自适应鲁棒滤波器提出了一种加窗Hilbert变换;Gholami等[6-7]利用混合范数稀疏性,提出稀疏短时傅里叶变换;Sattari等[8-9]考虑到地震数据频率的迅速变化,提出了一种新的基于快速稀疏的S变换。这些改进的方法使时频分辨率得到较大的提升,并且广泛应用于地震资料低频阴影分析、断层识别、弹性参数反演和河道检测等[10-12]。在实际应用中取得的效果证明了时频分析方法的有效性。高静怀等[13]将广义S变换应用于薄互层模型分析;陈学华等[14]利用高阶伪希尔伯特变换对河道、断层等不连续信息进行预测;对于依赖频率的AVO反演,时频分析方法则直接影响反演结果的分辨率[15-16]。此外,在流体流度属性的提取中,高精度时频分析方法也有广泛应用[17-21]。
随着地震勘探技术不断发展,地震资料解释的精度要求越来越高,需要利用更加有效的时频分析方法从地震数据中提取有效信息。因此,进一步改进和发展高分辨时频分析方法仍是开展地震资料精细储层描述的关键环节。本文在窗函数优化S变换[9]的基础上,提出通过引入新的窗函数调节参数,构建改进的窗参数优化S变换方法,能够根据实际信号的振幅谱自适应地求取最优窗参数,得到的时频谱具有更高的时频聚焦性和分辨率。通过合成信号对比分析,验证了该方法在低、高频端均具有较高分辨率;在实际地震资料的河道检测中能更好地刻画河道的空间展布特征,显示的地质细节特征更清晰,利于地震资料的精细解释。
1 方法原理Stockwell等[3]首次提出了时频分辨率随频率变化的时频表示方法——S变换。它所选取的窗函数随频率的增加而自适应地调节时窗宽度。在S变换中,高斯窗函数的表达式为
| $ w\left( t \right) = \frac{1}{{\sigma \sqrt {2\pi } }}\exp \left( { - \frac{{{t^2}}}{{2{\sigma ^2}}}} \right) $ | (1) |
式中:t为时间;σ为窗函数的调节尺度参数。
为了使窗函数随频率变化,定义σ为随频率f变化的函数,即
| $ \sigma \left( f \right) = \frac{1}{{\left| f \right|}} $ | (2) |
S变换的窗函数会根据频率的增加而减小时宽,但在时域压缩的同时会在频域拉伸,存在时间分辨率和频率分辨率不相容的问题。Sattari等[9]在S变换的基础上,提出窗参数优化S变换,将传统S变换中仅随时间或频率变化产生最优窗的问题转化为一个二维的问题。通过优化的窗函数定位局部的强振幅频率分量,并对弱振幅频率分量进行模糊处理,从而控制二者在时频谱上的影响区域。由于振幅谱中包含了频率和振幅的信息,因此将其作为优化窗函数的参照。基于上述思想,本文设计了根据实际地震信号的振幅谱自适应确定最优窗参数的流程,并基于求取的最优化窗参数构建了改进的窗参数优化S变换方法。优化流程如下。
(1) 对原始信号x(t)求取振幅谱
| $ X\left( f \right) = {\text{abs}}\left\{ {{\text{FT}}\left[ {x\left( t \right)} \right]} \right\} $ | (3) |
式中FT表示傅里叶变换。
(2) 对振幅谱X(f)进行平滑处理
| $ {X_{\text{s}}}\left( f \right) = {\text{smooth}}\left[ {X\left( f \right)} \right] $ | (4) |
(3) 保证平滑后的结果均大于0,即
| $ {\hat X_{\text{s}}}\left( f \right) = {X_{\text{s}}}\left( f \right) - \min \left[ {{X_{\text{s}}}\left( f \right)} \right] $ | (5) |
(4) 归一化
| $ \hat X_{\text{s}}^{\text{n}}\left( f \right) = \frac{{{{\hat X}_{\text{s}}}\left( f \right)}}{{\max \left[ {{{\hat X}_{\text{s}}}\left( f \right)} \right]}} $ | (6) |
(5) 通过参数r将
| $ \hat X_{{\text{sn}}}^r\left( f \right) = \left[ {r\hat X_{\text{s}}^{\text{n}}\left( f \right)} \right] + 1 $ | (7) |
式中r为可调节参数。通常对于带限信号,r取1或2;对于地震信号,r取3或4;对于带宽信号,r取5~10。
(6) 求得随频率变化的最优窗参数
| $ s\left( f \right) = \frac{N}{2}\frac{1}{{\hat X_{{\text{sn}}}^r\left( f \right)}} $ | (8) |
式中N表示离散信号点的个数。
通过r优化后的窗参数优化S变换,使信号时频聚焦性和分辨率有了一定的提高,但仍有改进的空间。之后引入λ、p(λ>0, 0.5≤p≤1.5)两个参数,共同调节窗参数s(f)。在实际应用中,根据实际信号的特征灵活选择λ、p,当λ取值过大时,可适当调整p值,从而得到最佳的窗参数。
λ、p两个参数的进一步优化,使改进后的调节参数可以根据实际应用中非平稳信号的频率分布特点和时频分析的侧重点,调节窗函数随频率变化的速度,能够灵活地适应具体信号。
进一步构建出改进的窗参数优化S变换的调节参数为
| $ {\sigma _{{\text{opt}}}} = \frac{{{{\left[ {s\left( f \right)} \right]}^p}}}{\lambda } $ | (9) |
由此得到改进的窗函数
| $ w\left( {t, f} \right) = \frac{\lambda }{{\sqrt {2\pi} {{\left[ {s\left( f \right)} \right]}^p}}}\exp \left\{ { - \frac{{{\lambda ^2}{t^2}}}{{2{{\left[ {s\left( f \right)} \right]}^{2p}}}}} \right\} $ | (10) |
得到改进的窗参数优化S变换表达式
| $ \begin{gathered} {\text{MS}}{{\text{T}}_{{\text{opt}}}}\left( {f,\tau } \right) = \int_{ - \infty }^{ + \infty } {x\left( t \right)} \frac{\lambda }{{\sqrt {2\pi } {{\left[ {s\left( f \right)} \right]}^p}}} \times \hfill \\ \;\;\;\;\;\;\;\;\exp \left\{ { - \frac{{{\lambda ^2}{{\left( {t - \tau } \right)}^2}}}{{2{{\left[ {s\left( f \right)} \right]}^{2p}}}}} \right\}\exp \left( { - {\text{i2}}\pi ft} \right)dt \hfill \\ \end{gathered} $ | (11) |
式中τ为窗函数中心点,控制窗函数在时间t上的移动。
图 1显示不同处理流程对窗参数的优化效果。图 1a为合成信号时域波形,对合成信号分别做S变换、窗参数优化S变换和改进的窗参数优化S变换,并与信号的振幅谱(图 1b)进行对比。由图可以看出,窗参数的变化具有对称性,其中S变换的窗参数呈线性变化(图 1c),进行优化后的窗参数随信号振幅谱自适应变化(图 1d),本文方法对优化的窗参数又有进一步改进,得到的窗参数能够更好地适应信号的突变(图 1e)。

|
图 1 信号振幅与不同处理方法窗宽的关系 (a)信号时域波形;(b)信号振幅谱;(c)S变换窗宽;(d)窗参数优化S变换窗宽;(e)本文方法S变换窗宽 |
优化后的窗函数可以根据实际信号的振幅区分不同的频率分量,同时在时间和频率域也具有自适应性。λ和p两个可调节参数的引入,使变换处理更具灵活性,时频聚集性更好,对非平稳信号中的各种分量区分能力更强,因而该方法得到的时频谱具有较高的时频分辨率。此外,当λ=1、p=1时,该方法即等价于窗参数优化S变换。
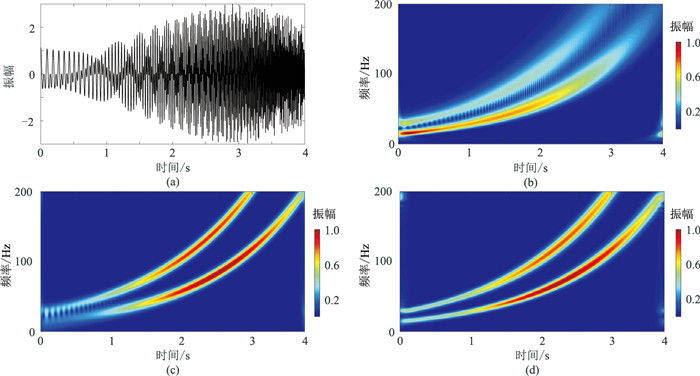
2 模型试算与分析为了便于分析本文方法的效果,设计了一个合成的非平稳信号进行模型试算。信号由两个不同频率成分的Chrip信号组成(图 2a)。对该信号分别做S变换、窗参数优化S变换(r=10)和改进的窗参数优化S变换(r=10,λ=6,p=0.5),分别得到对应的时频谱(图 2b~图 2d)。对比可知,窗参数优化S变换(图 2c)相比S变换(图 2b)具有更高的频率分辨率,尤其在高频部分优势更加明显,原因在于窗参数优化S变换在S变换的基础上对强振幅频率分量进行了适应性调节,因此得到的时频谱分辨率更高,聚焦性更好。而相比窗参数优化S变换的结果,改进的窗参数优化S变换(图 2d)不仅在高频端保持了很高的分辨率,在低频端分辨率也有明显的提升,能够更清楚地分离两个不同频率分量的信号,说明本文方法具有更强的信号区分能力。
|
图 2 合成的Chrip非平稳信号及不同方法处理的时频谱 (a)合成的Chrip非平稳信号;(b)S变换时频谱;(c)窗参数优化S变换时频谱;(d)本文方法S变换时频谱 |
将本文方法应用到某海上工区的实际地震资料处理。图 3a为工区内提取的原始地震剖面(图中蓝色线为解释的目的层),对地震数据分别做S变换、窗参数优化S变换(r=3)和改进的窗参数优化S变换(r=3,λ=8,p=0.5)后,抽取40Hz的共频率剖面进行对比分析。由图 3可见,改进的窗参数优化S变换得到的共频率剖面(图 3d)分辨率更高,并且具有很好的横向连续性,可以更好地表现地震记录随时间的变化。说明本文方法在提升时频聚焦性和时频分辨率方面效果更佳,能更好地适应非平稳信号的突变。

|
图 3 原始地震剖面及不同方法处理后的40Hz共频剖面 (a)原始地震剖面;(b)S变换共频率剖面;(c)窗参数优化S变换共频率剖面;(d)本文方法S变换共频率剖面 |
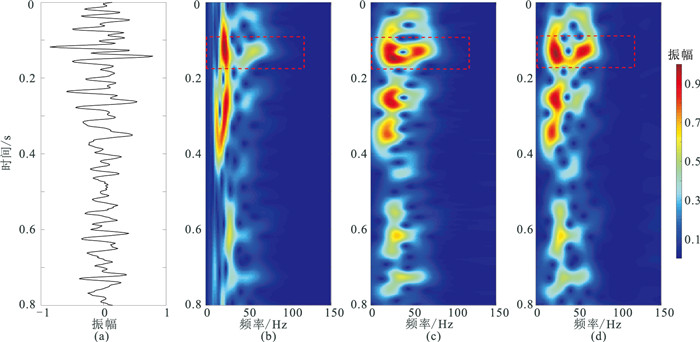
从图 3所示剖面中抽取第500道地震记录进行单道时频分析,结果显示,本文方法S变换结果同样显示出更好的时频聚焦性和更高的分辨率,频谱能够更加清晰地反映地震记录的变化(图 4d中红色虚线框标识处),说明改进的窗参数优化S变换在实际应用中更具优势。
|
图 4 单道地震记录及其不同方法处理的时频谱 (a)单道地震记录;(b)S变换时频谱;(c)窗参数优化S变换时频谱;(d)本文方法S变换时频谱 |
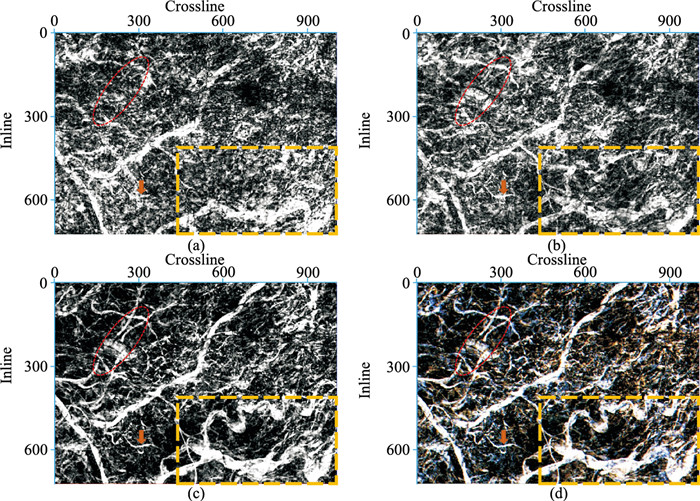
为进一步说明本文方法的实用性和优越性,将上述三种S变换方法应用于整个工区三维地震数据体处理。图 5为原始地震数据体中抽取的沿层切片(图中黑线为图 3选取的剖面位置)。由图可见,该地区河道较为发育,但是切片上显示的河道特征比较模糊,难以获得有效的细节信息。分别采用不同方法对三维数据进行瞬时谱分解,然后从不同方法处理得到的40Hz数据体中抽取沿层切片,进行河道特征分析。结果显示,在常规S变换(图 6a)和窗参数优化S变换(图 6b)结果中, 能够显示出较大尺度的河道(图中黄色矩形虚线框所示),但是背景比较模糊;在本文方法处理的结果中,除了清晰显示较大尺度的河道外,还能见到一些更小细节的河道(图 6c中红色椭圆虚线框所示)。此外,从图 6c中还观察到一些隐蔽的河道(图中橙色箭头所示),而该特征未在图 6a和图 6b中清晰显示。说明改进的窗参数优化S变换结果能够更加清晰地显示河道的形态和分布,刻画更多的细节特征。图 6d为应用本文方法对数据体进行分频处理后,对40、60、80Hz的单频振幅谱进行RGB融合[22-24]得到的切片。图中同样显示出了隐蔽河道的位置和细节,且更为清晰。

|
图 5 原始地震数据沿目的层的振幅切片 |
|
图 6 不同方法处理数据体抽取的沿层切片 (a)S变换;(b)窗参数优化S变换;(c)本文方法S变换;(d)RGB融合 |
本文基于窗参数优化S变换,通过引入新的调节参数,构建了一种改进的窗参数优化S变换方法,合成信号和实际资料的应用结果均表明该方法具有时频分辨率高和能量聚集性好的优势。在三维地震资料的河道检测中,改进的窗参数优化S变换的处理结果效果更好,能够更清晰地刻画出河道的形态,显示河道的连续性,为地震资料精细储层描述提供了有力的技术支持。此外,该方法在地震属性分析、弹性参数反演等方面也具有良好的应用前景。
| [1] |
Gabor D. Theory of communication[J]. Journal of the Institution of Electrical Engineers-Part Ⅲ: Radio and Communication Engineering, 1946, 93(26): 429-457. |
| [2] |
Morlet J, Arens G, Fourgeau E, et al. Wave propagation and sampling theory-Part Ⅰ: Complex signal and scattering in multilayered media[J]. Geophysics, 1982, 47(2): 203-221. DOI:10.1190/1.1441328 |
| [3] |
Stockwell R G, Mansinha L, Lowe R P. Localization of the complex spectrum: the S transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001. DOI:10.1109/78.492555 |
| [4] |
陈学华, 贺振华, 黄德济. 基于广义S变换的地震资料高效时频谱分解[J]. 石油地球物理勘探, 2008, 43(5): 53-57. CHEN Xuehua, HE Zhenhua, HUANG Deji. Efficient time-spectrum decomposition of seismic data based on generalized S transform[J]. Oil Geophysical Prospecting, 2008, 43(5): 53-57. |
| [5] |
Lu W K, Zhang C K. Robust estimation of instantaneous phase using a time-frequency adaptive filter[J]. Geophysics, 2013, 78(1): O1-O7. DOI:10.1190/geo2011-0435.1 |
| [6] |
Gholami A. Sparse time-frequency decomposition and some applications[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(6): 3598-3604. DOI:10.1109/TGRS.2012.2220144 |
| [7] |
Radad M, Gholami A, Siahkoohi H R. S-transform with maximum energy concentration: Application to non-stationary seismic deconvolution[J]. Journal of Applied Geophysics, 2015, 118: 155-166. DOI:10.1016/j.jappgeo.2015.04.010 |
| [8] |
Sattari H, Gholami A, Siahkoohi H R. Seismic data analysis by adaptive sparse time-frequency decomposition[J]. Geophysics, 2013, 78(5): V207-V217. DOI:10.1190/geo2012-0550.1 |
| [9] |
Sattari H. High-resolution seismic complex trace analysis by adaptive fast sparse S-transform[J]. Geophysics, 2017, 82(1): V51-V67. DOI:10.1190/geo2015-0425.1 |
| [10] |
陈学华, 贺振华, 黄德济, 等. 时频域油气储层低频阴影检测[J]. 地球物理学报, 2009, 52(1): 215-221. CHEN Xuehua, HE Zhenhua, HUANG Deji, et al. Low frequency shadow detection of oil and gas reservoirs in time-frequency domain[J]. Chinese Journal of Geophysics, 2009, 52(1): 215-221. |
| [11] |
陈波, 魏小东, 任敦占, 等. 基于谱分解技术的小断层识别[J]. 石油地球物理勘探, 2010, 45(6): 890-894. CHEN Bo, WEI Xiaodong, REN Dunzhan, et al. Identification of small faults based on spectral decomposition[J]. Oil Geophysical Prospecting, 2010, 45(6): 890-894. |
| [12] |
黄捍东, 张如伟, 孟宪军, 等. 基于小波变换的叠前地震弹性参数反演[J]. 石油地球物理勘探, 2008, 43(5): 562-567. HUANG Handong, ZHANG Ruwei, MENG Xianjun, et al. Prestack seismic elastic parameter inversion based on wavelet transform[J]. Oil Geophysical Prospecting, 2008, 43(5): 562-567. DOI:10.3321/j.issn:1000-7210.2008.05.013 |
| [13] |
高静怀, 陈文超, 李幼铭, 等. 广义S变换与薄互层地震响应分析[J]. 地球物理学报, 2003, 46(4): 526-532. GAO Jinghuai, CHEN Wenchao, LI Youming, et al. Generalized S transform and analysis of thin interbed seismic response[J]. Chinese Journal of Geophysics, 2003, 46(4): 526-532. DOI:10.3321/j.issn:0001-5733.2003.04.015 |
| [14] |
陈学华, 贺振华, 黄德济. 地震资料的高阶伪希尔伯特变换边缘检测[J]. 地球物理学进展, 2008, 23(4): 1106-1110. CHEN Xuehua, HE Zhenhua, HUANG Deji. Seismic data edge detection based on higher-order pseudo Hilbert transform[J]. Progress in Geophysics, 2008, 23(4): 1106-1110. |
| [15] |
Luo C, Li X, Huang G. Hydrocarbon identification by application of improved sparse constrained inverse spectral decomposition to frequency-dependent AVO inversion[J]. Journal of Geophysics and Engineering, 2018, 15(4): 1446-1459. DOI:10.1088/1742-2140/aab1d6 |
| [16] |
罗鑫, 陈学华, 张杰, 等. 基于依赖频率AVO反演的高含气饱和度储层预测方法[J]. 石油地球物理勘探, 2019, 54(2): 356-364. LUO Xin, CHEN Xuehua, ZHANG Jie, et al. Prediction method of high gas saturation reservoir based on frequency dependent AVO inversion[J]. Oil Geophy-sical Prospecting, 2019, 54(2): 356-364. |
| [17] |
陈学华, 贺振华, 朱四新, 等. 地震低频信息计算储层流体流度的方法及其应用[J]. 应用地球物理, 2012, 9(3): 326-332. CHEN Xuehua, HE Zhenhua, ZHU Sixin, et al. Seismic low-frequency-based calculation of reservoir fluid mobility and its applications[J]. Applied Geophysics, 2012, 9(3): 326-332. |
| [18] |
张生强, 韩立国, 李才, 等. 基于高分辨率反演谱分解的储层流体流度计算方法研究[J]. 石油物探, 2015, 54(2): 142-149. ZHANG Shengqiang, HAN Liguo, LI Cai, et al. Computation method for reservoir fluid mobility based on high-resolution inversion spectral decomposition[J]. Geophysical Prospecting for Petroleum, 2015, 54(2): 142-149. DOI:10.3969/j.issn.1000-1441.2015.02.004 |
| [19] |
赵子豪, 李凌, 马跃华, 等. 辫状河沉积储层预测技术——以大港探区孔店油田为例[J]. 石油地球物理勘探, 2017, 52(1): 152-159. ZHAO Zihao, LI Ling, MA Yuehua, et al. Braided river sedimentary reservior prediction: an example of Kongdian Oilfield in Dagang[J]. Oil Geophysical Prospecting, 2017, 52(1): 152-159. |
| [20] |
刘杰, 张懿疆, 王秀玲, 等. 利用反褶积广义S变换提取流体流度属性[J]. 石油地球物理勘探, 2019, 54(3): 617-623. LIU Jie, ZHANG Yijiang, WANG Xiuling, et al. Re-servoir fluid mobility extration based on the deconvolution generalized S-transform[J]. Oil Geophysical Prospecting, 2019, 54(3): 617-623. |
| [21] |
黄德智, 韩立国, 李辉峰, 等. 基于S变换自适应滤波迭代的多源地震数据分离[J]. 石油地球物理勘探, 2020, 55(6): 1253-1262. HUANG Dezhi, HAN Liguo, LI Huifeng, et al. Deblending of seismic data based on S-transform adaptive filtering iteration[J]. Oil Geophysical Prospecting, 2020, 55(6): 1253-1262. |
| [22] |
陈学华, 钟文丽, 贺振华, 等. 瞬时谱数据的谱加权自适应带通滤波融合[J]. 石油地球物理勘探, 2012, 47(3): 452-456. CHEN Xuehua, ZHONG Wenli, HE Zhenhua, et al. Spectra-weighted adaptive band-pass filtering fusion of instantaneous spectral data[J]. Oil Geophysical Prospecting, 2012, 47(3): 452-456. |
| [23] |
曹鉴华. RGB混频显示技术及其在河道识别中的应用[J]. 勘探地球物理进展, 2010, 33(5): 355-358. CAO Jianhua. RGB color blending and its application in channel recognition[J]. Progress in Exploration Geophysics, 2010, 33(5): 355-358. |
| [24] |
陈珊, 于兴河, 刘力辉, 等. 基于匹配追踪的RGB融合技术及在河道刻画中的应用[J]. 地球学报, 2015, 36(1): 111-114. CHEN Shan, YU Xinghe, LIU Lihui, et al. RGB ploting technique based on matching pursuit algorithm and its application to channel characterization[J]. Acta Geoscientica Sinica, 2015, 36(1): 111-114. |



 陈学华, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院5301室, 610059。Email:
陈学华, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院5301室, 610059。Email: 