② 页岩油气富集机理与有效开发国家重点实验室 北京 102206;
③ 国家能源页岩油研发中心 北京 102206
② State Key Laboratory of Shale Oil and Gas Enrichment Mechanisms and Effective Development, Beijing 102206, China;
③ State Energy Center for Shale Oil Research and Development, SINOPEC, Beijing 102206, China
地震储层预测技术应用于致密砂岩油气藏时,由于储层本身的物理性质、特征(如储层与围岩的纵波阻抗接近或重叠区域大),常用的叠后纵波阻抗反演技术难以取得好的预测效果[1-5]。在此情况下需要进行叠前反演,联合应用储层的纵、横波阻抗、泊松比等弹性参数对储层及流体进行预测[6-10]。在叠前反演中,最为重要和基础的工作是通过对已钻井的测井资料进行岩石物理建模,获得已钻井的横波信息。岩石物理建模是致密砂岩储层地震预测中的基础,不可回避,因此得到越来越多的重视。
对砂泥岩岩石物理研究的方法可以分为两类。一类以岩石物理测试数据为基础,建立砂泥岩弹性参数与岩石物性、矿物组分间的关系,并最终以经验公式的形式显式地表达这种关系,其中以Nur等[11-12]、Krief等[13]、Han等[14]的方法为代表;另一类则是以等效介质理论为基础,从测井及解释数据出发,建立地层弹性参数与地层物性参数间的联系,其中以Xu等[15-16]提出的岩石物理模型(Xu-White模型)最具代表性,至今仍被广泛应用[17-18]。
在第一类方法中,Nur等[11-12]提出了临界孔隙度模型,建立了岩石骨架速度与岩石基质速度和孔隙度间的关系。Krief等[13]以Raymer等[19]的数据为基础提出干岩石的体积模量等于基质体积模量乘以一个孔隙度的幂函数,在孔隙度远小于临界孔隙度的条件下,该模型与临界孔隙度模型结果相近。Han等[14]在研究中建立了纵波速度与孔隙度以及泥质含量间的关系。第一类方法由于是建立在某个地区有限的岩心测试数据基础上,使用时必须利用本区的测试数据或测井数据对相应的经验公式进行校验,并调整相应的经验系数。
第二类方法中,Xu等[15-16]使用了Voigt-Reuss-Hill(V-R-H)模型、Kuster-Toksöz(K-T)模型和微分等效介质(DEM)模型,通过测井解释的矿物组分和孔隙度等参数重构地层的纵、横波速度;王震宇等[20]在致密砂岩的岩石物理建模中使用自洽模型计算岩石的体积模量;刘振峰[21]则考虑致密砂岩储层可能发育裂缝的特点,将各向异性理论引入到致密砂岩岩石物理建模中。
第二类方法由于不受测试数据的限制,岩石物理建模需要的输入数据易于获得,因而得到广泛应用,成为叠前反演必需的技术环节和手段。但是这类常规岩石物理建模方法应用于致密砂岩仍面临如何准确获取岩石基质弹性参数的挑战。对于众多的岩石物理建模方法,无论使用何种模型,流程如何变化,都需要利用岩石的矿物组分估算岩石基质的弹性模量。现有的岩石物理建模方法通常是将组成岩石的矿物体积百分含量和对应的各矿物弹性模量看作已知直接代入,或是对每种矿物的弹性模量利用经验进行选择。这些方法在实际应用中存在许多困难。对于致密砂岩,应用这种方法更困难,其中最主要的限制是对于矿物成分的解释。
通常测井资料解释中将致密砂岩的组成矿物解释为砂质成分和泥质成分两种,并通过放射性测井等资料确定砂质成分和泥质成分的体积百分比。但是这种划分极其粗略,砂质成分既可以由纯的石英矿物组成,也可以由石英与长石等矿物组成,各种矿物的体积百分比也因不同的成因条件而千差万别。在此条件下,试图以单纯石英矿物的体积模量替代砂质成分的体积模量必然导致结果的偏差。对于泥质成分,由于黏土矿物的复杂性,问题更为突出。因此,现有的岩石物理建模方法不适用致密砂岩。
张金强等[22]针对碳酸盐岩储层的某些特定情形提出了利用统计方法获取岩石基质模量的方法,但该方法同样不适用于致密砂岩的复杂矿物条件。为此,本文通过联合应用临界孔隙度模型和Gassmann方程,提出了一种自适应估算泥质与砂质成分弹性模量的方法。
1 自适应岩石物理建模方法 1.1 常规岩石物理建模方法回顾通过对常规岩石物理建模方法流程的回顾,可以更为清楚地认识在致密砂岩储层领域所面临的问题与挑战。以应用Xu-White模型进行岩石物理建模为例,其基本流程包括以下关键环节。
(1) 岩石基质弹性模量计算。假设岩石基质由N种矿物组成,每种矿物的体积含量为Vi,则岩石基质的弹性模量可以由下式计算
| $ X_{\mathrm{m}}=\frac{1}{2}\left(\sum\limits_{i=1}^{N} X_{i} V_{i}+\frac{1}{\sum\limits_{i=1}^{N} \frac{V_{i}}{X_{i}}}\right) $ | (1) |
式中Xm、Xi分别为岩石基质和第i种矿物的弹性模量,既可以是体积模量,也可以是剪切模量,或者由二者线性组合形成其他弹性模量。式(1)是经典的V-R-H模型,利用Voigt界限和Reuss界限的平均计算混合物的体积模量。
(2) 岩石骨架弹性模量计算。在得到岩石基质的弹性模量后,利用K-T模型和微分等效介质理论,将孔隙加入岩石基质。根据K-T模型,有
| $ K_{\mathrm{d}}-K_{\mathrm{m}}=\frac{1}{3}\left(K^{\prime}-K_{\mathrm{m}}\right) \frac{3 K_{\mathrm{d}}+4 \mu_{\mathrm{m}}}{3 K_{\mathrm{m}}+4 \mu_{\mathrm{m}}} \sum\limits_{l} \phi_{l} T_{1}\left(\alpha_{l}\right) $ | (2) |
| $ \begin{aligned} &\mu_{\mathrm{d}}-\mu_{\mathrm{m}}=\frac{1}{5}\left(\mu^{\prime}-\mu_{\mathrm{m}}\right) \times \\ &\frac{6 \mu_{\mathrm{d}}\left(K_{\mathrm{m}}+2 \mu_{\mathrm{m}}\right)+\mu_{\mathrm{m}}\left(9 K_{\mathrm{m}}+8 \mu_{\mathrm{m}}\right)}{5 \mu_{\mathrm{m}}\left(3 K_{\mathrm{m}}+4 \mu_{\mathrm{m}}\right)} \sum\limits_{l} \phi_{l} F\left(\alpha_{l}\right) \end{aligned} $ | (3) |
式中:Kd、Km、K′分别为岩石骨架、基质和孔隙充填物的体积模量;μd、μm、μ′则为相应的剪切模量;ϕl为岩石第l种孔隙充填物的体积百分含量;αl为对应的横纵比;F(αl)=T2(αl)-T1(αl)/3;T1、T2是αl的函数,具体形式见附录A。在这一环节中,将孔隙充填物的体积模量与剪切模量都设为零。K-T模型的应用条件为ϕ/α≪1,即孔隙度与孔隙横纵比之比远小于1。实际应用中,这一条件较难满足,为此利用微分等效介质理论进行处理,即将每种基质的孔隙分成若干份,依次将孔隙加入基质中,每次加入一份孔隙后基质的弹性模量进行更新。
(3) 利用Gassmann方程计算孔隙充填流体后饱和流体岩石的弹性模量及速度。根据Gassmann方程,流体饱和岩石的弹性模量是岩石骨架、岩石基质以及孔隙流体体积模量的函数
| $ K_{\mathrm{s}}=K_{\mathrm{d}}+\frac{\left(1-\frac{K_{\mathrm{d}}}{K_{\mathrm{m}}}\right)^{2}}{\frac{\phi}{K_{\mathrm{f}}}+\frac{1-\phi}{K_{\mathrm{m}}}-\frac{K_{\mathrm{d}}}{K_{\mathrm{m}}^{2}}} $ | (4) |
| $ \mu_{\mathrm{s}}=\mu_{\mathrm{d}} $ | (5) |
式中:Ks、μs为流体饱和岩石的体积模量和剪切模量;ϕ为总孔隙度;Kf为流体的体积模量。故流体饱和岩石的纵波速度和横波速度分别为
| $ \left\{\begin{array}{l} v_{\mathrm{P}}=\sqrt{\frac{K_{\mathrm{s}}+4 \mu_{\mathrm{s}} / 3}{\rho}} \\ v_{\mathrm{S}}=\sqrt{\frac{\mu_{\mathrm{s}}}{\rho}} \end{array}\right. $ | (6) |
在常规岩石物理建模的三个关键环节中,人们更多地关注了第二个环节。如针对微分等效介质理论对于不同孔隙添加顺序结果会出现不同的缺陷,有学者提出了应用自洽理论进行建模的思路,也获得了一定的应用。但是,在实践中第一个环节面临更大的挑战。在第一个环节,首先假设组成岩石基质的矿物成分及其体积百分比是已知的,这一条件较为苛刻。实际测井数据解释仅可以获得泥质和砂质的百分含量,不能获得每种矿物的百分含量,难以满足高精度岩石物理建模要求。因为砂质成分可以由石英、长石或其他碎屑颗粒组成,黏土可以由高岭石、云母、绿泥石等复杂矿物组成。为应对这一困难,常规岩石物理建模通常采用两种方法。第一种方法认为砂质成分仅由石英矿物颗粒组成,并通过交会图的方法获得干黏土的模量参数;第二种方法,根据地质分析资料(如X射线衍射分析)确定砂质和泥质的平均矿物组成,并在整个工区内应用。第一种方法所引入的误差是显而易见的,第二种方法从某种程度上减少了第一种方法造成的误差,但是对于陆相致密砂岩储层,由于具有沉积相带横向变化快的特点,难以利用有限的地质分析资料确定砂质和泥质成分的矿物组成,因此仍会在建模过程中引入较大误差。另外,实际应用中,地质分析资料也存在缺失或获取困难等问题。
1.2 致密砂岩自适应岩石物理建模方法假设地层在一定深度范围内(可以是一个沉积段、小层,也可以人工划分)稳定沉积,测井解释的砂质成分、泥质成分分别由特定不变的矿物组分组成,这样可以将二者等效为两种介质。若能通过已有数据反推得到两种等效介质的弹性模量,就解决了上文所述岩石物理建模中面临的实际问题。具体步骤如下。
(1) 岩石基质弹性模量的估计。根据临界孔隙度模型,有
| $ K_{\mathrm{d}}=K_{\mathrm{m}}\left(1-\frac{\phi}{\phi_{\mathrm{c}}}\right) $ | (7) |
| $ \mu_{\mathrm{d}}=\mu_{\mathrm{m}}\left(1-\frac{\phi}{\phi_{\mathrm{c}}}\right) $ | (8) |
式中ϕc为临界孔隙度,对于致密砂岩一般约为0.4。
利用式(6)可根据纵、横波速度和密度数据求取流体饱和岩石的弹性模量Ks、μs,再根据式(5)可获得岩石骨架模量μd,然后利用式(8)可得到μm。
将式(7)代入式(4),经简单运算,可得
| $ \begin{aligned} &(1-x) \phi K_{\mathrm{m}}^{2}-\left[K_{\mathrm{s}} \phi-K_{\mathrm{f}}(1-x)(x-\phi)-\right. \\ &\left.K_{\mathrm{f}} x^{2}\right] K_{\mathrm{m}}-K_{\mathrm{f}} K_{\mathrm{s}}(x-\phi)=0 \end{aligned} $ | (9) |
式中x=ϕ/ϕc。式(9)是关于Km的二次方程。解式(9)可得到方程的两个根,取其中正值为Km的解。分析式(9)中Km各次项的系数,可以看出,当孔隙度ϕ等于零时,各次项的系数也等于零,此时方程无解。为防止这种情况发生,对于解释孔隙度极小的曲线段,可根据物理上的含义,令Km=Ks。
(2) 砂质及泥质成分弹性模量上限、下限的求取。在得到岩石基质的弹性模量Km、μm后,结合测井解释的泥质含量曲线,可以通过最小二乘法求取砂质及泥质成分的等效弹性模量。第一步中应用临界孔隙度模型,而临界孔隙度模型是以成分较纯的砂岩数据为基础得出的经验公式,未考虑复杂组分和孔隙结构对岩石骨架模量的影响,因此会给计算引入误差。鉴于此,分别利用Voigt上限公式和Reuss下限公式进行反演。应用Voigt上限公式求取的砂质、泥质矿物的弹性模量作为下限,应用Reuss下限公式求取的弹性模量作为上限。以应用Voigt上限公式求取砂、泥质体积模量的过程为例说明具体求解方法。
设在一定深度范围内,有L个样点,其基质的体积模量可表示为Km∈R1×L。相应的测井解释泥质含量为Vsh∈R1×L,设砂质和泥质成分的体积模量分别为Ksand、Ksh,则根据Voigt上限公式,有
| $ \boldsymbol{K}_{\mathrm{m}}=K_{\mathrm{sand}}\left(\boldsymbol{I}-\boldsymbol{V}_{\mathrm{sh}}\right)+K_{\mathrm{sh}} \boldsymbol{V}_{\mathrm{sh}} $ | (10) |
式中I为元素全部为1的向量。则求解Ksand、Ksh就转化为标准的最小二乘问题
| $ \varPhi_{1}=\left\|\boldsymbol{K}_{\mathrm{m}}-K_{\text {sand }}\left(\boldsymbol{I}-\boldsymbol{V}_{\mathrm{sh}}\right)+K_{\mathrm{sh}} \boldsymbol{V}_{\mathrm{sh}}\right\|_{2}^{2} $ | (11) |
(3) 利用最优化方法确定砂质、泥质成分的弹性模量。由于泥质、砂质成分弹性模量与岩石速度间是复杂的非线性关系,需要用全局寻优的算法进行求解。综合考虑计算的全局收敛性和计算成本,本文选用模拟退火算法。正演采用式(1)~式(6)所述流程,同时定义目标函数为
| $ \varPhi_{2}=\left\|\boldsymbol{v}_{\mathrm{P}}-\boldsymbol{v}^{\prime}{}_{\mathrm{P}}\right\|^{2}+\left\|\boldsymbol{v}_{\mathrm{S}}-\boldsymbol{v}^{\prime}{}_{\mathrm{S}}\right\|^{2} $ | (12) |
式中:vP、vS分别为建模深度段内实测的L个样点的纵、横波速度;v′P、v′S为对应的建模速度。
考虑到步骤(1)、步骤(2)中应用经验公式可能引入的计算误差,可以对求取的砂质和泥质成分的弹性模量范围进行适当放大,保证方法的容错性。
(4) 砂质、泥质成分弹性模量的微调。利用以上三步可以大致得到全局最优点附近的参数值,可以采用一定的策略在结果附近对反演的参数进行微调。一个较为简便的策略是:分别保持砂质、泥质成分的纵波模量不变,小幅度调整砂质、泥质成分的体积模量和剪切模量。其中,纵波模量的定义为
| $ M=K+\frac{4}{3} \mu $ | (13) |
按照这个策略,如果小幅增大泥质成分剪切模量(如+0.01GPa),就要相应地减小泥质成分体积模量(-0.013GPa),反之亦然。这个过程可以对砂质成分和泥质成分分别进行。
通过以上四步,解决了砂质、泥质成分弹性模量选取的难题。然后,可以利用常规方法完成相应的建模过程。
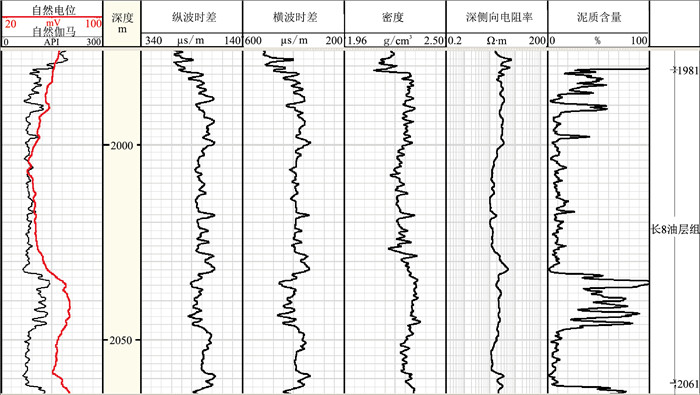
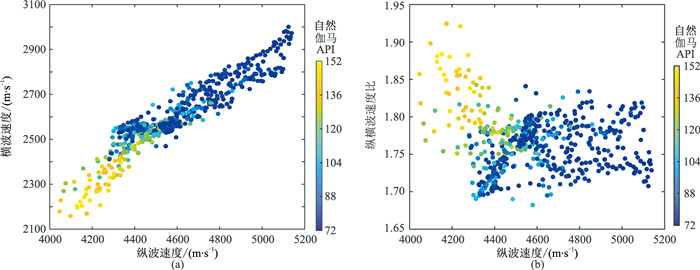
2 自适应岩石物理建模实际算例利用所提方法,对鄂尔多斯盆地南缘M靶区的X1井进行岩石物理建模。主要目的层为延长组长8油层组。该段地层主要由河流—三角洲相中砂岩、细砂岩构成,交错层理发育,夹灰黑色、灰色和黑色泥岩。自然电位曲线呈平缓波状夹齿状或漏斗状低值异常,自然伽马值整体偏高,砂岩段一般在70~100API之间;电阻率曲线呈齿状中高阻。在砂岩段密度有降低的趋势。图 1为X1井长8油层组的测井曲线,可以看出,长8油层组主要由砂岩构成,泥质含量不高。该井有偶极横波测井资料,横波时差曲线与纵波时差曲线形态相关度高。绘制该井段纵横波速度交会图(图 2a),可以看出泥岩(高GR值)具有较低的纵、横波速度。同时,在纵波速度与纵横波速度比交会图(图 2b)上,泥岩与砂岩的表现出一定的分异,泥岩整体表现出较高的纵横波速度比,但存在一定程度的混叠,且规律性不强,难以进行合理的、有明确地质意义的解释。
|
图 1 X1井测井曲线 |
|
图 2 X1井实测数据交会分析 (a)纵波速度与横波速度;(b)纵波速度与纵横波速度比 |
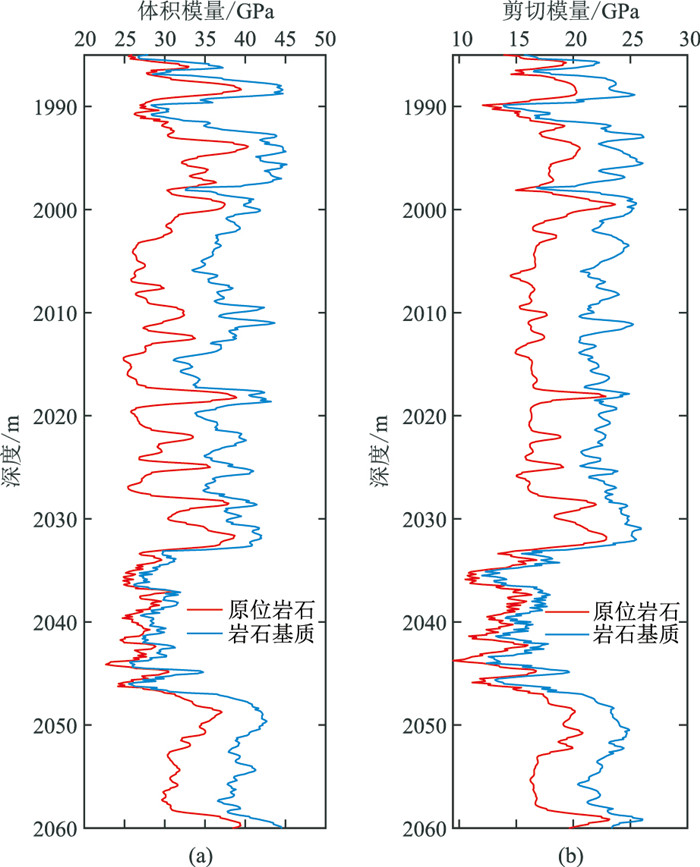
应用本文提出的方法对X1井进行岩石物理建模。首先,根据式(6),计算岩石的剪切模量和体积模量,然后利用式(5)和式(8)得到岩石基质的剪切模量,进而利用式(9)求取岩石基质的体积模量。图 3为原位岩石弹性模量(红色曲线)与计算的基质弹性模量(蓝色曲线)间的对比,可以看出,砂岩段基质弹性模量明显大于岩石的弹性模量,而对于泥岩段,由于本区泥岩压实强烈,孔隙度低,故基质弹性模量与岩石弹性模量非常接近;泥岩段(深度约为2033~2047m)基质的体积模量和剪切模量明显低于相邻砂岩段。
|
图 3 原位岩石与计算的基质的弹性模量对比 (a)体积模量;(b)剪切模量 |
第二,以岩石基质的弹性模量和解释的泥质含量曲线作为输入,分别应用Voigt公式和Reuss公式,并利用最小二乘法求取泥质和砂质成分的弹性模量的下限和上限。在该算例中,求得的泥质成分与砂质成分弹性模量的上、下限值如表 1所示。
|
|
表 1 砂质、泥质成分弹性模量上、下限 |
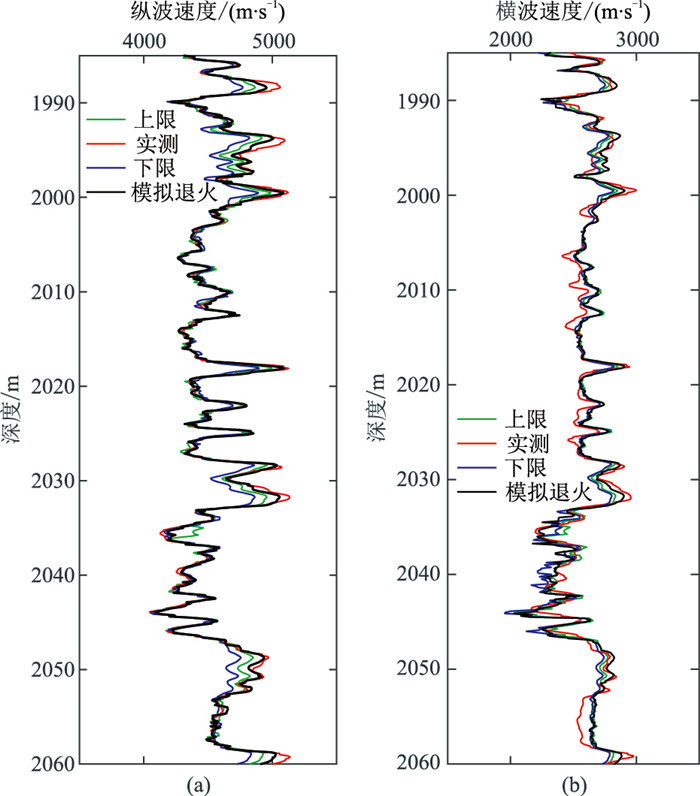
第三,利用模拟退火算法求取砂质与泥质成分的弹性模量。考虑到步骤二中存在的误差会导致求取的上、下限值存在误差,在模拟退火算法的求解中,将上限上浮20%,下限下调20%,这样放大了求解区间,增加了方法的容错性。利用模拟退火算法得到泥质和砂质成分的体积模量分别为19.34、46.55GPa,剪切模量为9.42、25.16GPa。图 4为实测纵横波速度曲线与本文模拟退火算法求得的弹性模量进行岩石物理建模及应用表 1中的上限和下限进行岩石物理建模的结果对比。可以看出,利用模拟退火算法求得的砂、泥质弹性模量进行岩石物理建模,其精度明显高于直接利用上、下限进行岩石物理建模的结果。
|
图 4 实测纵横波速度与岩石物理建模结果对比 (a)纵波速度;(b)横波速度 |
最后,对上一步求得的结果进行微调,即
| $ \left\{\begin{array}{l} \boldsymbol{K}=\boldsymbol{K}_{0}+\frac{4}{3} n \boldsymbol{b} \\ \boldsymbol{\mu}=\boldsymbol{\mu}_{0}+\frac{4}{3} n \boldsymbol{b} \end{array}\right. $ | (14) |
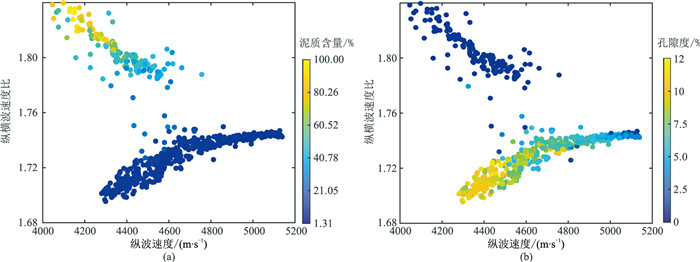
式中:K0、μ0为模拟退火求得的砂、泥质体积模量和剪切模量组成的向量;n为自然数;向量b可取四种形式:(0.1,0.1)T、(-0.1,-0.1)T、(0.1,-0.1)T、(-0.1,-0.1)T,本文取第三种。在此条件下,衡量建模结果精度的目标函数会出现一定程度的降低,当n=7时,目标函数降到最低。据此得到泥质和砂质成分的体积模量分别为20.27、45.61GPa,剪切模量为8.72、25.86GPa。最终岩石物理建模成果及误差曲线如图 5所示。由图可见,纵波速度、横波速度的建模结果与实测结果吻合度很高,从误差曲线看,纵波建模精度高于横波建模,但整体都较高,误差基本在5%以下。尽管建模结果与实测结果整体上非常接近,但由于利用了测井曲线中误差较小(受井眼环境影响小)的放射性测井曲线解释的泥质含量曲线进行建模,建模结果修正了实测结果中可能存在的受环境影响的误差,因此在建模后的交会图上不同岩性的区分更为明显(图 6)。在以泥质含量为色标的建模后的纵波速度与纵横波速度比交会图(图 6a)上,泥岩段(高泥质含量)表现为明显的低速、高纵横波速度比特点,且随着泥质含量的增高,有纵横波速度比升高、纵波速度降低的趋势。砂岩段与泥岩段在交会图上分异明显,表现为中—高速度、低纵横波速度比的特点,并且随着孔隙度增加纵横波速度比有降低的趋势(图 6b)。通过对X1井的岩石物理建模确定了泥质与砂

|
图 5 岩石物理建模最终结果与实测速度曲线的对比 (a)纵波速度;(b)横波速度;(c)相对误差 |
|
图 6 岩石物理建模后纵波速度与纵横波速度比交会图 (a)以泥质含量为色标;(b)以孔隙度为色标 |
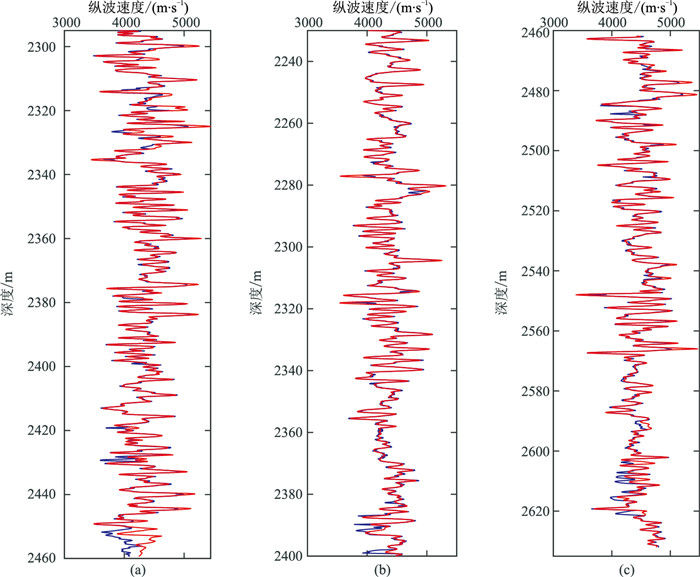
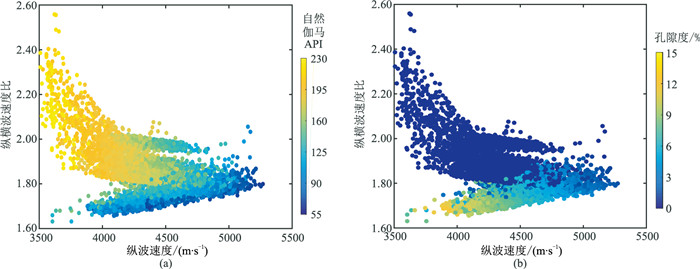
质成分的体积模量和剪切模量等建模参数,应用这些建模参数对工区其他无横波测井资料的井进行岩石物理建模以估计缺失的横波测井数据。图 7为部分井岩石物理建模后的纵波速度与实测速度的对比,二者吻合很好,展示了方法的稳定性和可靠性。图 8为工区内五口井岩石物理建模后的纵波速度与纵横波速度比的交会图。对比图 8与图 2b、图 6可以看出,无横波资料井建模后得到交会图形态与实测井的形态相似,表现出明显的规律性。泥岩(高伽马值)表现出较高的纵横波速度比和较低的纵波速度,并随砂质含量增加(伽马值变小)速度增大,纵横波速度比降低。而砂岩段整体表现为低纵横波速度比的特点,随孔隙度减小速度增高,纵横波速度比亦增高。
|
图 7 工区内另外三口井的岩石物理建模后的纵波速度曲线(蓝色)与实测曲线(红色)的对比 (a)X2井;(b)X3井;(c)X4井 |
|
图 8 工区内五口井岩石物理建模后纵波速度与纵横波速度比交会图 (a)以伽马值为色标;(b)以孔隙度为色标 |
以上规律对利用地震资料进行优质储层预测至关重要。
3 结论在现实实践中利用岩石物理建模方法估算缺失的横波测井资料仍面临诸多挑战。对于矿物组成复杂的致密砂岩储层,精确地估计砂、泥成分的弹性模量是成功应用岩石物理建模方法的基础,也是实践中不可回避的难点。本文给出了自适应的岩石物理建模方法以克服这一困难,即:通过联立Gassman方程与临界孔隙度模型进行岩石基质模量的估算,再通过最小二乘方法估计砂、泥质成分弹性模量的上、下限,然后通过全局寻优算法最终确定砂、泥质成分弹性模量。应用该方法对鄂尔多斯南部M工区进行岩石物理建模,结果可更清晰地展示储层物性与储层弹性参数间的相互关系,并方便、可靠地估算了缺失的横波资料。
本文方法具有简便、实用的特点,除要求一口井有横波测井资料外,其他井只要有常规测井资料和常规解释资料即可。
附录A 函数T1和T2的具体表达式在K-T模型中出现的T1和T2,是岩石基质、岩石椭球状包含物弹性模量及椭球体横纵比(椭球体短轴与长轴之比)的函数。具体形式为
| $ T_{1}=\frac{3 H_{1}}{H_{3}} $ | (A-1) |
| $ T_{2}=\frac{2}{H_{3}}+\frac{1}{H_{4}}+\frac{H_{4} H_{5}+H_{6} H_{7}-H_{8} H_{9}}{H_{2} H_{4}}+\frac{1}{3} T_{1} $ | (A-2) |
式中
| $ H_{1}= 1+A\left[\frac{3}{2}(f+\theta)-R\left(\frac{3}{2} f+\frac{5}{2} \theta-\frac{4}{3}\right)\right] $ | (A-3) |
| $ \begin{aligned} H_{2}=& 1+A\left[\frac{3}{2}(f+\theta)-R\left(\frac{3}{2} f+\frac{5}{2} \theta\right)\right]+\\ & B(3-4 R)+\frac{1}{2} A(A+3 B)(3-4 R) \times \\ &\left[f+\theta-R\left(f-\theta+2 \theta^{2}\right)\right] \end{aligned} $ | (A-4) |
| $ H_{3}=1+A\left[1-\left(f+\frac{3}{2} \theta\right)+R(f+\theta)\right] $ | (A-5) |
| $ H_{4}=1+\frac{1}{4} A[1-(f+3 \theta)-R(f-\theta)] $ | (A-6) |
| $ H_{5}=A\left[-f+R\left(f+\theta-\frac{4}{3}\right)\right]+B \theta(3-4 R) $ | (A-7) |
| $ H_{6}=1+A[1+f-R(f+\theta)]+B(1-\theta)(3-4 R) $ | (A-8) |
| $ H_{7}=2+\frac{1}{4} A[3 f+9 \theta-R(3 f+5 \theta)]+B \theta(3-4 R) $ | (A-9) |
| $ \begin{aligned} H_{8}=&A\left[1-2 R+\frac{1}{2} f(R-1)+\frac{1}{2} \theta(5 R-3)\right] \\ &+B(1-\theta)(3-4 R) \end{aligned} $ | (A-10) |
| $ H_{9}=A[(R-1) f-R \theta]+B \theta(3-4 R) $ | (A-11) |
| $ A=\frac{\mu_{l}}{\mu_{\mathrm{m}}}-1 $ | (A-12) |
| $ B=\frac{1}{3}\left(\frac{K_{l}}{K_{\mathrm{m}}}-\frac{\mu_{l}}{\mu_{\mathrm{m}}}\right) $ | (A-13) |
| $ R=\frac{3 \mu_{\mathrm{m}}}{3 K_{\mathrm{m}}+4 \mu_{\mathrm{m}}} $ | (A-14) |
| $ \theta=\frac{\alpha_{l}^{2}}{\left(1-\alpha_{l}^{2}\right)^{3 / 2}} \frac{3}{2}\left[\arccos \alpha_{l}-\left(1-\alpha_{l}^{2}\right)^{\frac{1}{2}}\right] $ | (A-15) |
| $ f=\frac{\alpha_{l}^{2}}{1-\alpha_{l}^{2}}(3 \theta-2) $ | (A-16) |
在应用K-T模型将孔隙充填物加入岩石基质过程中,令孔隙充填物的模量为零,这样有A=-1、B=0。
| [1] |
陈祖庆, 杨鸿飞, 王静波. 基于叠前反演的致密砂岩含气储层识别技术研究[J]. 天然气技术与经济, 2015, 9(4): 18-22. CHEN Zuqing, YANG Hongfei, WANG Jingbo. Identifying tight sandstone gas reservoir based on prestack inversion[J]. Natural Gas Technology and Economy, 2015, 9(4): 18-22. |
| [2] |
张盟勃, 史松群, 潘玉. 叠前反演技术在苏里格地区的应用[J]. 岩性油气藏, 2007, 19(4): 91-94. ZHANG Mengbo, SHI Songqun, PAN Yu. Application of prestack inversion in Sulige area[J]. Lithologic Reservoirs, 2007, 19(4): 91-94. |
| [3] |
蒋学峰. 叠前反演技术在致密油甜点预测中的应用[J]. 石油化工高等学校学报, 2018, 31(3): 76-80. JIANG Xuefeng. Application of pre-stack inversion technology in tight oil dessert prediction[J]. Journal of Petrochemical Universities, 2018, 31(3): 76-80. |
| [4] |
王霞, 张延庆, 于志龙, 等. 叠前反演结合地质统计模拟预测薄储层[J]. 石油地球物理勘探, 2011, 46(5): 744-748. WANG Xia, ZHANG Yanqing, YU Zhilong, et al. Thin reservoir prediction by prestack inversion combined with geostatistic simulation[J]. Oil Geophysical Prospecting, 2011, 46(5): 744-748. |
| [5] |
汪关妹, 张万福, 张宏伟, 等. 致密砂岩气地震预测关键技术及效果[J]. 石油地球物理勘探, 2020, 55(增刊): 72-79. WANG Guanmei, ZHANG Wanfu, ZHANG Hongwei, et al. Key technology and effect of prediction of tight sandstone gas based on seismic data[J]. Oil Geophysical Prospecting, 2020, 55(S): 72-79. |
| [6] |
邹玮, 张雷, 姜勇, 等. 叠前反演在西湖凹陷A构造低渗气层边界识别中的应用[J]. 海洋石油, 2015, 35(2): 46-49. ZOU Wei, ZHANG Lei, JIANG Yong, et al. Application of pre-stack inversion to identification of the boundary of low permeability gas reservoir in Xihu sag[J]. Offshore Oil, 2015, 35(2): 46-49. |
| [7] |
刘建辉, 明君, 彭刚, 等. 叠前联合反演技术在渤海中深层储层预测中的应用[J]. 海洋地质前沿, 2017, 33(4): 62-69. LIU Jianhui, MING Jun, PENG Gang, et al. Application of pre-stack joint inversion to mid-deep reservoir prediction in Bohai Bay[J]. Marine Geology Letters, 2017, 33(4): 62-69. |
| [8] |
王斌, 陈祥忠, 陈娟, 等. 四川盆地侏罗系致密砂岩弹性特征及岩石物理建模[J]. 地球物理学报, 2020, 63(12): 4528-4539. WANG Bin, CHEN Xiangzhong, CHEN Juan, et al. Elastic characteristics and petrophysical modeling of the Jurassic tight sandstone in Sichuan Basin[J]. Chinese Journal of Geophysics, 2020, 63(12): 4528-4539. |
| [9] |
刘萱, 谢占安, 张国栋, 等. 南堡油田叠前反演技术与储层预测[J]. 天然气工业, 2007, 27(增刊A): 439-442. LIU Xuan, XIE Zhan'an, ZHANG Guodong, et al. Prestack inversion and reservoirs prediction in Nanpu Oilfiled[J]. Natural Gas Industry, 2007, 27(SA): 439-442. |
| [10] |
李坤, 印兴耀. 混合概率模型驱动的叠前地震反演方法[J]. 石油地球物理勘探, 2020, 55(4): 839-853. LI Kun, YIN Xingyao. Prestack seismic inversion driven by mixture probabilistic models[J]. Oil Geophysical Prospecting, 2020, 55(4): 839-853. |
| [11] |
Nur A, Mavko G, Dvorkin J, et al. Critical porosity: the key to relating physical properties to porosity in rocks[C]. SEG Technical Program Expanded Abstracts, 1995, 14: 145-147.
|
| [12] |
Nur A, Marion D, Yin H. Wave velocities in sediments//Shear Waves in Marine Sediments[M]. Dordrecht: Kluwer Academic Publishers, 1991: 131-140.
|
| [13] |
Krief M, Garat J, Stellingwerff J, et al. A petrophysical interpretation using the velocities of P and S waves (full-waveform sonic)[J]. Log Analyst, 1991, 31(2): 355-369. |
| [14] |
Han D H, Nur A, Morgan D. Effects of porosity and clay content on wave velocities in sandstones[J]. Geo-physics, 1986, 51(10): 2093-2107. |
| [15] |
Xu S Y, White R E. A new velocity model for clay-sand mixtures[J]. Geophysical Prospecting, 1995, 43(1): 91-118. |
| [16] |
Xu S Y, White R E. A physical model for shear-wave velocity prediction[J]. Geophysical Prospecting, 1996, 44(4): 687-717. |
| [17] |
刘浩杰. 地震岩石物理研究综述[J]. 油气地球物理, 2009, 7(3): 1-8. LIU Haojie. Summarization of seismic rock physics research[J]. Petroleum Geophysics, 2009, 7(3): 1-8. |
| [18] |
马中高, 张金强, 蔡月晖, 等. 大牛地气田二叠系下石盒子组致密砂岩储层含气性识别因子研究[J]. 石油物探, 2012, 51(4): 414-419. MA Zhonggao, ZHANG Jinqiang, CAI Yuehui, et al. Study on gas identification factor of tight sandstone reservoirs in Lower Shihezi formation from Daniudi Gasfield, Ordos Basin[J]. Geophysical Prospecting for Petroleum, 2012, 51(4): 414-419. |
| [19] |
Raymer L L, Hunt E R, Gardner J S. An improved sonic transit time-to-porosity transform[C]. 21st Annual Logging Symposium of Society of Professitional Well Log Analysts, 1980.
|
| [20] |
王震宇, 刘俊州. 岩石物理建模技术在致密砂岩储层预测中的应用——以鄂尔多斯盆地北部H区块为例[J]. 物探化探计算技术, 2019, 41(1): 34-40. WANG Zhenyu, LIU Junzhou. Application of rock physics modeling in the prediction of tight sandstone reservoir: A case study of H block, Northern Erdos Basin[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2019, 41(1): 34-40. |
| [21] |
刘振峰, 张金强, 韩磊, 等. 鄂南长7段致密油地震流体识别技术应用实践[J]. 石油与天然气地质, 2018, 39(3): 541-548. LIU Zhenfeng, ZHANG Jinqiang, HAN Lei, et al. Geophysical fluid recognition for tight oil in Chang 7 Member, south Ordos Basin[J]. Oil & Gas Geology, 2018, 39(3): 541-548. |
| [22] |
张金强, 曲寿利, 孙建国, 等. 一种碳酸盐岩储层中的流体替换方法[J]. 石油地球物理勘探, 2010, 45(3): 406-409. ZHANG Jinqiang, QU Shouli, SUN Jianguo, et al. A fluid substitution realization method in carbonate re-servoir[J]. Oil Geophysical Prospecting, 2010, 45(3): 406-409. |



 张金强, 北京市昌平区沙河镇百沙路5号中国石化科学技术研究中心, 102206。Email:
张金强, 北京市昌平区沙河镇百沙路5号中国石化科学技术研究中心, 102206。Email: 