② 青岛海洋科学与技术试点国家实验室, 山东青岛 266580;
③ 中国石化石油物探技术研究院, 江苏南京 211103;
④ 山东省第一地质矿产勘查院, 山东济南 250014
② Pilot National Laboratory for Marine Science and Technology(Qingdao), Qingdao, Shandong 266580, China;
③ SINOPEC Geophysical Research Institute, Nanjing, Jiangsu 211103, China;
④ Institute of Geology and Mineral Resourcess Shandong Province, Jinan, Shandong 250014, China
传统地震偏移成像理论一般是基于地下介质为各向同性、完全弹性的假设,而真实地下内部介质广泛存在黏滞性及不同强度的各向异性[1]。黏滞性易于吸收地震信号的高频能量,导致地震波传播过程中振幅衰减及相位畸变,降低中深层成像分辨率。速度各向异性会使地震波在传播过程中旅行时曲线偏离,导致成像剖面绕射波不能完全收敛,成像效果变差。因此,对黏滞—各向异性介质的研究具有重要理论意义和现实应用价值[2]。其中,黏滞—各向异性介质的高精度和高效率偏移成像方法,近年来逐渐成为研究热点。
高斯束是一种兼具灵活性与高效性的偏移成像方法。Červený[3]最早将其应用于地球物理学领域,并做了卓有成效的研究[4-5];Hill[6-7]基于高斯束叠加表征的格林函数最先提出高斯束偏移基本框架,且采用局部倾斜叠加原理,使高斯束偏移具有方向选择性;Hale[8]系统地比较了Kirchhoff、倾斜叠加和高斯波束局部倾斜叠加三种偏移法的计算精度、效率及其算子对复杂模型的适应性。
随着人们针对复杂地表、成像精度和计算效率等方面持续地开展深入研究,高斯束偏移法得以更广泛地应用于地震勘探成像处理。Nowack等[9]和Gray[10]改进了Hill的局部倾斜叠加并提出共炮域高斯束叠前深度偏移法;Gray等[11]借鉴广义真振幅单程偏移法思想发展了真振幅高斯束偏移法;李振春等[12]实现了互相关条件下的保幅高斯束偏移,并给出了角道集提取方法;黄建平等[13]结合高斯束偏移与逆时偏移,提出具有更高精度的格林函数高斯束逆时偏移法;高成等[14]改变成像公式的积分顺序,实现了具有较高计算效率的二维时间域高斯束叠前深度偏移;秦宁[15]将时间域高斯束叠前深度偏移方法针对各向异性复杂构造数据进行了尝试与改进;Yang等[16]通过引入Gabor分解重构地震子波改变对正向波场的稀疏分解,提出基于子波重构理论的时空域高斯束偏移法。Huang等[17]利用矢量高斯束构建波场,实现了基于起伏地表的弹性波高斯束偏移。
针对具有各向异性和(或)黏滞性的复杂介质的束偏移方法,人们也做了大量研究。Alkhalifah[18]基于Červený[3]和Hanyga[19]提出的各向异性射线追踪体系,发展了各向异性高斯束叠后深度偏移算法;Zhu等[20]通过引入相速度和群速度简化各向异性射线追踪,解决了基于弹性参数计算过程繁杂的难题。吴娟等[21]通过校正高斯束复值旅行时,实现了适用于黏声介质的高斯束叠前深度偏移;韩建光等[22]和代福材等[23]也分别针对各向异性介质和黏滞性介质的高斯束偏移方法开展了有现实意义的研究。
近年来,新型波束构建策略的研究进展迅速。张瑞等[24]将控制束偏移应用于低信噪比数据,去噪的同时显著地提高信噪比;Gao等[25]提出快速束偏移以提高成像计算效率;Nowack[26]为了提高成像精度,基于深度聚焦思想提出了聚焦束偏移法;Yang等[27]进一步改进动态聚焦束,以模型速度场信息限制波束宽度、优化波束形态,形成自适应聚焦束偏移法,并展示了自适应聚焦束偏移的优势;李胜雅等[28]将自适应聚焦束拓展到各向异性介质,显著改善成像效果。目前,针对复杂介质(即同时考虑介质的各向异性和黏滞性)的新型波束偏移方法尚不多见。
通过充分调研上述文献,本文以常规频率域自适应聚焦束偏移法为基础,利用基于弹性参数的各向异性射线追踪体系和黏滞性介质中Q值衰减补偿策略,通过引入相应变换,实现了一种适用于黏声VTI介质的时间域自适应聚焦束偏移。即能同时处理黏滞性和各向异性的影响,且引入的傅里叶变换和Hilbert变换能降低计算维度,提高偏移算法的计算效率。利用黏声VTI洼陷模型测试了所提方法的有效性,通过更复杂的黏声VTI SEG/Hess模型验证了该方法的适应性;再与频率域类偏移方法对比,表明本文方法具有更高的计算效率;最后,通过实际地震资料的成像处理,表明所提方法具有良好应用效果。
1 方法原理 1.1 黏声VTI介质射线追踪以及衰减补偿束偏移射线追踪的过程是通过求解射线追踪方程获得中心射线的路径、振幅和旅行时,在不同介质中需采用不同的射线追踪方程。对于二维黏声VTI介质,黏滞性和各向异性都会对射束产生影响,且从已有研究成果可知黏滞性与各向异性对射线的影响是不同的。
Aki等[29]认为,地震波在黏声介质中的传播可看成是在声介质以一个复速度传播,在黏滞性较弱(1/Q≫1)时,该复速度可表示为
| $ v_{\mathrm{c}}=v_{0}\left[1-\frac{\mathrm{i}}{2} Q^{-1}(\boldsymbol{x})+\frac{1}{{\rm{ \mathsf{ π} }}} Q^{-1}(\boldsymbol{x}) \ln \frac{\omega}{\omega_{\mathrm{ref}}}\right] $ | (1) |
式中:x=(x,z)表示介质中一点;ω为圆频率;ωref为参考圆频率;v0为地震波在声介质中的传播速度;i为虚数单位。该式表达了地震波在黏滞性介质中传播的特点,其中复速度的虚部表示地震波沿射线路径的振幅衰减,实部表征频散关系。
对式(1)做一阶展开,表明黏滞性较弱时,在介质中传播的射线路径并未发生改变,复值速度的影响首先是针对射线旅行时,进而针对波形。利用复值速度可推导出体现衰减的旅行时表达式[30]
| $ T_{\mathrm{c}}(\boldsymbol{x})=T_{0}(\boldsymbol{x})+\frac{\mathrm{i}}{2} T_{Q}(\boldsymbol{x})-\frac{1}{{\rm{ \mathsf{ π} }}} T_{Q}(\boldsymbol{x}) \ln \frac{\omega}{\omega_{\mathrm{ref}}} $ | (2) |
式中:Tc(x)、T0(x)分别为射线在黏声介质和声介质中的旅行时;TQ(x)为与品质因子有关的旅行时
| $ T_{Q}(\boldsymbol{x})=\int \frac{1}{Q(\boldsymbol{x}) v_{0}(\boldsymbol{x})} \mathrm{d} s $ | (3) |
式中s为中心射线弧长。从式(3)可知,射线追踪时只需计算额外一小部分的计算量TQ,并对式(2)中TQ取反号进行补偿,即可得到衰减补偿旅行时。
各向异性介质的影响则相反,它仅改变射线传播路径,不会影响旅行时[3],因此本文采用基于弹性参数表征的各向异性射线追踪方程,依此修改射线复值旅行时,校正黏声VTI介质影响。
基于各向异性介质地震波传播方程,Červený[3]给出各向异性运动学射线追踪方程组,结合式(3),构成二维黏声VTI介质运动学射线追踪方程组
| $ \left\{\begin{array}{l} \frac{\mathrm{d} x_{i}}{\mathrm{~d} t}=a_{i j k l} \varGamma_{l} g_{j} g_{k} \\ \frac{\mathrm{d} \varGamma_{i}}{\mathrm{~d} t}=-\frac{1}{2} \frac{\partial a_{m i j k}}{\partial x_{i}} \varGamma_{m} \varGamma_{l} g_{j} g_{k} \\ T_{Q}(\boldsymbol{x})=\int \frac{1}{Q(\boldsymbol{x}) v_{0}(\boldsymbol{x})} \mathrm{d} s \end{array}\right. $ | (4) |
式中:aijkl=cijkl/ρ为密度归一化弹性参数,其中cijkl、ρ分别代表弹性参数和密度;γi代表慢度矢量的分量;gj (j=1,3)为Christoffel矩阵Γ(Γik= aijklγjγl)的特征向量分量,在二维情况下满足
| $ \left\{\begin{array}{l} g_{1} g_{1}=\frac{\varGamma_{33}-1}{\varGamma_{11}+\varGamma_{33}-2} \\ g_{3} g_{3}=\frac{\varGamma_{11}-1}{\varGamma_{11}+\varGamma_{33}-2} \\ g_{1} g_{3}=\frac{-\varGamma_{13}}{\varGamma_{11}+\varGamma_{33}-2} \end{array}\right. $ | (5) |
对于各向异性介质中动力学射线追踪方程,由于射线中心坐标系不再正交,其实现过程较复杂。Hanyga[19]引入沿中心射线的权值以解决非正交性,给出各向异性介质动力学追踪方程组
| $ \left\{\begin{array}{l} \frac{\mathrm{d} q}{\mathrm{~d} t}=W q+V p \\ \frac{\mathrm{d} p}{\mathrm{~d} t}=-V p-H q \end{array}\right. $ | (6) |
式中:p和q为动力学射线追踪参量;W、V、H分别为
| $ \left\{\begin{array}{l} W=\frac{1}{2} \frac{\partial^{2} G_{1}}{\partial p_{n}^{2}}-\frac{1}{4}\left(\frac{\partial G_{1}}{\partial p_{n}}\right)^{2} \\ H=\frac{1}{2} \frac{\partial^{2} G_{1}}{\partial n^{2}}-\frac{1}{4}\left(\frac{\partial G_{1}}{\partial p_{n}}\right)^{2} \\ V=\frac{1}{2} \frac{\partial^{2} G_{1}}{\partial p_{n} \partial n}-\frac{1}{4} \frac{\partial G_{1}}{\partial p_{n}} \frac{\partial G_{1}}{\partial n} \end{array}\right. $ | (7) |
式中:pn是沿射线中心坐标系法线方向n上的射线参量;n表示法线方向上距离中心射线的长度;G1为P波的程函数,它在二维介质的表达式为
| $ G_{1}=\varGamma_{11} g_{1} g_{1}+2 \varGamma_{13} g_{1} g_{3}+\varGamma_{33} g_{3} g_{3} $ | (8) |
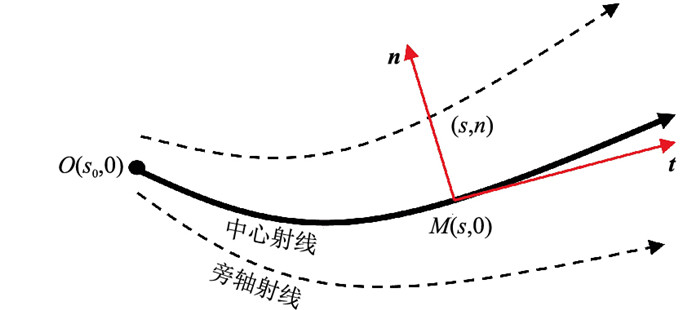
自适应聚焦束[27]的特点是考虑了速度的影响,束参数能根据局部速度动态地改变,进而使地震波束的有效半宽度控制在一个波长范围内。在图 1中的二维射线中心坐标系(s,n)下,利用动力学射线追踪方程从点O(s0,0)沿中心射线求取点M(s,0)的p和q值,则自适应聚焦束在点M的动态复值束参数表达式为
| $ \kappa(s)=\frac{-q_{2}(s)-\mathrm{i} \omega_{\mathrm{ref}} h^{2}(s) p_{2}(s)}{q_{1}(s)+\mathrm{i} \omega_{\mathrm{ref}} h^{2}(s) p_{1}(s)} $ | (9) |
|
图 1 二维射线中心坐标系 |
其中地下聚焦点M的束腰宽度h(s)的表达式为
| $ h(s)=\frac{2 {\rm{ \mathsf{ π} }} v(s)}{\omega_{\mathrm{ref}}} $ | (10) |
式(9)中动态束参数κ(s)不再是常数,而是与射线弧长s有关的复变量,它可自适应地计算束宽,使得波束能量更好地聚焦于射线中心邻域之内,称之为自适应聚焦参数。根据高斯束构建方案,基于自适应聚焦参数能构建出自适应聚焦束传播的表达式
| $ \begin{gathered} U(s, n, \omega)=\sqrt{\frac{\kappa\left(s_{0}\right) v(s)}{\left[\kappa(s) q_{1}(s)+q_{2}(s)\right] v\left(s_{0}\right)}} \times \\ \exp \left[\mathrm{i} \omega t(s)+\frac{1}{2} \mathrm{i} \omega n^{2} \frac{\kappa(s) p_{1}(s)+p_{2}(s)}{\kappa(s) q_{1}(s)+q_{2}(s)}\right] \end{gathered} $ | (11) |
自适应聚焦束表征的格林函数原理是利用一系列炮点出射的、且不同出射角度的自适应聚焦束的叠加积分来表示,其中为了计算方便利用射线中心坐标系与笛卡尔坐标系参量之间的转换关系,可得到从x0点传播至x点由自适应聚焦束构建的关于笛卡尔坐标系参量的格林函数表达式
| $ \begin{aligned} &G\left(\boldsymbol{x}, \boldsymbol{x}_{0} ; \omega\right)=\frac{\mathrm{i}}{4 {\rm{ \mathsf{ π} }}} \int A\left(\boldsymbol{x}, \boldsymbol{x}_{0}\right) \exp \left[\mathrm{i} \omega T\left(\boldsymbol{x}, \boldsymbol{x}_{0}\right)\right] \mathrm{d} \theta \\ &\quad=\frac{\mathrm{i}}{4 {\rm{ \mathsf{ π} }}} \int \mathrm{d} \theta \sqrt{\frac{\kappa\left(\boldsymbol{x}_{0}\right) v(\boldsymbol{x})}{\left[\kappa(\boldsymbol{x}) q_{1}(\boldsymbol{x})+q_{2}(\boldsymbol{x})\right] v\left(\boldsymbol{x}_{0}\right)}} \times \\ &\exp \left\{\mathrm{i} \omega\left[t\left(\boldsymbol{x}, \boldsymbol{x}_{0}\right)+\frac{1}{2} n^{2} \frac{\kappa(\boldsymbol{x}) p_{1}(\boldsymbol{x})+p_{2}(\boldsymbol{x})}{\kappa(\boldsymbol{x}) q_{1}(\boldsymbol{x})+q_{2}(\boldsymbol{x})}\right]\right\} \end{aligned} $ | (12) |
式中:x此处为地下成像点;θ为中心射线出射角;A、T分别为自适应聚焦束复值振幅和旅行时。
根据黏声介质对地震波束复值旅行时的影响,可通过将衰减算子取反号进行补偿,即令式(2)表达式中带有TQ项反号,将其代替自适应聚焦束中心射线旅行时,进而得到自适应聚焦束构建的黏声介质补偿后的格林函数表达式
| $ \begin{aligned} &G\left(\boldsymbol{x}, \boldsymbol{x}_{0} ; \omega\right)=\frac{\mathrm{i}}{4 {\rm{ \mathsf{ π} }}} \int \mathrm{d} \theta A\left(\boldsymbol{x}, \boldsymbol{x}_{0}\right) \times \exp \left[\mathrm{i} \omega T\left(\boldsymbol{x}, \boldsymbol{x}_{0}\right)+\right. \\ &\left.\quad \frac{\omega}{2} T_{Q}\left(\boldsymbol{x}, \boldsymbol{x}_{0}\right)+\frac{\mathrm{i} \omega}{{\rm{ \mathsf{ π} }}} T_{Q}\left(\boldsymbol{x}, \boldsymbol{x}_{0}\right) \ln \frac{\omega}{\omega_{\mathrm{ref}}}\right] \end{aligned} $ | (13) |
式中:
自适应聚焦束偏移流程:首先通过自适应聚焦束表征的格林函数在炮点和检波点处构建上行、下行波场;然后对上行、下行波场利用互相关成像条件进行成像。对于各向异性的影响只需改变射线追踪即可达到校正效果。但由于吸收衰减作用于地震波在地下传播的全过程,因此借鉴单程波偏移补偿原理,需对炮点波场和检波点波场分别进行补偿,才能得到想要的偏移成像结果。
考虑二维情况下,炮点坐标为xs=(xs,0),检波点坐标为xr=(xr,0),地下成像点坐标为x=(x,z),依据Zhang等[31]给出的二维频率域互相关成像条件
| $ I\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{s}}\right)=-\mathrm{i} \int \mathrm{d} \omega \operatorname{sgn}(\omega) P_{\mathrm{U}}\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{r}} ; \omega\right) P_{\mathrm{D}}^{*}\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{s}} ; \omega\right) $ | (14) |
式中:上标“*”代表复共轭;PU、PD分别为上行、下行波场,Gray等[11]给出其表达式
| $ \begin{aligned} P_{\mathrm{U}}\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{r}} ; \omega\right)=&-2 \mathrm{i} \omega \int \mathrm{d} \boldsymbol{x}_{\mathrm{r}} p_{\mathrm{U}}\left(\boldsymbol{x}_{\mathrm{r}}, \boldsymbol{x}_{\mathrm{s}} ; \omega\right) \times \\ & \frac{\cos \theta_{\mathrm{r}}}{v_{\mathrm{r}}} G^{*}\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{r}} ; \omega\right) \end{aligned} $ | (15) |
| $ P_{\mathrm{D}}^{*}\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{s}} ; \omega\right)=2 \frac{\cos \theta_{\mathrm{s}}}{v_{\mathrm{s}}} \mathrm{i} \omega G^{*}\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{s}} ; \omega\right) $ | (16) |
式中:pU(x, xs; ω)是对地震记录做傅里叶变换后结果;vs和vr分别是炮点和检波点处的速度;θs和θr分别为炮点和检波点处的射线出射角;G(x, xs; ω)为自适应聚焦束表征的黏声介质格林函数。
假定As和Ar、Ts和Tr分别为在黏滞性介质中xs和xr处的复值振幅和旅行时,TQ,s和TQ,r分别为从xs和xr射线追踪求取的与品质因子有关的旅行时,则补偿后的格林函数表达式为
| $ \left\{\begin{array}{l} G\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{s}} ; \omega\right)=\frac{\mathrm{i}}{4 {\rm{ \mathsf{ π} }}} \int \mathrm{d} \theta_{\mathrm{s}} \times \\ \quad A_{\mathrm{s}} \exp \left[\mathrm{i} \omega\left(T_{\mathrm{s}}-\frac{\mathrm{i}}{2} T_{Q, \mathrm{~s}}+\frac{1}{{\rm{ \mathsf{ π} }}} T_{Q, s} \ln \frac{\omega}{\omega_{\mathrm{ref}}}\right)\right] \\ G\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{r}} ; \omega\right)=\frac{\mathrm{i}}{4 {\rm{ \mathsf{ π} }}} \int \mathrm{d} \theta_{\mathrm{r}} \times \\ \quad A_{\mathrm{r}} \exp \left[\mathrm{i} \omega\left(T_{\mathrm{r}}-\frac{\mathrm{i}}{2} T_{Q, \mathrm{r}}+\frac{1}{{\rm{ \mathsf{ π} }}} T_{Q, \mathrm{r}} \ln \frac{\omega}{\omega_{\mathrm{ref}}}\right)\right] \end{array}\right. $ | (17) |
其中
| $ \left\{\begin{array}{l} A_{\mathrm{s}}(\omega)=\operatorname{Re}\left(A_{\mathrm{s}}|\omega|\right)+\mathrm{i} \operatorname{sgn}(\omega) \operatorname{Im}\left(A_{\mathrm{s}}|\omega|\right) \\ A_{\mathrm{r}}(\omega)=\operatorname{Re}\left(A_{\mathrm{r}}|\omega|\right)+\mathrm{i} \operatorname{sgn}(\omega) \operatorname{Im}\left(A_{\mathrm{r}}|\omega|\right) \end{array}\right. $ | (18) |
通过式(18)负频率下的复值振幅等于正频率下复值振幅的复共轭,同时考虑到exp(iτ)*=exp(-iτ*),则可得格林函数的复共轭
| $ \left\{\begin{aligned} G^{*}\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{s}} ; \omega\right)=& \frac{\mathrm{i}}{4 {\rm{ \mathsf{ π} }}} \int \mathrm{d} \theta_{\mathrm{s}} A_{\mathrm{s}}^{*} \exp \left[-\mathrm{i} \omega\left(T_{\mathrm{s}}^{*}+\right.\right.\\ &\left.\left.\frac{1}{{\rm{ \mathsf{ π} }}} T_{Q, \mathrm{~s}}^{*} \ln \frac{\omega}{\omega_{\mathrm{ref}}}\right)+\frac{\omega}{2} T_{Q, \mathrm{~s}}^{*}\right] \\ G^{*}\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{r}} ; \omega\right)=& \frac{\mathrm{i}}{4 {\rm{ \mathsf{ π} }}} \int \mathrm{d} \theta_{\mathrm{r}} A_{\mathrm{r}}^{*} \exp \left[-\mathrm{i} \omega\left(T_{\mathrm{r}}^{*}+\right.\right.\\ &\left.\left.\frac{1}{{\rm{ \mathsf{ π} }}} T_{Q, \mathrm{r}}^{*} \ln \frac{\omega}{\omega_{\mathrm{ref}}}\right)+\frac{\omega}{2} T_{Q, \mathrm{r}}^{*}\right] \end{aligned}\right. $ | (19) |
将式(19)代入式(14),可得常规频率域黏声自适应聚焦束偏移公式
| $ \begin{aligned} I\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{s}}\right)=& \frac{1}{4 {\rm{ \mathsf{ π} }}^{2}} \int \mathrm{d} \boldsymbol{x}_{\mathrm{r}} \int \mathrm{d} \omega \mathrm{i} \omega|\omega| \times \frac{\cos \theta_{\mathrm{s}}}{v_{\mathrm{s}}} \int \mathrm{d} \theta_{\mathrm{s}} A_{\mathrm{s}}^{*} \times \\ & \exp \left[-\mathrm{i} \omega\left(T_{\mathrm{s}}^{*}+\frac{1}{{\rm{ \mathsf{ π} }}} T_{Q, \mathrm{~s}}^{*} \ln \frac{\omega}{\omega_{\mathrm{ref}}}\right)+\frac{\omega}{2} T_{Q, \mathrm{~s}}^{*}\right] \times \\ & \frac{\cos \theta_{\mathrm{r}}}{v_{\mathrm{r}}} \int \mathrm{d} \theta_{\mathrm{r}} A_{\mathrm{r}}^{*} \exp \left[-\mathrm{i} \omega\left(T_{\mathrm{r}}^{*}+\frac{1}{{\rm{ \mathsf{ π} }}} T_{Q, \mathrm{r}}^{*} \ln \frac{\omega}{\omega_{\mathrm{ref}}}\right)+\right.\\ &\left.\frac{\omega}{2} T_{Q, \mathrm{r}}^{*}\right] \times p_{\mathrm{U}}\left(\boldsymbol{x}_{\mathrm{r}}, \boldsymbol{x}_{\mathrm{s}} ; \omega\right) \end{aligned} $ | (20) |
由于自适应聚焦束偏移在整个射线路径中自适应地聚焦,为避免偏移过程中需进行数次τ-p变换与二次相位校正,该常规频率域方法不采用加窗倾斜叠加,而是利用传统Kirchhoff偏移单道输入的偏移成像框架,但计算效率改善甚微。因此,本文进一步调整偏移成像公式顺序,引入相应变换降低频率域自适应聚焦束偏移的积分维度,实现具有较高计算效率的时间域黏声VTI自适应聚焦束偏移。
为了简化式(20),先交换公式积分顺序,且令A=AsAr, T=Ts+Tr, TQ=TQ, s*+TQ, r*得到
| $ \begin{aligned} I\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{s}}\right)=& \frac{1}{4 {\rm{ \mathsf{ π} }}^{2}} \int \mathrm{d} \boldsymbol{x}_{\mathrm{r}} \int \mathrm{d} \theta_{\mathrm{s}} \int \mathrm{d} \theta_{\mathrm{r}} \int \mathrm{d} \omega \mathrm{i} \omega \frac{\cos \theta_{\mathrm{s}}}{{v}_{\mathrm{s}}} \frac{\cos \theta_{\mathrm{r}}}{v_{\mathrm{r}}} \times \\ & A^{*} \exp \left[-\mathrm{i} \omega\left(T^{*}+\frac{1}{{\rm{ \mathsf{ π} }}} T_{Q} \cdot \ln \frac{\omega}{\omega_{\mathrm{ref}}}\right)+\right.\\ &\left.\frac{\omega}{2} T_{Q}\right] W\left(\boldsymbol{x}_{\mathrm{r}}, \boldsymbol{x}_{\mathrm{s}} ; \omega\right) \end{aligned} $ | (21) |
其中频率加权地震数据W表示为
| $ W\left(\boldsymbol{x}_{\mathrm{r}}, \boldsymbol{x}_{\mathrm{s}} ; \omega\right)=|\omega| p_{\mathrm{U}}\left(\boldsymbol{x}_{\mathrm{r}}, \boldsymbol{x}_{\mathrm{s}} ; \omega\right) $ | (22) |
式(21)为四重积分,被积函数中
| $ I\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{s}}\right)=\frac{1}{4 {\rm{ \mathsf{ π} }}^{2}} \int \mathrm{d} \boldsymbol{x}_{\mathrm{r}} \int \mathrm{d} \theta_{\mathrm{s}} \int \mathrm{d} \theta_{\mathrm{r}} \frac{\cos \theta_{\mathrm{s}}}{v_{\mathrm{s}}} \frac{\cos \theta_{\mathrm{r}}}{v_{\mathrm{r}}} I_{0}\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{s}}\right) $ | (23) |
其最内层积分表达式为
| $ \begin{aligned} I_{0}\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{s}}\right)=& \int \mathrm{d} \omega \mathrm{i} \omega A^{*} \times \exp \left[-\mathrm{i} \omega\left(T^{*}+\right.\right.\\ &\left.\left.\frac{1}{{\rm{ \mathsf{ π} }}} T_{Q} \ln \frac{\omega}{\omega_{\mathrm{ref}}}\right)+\frac{\omega}{2} T_{Q}\right] W\left(\boldsymbol{x}_{\mathrm{r}}, \boldsymbol{x}_{\mathrm{s}} ; \omega\right) \end{aligned} $ | (24) |
考虑到振幅和旅行时都为复值,将其拆成实部加虚部形式,则令TRe=Re(Ts+Tr)、TIm=Im(Ts+Tr)、ARe=Re(AsAr)及AIm=sgn(ω)×Im(AsAr),代入式(24)整理可得
| $ \begin{aligned} I_{0}\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{s}}\right)=& \int \mathrm{i} \omega \mathrm{d} \omega\left[A_{\mathrm{Re}}-\mathrm{i} \operatorname{sgn}(\omega) A_{\mathrm{Im}}\right] \times \\ & \exp \left[-\mathrm{i} \omega\left(T_{\mathrm{Re}}+\frac{1}{{\rm{ \mathsf{ π} }}} T_{Q} \ln \frac{\omega}{\omega_{\mathrm{ref}}}\right)-\right.\\ &\left.\omega T_{\mathrm{Im}}+\frac{\omega}{2} T_{Q}\right] W\left(\boldsymbol{x}_{\mathrm{r}}, \boldsymbol{x}_{\mathrm{s}} ; \omega\right) \end{aligned} $ | (25) |
进一步可写成
| $ I_{0}\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{s}}\right)=I_{1}\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{s}}\right)+I_{2}\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{s}}\right) $ | (26a) |
| $ \begin{aligned} I_{1}\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{s}}\right)=& \int \mathrm{i} \omega W\left(\boldsymbol{x}_{\mathrm{r}}, \boldsymbol{x}_{\mathrm{s}} ; \omega\right) A_{\mathrm{Re}} \times \\ & \exp \left[-\mathrm{i} \omega\left(T_{\mathrm{Re}}+\frac{1}{{\rm{ \mathsf{ π} }}} T_{Q} \cdot \ln \frac{\omega}{\omega_{\mathrm{ref}}}\right)-\right.\\ &\left.\omega\left(T_{\mathrm{Im}}-\frac{1}{2} T_{Q}\right)\right] \mathrm{d} \omega \end{aligned} $ | (26b) |
| $ \begin{aligned} I_{2}\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{s}}\right)=& \int \mathrm{i} \omega W\left(\boldsymbol{x}_{\mathrm{r}}, \boldsymbol{x}_{\mathrm{s}} ; \omega\right)\left[-\mathrm{i} \operatorname{sgn}(\omega) A_{\mathrm{Im}}\right] \times \\ & \exp \left[-\mathrm{i} \omega\left(T_{\mathrm{Re}}+\frac{1}{{\rm{ \mathsf{ π} }}} T_{Q} \ln \frac{\omega}{\omega_{\mathrm{ref}}}\right)-\right.\\ &\left.\omega\left(T_{\mathrm{Im}}-\frac{1}{2} T_{Q}\right)\right] \mathrm{d} \omega \end{aligned} $ | (26c) |
由傅里叶逆变换的定义
| $ f(t)=\frac{1}{2 {\rm{ \mathsf{ π} }}} \int W(\omega) \exp (-\mathrm{i} \omega t) \mathrm{d} \omega $ |
得知I1(x, xs)的表达式可转换为
| $ \begin{aligned} 2 {\rm{ \mathsf{ π} }} A_{\mathrm{R}} \widetilde{w}&\left(T_{\mathrm{Re}}, T_{\mathrm{Im}}, T_{Q}\right)=\int \mathrm{i} \omega W\left(\boldsymbol{x}_{\mathrm{r}}, \boldsymbol{x}_{\mathrm{s}} ; \omega\right) \times \\ &\exp \left(-\omega T_{\mathrm{Im}}+\frac{\omega}{2} T_{Q}\right) \times \\ &A_{\mathrm{Re}} \exp \left[-\mathrm{i} \omega\left(T_{\mathrm{Re}}+\frac{1}{{\rm{ \mathsf{ π} }}} T_{Q} \ln \frac{\omega}{\omega_{\mathrm{ref}}}\right)\right] \mathrm{d} \omega \end{aligned} $ | (27) |
根据文献[8],式(26c)在频率域乘以-isgn(ω)相当于时间域的Hilbert变换,故式(26c)中I2(x, xs)可表示为
| $ \begin{aligned} 2 {\rm{ \mathsf{ π} }} A_{\operatorname{Im}} w_{\mathrm{H}}&\left(T_{\mathrm{Re}}, T_{\mathrm{Im}}, T_{Q}\right)=\\ & \int \mathrm{i} \omega W\left(\boldsymbol{x}_{\mathrm{r}}, \boldsymbol{x}_{\mathrm{s}} ; \omega\right)\left[-\mathrm{i} \operatorname{sgn}(\omega) A_{\mathrm{Im}}\right] \times \\ & \exp \left(-\omega T_{\mathrm{Im}}+\frac{\omega}{2} T_{Q}\right) \times \\ & \exp \left[-\mathrm{i} \omega\left(T_{\mathrm{Re}}+\frac{1}{{\rm{ \mathsf{ π} }}} T_{Q} \ln \frac{\omega}{\omega_{\mathrm{ref}}}\right)\right] \mathrm{d} \omega \end{aligned} $ | (28) |
据傅里叶逆变换和Hilbert变换,可将式(25)简化为
| $ \begin{aligned} I_{0}\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{s}}\right)=& 2 {\rm{ \mathsf{ π} }}\left[A_{\mathrm{Re}} \widetilde{w}\left(\boldsymbol{x}_{\mathrm{r}}, \boldsymbol{x}_{\mathrm{s}} ; T_{\mathrm{Re}}, T_{\mathrm{Im}}, T_{Q}\right)+\right.\\ &\left.A_{\operatorname{Im}} w_{\mathrm{H}}\left(\boldsymbol{x}_{\mathrm{r}}, \boldsymbol{x}_{\mathrm{s}} ; T_{\mathrm{Re}}, T_{\mathrm{Im}}, T_{Q}\right)\right] \end{aligned} $ | (29) |
式(27)~式(29)中,
然后将式(29)代入式(23),将频率域积分转化为时间域,使得四重积分简化为三重积分,得到最终的时间域黏声自适应聚焦束偏移成像公式
| $ \begin{aligned} I\left(\boldsymbol{x}, \boldsymbol{x}_{\mathrm{s}}\right)=& \frac{1}{2 {\rm{ \mathsf{ π} }}} \int \mathrm{d} \boldsymbol{x}_{\mathrm{r}} \int \mathrm{d} \theta_{\mathrm{s}} \int \mathrm{d} \theta_{\mathrm{r}} \frac{\cos \theta_{\mathrm{s}}}{v_{\mathrm{s}}} \frac{\cos \theta_{\mathrm{r}}}{v_{\mathrm{r}}} \times \\ &\left[A_{\mathrm{Re}} \widetilde{\omega}\left(\boldsymbol{x}_{\mathrm{r}}, \boldsymbol{x}_{\mathrm{s}} ; T_{\mathrm{Re}}, T_{\mathrm{Im}}, T_{Q}\right)+\right.\\ &\left.A_{\operatorname{Im}} w_{\mathrm{H}}\left(\boldsymbol{x}_{\mathrm{r}}, \boldsymbol{x}_{\mathrm{s}} ; T_{\mathrm{Re}}, T_{\mathrm{Im}}, T_{Q}\right)\right] \end{aligned} $ | (30) |
该式为单炮偏移结果。最后,对所有炮的偏移结果进行叠加,得到最终偏移成像剖面。
2 数值算例为了验证本文时间域黏声VTI介质自适应聚焦束偏移方法的有效性、适用性和优越性,分别针对黏声VTI洼陷模型和黏声VTI SEG/Hess模型进行了测试,还对实际资料进行了处理。
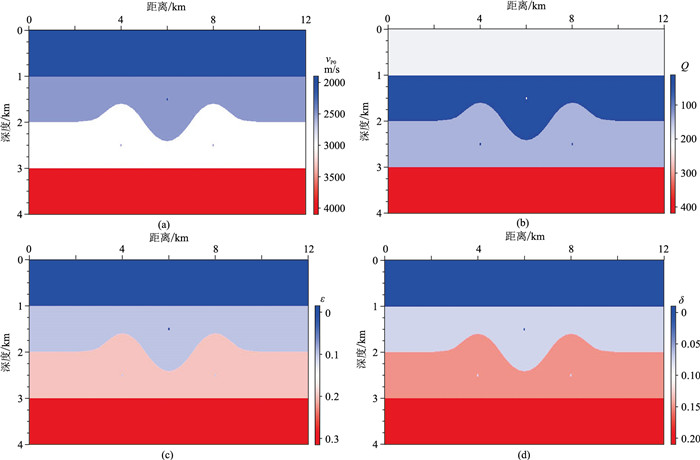
2.1 黏声VTI洼陷模型选取的黏声VTI洼陷模型(图 2)的尺寸为1201×401,网格间距是10m。模型第一层表现为各向同性,其余三层为各向异性,此外还含三个绕射体。
|
图 2 黏声VTI洼陷模型 (a)vP0; (b)Q; (c)ε; (d)δ |
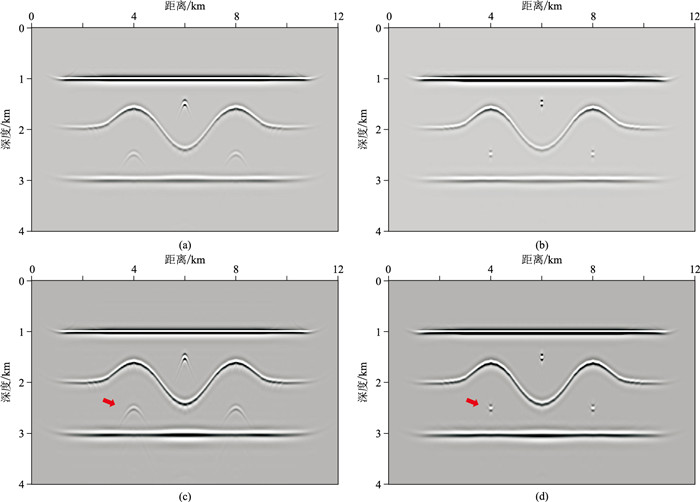
采用黏声VTI介质有限差分法做正演模拟,设计观测系统为中间激发,两边接收;共激发161炮,炮间距为50m;每炮401道接收,道间距为10m;每道记录时长为3s,时间采样间隔为1ms。观察利用不同自适应聚焦束偏移法所得处理结果(图 3)可见:如果忽略各向异性影响,会出现绕射波不能完全收敛(图 3c中红色箭头指向处);若忽略黏滞性影响,会出现中深层能量较弱、相位畸变等问题(图 3b);而本文方法成像结果(图 3d)不仅绕射波较好地收敛,深层能量也得到有效补偿,同时相位得到校正,即成像位置更接近于真实界面。
|
图 3 黏声VTI洼陷模型四种方法偏移成像结果 (a)频率域自适应聚焦束偏移;(b)频率域VTI自适应聚焦束偏移;(c)频率域黏声自适应聚焦束偏移;(d)本文方法 |
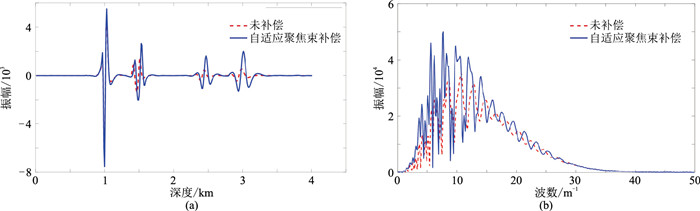
图 4是从图 3b和图 3d中抽取6km处的单道波振幅谱的对比,表明本文方法具有较强振幅补偿和校正的能力。
|
图 4 偏移剖面6km处单道波形(a)及其振幅谱(b)的对比 |
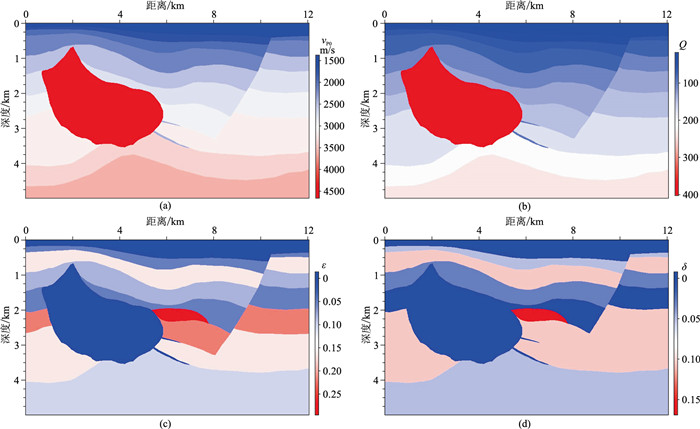
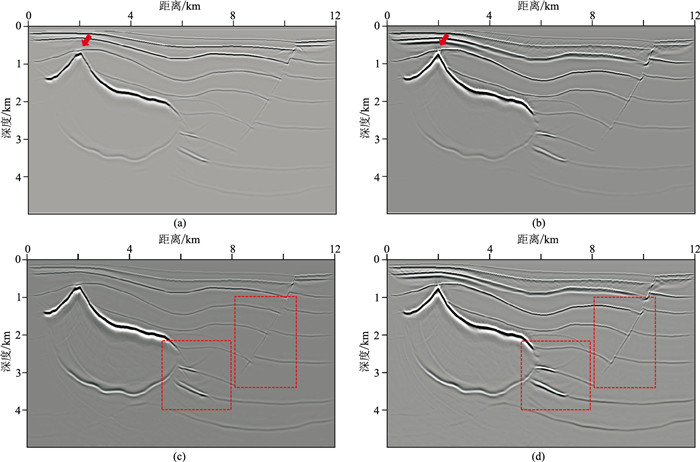
为了验证本文方法对复杂介质的适应性,选用抽稀的国际标准各向异性SEG/Hess模型,且通过李氏经验公式[32]求取Q值,构建如图 5所示的复杂黏声VTI SEG/Hess模型。该模型含有断层、被各向异性包围的盐丘构造及盐丘尾部的岩性尖灭。模型尺寸为1206×500,网格间距为10m;设计观测系统为中间激发,两边接收,共302炮,每炮401道接收,道间距为20m;每道采样点数为2001,采样间隔为0.5ms。通过黏声VTI高阶有限差分正演模拟获取地震炮记录,分别采用频率域声波各向同性、频率域声波VTI、频率域黏声各向同性、时间域黏声VTI等四种自适应聚焦束方法对正演炮记录做偏移处理。观察所得成像(图 6)结果可见:图 6a中深层能量较弱,断层未准确归位,构造成像效果欠佳;图 6c中虽考虑了地层衰减,但黏滞性补偿并未改变射线路径,故未能修正各向异性影响,仍存在绕射波无法正确归位现象;图 6b仅考虑了各向异性影响,盐丘轮廓虽较准确、清晰(红色箭头处),但能量未得到充分补偿;而本文方法由于同时考虑了黏滞性和各向异性的影响,不仅构造成像准确、清晰(图 6d),偏移能量聚焦,而且弥补了能量损失,得到了较高精度的偏移成像剖面。
|
图 5 黏声VTI SEG-Hess模型 (a)vP0; (b)Q; (c)ε; (d)δ |
|
图 6 黏声VTI SEG-Hess模型四种方法偏移成像结果 (a)频率域自适应聚焦束偏移;(b)频率域VTI自适应聚焦束偏移;(c)频率域黏声自适应聚焦束偏移;(d)本文方法 |
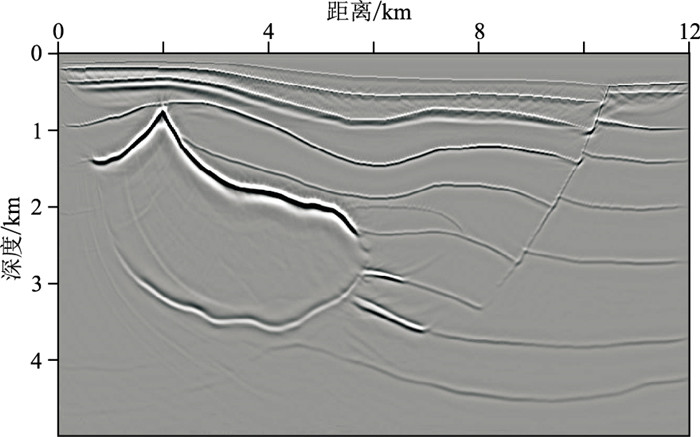
图 7为频率域黏声VTI自适应聚焦束方法的偏移结果,通过与本文方法偏移结果(图 6d)进行对比,同时比较两种方法的计算效率(表 1),可见在确保成像精度前提下,本文方法的计算效率具有明显的优势。
|
图 7 频率域黏声VTI自适应聚焦束偏移成像结果 |
|
|
表 1 两种偏移方法计算时间对比 |
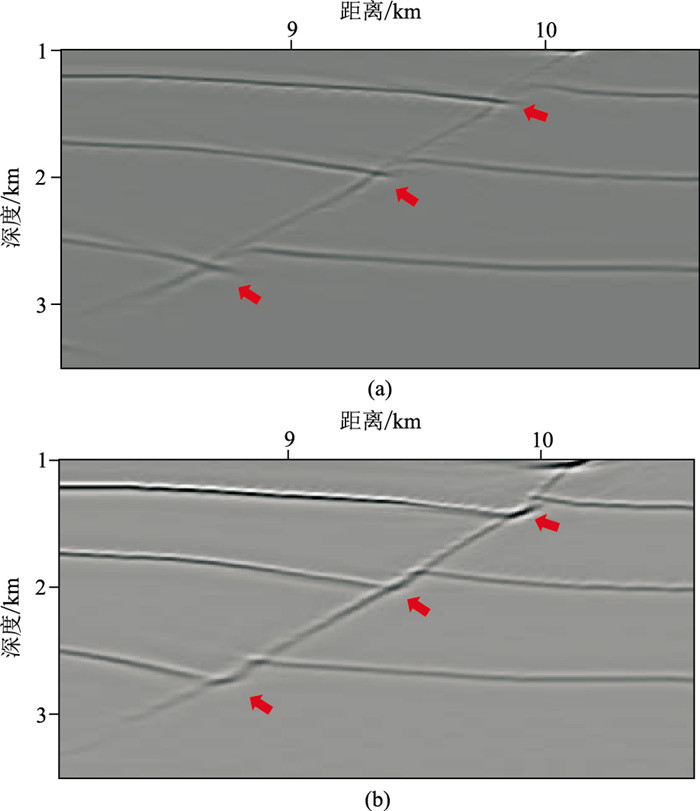
此外,为了更直观地对比本文方法对各向异性的处理能力,将图 6c和图 6d中红色虚线区域进行局部放大(图 8、图 9),可见本文方法处理结果(图 8b、图 9b)中绕射波能更好收敛,断层构造成像准确、清晰,最终偏移剖面质量显著提高。

|
图 8 黏声VTI SEG-Hess模型盐丘尾部尖灭成像结果的局部放大 (a)频率域黏声自适应聚焦束偏移;(b)本文方法 |
|
图 9 黏声VTI SEG-Hess模型断层处成像结果的局部放大 (a)频率域黏声自适应聚焦束偏移;(b)本文方法 |
采用含有黏滞性和弱各向异性特征的M探区数据测试本文方法对实际资料的处理能力。试验区域的深度和横向距离分别是6.0km和25.0km,地震记录共有103炮,炮间距为50m,接收道数为140,采样时长为3.6s,采样间隔为2ms。
从选取的第50、第51炮记录(图 10)可见,有效波的同相轴较清晰,浅层存在一定噪声,中深部信息欠充分,资料整体信噪比较高,可用于成像算法的测试和对比分析。分别用频率域各向同性自适应聚焦束偏移[27]和时间域黏声VTI自适应聚焦束偏移两种方法对该实际记录做偏移处理。从最终偏移成像剖面(图 11)可见,与各向同性自适应聚焦束偏移相比,本文方法所得偏移结果(图 11b)的浅层和中深层同相轴(红色箭头处)的能量得到明显补偿,同相轴更连续,偏移剖面质量得到提高。
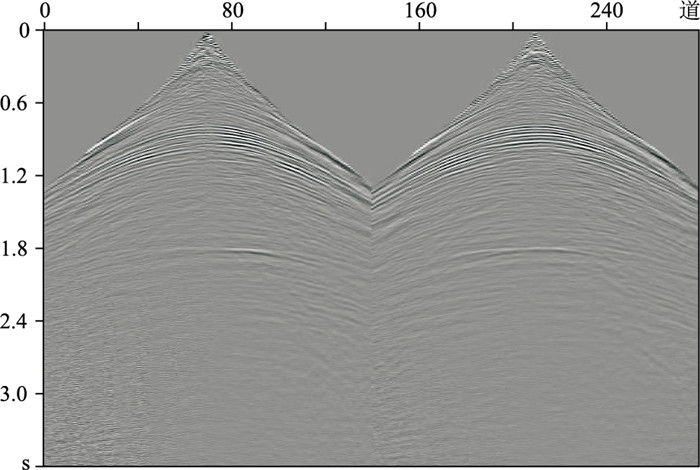
|
图 10 M探区实际地震资料(第50、第51炮) |
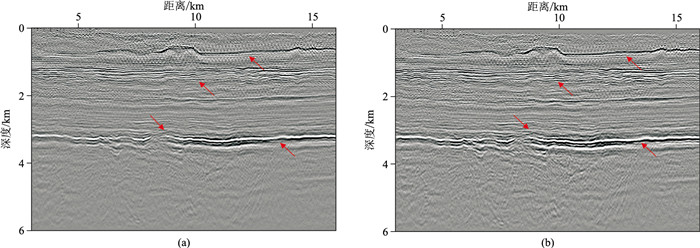
|
图 11 M探区偏移成像结果 (a)频率域各向同性自适应聚焦束偏移;(b)本文方法 |
本文利用各向异性射线追踪方程和黏滞介质吸收衰减补偿特性,给出了黏滞—各向异性射线追踪方程,推导了黏声自适应聚焦束表征的格林函数,并引入傅里叶逆变换和Hilbert变换降低频率域自适应聚焦束积分维度,从而实现了一种较为快速的时间域黏声VTI介质自适应聚焦束偏移。
模型数据和实际地震资料测试结果表明,本文方法对黏滞—各向异性介质具有较强适应性,能同时校正黏滞性和各向异性的影响,使绕射波准确归位,断层处成像清晰,深层能量得到补偿,显著提高成像质量。在计算效率方面,本文方法在保持传统频率域偏移方法较强适应性基础上,计算效率得到明显提升。
然而,补偿后的深层同相轴的能量仍存在欠均衡现象,可考虑引入最小二乘思想进行改善;此外,将本文方法扩展到三维空间,研发三维成像算法,也是下一步研究的方向。
| [1] |
Carcione J M. Wave propagation in anisotropic linear viscoelastic media: theory and simulated wavefields[J]. Geophysical Journal International, 1990, 101(3): 739-750. DOI:10.1111/j.1365-246X.1990.tb05580.x |
| [2] |
严红勇, 刘洋. 黏弹TTI介质中旋转交错网格高阶有限差分数值模拟[J]. 地球物理学报, 2012, 55(4): 1354-1365. YAN Hongyong, LIU Yang. Rotated staggered grid high-order finite-difference numerical modeling for wave propagation in viscoelastic TTI media[J]. Chinese Journal of Geophysics, 2012, 55(4): 1354-1365. DOI:10.6038/j.issn.0001-5733.2012.04.031 |
| [3] |
Červený V. Seismic rays and ray intensities in inhomogeneous anisotropic media[J]. Geophysical Journal International, 1972, 29(1): 1-13. DOI:10.1111/j.1365-246X.1972.tb06147.x |
| [4] |
Červený V, Vaněk J. Expansion of a plane wave into Gaussian beams[J]. Studia Geophysica et Geodaetica, 1982, 26(2): 120-131. DOI:10.1007/BF01582305 |
| [5] |
Červený V, Popov M M, Pšeník I. Computation of wave fields in inhomogeneous media-Gaussian beam approach[J]. Geophysical Journal International, 1982, 70(1): 109-128. DOI:10.1111/j.1365-246X.1982.tb06394.x |
| [6] |
Hill N R. Gaussian beam migration[J]. Geophysics, 1990, 55(11): 1416-1428. DOI:10.1190/1.1442788 |
| [7] |
Hill N R. Prestack Gaussian beam depth migration[J]. Geophysics, 2001, 66(4): 1240-1250. DOI:10.1190/1.1487071 |
| [8] |
Hale D. Migration by the Kirchhoff, Slant Stack, and Gaussian Beam Methods[R]. Center for Wave Phenomena, Colorado School of Mines, 1992.
|
| [9] |
Nowack R L, Sen M K, Stoffa P L. Gaussian beam migration for sparse common-shot and common-receiver data[C]. SEG Technical Program Expanded Abstracts, 2003, 22: 1114-1117.
|
| [10] |
Gray S H. Gaussian beam migration of common-shot records[J]. Geophysics, 2005, 70(4): S71-S77. DOI:10.1190/1.1988186 |
| [11] |
Gray S H, Bleistein N. True-amplitude Gaussian-beam migration[J]. Geophysics, 2009, 74(2): S11-S23. DOI:10.1190/1.3052116 |
| [12] |
李振春, 岳玉波, 郭朝斌, 等. 高斯波束共角度保幅深度偏移[J]. 石油地球物理勘探, 2010, 45(3): 360-365. LI Zhenchun, YUE Yubo, GUO Chaobin, et al. Common angle domain preserved amplitude Gaussian beam depth migration[J]. Oil Geophysical Prospecting, 2010, 45(3): 360-365. |
| [13] |
黄建平, 张晴, 张凯, 等. 格林函数高斯束逆时偏移[J]. 石油地球物理勘探, 2014, 49(1): 101-106. HUANG Jianping, ZHANG Qing, ZHNAG Kai, et al. Reverse time migration with Gaussian beams based on the Greeen functions[J]. Oil Geophysical Prospecting, 2014, 49(1): 101-106. |
| [14] |
高成, 孙建国, 齐鹏, 等. 2D共炮时间域高斯波束偏移[J]. 地球物理学报, 2015, 58(4): 1333-1340. GAO Cheng, SUN Jianguo, QI Peng, et al. 2-D Gau-ssian beam migration of common-shot records in time domain[J]. Chinese Journal of Geophysics, 2015, 58(4): 1333-1340. |
| [15] |
秦宁. 声波各向异性时间域高斯束叠前深度偏移[J]. 石油地球物理勘探, 2020, 55(4): 813-820. QIN Ning. Time domain Gaussian beam prestack depth migration for acoustic anistropic media[J]. Oil Geophysical Prospecting, 2020, 55(4): 813-820. |
| [16] |
Yang J D, Huang J, Wang X, et al. Prestack depth migration method using the time-space Gaussian beam[C]. SEG Technical Program Expanded Abstracts, 2015, 34: 4303-4307.
|
| [17] |
Huang J P, Duan X Y, Yuan M L, et al. Elastic Gau-ssian beam migration method for rugged topography[C]. Extended Abstracts of 75th EAGE Confe-rence & Exhibition, 2013.
|
| [18] |
Alkhalifah T. Gaussian beam depth migration for anisotropic media[J]. Geophysics, 1995, 60(5): 1474-1484. DOI:10.1190/1.1443881 |
| [19] |
Hanyga A. Gaussian beams in anisotropic elastic media[J]. Geophysical Journal International, 1986, 85(3): 473-504. DOI:10.1111/j.1365-246X.1986.tb04528.x |
| [20] |
Zhu T, Gray S H, Wang D. Prestack Gaussian-beam depth migration in anisotropic media[J]. Geophysics, 2007, 72(3): S133-S138. DOI:10.1190/1.2711423 |
| [21] |
吴娟, 陈小宏, 白敏. 黏滞声波高斯束叠前深度偏移[J]. 吉林大学学报(地球科学版), 2015, 45(5): 1530-1538. WU Juan, CHEN Xiaohong, BAI Min. Viscoacoustic Gaussian beam prestack depth migration[J]. Journal of Jilin University(Earth Science Edition), 2015, 45(5): 1530-1538. |
| [22] |
韩建光, 王赟, 张晓波, 等. VTI介质高斯束叠前深度偏移[J]. 石油地球物理勘探, 2015, 50(2): 267-273. HAN Jianguang, WANG Yun, ZHANG Xiaobo, et al. Guassian beam prestack depth migration in VTI media[J]. Oil Geophysical Prospecting, 2015, 50(2): 267-273. |
| [23] |
代福材, 黄建平, 李振春, 等. 角度域黏声介质高斯束叠前深度偏移方法[J]. 石油地球物理勘探, 2017, 52(2): 283-293. DAI Fucai, HUANG Jianping, LI Zhenchun, et al. Angle domain prestack Gaussian beam migration for visco-acoustic media[J]. Oil Geophysical Prospecting, 2017, 52(2): 283-293. |
| [24] |
张瑞, 黄建平, 李振春, 等. 相似系数阈值滤波的数据驱动控制束偏移[J]. 石油地球物理勘探, 2019, 54(6): 1267-1279. ZHANG Rui, HUANG Jianping, LI Zhenchun, et al. A data-driven controlled beam migration based on the semblance threshold filtering[J]. Oil Geophysical Prospecting, 2019, 54(6): 1267-1279. |
| [25] |
Gao F, Zhang P, Wang B, et al. Fast beam migration: A step toward interactive imaging[C]. SEG Technical Program Expanded Abstracts, 2006, 25: 2470-2474.
|
| [26] |
Nowack R L. Focused Gaussian beams for seismic imaging[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 2376-2380.
|
| [27] |
Yang J D, Huang J P, Wang X, et al. An amplitude-preserved adaptive focused beam seismic migration method[J]. Petroleum Science, 2015, 12(3): 417-427. DOI:10.1007/s12182-015-0044-7 |
| [28] |
李胜雅, 吕庆达, 黄建平, 等. VTI介质自适应聚焦束偏移[J]. 石油地球物理勘探, 2020, 55(1): 92-100. LI Shengya, LYU Qingda, HUANG Jianping, et al. Adaptive focused beam migration in VTI media[J]. Oil Geophysical Prospecting, 2020, 55(1): 92-100. |
| [29] |
Aki K, Richards P G. Quantitative Seismology, Theory and Methods[M]. Freeman: W H, 1980.
|
| [30] |
Keers H, Vasco D W, Johnson L R. Viscoacoustic cro-sswell imaging using asymptotic waveforms[J]. Geophysics, 2001, 66(3): 861-870. DOI:10.1190/1.1444975 |
| [31] |
Zhang Y, Xu S, Bleistein N, et al. True-amplitude, angle-domain, common-image gathers from one-way wave-equation migrations[J]. Geophysics, 2007, 72(1): S49-S58. DOI:10.1190/1.2399371 |
| [32] |
李庆忠. 高分辨率地震资料处理[M]. 北京: 石油工业出版社, 1993.
|



 黄建平, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
黄建平, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: 