② 中国石化地球物理重点实验室, 江苏南京 211103
② SINOPEC Key Laboratory of Geophysics, Nanjing, Jiangsu 211103, China
地震波数值模拟对认识地震波传播规律和分析干扰波形成机理具有重要意义,因此常被用于优化观测系统和指导处理解释[1-5]。此外,地震波数值模拟也是逆时偏移和波形反演的重要内核[6]。目前已有许多基于波动方程的数值模拟方法,如:有限差分法(FDM)[7-10]、伪谱法(PSM)[11-12]、有限体积法(FVM)[13-14]、无网格法[15]、有限元法(FEM)[16-18],谱元法(SEM)[19-23]和间断Galerkin有限元方法(DGFEM)[24-27]。FDM因容易编程实现、易于并行等特点,目前应用最广泛。但是FDM对起伏地表的适应性有限,且准确模拟地表自由边界较为困难。PSM同样也存在边界条件难以准确模拟的问题,且三维计算需要全局通信,难于实现并行。FVM和FEM都可以使用非结构化的三角形(三维是四面体)网格以适应复杂的地表结构,且天然满足自由边界条件,但是FVM的高阶计算难于实现,较少应用于地震波模拟。FEM则需要存储大型稀疏矩阵并求逆,对计算资源要求极高。SEM和DGFEM是对FEM的改进。SEM使用GLL(Gauss Lobatto Legendre)插值点得到对角形式的质量矩阵,从而避免了矩阵求逆过程。但是经典的SEM使用的是四边形(三维是六面体)网格,对复杂地表的刻画缺乏灵活性。DGFEM在单元内部使用有限元方法处理,而在单元边界上使用FVM的数值流通量的方式。DGFEM集合了有限元方法的网格灵活性和高精度,同时又可以逐元求解,降低了对计算资源的消耗且便于并行计算。
数值稳定性、数值频散以及耗散问题是研究波动方程数值解的重要内容。有限元方法因使用的网格形态比较灵活,所以一般需构建周期性网格进行分析。四边形网格的模拟精度分析因为周期网格构建容易、基函数可以解耦等原因,已有大量研究[16, 28-32]。而对于三角形网格的数值精度研究较少,刘少林等[33]和曹丹平等[34]分析了经典FEM在不同形态的周期性三角形网格中的声波方程频散和稳定性条件,也有少量的关于三角形网格的SEM频散分析研究[35-37]。对于四边形网格的DGFEM,De Basabe等[38]分析了不同基函数对数值精度的影响;贺茜君等[39]分析了Runge-Kutta(RK)时间格式的频散和稳定性;Meng等[40]分析了不同基函数对频散和稳定性的影响。对于三角形网格的DGFEM,Hu等[41]分析了半离散声波方程的频散和耗散,但未考虑时间格式;Käser等[42]从实验角度分析了弹性波任意高阶导数法(Arbitrary high-order derivatives,ADER)时间格式的数值收敛率,但未分析频散和耗散;Delcourte等[43]分析了蛙跳(Frog-leap,FL)时间格式的基于中心数值流的收敛率;He等[44]分析了声波方程RK和ADER时间格式的数值精度。
本文针对弹性波的数值模拟精度问题,通过构造任意等腰三角形单元组成的周期性网格,可以方便地分析各种形态的三角形单元对数值模拟精度的影响。从理论和数值计算上分析了基于局部Lax-Friedrichs数值流和3阶总变差不增的Runge-Kutta(简称TVD RK)时间格式的三角形网格DGFEM弹性波模拟的数值频散、耗散和稳定性,可为基于三角形网格的DGFEM弹性波模拟提供参数选取指导。
1 数值模拟方法二维各向同性介质中的弹性波速度—应力方程为[42]
| $ \left\{\begin{array}{l} \frac{\partial \sigma_{x x}}{\partial t}-(\lambda+2 \mu) \frac{\partial v_{x}}{\partial x}-\lambda \frac{\partial v_{z}}{\partial z}=S_{1} \\ \frac{\partial \sigma_{z z}}{\partial t}-\lambda \frac{\partial v_{x}}{\partial x}-(\lambda+2 \mu) \frac{\partial v_{z}}{\partial z}=S_{2} \\ \frac{\partial \sigma_{x z}}{\partial t}-\mu\left(\frac{\partial v_{z}}{\partial x}+\frac{\partial v_{x}}{\partial z}\right)=S_{3} \\ \frac{\partial v_{x}}{\partial t}-\frac{1}{\rho}\left(\frac{\partial \sigma_{x x}}{\partial x}+\frac{\partial \sigma_{x z}}{\partial z}\right)=S_{4} \\ \frac{\partial v_{z}}{\partial t}-\frac{1}{\rho}\left(\frac{\partial \sigma_{x z}}{\partial x}+\frac{\partial \sigma_{z z}}{\partial z}\right)=S_{5} \end{array}\right. $ | (1) |
式中:λ、μ为拉梅常数;ρ是密度;σxx和σzz为正应力,σxz为剪切应力;vx和vz分别为质点速度的x和z分量;S1~S5表示外力震源。将式(1)改写成一阶线性双曲偏微分方程矩阵形式,有
| $ \frac{\partial \boldsymbol{u}}{\partial t}+\boldsymbol{P} \frac{\partial \boldsymbol{u}}{\partial x}+\boldsymbol{B} \frac{\partial \boldsymbol{u}}{\partial z}=\boldsymbol{S} $ | (2) |
式中:u=(σxx,σzz,σxz,vx,vz)T;P、B是式(1)中弹性参数的矩阵形式。
1.1 空间离散DGFEM的空间离散需要将计算空间划分成不重叠的子区域,即单元。本文讨论二维三角形网格,直接给出式(2)的DGFEM空间离散格式[36]
| $ \begin{aligned} &\frac{\partial \hat{u}_{g b}^{(m)}}{\partial t} M_{a b}+\sum\limits_{j=1}^{3}\left(H^{+j}\right)_{g l} \hat{u}_{l b}^{\left(m_{j}\right)} \frac{\left|\varepsilon_{j}\right|}{J} F_{a b}^{j, 0}+\\ &\sum\limits_{j=1}^{3}\left(H^{-j}\right)_{g l} \hat{u}_{l b}^{(m)} \frac{\left|\varepsilon_{j}\right|}{J} F_{a b}^{j, i}-P_{g q}^{*} \hat{u}_{q b}^{(m)} K_{a b}^{\zeta}-\\ &B_{g q}^{*} \hat{u}_{q b}^{(m)} K_{a b}^{\eta}=\int_{\varOmega^{(m)}} \phi_{a} S_{g} \mathrm{~d} \xi \mathrm{d} \eta \end{aligned} $ | (3) |
式中:m为本单元编号;ug(m)(ξ, η, t)=ûgb(m)(t)ϕb(ξ, η),ûgb(m)为本单元应力和速度的自由度,ϕb为基函数;a,b=1,2,…,N,N为单元内自由度数目;l,g,q=1,2,…,5;a,b,l,g,q均满足Einstein求和约定;i,j=1,2,3为单元内三条边的编号;mj和εj分别为本单元三条边对应的单元编号和边的长度;Ω(m)表示在本单元内部积分;J为Jacobi常数;ξ和η是参考单元内坐标;M是质量矩阵;Kξ和Kη是刚度矩阵;Fj,0是本单元的j边的数值流矩阵;Fj,i是与本单元第j边相邻的单元mj (相邻边在mj单元中为第i边)的数值流矩阵(本文使用局部Lax-Freidrichs数值流[27]);其余矩阵的表达式为
| $ \left\{\begin{array}{l} \left(H^{+j}\right)_{g l}=\frac{n_{x}^{j} P_{g l}+n_{z}^{j} B_{g l}+c_{\mathrm{P}} I_{g l}}{2} \\ \left(H^{-j}\right)_{g l}=\frac{n_{x}^{j} P_{g l}+n_{z}^{j} B_{g l}-c_{\mathrm{P}} I_{g l}}{2} \\ P_{g q}^{*}=P_{g q} \frac{\partial \xi}{\partial x}+B_{g q} \frac{\partial \xi}{\partial z} \\ B_{g q}^{*}=P_{g q} \frac{\partial \eta}{\partial x}+B_{g q} \frac{\partial \eta}{\partial z} \end{array}\right. $ | (4) |
其中:I为单位矩阵;cP为纵波速度;nxj和nzj分别为本单元j边的外法向单位矢量的x和z分量。更多关于DGFEM的细节及矩阵具体形式见文献[42]。本文使用的基函数由Jacobi多项式构造[45]。
1.2 时间离散间断有限元求解有多种时间离散方法,如ADER、LF和RK法。ADER法将时间导数转化到空间导数的计算上,可以达到时间和空间任意精度,但是实现复杂[42];LF时间格式通常和中心数值流一起使用[43, 46],且可以使用更大的时间步长从而提高计算效率,但是常用的LF时间格式精度只有二阶。本文使用RK法。
式(3)可简写为关于时间的常微分方程
| $ \frac{\partial \hat{\boldsymbol{u}}}{\partial t}=L(\hat{\boldsymbol{u}}) $ | (5) |
式中忽略了震源项,L是空间离散的线性系统。常用的3阶TVD RK时间离散格式[25, 39]为
| $ \left\{\begin{array}{l} \hat{\boldsymbol{u}}_{(1)}=\hat{\boldsymbol{u}}^{N_{t}}+\Delta t L\left(\hat{\boldsymbol{u}}^{N_{t}}\right) \\ \hat{\boldsymbol{u}}_{(2)}=\frac{3}{4} \hat{\boldsymbol{u}}^{N_{t}}+\frac{1}{4} \hat{\boldsymbol{u}}_{(1)}+\frac{1}{4} \Delta t L\left[\hat{\boldsymbol{u}}_{(1)}\right] \\ \hat{\boldsymbol{u}}^{N_{t}+1}=\frac{1}{3} \hat{\boldsymbol{u}}^{N_{t}}+\frac{2}{3} \hat{\boldsymbol{u}}_{(2)}+\frac{2}{3} \Delta t L\left[\hat{\boldsymbol{u}}_{(2)}\right] \end{array}\right. $ | (6) |
式中:Δt为时间步长;Nt为时间序号;û(1)和û(2)为两个辅助变量。
2 数值稳定性及精度分析 2.1 基于三角形网格的理论分析方法稳定性和数值精度的理论分析通常使用Von Neumann方法:假设研究区域为无界各向同性的均匀介质且无外力震源,分析平面波在研究区域的传播问题。
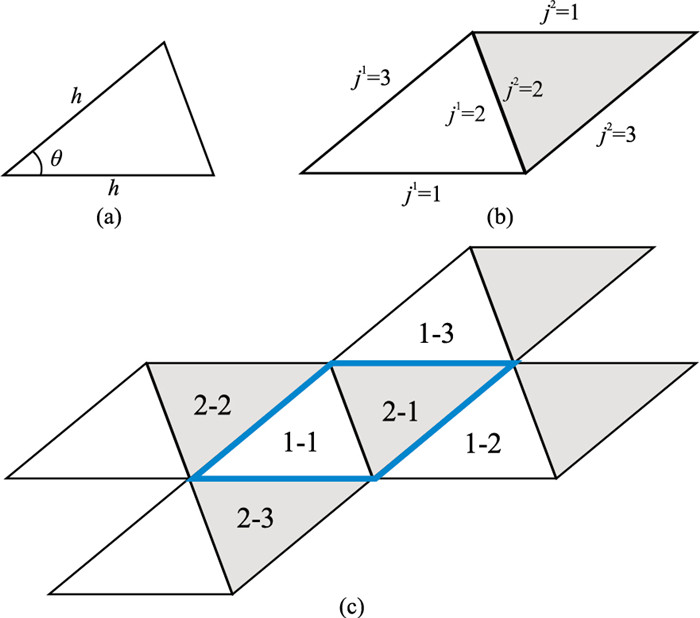
首先假设计算空间剖分为以顶角为θ、腰长为h的等腰三角形为基本单元的周期性网格(图 1),其中单元2-i是由单元1-i旋转所得,除此之外,单元完全相同。因此将单元1-1和单元2-1称为母单元,其他单元称为子单元。为了简化,将相邻的两类三角形组合在一起分析[41],即图 1中单元1-1和单元2-1作为整体进行分析。假设母单元中的边界顺序如图 1b所示,子单元边界顺序同母单元。
|
图 1 周期性三角形网格剖分示意图 (a)基本单元;(b)1类和2类母单元边界对应关系;(c)周期性网格模型 |
考虑平面简谐波
| $ \begin{aligned} &\hat{\boldsymbol{u}}=\boldsymbol{A} \exp [\mathrm{i}(\boldsymbol{k} \boldsymbol{x}-\omega t)]= \\ &\boldsymbol{A} \exp (-\mathrm{i} \omega t) \exp (\mathrm{i} \boldsymbol{k} \boldsymbol{x})=\boldsymbol{A}(t) \exp (\mathrm{i} \boldsymbol{k} \boldsymbol{x}) \end{aligned} $ | (7) |
则各子单元内的平面波与母单元平面波的相位关系如表 1所示。假设波的传播方向与x轴夹角为γ,则kxh=2πδcosγ,kzh=2πδsinγ,其中k为波数矢量,δ=h/W是采样率,W是波长。
|
|
表 1 各子单元与母单元的平面波相位关系 |
忽略震源项,单元1-2和单元2-1的间断Galerkin有限元法的半离散方程(式(3))可以写为
| $ \frac{\partial \hat{\boldsymbol{u}}}{\partial t}=\boldsymbol{Q} \hat{\boldsymbol{u}} $ | (8) |
式中
| $ \begin{aligned} \hat{\boldsymbol{u}}=&\left[\sigma_{x x}^{(1-1)} \sigma_{z z}^{(1-1)} \sigma_{x z}^{(1-1)} v_{x}^{(1-1)} v_{z}^{(1-1)}\right.\\ &\ \ \ \ \ \ \ \ \left.\sigma_{x x}^{(2-1)} \sigma_{z z}^{(2-1)} \sigma_{x z}^{(2-1)} v_{x}^{(2-1)} v_{z}^{(2-1)}\right]^{\mathrm{T}} \end{aligned} $ | (9) |
| $ \boldsymbol{Q}=\frac{h}{J}\left[\begin{array}{llll} \boldsymbol{M} & & & \\ & \boldsymbol{M} & & \\ & & \ddots & \\ & & & \boldsymbol{M} \end{array}\right]\left[\begin{array}{ll} \boldsymbol{\varGamma}_{11} & \boldsymbol{\varGamma}_{12} \\ \boldsymbol{\varGamma}_{21} & \boldsymbol{\varGamma}_{22} \end{array}\right] $ | (10) |
其中的子矩阵Γ11、Γ12、Γ21、Γ22表达式见附录A。
2.2 稳定性分析模拟时在网格尺寸h和介质速度cP已定的情况下,时间步长需满足Δt≤αmaxh/cP,其中α为Courant数,αmax=ΔtmaxcP/h是最大Courant数。DGFEM的3阶TVD RK方法可以写成[33]
| $ \begin{aligned} \hat{\boldsymbol{u}}^{N_{t}+1} &=\left[\boldsymbol{I}+\Delta t \boldsymbol{Q}+\frac{1}{2}(\Delta t)^{2} \boldsymbol{Q}^{2}+\frac{1}{6}(\Delta t)^{3} \boldsymbol{Q}^{3}\right] \hat{\boldsymbol{u}}^{N_{t}} \\ &=\boldsymbol{G} \hat{\boldsymbol{u}}^{N_{t}} \end{aligned} $ | (11) |
ûNt+1=exp(-iωt)ûNt代入上式,可得
| $ \exp \left(-\mathrm{i} \omega_{h} \Delta t\right) \hat{\boldsymbol{u}}^{N_{t}}=\boldsymbol{G} \hat{\boldsymbol{u}}^{N_{t}} $ | (12) |
式中ωh是与三角形腰长h有关的数值圆频率。可以看出,β=exp(-iωhΔt)是矩阵G的特征值。为了使模拟稳定,矩阵G的谱半径必须小于等于1,即|β|≤1[34]。需要注意的是,求解式(13)的特征值,系统会得到20N个特征值,要求每个特征值都满足|β|≤1,可用迭代方法求得最大Courant数αmax[40]。αmax越小说明模拟过程的稳定性越差,反之稳定性越强。
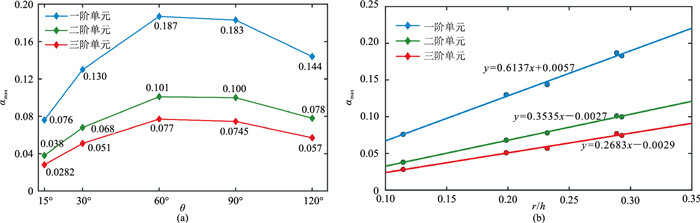
αmax随θ的变化曲线如图 2a所示,可见,当单元过于狭长或扁平时模拟的稳定性较差。图 2b为一、二、三阶单元αmax随r/h(r为内切圆半径)变化曲线,可知,各阶单元的αmax与r/h满足线性关系,其斜率分别为0.6137、0.3535、0.2683,约等于2/(2p+1),其中p为单元阶次。由Δt=αh/cP可知,Δt与三角形内切圆半径r也满足线性关系,即Δt∝2/(2p +1)r/cP。
|
图 2 不同阶单元αmax随θ(a)和r/h(b)的变化曲线 |
当时间步长Δt确定后,计算得到的数值圆频率与真实圆频率不完全相同,导致数值频散和耗散。理论分析同样用式(13)的特征值问题展开。将数值圆频率写为ωh=ωr+iωi,其中ωi对应了数值模拟的耗散部分,引起平面波振幅变化,ωr是频散部分,引起波速变化。将ωh代入式(7)可得
| $ \hat{\boldsymbol{u}}=\boldsymbol{A} \exp \left(\omega_{\mathrm{i}} t\right) \exp \left[\mathrm{i}\left(\boldsymbol{k} \boldsymbol{x}-\omega_{\mathrm{r}} t\right)\right] $ | (13) |
将ωh代入式(12)左侧,可得
| $ \exp \left(\omega_{\mathrm{i}} \Delta t\right)\left[\cos \left(\omega_{\mathrm{r}} \Delta t\right)-\mathrm{i} \sin \left(\omega_{\mathrm{r}} \Delta t\right)\right]=\beta_{\mathrm{r}}+\mathrm{i} \beta_{\mathrm{i}} $ | (14) |
进一步可得
| $ \omega_{\mathrm{r}}=\frac{1}{\Delta t} \arctan \left(-\frac{\beta_{\mathrm{i}}}{\beta_{\mathrm{r}}}\right) $ | (15) |
则数值频散系数d和耗散系数d′可分别表示为
| $ d=\frac{c_{h}}{c}=\frac{h \omega_{\mathrm{r}}}{2 {\rm{ \mathsf{ π} }} \delta c_{\mathrm{P}}}=\frac{\Delta t \omega_{\mathrm{r}}}{2 {\rm{ \mathsf{ π} }} \alpha \delta} $ | (16) |
| $ d^{\prime}=\exp \left(\omega_{\mathrm{i}} \Delta t\right)=\frac{\beta_{\mathrm{r}}}{\cos \left(\omega_{\mathrm{r}} \Delta t\right)} $ | (17) |
当d大于1时,相速度大于介质速度,相反则说明相速度小于介质速度。d越接近1,模拟精度越高。由于P波和S波具有相同的频率、不同的空间采样率,因此分别对P波和S波进行分析。
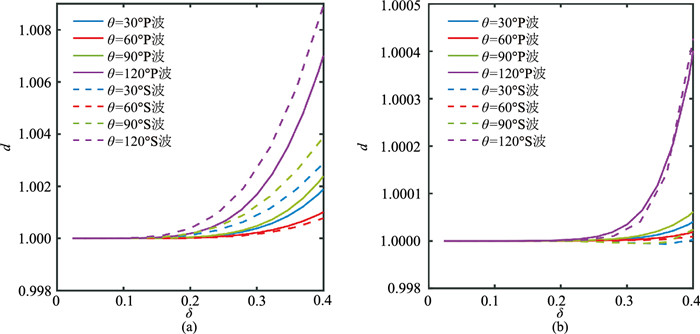
当Courant数α=0.03、平面波传播方向角γ=0°时,计算θ分别为30°、60°、90°、120°时的二阶和三阶单元的P波和S波频散系数d随δ的变化曲线(图 3)。由图 3可以看出,二阶单元在δ小于0.4时,P、S波频散系数的相对误差小于0.9%,三阶单元的相对误差则小于0.05%,体现了DGFEM的弱频散特性。二阶单元一个波长内有2~3个网格即可满足频散要求。此外,由二阶单元的频散结果可以看出,在γ=0°方向上传播的平面波,θ为60°时频散最弱,其次是30°、90°、120°;S波的频散强弱相对关系与P波一致。不同形态(顶角θ不同)三阶单元的纵波频散相对关系与二阶单元一致。
|
图 3 不同形态二阶(a)和三阶(b)单元的的P波和S波频散曲线 |
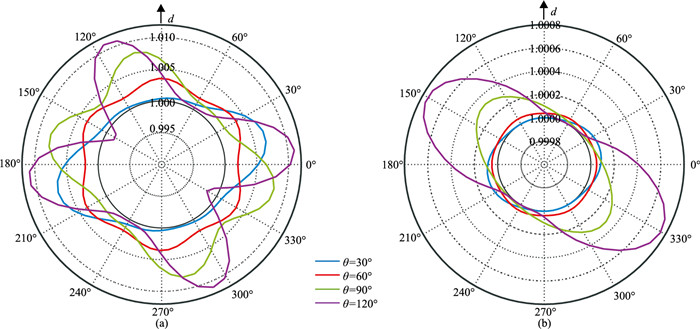
图 4是一阶单元和二阶单元频散系数随传播方向的变化曲线,由图中可以看出,当单元为等边三角形时,频散系数随传播方向变化的周期为60°,且沿单元边界方向传播时频散最小,而垂直网格线传播时频散最大。而经典有限元方法在等边三角形网格中基本没有数值各向异性。二者的区别可能是由DGFEM的数值流形式引起的。其他形态三角形单元的频散系数随传播方向的变化以180°为周期。等边三角形单元的频散曲线更接近圆形,数值各向异性最弱,而其他形态的三角形单元的频散多呈条带状,数值各向异性更强。在图 4b中,当θ=30°时频散曲线在γ=15°和195°处频散最大,即垂直于等腰三角形底边的方向,最小频散的方向为沿底边方向;当θ=90°时,最大频散的方向为γ=135°和225°,当θ=120°时,最大频散的方向为γ=150°和330°,即沿底边的传播方向频散最大,垂直于底边方向频散最小。
|
图 4 不同形态单元纵波频散系数随传播方向角γ的变化曲线 (a)一阶单元;(b)二阶单元。δ≈0.2 |
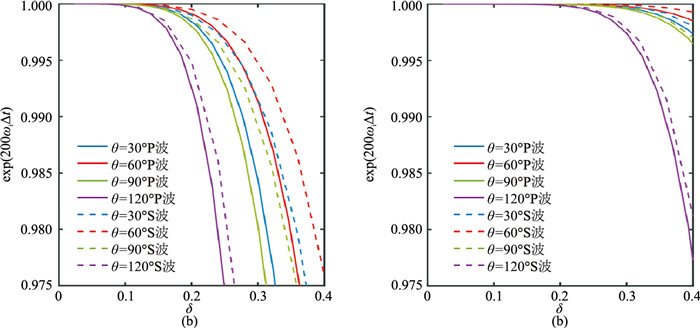
θ分别为30°、60°、90°、120°时,计算二阶和三阶单元的网格P波和S波的耗散系数随采样率的变化曲线(图 5),其中α=0.03。为了明显区分曲线,图 5是模拟了200个时间步长后的耗散曲线(即exp(200ωiΔt))。由图可见,随着δ的增加,数值耗散越强;对于相同的δ,S波的耗散略小于P波,通常情况下,同一介质内的S波采样率大于P波的采样率;另外,随着单元阶数的增大,耗散的影响减弱。通常地震波需要模拟几千甚至几万个时间步长,数值耗散将对模拟结果产生较大影响。
|
图 5 不同形态二阶(a)和三阶(b)单元的的P波和S波耗散曲线 |
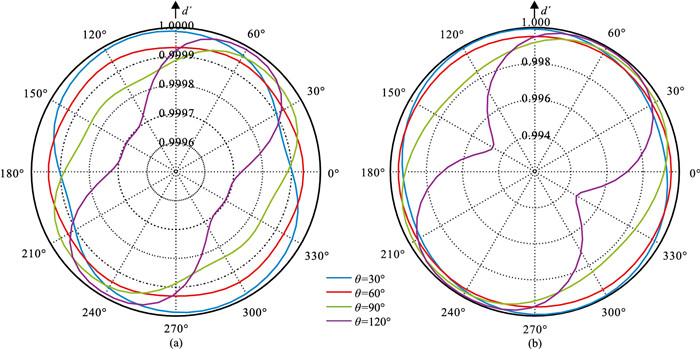
图 6为θ不同时,一阶单元网格的exp(ωiΔt)随传播方向的变化曲线,其中α=0.03、δP=0.11、δS=0.20。由图可见,耗散曲线的对称性与频散曲线(图 4)相同。单元顶角θ=60°时,耗散系数整体上更接近1。
|
图 6 不同形态一阶单元的耗散系数随传播方向角γ的变化曲线 (a)纵波;(b)横波 |
表 2梳理了上述周期性网格的理论分析结果。表中数值各向异性是基于已比较过的单元形态。
|
|
表 2 不同形态三角形单元的最大αmax及数值各向异性特征 |
首先通过模拟二维均匀各向同性介质平面波单频成分分析不同形态单元的误差。不考虑震源项,均匀各向同性介质中弹性平面波应力和速度分量的解析解表达式分别为
| $ \left\{\begin{aligned} \sigma_{x x}=&\left(\lambda+2 \mu n_{x}^{2}\right) \sin \left[2 {\rm{ \mathsf{ π} }} f_{0}\left(t-\frac{n_{x} x}{c_{\mathrm{P}}}-\frac{n_{z} z}{c_{\mathrm{P}}}\right)\right]- \\ &2 \mu n_{x} n_{z} \sin \left[2 {\rm{ \mathsf{ π} }} f_{0}\left(t-\frac{n_{x} x}{c_{\mathrm{S}}}-\frac{n_{z} z}{c_{\mathrm{S}}}\right)\right] \\ \sigma_{z z}=&\left(\lambda+2 \mu n_{z}^{2}\right) \sin \left[2 {\rm{ \mathsf{ π} }} f_{0}\left(t-\frac{n_{x} x}{c_{\mathrm{P}}}-\frac{n_{z} z}{c_{\mathrm{P}}}\right)\right]+ \\ & 2 \mu n_{x} n_{z} \sin \left[2 {\rm{ \mathsf{ π} }} f_{0}\left(t-\frac{n_{x} x}{c_{\mathrm{S}}}-\frac{n_{z} z}{c_{\mathrm{S}}}\right)\right] \\ \sigma_{x z}=&2 \mu n_{x} n_{z} \sin \left[2 {\rm{ \mathsf{ π} }} f_{0}\left(t-\frac{n_{x} x}{c_{\mathrm{P}}}-\frac{n_{z} z}{c_{\mathrm{P}}}\right)\right]+ \\ & \mu\left(n_{x}^{2}-n_{z}^{2}\right) \sin \left[2 {\rm{ \mathsf{ π} }} f_{0}\left(t-\frac{n_{x} x}{c_{\mathrm{S}}}-\frac{n_{z} z}{c_{\mathrm{S}}}\right)\right] \end{aligned}\right. $ | (18) |
| $ \left\{\begin{aligned} v_{x}=&-n_{x} c_{\mathrm{P}} \sin \left[2 {\rm{ \mathsf{ π} }} f_{0}\left(t-\frac{n_{x} x}{c_{\mathrm{P}}}-\frac{n_{z} z}{c_{\mathrm{P}}}\right)\right]+\\ & n_{z} c_{\mathrm{S}} \sin \left[2 {\rm{ \mathsf{ π} }} f_{0}\left(t-\frac{n_{x} x}{c_{\mathrm{S}}}-\frac{n_{z} z}{c_{\mathrm{S}}}\right)\right] \\ \tau_{z}=&-n_{z} c_{\mathrm{P}} \sin \left[2 {\rm{ \mathsf{ π} }} f_{0}\left(t-\frac{n_{x} x}{c_{\mathrm{P}}}-\frac{n_{z} z}{c_{\mathrm{P}}}\right)\right]-\\ & n_{x} c_{\mathrm{S}} \sin \left[2 {\rm{ \mathsf{ π} }} f_{0}\left(t-\frac{n_{x} x}{c_{\mathrm{S}}}-\frac{n_{z} z}{c_{\mathrm{S}}}\right)\right] \end{aligned}\right. $ | (19) |
上式每个分量都包含一个沿着(nx,nz)T方向传播的平面P波和S波。取t=0时刻的解析值作为数值模拟的初始条件。
分别用θ为30°、60°、90°的周期性网格进行均匀模型模拟,并对每个θ取其数值各向异性的两个对称轴的方向作为平面波传播方向,即θ=30°时,取γ=15°或105°;θ=60°时,取γ=0°或30°;θ=90°时,取γ=45°或135°。等腰三角形单元的腰长h分别设置为10.0、12.5、20.0、25.0m。均匀模型尺寸为5000m×5000m,cP=4000m/s、cS=2000m/s、ρ=2000kg/m3;模拟频率f0=40Hz,Δt=2ms,模拟时长tmax=250ms。
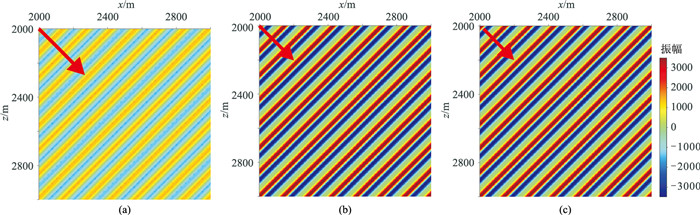
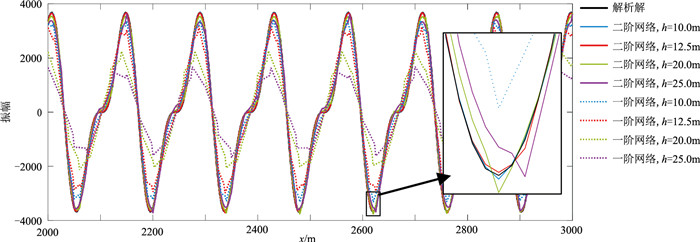
图 7为θ=90°、γ=45°时,tmax时刻的模拟波场与解析解的对比。由于没有使用吸收和周期性边界,所以取模型中没有受到边界反射干扰的区域。由图 7可以看出,使用一阶单元且h=25.0m时的模拟波场与解析解在能量上有很大差异,模拟误差主要来源于是数值耗散(纵波空间采样率为0.25,横波采样率为0.5)。使用二阶单元,h=10.0m时的模拟波场与解析解接近(纵、横波的空间采样率分别为0.1和0.2)。图 8为图 7深度为2000m处的波场,可见:二阶单元h=10.0m和h=12.5m两种网格的计算结果与解析解对应较好;当使用一阶单元时,即使空间采样率取0.1,也会产生很强的数值耗散。
|
图 7 θ=90°、γ=45°时tmax时刻的不同网格模拟的40Hz单频波场与解析解的对比 (a)一阶单元,h=25m;(b)二阶单元h=10m;(c)解析解。图中红色箭头表示传播方向 |
|
图 8 θ=90°、γ=45°时tmax时刻、深度2000m处不同网格模拟的波场与解析解的对比 |
使用Etienne等[46]的方法计算模拟结果x与解析解vx的误差,即
| $ E=\left[\int_{\varOmega}\left(\hat{v}_{x}-v_{x}\right)^{2} \mathrm{~d} \varOmega\right]^{\frac{1}{2}} $ | (20) |
式中Ω为选取的计算区域。具体地,当θ=30°时,Ω为4600m≤x≤4900m,1200m≤z≤1400m;当θ=60°时,Ω为3500m≤x≤4500m,2000m≤z≤3000m;当θ=90°时,Ω为2000m≤x≤3000m,2000m≤z≤3000m。
图 9、表 3给出了不同θ的一阶和二阶单元网格在不同传播方向上的模拟误差。可以看出,由于误差主要受数值耗散的影响,对于相同θ,两个对称轴方向上的误差相对关系与耗散随传播方向的变化曲线(图 5和图 6)一致;对于相同阶次的单元,其网格尺寸与误差在双对数坐标系下呈线性关系:一阶单元时,斜率约为2;二阶单元时,斜率约为4;单元从一阶提高到二阶,网格越小,误差减小越明显。

|
图 9 不同θ的时一阶和二阶单元网格在不同传播方向上的模拟误差随网格尺寸的变化曲线 蓝色、红色和紫色线分别代表顶角为60°、30°、90°的周期性网格结果,绿色为非规则网格结果 |
|
|
表 3 不同形态的一阶和二阶单元在不同传播方向上的误差统计 |
同时,计算了在一般性非规则网格中的3阶TVD RK时间格式的DGFEM的误差(图 9、表 4)。图 10是误差统计区域内的非结构性网格,呈无规律排列。图 9中非规则网格误差曲线同样表现为线性,而且在45°和135°两个方向上没有出现明显的数值各向异性。
|
|
表 4 非结构网格中一阶和二阶单元在45°和135°方向上的误差 |

|
图 10 模拟使用的非结构性网格 |
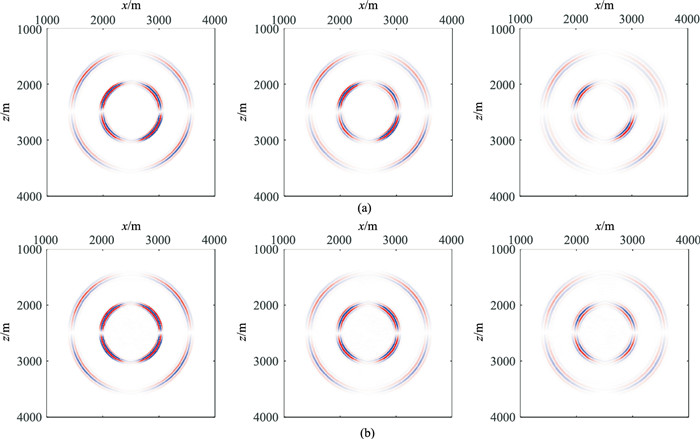
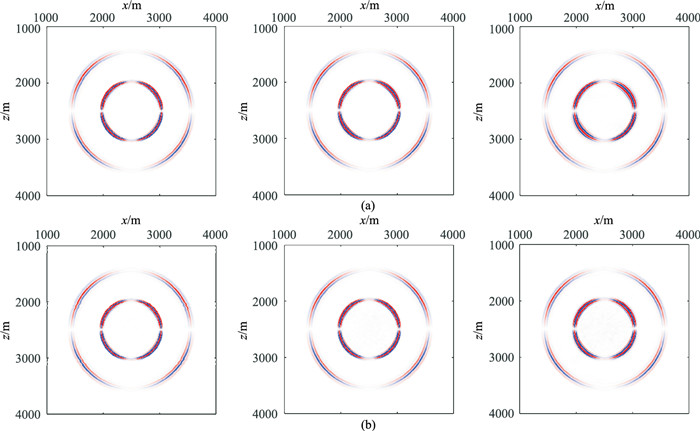
应用上述均匀各向同性介质模型进行点源激发模拟,以更加直观地说明网格对DGFEM的波场特征的影响。震源为主频40Hz的Ricker子波,时间步长Δt=8ms。图 11为h取不同值时一阶直角三角形周期性网格与一般非结构化网格模拟得到的0.3s时刻的vz波场快照对比。图 12为二阶直角三角形周期性网格与一般非结构化网格模拟得到的0.3s时刻的vz波场快照对比。由图 11可以看出,当网格阶数为一时,随着网格尺寸的增加,两种网格的波场能量总体都有所下降。由h=20.0m的直角三角形周期性网格模拟的波场快照(图 11a右和图 12a右)可以看出,在135°和315°方向,纵波和横波的波形变宽,旁瓣更加明显,能量比45°方向弱很多,这是数值耗散所致。而在图 11b右和图 12b右所示的h=20.0m的一般非结构化网格模拟的性网格的波场快照上,观察不到明显的方向差异,说明非结构数值各向异性不明显。图 12b右中有部分杂乱的波场,这是由于网格尺寸增大导致的点加载的震源噪声。通常可以将震源以高斯分布的方式加载在震源点附近的一定范围内以减弱这一噪声[27]。
|
图 11 取不同值时一阶直角三角形周期性网格(a)与一般非结构化网格(b)模拟的0.3s时刻的vz波场快照对比 左:h=10.0m;中:h=12.5m;右:h=20.0m |
|
图 12 h取不同值时二阶直角三角形周期性网格(a)与一般非结构化网格(b)模拟的0.3s时刻的vz波场快照对比 左:h=10.0m;中:h=12.5m;右:h=20.0m |
本文通过构造周期性三角形网格模型,分析了基于Runge-Kutta的间断Galerkin有限元方法的稳定性条件、数值频散以及数值耗散,得到以下结论和认识。
(1) DGFEM稳定模拟的最大时间步长Δtmax与单元内切圆半径存在线性关系。分析结果表明,等边三角形的稳定性条件最宽松。
(2) 从理论和实验角度说明了基于局部Lax-Friedrichs数值流的DGFEM的弱频散和强耗散特性,且在不同传播方向上,二者都表现出方向各向异性。数值各向异性呈双轴对称性。等边三角形网格的数值各向异性最弱,而直角三角形和钝角三角形网格表现出的数值各向异性较强。一般的非结构性网格由于网格排列没有一定规律,因此没有表现出明显的数值各向异性,说明在网格生成时,应尽量避免钝角三角形和呈大面积排列的直角三角形,以减小数值各向异性的影响。
(3) 误差分析显示,模拟误差与网格尺寸在双对数坐标系下呈线性关系。数值实验表明,模拟误差主要来源是基于局部Lax-Friedrichs数值流的数值耗散。实验中,使用一阶单元模拟的波场均有较强耗散。而选取二阶单元,一个横波波长内包含四个单元则耗散明显减弱。
关于其他数值流形式的频散和耗散特性,以及其对模拟精度的影响仍需进一步研究。
附录A 矩阵Γ11、Γ12、Γ21、Γ22的具体表达式式(11)中子矩阵Γ11,Γ12,Γ21,Γ22分别为
| $ \boldsymbol{\varGamma}_{11}=\left[\begin{array}{ccccc} \frac{c_{\mathrm{P}} \boldsymbol{C}_{3}}{2} & 0 & 0 & \tau_{1} \boldsymbol{C}_{1} & \tau_{2} \boldsymbol{C}_{2} \\ 0 & \frac{c_{\mathrm{P}} \boldsymbol{C}_{3}}{2} & 0 & \tau_{2} \boldsymbol{C}_{1} & \tau_{1} \boldsymbol{C}_{2} \\ 0 & 0 & \frac{c_{\mathrm{P}} \boldsymbol{C}_{3}}{2} & \tau_{3} \boldsymbol{C}_{2} & \tau_{3} \boldsymbol{C}_{1} \\ \tau_{0} \boldsymbol{C}_{1} & 0 & \tau_{0} \boldsymbol{C}_{2} & \frac{c_{\mathrm{P}} \boldsymbol{C}_{3}}{2} & 0 \\ 0 & \tau_{0} \boldsymbol{C}_{2} & \tau_{0} \boldsymbol{C}_{1} & 0 & \frac{c_{\mathrm{P}} \boldsymbol{C}_{3}}{2} \end{array}\right] $ | (A-1) |
| $ \begin{array}{l} \boldsymbol{\varGamma}_{12}=\left[\begin{array}{ccccc} -\frac{c_{\mathrm{P}} \boldsymbol{D}_{1}}{2} & 0 & 0 & \tau_{1} \boldsymbol{D}_{2} & \tau_{2} \boldsymbol{D}_{3} \\ 0 & -\frac{c_{\mathrm{P}} \boldsymbol{D}_{1}}{2} & 0 & \tau_{2} \boldsymbol{D}_{2} & \tau_{1} \boldsymbol{D}_{3} \\ 0 & 0 & -\frac{c_{\mathrm{P}} \boldsymbol{D}_{1}}{2} & \tau_{3} \boldsymbol{D}_{3} & \tau_{3} \boldsymbol{D}_{2} \\ \tau_{0} \boldsymbol{D}_{2} & 0 & \tau_{0} \boldsymbol{D}_{3} & -\frac{c_{\mathrm{P}} \boldsymbol{D}_{1}}{2} & 0 \\ 0 & \tau_{0} \boldsymbol{D}_{3} & \tau_{0} \boldsymbol{D}_{2} & 0 & -\frac{c_{\mathrm{P}} \boldsymbol{D}_{1}}{2} \end{array}\right] \end{array} $ | (A-2) |
| $ \boldsymbol{\varGamma}_{21}=\left[\begin{array}{ccccc} -\frac{c_{\mathrm{P}} \boldsymbol{D}^{\prime}{}_{1}}{2} & 0 & 0 & \tau_{1} \boldsymbol{D}_{4} & \tau_{2} \boldsymbol{D}_{5} \\ 0 & -\frac{c_{\mathrm{P}} \boldsymbol{D}^{\prime}{}_{1}}{2} & 0 & \tau_{2} \boldsymbol{D}_{4} & \tau_{1} \boldsymbol{D}_{5} \\ 0 & 0 & -\frac{c_{\mathrm{P}} \boldsymbol{D}^{\prime}{}_{1}}{2} & \tau_{3} \boldsymbol{D}_{5} & \tau_{3} \boldsymbol{D}_{4} \\ \tau_{0} \boldsymbol{D}_{4} & 0 & \tau_{0} \boldsymbol{D}_{5} & -\frac{c_{\mathrm{P}} \boldsymbol{D}^{\prime}{}_{1}}{2} & 0 \\ 0 & \tau_{0} \boldsymbol{D}_{5} & \tau_{0} \boldsymbol{D}_{4} & 0 & -\frac{c_{\mathrm{P}} \boldsymbol{D}^{\prime}{}_{1}}{2} \end{array}\right] $ | (A-3) |
| $ \begin{aligned} &\boldsymbol{\varGamma}_{22}=\left[\begin{array}{cccc} \frac{c_{\mathrm{P}} \boldsymbol{C}_{3}}{2} & 0 & 0 & -\tau_{1} \boldsymbol{C}_{1} & -\tau_{2} \boldsymbol{C}_{2} \\ 0 & \frac{c_{\mathrm{P}} \boldsymbol{C}_{3}}{2} & 0 & -\tau_{2} \boldsymbol{C}_{1} & -\tau_{1} \boldsymbol{C}_{2} \\ 0 & 0 & \frac{c_{\mathrm{P}} \boldsymbol{C}_{3}}{2} & -\tau_{3} \boldsymbol{C}_{2} & -\tau_{3} \boldsymbol{C}_{1} \\ -\tau_{0} \boldsymbol{C}_{1} & 0 & -\tau_{0} \boldsymbol{C}_{2} & \frac{c_{\mathrm{P}} \boldsymbol{C}_{3}}{2} & 0 \\ 0 & -\tau_{0} \boldsymbol{C}_{2} & -\tau_{0} \boldsymbol{C}_{1} & 0 & \frac{c_{\mathrm{P}} \boldsymbol{C}_{3}}{2} \end{array}\right] \end{aligned} $ | (A-4) |
其中
| $ \boldsymbol{C}_{1}=\left(\boldsymbol{K}^{\xi}-\frac{1}{2} \boldsymbol{F}^{2,0}+\frac{1}{2} \boldsymbol{F}^{3,0}\right) \sin \theta $ | (A-5) |
| $ \begin{aligned} \boldsymbol{C}_{2}=&-\boldsymbol{K}^{\xi} \cos \theta+\boldsymbol{K}^{\eta}+\frac{1}{2} \boldsymbol{F}^{1,0}- \\ &\boldsymbol{F}^{2,0} \sin \frac{\theta}{2}-\frac{1}{2} \boldsymbol{F}^{3,0} \cos \theta \end{aligned} $ | (A-6) |
| $ \boldsymbol{C}_{3}=-\boldsymbol{F}^{1,0}-2 \boldsymbol{F}^{2,0} \sin \frac{\theta}{2}-\boldsymbol{F}^{3,0} $ | (A-7) |
| $ \boldsymbol{D}_{1}=-\bf{F}^{1,1} \varphi_{\mathrm{B}}-2 \boldsymbol{F}^{2,2} \sin \frac{\theta}{2}-\boldsymbol{F}^{3,3} \varphi_{\mathrm{L}} $ | (A-8) |
| $ \boldsymbol{D}^{\prime}{}_{1}=-\boldsymbol{F}^{1,1} \varphi_{\mathrm{T}}-2 \boldsymbol{F}^{2,2} \sin \frac{\theta}{2}-\boldsymbol{F}^{3,3} \varphi_{\mathrm{R}} $ | (A-9) |
| $ \boldsymbol{D}_{2}=\frac{1}{2}\left(-\boldsymbol{F}^{2,2}+\boldsymbol{F}^{3,3} \varphi_{\mathrm{L}}\right) \sin \theta $ | (A-10) |
| $ \boldsymbol{D}_{3}=\frac{1}{2} \boldsymbol{F}^{1,1} \varphi_{\mathrm{B}}-\boldsymbol{F}^{2,2} \sin ^{2} \frac{\theta}{2}-\frac{1}{2} \boldsymbol{F}^{3,3} \varphi_{\mathrm{L}} \cos \theta $ | (A-11) |
| $ \boldsymbol{D}_{4}=\frac{1}{2}\left(\boldsymbol{F}^{2,2}-\boldsymbol{F}^{3,3} \varphi_{\mathrm{R}}\right) \sin \theta $ | (A-12) |
| $ \boldsymbol{D}_{5}=-\frac{1}{2} \boldsymbol{F}^{1,1} \varphi_{\mathrm{B}}+\boldsymbol{F}^{2,2} \sin ^{2} \frac{\theta}{2}+\frac{1}{2} \boldsymbol{F}^{3,3} \varphi_{\mathrm{R}} \cos \theta $ | (A-13) |
| $ \left\{\begin{array}{l} \tau_{0}=-\frac{1}{\rho} \\ \tau_{1}=-(\lambda+2 \mu) \\ \tau_{2}=-\lambda \\ \tau_{3}=-\mu \end{array}\right. $ | (A-14) |
| [1] |
裴正林, 王尚旭, 狄帮让, 等. 无组合检波采集方法的三维地震波数值模拟研究[J]. 石油地球物理勘探, 2005, 40(2): 138-142. PEI Zhenglin, WANG Shangxu, DI Bangrang, et al. Study on acquisition methods without geophone array by numeric modeling of 3D seismic wavefield[J]. Oil Geophysical Prospecting, 2005, 40(2): 138-142. DOI:10.3321/j.issn:1000-7210.2005.02.010 |
| [2] |
崔宏良, 王瑞贞, 陈敬国, 等. 可控震源地震勘探中的数值模拟法应用[J]. 石油地球物理勘探, 2017, 52(2): 209-213. CUI Hongliang, WANG Ruizhen, CHEN Jingguo, et al. Application of numerical simulation in vibroseis seismic acquisition[J]. Oil Geophysical Prospecting, 2017, 52(2): 209-213. |
| [3] |
何宝庆, 谢小碧. 宽线地震数据采集和处理的数值模拟[J]. 石油地球物理勘探, 2019, 54(3): 500-511. HE Baoqing, XIE Xiaobi. A numerical investigating on wide-line seismic data acquisition and processing[J]. Oil Geophysical Prospecting, 2019, 54(3): 500-511. |
| [4] |
马国旗, 曹丹平, 尹教建, 等. 分布式声传感井中地震信号检测数值模拟方法[J]. 石油地球物理勘探, 2020, 55(2): 311-320. MA Guoqi, CAO Danping, YIN Jiaojian, et al. Nume-rical simulation of detecting seismic signals in DAS wells[J]. Oil Geophysical Prospecting, 2020, 55(2): 311-320. |
| [5] |
王文枫, 岳大力, 赵继勇, 等. 利用地震正演模拟方法研究地层结构——以鄂尔多斯盆地合水地区延长组三段为例[J]. 石油地球物理勘探, 2020, 55(2): 411-418. WANG Wenfeng, YUE Dali, ZHAO Jiyong, et al. Research on stratigraphic structure based on seismic forward modeling: A case study of the third member of the Yanchang Formation in Heshui area, Ordos Basin[J]. Oil Geophysical Prospecting, 2020, 55(2): 411-418. |
| [6] |
Virieux J, Calandra H, Plessix R É. A review of the spectral, pseudo-spectral, finite-difference and finite-element modelling techniques for geophysical imaging[J]. Geophysical Prospecting, 2011, 59(5): 794-813. DOI:10.1111/j.1365-2478.2011.00967.x |
| [7] |
Kelly K R, Ward R W, Treitel S, et al. Synthetic seismograms: A finite-difference approach[J]. Geophy-sics, 1976, 41(1): 2-27. |
| [8] |
Dablain M A. The application of high-order differencing to the scalar wave equation[J]. Geophysics, 1986, 51(1): 54-66. DOI:10.1190/1.1442040 |
| [9] |
董良国, 马在田, 曹景忠. 一阶弹性波方程交错网格高阶差分解法[J]. 地球物理学报, 2000, 43(3): 411-419. DONG Liangguo, MA Zaitian, CAO Jingzhong, et al. A staggered-grid high-order difference method of one-order elastic wave equation[J]. Chinese Journal of Geophysics, 2000, 43(3): 411-419. DOI:10.3321/j.issn:0001-5733.2000.03.015 |
| [10] |
Yang D. A nearly analytic discrete method for acoustic and elastic wave equations in anisotropic media[J]. Bulletin of the Seismological Society of America, 2003, 93(2): 882-890. DOI:10.1785/0120020125 |
| [11] |
Kosloff D D, Baysal E. Forward modeling by a Fourier method[J]. Geophysics, 1982, 47(10): 1402-1412. DOI:10.1190/1.1441288 |
| [12] |
罗文山, 陈汉明, 王成祥, 等. 时间域黏滞波动方程及其数值模拟新方法[J]. 石油地球物理勘探, 2016, 51(4): 707-713. LUO Wenshan, CHEN Hanming, WANG Cheng-xiang, et al. A novel time-domain viscoacoustic wave equation and its numerical simulation[J]. Oil Geophysical Prospecting, 2016, 51(4): 707-713. |
| [13] |
Hermeline F. Two coupled particle-finite volume methods using Delaunay-Voronoï meshes for the approximation of Vlasov-Poisson and Vlasov-Maxwell equations[J]. Journal of Computational Physics, 1993, 106(1): 1-18. DOI:10.1006/jcph.1993.1086 |
| [14] |
Versteeg H K, Malalasekera W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method[M]. Harlow: Addison-Wesley, 1995.
|
| [15] |
贾晓峰, 胡天跃, 王润秋. 复杂介质中地震波模拟的无单元法[J]. 石油地球物理勘探, 2006, 41(1): 43-48. JIA Xiaofeng, HU Tianyue, WANG Runqiu. A mesh-free algorithm of seismic wave simulation in complex medium[J]. Oil Geophysical Prospecting, 2006, 41(1): 43-48. DOI:10.3321/j.issn:1000-7210.2006.01.009 |
| [16] |
Marfurt K J. Accuracy of finite-difference and finite-element modeling of scalar and elastic wave equations[J]. Geophysics, 1984, 49(5): 533-549. DOI:10.1190/1.1441689 |
| [17] |
Serón F J, Sanz F J, Kindelán M. Finite-element method for elastic wave propagation[J]. Communications in Applied Numerical Methods, 1990, 6(5): 359-368. DOI:10.1002/cnm.1630060505 |
| [18] |
薛东川, 王尚旭, 焦淑静. 起伏地表复杂介质波动方程有限元数值模拟方法[J]. 地球物理学进展, 2007, 22(2): 522-529. XUE Dongchuan, WANG Shangxu, JIAO Shujing. Wave equation finite-element modeling including rugged topography and complicated medium[J]. Progress in Geophysics, 2007, 22(2): 522-529. DOI:10.3969/j.issn.1004-2903.2007.02.026 |
| [19] |
Komatitsch D, Roland M, Tromp J, et al. Wave propagation in 2-D elastic media using a spectral element method with triangles and quadrangles[J]. Journal of Computational Acoustics, 2001, 9(2): 703-718. DOI:10.1142/S0218396X01000796 |
| [20] |
Komatitsch D, Tromp J. Spectral-element simulations of global seismic wave propagation, Ⅰ: Validation[J]. Geophysical Journal International, 2002, 149(2): 390-412. DOI:10.1046/j.1365-246X.2002.01653.x |
| [21] |
Komatitsch D, Vilotte J P. The spectral-element method: An efficient tool to simulate the seismic response of 2D and 3D geological structures[J]. Bulletin of the Seismological Society of America, 1998, 88(2): 368-392. |
| [22] |
Liu Y S, Teng J W, Lan H Q, et al. A comparative study of finite element and spectral element methods in seismic wavefield modeling[J]. Geophysics, 2014, 79(2): T91-T104. DOI:10.1190/geo2013-0018.1 |
| [23] |
Pasquetti R, Francesca R. Spectral element methods on triangles and quadrilaterals: comparisons and applications[J]. Journal of Computational Physics, 2004, 198(1): 349-362. DOI:10.1016/j.jcp.2004.01.010 |
| [24] |
Bernardo C, Shu C W. Runge-Kutta discontinuous Galerkin methods for convection-dominated problems[J]. Journal of Scientific Computing, 2001, 16(3): 173-261. DOI:10.1023/A:1012873910884 |
| [25] |
He X J, Yang D H, Wu H. A weighted Runge-Kutta discontinuous Galerkin method for wavefield modelling[J]. Geophysical Journal International, 2014, 200(3): 1389-1410. |
| [26] |
Reed W H, Hill T R. Triangular Mesh Methods for the Neutron Transport Equation[R]. Los Alamos Scientific Laboratory, Los Alamos, 1973.
|
| [27] |
薛昭, 董良国, 李晓波, 等. 起伏地表弹性波传播的间断Galerkin有限元数值模拟方法[J]. 地球物理学报, 2014, 57(4): 1209-1223. XUE Zhao, DONG Liangguo, LI Xiaobo, et al. Discontinuous Galerkin finite-element method for elastic wave modeling including surface topography[J]. Chinese Journal of Geophysics, 2014, 57(4): 1209-1223. |
| [28] |
De Basabe J D, Sen Mrinal K. Grid dispersion and stability criteria of some common finite-element methods for acoustic and elastic wave equations[J]. Geophy-sics, 2007, 72(6): T81-T95. |
| [29] |
Mulder W A. Spurious modes in finite-element discre-tizations of the wave equation may not be all that bad[J]. Applied Numerical Mathematics, 1999, 30(4): 425-445. DOI:10.1016/S0168-9274(98)00078-6 |
| [30] |
Sármány D, Botchev M A, Van Der Vegt J J W. Dispersion and dissipation error in high-order Runge-Kutta discontinuous Galerkin discretisations of the Maxwell equations[J]. Journal of Scientific Computing, 2007, 33(1): 47-74. DOI:10.1007/s10915-007-9143-y |
| [31] |
Seriani G, Oliveira S P. Dispersion analysis of spectral element methods for elastic wave propagation[J]. Wave Motion, 2008, 45(6): 729-744. DOI:10.1016/j.wavemoti.2007.11.007 |
| [32] |
Zyserman F I, Santos J E. Analysis of the numerical dispersion of waves in saturated poroelastic media[J]. Computer Methods in Applied Mechanics and Engineering, 2007, 196(45-48): 4644-4655. DOI:10.1016/j.cma.2007.05.021 |
| [33] |
刘少林, 李小凡, 刘有山, 等. 三角网格有限元法声波与弹性波模拟频散分析[J]. 地球物理学报, 2014, 57(8): 2620-2630. LIU Shaolin, LI Xiaofan, LIU Youshan, et al. Dispersion analysis of triangle-based finite element method for acoustic and elastic wave simulations[J]. Chinese Journal of Geophysics, 2014, 57(8): 2620-2630. |
| [34] |
曹丹平, 周建科, 印兴耀. 三角网格有限元法波动模拟的数值频散及稳定性研究[J]. 地球物理学报, 2015, 58(5): 1717-1730. CAO Danping, ZHOU Jianke, YIN Xingyao. The study for numerical dispersion and stability of wave motion with triangle-based finite element algorithm[J]. Chinese Journal of Geophysics, 2015, 58(5): 1717-1730. |
| [35] |
Liu T, Sen Mrinal K, Hu T Y, et al. Dispersion analysis of the spectral element method using a triangular mesh[J]. Wave Motion, 2012, 49(4): 474-483. DOI:10.1016/j.wavemoti.2012.01.003 |
| [36] |
Mazzieri I, Francesca R. Dispersion analysis of triangle-based spectral element methods for elastic wave propagation[J]. Numerical Algorithms, 2012, 60(4): 631-650. DOI:10.1007/s11075-012-9592-8 |
| [37] |
李琳, 刘韬, 胡天跃. 三角谱元法及其在地震正演模拟中的应用[J]. 地球物理学报, 2014, 57(4): 1224-1234. LI Lin, LIU Tao, HU Tianyue. Spectral element method with triangular mesh and its application in seismic modeling[J]. Chinese Journal of Geophysics, 2014, 57(4): 1224-1234. |
| [38] |
De Basabe J D, Sen Mrinal K, Wheeler M F. The interior penalty discontinuous Galerkin method for elastic wave propagation: Grid dispersion[J]. Geophysical Journal International, 2008, 175(1): 83-93. DOI:10.1111/j.1365-246X.2008.03915.x |
| [39] |
贺茜君, 杨顶辉, 吴昊. 间断有限元方法的数值频散分析及其波场模拟[J]. 地球物理学报, 2014, 57(3): 906-917. HE Xijun, YANG Dinghui, WU Hao. Numerical dispersion and wave-field simulation of the Runge-Kutta discontinuous Galerkin method[J]. Chinese Journal of Geophysics, 2014, 57(3): 906-917. |
| [40] |
Meng W J, Fu L Y. Numerical dispersion analysis of discontinuous Galerkin method with different basis functions for acoustic and elastic wave equations[J]. Geophysics, 2018, 83(3): T87-T101. DOI:10.1190/geo2017-0485.1 |
| [41] |
Hu F Q, Hussaini M Y, Rasetarinera P. An analysis of the discontinuous Galerkin method for wave propagation problems[J]. Journal of Computational Physics, 1999, 151(2): 921-946. DOI:10.1006/jcph.1999.6227 |
| [42] |
Käser M, Michael D. An arbitrary high-order discontinuous Galerkin method for elastic waves on unstructured meshes, I: The two-dimensional isotropic case with external source terms[J]. Geophysical Journal International, 2006, 166(2): 855-877. DOI:10.1111/j.1365-246X.2006.03051.x |
| [43] |
Delcourte S, Fezoui L, Glinsky-Olivier N. A high-order discontinuous Galerkin method for the seismic wave propagation[J]. ESAIM: Proceedings, 2009, 27: 70-89. DOI:10.1051/proc/2009020 |
| [44] |
He X J, Yang D H, Ma X, et al. Dispersion-dissipation analysis of the triangle-based discontinuous Galerkin method for scalar wave equation[J]. Geophysical Journal International, 2019, 218(2): 1174-1198. DOI:10.1093/gji/ggz170 |
| [45] |
Hermann V, Käser M, Castro C E. Non-conforming hybrid meshes for efficient 2-D wave propagation using the discontinuous Galerkin method[J]. Geophy-sical Journal International, 2011, 184(2): 746-758. DOI:10.1111/j.1365-246X.2010.04858.x |
| [46] |
Etienne V, Chaljub E, Virieux J, et al. An hp-adaptive discontinuous Galerkin finite-element method for 3-D elastic wave modelling[J]. Geophysical Journal International, 2010, 183(2): 941-962. DOI:10.1111/j.1365-246X.2010.04764.x |



 司文朋, 江苏省南京市江宁区上高路219号中国石化石油物探技术研究院, 211103。Email:
司文朋, 江苏省南京市江宁区上高路219号中国石化石油物探技术研究院, 211103。Email: 