② 中石化石油工程地球物理有限公司, 北京 100020;
③ 中国科学院地质与地球物理研究所油气资源研究室, 北京 100029;
④ 保定北奥石油物探特种车辆制造有限公司, 河北保定 072550
② SINOPEC Geophysical Corporation, Beijing 100020, China;
③ Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China;
④ Baoding Bei'ao Special Vehicle Manufacturing Co., Ltd, Baoding, Hebei 072550, China
近地表地层模型的建立对地球物理研究和岩土工程具有重要意义[1]。瑞雷波的频散曲线对横波速度具有较强敏感性,因此常利用它反演地层的横波速度[2]。与常规勘探方法相比,瑞雷波勘探技术具有分辨率高、应用范围广、检测设备简单且速度快等优点[3],在浅层勘探中得到了广泛应用。
对瑞雷波频散曲线进行反演是瑞雷波勘探的关键环节[4-5],反演算法可分为线性和非线性两大类。由于反演本身具有非线性和多极值特点[6],因此诸如最小二乘法[7]和Occam算法[8]等传统线性算法在求解时易陷入局部极小值。遗传算法[9-10]、模拟退火法[11-12]、BP神经网络法[13]、粒子群算法[14-15]等非线性算法虽不需满足观测值与未知量之间是线性关系的假设条件[16-17],且具有全局搜索的优势,但在求解复杂问题时会出现参数不易调整等弊端,限制了这类方法的应用范围[18]。
蜻蜓算法(Dragonfly algorithm,DA)是Mirjalili[19]于2016年提出的一种新型非线性算法,即以定义多个行为向量及其权重的方式模仿蜻蜓的飞行规律与协作模式,实现对搜索空间的“探索”与“开发”。然而在原算法的每步迭代过程中,所有蜻蜓个体的同类权重被赋予相同数值,这种无差别赋值方式可能在实际求解过程中降低算法寻找全局极小值的效率。为此,本文提出基于自适应权重的蜻蜓算法(Adaptive weight dragonfly algorithm,AWDA),以蜻蜓个体的适应度为依据,赋予与其相匹配的自适应权重,及时调整蜻蜓个体的搜索策略,达到提高求解效率的目的。
通常,基阶模式波的频散曲线更易于拾取,是求取地层横波速度的主要反演对象。当地下含有高速硬夹层或低速软夹层时,高阶模式波的频散能量在高频区域占据主导地位。研究[20-22]表明,高阶频散曲线蕴含丰富地质信息,若对基阶、高阶频散曲线进行联合反演可显著提高结果的精度。
因此,本文首先利用测试函数,对AWDA算法、改进的蜻蜓算法[23](Improved dragonfly algorithm,IDA)、改进的粒子群算法[24](Improved particle swarm optimization algorithm,IEPSO)和改进的自适应遗传算法[25](New improved adaptive genetic algorithm,NIAGA)分别进行对比测试,验证了本文所提算法具有更强寻找全局极小值能力。随后使用这一新型算法,通过理论及实际面波记录,分别对基阶和高阶瑞雷波频散曲线进行反演,新算法可显著提高地层横波速度反演结果的准确性和稳定性,取得了较为理想的应用效果。
1 基于自适应权重的蜻蜓算法 1.1 原理描述蜻蜓以群组方式进行迁徙和觅食两种运动,这两种运动规律能分别与非线性算法中的“探索”、“开发”阶段一一对应:迁徙中的蜻蜓群体通过远距离飞行可遍布整个搜索空间,这是“探索”的主要目标;处于觅食状态下的蜻蜓群体通过短距离移动可对其周围区域进行详细搜寻,这是“开发”的主要特征。在蜻蜓算法中[19],蜻蜓个体的运动轨迹通过避撞、结队、聚集、觅食和避敌这五种行为的共同作用,并赋予其相应的权重,从而实现对搜索空间的“探索”和“开发”。
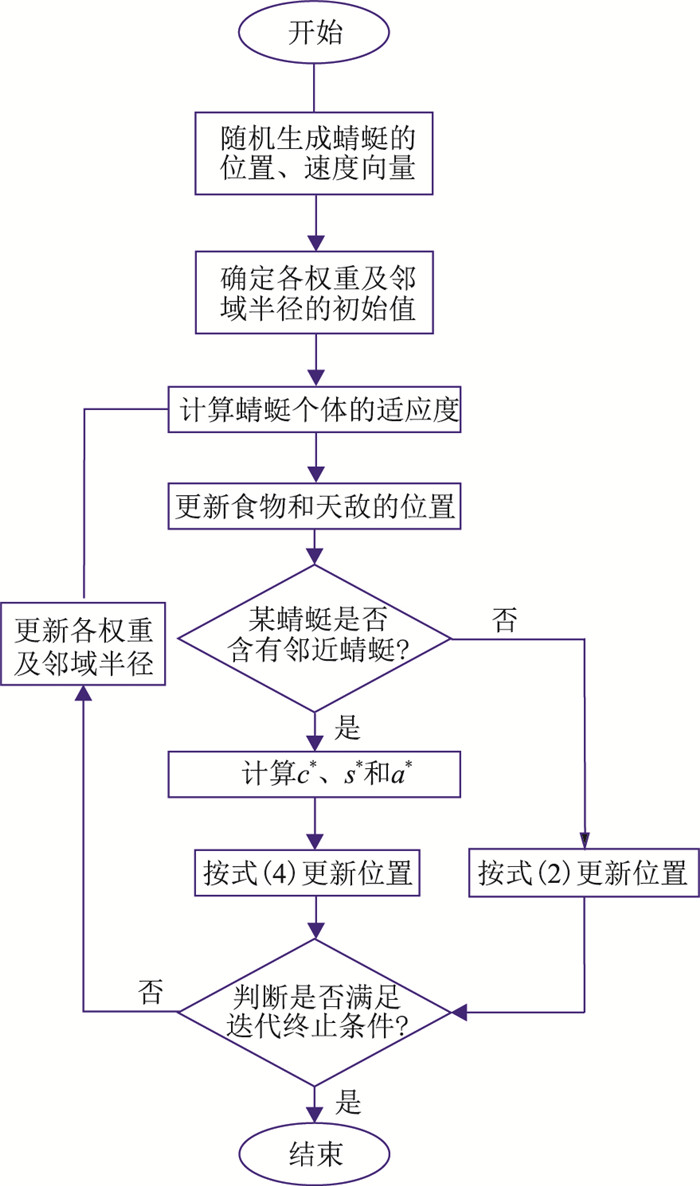
蜻蜓在飞行过程中受某种行为的影响程度由相应行为的权重决定,故对其进行合理的赋值尤为关键。针对原蜻蜓算法存在的同类权重无差别赋值问题,本文提出AWDA算法,即根据迭代过程中个体适应度之间的差异,自动调整原聚集、避撞和结队等三种权重,其具体运算流程(图 1)如下。
|
图 1 AWDA算法流程 |
(1) 初始化参数。假设蜻蜓的数量为n,搜索空间的维度为D,则蜻蜓的位置X及飞行速度V为
| $ \left\{\begin{array}{l} \boldsymbol{X}_{i}=\left(x_{i}^{1}, \cdots, x_{i}^{d}, \cdots, x_{i}^{D}\right) \\ \boldsymbol{V}_{i}=\left(v_{i}^{1}, \cdots, v_{i}^{d}, \cdots, v_{i}^{D}\right) \end{array}\right. $ | (1) |
式中:i=1,2,…,n,表示蜻蜓编号;d为D中任一维度。
根据具体问题,设定聚集权重c、避撞权重s、结队权重a、觅食权重f、避敌权重e、惯性权重w及邻域半径rc的初始值。
(2) 计算适应度。将所有蜻蜓个体的位置代入目标函数,计算其适应度。
(3) 更新蜻蜓个体的位置。当两只蜻蜓的距离小于邻域半径时,就认为这对蜻蜓是相邻的,与同一只蜻蜓相邻的所有蜻蜓就构成了一个子群体。
若某蜻蜓周围没有邻近个体时则将其命名为孤立个体,且通过Lévy飞行完成位置更新,其表达式为
| $ \boldsymbol{X}_{i}^{t+1}=\boldsymbol{X}_{i}^{t}+\text { Lévy }(D) \boldsymbol{X}_{i}^{t} $ | (2) |
Lévy飞行使个体进行大量的短距离局部搜索以及少量的长距离全局搜索,增强了个体飞行过程中的随机性和“探索”性[26]。
若该蜻蜓存在邻近个体,AWDA算法是通过各行为向量更新该蜻蜓的位置和飞行速度。因此,根据步骤(1)可定义避撞向量Si、结队向量Ai、聚集向量Ci、觅食向量Fi和避敌向量Ei的表达式为
| $ \left\{\begin{array}{l} \boldsymbol{S}_{i}=\sum\limits_{j=1}^{m}\left(\boldsymbol{X}_{i}-\boldsymbol{X}_{j}\right) \\ \boldsymbol{A}_{i}=\sum\limits_{j=1}^{m} \frac{\boldsymbol{V}_{j}}{m} \\ \boldsymbol{C}_{i}=\sum\limits_{j=1}^{m} \frac{\boldsymbol{X}_{j}}{m}-\boldsymbol{X}_{i} \\ \boldsymbol{F}_{i}=\boldsymbol{X}^{+}-\boldsymbol{X}_{i} \\ \boldsymbol{E}_{i}=\boldsymbol{X}^{-}+\boldsymbol{X}_{i} \end{array}\right. $ | (3) |
式中:Xj、Vj分别为第j个与当前个体相邻的蜻蜓的位置和飞行速度;m是相邻蜻蜓的数量;X+和X-分别表征食物和天敌的位置,将已记录的适应度最大的个体作为食物,适应度最小的个体作为天敌。
随后据下式更新蜻蜓的飞行速度和位置
| $ \left\{\begin{array}{l} \boldsymbol{V}_{i}^{t+1}=s_{i}^{*} \boldsymbol{S}_{i}+a_{i}^{*} \boldsymbol{A}_{i}+c_{i}^{*} \boldsymbol{C}_{i}+f_{i} \boldsymbol{F}_{i}+e_{i} \boldsymbol{E}_{i}+w_{i} \boldsymbol{V}_{i}^{t} \\ \boldsymbol{X}_{i}^{t+1}=\boldsymbol{X}_{i}^{t}+\boldsymbol{V}_{i}^{t+1} \end{array}\right. $ | (4) |
式中:t是当前迭代次数;ci*、si*和ai*分别是第i个蜻蜓个体的自适应的聚集权重、避撞权重和结队权重;原算法的觅食权重fi、避敌权重ei和惯性权重wi则保持不变。ci*、si*和ai*的表达式为
| $ \left\{\begin{array}{l} c_{i}^{*}=c_{i}\left\{b_{1}-[\operatorname{rankfit} 1(i)-1] \times \frac{b_{1}-b_{2}}{m}\right\} \\ s_{i}^{*}=s_{i}\left\{b_{1}-[\operatorname{rankfit} 2(i)-1] \times \frac{b_{1}-b_{2}}{n-1}\right\} \\ a_{i}^{*}=a_{i}\left\{b_{1}-[\operatorname{rankfit} 2(i)-1] \times \frac{b_{1}-b_{2}}{n-1}\right\} \end{array}\right. $ | (5) |
式中:ci、si和ai分别是原算法第i个蜻蜓个体的聚集权重、避撞权重和结队权重;b1和b2是常数,本文分别取为1.5和0.5,可根据具体问题对其进行相应的调整;函数rankfit1(i)代表将同一群体内所有蜻蜓的适应度从低到高排序时,第i个蜻蜓在其中的排名;函数rankfit2(i)代表将当前迭代中所有个体的适应度从低到高排序时,第i个蜻蜓个体在其中的排名。
在AWDA算法中,适应度大的个体会分配到较小聚集权重,抑制该个体向子群体中其他个体移动;而适应度小的个体则会分配到较大聚集权重,促使其飞向适应度更大的个体。此外,适应度较大的蜻蜓个体将保持小间距、低速度的飞行状态,对周围做细致搜寻,“开发”是其主要任务;而那些适应度较小的个体,扩大间距、提高飞行速度才能增加获取食物的可能性,“探索”对它们来说更为重要。如此,ADWA算法中的蜻蜓个体在迭代前期不但能对食物进行更高效的“开发”,中后期也会通过持续的“探索”以保存跳出局部极小值的能力。
(4) 终止迭代。当最优蜻蜓个体的适应度满足给定条件或达到最大迭代次数时,算法终止迭代并输出结果,否则返回步骤(2)继续迭代(图 1)。
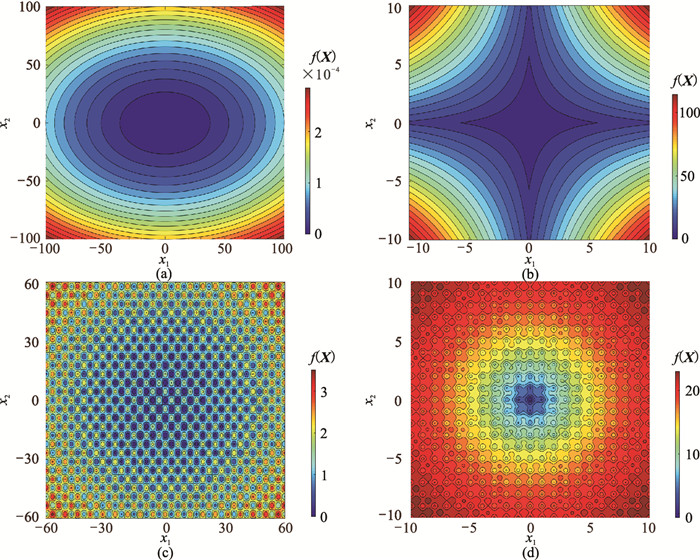
1.2 算法测试本文采用四个常用的测试函数[27]对AWDA、IDA、IEPSO及NIAGA等算法进行对比测试,以检验本文提出算法的有效性。测试函数的表达式及搜索区间如表 1所示,空间维度D均为2。其中:Shpere和Schwefel 2.22为单极值函数,该类函数仅含有一个极小值,主要测试算法的收敛性和“开发”能力;Griewank和Ackley为多极值函数,它们包含了一个全局极小值和多个局部极小值,检测算法的全局“探索”能力。四个测试函数的二维示意图如图 2所示。所有算法的个体总数设定为50,最大迭代次数均为200。IDA、IEPSO和NIAGA三种算法的其他参数则分别与参考文献[23-25]中的最佳参数组合设置保持一致。
|
|
表 1 测试函数 |
|
图 2 四种测试函数的示意图 (a)Sphere; (b)Schwefel 2.22; (c)Griewank; (d)Ackley |
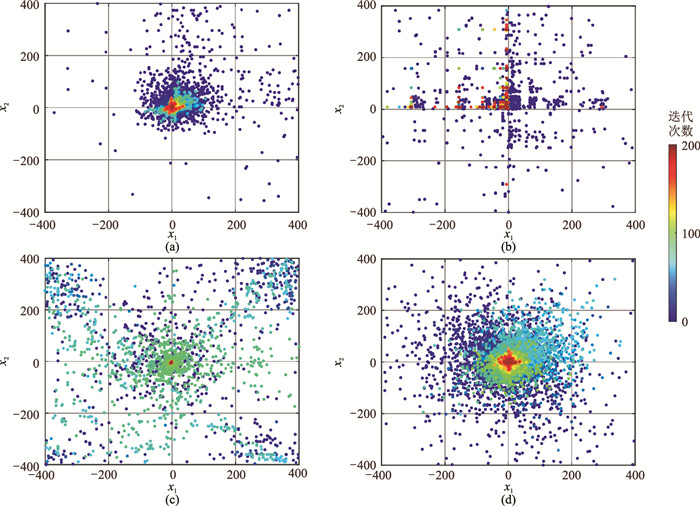
以各算法对Griewank函数的一次运算结果为例,统计了所有个体在迭代过程中的位置分布,据该结果能更清晰直观地分析算法对空间的“探索”与“开发”情形。IEPSO、NIAGA、IDA及AWDA四种算法求得的最小误差分别为0.0038、0.0364、0.0071和0.0003。如图 3所示,IEPSO算法在迭代前期无法对空间进行充分“探索”,有相当多的区域仅分布零星个体甚至没有个体,这可能会使算法最终无法寻找到全局极小值。NIAGA算法大概从第40次迭代开始,个体在若干局部极小值处呈现较强的聚集、重叠现象并一直持续到迭代结束,即表现出“早熟收敛”特征。由于该算法的选择、复制机制大幅度削弱了个体的多样性,导致算法在中后期出现严重的个体趋同现象,这意味着计算机在大部分时间内做着无谓的重复运算。此外,由于变异的触发概率较低,故通过变异跳出局部极小值从而继续搜寻全局极小值是非常困难的。IDA算法和AWDA算法凭借避撞机制在迭代过程中能很好地抑制蜻蜓之间的重叠,因而在迭代前期能对整个区间进行广泛的“探索”。在迭代后期,由于对食物周围的“探索”不足,导致IDA算法最终收敛于局部极小值(x1=-3.13,x2=4.43)。但AWDA算法能较好地解决上述问题,在迭代后期仍能保持一定的“探索”能力,最终收敛于全局极小值。
|
图 3 四种算法对Griewank函数寻优的个体历史位置分布图 (a)IEPSO; (b)NIAGA; (c)IDA; (d)AWDA |
考虑到求解的稳定性因素,各算法对测试函数均进行50次独立运算,并统计其误差均值和标准差(表 2)。对比可见,NIAGA算法求取的误差均值在上述四种算法结果中是最大的,IEPSO算法的求解能力优于IDA算法。相较于其他三种算法,AWDA算法的误差均值和标准差更小,显示出该算法具有更出色的搜寻全局极小值的能力。
|
|
表 2 各算法的寻优结果 |
频散曲线的正演是瑞雷波勘探技术中的重要部分。地质模型一般由纵波速度vP、横波速度vS、层厚H及密度ρ进行表征。将上述参数及频率代入频散方程中,求解该方程即可计算该频率的瑞雷波相速度,以此获得频散曲线。反演的目的是寻找与已知频散曲线匹配最好的地质模型。由于瑞雷波频散曲线的反演问题是多极值的,为了降低反演难度,又因为横波速度和层厚与瑞雷波频散曲线的关系最为紧密,本文仅对这两个参数进行计算,而影响较小的纵波速度和密度可根据先验信息确定[28]。
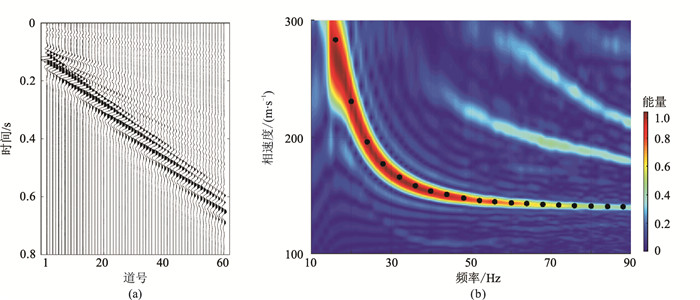
2.1 基阶频散曲线反演结果模型A为四层横波速度递增模型[18],各地层参数和反演搜索范围如表 3所示。利用交错网格有限差分方法[29]生成其理论面波记录(图 4a),采用相移法[30]获得该地震记录的瑞雷波频散能量谱(图 4b),可见频散能量的极大值能准确对应由地层模型正演得到的理论频散曲线(图 4b中黑点),这说明使用相移法提取频散曲线是可靠的。
|
|
表 3 模型A地质参数及反演搜索范围 |
|
图 4 模型A的理论面波炮集记录(a)及相移法获得的频散能量谱(b) 黑点是根据Knopoff方法计算的理论频散点。图 7同 |
对个体做定量评估,即构建目标函数是频散曲线反演的关键部分。目前最常用的是均方差函数,其基阶频散曲线反演的个体目标函数为
| $ \varepsilon=\sqrt{\frac{\sum\limits_{j=1}^{M}\left(c_{\mathrm{obs} j}-c_{\mathrm{cal} j}\right)^{2}}{M}} $ | (7) |
式中:cobs是实际提取的瑞雷波相速度;ccal是正演算出的瑞雷波相速度;M为频散曲线的频率点总数。
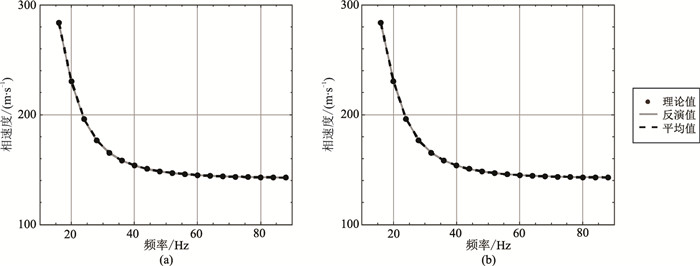
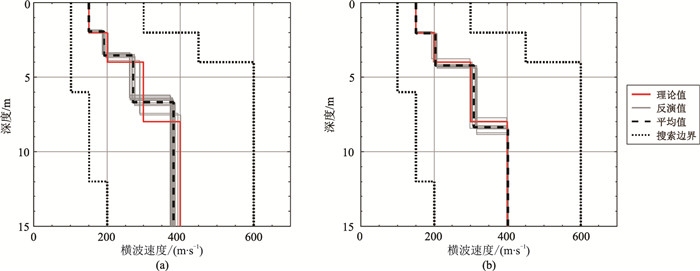
前文述及,IEPSO算法具有相对较强的“寻解”能力,因此本文分别采用该算法和AWDA算法反演频散曲线,以对比验证AWDA算法的反演效果。以上述两种算法分别进行50次独立计算,结果显示该两种算法反演得到的频散曲线(图 5)与理论值均有较高拟合度,但通过AWDA算法所得地层横波速度剖面(图 6b)的效果明显优于IEPSO算法结果(图 6a),各独立运算结果也更集中地分布于理论值周围。这从侧面反映出瑞雷波频散曲线的反演具有很强的多极值特性,而AWDA算法能有效地克服此不足,寻找到适应度更高的结果。从表 4的反演结果统计可知,AWDA算法计算的地层参数的平均相对误差为2.75%,显著低于IEPSO算法结果的9.03%。
|
图 5 模型A的IEPSO(a)和AWDA(b)频散曲线反演结果 |
|
图 6 模型A的IEPSO(a)和AWDA(b)横波速度反演结果 |
|
|
表 4 模型A反演结果统计 |
层状介质中瑞雷波存在多种传播模式[31-32],即在同一频率下存在多个相速度值,速度从低到高依次为基阶、一阶高阶、二阶高阶……等模式。在某些地质条件下,高阶频散能量在中、高频段占据主导地位。若将高阶频散曲线纳入反演中,就能增强对反演结果的约束,获得更准确的横波速度数据。
多阶频散曲线反演中个体的目标函数为
| $ \varepsilon=\frac{1}{L} \sum\limits_{k=1}^{L} \sqrt{\frac{\sum\limits_{j=1}^{M_{k}}\left(c_{\mathrm{obs} j}^{k}-c_{\mathrm{calj}}^{k}\right)^{2}}{M_{k}}} $ | (8) |
式中:L为频散曲线总数;Mk为第k条频散曲线的频率点总数。
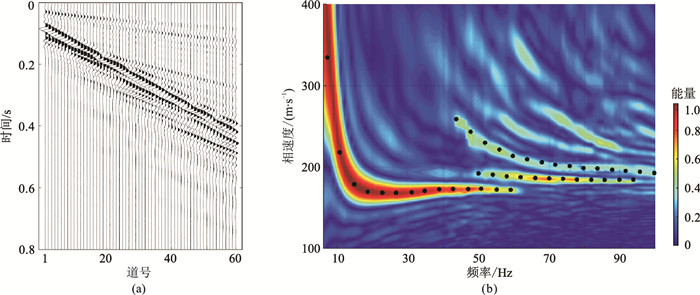
模型B为含软夹层的五层模型,人工铺设路面的地层结构即与此类似。地层参数和反演搜索范围如表 5所示;所得理论面波记录及生成的频散能量谱如图 7所示,可见基阶频散能量主要分布于低频区域,而高阶频散能量在50Hz以上更活跃(提取的基阶、一阶高阶和二阶高阶频散曲线如黑点连线)。
|
|
表 5 模型B地质参数及反演搜索范围 |
|
图 7 模型B的理论面波炮集记录(a)及相移法获得的频散能量谱(b) |
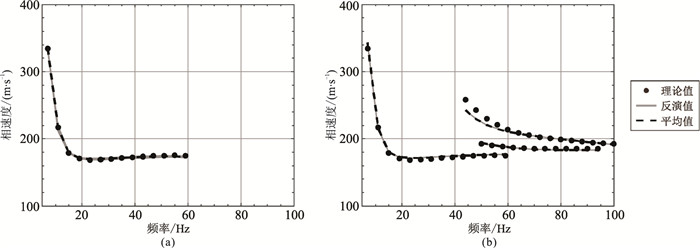
本文首先分别计算了IEPSO算法对基阶、多阶频散曲线的反演结果(图 8),可见IEPSO算法反演基阶频散曲线的结果与理论值的拟合度较好,但仍能观察到20~60Hz频段的反演结果与理论值存在一定程度偏差,虽呈现出反映低速夹层的“之”字形结构[33],但并不如理论值那样明显。此外,多阶频散曲线反演结果中40~60Hz频段的二阶高阶频散曲线与理论值存在明显偏差。
|
图 8 模型B的IEPSO算法的基阶(a)和多阶(b)频散曲线反演结果 |
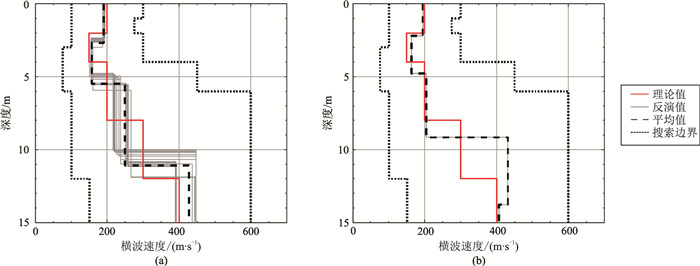
横波速度反演结果如图 9所示,可见IEPSO算法的两类反演结果与理论值的拟合度均较低。
|
图 9 模型B的IEPSO算法对基阶(a)和多阶(b)频散曲线反演得到的横波速度 |
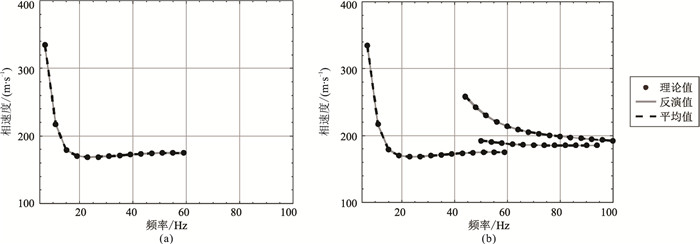
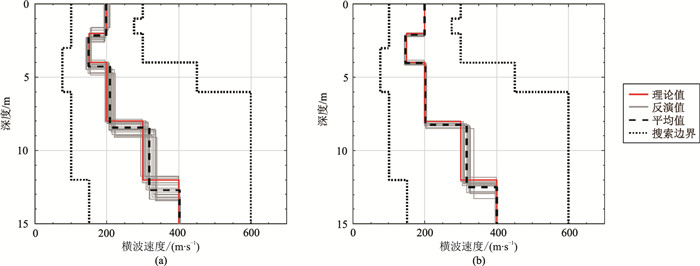
随后应用AWDA算法分别求得基阶(图 10a)及多阶(图 10b)频散曲线反演结果,可见两种情形的频散曲线与理论值均有较高拟合度;从横波速度反演结果(图 11)不难发现,多阶频散曲线的反演结果与理论值的拟合情况明显更好。对上述反演结果的统计(表 6)表明,相比仅反演基阶频散曲线的结果,反演多阶频散曲线结果中的第一层和第三层横波速度的标准差分别由4.15和8.43降至0.91和2.24。
|
图 10 模型B的AWDA算法的基阶(a)和多阶(b)频散曲线反演结果 |
|
图 11 模型B的AWDA算法对基阶(a)和多阶(b)频散曲线反演得到的横波速度 |
|
|
表 6 模型A反演结果统计 |
以上结果说明AWDA算法的求解能力明显高于IEPSO算法,且反演多阶频散曲线可进一步提高结果的准确度和稳定性。
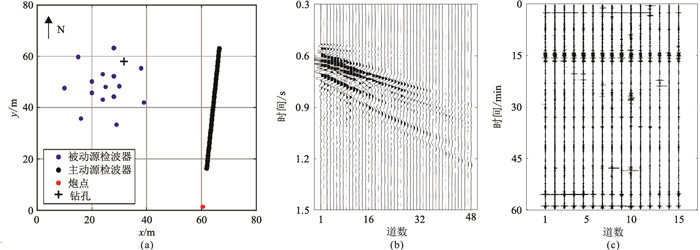
3 实际测试依据实际地震数据,进一步验证AWDA算法反演瑞雷波频散曲线的效果。数据来自欧洲研究机构发起的InterPacific项目[34-35],测量地点位于意大利北部城镇Mirandola。为增加勘探深度,同时使用主动源和被动源地震记录提取频散曲线。从检波器阵列及钻孔位置(图 12a)可见:主动源阵列由48个4.5Hz的垂向检波器以1m间隔线性摆放,震源采用8kg重锤敲击地面方式,最小炮检距为15m,采样间隔为0.25ms,采集时长为2s;被动源阵列采用两个半径分别为5m和15m的共中心圆环,采样间隔为5ms,采集时长为60min。得到主动源(图 12b)和被动源(图 12c)地震记录。
|
图 12 Mirandola地区实际面波勘探的检波器阵列(a)及主动源(b)、被动源(c)地震记录 |
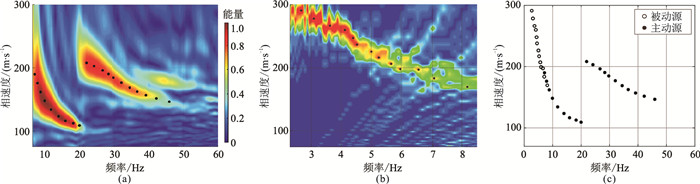
图 13a是主动源地震记录通过相移法生成的频散能量谱,易见频散能量可分为两部分,即7~20Hz的基阶频散能量和22~45Hz的高阶频散能量。为准确利用该高阶频散能量,对实际数据做两步法反演[36]:①对上述基阶频散曲线进行反演,得到横波速度模型;②对步骤①中反演得到的横波速度模型做正演,计算其多阶理论频散曲线,随后与上述高阶频散曲线进行比照,确定该高阶频散曲线的模态,再对基阶和高阶频散曲线进行联合反演,作为多阶频散曲线的反演结果。利用Geopsy软件中的MSPAC模块[37]提取被动源地震数据的频散曲线,并得到相应的频散能量谱(图 13b)。主、被动源方法提取的多阶频散曲线如图 13c所示,可见包含丰富的低频信息,能显著提高瑞雷波勘探深度。
|
图 13 主动源(a)、被动源(b)的频散能量谱以及联合方法提取的频散曲线(c) |
在实际面波勘探中,根据所提取的频散曲线需确定最大勘探深度。通常最大勘探深度为基阶频散曲线最大波长的1/3~1/2 [38],本文选择42m为此轮反演最大勘探深度。由于横波速度和层厚与瑞雷波频散曲线的关系最紧密[2],故通过反演频散曲线仅计算最大勘探深度以上地层的横波速度和层厚,而将影响较小的纵波速度和密度设为合理的固定值。
根据横波测井数据将勘探空间划分为4层,各层横波速度和层厚的搜索范围、纵波速度及密度的设定如表 7所示。若缺少横波测井资料,可根据现场实际地质情况,结合提取的频散曲线所包含的速度信息,设置一组搜索模型并分别进行反演,以获得拟合度较高结果。之后,可对拟合度较高的反演结果的搜索模型进行更细致合理的调整并再做反演运算,以便得到更能反映地下真实情况的结果。
|
|
表 7 反演搜索范围及模型参数设置 |
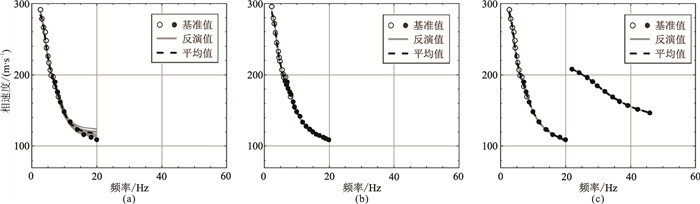
本文使用IEPSO算法对提取的基阶频散曲线进行反演,并与AWDA算法的结果进行对比。算法的参数设置与理论地层模型测试一致。首先计算两种算法对基阶频散曲线的反演结果,根据该反演结果正演计算多阶频散曲线,经过比照确定所提取的高阶频散曲线为二阶高阶频散曲线。随后利用AWDA算法对基阶、二阶高阶频散曲线进行联合反演。对于频散曲线,IEPSO算法计算的结果(图 14a)在10Hz以下与基准值的拟合度相较好,但在10Hz以上出现明显偏差,最大误差达2.12%。AWDA算法反演基阶频散曲线的结果(图 14b)与基准值的吻合情况优于前者,最大误差不超过0.73%。AWDA算法反演多阶频散曲线的结果(图 14c)同样能很好地拟合提取的频散曲线,最大误差仅为0.55%。
|
图 14 实际资料频散曲线反演结果 (a)IEPSO算法对基阶频散曲线的反演;(b)AWDA算法对基阶频散曲线的反演;(c)AWDA算法对多阶频散曲线的反演 |
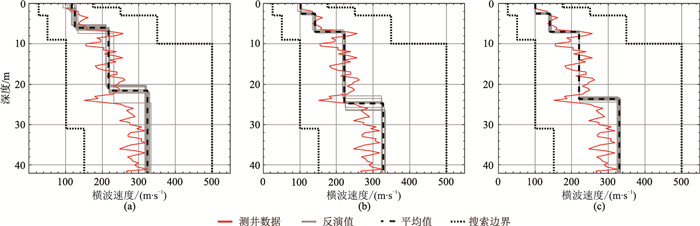
从IEPSO算法反演所得横波速度剖面(图 15a)可见,各独立运算结果在浅层横波速度及第三层厚度的确定与横波测井数据存在一定程度偏差和波动。再看AWDA算法基阶频散曲线反演结果(图 15b),浅层横波速度的稳定性得到提升,且更接近于横波测井资料。第三层厚度值虽仍存在一定波动,但与IEPSO算法结果相比更准确。从图 15c可见,利用AWDA算法对多阶频散曲线进行反演可进一步提高地层速度结构的稳定性,且对第三层厚度稳定性的提升尤为明显。
|
图 15 不同方法针对实际资料反演的横波速度 (a)IEPSO算法对基阶频散曲线的反演;(b)AWDA算法对基阶频散曲线的反演;(c)AWDA算法对多阶频散曲线的反演 |
总之,实际资料测试结果再次验证,相比本文提及的其他非线性算法,使用AWDA算法反演瑞雷波频散曲线能显著提高结果的准确性。
4 结论与讨论本文根据蜻蜓个体的适应度对行为权重进行调控,构建了AWDA算法。即通过各行为机制的相互配合,不断调整各行为所占比重,从而灵活地在迭代过程中更改“搜索”策略。将该算法用于瑞雷波频散曲线反演,与IEPSO算法相比,AWDA算法计算的频散曲线与基准值的误差更小,反演得到的地层速度结构与横波测井数据更接近,证明了该算法的可行性及有效性。
此外,对多阶瑞雷波频散曲线的反演能获得更准确、稳定的地层速度结构。
当然,AWDA算法也存在一些缺陷,如计算耗时相对较长,对自适应行为权重赋值范围的设定多基于经验。对这些问题的持续关注和深入研究无疑会大幅度提高AWDA算法的求解能力和计算效率。
| [1] |
Pan Y, Gao L, Bohlen T. High-resolution characteri-zation of near-surface structures by surface-wave inversions: from dispersion curve to full waveform[J]. Surveys in Geophysics, 2019, 40(2): 167-195. DOI:10.1007/s10712-019-09508-0 |
| [2] |
Xia J, Miller R D, Park C B. Estimation of near-surface shear-wave velocity by inversion of Rayleigh waves[J]. Geophysics, 1999, 64(3): 691-700. DOI:10.1190/1.1444578 |
| [3] |
祁生文, 孙进忠, 何华. 瑞雷波勘探的研究现状及展望[J]. 地球物理学进展, 2002, 17(4): 630-635. QI Shengwen, SUN Jinzhong, HE Hua. Review of Rayleigh wave exploration[J]. Progress in Geophy-sics, 2002, 17(4): 630-635. DOI:10.3969/j.issn.1004-2903.2002.04.011 |
| [4] |
Cox B R, Beekman A N. Intramethod variability in ReMi dispersion measurements and VS estimates at shallow bedrock sites[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(4): 354-362. DOI:10.1061/(ASCE)GT.1943-5606.0000436 |
| [5] |
Comina C, Foti S, Boiero D, et al. Reliability of VS, 30 evaluation from surface-wave tests[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 137(6): 579-586. |
| [6] |
Wathelet M, Jongmans D, Ohrnberger M. Surface-wave inversion using a direct search algorithm and its application to ambient vibration measurements[J]. Near Surface Geophysics, 2004, 2(4): 211-221. DOI:10.3997/1873-0604.2004018 |
| [7] |
刘云祯, 王振东. 瞬态面波法的数据采集处理系统及其应用实例[J]. 物探与化探, 1996, 20(1): 28-34. LIU Yunzhen, WANG Zhendong. Data collection and processing system of transient surface wave method and examples of its application[J]. Geophysical and Geochemical Exploration, 1996, 20(1): 28-34. |
| [8] |
Song X, Gu H, Liu J, et al. Estimation of shallow subsurface shear-wave velocity by inverting fundamental and higher-mode Rayleigh waves[J]. Soil Dynamics and Earthquake Engineering, 2007, 27(7): 599-607. DOI:10.1016/j.soildyn.2006.12.003 |
| [9] |
Moro G D, Pipan M, Gabrielli P. Rayleigh wave dispersion curve inversion via genetic algorithms and marginal posterior probability density estimation[J]. Journal of Applied Geophysics, 2007, 61(1): 39-55. DOI:10.1016/j.jappgeo.2006.04.002 |
| [10] |
Matteo P, Dario A. Combining genetic and linearized algorithms for a two-step joint inversion of Rayleigh wave dispersion and H/V spectral ratio curves[J]. Geophysical Journal International, 2007, 69(1): 189-200. |
| [11] |
Ryden N, Park C B. Fast simulated annealing inversion of surface waves on pavement using phase-velocity spectra[J]. Geophysics, 2006, 71(4): R49-R58. DOI:10.1190/1.2204964 |
| [12] |
Calderón-macías C, Luke B. Improved parameterization to invert Rayleigh-wave data for shallow profiles containing stiff inclusions[J]. Geophysics, 2007, 72(1): U1-U10. DOI:10.1190/1.2374854 |
| [13] |
曹旭, 熊章强, 张大洲. 基于BP神经网络的瑞雷面波智能优化反演[J]. 工程地球物理学报, 2015, 12(4): 514-519. CAO Xu, XIONG Zhangqiang, ZHANG Dazhou. The Rayleigh surface wave intelligent inversion based on the BP artificial neural network[J]. Chinese Journal of Engineering Geophysics, 2015, 12(4): 514-519. DOI:10.3969/j.issn.1672-7940.2015.04.017 |
| [14] |
Song X, Tang L, Lv X, et al. Application of particle swarm optimization to interpret Rayleigh wave dispersion curves[J]. Journal of Applied Geophysics, 2012, 84: 1-13. DOI:10.1016/j.jappgeo.2012.05.011 |
| [15] |
蔡伟, 宋先海, 袁士川, 等. 利用粒子群优化算法快速、稳定反演瑞雷波频散曲线[J]. 石油地球物理勘探, 2018, 53(1): 25-34. CAI Wei, SONG Xianhai, YUAN Shichuan, et al. Fast and stable Rayleigh-wave dispersion-curve inversion based on particle swarm optimization[J]. Oil Geo-physical Prospecting, 2018, 53(1): 25-34. |
| [16] |
Cercato M. Addressing non-uniqueness in linearized multichannel surface wave inversion[J]. Geophysical Prospecting, 2008, 57(1): 27-47. |
| [17] |
Foti S, Comina C, Boiero D, et al. Non-uniqueness in surface-wave inversion and consequences on seismic site response analyses[J]. Soil Dynamics & Earthquake Engineering, 2009, 29(6): 982-993. |
| [18] |
于东凯, 宋先海, 张学强, 等. 蚱蜢算法在瑞雷波频散曲线反演中的应用[J]. 石油地球物理勘探, 2019, 54(2): 288-301. YU Dongkai, SONG Xianhai, ZHANG Xueqiang, et al. Rayleigh wave dispersion inversion based on gras-shopper optimization algorithm[J]. Oil Geophysical Prospecting, 2019, 54(2): 288-301. |
| [19] |
Mirjalili S. Dragonfly algorithm: a new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems[J]. Neural Computing and Applications, 2016, 27(4): 1053-1073. DOI:10.1007/s00521-015-1920-1 |
| [20] |
Beaty K S, Schmitt D R, Sacchi M. Simulated annealing inversion of multimode Rayleigh wave dispersion curves for geological structure[J]. Geophysical Journal International, 2002, 151(2): 622-631. DOI:10.1046/j.1365-246X.2002.01809.x |
| [21] |
Maraschini M, Ernst F, Foti S, et al. A new misfit function for multimodal inversion of surface waves[J]. Geophysics, 2010, 75(4): G31-G43. DOI:10.1190/1.3436539 |
| [22] |
Lin S, Ashlock J C. Multimode Rayleigh wave profiling by hybrid surface and borehole methods[J]. Geophysical Journal International, 2014, 197(2): 1184-1195. DOI:10.1093/gji/ggu051 |
| [23] |
Li L L, Zhao X, Tseng M L, et al. Short-term wind power forecasting based on support vector machine with improved dragonfly algorithm[J]. Journal of Cleaner Production, 2020, 242: 118447. DOI:10.1016/j.jclepro.2019.118447 |
| [24] |
Lv X, Wang Y, Deng J, et al. Improved particle swarm optimization algorithm based on last-eliminated principle and enhanced information sharing[J]. Computational Intelligence and Neuroscience, 2018, 12: 1-17. |
| [25] |
吴聪, 陈侃松, 姚静. 基于改进自适应遗传算法的物流配送路径优化研究[J]. 计算机测量与控制, 2018, 26(2): 236-240. WU Cong, CHEN Kansong, YAO Jing. Study on optimization of logistics distribution route based on improved adaptive genetic algorithm[J]. Computer Measurement & Control, 2018, 26(2): 236-240. |
| [26] |
Yang X S. Firefly Algorithm, Lévy Flight and Global Optimization[M]. Springer, 2010, 209-218.
|
| [27] |
Yu W J, Li X B, Cai H B, et al. An improved artificial bee colony algorithm based on factor library and dynamic search balance[J]. Mathematical Problems in Engineering, 2018. DOI:10.1155/2018/3102628 |
| [28] |
Foti S, Hollender F, Garofalo F, et al. Guidelines for the good practice of surface wave analysis: a product of the InterPACIFIC project[J]. Bulletin of Earthquake Engineering, 2017, 16(6): 2367-2420. DOI:10.1007/s10518-017-0206-7 |
| [29] |
Levander A R. Fourth-order finite-difference P-SV seismograms[J]. Geophysics, 1988, 53(11): 1425-1436. DOI:10.1190/1.1442422 |
| [30] |
Park C B, Miller R D, Xia J. Multichannel analysis of surface waves[J]. Geophysics, 1999, 64(3): 800-808. DOI:10.1190/1.1444590 |
| [31] |
Socco L V, Foti S, Boiero D. Surface-wave analysis for building near-surface velocity models-established approaches and new perspectives[J]. Geophysics, 2010, 75(5): A83-A102. |
| [32] |
尹晓菲, 胥鸿睿, 郝晓菡, 等. 水平层状模型中多模式瑞雷波和拉夫波相速度频散曲线的灵敏度分析[J]. 石油地球物理勘探, 2020, 55(1): 136-146. YIN Xiaofei, XU Hongrui, HAO Xiaohan, et al. Sensitivity analysis of multi-mode Rayleigh and Love wave phase-velocity dispersion curves in horizontal layered models[J]. Oil Geophysical Prospecting, 2020, 55(1): 136-146. |
| [33] |
张碧星, 鲁来玉, 鲍光淑. 瑞利波勘探中"之"字形频散曲线研究[J]. 地球物理学报, 2002, 45(2): 263-274. ZHANG Bixing, LU Laiyu, BAO Guangshu. A study on zigzag dispersion curves in Rayleigh wave exploration[J]. Chinese Journal of Geophysics, 2002, 45(2): 263-274. DOI:10.3321/j.issn:0001-5733.2002.02.013 |
| [34] |
Garofalo F, Foti S, Hollender F, et al. InterPACIFIC project: Comparison of invasive and non-invasive methods for seismic site characterization.Part Ⅰ: Intra-comparison of surface wave methods[J]. Soil Dynamics & Earthquake Engineering, 2016, 82(1): 222-240. |
| [35] |
Garofalo F, Foti S, Hollender F, et al. InterPACIFIC project: Comparison of invasive and non-invasive methods for seismic site characterization.Part Ⅱ: Inter-comparison between surface-wave and borehole methods[J]. Soil Dynamics & Earthquake Enginee-ring, 2016, 82(4): 241-254. |
| [36] |
杨博, 熊章强, 张大洲, 等. 利用自适应混沌遗传粒子群算法反演瑞雷面波频散曲线[J]. 石油地球物理勘探, 2019, 54(6): 1217-1227. YANG Bo, XIONG Zhangqiang, ZHANG Dazhou, et al. Rayleigh surface-wave dispersion curve inversion based on adaptive chaos genetic particle swarm optimization algorithm[J]. Oil Geophysical Prospecting, 2019, 54(6): 1217-1227. |
| [37] |
Wathelet M, Jongmans D, and Ohrnberger M. Direct inversion of spatial autocorrelation curves with the neighborhood algorithm[J]. Bulletin of the Seismological Society of America, 2005, 95(5): 1787-1800. DOI:10.1785/0120040220 |
| [38] |
Cox B R, Teague D P. Layering ratios: a systematic approach to the inversion of surface wave data in the absence of a priori information[J]. Geophysical Journal International, 2016, 207(1): 422-438. DOI:10.1093/gji/ggw282 |



 何川, 北京市海淀区颐和园路5号北京大学地球与空间科学学院, 100871。Email:
何川, 北京市海淀区颐和园路5号北京大学地球与空间科学学院, 100871。Email: 