② 中国石油大学(北京)地球物理学院, 北京 102249
② College of Geophysics, China University of Petroleum(Beijing), Beijing 102249, China
奥地利数学家Radon于上世纪初提出了Radon变换理论,经过不断的发展完善,逐渐从数学领域沿用到其他领域。Claerbout等[1]将Radon变换引入地震勘探领域,极大地促进了Radon变换在地震资料处理方面的应用,如多次波压制、缺失地震道重建、平面波分解以及去噪,且该变换可在时域、频域及混合域实现。
由于线性Radon变换和抛物Radon变换具有时不变特性,故可在频域快速求解。Hampson[2]提出抛物Radon变换并将其应用于多次波压制,且在频域用最小二乘(Least square,LS)算法求解,但该方法的分辨率并不高;之后,Sacchi等[3-4]结合贝叶斯原理,通过引入模型的先验信息提高Radon变换的分辨率。由于高分辨率Radon变换迭代过程涉及矩阵求逆运算,导致其计算量较大,为此采用低频约束方法,即用上一频率计算结果约束当前频率的计算[5-6]。刘喜武等[7]利用稀疏约束共轭梯度算法求解Radon变换,与阻尼LS算法相比,提高了Radon变换的分辨率和计算效率;王维红等[8]提出基于Levinson递推法的加权抛物Radon变换叠前地震数据重建方法,与传统的高分辨率Radon变换方法相比,计算效率有所提升;薛亚茹等[9]将传统抛物Radon变换与正交多项式相结合,克服了空间假频,并保留地震波的AVO特性;之后,王亮亮等[10]在此基础上引入新变量,消除了变换算子对频率的依赖,提高了计算效率。由于L1范数不具有真正意义上的稀疏性,薛亚茹等[11]引入SL0范数约束,并通过最速下降法和梯度投影原理实施了高分辨率Radon变换。
由于Radon模型在时域比在频域更具有稀疏性,Cary[12]和Schonewille等[13]在时域实现了Radon变换,提高了其分辨率,但收敛速度较慢;巩向博等[14]提出各向异性Radon变换,通过最优相似系数加权Gauss-Seidel迭代算法,提高了Radon变换计算效率。结合Radon变换在时域的稀疏性及在频域的计算高效性,Trad等[15]在频域实现Radon变换的正向和反向过程,并利用迭代加权最小二乘法(Iterative reweighted least square,IRLS)在时域求解稀疏Radon变换,充分兼顾时域Radon变换和频域Radon变换的优点;此后,Lu[16]用迭代收缩算法(Iterative-shrinkage algorithms)代替IRLS,进一步提高混合域Radon变换的计算效率;在此基础上,Wang等[17]针对噪声偏离高斯分布的Radon变换,引入Bregman方法,提高了混合域Radon变换的鲁棒性;巩向博等[18]在混合域实现双曲Radon变换,并引入快速迭代软阈值算法(Fast iterative shrinkage-thresholding algorithm,FISTA)加快反演收敛速度。随着Radon变换在地震数据领域的更广泛应用,近年来还研发出基于字典学习的用于去噪和插值的Radon变换,通过稀疏表征地震数据并结合K-SVD方法实现求解[19-21]。由于高分辨率Radon变换计算量较大且计算结果易受正则化影响,也有学者提出在压缩感知框架下处理地震数据,利用匹配追踪等算法,以提高地震数据处理的计算精度和效率[22-26]。
本文分析了迭代软阈值法(Iterative soft threshold algorithm,ISTA)和IRLS实现Radon变换的基本原理,提出将IRLS的加权矩阵思想引入ISTA方法中,形成加权迭代软阈值法(Reweighted-Iterative soft threshold algorithm,R-ISTA),以进一步提高Radon变换分辨率。
1 方法原理 1.1 Radon变换反演基本原理在地震勘探领域,常用的Radon变换有线性Radon变换、抛物Radon变换和双曲Radon变换。抛物Radon变换将动校正后的同相轴沿时距曲线进行叠加,得到Radon参数。由于采集到的地震数据为离散数据,一般采用离散Radon变换,Radon正变换离散形式为
| $ d\left(t, h_{i}\right)=\sum\limits_{j=1}^{N_{q}} m\left(\tau=t-q_{j} h_{i}^{2}, q_{j}\right) $ | (1) |
式中:m为Radon域数据;d为时空域地震数据;q为曲率参数;h为炮检距;t为时间;τ为时空域双重旅行时截距;Nq为Radon域曲率参数个数。
抛物Radon变换具有时不变性,可将其变换到频域进行计算,以提高计算效率。对式(1)做傅里叶变换得到对应的频域Radon正变换公式
| $ D\left(\omega, h_{i}\right)=\sum\limits_{j=1}^{N_{q}} M\left(\omega, q_{j}\right) \mathrm{e}^{-\mathrm{i} \omega \alpha_{j} h_{i}^{2}} $ | (2) |
可写成如下矩阵形式
| $ \boldsymbol{D}=\boldsymbol{L} \boldsymbol{M} $ | (3) |
其中Radon变换算子矩阵L的具体表达式为
| $ \boldsymbol{L}=\left[\begin{array}{cccc} \mathrm{e}^{-\mathrm{i} \omega q_{1} h_{1}^{2}} & \mathrm{e}^{-\mathrm{i} \omega q_{2} h_{1}^{2}} & \cdots & \mathrm{e}^{-\mathrm{i} \omega q_{N_q} h_{1}^{2}} \\ \mathrm{e}^{-\mathrm{i} \omega q_{1} h_{2}^{2}} & \mathrm{e}^{-\mathrm{i} \omega q_{2} h_{2}^{2}} & \cdots & \mathrm{e}^{-\mathrm{i} \omega q_{N_{q}} h_{2}^{2}} \\ & & \vdots & \\ \mathrm{e}^{-\mathrm{i} \omega q_{1} h_{N_{h}}^{2}} & \mathrm{e}^{-\mathrm{i} \omega q_{2} h_{N_h}^{2}} & \cdots & \mathrm{e}^{-\mathrm{i} \omega q_{{N}_{q}} h_{N_h}^{2}} \end{array}\right] $ | (4) |
式中Nh为道数。
由于矩阵L通常不是方阵,无法求逆,其LS解分辨率低,基于L1范数的稀疏正则化是现今常用的高分辨率反演方法。构造高分辨率反演目标函数为
| $ J=\|\boldsymbol{D}-\boldsymbol{L} \boldsymbol{M}\|_{2}^{2}+\lambda\|\boldsymbol{M}\|_{2}^{2} $ | (5) |
式中λ为拉格朗日因子,且有λ>0,用于平衡模型的准确度和稀疏性。ISTA是上述优化问题常用求解方法之一[27-30],该算法求解过程不涉及矩阵求逆,计算效率高,每次迭代过程中经矩阵乘法后通过软阈值函数逐渐逼近所求变量,其迭代式为
| $ \boldsymbol{M}^{n+1}=S_{\sigma}\left[\boldsymbol{M}^{n}+\eta \boldsymbol{L}^{\mathrm{H}}\left(\boldsymbol{D}-\boldsymbol{L} \boldsymbol{M}^{n}\right)\right] $ | (6) |
式中:n为迭代次数;η为正参数,通常取为LHL最大特征值的倒数;Sσ为软阈值函数,其表达式为
| $ S_{\sigma}(\boldsymbol{M}, \sigma)=\operatorname{sign}(\boldsymbol{M}) \max \{0,|\boldsymbol{M}|-\sigma\} $ | (7) |
式中:sign为符号函数;σ为阈值,该值与上一次迭代结果有关,即达到自适应阈值的目的,其经验表达式为
| $ \sigma=0.01 \max \left(\left|\boldsymbol{M}^{n}\right|\right) $ | (8) |
由于矩阵L具有非正交性,式(6)中共轭算子LH降低了Radon变换的分辨率,使得上述算法应用于Radon变换反演时收敛速度较慢。
1.2 基于R-ISTA算法的高分辨Radon变换IRLS是高分辨Radon变换的另一种常用方法[31]。Sacchi等[3-4]基于贝叶斯原理,将模型先验信息与Radon变换相结合,将前一次迭代结果作为下一次反演的加权矩阵;经过若干次迭代之后,得到高分辨率的Radon变换。
据式(3)构造如下目标函数
| $ J=\|\boldsymbol{D}-\boldsymbol{L} \boldsymbol{M}\|_{2}^{2}+\mu\left\|\boldsymbol{W_{M}} \boldsymbol{M}\right\|_{2}^{2} $ | (9) |
式中:μ为阻尼因子,取值范围是0.01~1.00;WM为数据M的协方差矩阵。将式(9)最小化,可得
| $ \boldsymbol{M}=\left(\boldsymbol{L}^{\mathrm{H}} \boldsymbol{L}+{\mu} \boldsymbol{W}\right)^{-1} \boldsymbol{L}^{\mathrm{H}} \boldsymbol{D} $ | (10) |
式中W=WMHWW,是一个权重对角矩阵。
为克服ISTA中Radon共轭算子分辨率低的问题,引入IRLS的Radon变换中权重矩阵思想,将IRLS的加权反演矩阵引入ISTA中,得到R-ISTA公式,即改进的式(6)表达式
| $ \boldsymbol{M}^{n+1}=S_{\sigma}\left\{\boldsymbol{M}^{n}+\eta \boldsymbol{B}^{-1}\left[\boldsymbol{L}^{\mathrm{H}}\left(\boldsymbol{D}-\boldsymbol{L} \boldsymbol{M}^{n}\right)\right]\right\} $ | (11) |
与式(6)所示传统的ISTA公式相比,本文引入与加权矩阵相关的反演矩阵
| $ \boldsymbol{B}=\boldsymbol{L}^{\mathrm{H}} \boldsymbol{L}+\mu \boldsymbol{W} $ | (12) |
式中对角矩阵W的对角元素与前一次迭代Radon域数据M有关,用来聚焦Radon域能量,即
| $ \boldsymbol{W}_{i i}=\frac{1}{\left|\boldsymbol{M}_{i}\right|^{2}+b^{2}} $ | (13) |
式中b是稳定因子。
与传统ISTA方法相比,本文所提R-ISTA方法通过引入权重矩阵使Radon域能量聚焦,当上一次迭代得到的Radon域数据M部分能量较低时,则相应的权重矩阵较大。类似地,当前一次迭代得到的M数据部分能量较高时,其对应的权重矩阵较小;随后经矩阵求逆运算,使得数据M中能量强的部分继续加强,能量弱的部分进一步减弱,以此达到高分辨率Radon变换的目的。
1.3 基于主频约束的R-ISTA高分辨Radon变换迭代加权方法对每个频率都需计算反演权重矩阵(式(12)),还需做求逆运算,故计算量较大。为了降低运算耗时,可用单个频率的运行结果约束其他频率,避免逐个分别对每一频率计算权重矩阵,这样就可提高Radon变换计算效率[5-6, 32]。
为提高R-ISTA的计算效率,本文设计了适用于多次波压制的主频约束R-ISTA。首先选取地震数据的主频进行迭代训练,在分辨率达到要求后停止迭代,并保存其迭代得到的最终权重矩阵,然后用该频率训练得到的权重矩阵去约束其他所有频率的反演。基于主频约束的R-ISTA迭代公式为
| $ \boldsymbol{M}^{n+1}=\boldsymbol{S}_{\sigma}\left\{\boldsymbol{M}^{n}+\eta \boldsymbol{B}_{\text {main }}^{-1}\left[\boldsymbol{L}^{\mathrm{H}}\left(\boldsymbol{D}-\boldsymbol{L} \boldsymbol{M}^{n}\right)\right]\right\} $ | (14) |
式中Bmain为定值,不随迭代次数变化,其表达式为
| $ \boldsymbol{B}_{\operatorname{main}}=\boldsymbol{L}^{\mathrm{H}} \boldsymbol{L}+\mu \boldsymbol{W}_{\operatorname{main}} $ | (15) |
式中Wmain为主频训练迭代得到的加权矩阵,此后其值不再随频率变化。由于只需进行一次求逆运算,所以计算量大幅度减少。
基于主频约束的R-ISTA压制多次波的步骤如下:
(1) 设置初始参数,通过傅里叶变换把时空域地震数据d变换到频域D=F(d);
(2) 选择主频对应的频域数据Dmain,利用式(11)获得该主频的Radon参数,保存其加权参数矩阵Wii=(|Mi|2+b2)-1,以此约束其他频率的反演;
(3) 对频域所有地震数据D,由LS计算其迭代初始值M0=(LHL+μI)-1LHD;将M0代入主频约束R-ISTA迭代式(式(14)),其中伪逆矩阵由式(15)计算,迭代至收敛,得到Radon域数据Mn;
(4) 在Radon域分离一次波与多次波,实现多次波压制。
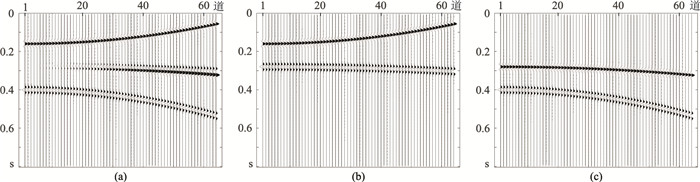
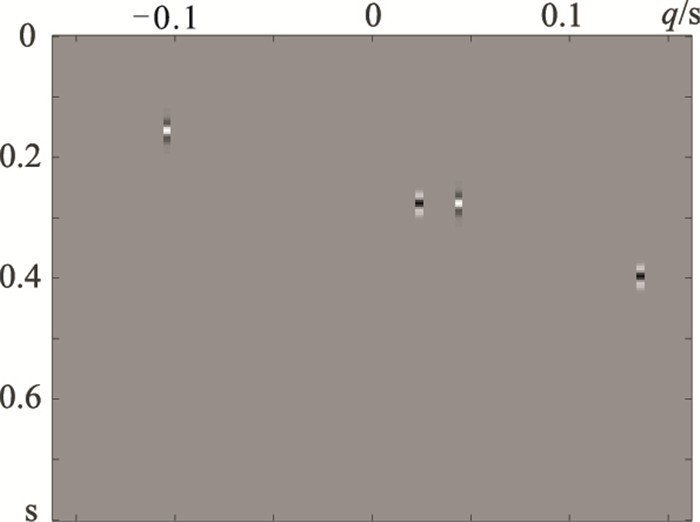
2 数据实验 2.1 模拟数据为比较ISTA、IRLS及R-ISTA三种方法实现Radon变换的分辨率及压制多次波的效果,构建如图 1a所示的模拟地震数据:采用主频为30Hz的Ricker子波,采样点数为200,采样间隔为4ms,共计64道;共含4条同相轴,其中一次波(图 1b)和多次波(图 1c)各两条。针对图 1a模拟数据对应的原始Radon数据(图 2),分别用ISTA、主频约束IRLS及主频约束R-ISTA三种方法进行处理,反演得到对应的Radon域数据(图 3a~图 3c)及其与原始Radon域数据的误差(图 3d~图 3f)。其中:ISTA和主频约束R-ISTA的迭代次数为10;主频约束IRLS的主频迭代也为10次,其他频率反演无需迭代。
|
图 1 模拟地震数据 (a)合成地震记录;(b)一次波记录;(c)多次波记录 |
|
图 2 原始Radon域数据 |

|
图 3 不同方法反演得到的Radon域数据(上)及其与原始数据的差值(下) (a)、(d)ISTA;(b)、(e)主频约束IRLS;(c)、(f)主频约束R-ISTA |
观察、对比可见:ISTA反演得到的Radon域数据能量较分散,分辨率较低,无法分离剩余时差差异较小的两同相轴;主频约束IRLS虽可将其分离,但还是存在能量扩散现象;而主频约束R-ISTA反演得到的Radon参数能量集中,分辨率高。
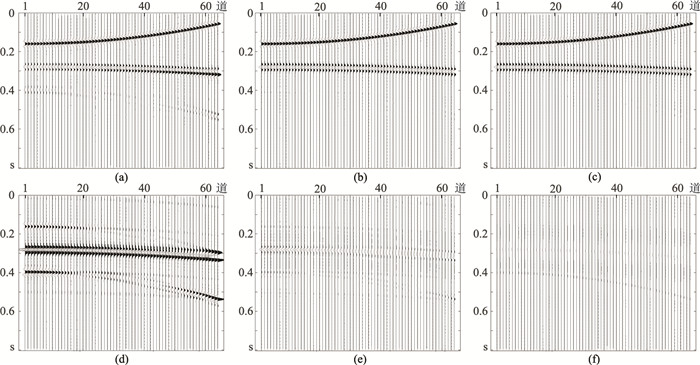
进一步分析反演所得结果(图 3),可知一次波与多次波已分离,去除其中一次波,经Radon反变换可得到时域多次波数据,从原始地震数据减去多次波数据,即可达到去除多次波的效果。分别用ISTA、主频约束IRLS和主频约束R-ISTA处理模拟地震数据后,恢复出图 4a~图 4c所示的多次波数据,用原始多次波数据(图 1c)分别减去上述三种方法恢复的多次波数据,得到图 4d~图 4f所示的(放大了5倍的)多次波残差数据。从原始地震数据(图 1a)减去三种方法恢复的多次波数据(图 4a~图 4c),可得到三种方法估计的一次波数据(图 5a~图 5c)及其与原始一次波(图 1b)的残差(图 5e~图 5f,放大了5倍)。

|
图 4 不同方法恢复的多次波数据(上)及其与原始多次波数据的差值(下,放大5倍) (a)、(d)ISTA;(b)、(e)主频约束IRLS;(c)、(f)主频约束R-ISTA |
|
图 5 不同方法恢复的一次波数据(上)及其与原始一次波数据的差值(下,放大5倍) (a)、(d)ISTA;(b)、(e)主频约束IRLS;(c)、(f)主频约束R-ISTA |
从图 4d~图 4f可观察到,主频约束IRLS和主频约束R-ISTA恢复的多次波更接近于真实值,ISTA恢复的多次波与真实值相差较大。观察图 5e~图 5f,可发现在一次波同相轴与多次波同相轴相邻位置,ISTA方法的多次波残留明显,且一次波数据有丢失;主频约束IRLS和主频约束R-ISTA两种方法对多次波压制效果都优于ISTA,但主频约束IRLS方法(图 5e)仍残存明显一次波数据;而图 5f中则基本看不到一次波残留,因此主频约束R-ISTA恢复的一次波数据更接近实际一次波数据。
用信噪比衡量不同方法对多次波的压制效果,信噪比定义为
| $ \mathrm{SNR}=20 \lg \frac{\|\boldsymbol{d}\|_{2}}{\left\|\boldsymbol{d}-\boldsymbol{d}_{m}\right\|_{2}} $ | (16) |
式中:d为原始一次波数据;dm为不同方法各自得到的一次波数据。本次采用的三种方法所用数据的信噪比如表 1所示,可见主频约束R-ISTA得到的信噪比为31.0404dB,远大于ISTA的7.7926dB,同样高于主频约束IRLS的21.6724dB。因此,主频约束R-ISTA对多次波的压制效果优于另两种方法。
|
|
表 1 加噪前后三种方法得到一次波的信噪比 |
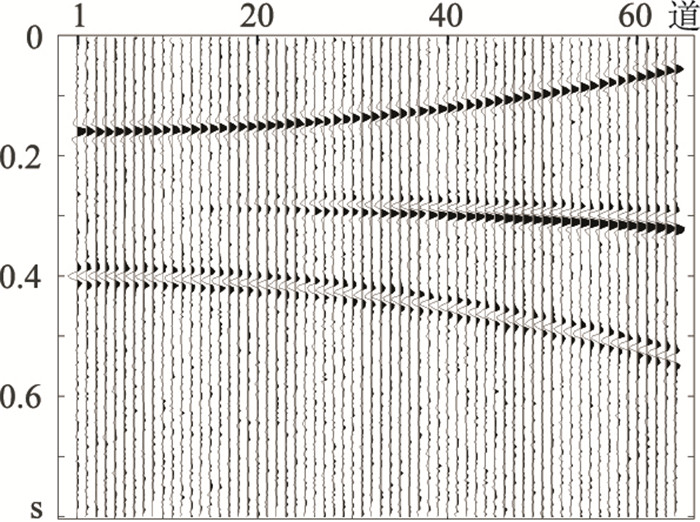
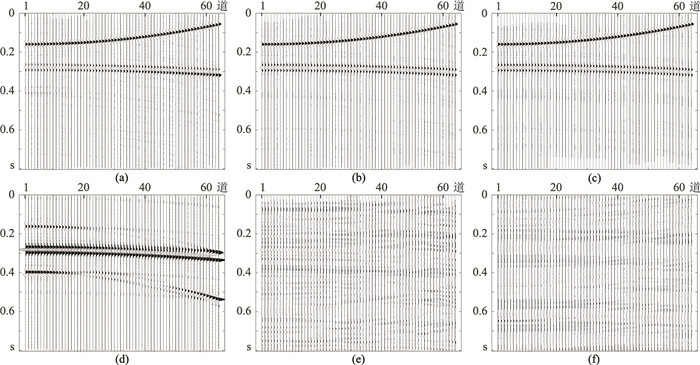
为评估R-ISTA的抗噪性能,针对图 1a模拟数据加入高斯白噪声,得到图 6所示含噪地震数据。根据信噪比定义式(式(16))算出该数据的信噪比为0dB。分别用ISTA、主频约束IRLS及主频约束R-ISTA压制多次波,得到一次波(图 7a~图 7c)及其误差数据(图 7d~图 7f),三种方法去噪后信噪比见表 1。从图 7及表 1可见,主频约束R-ISTA的去噪效果略优于主频约束IRLS,且都远优于ISTA。
|
图 6 含高斯白噪模拟地震数据 |
|
图 7 针对含噪地震数据用不同方法恢复的一次波数据(上)及其与原始一次波数据的差值(下,放大5倍) (a)、(d)ISTA;(b)、(e)主频约束IRLS;(c)、(f)主频约束R-ISTA |
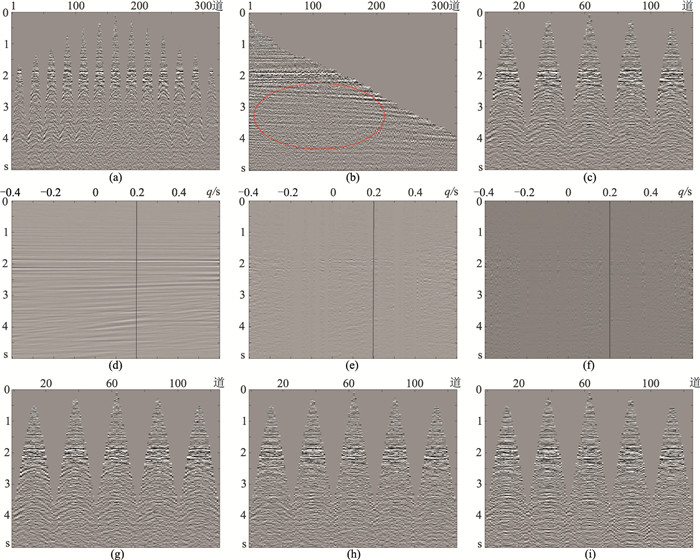
选取M地区三维实际地震数据(图 8a),共计13炮,每炮25道,采样点数为2501,采样间隔为2ms。图 8b为对原始数据按炮点距离排序后的实际数据。经动校正后,一次波同相轴基本被校平,曲率较小,而多次波仍有剩余时差,曲率较大,故可根据曲率的不同分离一次波与多次波。从图 8b可见多次波主要存在于图像中部(红色椭圆)区域,为便于对多次波压制过程做数据分析,选择仅展示图 8c所示的中间5炮数据。该数据Radon变换曲率参数q取值范围是-0.4~0.6s。图 8d~图 8f分别为ISTA、主频约束IRLS和主频约束R-ISTA三种方法反演的Radon域数据,切除0.2s以下部分(黑线左侧区域),即可获取多次波对应的Radon域数据;再经Radon反变换得到多次波数据,用原始数据减去多次波数据即可得三种方法压制多次波后结果(图 8g~图 8i)。
|
图 8 实际地震数据 (a)原始数据;(b)按炮点距离排序的实际数据;(c)取中间5炮数据;(d)、(e)、(f)对应ISTA、主频约束IRLS、主频约束R-ISTA方法反演的Radon域数据;(g)、(h)、(i)对应ISTA、主频约束IRLS、主频约束R-ISTA方法压制多次波后数据 |
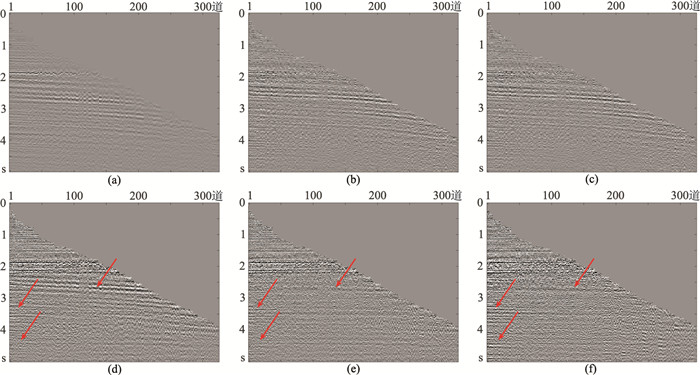
由于从图 8g~图 8i难以判明三种方法优劣性,故用上述三种方法处理13炮数据后,再按炮点距离排序,得到图 9a~图 9c所示多次波数据;进而获得三种方法去除多次波后的数据(图 9d~图 9f)。其中:ISTA迭代20次;主频约束R-ISTA迭代5次;主频约束IRLS的主频迭代10次,其他频率反演无需迭代。观察图 8d~图 8f中三种方法反演的Radon域数据,可见主频约束R-ISTA求取的Radon域数据比另两种方法更稀疏,去除多次波后可保留更多一次波信息;从图 9d~图 9f中箭头所指部分可见,与原始数据相比,经三种方法处理后,ISTA对多次波的压制效果欠佳,另两种方法的压制多次波效果较理想,且主频约束R-ISTA比主频约束IRLS的一次波同相轴更清晰。
|
图 9 按炮点距离排序地震数据不同方法去除的多次波(上)及剩余数据(下) (a)、(d)ISTA;(b)、(e)主频约束IRLS;(c)、(f)主频约束R-ISTA |
已知ISTA的收敛速度为O1(1/k,其中k为迭代次数,下同),即为次线性收敛;FISTA的收敛速度为O2(1/k2)[28];IRLS为指数收敛[33]。本文以均方误差为收敛性能的评判指标,其表达式为
| $ \mathrm{MSE}=\frac{1}{N} \sum\limits_{i=1}^{N}\left(m_{i}-\bar{m}_{i}\right)^{2} $ | (17) |
式中:mi为原数据;mi为算法恢复所得数据;N为数据总数。
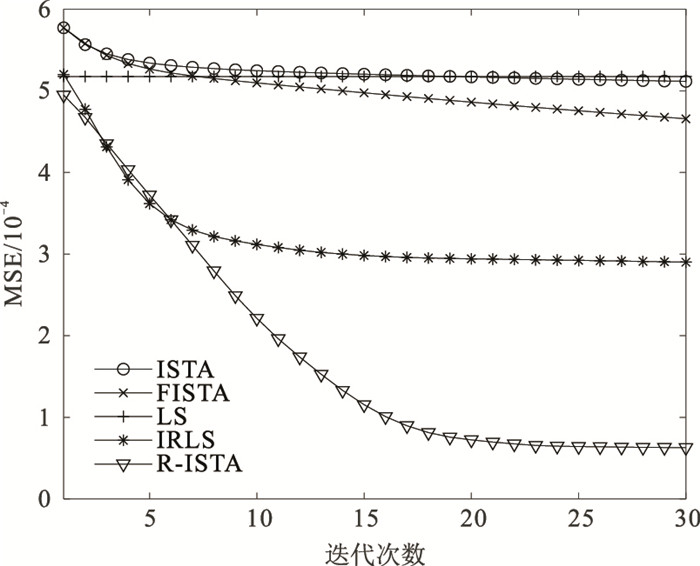
将R-ISTA与收敛速度已知的ISTA、FISTA、IRLS及基础的LS对比,得到图 10所示的收敛速度图。可见FISTA收敛速度快于ISTA,且此两者的精度略高于LS。迭代初始,IRLS和R-ISTA的收敛速度相差不大,且都快于ISTA;迭代12次之后,IRLS趋于收敛,R-ISTA的均方误差则继续下降,迭代20次趋于收敛;最终,R-ISTA的均方误差小于另四种算法。
|
图 10 ISTA、FISTA、LS、IRLS、R-ISTA收敛速度 |
从表 2可见,对于相同迭代次数(1次迭代除外),ISTA的运行速度明显快于R-ISTA和IRLS,这是由于ISTA不需进行矩阵求逆运算,而IRLS和R-ISTA的每次迭代过程,都需计算伪逆矩阵B=LHL+μW,当待处理数据较复杂时,其计算量更大。本次计算环境为Intel Core i5,主频为2.3 GHz,采用Windows平台下的Matlab实现。
|
|
表 2 三种算法的运算时间对比 |
为减小R-ISTA计算量,本文在R-ISTA基础上引入主频约束,此时伪逆矩阵Bmain=LHL+μWmain只需求解一次,计算量显著减少,主频约束对运行速度的影响见表 3。可见当只进行一次迭代时,主频约束对运行时间影响不大;随着迭代次数的增加,对无主频约束的R-ISTA而言,伪逆矩阵要随之计算更新,导致其计算量显著增大;而有主频约束的R-ISTA由于只需求解一次伪逆矩阵,之后不再随迭代次数增加而更新,且软阈值函数的相关计算量较小,当处理大量数据时,其计算量增加缓慢。
|
|
表 3 有/无主频约束R-ISTA方法的迭代时间 |
本文将高分辨Radon变换中加权矩阵的思想引入ISTA方法,利用Radon参数的先验信息约束反演误差函数,提出R-ISTA方法,解决了传统软阈值算法用于Radon变换表现的分辨率低及收敛速度慢问题。模拟数据和实际资料处理结果表明,与ISTA和IRLS相比,所提R-ISTA的Radon变换的分辨率有所提升,且具有更强压制多次波能力。
由于R-ISTA方法对于每一个频率仍需计算加权矩阵并进行矩阵求逆运算,计算量较大,因此本文在压制多次波时,引入主频约束思想,提高了R-ISTA方法对大型数据的处理能力。
| [1] |
Claerbout J F, Johnson A G. Extrapolation of time-dependent waveforms along their path of propagation[J]. Geophysical Journal of the Royal Astronomical Society, 1971, 26(1-4): 285-293. |
| [2] |
Hampson D. Inverse velocity stacking for multiple elimination[J]. Journal of the Canadian Society of Exploration Geophysicists, 1986, 22(1): 44-45. |
| [3] |
Sacchi M D, Ulrych T. High resolution velocity ga-thers and offset space reconstruction[J]. Geophysics, 1995, 60(4): 1169-1177. DOI:10.1190/1.1443845 |
| [4] |
Sacchi M D, Porsani M J. Fast high resolution parabolic Radon transform[C]. SEG Technical Program Expanded Abstracts, 1999, 18: 1477-1480.
|
| [5] |
Herrmann P. De-aliased, high-resolution radon transforms[C]. SEG Technical Program Expanded Abstracts, 2000, 19: 1953-1956.
|
| [6] |
刘仕友, 马继涛, 孙万元, 等. 基于低频约束的高分辨率Radon变换多次波压制方法研究[J]. 物探化探计算技术, 2019, 41(3): 293-298. LIU Shiyou, MA Jitao, SUN Wanyuan, et al. Multiple attenuation using low frequency constrained high-resolution parabolic Radon transform[J]. Techniques for Geophysical and Geochemical Exploration, 2019, 41(3): 293-298. DOI:10.3969/j.issn.1001-1749.2019.03.02 |
| [7] |
刘喜武, 刘洪, 李幼铭. 高分辨率Radon变换方法及其在地震信号处理中的应用[J]. 地球物理学进展, 2004, 19(1): 8-15. LIU Xiwu, LIU Hong, LI Youming. High resolution Radon transform and its application in seismic signal processing[J]. Progress in Geophysics, 2004, 19(1): 8-15. DOI:10.3969/j.issn.1004-2903.2004.01.002 |
| [8] |
王维红, 裴江云, 张剑锋. 加权抛物Radon变换叠前地震数据重建[J]. 地球物理学报, 2007, 50(3): 851-859. WANG Weihong, PEI Jiangyun, ZHANG Jianfeng, et al. Prestack seismic data reconstruction using weighted parabolic Radon transform[J]. Chinese Journal of Geophysics, 2007, 50(3): 851-859. DOI:10.3321/j.issn:0001-5733.2007.03.026 |
| [9] |
薛亚茹, 唐欢欢, 陈小宏. 高阶高分辨率Radon变换地震数据重建方法[J]. 石油地球物理勘探, 2014, 49(1): 95-100. XUE Yaru, TANG Huanhuan, CHEN Xiaohong. Reconstruction method of seismic data using high-order high resolution Radon transform[J]. Oil Geophysical Prospecting, 2014, 49(1): 95-100. |
| [10] |
王亮亮, 毛伟建, 唐欢欢, 等. 快速3D抛物Radon变换地震数据保幅重建[J]. 地球物理学报, 2017, 60(7): 2801-2812. WANG Liangliang, MAO Weijian, TANG Huanhuan, et al. Amplitude preserved seismic data reconstruction by fast 3D parabolic Radon transform[J]. Chinese Journal of Geophysics, 2017, 60(7): 2801-2812. |
| [11] |
薛亚茹, 王敏, 陈小宏. 基于SL0的高分辨率Radon变换及数据重建[J]. 石油地球物理勘探, 2018, 53(1): 1-7. XUE Yaru, WANG Min, CHEN Xiaohong. High re-solution Radon transform based on SL0 and its application in data reconstruction[J]. Oil Geophysical Prospecting, 2018, 53(1): 1-7. |
| [12] |
Cary P W. The simplest discrete Radon transform[C]. SEG Technical Program Expanded Abstracts, 1998, 17: 1999-2002.
|
| [13] |
Schonewille M, Aaron P, Allen T. Applications of time-domain high-resolution Radon demultiple[C]. SEG Technical Program Expanded Abstracts, 2007, 26: 1-5.
|
| [14] |
巩向博, 韩立国, 李洪建. 各向异性Radon变换及其在多次波压制中的应用[J]. 地球物理学报, 2014, 57(9): 2928-2936. GONG Xiangbo, HAN Liguo, LI Hongjian. Anisotropic Radon transform and its application to demultiple[J]. Chinese Journal of Geophysics, 2014, 57(9): 2928-2936. |
| [15] |
Trad D, Ulrych T and Sacchi M. Latest views of the sparse Radon transform[J]. Geophysics, 2003, 68(10): 386-399. |
| [16] |
Lu W K. An accelerated sparse time-invariant Radon transform in the mixed frequency-time domain based on iterative 2D model shrinkage[J]. Geophysics, 2013, 78(4): V147-V155. DOI:10.1190/geo2012-0439.1 |
| [17] |
Wang B, Zhang Y, Lu W, et al. A robust and efficient sparse time-invariant Radon transform in the mixed time-frequency domain[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(10): 7558-7566. DOI:10.1109/TGRS.2019.2914086 |
| [18] |
巩向博, 韩立国, 王升超. 混合域高分辨率双曲Radon变换及其在多次波压制中的应用[J]. 石油物探, 2016, 55(5): 711-718. GONG Xiangbo, HAN Liguo, WANG Shengchao. High-resolution hyperbolic Radon transform and its application in multiple suppression[J]. Geophysical Prospecting for Petroleum, 2016, 55(5): 711-718. DOI:10.3969/j.issn.1000-1441.2016.05.010 |
| [19] |
Zhu L C, Liu E T, McClellan J H. Seismic data denoising through multiscale and sparsity-promoting dictionary learning[J]. Geophysics, 2015, 80(6): WD45-WD57. DOI:10.1190/geo2015-0047.1 |
| [20] |
Zhu L C, Liu E T, McClellan J H. Joint seismic data denoising and interpolation with double-sparsity dictionary learning[J]. Journal of Geophysics and Engineering, 2017, 14(4): 802-810. DOI:10.1088/1742-2140/aa6491 |
| [21] |
李慧, 韩立国, 张良, 等. Radon域下的K-SVD字典的混采分离[J]. 世界地质, 2019, 38(1): 256-267. LI Hui, HAN Liguo, ZHANG Liang, et al. Separation of blended seismic acquisition with K-SVD dictionary in Radon domain[J]. Global Geology, 2019, 38(1): 256-267. DOI:10.3969/j.issn.1004-5589.2019.01.025 |
| [22] |
兰南英, 张繁昌, 张益明, 等. 快速结构字典学习三维地震数据重建方法[J]. 石油地球物理勘探, 2020, 55(1): 1-9. LAN Nanying, ZHANG Fanchang, ZHANG Yiming, et al. 3D seismic data reconstruction based on a fast structure dictionary learning method[J]. Oil Geophy-sical Prospecting, 2020, 55(1): 1-9. |
| [23] |
王雄文, 王华忠. 基于压缩感知的高分辨率平面波分解方法研究[J]. 地球物理学报, 2014, 57(9): 2946-2960. WANG Xiongwen, WANG Huazhong. A research of high-resolution plane-wave decomposition based on compressed sensing[J]. Chinese Journal of Geophy-sics, 2014, 57(9): 2946-2960. |
| [24] |
Latif A, Mousa W A. An efficient undersampled high-resolution Radon transform for exploration seismic data processing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(2): 1010-1024. DOI:10.1109/TGRS.2016.2618848 |
| [25] |
魏亚杰, 张盼, 许卓. 基于稀疏约束反演的三维混采数据分离[J]. 地球物理学报, 2019, 62(10): 4000-4009. WEI Yajie, ZHANG Pan, XU Zhuo. Separation of 3D blending seismic data based on sparse constrained inversion[J]. Chinese Journal of Geophysics, 2019, 62(10): 4000-4009. DOI:10.6038/cjg2019M0501 |
| [26] |
赵子越, 李振春, 张敏. 利用压缩感知技术的离散正交S变换地震数据重建[J]. 石油地球物理勘探, 2020, 55(1): 29-35. ZHAO Ziyue, LI Zhenchun, ZHANG Min. Seismic data reconstruction using discrete orthonormal S-transform based on compressive sensing[J]. Oil Geo-physical Prospecting, 2020, 55(1): 29-35. |
| [27] |
Daubechies I, Defrise M, Mol C D. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J]. Communications on Pure and Applied Mathematics, 2010, 57(11): 1413-1457. |
| [28] |
Donoho D L. De-noising by soft thresholding[J]. IEEE Transactions on Information Theory, 2006, 41(3): 613-627. |
| [29] |
Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(1): 183-202. DOI:10.1137/080716542 |
| [30] |
潘树林, 闫柯, 李凌云, 等. 自适应步长FISTA算法稀疏脉冲反褶积[J]. 石油地球物理勘探, 2019, 54(4): 737-743. PAN Shulin, YAN Ke, LI Lingyun, et al. Sparse-spike deconvolution based on adaptive step FISTA algorithm[J]. Oil Geophysical Prospecting, 2019, 54(4): 737-743. |
| [31] |
Scales J A, Gersztenkorn A, Treitel S. Fast Lp solution of large, sparse, linear systems: Application to seismic travel time tomography[J]. Journal of Computational Physics, 1988, 75(2): 314-333. DOI:10.1016/0021-9991(88)90115-5 |
| [32] |
Chen Z H, Lu W K. Non-iterative high resolution Radon transform[C]. Extended Abstracts of 73rd EAGE Conference and Exhibition, 2011, 4803-4807.
|
| [33] |
Daubechies I, Devore R, Fornasier M, et al. Iteratively reweighted least squares minimization for sparse recovery[J]. Communications on Pure and Applied Mathematics, 2010, 63(1): 1-38. |



 郭蒙军, 北京市昌平区府学路18号中国石油大学(北京)信息科学与工程学院, 102249。Email:
郭蒙军, 北京市昌平区府学路18号中国石油大学(北京)信息科学与工程学院, 102249。Email: 