② 青岛海洋科学与技术试点国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266061;
③ 休斯顿大学地球与大气科学系, 得克萨斯休斯顿 77204;
④ 东方地球物理公司物探技术研究中心, 河北涿州 072751
② Laboratory for Marine Mineral Resources, Pilot National Laboratry for Marine Science and Tech-nologyc(Qingdao), Qingdao, Shandong 266061, China;
③ Department of Earth and Atmospheric Sciences, University of Houston, Houston 77204, America;
④ BGP R<D Center, CNPC, Zhouzhou, Hebei 072751, China
随着地震勘探逐渐发展,传统的海面拖缆地震采集方式已不能满足勘探需求。随着技术的进步,逐步提出了海底地震仪(Ocean Bottom Seismograph,OBS)、海底电缆(Ocean Bottom Cable,OBC)、海底节点(Ocean Bottom Node,OBN)等地震采集方式[1-5]。这些新技术的出现为海洋油气勘探带来了革命性的变化:地震勘探的深度可达莫霍面;由于接收器位于海底,地震资料的信噪比更高,能够获得高质量的多分量地震数据;采集方位角更宽,照明度更高等。
但是,对于海面激发、海底接收的OBN地震采集方式,接收设备需要部署在海底,由于复杂海洋环境的影响,检波点的位置可能发生偏离,需要使用一定的技术手段确定检波点的准确坐标,这一过程通常叫做二次定位[6-7]。为了解决二次定位的问题,发展了声波二次定位[8]和初至波二次定位[9]方法。前者利用专门的硬件,通过声波旅行时确定检波点位置;后者利用地震记录中的初至波旅行时进行二次定位。声波二次定位具有较高的精度,但是费用较高,因此初至波二次定位是目前应用较广的二次定位方法。
关于地震初至波二次定位,前人已经提出了多种方法,如正四面体法[10]、搜索法[11]、拟合曲面法[12]、混合定位法[13]、矢量合成法[14]、等效速度法[15-16]等。但大多数研究重点强调了各种方法的原理和实现过程,在实际资料的应用过程中如何进行质量监控以取得好的应用效果,却鲜有系统性研究[17-18]。等效速度法是最新提出的二次定位方法,它不仅能够进行三维海底检波点的定位,而且因考虑了地震波在海水中传播速度的影响,具有更高的定位精度。基于此,本文在等效速度法的基础上,研究了影响海底检波点二次定位质量的控制因素,如初至波旅行时拾取精度、观测系统、旅行时系统误差等。结果表明:直达波旅行时拾取精度对二次定位的精度具有至关重要的影响;把炮点和检波点分别投影到x轴、y轴和z轴,炮点相对于检波点的分布越均匀对称,则该方向定位精度就越高;较难发现旅行时系统性误差,但对z方向定位精度有较大影响。最终给出了做好OBN二次定位质量监控的方法与建议:首先,对初至旅行时进行筛选,保证用于二次定位的初至旅行时拾取质量;然后在计算过程中添加系统时移量这一未知数,用于计算可能存在的初至旅行时的系统时移,并尽可能选择相对于检波点均匀对称的炮点的初至时间参与计算;最后,通过对比二次定位前、后共检波点道集直达波双曲动校正后形态以及旅行时误差的空间分布、数理统计等,可以对二次定位质量进行监控。
1 二次定位影响因素分析 1.1 初至旅行时对二次定位精度的影响初至波旅行时是进行检波点二次定位的基础,因此在进行二次定位之前,需要先进行初至拾取。无论是人工拾取还是软件自动拾取,总会存在拾取不准的可能。典型的情况有:①初至拾取存在跳点,导致个别地震道拾取的初至旅行时与真实值相差较大;②在地震记录信噪比较低的区域,初至拾取质量较差。针对这两种情况,需要把相应的初至信息舍弃,消除其对二次定位结果的不利影响。
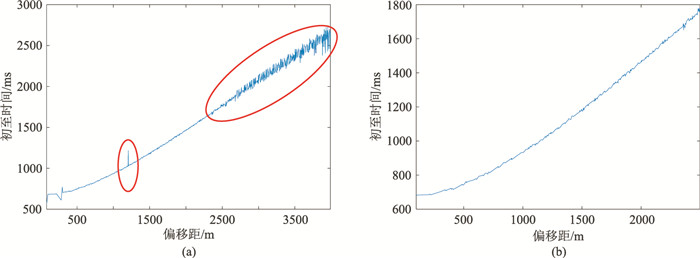
图 1为初至筛选前、后的旅行时曲线。对于检波点位于海底、炮点位于海面的观测系统,理想情况下,如果初至旅行时拾取准确且检波点坐标准确,初至时间随偏移距变化曲线应该是双曲线[19]。如果仅仅是检波点坐标不准,而初至拾取准确,则初至旅行时曲线大体形状仍是双曲线,只是稍有波动,这是检波点坐标不准导致偏移距不准造成的,且在整个偏移距范围内这种波动的幅度应该一致。图 1a中红色圆圈内初至拾取效果不好,与实际情况有较大差异,应予以剔除。剔除的原则有两种:①根据道头中的炮点和检波点坐标计算该道的直达波理论旅行时,并计算与实际拾取旅行时的差,如果误差绝对值小于一定数值,如100ms(可根据区域内检波点坐标误差调整,以免把正常初至信息剔除),则予以保留,如果误差绝对值超过该值,则予以剔除,这样可以去掉初至拾取中的个别跳点、0值、负值、99999等异常值,从而减小对定位精度的不利影响。②对于超过一定偏移距的初至进行剔除,比如超过3000m或3倍水深的初至信息,这样可以删除远偏移距低信噪比以及部分折射波初至信息。
|
图 1 筛选前(a)、后(b)初至曲线 |
表 1为初至旅行时筛选前、后定位结果的对比,该数据检波点初始坐标三个方向上都有一定的误差。直接用拾取的初至时间进行二次定位计算,得到的检波点坐标误差大,可见初至旅行时的准确性对定位精度至关重要。依据上述两个原则,把初至拾取误差较大的部分删除,重新进行二次定位计算,定位误差在2m以内,精度大大提高。
|
|
表 1 初至旅行时筛选前、后定位结果对比 |
由此可见,在初至拾取后需要进行异常点的甄别与删除,以确保定位精度。
1.2 炮点与检波点空间分布关系对OBN检波点二次定位精度的影响除了初至旅行时的准确性会对OBN检波点定位精度带来明显影响外,观测系统即炮点相对于检波点的分布关系也会对定位结果产生一定的影响。观测系统对定位结果的影响主要体现在抗旅行时误差的能力方面。对于一个检波点,观测角度越均匀、越对称,则抗旅行时误差的能力越强。
从地震数据中拾取的初至时间,总会或大或小存在一定噪声,这种噪声是指旅行时拾取的误差。旅行时误差产生的原因通常有:①地震数据存在一定的噪声,从而导致初至位置不明确,实际拾取的位置与真实位置存在一定偏差;②地震数据通常为离散数据,最终拾取旅行时的精度必定受到采样间隔的限制。
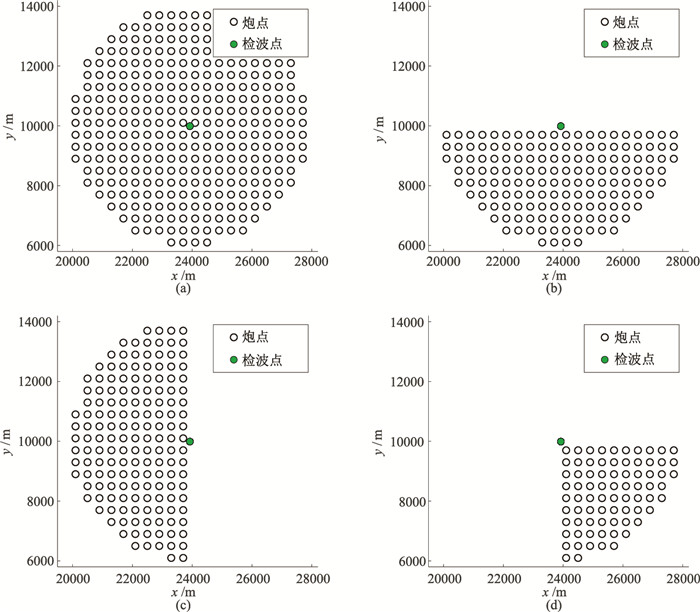
为阐述炮检点空间分布关系对二次定位精度的影响,建立如图 2a所示的观测系统,其中检波点的真实坐标为(23900.00m,10000.00m,1420.00m),在海面上4000m偏移距内以50m间隔进行放炮,声波在海水中的传播速度为1490m/s。用炮检点真实坐标以及声波在海水中的传播速度计算获得每炮的直达波旅行时,然后人为加入±8ms的随机误差,用图 2中4个观测系统数据分别进行二次定位,结果如表 2所示。其中检波点初始坐标为(23923.90m,9990.70m,1406.00m),海水速度的初始值为1500m/s。由表 2可以看出,图 2a观测系统的定位精度最高,图 2b观测系统的y坐标及图 2c观测系统的x坐标定位有较大误差,图 2d观测系统的x和y坐标定位误差都较大。可见观测方位角不均匀会对定位精度产生较大影响。
|
图 2 同一检波点不同炮点观测系统分布 (a)全方位均匀分布;(b)下半部分均匀分布;(c)左半部分均匀分布;(d)右下部分均匀分布 |
|
|
表 2 不同观测系统的定位精度对比 |
为此,建议在实际资料OBN共接收点二次定位时,选择方位角均匀分布的炮点信息参与反演,可以确保定位精度。
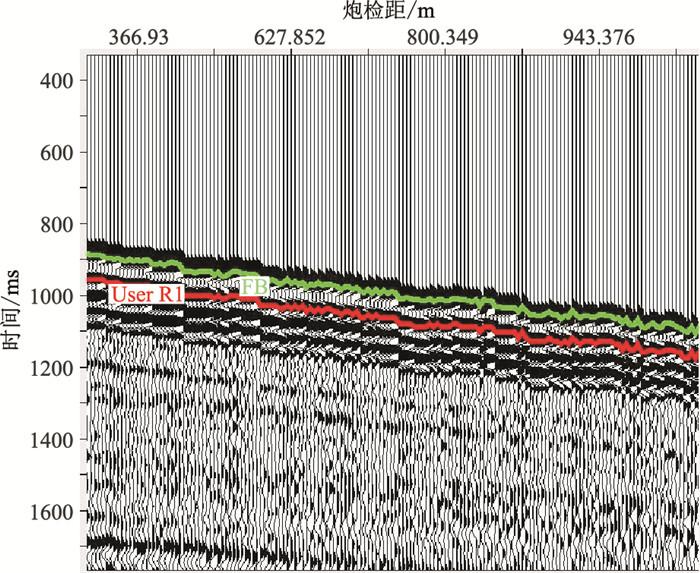
1.3 旅行时系统误差对二次定位精度的影响通常地震初至波拾取的是第一个起跳点的峰值位置,以此作为地震初至波的旅行时,这样做有一个前提,那就是地震子波为零相位子波,而实际地震子波通常是混合相位的,这就导致实际拾取的初至时间和真实的初至时间有一定的时差。此外,由于仪器系统的原因,也可能导致开始记录时间不为0时刻。但总体来讲,对于同一个工区同一套设备采集的地震数据,这种系统性误差是相对固定的。对于存在系统性误差的初至时间,需要对行整体时移处理后才能进行二次定位计算,否则将会影响二次定位的精度,尤其是深度方向的精度。图 3为OBN检波点二次定位的试验数据,虽然初至信噪比较高且拾取质量较好,但实际拾取的初至(绿线)与根据炮点和检波点实际坐标计算的真实初至(红线)存在一定的系统误差。
|
图 3 实际拾取旅行时(绿线)与计算的旅行时(红线)对比 |
旅行时系统误差的存在较为隐蔽,一般不容易从初至拾取环节检查出来,且对z方向的定位影响远大于x和y方向,这是炮点相对于检波点,因为在x和y方向一定范围内都有分布,而在z方向只有海平面这一位置有观测值,因此在z方向上定位的抗噪能力最弱。在进行二次定位时可以用以下方法甄别是否存在整体时移问题:首先删除初至拾取存在明显错误的部分,即首先保证用于二次定位计算的初至质量;然后在直达波范围内(一般和水深有关)选用不同偏移距之内的初至数据进行二次定位计算,分析计算结果。理论上,如果初至旅行时拾取准确且不存在整体时移,那么不同偏移距内旅行时数据计算得到的结果相差不大。如果结果当中x和y变化不大,而z值存在规律性变化,则需要进行整体时移。具体表现为:如果远偏移距得到的深度小,近偏移距得到的深度大,说明实际拾取的旅行时偏小,初至时间需要整体增加,反之则需要整体减小。
表 3为共检波点道集采用不同偏移距初至数据进行二次定位计算的结果,由表可以看出,随着偏移距的减小,二次定位结果在x和y方向变化不大(1m以内),在z方向却呈现递增趋势,且等效速度也呈现递增趋势,由此可以判断所拾取的初至旅行时比真实值偏小,旅行时需要进行整体时移处理。
|
|
表 3 旅行时存在系统性误差时选用不同偏移距初至数据定位结果对比 |
系统性误差的时移量可以在二次定位计算过程中求解,以减小人为给定造成的不确定性,具体实现方法如下。
假设对于同一个检波点,每一炮直达波旅行时都有一个固定的时移量Δt,根据已知的炮点位置、海水速度、直达波旅行时,可以得到以下方程组
| $ \left\{\begin{array}{c} \left(x-x_{1}\right)^{2}+\left(y-y_{1}\right)^{2}+\left(z-z_{1}\right)^{2}=v^{2}\left(t_{1}+\Delta t\right)^{2} \\ \left(x-x_{2}\right)^{2}+\left(y-y_{2}\right)^{2}+\left(z-z_{2}\right)^{2}=v^{2}\left(t_{2}+\Delta t\right)^{2} \\ \vdots \\ \left(x-x_{n}\right)^{2}+\left(y-y_{n}\right)^{2}+\left(z-z_{n}\right)^{2}=v^{2}\left(t_{n}+\Delta t\right)^{2} \end{array}\right. $ | (1) |
式中:(x,y,z)为检波点坐标;(xi,yi,zi)为第i炮的炮点坐标;ti为拾取的第i炮的直达波旅行时;n为炮点个数;v为海水等效速度。写成统一的形式,有
| $ \begin{aligned} &f_{i}\left(x_{i}, y_{i}, z_{i}, v, \Delta t\right)=\left(x-x_{i}\right)^{2}+\left(y-y_{i}\right)^{2}+ \\ &\quad\left(z-z_{i}\right)^{2}-v^{2}\left(t_{i}+\Delta t\right)^{2} \end{aligned} $ | (2) |
问题变为求目标函数fi(xi,yi,zi, v, Δt)的极小值。理想情况下,fi(xi,yi,zi, v, Δt)=0。该方程组是一个五元二次方程组,本文用牛顿法[20]求解。
对每个fi都在初值(x0,y0,z0, v0, Δt0)附近用Taylor级数展开,并取其线性部分,有
| $ \left\{\begin{array}{c} \frac{\partial f_{1}}{\partial x}\left(x-x_{0}\right)+\frac{\partial f_{1}}{\partial y}\left(y-y_{0}\right)+\frac{\partial f_{1}}{\partial z}\left(z-z_{0}\right)+ \\ \frac{\partial f_{1}}{\partial_{v}}\left(v-v_{0}\right)+\frac{\partial f_{1}}{\partial(\Delta t)}\left(\Delta t-\Delta t_{0}\right)=-f_{1, 0} \\ \frac{\partial f_{2}}{\partial x}\left(x-x_{0}\right)+\frac{\partial f_{2}}{\partial y}\left(y-y_{0}\right)+\frac{\partial f_{2}}{\partial z}\left(z-z_{0}\right)+ \\ \frac{\partial f_{2}}{\partial v}\left(v-v_{0}\right)+\frac{\partial f_{2}}{\partial(\Delta t)}\left(\Delta t-\Delta t_{0}\right)=-f_{2, 0} \\ \vdots \\ \frac{\partial f_{n}}{\partial x}\left(x-x_{0}\right)+\frac{\partial f_{n}}{\partial y}\left(y-y_{0}\right)+\frac{\partial f_{n}}{\partial z}\left(z-z_{0}\right)+ \\ \frac{\partial f_{n}}{\partial v}\left(v-v_{0}\right)+\frac{\partial f_{n}}{\partial(\Delta t)}\left(\Delta t-\Delta t_{0}\right)=-f_{n, 0} \end{array}\right. $ | (3) |
式中fi, 0为fi在(x0,y0,z0, v0, Δt0)处的取值。写成矩阵形式为
| $ \left(\begin{array}{c} \frac{\partial f_{1}}{\partial x} & \frac{\partial f_{1}}{\partial y} & \frac{\partial f_{1}}{\partial z} & \frac{\partial f_{1}}{\partial v} & \frac{\partial f_{1}}{\partial(\Delta t)} \\ \frac{\partial f_{2}}{\partial x} & \frac{\partial f_{2}}{\partial y} & \frac{\partial f_{2}}{\partial z} & \frac{\partial f_{2}}{\partial v} & \frac{\partial f_{2}}{\partial(\Delta t)} \\ {}&{}&{\vdots}&{}&{}\\ \frac{\partial f_{n}}{\partial x} & \frac{\partial f_{n}}{\partial y} & \frac{\partial f_{n}}{\partial z} & \frac{\partial f_{n}}{\partial v} & \frac{\partial f_{n}}{\partial(\Delta t)} \end{array}\right)\left(\begin{array}{c} x-x_{0} \\ y-y_{0} \\ z-z_{0} \\ v-v_{0} \\ \Delta t-\Delta t_{0} \end{array}\right)=\left(\begin{array}{c} -f_{1, 0} \\ -f_{2, 0} \\ \vdots \\ -f_{n, 0} \end{array}\right) $ | (4) |
其系数矩阵为Jacobi矩阵,各元素的取值为
| $ \left\{\begin{array}{l} \frac{\partial f_{i}}{\partial x}=2\left(x_{0}-x_{i}\right) \\ \frac{\partial f_{i}}{\partial y}=2\left(y_{0}-y_{i}\right) \\ \frac{\partial f_{i}}{\partial z}=2\left(z_{0}-z_{i}\right) \\ \frac{\partial f_{i}}{\partial v}=2\left(v_{0}-v_{i}\right) \\ \frac{\partial f_{i}}{\partial(\Delta t)}=2\left[(\Delta t)_{0}-(\Delta t)_{i}\right] \end{array}\right. $ | (5) |
式(4)为一个超定线性方程组,可用高斯消元法求解。
通过在二次定位计算过程中加入时移量这一变量,可求得系统性误差时移量。最终反演的时移量为+67ms,二次定位的结果误差在1m以内,与真实值非常接近(表 3)。
2 处理员质量监控除了上述在计算过程中进行二次定位的质量监控外,处理员还可以根据地震数据的其他特征评价结果的好坏,主要有两种方法。
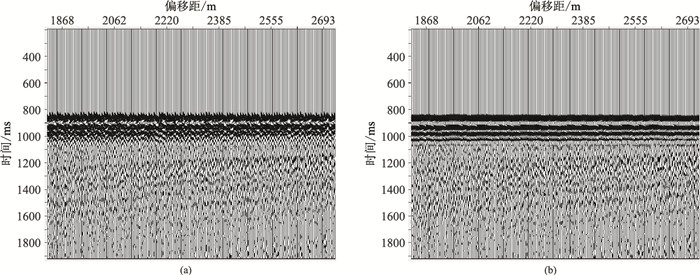
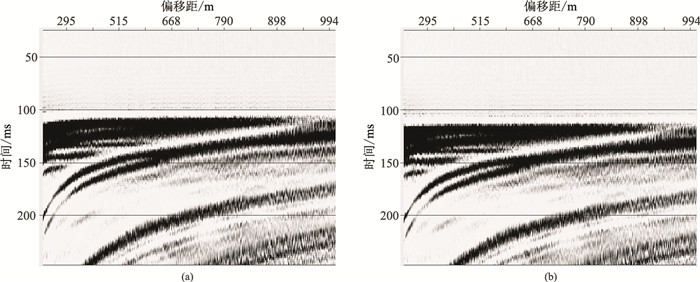
第一种方法是二次定位前、后分别对检波点道集进行双曲动校正,校正速度采用二次定位得到的等效速度进行。如果直达波的时距曲线形态变得更加趋近于水平,则表明二次定位后坐标更准。对于二次定位前坐标不准导致直达波不平的原因有两种:第一种是水平方向坐标有较大误差,此时根据偏移距排列的共检波点道集直达波呈现参差不齐的形状,如图 4a所示;第二种是水平方向误差不大,而垂直方向有一定的误差,此时主要表现为直达波的形态下拉或上翘,如图 5a所示。经过二次定位之后,同样会变得更加水平。
|
图 4 检波点横坐标不准时二次定位前(a)、后(b)的直达波形态(动校正后) |
|
图 5 检波点z坐标不准时二次定位前(a)、后(b)的直达波形态(动校正后) |
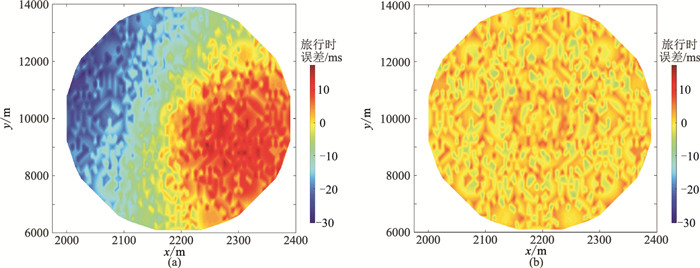
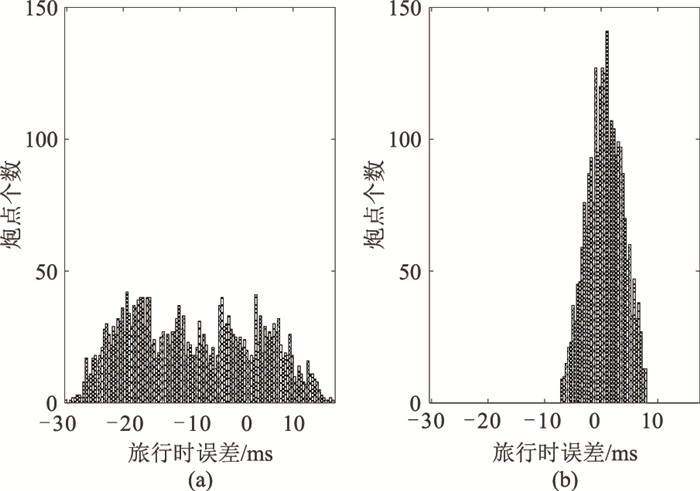
第二种方法是根据旅行时拟合情况评价二次定位结果。理论上,如果直达波旅行时拾取准确,且最终定位准确的话,炮点到检波点的理论直达波旅行时和实际拾取旅行时之差应该为0。图 6为二次定位前、后各炮点到检波点的旅行时误差。在二次定位之前的理论旅行时与拾取旅行时之差分布在-30.35~17.48ms之间,其空间上的分布存在一定规律:左侧偏上部分为负值,右侧偏下部分为正值,其他区域在两者之间渐变,可见当前x坐标值比真实值大,y坐标值偏小。二次定位之后二者之差在-6.99~7.93ms之间,且空间上呈随机分布。图 7为二次定位前、后旅行时误差统计,可见二次定位前旅行时误差分布范围较广,在-30.35~17.48ms之间;二次定位之后旅行时误差分布范围变窄,在0值附近,与理论情况更为接近。
|
图 6 二次定位前(a)、后(b)旅行时误差对比 |
|
图 7 二次定位前(a)、后(b)旅行时误差分布范围统计直方图 |
(1) 通过人工或自动删除初至旅行时拾取明显错误的部分信息,能够大大提高OBN检波点定位精度;
(2) 选择相对于OBN检波点均匀对称的炮点进行二次定位计算,能够一定程度上提高抗旅行时误差的能力,提高定位精度;
(3) 判断是否需要进行旅行时的整体时移,对于准确进行检波点深度方向的定位尤其重要;
(4) 通过对比二次定位前、后共检波点道集直达波双曲动校正后形态、旅行时误差的空间分布、数理统计等,可以方便处理人员对二次定位进行质量监控、结果评价,以确保二次定位的精度。
| [1] |
韩立强, 常稳. 海底电缆初至波二次定位技术的应用[J]. 石油物探, 2003, 42(4): 501-504. HAN Liqiang, CHANG Wen. Application of first break second positioning technique in OBC[J]. Geophysical Prospecting for Petroleum, 2003, 42(4): 501-504. DOI:10.3969/j.issn.1000-1441.2003.04.015 |
| [2] |
李丽青, 陈玺, 伍宗良, 等. 深水环境下OBS的二次定位技术[J]. 海洋地质前沿, 2013, 29(11): 54-61. LI Liqing, CHEN Xi, WU Zongliang, et al. Technique for relocating OBS in deep water environment[J]. Marine Geology Frontiers, 2013, 29(11): 54-61. |
| [3] |
敖威, 赵明辉, 丘学林, 等. 西南印度洋中脊三维地震探测中炮点与海底地震仪的位置校正[J]. 地球物理学报, 2010, 53(12): 2982-2991. AO Wei, ZHAO Minghui, QIU Xuelin, et al. The correction of shot and OBS position in the 3D seismic experiment of the SW Indian Ocean ridge[J]. Chinese Journal of Geophysics, 2010, 53(12): 2982-2991. DOI:10.3969/j.issn.0001-5733.2010.12.022 |
| [4] |
张莉, 赵明辉, 王建, 等. 南海中央次海盆OBS位置校正及三维地震探测新进展[J]. 地球科学——中国地质大学学报, 2013, 38(1): 33-42. ZHANG Li, ZHAO Minghui, WANG Jian, et al. Correction of OBS position and recent advanced of 3D seismic exploration in the Central Sub-Basin of South China Sea[J]. Earth Science: Journal of China University of Geosciences, 2013, 38(1): 33-42. |
| [5] |
刘斌. 海底地震仪重新定位: 以东沙群岛海域为例[J]. 热带海洋学报, 2015, 34(2): 66-70. LIU Bin. Ocean bottom seismometer relocation: Using Dongsha sea area as an example[J]. Journal of Tropical Oceanography, 2015, 34(2): 66-70. DOI:10.3969/j.issn.1009-5470.2015.02.008 |
| [6] |
葛晓丹. 浅海地震勘探海底电缆初至波二次定位方法研究[D]. 山东青岛: 中国海洋大学, 2015. GE Xiaodan. A Study on the Second Positioning Technique for the First Break in OBC Seismic Exploration of Shallow Sea[D]. Ocean University of China, Qingdao, Shandong, 2015. |
| [7] |
刘慧敏, 王振杰, 吴绍玉, 等. 顾及声线弯曲的浅海多目标水声定位算法[J]. 石油地球物理勘探, 2019, 54(1): 9-15. LIU Huimin, WANG Zhenjie, WU Shaoyu, et al. A positioning determination of multi-transponders with sound ray bending in shallow waters[J]. Oil Geophy-sical Prospecting, 2019, 54(1): 9-15. |
| [8] |
刘慧敏, 王振杰, 赵爽. 深度约束的浅海多目标声学定位方法[J]. 石油地球物理勘探, 2019, 54(6): 1181-1187. LIU Huimin, WANG Zhenjie, ZHAO Shuang. A depth-constraint multi-target positioning acoustic approach in shallow waters[J]. Oil Geophysical Prospecting, 2019, 54(6): 1181-1187. |
| [9] |
徐维秀. 浅水域检波点自动重定位技术[J]. 石油地球物理勘探, 2011, 46(1): 6-11. XU Weixiu. Automatic repositioning technique for shallow water receiver points[J]. Oil Geophysical Prospecting, 2011, 46(1): 6-11. |
| [10] |
杨正华, 张慧静. 海底电缆地震勘探中近正四面体法二次定位技术[J]. 石油地球物理勘探, 2013, 48(2): 163-170. YANG Zhenghua, ZHANG Huijing. An approximate tetrahedron method for the secondary positioning in OBC seismic survey[J]. Oil Geophysical Prospecting, 2013, 48(2): 163-170. |
| [11] |
倪成洲, 全海燕, 陈刚, 等. 一种高精度初至波二次定位新方法——搜索法[J]. 石油地球物理勘探, 2008, 43(2): 131-133. NI Chengzhou, QUAN Haiyan, CHEN Gang, et al. A new method for high-precision first break secondary positioning: Search method[J]. Oil Geophysical Prospecting, 2008, 43(2): 131-133. DOI:10.3321/j.issn:1000-7210.2008.02.002 |
| [12] |
肖永新, 杨海申, 蒋先艺, 等. OBC勘探中扫描拟合二次定位方法[J]. 石油地球物理勘探, 2012, 47(3): 366-370. XIAO Yongxin, YANG Haishen, JIANG Xianyi, et al. A secondary positioning method by grid scanning and curved-surface fitting in OBC survey[J]. Oil Geophysical Prospecting, 2012, 47(3): 366-370. |
| [13] |
马德堂, 赵会兵, 伍忠良. 基于直达波旅行时的OBS混合定位方法[J]. 石油地球物理勘探, 2013, 48(5): 677-681. MA Detang, ZHAO Huibing, WU Zhongliang. An OBS positioning mixed method based on travel-time of direct wave[J]. Oil Geophysical Prospecting, 2013, 48(5): 677-681. |
| [14] |
杨海申, 徐丽军, 马杰, 等. 矢量叠加初至波定位方法及精度评价[J]. 石油地球物理勘探, 2021, 56(1): 49-56. YANG Haishen, XU Lijun, MA Jie, et al. First-break positioning and accuracy evaluation based on vector superposition[J]. Oil Geophysical Prospecting, 2021, 56(1): 49-56. |
| [15] |
王忠成, 周华伟, 童思友, 等. 深水海底节点二次定位方法[J]. 石油地球物理勘探, 2020, 55(2): 242-247. WANG Zhongcheng, ZHOU Huawei, Tong Siyou, et al. Secondary positioning of deep ocean bottom nodes[J]. Oil Geophysical Prospecting, 2020, 55(2): 242-247. |
| [16] |
韩复兴, 孙建国, 王坤. 深海声道对波场传播的影响[J]. 石油地球物理勘探, 2014, 49(3): 444-450. HAN Fuxing, SUN Jianguo, WANG Kun. Deep sea channel influence on wave field energy propagation[J]. Oil Geophysical Prospecting, 2014, 49(3): 444-450. |
| [17] |
徐维秀, 段卫星, 刘治红, 等. 提高初至波二次定位精度技术的探讨[J]. 石油物探, 2009, 48(3): 239-243. XU Weixiu, DUAN Weixing, LIU Zhihong, et al. Discussion on the technology for improving the accuracy of secondary positioning with first break[J]. Geophysical Prospecting for Petroleum, 2009, 48(3): 239-243. |
| [18] |
易昌华, 任文静, 王钗. 二次水声定位系统误差分析[J]. 石油地球物理勘探, 2009, 44(2): 136-139. YI Changhua, REN Wenjing, WANG Chai. Analysis on error of secondary acoustic positioning system[J]. Oil Geophysical Prospecting, 2009, 44(2): 136-139. |
| [19] |
陆基孟. 地震勘探原理[M]. 山东东营: 石油大学出版社, 2009.
|
| [20] |
徐萃薇, 孙绳武. 计算方法引论[M]. 北京: 高等教育出版社, 2007.
|



 童思友, 山东省青岛市崂山区松岭路238号中国海洋大学海洋地球科学学院, 266100。Email:
童思友, 山东省青岛市崂山区松岭路238号中国海洋大学海洋地球科学学院, 266100。Email: 