② 东方地球物理公司研究院地质研究中心, 河北涿州 072751
② BGP Geological Research Center, BGP, CNPC, Zhuozhou, Hebei 072751, China
地震波阻抗反演以地震资料为基础,通过综合利用地质和测井资料从有限频宽的地震数据中恢复得到宽频带波阻抗数据,现已广泛应用于油气勘探阶段的储层定性、定量预测和油气开发阶段的井网部署、储量计算、油藏动态监测等方面[1-2]。由于实际地球物理问题十分复杂,人们对其认知通常又十分模糊,这使得在反演波阻抗时构建的模型大多是近似的。而深度学习算法可从大量已有数据中学习到隐含知识,从而使所构建数学模型更有利于对那些知识背景不清晰、模型欠精确的问题进行求解,因此该算法适用于波阻抗反演。
深度学习源于神经网络研究,此概念由Hinton等[3]率先提出。相比于提升方法、支持向量机、最大熵方法等通过人工抽取样本特征且只能学习到没有层次结构的单层特征的“浅层学习”方法而言,深度学习通过对输入样本逐层进行特征变换以学习得到数据的层次化特征表示[4-6]。深度学习模型的复杂度高,非线性层级数大,可实现对复杂函数的逼近,但通常复杂模型的训练效率低、易陷入过拟合。而随着云计算、大数据时代的到来,高性能计算集群有效地缓解了训练的低效性,海量训练数据降低了过拟合风险,促进了深度学习的研究与应用的逐步升温[7]。目前深度学习已广泛应用于计算机视觉[8]、图像处理[9]、语音识别[10]和自然语言处理[11]等领域,并给这些领域带来了巨大的变革。
神经网络技术在油气地球物理领域应用较早,印兴耀等[12-14]在上世纪90年代初就开展了基于神经网络的储层预测技术研究,并取得良好应用效果。近年来随着深度学习的兴起,国内外众多学者基于此开展了大量研究,如利用深度学习算法识别断层和盐体[15-17],进行地震相分类[18],提取弹性参数[19-20],进行储层预测等[21-22];在波阻抗反演方面,依据算法所采用的学习方式分为三类主要方法:基于监督学习的波阻抗反演[23]、基于无监督学习的波阻抗反演[24]和基于半监督学习的波阻抗反演[25-26]。
基于监督学习的波阻抗反演方法需耗费大量时间制作标签数据(通常来源于测井波阻抗数据)集,且标签数据的质量也会影响网络的反演精度。无监督学习波阻抗反演方法将物理模型与神经网络结合,在网络学习过程中引入正演模型。这种无监督学习方式减少了网络对标签数据的依赖,但同时因缺少真实标签数据的约束,故其反演精度通常低于监督学习地震反演方法。
半监督学习波阻抗反演方法结合监督学习反演方法与无监督学习反演方法的优势,同时使用大量无标签数据(指无对应测井数据的地震数据)和少量有标签数据(有对应测井数据的地震数据)对网络模型进行训练。训练时将地震数据输入网络模型,得到估计的波阻抗;将该波阻抗再输入到正演模型,得到合成记录;通过对比合成记录与输入记录、标签数据与网络估计的波阻抗数据计算损失函数优化网络模型。因此,半监督学习反演方法既减少了训练时获取大量波阻抗的难度,又将井中波阻抗作为标签约束网络反演,保证了反演精度。但此类方法仍存在一些问题:①在构造复杂区,数据特征也十分复杂,在训练网络模型时,为了更精确地表征地震数据与波阻抗数据之间的映射关系,可能会丢失较多局部特征,使网络反演结果丧失一些细节信息。尽管可通过增加网络深度或延长训练周期以便于网络学习这些局部特征,但由于数据量限制,很容易陷入过拟合。②由于地震数据采集设备的限制及处理过程中的低频损失,获取的地震数据通常缺少低频成分,由于深度学习的基础是数据,若仅据带限地震数据对网络模型进行训练,则网络所预测的波阻抗也会缺少低频成分。而低频成分蕴含地质构造的基本信息,缺失该成分在一定程度上会降低基于波阻抗反演结果开展储层预测的精度。③受现场环境及采集条件影响,所采集原始数据通常包含大量噪声,尽管可在处理阶段降噪,但这样也会损害其中的有效信息,如何提高网络模型对含噪地震数据的反演精度,也是亟待解决的问题之一。
为此,本文提出基于先验约束的深度学习波阻抗反演方法,即根据待反演区地震相类型对其进行区域划分,并为每个区域生成相应子网络,使每个子网络仅用于对应区域反演任务;将初始模型用作一类特殊标签以丰富反演结果的低频信息、提高反演结果横向连续性;在模型中引入具有生物真实性的强抗噪神经元激活函数Rand Softplus[27]以提高其抗噪性能。最后将上述方法针对Marmousi 2模型进行测试,并将其成功地应用于M油田的实际地震数据的反演。
1 方法原理 1.1 反演流程反演的具体流程主要包括五个方面。
(1) 区域分割:将已取得的地震相分类结果作为最初的区域分割结果,为保证每个分割区域内具有较充足数据量并存在一定数量的井数据,合并相邻的内部反射结构类似且面积较小的区域。
(2) 数据预处理:首先对地震数据与测井数据进行标准化处理,再进行井震标定,构建时深关系,然后根据每个区域内的测井数据与地震数据为每个区域提取区域子波并构建区域子波集,最后根据测井数据与构造解释结果构建初始模型。
(3) 训练反演模块:反演模块由一系列网络模型构成,这些网络模型是根据区域分割结果自动生成的,每个网络模型唯一对应一个分割区域。网络模型的输入是地震数据,输出是波阻抗数据,训练时使用与网络模型对应分割区域内的训练数据,并采取半监督学习方式训练这些网络模型。
(4) 波阻抗反演:将地震数据依据区域分割结果输入到反演模块的对应网络模型中,再合并反演模块中所有网络模型预测的波阻抗以获得最终反演结果,最后对反演结果进行反标准化处理。
(5) 评价反演结果:利用均方误差、相关系数和确定系数三项指标定量地评价反演结果。
1.2 网络模型循环神经网络(RNN)具有一个隐藏状态向量,可在序列数据之间传递,使其能捕获序列数据中的长距离依赖关系。而卷积神经网络(CNN)使用固定大小的卷积核并通过滑动窗口方式对输入数据进行处理,故在局部特征提取方面有较大优势。本文充分考虑了二者的优势而构建了深度学习网络模型框架(图 1),包含全局特征提取层、局部特征提取层和回归层三个主要部分。
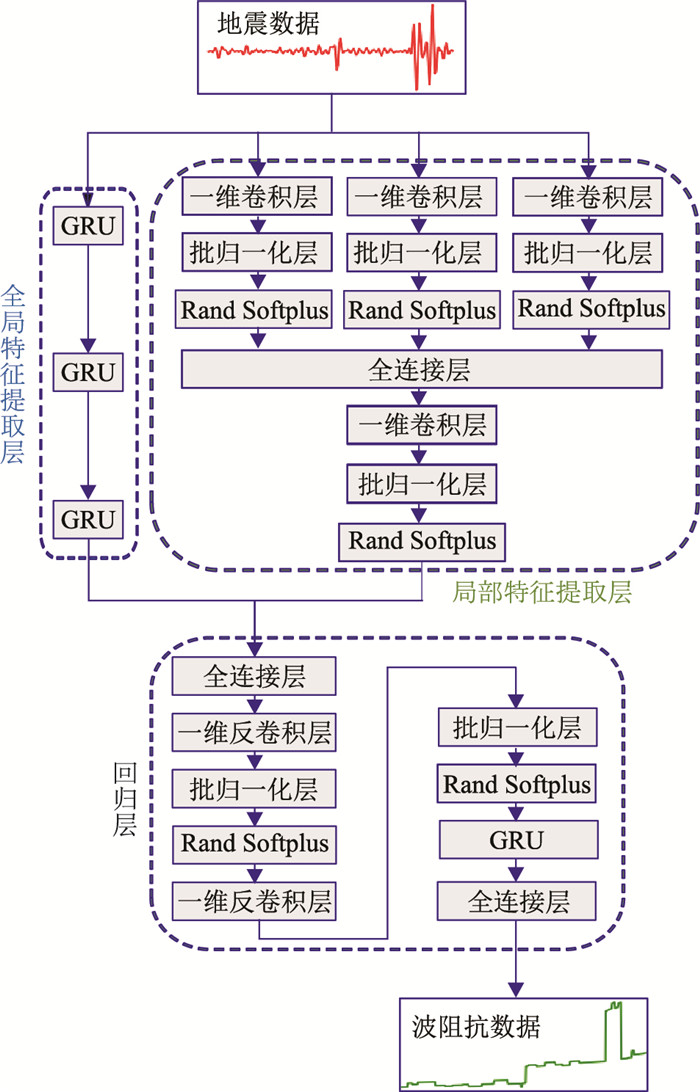
|
图 1 深度学习网络模型框架 |
全局特征提取层的功能是提取输入地震数据中长时间依赖关系,即全局特征,由一系列GRU (Gate recurrent unit)[28]构成。GRU是RNN的一种,用于处理长期记忆与反向传播时梯度消失的问题,它使用重置门和更新门控制信息流动。
在图 2所示结构中,前向传播过程可表示为
| $ \left\{\begin{array}{l} u_{t}=\operatorname{sigmoid}\left(W_{x u} x_{t}+W_{h u} h_{t-1}+b_{u}\right) \\ r_{t}=\operatorname{sigmoid}\left(W_{x r} x_{t}+W_{h r} h_{t-1}+b_{r}\right) \\ \tilde{h}_{t}=\tanh \left[W_{x h} x_{t}+W_{h h}\left(r_{t} \odot h_{t-1}\right)+b_{h}\right] \\ h_{t}=u_{t} h_{t-1}+\left(1-u_{t}\right) \odot \tilde{h}_{t} \end{array}\right. $ | (1) |
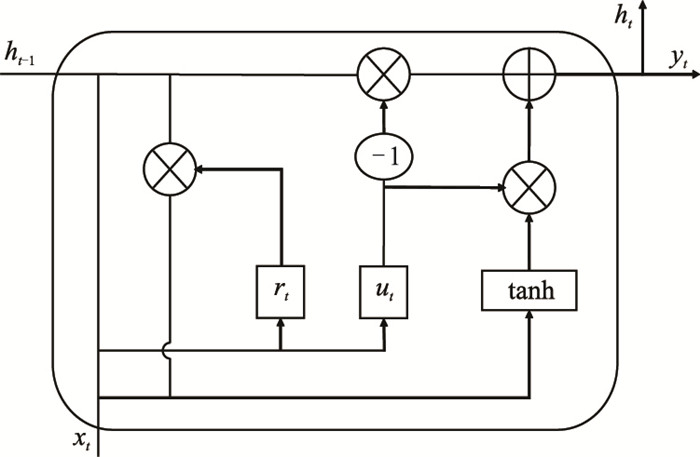
|
图 2 GRU结构示意图 |
式中:rt、ut分别为重置门和更新门的门控信号,rt门控信号用于控制是否忽略之前的隐藏状态,而ut用于控制隐藏状态变量的更新;xt、yt、ht、ht-1分别为当前时刻的输入、输出、状态变量及前一时刻状态变量;W和b分别是权值矩阵和偏置向量。
1.2.2 局部特征提取层局部特征提取层的功能是提取输入地震数据的局部特征。由于卷积层中的膨胀系数(dilation)可控制卷积核的感受野大小,所以首先利用一组膨胀系数不同的并行卷积块提取地震数据中不同尺度的局部特征,再使用一个全连接层和一个卷积块组合局部特征。这里的卷积块由一维卷积层(Conv1d)、批归一化层(Batch normalization)[29]和Rand Softplus激活函数组成。
卷积层由包含多个神经元的特征面组成,每个神经元通过卷积核与前一层特征面局部区域相连以提取输入特征[30]。卷积层的前向传播过程表示为
| $ \boldsymbol{y}_{l}=\boldsymbol{y}_{l-1} * \mathrm{~W}_{1}+\boldsymbol{b}_{1} $ | (2) |
式中:yl-1、yl分别为第l-1、第l层输出;Wl、bl是第l层卷积核和偏置向量;“*”是卷积运算符。
批归一化层用于处理中间层数据分布变化问题,加速网络的收敛速度。其定义为
| $ y=\frac{\lambda(x-\mu)}{\sqrt{\sigma^{2}+\varepsilon}}+\psi $ | (3) |
式中:μ、σ分别为输入数据的均值和标准差;ε是常量,用于保证分式中的分母不为0;λ、ψ均为可学习参数。
激活函数是网络模型的重要组成部分,是网络非线性的来源,使网络能逼近高度非线性函数。常用的激活函数有Tanh、Relu、Softplus等。由于这些激活函数只是对生物神经元输出相应特性的高度简化与模拟,使用这些激活函数的网络模型在抗噪性、不确定性信息处理及功耗等方面与人脑仍存在巨大差距。Rand Softplus激活函数通过引入反映生物神经元随机性的参数,将Relu与Softplus函数有机结合,使其具有强抗噪能力,定义为
| $ f(x)=(1-\eta) \max (0, x)+\eta \ln \left(1+\mathrm{e}^{x}\right) $ | (4) |
式中:x为神经元输入值;η为生物神经元随机性参数,其值与输入数据的噪声水平有关,详细的计算步骤[27]如下。
(1) 计算神经网络输入数据所含噪声标准差
| $ \sigma_{j}=\sqrt{\sum\limits_{i} \frac{1}{2} W_{i j}^{2} x_{i}} $ | (5) |
(2) 调整噪声标准差:由于同一层内部分标准差远大于该层均值,为避免归一化操作导致其分布不均匀,将大于2倍均值的标准差设定为2倍均值。
(3) 噪声标准差归一化处理:随着网络深度增加噪声标准差呈逐渐减小趋势,为此对噪声标准差做归一化处理,从而得到参数η。
(4) η置零操作:为控制网络的稀疏性,设置比例系数阈值ηth,将η中小于ηth的部分置为0。
1.2.3 回归层回归层的功能是将数据从特征域映射到目标域,即首先使用一个全连接层来组合全局特征提取层和局部特征提取层所提取的特征。由于在特征提取时改变了输入数据尺寸,所以再使用一组串行反卷积块对合并后特征进行上采样,使其具有与标签数据相同的采样率;再使用一个GRU和一个全连接层将上采样后数据从特征域映射到目标域。其中反卷积块由反卷积层、批归一化层和Rand Softplus激活函数组成。反卷积层与卷积层思路类似,仅是运算不同,可将其理解为卷积层的逆过程,其前向传播过程与卷积层的反向传播过程相同,反向传播过程与卷积层的前向传播过程相同[31]。
1.3 反演框架本文采用半监督学习方式,并构建图 3所示的基于先验信息约束的半监督学习反演框架。
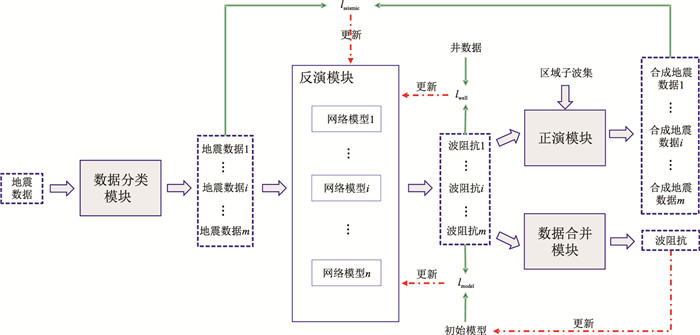
|
图 3 本文方法反演框架 |
该反演框架由数据分类、反演、正演和数据合并等四个主要模块组成。数据分类模块的功能是将输入地震数据按区域分割结果进行分类。为消除分块训练后的拼接痕迹,在对区域边界处数据进行分类时,对数据向上、向下延拓半个子波长度;当可延拓长度小于半个子波长度时,延拓至整个二维剖面边界处;最后将分类后数据依次输入到反演模块的相应网络模型中。反演模块由n个网络模型组成,每个网络模型(图 1)对应一个分割区域,网络模型的输入是地震数据,输出是波阻抗,训练时使用相同分割区域内的训练数据训练相应网络模型。数据合并模块的功能是根据区域分割结果将各分割区域内的波阻抗数据或地震数据进行合并,从而得到与输入地震数据对应的波阻抗数据或合成地震数据。正演模块的功能是将波阻抗进行正演,从而得到合成地震记录。即首先根据
| $ R(t)=\frac{I_{\mathrm{P}}(t+\Delta t)-I_{\mathrm{P}}(t)}{I_{\mathrm{P}}(t+\Delta t)+I_{\mathrm{P}}(t)} $ | (6) |
将输入的波阻抗转换为反射系数;然后从区域子波集中选取与输入波阻抗数据属同一分割区域的区域子波;最后将反射系数与区域子波进行褶积,得到合成地震记录。式中IP为纵波阻抗序列。
训练时,反演模块中各个网络模型内部可学习参数的优化受以下三个过程的综合影响:
(1) 无标签地震数据输入到数据分类模块后,地震数据按所属区域类别输入到反演模块的相应网络模型中,得到多组预测波阻抗数据,这些波阻抗数据经过正演模块后又得到多组合成地震数据,通过计算合成地震数据与分类后输入地震数据之间的均方误差(lseismic),更新反演模块中相应网络模型内部参数。
(2) 将井旁道地震数据输入数据分类模块进行分类,同样将分类后地震数据按类别输入到反演模块的相应网络模型中,得到多组预测波阻抗数据,通过计算这些预测波阻抗数据与相应井段之间的均方误差(lwell),更新反演模块中相应网络模型内部参数。
(3) 将所有地震数据输入到数据分类模块中进行分类,再按类别将地震数据输入到反演模块的相应网络模型中,得到多组预测波阻抗数据,计算这些预测波阻抗与对应初始模型数据之间的均方误差(lmodel),从而更新反演模块中相应网络模型内部参数。
在训练初期,初始模型可使网络快速收敛到某一局部低值,但由于初始模型与地下真实波阻抗存在一定差距,若在训练后期仍将其作为标签对网络进行训练,则会使反演模块的预测结果过度模型化,因此应随着训练的进行对初始模型进行更新。本次采取每隔一定训练周期将反演模块预测的多组波阻抗输入到数据合并模块中进行合并,再用合并后波阻抗数据更新初始模型。
综上,构建如下损失函数
| $ l=\left\{\begin{array}{l} \alpha \mathrm{L}\left(s_{1}, \widetilde{s_{1}}\right)+\beta \mathrm{L}\left(p_{1}, \widetilde{p_{1}}\right)+\gamma \mathrm{L}\left(m_{1}, \widetilde{m_{1}}\right) \\ \alpha \mathrm{L}\left(s_{2}, \widetilde{s_{2}}\right)+\beta \mathrm{L}\left(p_{2}, \widetilde{p_{2}}\right)+\gamma \mathrm{L}\left(m_{2}, \widetilde{m_{2}}\right) \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots \\ \alpha \mathrm{L}\left(s_{i}, \widetilde{s}_{i}\right)+\beta \mathrm{L}\left(p_{i}, \widetilde{p_{i}}\right)+\gamma \mathrm{L}\left(m_{i}, \widetilde{m_{i}}\right) \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots \\ \alpha \mathrm{L}\left(s_{n}, \widetilde{s_{n}}\right)+\beta \mathrm{L}\left(p_{n}, \widetilde{p_{n}}\right)+\gamma \mathrm{L}\left(m_{n}, \widetilde{m_{n}}\right) \end{array}\right. $ | (7) |
即通过最小化式(7)来优化反演模块中各网络模型内部参数。式中:si、
| $ \mathrm{L}(a, \tilde{a})=\frac{1}{N} \sum\limits_{i=1}^{N}\left(a_{i}-\widetilde{a}_{i}\right)^{2} $ | (8) |
式中a和
反演模块中网络模型优化完成后,便可利用上述反演框架开展波阻抗反演,其具体过程是:将待反演地震数据输入到数据分类模块进行分类,即将地震数据按类别输入到反演模块的相应网络模型中;通过反演模块得到一组预测波阻抗数据;再将这组预测波阻抗输入到数据合并模块,得到反演结果;最后再对该反演结果进行定量评价。
1.4 反演结果的评价反演模块经训练后,地震数据通过数据分类、反演、合并模块可得到预测波阻抗数据,地震数据通过数据分类、反演、正演、合并模块可得到合成地震数据。通过计算真实波阻抗与预测波阻抗、输入地震数据与合成地震数据的均方误差(MSE)、相关系数(PCC)和确定系数(R2),定量评价反演结果。
(1) MSE是预测数据与真实数据对应点误差的平方和,其值越小说明预测数据与原始数据拟合越好,其定义如式(8)所示。
(2) PCC表征变量之间相关程度,值域为[-1, 1],取值为正、负时分别表示两变量正、负相关,取值为0时表示不相关。定义μa、
| $ \operatorname{PCC}(a, \widetilde{a})=\frac{1}{N} \frac{\sum\limits_{i=1}^{N}\left(a_{i}-\mu_{a}\right)\left(\widetilde{a}_{i}-\mu_{\tilde{a}}\right)}{\sqrt{\sum\limits_{i=1}^{N}\left(a_{i}-\mu_{a}\right)^{2}} \sqrt{\sum\limits_{i=1}^{N}\left(\tilde{a}_{i}-\mu_{\tilde{a}}\right)^{2}}} $ | (9) |
(3) R2用于评价变量之间的拟合优度,值域为[0, 1],其值越大,表明变量之间拟合优度越大,自变量对因变量的解释程度越高,自变量引起的变动占总变动的百分比越高。其定义为
| $ R^{2}(a, \widetilde{a})=1-\frac{\sum\limits_{i=1}^{N}\left(a_{i}-\tilde{a}_{i}\right)^{2}}{\sum\limits_{i=1}^{N}\left(a_{i}-\mu_{a}\right)^{2}} $ | (10) |
选取Marmousi 2模型(图 4a),生成波阻抗数据(图 4b),再根据下式对波阻抗数据做标准化处理
| $ y=\frac{x-\mu}{\sigma} $ | (11) |
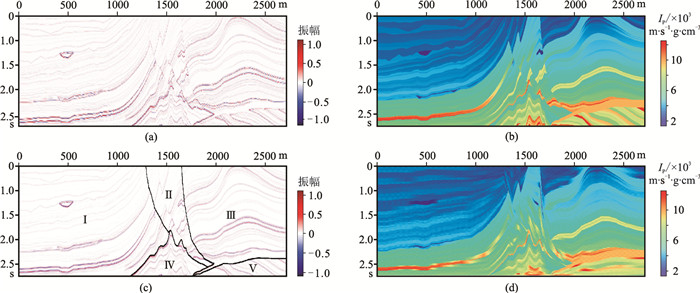
|
图 4 Marmousi2模型数据 (a)零炮检距地震数据;(b)波阻抗数据;(c)区域分割结果;(d)初始模型 |
式中x是任意输入数据。将标准化后的波阻抗数据与主频为30Hz的Ricker子波输入到正演模块,得到相应的正演地震数据;再对该地震数据进行滤波,使其缺失5Hz以下频带(图 4a)。将地震相划分结果作为区域分割结果的初值,对相邻的内部反射结构类似且面积较小的区域进行合并,如将剖面左侧的透镜体与周围区域进行合并(图 4c区域Ⅰ)、将剖面中部的两个断层结构进行合并(图 4c区域Ⅱ),得到最终的区域分割结果(图 4c)。均匀地抽取20道的波阻抗作为伪井数据。然后进行层位解释及断层解释,据此将二维剖面分割为多个区块。针对具有测井数据的区块,将测井数据在该区块内进行内插外推;而对于无测井数据的区块,则根据相邻区块内的数据对该区块做插值或延伸,生成图 4d所示的初始模型。
使用地震数据、伪井、初始模型和子波训练反演模块中的网络模型,训练时将迭代周期设置为1000,每个迭代周期的批训练量为50,损失函数中的α、β、γ分别设置为1.0、1.0、0.1,训练时每隔50个迭代周期更新一次初始模型。随后用训练好的反演模块进行波阻抗反演(图 5a,设定为Result1)。
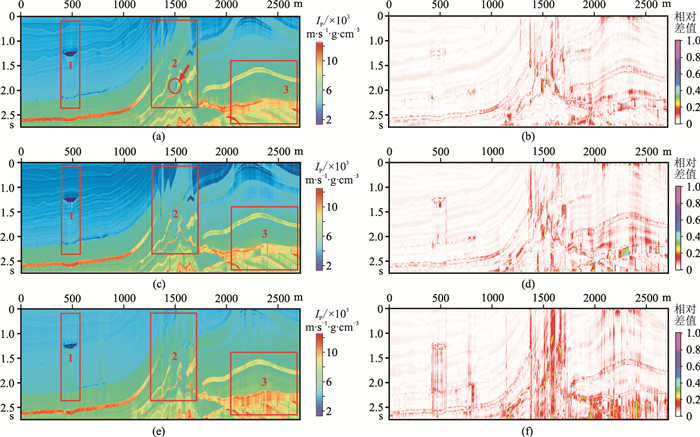
|
图 5 不同先验信息约束条件下的反演结果(左)及其与真实波阻抗的相对差值(右) (a)、(b)α=1.0、β=1.0、γ=0.1,区域分割约束+初始模型约束;(c)、(d)α=1.0、β=1.0、γ=0,初始模型约束;(e)、(f)α=1.0、β=1.0、γ=0,无约束 |
基于上述反演框架,首先测试无初始模型约束条件下反演效果,即将γ设置为0,得到了图 5c所示反演结果(设定为Result2);然后测试无初始模型和区域分割结果约束条件下的反演效果,即将γ设置为0且不进行区域分割(认为整个地震剖面属于同一区域),得到图 5e所示反演结果(设定为Result3)。表 1显示不同先验约束条件下网络在训练阶段与预测阶段的计算时长(Intel i7 9700、Nvidia GeForce GTX 1050Ti),发现引入各种先验信息约束后,网络的计算时间仍保持在可接受范围内。
|
|
表 1 不同先验约束下网络的训练和预测阶段运行时长 |
为了更直观地对比不同先验约束条件下的反演效果,根据
| $ I_{P, \text { dif }}=\frac{\left|I_{\mathrm{P}, \text { est }}-I_{\mathrm{P}, \text { true }}\right|}{\max \left(\left|I_{\mathrm{P}, \mathrm{est}}-I_{\mathrm{P}, \text { true }}\right|\right)} $ | (12) |
分别计算Result1、Result2与Result3与真实波阻抗的相对差值,结果如图 5b、图 5d和图 5f所示。
由于事先已知模型的波阻抗,可通过计算Result1、Result2和Result3与真实波阻抗的MSE、PCC和R2平均值定量评价不同约束条件下网络模型的反演效果。表 2、表 3和表 4分别为Result1、Result2和Result3与真实波阻抗在整个剖面上以及在图 5中红色矩形1、2、3标示区域的MSE、PCC和R2平均值。
|
|
表 2 Result1的定量评价 |
|
|
表 3 Result2的定量评价 |
|
|
表 4 Result3的定量评价 |
分析、对比图 5中不同先验约束条件下的反演结果及表 2~表 4中定量评价结果,可直观地发现,充分利用初始模型和区域分割结果等先验信息能较大程度上消除反演结果中纵向抖动现象,提高反演结果的横向连续性;且在一些构造复杂部位,这种效果改善更明显。如图 5a、图 5c和图 5e中红色矩形1、2、3标示区域,这主要是由于该区域地下构造较复杂,存在构造突变和断层,此时初始模型和区域分割结果向网络提供基本构造信息,并对网络预测结果做出明确的空间约束。而且反演模块中每个网络模型只负责构造形态相似区域的反演,使这些网络模型能从训练数据中捕捉更多局部特征,在使用训练好的网络模型进行反演时,其反演结果的细节信息也会更丰富,即反演精度更高。
但在图 5a中红色箭头所指区域的反演效果却出现了退化,这主要是由于在进行区域分割时该处(图 4cⅠ区域)纵向长度较短,由于地震数据的自相关性,当将该处地震数据输入到网络模型时,网络易将该处地震数据与其他某些道集数据相混淆,所以呈现反演精度降低的现象。
2.2 含噪声条件下的波阻抗反演为测试网络模型对噪声数据的适应能力,向原地震数据中分别加入4%、8%、12%的高斯随机噪声,然后在网络模型中分别使用Rand Softplus和Tanh激活函数对含噪地震数据进行反演。图 6显示0、4%、8%和12%含噪条件下使用Rand Softplus和Tanh两种激活函数的反演结果。图 7为上述反演结果与真实波阻抗的相对差值。表 5和表 6归纳在上述噪声条件下所得反演结果的定量评价。
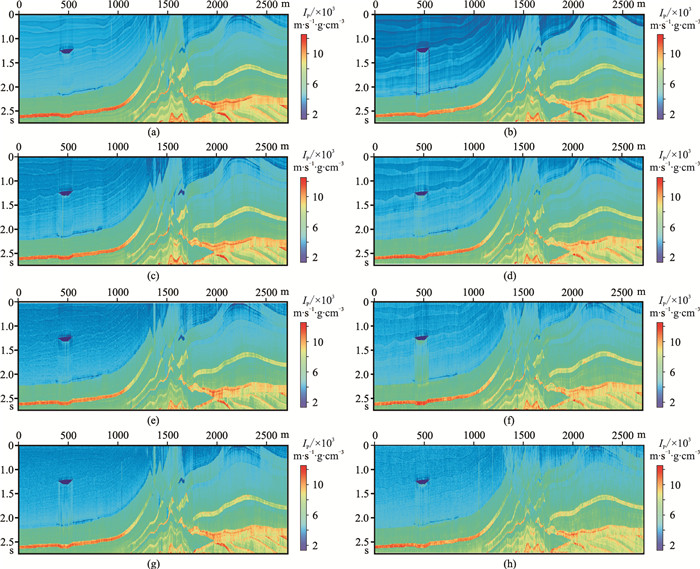
|
图 6 不同噪声条件下使用Rand Softplus(左)和Tanh(右)激活函数的网络模型的反演结果 (a)、(b)α=1.0、β=1.0、γ=0.1,不含噪;(c)、(d)α=0.8、β=1.0、γ=0.1,含噪4%;(e)、(f)α=0.6、β=1.0、γ=0.1,含噪8%;(g)、(h)α=0.4、β=1.0、γ=0.1,含噪12% |
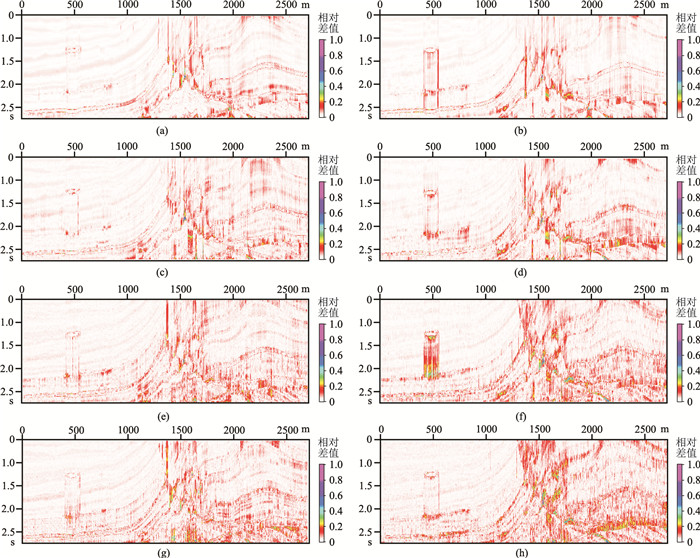
|
图 7 图 6所得反演结果与真实波阻抗的相对差值 (a)、(b)α=1.0、β=1.0、γ=0.1,不含噪;(c)、(d)α=0.8、β=1.0、γ=0.1,含噪4%;(e)、(f)α=0.6、β=1.0、γ=0.1,含噪8%;(g)、(h)α=0.4、β=1.0、γ=0.1,含噪12% |
|
|
表 5 基于Rand Softplus激活函数的反演结果定量评价 |
|
|
表 6 基于Tanh激活函数的反演结果定量评价 |
从图 6、图 7对应的反演结果及相对差值可直观地看出,在相同噪声条件下,相比于Tanh激活函数,使用Rand Softplus激活函数的网络模型具有较好反演效果。结合表 5、表 6中的定量评价结果还可发现,在低噪声条件(0、4%)下,相比于Tanh激活函数,Rand Softplus激活函数对网络模型的反演精度提升的幅度并不大,MSE分别减少了0.29%、0.19%,PCC分别提高了0.08%、0.24%,
将本文反演方法应用于M油田实际三维地震数据。所选测线(图 8)穿过3口井(W1、W2、W3),包含427个CDP,纵向时间长度为378ms、采样间隔为2ms。区内Hor3界面(红线)的上部与下部地震数据的反射结构有较大差异,下部振幅强度大、连续性好、内部反射结构有序;而上部振幅强度小、连续性差、内部反射结构相对杂乱,因此以Hor3为分界线将该剖面分为上、下两个区域。本次将W1和W3设定为训练井,W2作为测试井,训练井用作网络标签,而测试井不参与子波提取、初始模型构建与反演模块的训练。
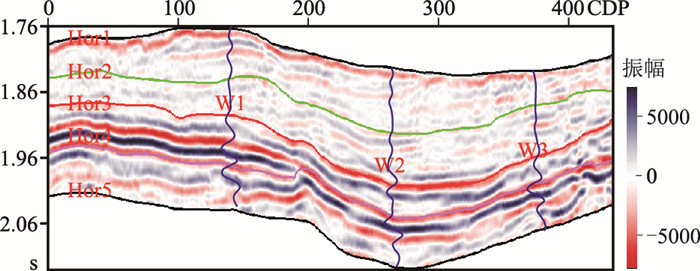
|
图 8 地震数据、测井数据与地震层位解释结果 |
首先对数据进行预处理。
(1) 据式(11)对井数据、地震数据做标准化处理。
(2) 井震标定,构建时深关系;再从井旁地震道分别提取Hor3层上、下相邻区域的子波(图 9)。
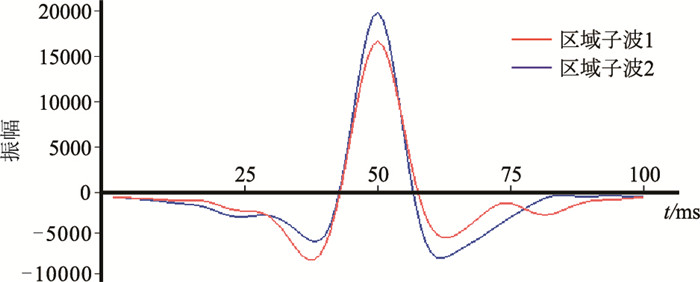
|
图 9 Hor3层上、下相邻区域的子波 |
(3) 当标签数据与输入地震数据的频谱范围差异较大时,不利于网络快速收敛,还会降低网络预测精度[33],因此需滤去测井数据中的高频成分。
(4) 根据地震层位解释结果,并综合利用测井数据,构建初始模型(图 10)。
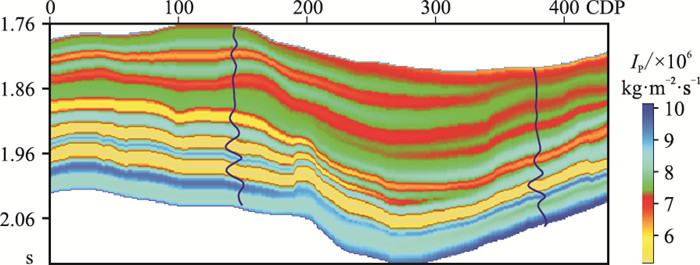
|
图 10 本文方法构建的初始模型 |
然后用区域子波、井数据、地震数据与初始模型训练反演模块中的网络模型,训练周期为500,每个周期的批训练量为20,损失函数中的α、β、γ分别设定为0.2、1.0、0.1,训练时每隔30个周期更新一次初始模型。
最后,用训练好的反演模块对地震数据做反演。将反演结果(图 11a)输入正演模型中,得到合成地震记录(图 11c),并进而求得输入地震记录与合成地震记录间的相对差值(图 11d)及其量化评价指标MSE、PCC和
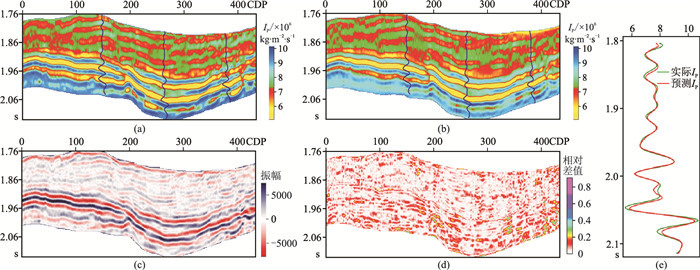
|
图 11 本文方法在实际数据中的应用 (a)基于先验约束的深度学习地震反演结果;(b)基于稀疏脉冲反演结果;(c)合成地震记录;(d)合成地震记录与输入地震记录的相对差值;(e)验证井处的反演结果与验证井的波阻抗 |
从上述反演结果可知,本文反演方法不仅在训练数据集中有标记数据上具有较好反演效果,且在无标记数据上仍能取得较高反演精度。合成地震记录与输入地震记录的对比结果(图 11d)充分证明了本文方法反演结果的合理性与准确性;与稀疏脉冲反演法结果(图 11b)相比,本文方法反演结果中横向连续性更好,且层与层之间的粘连效应较弱。
4 结论在深度学习地震反演算法中,本文尝试引入不同的先验约束条件,由此提出一种基于先验约束的深度学习地震反演方法。为增强算法的稳定性与抗噪性,并减少算法对标签数据的依赖性,在网络模型中选用了强抗噪性的Rand Softplus激活函数,且采取半监督学习方式对网络模型进行训练。经过理论分析与实验测试取得以下认识和结论:
(1) 采用区域分割策略后,每个网络模型只需负责数据特征相似区域的反演,这使网络模型能从训练数据中提取更多有效信息,从而丰富了反演结果的细节信息,提高了反演精度。但由于地震数据的自相关性,在一些纵向长度较短的地震道,反演精度会有所退化。
(2) 将初始模型作为一种特殊标签来约束网络的反演过程,可使网络充分利用初始模型中含有的低频分量和构造细节信息,从而丰富了反演结果的低频信息,提高了反演结果的横向连续性。
(3) Rand Softplus激活函数通过引入反映数据随机性的参数,提高了网络对噪声数据的适应能力。尤其是在强噪声条件下,该激活函数对反演精度的提升更为明显。
| [1] |
张永刚. 地震波阻抗反演技术的现状和发展[J]. 石油物探, 2002, 41(4): 385-390. ZHANG Yonggang. The present and future of wave impedance inversion technique[J]. Geophysical Prospecting for Petroleum, 2002, 41(4): 385-390. DOI:10.3969/j.issn.1000-1441.2002.04.001 |
| [2] |
叶云飞, 崔维, 张益明, 等. 低频模型对波阻抗反演结果定量解释的影响[J]. 中国海上油气, 2014, 26(6): 32-36. YE Yunfei, CUI Wei, ZHANG Yiming, et al. Impacts of low-frequency models on the quantitative interpretation of acoustic impedance inversion[J]. China Offshore Oil and Gas, 2014, 26(6): 32-36. |
| [3] |
Hinton G E, Osindero S, Teh Y W. A Fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18(7): 1527-1554. DOI:10.1162/neco.2006.18.7.1527 |
| [4] |
Lowe D G. Distinctive image features from scale-invariant key points[J]. International Journal of Computer Vision, 2006, 60(2): 91-110. |
| [5] |
Dalal N and Triggs B. Histograms of oriented gradients for human detection[C]. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, 2005, 1: 886-893.
|
| [6] |
Ojala T, Pietikainen M, Maenpaa T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2002, 24(7): 971-987. |
| [7] |
周志华. 机器学习[M]. 北京: 清华大学出版社, 2016.
|
| [8] |
卢宏涛, 张秦川. 深度卷积神经网络在计算机视觉中的应用研究综述[J]. 数据采集与处理, 2016, 31(1): 1-17. LU Hongtao, ZHANG inchuan. Applications of deep convolutional neural network in computer vision[J]. Journal of Data Acquisition and Processing, 2016, 31(1): 1-17. |
| [9] |
曹林林, 李海涛, 韩颜顺, 等. 卷积神经网络在高分遥感影像分类中的应用[J]. 测绘科学, 2016, 41(9): 170-175. CAO Linlin, LI Haitao, HAN Yanshun, et al. Application of convolutional neural networks in classification of high resolution remote sensing imagery[J]. Science of Surveying and Mapping, 2016, 41(9): 170-175. |
| [10] |
侯一民, 周慧琼, 王政一. 深度学习在语音识别中的研究进展综述[J]. 计算机应用研究, 2017, 34(8): 2241-2246. HOU Yimin, ZHOU Huiqiong, WANG Zhengyi. Overview of speech recognition based on deep learning[J]. Application Research of Computers, 2017, 34(8): 2241-2246. DOI:10.3969/j.issn.1001-3695.2017.08.001 |
| [11] |
奚雪峰, 周国栋. 面向自然语言处理的深度学习研究[J]. 自动化学报, 2016, 42(10): 1445-1465. XI Xuefeng, ZHOU Guodong. A survey on deep learning for natural language processing[J]. Acta Automatica Sinica, 2016, 42(10): 1445-1465. |
| [12] |
印兴耀, 吴国忱, 张洪宙. 神经网络在储层横向预测中的应用[J]. 石油大学学报(自然科学版), 1994, 18(5): 20-26. YIN Xingyao, WU Guochen, ZHANG Hongzhou. The application of neural networks in the reservior prediction[J]. Journal of the University of Petroleum, China, 1994, 18(5): 20-26. |
| [13] |
印兴耀, 杨风丽, 吴国忱. 神经网络在CB油田储层预测和储层厚度计算中的应用[J]. 石油大学学报(自然科学版), 1998, 22(2): 17-20. YIN Xingyao, YANG Fengli, WU Guochen. Application of neural network to predicting reservoir and calculating thickness in CB oilfield[J]. Journal of the University of Petroleum, China, 1998, 22(2): 17-20. |
| [14] |
张繁昌, 印兴耀, 吴国忱, 等. 用模拟退火神经网络技术进行波阻抗反演[J]. 石油大学学报(自然科学版), 1997, 21(6): 16-18. ZHANG Fanchang, YIN Xingyao, WU Guochen, et al. Impedance inversion by using annealing neutral network[J]. Journal of the University of Petroleum, China, 1997, 21(6): 16-18. |
| [15] |
Zheng Y, ZHANG Q, Yusifov A, et al. Applications of supervised deep learning for seismic interpretation and inversion[J]. The Leading Edge, 2019, 38(7): 526-533. DOI:10.1190/tle38070526.1 |
| [16] |
Huang Lei, Dong X and Clee T E. A scalable deep learning platform for identifying geologic features from seismic attributes[J]. The Leading Edge, 2017, 36(3): 249-256. DOI:10.1190/tle36030249.1 |
| [17] |
张玉玺, 刘洋, 张浩然, 等. 基于深度学习的多属性盐丘自动识别方法[J]. 石油地球物理勘探, 2020, 55(3): 475-483. ZHANG Yuxi, LIU Yang, ZHANG Haoran, et al. Multi-attribute automatic interpretation of salt domes based on deep learning[J]. Oil Geophysical Prospecting, 2020, 55(3): 475-483. |
| [18] |
闫星宇, 顾汉明, 罗红梅, 等. 基于改进深度学习方法的地震相智能识别[J]. 石油地球物理勘探, 2020, 55(6): 1169-1177. YAN Xingyu, GU Hanming, LUO Hongmei, et al. Intelligent seismic facies classification based on an improved deep learning method[J]. Oil Geophysical Prospecting, 2020, 55(6): 1169-1177. |
| [19] |
Moya A, Irikura K. Inversion of a velocity model using artificial neural networks[J]. Computers & Geo-sciences, 2010, 36(12): 1474-1483. |
| [20] |
Alfarraj M, Alregib G. Petrophysical-property estimation from seismic data using recurrent neural networks[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 2141-2146.
|
| [21] |
林年添, 张栋, 张凯, 等. 地震油气储层的小样本卷积神经网络学习与预测[J]. 地球物理学报, 2018, 61(10): 4110-4125. LIN Niantian, ZHANG Dong, ZHANG Kai, et al. Predicting distribution of hydrocarbon reservoirs with seismic data based on learning of the small-sample convolution neural network[J]. Chinese Journal of Geophysics, 2018, 61(10): 4110-4125. DOI:10.6038/cjg2018J0775 |
| [22] |
付超, 林年添, 张栋, 等. 多波地震深度学习的油气储层分布预测案例[J]. 地球物理学报, 2018, 61(1): 293-303. FU Chao, LIN Niantian, ZHANG Dong, et al. Prediction of reservoirs using multi-component seismic data and the deep learning method[J]. Chinese Journal of Geophysics, 2018, 61(1): 293-303. |
| [23] |
Das V, Pollack A, Wollner U, et al. Convolutional neural network for seismic impedance inversion[J]. Geophysics, 2019, 84(6): R869-R880. DOI:10.1190/geo2018-0838.1 |
| [24] |
Biswas R, Sen M K, Das V, et al. Pre-stack and post-stack inversion using a physics-guided convolutional neural network[J]. Interpretation, 2019, 7(3): SE161-SE174. DOI:10.1190/INT-2018-0236.1 |
| [25] |
Alfarraj M, Alregib G. Semi-supervised learning for acoustic impedance inversion[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 1949-4645.
|
| [26] |
Wang Y, Ge Q, Lu W, et al. Well-logging constrained seismic inversion based on closed-loop convolutional neural network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(8): 1-11. DOI:10.1109/TGRS.2020.3003152 |
| [27] |
麦应潮, 陈云华, 张灵. 具有生物真实性的强抗噪性神经元激活函数[J]. 计算机科学, 2019, 46(7): 206-210. MAI Yingchao, CHEN Yunhua, ZHANG Ling. Bio-inspired activation function with strong anti-noise ability[J]. Computer Science, 2019, 46(7): 206-210. |
| [28] |
Cho K, Van Merrienboer B, Gulcehre C, et al. Lear-ning phrase representations using RNN encoder-decoder for statistical machine translation[J]. arXiv Preprint arXiv: 1406.1078(2014).
|
| [29] |
Ioffe S, Szegedy C. Batch normalization: accelerating deep network training by reducing internal covariate shift[C]. Proceedings of the 32nd International Conference on Machine Learning, 2015, 448-456.
|
| [30] |
周飞燕, 金林鹏, 董军. 卷积神经网络研究综述[J]. 计算机学报, 2017, 40(6): 1229-1251. ZHOU Feiyan, JIN Linpeng, DONG Jun. Review of convolutional neural network[J]. Chinese Journal of Computer, 2017, 40(6): 1229-1251. |
| [31] |
Zeiler M, Krishnan D, Taylor W, et al. Deconvolutional networks[C]. 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2010, 2528-2535.
|
| [32] |
Kingma D P, Ba J. Adam: A method for stochastic optimization[J]. arXiv Preprint arXiv: 1412.6980(2014).
|
| [33] |
Chaki S, Routray A, Mohanty W K. A novel preprocessing scheme to improve the prediction of sand fraction from seismic attributes using neural networks[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(4): 1808-1820. DOI:10.1109/JSTARS.2015.2404808 |



 印兴耀, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
印兴耀, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: 