地震波阻抗反演将地震数据转换成反映地层物性参数的阻抗信息,是岩层和储层精细刻画的关键技术。近半个世纪以来,阻抗反演技术从直接反演发展到基于模型的反演,从线性反演发展到非线性反演,从叠后反演发展到叠前反演,受到了广泛的关注[1]。
近年来,以卷积神经网络(CNN)为代表的深度学习方法在解决地震反演问题中得到了成功的应用[2-8]。这类方法大多基于有监督学习,即利用网络从给定的数据和反演结果(标签)凭经验寻找二者之间的联系,从而得到预测网络模型。深度网络由多隐藏层构成,通过最小化网络预测结果与标签之间的误差迭代更新内部参数,该训练过程需要足够多的标签。在标签足够多和质量足够好的情况下,与传统地球物理反演方法相比,深度学习方法可以产生精度更高的反演结果。Das等[9]利用Kennett反射率法产生合成数据,结合阻抗标签训练CNN并测试了网络模型的稳健性;Mustafa等[10]把地震数据和声波阻抗当作序列数据,使用时域卷积网络(TCN)模型学习二者之间的映射关系;Du等[11]提出用残差网络进行叠前反演,获得了P波阻抗、S波阻抗等岩性和物性参数;孙宇航等[12]基于序列数据假设,利用测井数据训练门控单元(GRU)神经网络预测横波速度;王俊等[13]将GRU网络用于测井曲线重构。
在前人基于深度学习的波阻抗反演研究中,网络的训练样本大多从合成数据中获得,很难直接用于实际数据。而实际标签样本从测井数据中生成,由于成本的原因,可用的测井曲线通常数量少,不足以充分训练网络,容易产生过拟合。因此,利用大量合成数据对网络进行预训练后,应用少量实际标签对网络进行迁移学习,是提升网络实际数据反演精度的有效策略[14-16]。
在制作合成数据标签时,保证标签的典型性和多样性,避免大量特征相近标签的出现,是提升网络收敛速度的关键。本文提出基于数据增广和主动学习的策略进行波阻抗反演网络训练。主动学习[17-18]不仅可以有效减少标签数量,而且能够优选出典型标签。通过对这些优选单道阻抗标签数据以内插重采样的方法进行增广,可对深度神经网络进行有效训练。Marmousi 2模型测试结果表明,仅用14道阻抗增广后的数据训练网络,即可获得整个模型3400道数据的高精度反演结果。
1 内插重采样的波阻抗增广方法 1.1 增广原理一般常用的增广方式有裁剪、复制、增强特征、统计分布再抽样等,通过增加数据多样性提高网络模型泛化能力。对于时间序列源数据,增广方式主要从采样频率和时间窗着手,常见的增广方式有缩小采样频率的上采样、放大采样频率的下采样和同等采样频率的重采样。插值方法也有许多种,常用的有线性插值、三次样条插值等。为保证时间维度上的走势一致性,本文采用三次样条插值[19]。
用N维列向量d、r、I分别表示地震剖面的一道数据及对应的反射系数序列和波阻抗,通过Toe-plitz型子波矩阵W,可将地震子波与反射系数序列的卷积运算写为[20-21]
| $ \boldsymbol{d}=\boldsymbol{W} * \boldsymbol{r} $ | (1) |
I与r的关系可表示为
| $ I(t)=I(t-1) \cdot \frac{1+r(t-1)}{1-r(t-1)} $ | (2) |
引入时移循环矩阵K为随机核,与式(1)等号两边相乘。对于时不变地震子波,K与W可交换次序[22],可得
| $ \boldsymbol{K} * \boldsymbol{d}=\boldsymbol{W} * \boldsymbol{K} * \boldsymbol{r} $ | (3) |
引入新变量
| $ \widetilde{\boldsymbol{d}}=\boldsymbol{W} * \tilde{\boldsymbol{r}} $ | (4) |
由式(4)可得一组新的地震道和反射系数序列
若直接利用纵向内插重采样对反射系数进行增广,由式(2)可知,任意一个r(t)(1≤t≤N)的微小变化均会对后续波阻抗的计算产生影响,则增广出的反射系数
同样可以按照纵向内插重采样的方法,对波阻抗I直接进行增广,生成对应的一组{I,
上述纵向内插重采样的具体步骤如下:
(1) 任取一个N维波阻抗I,通过三次样条插值为N*维波阻抗(本文实验中,取N*=10N);
(2) 对N*维波阻抗沿时间方向随机重采样N个,组成新的N维列向量
(3) 利用增广后的波阻抗
(4) 利用{r,
重复以上四步可求出若干组{
在实际应用中,子波在水平或垂直方向上经常发生变化。地质和岩性的非平稳性变化会给估计子波带来挑战。本文增广方法的最大优势是可以避开关于地震子波W的大量运算,从而减小误差[23]。
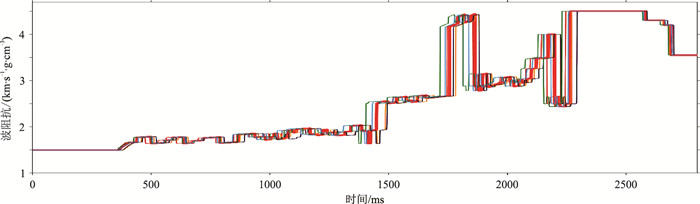
1.2 初步验证在Marmousi 2剖面上任取一道波阻抗I,对其进行5道增广后,结果如图 1所示,可以看出增广后的波阻抗
|
图 1 原始波阻抗曲线(红色粗线)与增广后曲线对比 |
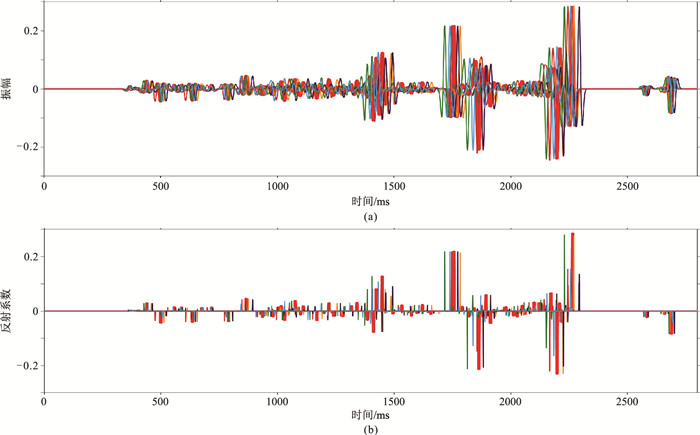
由增广后的波阻抗
|
图 2 增广地震道(a)和反射系数(b)与原始曲线(红色粗线)的对比 |
全卷积网络(FCN)是一种没有全连接层的卷积神经网络,能够根据任意大小的输入进行预测,可用于解决反演问题[24]。在深度学习中,基于恒等映射的残差网络可缓解网络随着层数增加出现性能退化的现象[25]。结合这两种网络优点而设计的全卷积残差网络(FCRN),在提高预测精度的同时,缓解了网络训练困难的问题[26]。
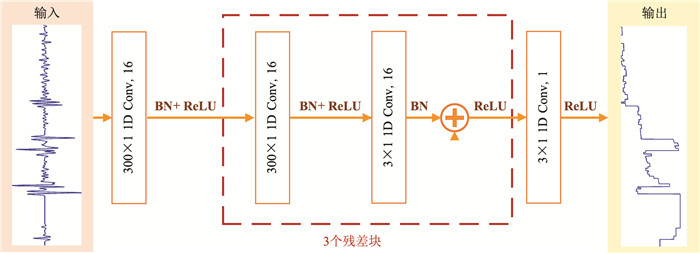
FCRN结构如图 3所示,由首尾两个一维卷积层(Conv)和中间三个残差块组成。首端卷积层由16个大小为300×1的核组成;每个残差块由两个一维卷积层组成,其中第一层拥有16个大小为300×1的核,第二层拥有16个大小为3×1的核;末端卷积层拥有1个大小为3×1的核。所有卷积层中使用零填充,以保证每个卷积层的输入和输出大小相同。为了加快网络收敛速度,FCRN选择了整流线性激活单元(ReLU);并且除了最后一层外,对所有卷积层的输出应用了批量归一化处理(BN)[27-28]。
|
图 3 FCRN结构[24] |
Wu等[26]提出的FCRN网络是以单道对单道的形式进行训练的,即在训练集中,一道地震数据输入对应一道波阻抗输出。令Ireal(d)表示地震道d对应的波阻抗真值,F表示训练出的反演网络,Θ表示网络参数的集合,则可用FΘ (d)表示网络预测出的一道波阻抗。网络的损失函数可用均方误差计算,定义为
| $ \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}=\left\|\boldsymbol{F}_{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}}(\boldsymbol{d})-\boldsymbol{I}^{\mathrm{rel}}(\boldsymbol{d})\right\|_{2}^{2} $ | (5) |
由于小批量训练方法能够提高网络的泛化能力,本文设置Batch(批处理)大小为10;更新权重部分选择Adam算法优化网络中的参数,权重衰减设置为10-7;Epoch(训练集中的样本遍历次数)的数目设为10,学习率设置为0.001。为避免过拟合,当验证损失开始增加时,停止网络训练[29-30]。
2.2 基于主动学习的网络迭代主动学习是机器学习算法之一。在数据集十分庞大时,可利用较少的训练数据,在更短时间内获得相同甚至更好的学习效果。减少标签数据、利用很少的数据训练出强泛化能力的模型,是主动学习最大的优势。
在实际训练过程中,训练一次后的网络尽管在训练集上表现良好,但在验证集上仍与目标值存在一定差距。这时便需要借鉴主动学习的思想,根据误差对此次训练集中的数据进行调整,直至下一次训练出的网络在验证集上的误差小于目标误差值。
2.2.1 初始选择策略在第一次迭代之前,需要人工筛选出需要标注的数据。按照波阻抗剖面的分布,可在横向上选择M个具有代表性的位置,记为[p1,p2,…,pM];然后将这些位置处的数据作为初始值,对此M个位置的地震数据和波阻抗增广为M+组{
每一次训练完成后,生成的网络会预测出一个新的波阻抗剖面。设波阻抗剖面共有L道数据,Iipre表示第i次训练后网络预测出的波阻抗剖面,可以推出在整个剖面验证集上的单道误差Eis(l)为
| $ E_{i}^{\mathrm{s}}(l)=\left\|\boldsymbol{I}^{\mathrm{real}}(l)-\boldsymbol{I}_{i}^{\mathrm{pre}}(l)\right\|_{2}^{2} \quad(l=1, 2, \cdots, L) $ | (6) |
则第i次预测整体误差为
| $ E_{i}^{\mathrm{all}}=\frac{\sum\limits_{l=1}^{L} E_{i}^{\mathrm{s}}(l)}{L} $ | (7) |
通过观察整体误差的变化,便可知道当前预测的整体效果。而主动学习每次选择新数据进行标注并加入原训练集时,应该选择误差最大位置处的数据。所以除了整体误差,还应增加最大误差Eimax作为迭代时主动学习选择数据的判断标准。
为避免峰值误差对判断的负面影响,减少主动学习迭代次数,本文引入平滑窗的概念,对剖面上的单道误差做平滑处理,改进最大误差的计算方法。
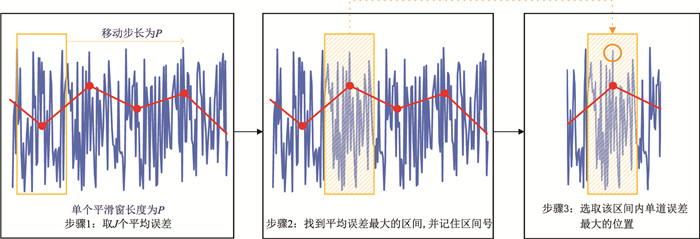
首先,选择P道为平滑窗口,即每P道计算一个平均误差,且设置平滑窗的移动步长为P,一共得到J(J=L/P)个平均误差Ejave(本实验设置P为50);其次,找到J个平均误差中最大的Emaxave及其所在的窗口jmax;最后,在窗口jmax内寻找单道预测误差最大的道,其道号记limax,即为主动学习迭代中要选取的新数据。图 4为主动学习样本选择流程,并且每轮迭代将新选取样本加入到训练集中,形成新的训练样本。
|
图 4 主动学习每次迭代后选取新数据的流程 蓝线为单道预测误差曲线,红线为平均误差曲线 |
设函数Φ为本文实验的误差计算函数,其输入为Ireal和Iipre,输出为Eiall、Eimax和limax,则第i次网络训练后的误差计算结果可写为
| $ \left[E_{i}^{\mathrm{all}}, E_{i}^{\max }, l_{i}^{\max }\right]=\mathit{\Phi }\left(\boldsymbol{I}^{\mathrm{real}}, \boldsymbol{I}_{i}^{\mathrm{pre}}\right) $ | (8) |
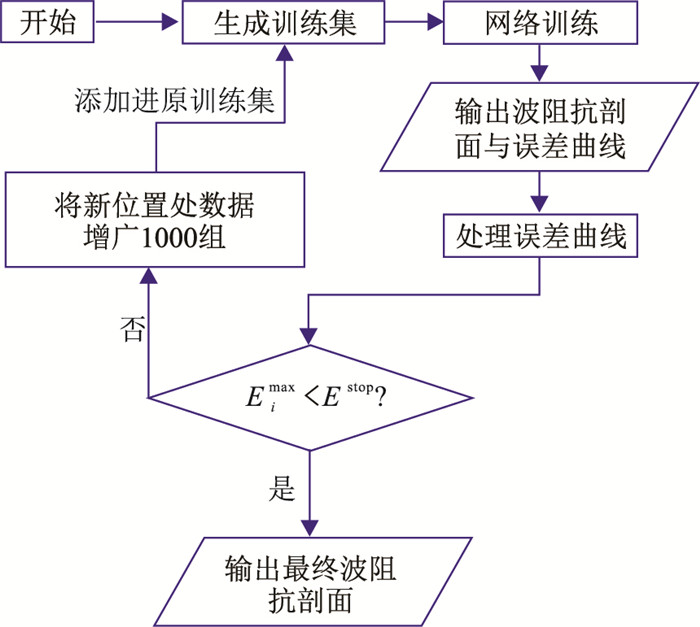
此外,还需设置迭代终止条件Estop。新的一次迭代前需判断当前Eimax与Estop关系。若Eimax>Estop,则将第limax道数据和阻抗均增广到M+道,加入上一次训练集作为新训练集,继续迭代;若Eimax>Estop,则停止迭代,输出当前预测剖面Iipre和最优反演网络FΘ*。本文基于数据增广和主动学习的地震波阻抗反演方法流程如图 5所示。
|
图 5 反演网络迭代总流程 |
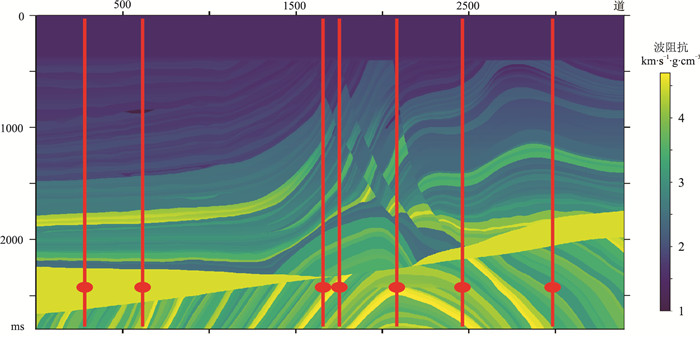
本文实验的所有数据基于减采样后的Mar-mousi 2模型[31](图 6),横向共有3400道,纵向有2800个时间采样点,采样间隔为1ms。
|
图 6 Marmousi 2波阻抗模型及初始训练样本位置(红色竖线所示) |
在网络迭代之前,人工选取了7道作为训练样本,其道号分别为249、599、1674、1799、2199、2499、2999。
对这7个初始样本数据(包括地震数据和波阻抗)均增广到1000道,共获得7000组
|
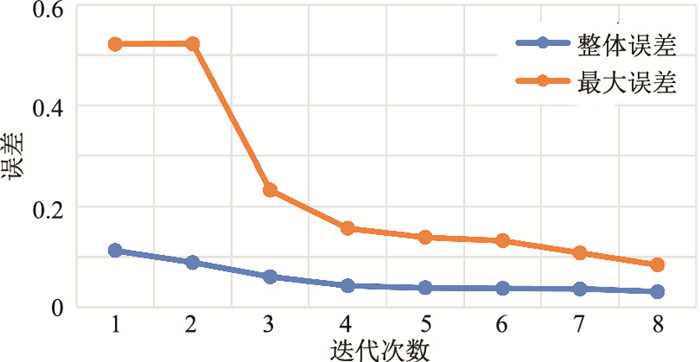
图 7 网络迭代误差曲线随迭代次数的变化 |
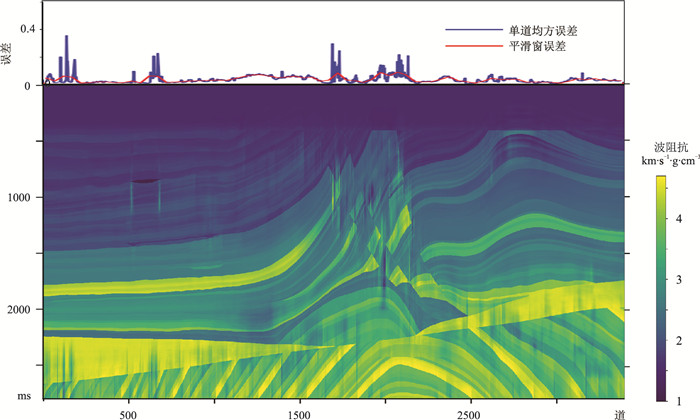
从图 7可以看出,当迭代到第8次,即训练集为14×1000组时,最大误差Eimax降至0.0841,小于预定的极限误差Estop=0.1,则此时停止迭代。第8次迭代时训练样本为第249、599、1674、1799、2199、2499、2999、1973、1889、1854、2068、2899、2651和2466道。图 8为本文方法反演的最佳剖面及误差曲线,与真值的整体误差为0.0309,最大误差为0.0841,整体反演效果良好。
|
图 8 纵向数据增广波阻抗预测剖面及误差曲线 |
与纵向内插重采样不同,横向数据增广的过程如下。
假设现有7道波阻抗数据,其位置与图 6相同,将其按位置顺序展开如图 9a所示。在横向上,采用最简单的线性内插方法,内插成7×100道作为示例,如图 9b所示。

|
图 9 7道波阻抗信息(a)及其横向内插结果(b) |
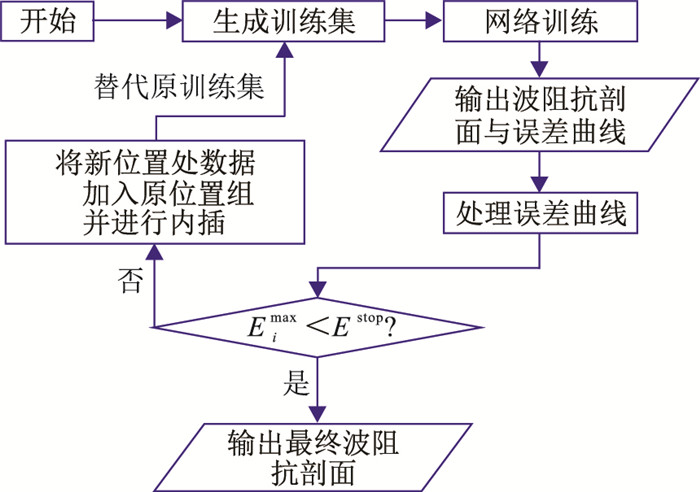
当主动学习根据图 4流程完成一次对新位置的选取后,横向增广要将新位置按横坐标插入训练集中,再进行内插。横向数据增广和主动学习的地震波阻抗反演的流程如图 10所示。
|
图 10 横向内插数据增广和主动学习的波阻抗反演流程 |
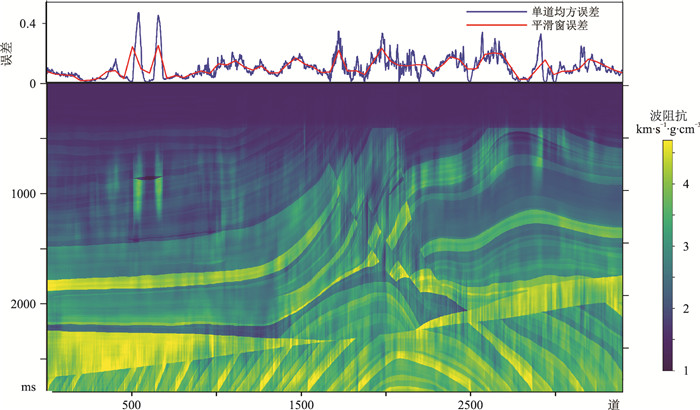
横向内插数据增广和主动学习的地震波阻抗反演8次迭代后得到的结果如图 11所示。其最大误差为0.3139,整体误差为0.1197,均高于图 8中的误差。说明本文所提出的内插重采样波阻抗增广方法优于横向内插方法。
|
图 11 横向数据增广波阻抗预测剖面及其误差曲线 |
与主动学习不同,非主动学习网络训练方法采用随机选择初始训练样本进行数据增广训练网络;且前后迭代之间并无任何关系,每一次的网络训练都是独立的,重新随机选取训练样本。
随机迭代的效果在同样规模的训练集下,预测精度低于主动学习方法。将14×1000道的数据规模作为标准,考察在同样数据规模下的随机选择样本网络预测效果。但由于没有借助主动学习策略,其预测效果欠佳,并不具有可比性。
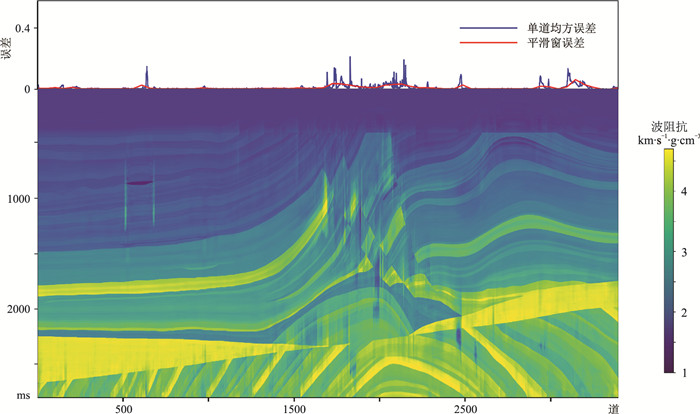
在随机选择140个位置,每个位置增广100道数据时,反演结果如图 12所示,最大误差为0.0609,整体误差为0.0218,比图 8的最大误差和整体误差略小。
|
图 12 随机迭代方法的波阻抗反演剖面及误差 |
对比图 12与图 8可知,虽然随机迭代的整体预测效果与主动学习迭代效果相近,但随机迭代选取了140个位置的数据,主动学习迭代只选取了14个位置的数据。而且,基于随机样本选取的预测结果误差主要集中于结构复杂横向变化剧烈的1600~2200道。该结果说明主动学习迭代方式可挑选更为典型的训练样本,使预测误差在整个数据集上得到有效控制,而不是集中于少数变化强烈位置。
5 结束语本文首先在理论上推导了单道内插重采样的增广方法,生成了反演网络训练集;然后应用主动学习,配置了反演网络参数并确定了参数更新方式。Marmousi 2模型实验结果表明,本文提出的算法只需14道真实的地震波阻抗信息,就可以反演出相对真实的波阻抗剖面。
本文并未对网络性能提升以及泛化能力展开研究。首先,可以通过优化FCRN网络结构的方式,提高反演精度,减少迭代次数,并使反演误差在整个剖面上较为均衡,更有利于实际应用;其次,对实际数据进行增广,并与迁移学习结合,检验本文方法在实际数据上波阻抗反演效果;再次,本文仅为单参数反演,在对多个弹性参数进行反演时如何利用主动学习策略对网络进行训练,也是值得研究的方向之一。
| [1] |
Russell B H. Introduction to Seismic Inversion Me-thods[M]. SEG, 1988.
|
| [2] |
Araya-Polo M, Jennings J, Adler A, et al. Deep-lear-ning tomography[J]. The Leading Edge, 2018, 37(1): 58-66. DOI:10.1190/tle37010058.1 |
| [3] |
Bergen K J, Johnson P A, De Hoop M V, et al. Machine learning for data-driven discovery in solid Earth geoscience[J]. Science, 2019, 363(6433): eaau0323. DOI:10.1126/science.aau0323 |
| [4] |
Karpatne A, Ebert-Uphoff I, Ravela S, et al. Machine learning for the geosciences: Challenges and opportunities[J]. IEEE Transactions on Knowledge & Data Engineering, 2017, 31(8): 1544-1554. |
| [5] |
Yang F, Ma J. Deep-learning inversion: a next generation seismic velocity-model building method[J]. Geophysies, 2019, 84(4): R583-R589. DOI:10.1190/geo2018-0249.1 |
| [6] |
Wang Y, Ge Q, Lu W, et al. Well-logging constrained seismic inversion based on closed-loop convolutional neural network[J]. IEEE Transactions on Geosience and Remote Sensing, 2020, 58(8): 5564-5574. DOI:10.1109/TGRS.2020.2967344 |
| [7] |
Fabien-Ouellet G, Sarkar R. Seismic velocity estimation: A deep recurrent neural-network approach[J]. Geophysics, 2020, 85(1): U21-U29. DOI:10.1190/geo2018-0786.1 |
| [8] |
Park M J, Sacchi M D. Automatic velocity analysis using convolutional neural network and transfer lear-ning[J]. Geophysics, 2020, 85(1): V33-V43. DOI:10.1190/geo2018-0870.1 |
| [9] |
Das V, Pollack A, Wollner U, et al. Convolutional neural network for seismic impedance inversion[J]. Geophysics, 2019, 84(6): R869-R880. DOI:10.1190/geo2018-0838.1 |
| [10] |
Mustafa A, Alfarraj M, Al Regib G. Estimation of acoustic impedance from seismic data using temporal convolutional network[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 2554-2557.
|
| [11] |
Du J, Liu J, Zhang G, et al. Pre-stack seismic inversion using SeisInv-ResNet[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 2338-2342.
|
| [12] |
孙宇航, 刘洋. 利用GRU神经网络预测横波速度[J]. 石油地球物理勘探, 2020, 55(3): 484-492. SUN Yuhang, LIU Yang. Prediction of S-wave velo-city based on GRU neural network[J]. Oil Geophy-sical Prospecting, 2020, 55(3): 484-492. |
| [13] |
王俊, 曹俊兴, 尤加春. 基于GRU神经网络的测井曲线重构[J]. 石油地球物理勘探, 2020, 55(3): 510-520. WANG Jun, CAO Junxing, YOU Jiachun. Reconstruction of logging traces based on GRU neural network[J]. Oil Geophysical Prospecting, 2020, 55(3): 510-520. |
| [14] |
Ali S, Mathias L, Felix J H. The importance of transfer learning in seismic modeling and imaging[J]. Geo-physics, 2019, 84(6): A47-A54. |
| [15] |
张政, 严哲, 顾汉明. 基于残差网络与迁移学习的断层自动识别[J]. 石油地球物理勘探, 2020, 55(5): 950-956. ZHANG Zheng, YAN Zhe, GU Hanming. Automatic fault recognition with residual network and transfer learning[J]. Oil Geophysical Prospecting, 2020, 55(5): 950-956. |
| [16] |
Park M J, Sacchi M D. Automatic velocity analysis using convolutional neural network and transfer lear-ning[J]. Geophysics, 2020, 85(1): V33-V43. DOI:10.1190/geo2018-0870.1 |
| [17] |
Wu D, Lin C T, Huang J. Active learning for regression using greedy sampling[J]. Information Sciences, 2019, 474: 90-105. DOI:10.1016/j.ins.2018.09.060 |
| [18] |
Cao X, Yao J, Xu Z, et al. Hyperspectral image classification with convolutional neural network and active learning[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(7): 4604-4616. DOI:10.1109/TGRS.2020.2964627 |
| [19] |
McKinley S, Levine M. Cubic spline interpolation[J]. College of the Redwoods, 1998, 45(1): 1049-1060. |
| [20] |
Gray R M. Toeplitz and circulant matrices: A review[J]. Foundations & Trends in Communications & Information Theory, 2006, 2(3): 155-239. |
| [21] |
汪玲玲, 高静怀, 赵谦, 等. 基于矩阵Toeplitz稀疏分解的相对波阻抗反演方法[J]. 地球物理学报, 2017, 60(2): 639-654. WANG Lingling, GAO Jinghuai, ZHAO Qian, et al. Relative acoustic impedance inversion via Toeplitz-sparse matrix factorization[J]. Chinese Journal of Geophysics, 2017, 60(2): 639-654. |
| [22] |
Wang K, Bandura L, Bevc D, et al. End-to-end deep neural network for seismic inversion[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 4983-4986.
|
| [23] |
梁光河. 地震子波提取方法研究[J]. 石油物探, 1998, 37(1): 31-39. LIANG Guanghe. On the methods of seismic wavelet extraction[J]. Geophysical Prospecting for Petro-leum, 1998, 37(1): 31-39. |
| [24] |
Long J, Shelhamer E, Darrell T. Fully convolutional networks for semantic segmentation[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2015, 3431-3440.
|
| [25] |
He K, Zhang X, Ren S, et al. Deep residual learning for image recognition[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, 770-778.
|
| [26] |
Wu B, Meng D, Wang L, et al. Seismic impedance inversion using fully convolutional residual network and transfer learning[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(12): 2140-2144. DOI:10.1109/LGRS.2019.2963106 |
| [27] |
Xu B, Wang N, Chen T, et al. Empirical evaluation of rectified activations in convolutional network[CS/ML]. arxiv. org/abs/1505.00853, 2015-05-05.
|
| [28] |
Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift[C]. Proceedings of the 32nd International Conference on Machine Learning, 2015, 448-456.
|
| [29] |
Keskar N S, Mudigere D, Nocedal J, et al. On large-batch training for deep learning: Generalization gap and sharp minima[C]. International Conference on Learning Representations, 2017, 1-16.
|
| [30] |
Kingma D P, Ba J. Adam: A method for stochastic optimization[CS/ML]. arxiv. org/abs/1412.6980, 2014-12-22.
|
| [31] |
Martin G S, Wiley R, Marfurt K J. Marmousi 2:An elastic upgrade for Marmousi[J]. The Leading Edge, 2006, 25(2): 156-166. DOI:10.1190/1.2172306 |



 曹相湧, 陕西省西安市碑林区咸宁西路28号西安交通大学数学与统计学院, 710049。Email:
曹相湧, 陕西省西安市碑林区咸宁西路28号西安交通大学数学与统计学院, 710049。Email: 