② 中国石油大学(北京)CNPC物探重点实验室, 北京 102249;
③ 中国石油大学(北京)油气资源与探测国家重点实验室, 北京 102249
② CNPC Key Laboratory of Geophysical Prospecting, China University of Petroleum(Beijing), Beijing 102249, China;
③ State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum(Beijing), Beijing 102249, China
断层解释是地震资料解释的关键环节之一。传统方法是:首先通过人工在二维地震剖面上根据同相轴的不连续性识别断层,再在三维空间进行断层组合。目前,可以在常规地震波形剖面的基础上增加不同的地震属性进行断层联合解释,如相干[1-4]、方差[5]、曲率[6]等属性。其中,Bahorich等[1]提出的基于互相关C1相干体技术计算速度快,但受相干噪声干扰明显;Marfurt等[2]提出的基于多道相似性C2相干体技术在保证计算速度及适用性的同时,弥补了C1相干算法由于采样少造成的抗噪性低的不足,但对波形和横向振幅的变化敏感;为了进一步提高相干体技术的分辨率,Gersztenkorn等[3]提出了基于本征结构的C3相干技术,通过计算协方差求取相干值,但运算速度相对较慢。而方差体技术[5]是一种基于概率方差分析的不连续性检测,它通过计算相邻地震道之间的方差表示反射特征的差异,从而完成断层的识别。
除了上述与地震属性相关的方法识别断层外,还可以通过边缘检测[7]、数据目标特殊处理、模型正演分析[8]和全三维解释[9]等技术提高断层识别的准确性和可靠性[10]。其中,边缘检测技术起源于图像处理领域,主要用于检测图像中的灰度突变,可检测地震数据中的反射同相轴不连续。通常情况下,断裂等一些特殊地质体在地震剖面上会表现出同相轴不连续的特点,经过边缘检测技术处理后,这些不连续的边缘特性会得到凸显,但缺点在于检测的对象不是地震数据本身,而是经过处理后(如滤波、相干等)的地震数据图像。
目前,利用地震数据解释断层主要还是依靠人工,工作量大且费时。随着人工智能技术的发展,如何自动、快速地识别断层,成为了地球物理勘探领域研究的热点之一。断层的自动识别主要包括深度学习网络的选取及优化、样本标签数据集的生成和损失函数的选取等三个方面。
在深度学习网络的选取方面,董守华等[11]应用BP神经网络探索了断层自动检测方法;Chehrazi等[12]采用多层感知器(MLP)的网络结构训练断层自动识别模型;Huang等[13]首次将卷积神经网络(CNN)成功应用于断层识别中;Zhao等[14]将CNN断层识别与图像处理相结合,提高了断层识别精度;Wu等[15]改进了U型神经网络(U-Net),充分利用地震数据的三维空间特征,大幅度提高了模型训练的预测精度和效率;Liu等[16]在Wu等[15]提出的U-Net的基础上,引入了ResNet-34[17]中的残差模块,进一步提高了断层自动识别的精度。
在样本标签数据集的制作方面,Tingdahl等[18]通过地震属性优选制作样本标签数据集;Zhang等[19]提出了一种正演合成断层地震记录作为样本标签的方法,将有限差分声波方程正演得到含断层的地震数据作为训练集;Xiong等[20]利用骨架化地震相干自校正结果作为训练样本,将一个中心点的主测线和联络线、时间切片的地震数据作为三通道输入;Wu等[15]提出了合成地震记录并用U型神经网络进行训练的方法,通过定义反射系数层、加入纵向剪切、加入横向剪切、加入断层、褶积运算、加入噪声等六个步骤,获得了更符合地质意义以及更多样化的样本和标签信息。
在损失函数方面,董守华等[11]采用平方误差函数作为网络的损失函数,将网络的参数调整与梯度优化相结合;Zhang等[19]采用符合机器学习特征的规则化最小平方高斯内核函数作为损失函数;Araya-Polo等[21]采用瓦瑟斯坦(Wasserstein)损失函数作为目标函数,克服了交叉熵损失函数无法考虑相邻样本之间联系的缺点,使训练的模型更符合断层的地质意义;Wu等[15]在考虑地震数据中正、负样本不均衡的情况下,使用平衡交叉熵损失函数。
虽然利用深度学习检测断层技术已获得较大进展,但在实际资料应用中还存在模型训练难度大、预测效果不理想等问题,因此本文构建了新的网络结构ResU-Net用于地震数据断层检测。该网络结构将U-Net与Res-50的残差模块相结合,在增加网络深度的同时,优化模型以降低训练难度和计算量;针对合成地震数据集中正、负样本极度不均衡(断层点的数量远远少于非断层点)的情况,应用带有权重的交叉熵损失函数,提高了断层样本对损失函数的影响;同时选择适当的输入大小、重叠边界处理方法以及进行不规则输入数据的扩充后,通过搭建的网络训练得到的模型可快速、准确地检测断层。
1 方法原理 1.1 网络结构利用CNN识别断层的方法分为两种:第一种是当作图像分类问题,主要思路是判断一个剖面的中心点是否为断层点,然后逐点移动剖面,进行逐点预测[13, 20];第二种是当作语义分割问题,输入二维或者三维的数据体,输出对应大小的预测结果[15-16]。相较于前者,后者拥有更高的预测精度和更快的训练速度。因此,本文采用语义分割的思路进行断层自动识别。
1.1.1 U-NetU-Net于2015年由Ronneberger等[22]提出,是基于全卷积神经网络(FCN)[23]拓展、修改而来,由编码器和解码器两部分组成。其中,编码器部分是典型的卷积结构,包含两个连续的3×3卷积核层,卷积后的特征图像经ReLU函数进行非线性激活;下采样方法采用最大池化,每次下采样操作都将特征图像通道数增加2倍,同时将图像尺寸缩小2倍;在解码器部分对特征图像反卷积,特征图像的尺寸扩大2倍,与对应编码器中的特征图像拼接,提取低维特征信息,对拼接后的特征图像进行两次连续卷积操作,最后使用ReLU函数激活。在最后的输出层中利用1×1卷积核对特征图像进行卷积,生成与输入数据相同的维数,还原图像的原始尺寸。在编码器部分的每次池化之前,特征图像都将被保存,并通过跳跃连接的方式将保存的特征图像传递给对应尺度的解码器部分,为解码器提供不同尺度的特征信息。通过跳跃连接的方式恢复由于池化处理降低分辨率而损失的空间信息,可为解码器提供不同分辨率的图像特征。
1.1.2 残差模块机器学习算法的网络达到一定深度之后,就会出现梯度消失、梯度爆炸等问题,从而产生错误的训练结果。为此,He等[17]提出了能够解决网络过深问题的残差神经网络。如果网络中的深层是恒等映射,那么模型就退化为一个浅层网络。因此,需要解决的问题是学习过程中的恒等映射函数。如果把网络设计为H(x)=F(x)+x,那么可将它转换为学习一个残差函数F(x)=H(x)-x(其中x为网络的输入)。只要F(x)=0就构成了一个恒等映射H(x)=x,从而使结果更容易拟合。由此,He等[17]提出了包含残差函数的两个残差模块,分别为Res-34和Res-50(图 1)。对比Res-34和Res-50两个残差模块,可以发现Res-34模块主要由两个3×3的卷积核构成;而Res-50模块中间为一个3×3的卷积核,首端和末端均为1×1的卷积核,目的是削减和恢复四倍的特征图像通道数量。

|
图 1 Res-34(左)与Res-50(右)残差模块结构对比 |
在残差模块的时间复杂度对比方面,主要考虑卷积层中的乘法次数。假设在残差模块中完成特征图像通道数为64的运算,图 1中两个残差模块红色部分的时间复杂度是一样的,其余部分中,Res-34模块可以分解为3×3×64×64次乘法运算,而Res-50模块为(4+4)×64×64次乘法运算。因此,对于二维数据的卷积核计算,两种残差模块的时间复杂度基本相同。但是,对于三维卷积核,红色部分抵消之后,Res-34模块的时间复杂度为3×3×3×64×64,而Res-50模块的时间复杂度不变,因此Res-34模块的时间复杂度为Res-50模块的3.375倍。对于三维地震数据体的断层检测而言,选择Res-50模块会比Res-34模块减少计算时间,可以加深网络结构以提高学习能力。
1.1.3 ResU-Net网络结构通过上述分析,本文以U-Net网络为基础,引入Res-50残差模块构建新的网络结构,即ResU-Net,如图 2所示。
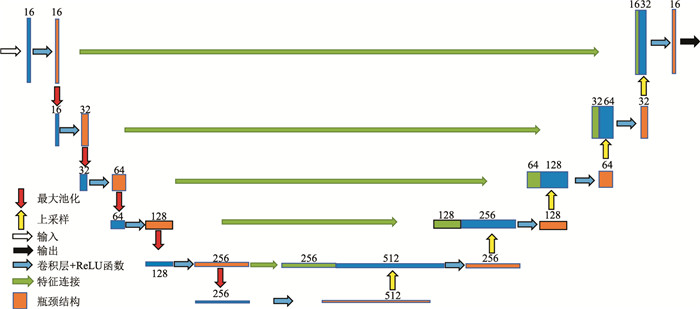
|
图 2 ResU-Net网络结构示意图 |
Res-50模块通过1×1×1卷积核升、降特征图像的通道数,可以在保证特征学习能力的前提下大幅减少运算量。因此,本文构建了包含45个卷积层的深层神经网络,特征图像通道数从16开始、以2的倍数升高至512。
在编码器部分(图 2左侧),每一个步骤均包含三个卷积层,依次为1×1×1、3×3×3和1×1×1,并将输出与残差模块的输入计算残差。每一个卷积层之后都加入一个ReLU函数,最后利用一个2×2×2的最大池化层用于下采样。这样就可以在每一步骤之后将特征层的数量加大一倍。
在解码器部分(图 2右侧)的每一步骤都包含一个2×2×2的上采样操作、一个与左侧收缩路径中的特征连接和三个卷积层(依次为1×1×1、3×3×3、1×1×1),并将输出与残差模块的输入计算残差。每一个卷积层之后都加入一个ReLU函数。输出层采用一个包含Sigmoid函数的1×1×1卷积层,最终输出断层概率值。
1.2 损失函数损失函数最小化可使模型达到收敛状态,减少模型预测值的误差。本文采用的损失函数为Xie等[24]提出的平衡交叉熵损失函数,即
| $ \begin{aligned} L=&-\beta \sum\limits_{i=0}^{N} y_{i} \ln p_{i}-\\ &(1-\beta) \sum\limits_{i=0}^{N}\left(1-y_{i}\right) \ln \left(1-p_{i}\right) \end{aligned} $ | (1) |
式中:N为输入三维地震体数据点个数;β为非断层点与样本数的比;pi是预测为断层点的概率(0<pi<1);yi是标签值(1为断层点,0为非断层点)。
增加β可以使模型在训练过程中更加侧重于标签少的样本的学习,适合正、负样本不均衡的情况。在数据训练集中,非断层点(标签为0)远大于断层点(标签为1)的数量,因而应用平衡交叉熵损失函数能够增加模型对断层点的学习能力,以便更好地识别断层。
1.3 模型训练模型训练采用的数据集为Wu等[15]开源的合成地震记录数据集,共有220个三维合成地震记录以及与之对应的标签集,每个数据集大小为128×128×128。其中,200个作为训练集,剩余的20个作为测试集。图 3展示了剖面、时间切片以及对应的断层标签。
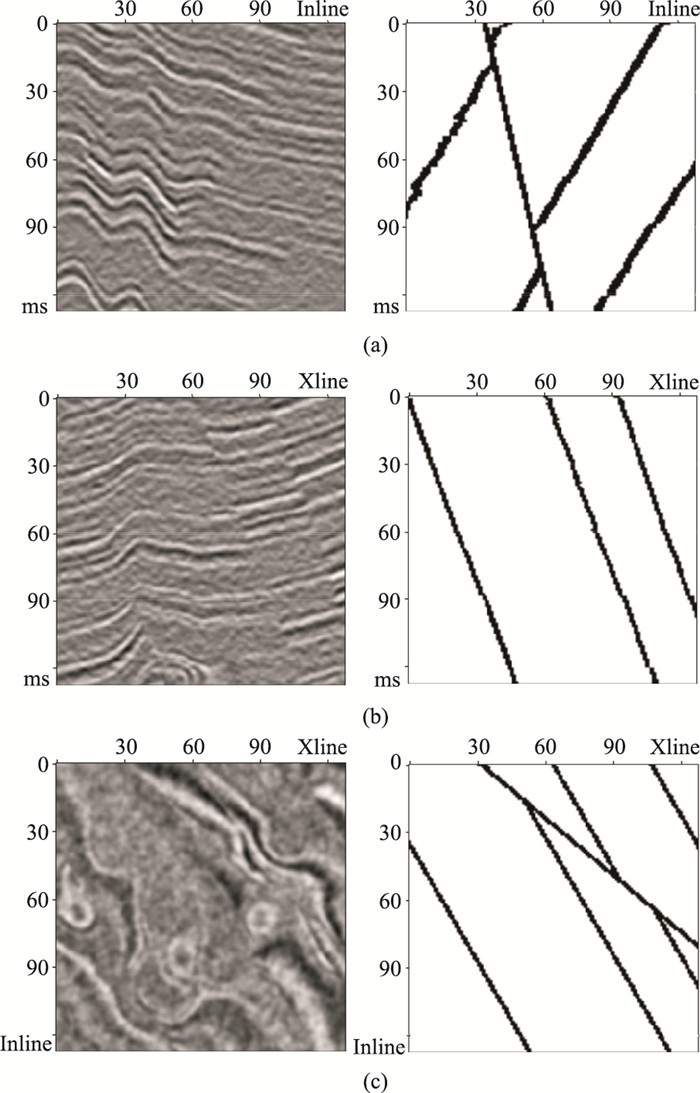
|
图 3 模型训练样本数据(左)及对应断层标签(右) (a)Xline剖面;(b)Inline剖面;(c)时间切片 |
在训练之前,首先对样本标签数据体进行预处理。考虑到不同地震图像的振幅值之间可能存在很大差异,因而对所有训练的地震图像进行归一化处理,每幅图像用平均值减去标准差。同时,为了增加数据的多样性,提高训练模型的泛化能力,对数据集进行增强处理,将样本标签数据集沿z轴进行90°、180°和270°旋转,目的是避免插值引起的伪影。
在模型数据训练中,本文对比了两个网络模型的训练效果。第一个网络模型为包含45个卷积层的ResU-Net;第二个网络模型是在第一个网络模型的基础上,将映射计算方式改为H(x)=x的U-Net。在模型训练中采用相同的参数(表 1)。采用数据增强之后的800个合成地震记录数据体(前文的220个数据集中的200个作为训练集,数据增强处理将训练集扩充了四倍),在显存为11GB的GPU-RTX2080Ti中训练了25个周期,每训练完1个周期均采用20个合成地震记录数据集作为验证集进行验证。
|
|
表 1 模型训练参数表 |
经过25个周期训练,两个网络模型均达到收敛,并在验证集上均取得了约93%的准确率和0.025的损失。
随机在验证集中选取一条地震剖面,断层预测结果如图 4所示。由图可见,两个网络模型预测结果基本一致,均可以从地震剖面中识别断层。在相同条件下,训练得到的模型具有相同的训练时间和时间复杂度(3.1×109),这也印证了前文对残差模块的分析。残差模块恒等映射与普通卷积层计算恒等映射具有相同的模型参数和计算量,即残差模块并不会增加模型的参数和训练时间,只是更换了卷积层计算映射的方式。相较于包含7个Res-34结构、时间复杂度为7.3×109的ResU-Net(包含Res-34残差模块),本文的包含Res-50残差模块ResU-Net能够在很大程度上减少参数数量,节余的计算量可以加入更多的Res-50残差模块而更好地学习断层特征,并且拥有更少的训练时间和更小的时间复杂度。

|
图 4 不同训练模型验证集地震剖面断层预测结果对比 (a)地震数据剖面;(b)标签;(c)U-Net模型;(d)ResU-Net模型 |
选取三个断层比较发育的三维实际地震数据(图 5)进行测试以验证模型的断层预测效果及泛化能力。
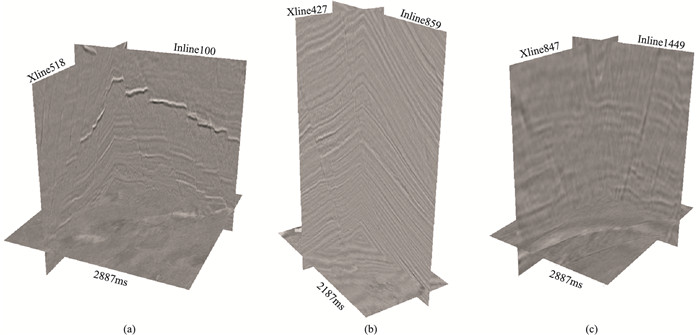
|
图 5 实际地震数据体 (a)Inline为1~300,Xline为419~718,时间为2800~3697ms;(b)Inline为760~1068,Xline为425~594,时间为2100~3398ms;(c)Inline为1385~1640,Xline为798~1054,时间为2799~3372ms |
在实际数据的处理过程中,需要根据训练模型的输入大小进行数据的组合、拼接,不同大小的模型输入、不同的拼接方法均会对预测结果产生很大的影响。
本文利用第一个数据进行模型大小的对比、分析。第一个三维数据的大小为300×300×300,为了充分利用GPU的计算效率,将网络的输入分别设置为64×64×64、128×128×128、256×256×256并进行测试。从预测所用的时间来看,这三种情况下都在5s之内完成了测试,所用时间相近。测试结果如图 6所示。由图可见,以64×64×64作为输入效果最差,断层连续性被严重破坏;而以256×256×256作为输入效果最好,断层识别精度高,预测的断层更加连续(图 6箭头处)。测试结果表明,网络输入越大,地震数据信息及断层特征更丰富,检测到的断层更连续、准确。
一般情况下,使用训练好的模型进行实际数据应用时,如果三维地震数据某个维度的大小超过了256,则在这个维度上选取256作为输入的大小就可以得到相对优异的预测结果。因此,可以通过分块预测、采用边界加权叠加的方法进行输出数据的拼接。图 7对比了数据输出时分别采用和不采用加权叠加方法得到的结果。如果不做任何处理直接进行拼接,将会在拼接处出现如图 7a箭头所示的断层不连续的现象。在加权函数选取中,本文选取高斯权重函数进行加权叠加,使预测断层更加连续,拼接痕迹明显减少(图 7b)。

|
图 7 不同拼接方式预测结果对比 (a) 时间切片;(b)直接拼接;(c)边界高斯加权拼接 |
在实际数据应用中,如果以200×200×200的大小作为输入(图 8a)时,就会出现断层无法预测的现象,原因是网络需要进行5次池化层的操作,即将原始输入的图像缩小了25(32)倍,32无法被200整除,所以导致200×200×200大小的数据无法预测。本文将这定义为数据不规则情况下的预测问题。为了解决这个问题,将数据向上扩展到最近的一个能够被32整除的数据,即224,被扩充的部分数值为原始矩阵的均值。与128×128×128大小作为输入并进行重叠边界处理后的结果(图 8b)相比,将数据扩充以224×224×224作为输入识别的断层(图 8c)更加连续,准确性更高。

|
图 8 数据不规则预测结果对比 (a)地震数据剖面;(b)使用大小128输入并拼接;(c)边缘数据扩充到224作为输入 |
残差模块的加入可提升断层识别能力。实际数据应用中采用256×256×256大小作为输入,重叠部分拼接长度为15,整个预测过程在几秒内即可完成。图 9展示了其在两个训练模型上的应用结果对比。可以看出,相较于U-Net网络,ResU-Net预测断层更准确、连续性更好(图 9中黑色虚线圆圈标注处);同时,ResU-Net网络预测的断层线更细致(图 9中箭头处)。

|
图 9 两个网络训练模型的实际数据应用效果对比 (a)地震数据剖面;(b)U-Net(Conv 45)预测结果;(c)ResU-Net(Res-50)预测结果 |
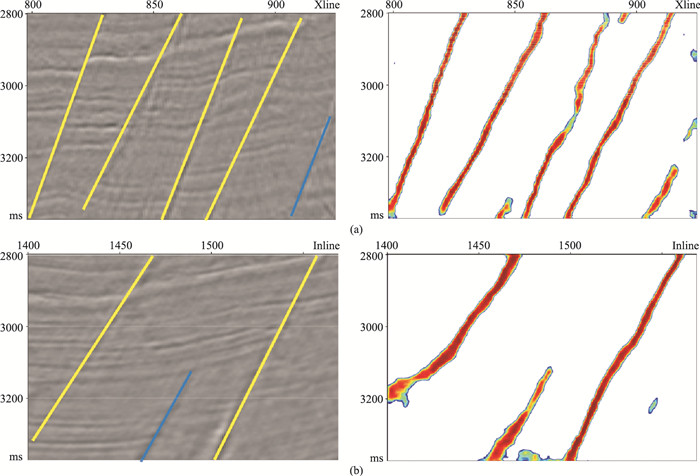
为了证明模型的泛化能力,利用其他两个三维数据进行测试,图 10和图 11分别为对应于图 5b和图 5c的三维数据体断层预测结果。结果表明,两个三维数据体的断层预测结果与实际数据体断层解释结果一致,验证了本文网络模型在实际数据应用中具有良好的泛化能力。
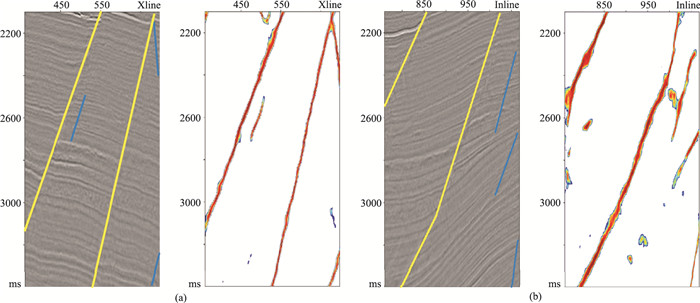
|
图 10 图 5b三维数据体地震剖面(左)及断层预测结果(右)对比 (a)Inline测线;(b)Xline测线 |
|
图 11 图 5c三维数据体地震剖面(左)及断层预测结果(右)对比 (a)Inline测线;(b)Xline测线 |
网络模型的抗噪能力是机器学习应用于断层检测过程中非常重要的一个方面,通过加入随机噪声的实际数据进行训练可检验模型的抗噪能力。首先向地震数据中加入一定强度的高斯噪声(15dB和10dB),为了方便凸显不同信噪比条件下剖面的差异,选择地震波形显示方式进行展示(图 12)。与图 12a中Inline地震剖面相比,图 12b、图 12c中同相轴很模糊,有效信号被噪声掩盖,构造特征无法凸显。将这三组数据输入到本文提出的网络模型中进行断层预测。可以看出,尽管在地震数据中存在较强噪声干扰的情况下,信噪比为15dB地震数据(图 12b右)与原始地震数据的预测结果(图 12a右)基本一致,与人工解释断层结果也吻合较好,表明本文网络模型抗噪能力强。而在信噪比为10dB的情况下,也能够将大部分断层准确识别(图 12c右),但是在黑色虚线圆圈标注处的断层未能很好地识别。这可能因为此区域噪声对同向轴干扰相对较强,从而影响了模型对断层识别的效果。考虑到训练样本标签数据集的合成过程中已经加入了一定强度的随机噪声,因此向数据集中加入多种噪声、对预测数据采取更好的去噪处理是进一步提高断层识别精度的两个重要手段。

|
图 12 不同信噪比条件数据体(左)及断层预测预测结果(右)对比 (a)原始实际数据;(b)信噪比为15dB;(c)信噪比为10dB |
本文结合U-Net与Res-50残差模块提出了一种运算高效且泛化能力强的地震数据断层检测深度学习网络。利用合成数据集进行网络训练建立的断层检测模型,在不同的三维数据体上的测试应用均取得较好的结果,预测的断层准确性高、连续性好,并且抗噪能力强。
| [1] |
Bahorich M, Farmer S. 3-D seismic discontinuity for faults and stratigraphic features: The coherence cube[J]. The Leading Edge, 1995, 14(10): 1053-1058. DOI:10.1190/1.1437077 |
| [2] |
Marfurt K J, Kirlin R L, Farmer S L, et al. 3-D seismic attributes using a semblance based coherency algorithm[J]. Geophysics, 1998, 63(4): 1150-1165. DOI:10.1190/1.1444415 |
| [3] |
Gersztenkorn A, Marfurt K J. Eigenstructure-based coherence computations as an aid to 3-D structural and stratigraphic mapping[J]. Geophysics, 1999, 64(5): 1468-1479. DOI:10.1190/1.1444651 |
| [4] |
Yang L, Gao J, Liu N, et al. A coherence algorithm for seismic data analysis based on the mutual information[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(6): 967-971. DOI:10.1109/LGRS.2018.2886768 |
| [5] |
仲伟军, 姚卫江, 贾春明, 等. 地震多属性断裂识别技术在中拐凸起石炭系中的应用[J]. 石油地球物理勘探, 2017, 52(增刊2): 135-139. ZHONG Weijun, YAO Weijiang, JIA Chunming, et al. Fault and fracture identification in Carboniferous, Zhongguai Uplift, Junggar Basin with seismic multi-attributes[J]. Oil Geophysical Prospecting, 2017, 52(S2): 135-139. |
| [6] |
Andy R. Curvature attributes and their application to 3D interpreted horizons[J]. First Break, 2001, 19(2): 85-100. DOI:10.1046/j.0263-5046.2001.00142.x |
| [7] |
吕丙南, 陈学华, 徐赫, 等. 空间域加窗二维希尔伯特变换在三维地震资料体边缘检测中的应用[J]. 石油地球物理勘探, 2020, 55(3): 661-668. LYU Bingnan, CHEN Xuehua, XU He, et al. Application of spatial-windowed 2D Hilbert transform in vo-lumetric edge detection of 3D seismic data[J]. Oil Geophysical Prospecting, 2020, 55(3): 661-668. |
| [8] |
姜岩, 程顺国, 王元波, 等. 大庆长垣油田断层阴影地震正演模拟及校正方法[J]. 石油地球物理勘探, 2019, 54(2): 320-329. JIANG Yan, CHENG Shunguo, WANG Yuanbo, et al. Seismic forward modeling for correction of fault shadow zones in Changyuan Oilfield, Daqing[J]. Oil Geophysical Prospecting, 2019, 54(2): 320-329. |
| [9] |
冯连勇, 黎莉, 裴勇. 胜利油田岩性油藏勘探中的地震技术[J]. 石油地球物理勘探, 2006, 41(2): 211-215. FENG Lianyong, LI Li, PEI Yong. Seismic technology in lithologic reservoir prospecting of Shengli oilfield[J]. Oil Geophysical Prospecting, 2006, 41(2): 211-215. DOI:10.3321/j.issn:1000-7210.2006.02.019 |
| [10] |
袁联生. 塔里木盆地玉北地区中下奥陶统断溶体识别[J]. 石油物探, 2020, 59(4): 628-636. YUAN Liansheng. Identifying fault-karst reservoirs in Middle-Lower Ordovician carbonates[J]. Geophysical Prospecting for Petroleum, 2020, 59(4): 628-636. DOI:10.3969/j.issn.1000-1441.2020.04.013 |
| [11] |
董守华, 石亚丁, 汪洋. 地震多参数BP人工神经网络自动识别小断层[J]. 中国矿业大学学报, 1997, 26(3): 16-20. DONG Shouhua, SHI Yading, WANG Yang. Automatic recognition of small fault by BP artificial ner-vous network from multiple seismic parameters[J]. Journal of China University of Mining & Technology, 1997, 26(3): 16-20. |
| [12] |
Chehrazi A, Rahimpour-Bonab H, Rezaee M R. Seismic data conditioning and neural network-based attribute selection for enhanced fault detection[J]. Petroleum Geoscience, 2013, 19(2): 169-183. DOI:10.1144/petgeo2011-001 |
| [13] |
Huang L, Dong X, Clee T E. A scalable deep learning platform for identifying geologic features from seismic attributes[J]. The Leading Edge, 2017, 36(3): 249-256. DOI:10.1190/tle36030249.1 |
| [14] |
Zhao T, Mukhopadhyay P. A fault-detection workflow using deep learning and image processing[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 1966-1970.
|
| [15] |
Wu X, Liang L, Shi Y, et al. FaultSeg3D: Using synthetic data sets to train an end-to-end convolutional neural net-work for 3D seismic fault segmentation CNN for 3D fault segmentation[J]. Geophysics, 2019, 84(3): IM35-IM45. DOI:10.1190/geo2018-0646.1 |
| [16] |
Liu N, He T, Tian Y, et al. Common azimuth seismic data fault analysis using residual U-Net[J]. Interpretation, 2020, 8(3): 1-41. |
| [17] |
He K, Zhang X, Ren S, et al. Deep residual learning for image recognition[C]. Computer Vision and Pattern Recognition, 2016, 770-778.
|
| [18] |
Tingdahl K M, De R M. Semi-automatic detection of faults in 3D seismic data[J]. Geophysical Prospecting, 2005, 53(4): 533-542. DOI:10.1111/j.1365-2478.2005.00489.x |
| [19] |
Zhang C, Frogner C, Araya-Polo M, et al. Machine-learning based automated fault detection in seismic traces[C]. Extended Abstracts of 76th EAGE Conference and Exhibition, 2014.
|
| [20] |
Xiong W, Ji X, Ma Y, et al. Seismic fault detection with convolutional neural network[J]. Geophysics, 2018, 83(5). |
| [21] |
Araya-polo M, Dahlke T, Frogner C, et al. Automated fault detection without seismic processing[J]. The Leading Edge, 2017, 36(3): 208-214. DOI:10.1190/tle36030208.1 |
| [22] |
Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation[C]. International Conference on Medical Image Com-puting and Computer-Assisted Intervention, 2015, 234-241.
|
| [23] |
Long J, Shelhamer E, Darrell T. Fully Convolutional Networks for Semantic Segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 39(4): 640-651. |
| [24] |
Xie S, Tu Z. Holistically-nested edge detection[J]. International Journal of Computer Vision, 2017, 125(5): 3-18. |



 杨佳润, 北京市昌平区府学路18号中国石油大学(北京)CNPC物探重点实验室, 102249。Email:
杨佳润, 北京市昌平区府学路18号中国石油大学(北京)CNPC物探重点实验室, 102249。Email: 
