② 中国科学技术大学地球和空间科学学院, 安徽合肥 230026;
③ 中国石化石油勘探开发研究院, 北京 100083;
④ 中石油塔里木油田分公司勘探开发研究院, 新疆库尔勒 841000
② School of Earth and Space Sciences, University of Science and Technology of China, Hefei, Anhui 230026, China;
③ SINOPEC Petroleum Exploration and Production Research Institute, Beijing 100083, China;
④ Research Institute of Petroleum Exploration and Development, PetroChina Tarim Oilfield Company, Korla, Xinjiang 841000, China
目前,中国东部各油气田的主力区块已经达到中、高勘探程度,勘探方向从以构造油气藏为主转向以岩性地层油气藏为主[1]。准确地预测岩性是岩性地层油气藏勘探的重要环节,同时也是储层特征研究、储量计算和地质建模的基础[2]。
在地震储层预测领域,岩性预测主要有地震属性分析和地震反演两种方法。在地震属性分析方面,赵谦等[3]利用地震波波形分类识别砂、泥岩;黄凤祥等[4]利用均方根振幅属性识别基性侵入岩。在地震反演方面,孙明等[5]应用叠后纵波阻抗反演预测目的层段的岩性;黄饶等[6]通过叠前同时反演预测目标层岩性。
以上列举的地震岩性预测方法虽然在实际应用中都取得了较好的效果,但也存在着一定的局限性。洪忠等[7]基于大量实践认为,不同岩相的地震振幅、频率、相位、时间厚度等差异是应用波形分类方法的前提,当岩相间的地震响应差别不明显或同一岩相横向波形变化较快,而无法建立统一的岩相地震波形特征时,根据波形分类的结果不能准确地划分岩相,也没有明确的地质意义。基于地震属性分析的岩性预测方法的局限性主要在于:所选取的地震属性可能对岩性不敏感,通过单一属性难以准确预测岩性。对于基于地震反演的岩性预测方法来说,在统计各种岩性的某一弹性参数范围或进行弹性参数交会分析时,会受限于弹性参数重叠的情况[8]。此外,在利用交会图划分岩性时,一般都采取粗略的描述或者手工勾绘,这种方法存在很大的不确定性[9]。
近年来,机器学习算法的飞速发展受到了各行业的关注。在地震储层预测领域,一些学者将机器学习算法应用于岩性预测。李国和等[10]以全频和分频振幅数据作为输入、以岩性数据作为输出、以深度置信网络(Deep Belief Networks)作为分类识别模型,利用地震数据识别岩性。张国印等[11]将测井数据和井旁地震道时频谱分别作为标签和输入,训练卷积神经网络(Convolutional Neural Networks,CNN),充分挖掘地震数据高频和低频信息并预测岩性。杨璐等[12]建立多种地震属性与岩性类别标签之间的随机森林(Random Forests,RF)分类模型并用于岩性预测。基于机器学习的岩性预测方法的优势在于:①扩展了岩性划分的特征空间维度,单一地震属性或单一岩石弹性参数为一维,弹性参数交会分析方法为二维,而机器学习算法可在三维甚至更高维度的特征空间划分岩性;②与在交会图上采取粗略描述或者手工勾绘的传统方法相比,机器学习算法降低了人为因素带来的不确定性。
目前应用于岩性预测的机器学习算法主要是有监督分类算法,需要使用已经标记好类别的样本训练分类器,使分类器有能力预测未知类别的样本。但这类方法存在一个缺陷,即在不同类别样本数量差别很大的不平衡样本集上训练时,往往会出现分类面向多数类样本偏倚的现象,而少数类样本无法获得理想的分类效果[13]。对于岩性预测而言,当样本集中目标岩性(如砂岩)样本过少,而非目标岩性(如泥岩)样本过多时,将会使预测结果向非目标岩性偏倚,导致目标岩性的预测准确率较低。
为了解决这一问题,本文提出一种针对不平衡样本集的随机森林岩性预测方法。首先,以录井岩性数据作为岩性样本标签,以井旁道地震属性和岩石弹性参数作为岩性样本特征构建岩性样本集;其次,将近邻清除算法(Near Miss, NM)[14]与合成少数类过采样算法(Synthetic Minority Over-sampling Technique, SMOTE)[15]相结合,形成NM-SMOTE算法,对岩性样本集进行平衡化;然后,用平衡化的岩性样本集训练随机森林分类器,建立多种地震属性、弹性参数与岩性之间的非线性关系;最后,将目标区的地震属性和弹性参数输入随机森林分类器预测岩性,以期获得与地震资料吻合程度更高的岩性数据体。
1 方法原理 1.1 井震数据匹配选取录井岩性数据作为岩性样本标签。一般来说,录井数据中记录的是各种岩性的顶、底界深度。为了获得足够多的岩性样本,需要在各种岩性的顶、底界之间按照测井数据的采样率(以0.125m为间隔)均匀插值。然后,通过井震标定获得准确的时深关系,将录井岩性数据从深度域转换到时间域。由于地震数据与录井岩性数据的时间采样率不同,因此还需要对录井岩性数据重采样,将其转换为与地震数据相同的采样率(2ms)。
前人研究[3-6]表明,利用地震属性和反演所得的弹性参数皆可预测岩性。因此,本文从井旁道中提取多种地震属性和弹性参数作为岩性样本特征,与转换到时间域且重采样后的录井岩性数据组成样本集。岩性样本特征与标签的匹配方式为“点-点”匹配,即对于某一口井来说,将同一时间采样点上的地震属性、弹性参数和录井岩性数据进行匹配,形成该井的岩性样本集,如图 1所示。
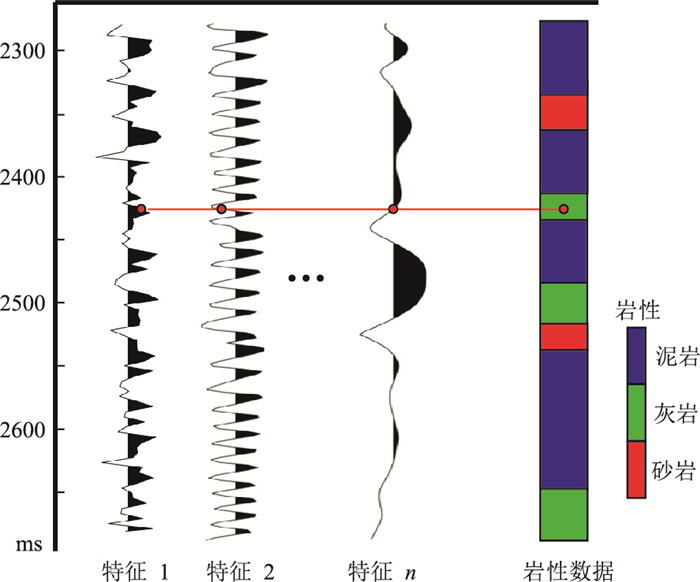
|
图 1 岩性样本特征与标签的“点-点”匹配方法将泊松比、能量半衰时、瞬时振幅等作为不同特征 |
NM-SMOTE算法是一种对多数类样本欠采样(Under-sampling)、同时对少数类样本过采样(Over-sampling)的平衡化算法。由于NM-SMOTE算法需要计算特征空间中样本之间的距离,因此引入特征空间中样本距离的概念,即在由m个特征组成的特征空间中,任意两个样本的坐标可以表示为x1(f11, f12, …, f1m)和x2(f21, f22, …, f2m),x1和x2的距离为
| $ D\left(x_{1}, x_{2}\right)=\sqrt{\sum\limits_{i=1}^{m}\left(f_{1 i}-f_{2 i}\right)^{2}} $ | (1) |
式中:f1i和f2i分别表示样本x1和x2的各个特征;m为特征个数。NM-SMOTE算法的步骤如下。
(1) 根据样本不平衡比例,设置多数类样本欠采样后的数量NU和少数类样本过采样后的数量NO,NU与NO应相对平衡。
(2) 对于少数类样本,利用SMOTE增加样本数量。SMOTE算法为:①在特征空间中,随机选取一个少数类样本x,利用式(1)计算x与其他所有少数类样本的距离,得到与x距离最近的k个少数类样本;②在k个少数类样本中随机选取一个少数类样本x',在x与x'之间的某一点上合成新的少数类样本xnew,即
| $ x_{\text {new }}=x+\operatorname{rand}(0, 1) \times\left(x^{\prime}-x\right) $ | (2) |
式中rand(0, 1)表示0~1之间的随机数;③重复步骤①~②,直到少数类样本的数量增加到预设值NO为止。
(3) 对于多数类样本,利用NM算法减少样本数量:①在特征空间中,由式(1)计算每个多数类样本和与之距离最近的k个少数类样本的平均距离;②删除与最近的k个少数类样本平均距离最短的多数类样本;③重复步骤②,直到多数类样本的数量减少到预设值NU为止。
图 2展示了当m=2时,利用NM-SMOTE算法对一个不平衡样本集进行平衡化的过程。由图 2a可以看出,受样本数量不平衡的影响,在特征空间中无法正确地划分两类样本的分类区域。若在此不平衡样本集上训练分类器,则少数类样本会被误分为多数类样本。根据NM-SMOTE算法步骤,首先对少数类样本进行SMOTE过采样(图 2b),增加样本数量(图 2c);然后对多数类样本进行NM欠采样(图 2d),减少样本数量(图 2e)。在使用NM-SMOTE平衡化算法后,样本集中的两类样本数量达到平衡状态,并且在特征空间中能够更好地区分。利用该样本集训练分类器,可有效地降低少数类样本被误分的风险。
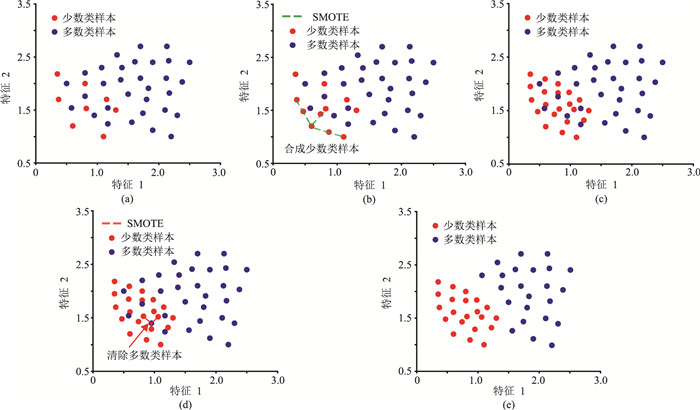
|
图 2 NM-SMOTE算法步骤 (a)不平衡样本集;(b)SMOTE过采样;(c)通过SMOTE增加少数类样本;(d)NM欠采样;(e)两类样本数量达到平衡 |
随机森林分类器(Random Forests Classifier,RFC)[16]是一种集成了多个决策树的机器学习算法。RFC通过Bootstrap抽样[17](有放回地随机抽样)从原始样本集中抽取多个子集用于构建决策树,每一个决策树在节点分裂时都通过随机特征选取的方式寻找最优的分割方案。与单个决策树分类器相比,RFC具有预测精度高且不容易出现过拟合的优点。RFC在训练过程中,可以同时计算每一种样本特征的重要性,重要性越高的样本特征对RFC的预测准确率影响越大。在此基础上,本文设计了一种根据样本特征重要性优化RFC的方法,可以在训练RFC的同时优选样本特征,提升RFC的预测准确率。
针对不平衡岩性样本集,从中随机选取一部分(如75%)样本作为训练样本集,记为Ωa,剩余样本作为测试样本集Ωb。假设Ωa中共有m个岩性样本特征,对Ωa进行NM-SMOTE平衡化,得到Ω'a,用于训练RFC,获得m个岩性样本特征的重要性。然后,基于RFC输出的特征重要性优化分类器,同时优选岩性样本特征,主要步骤为:
(1) 基于十折交叉验证[18]的思想,将未经平衡化的训练样本集Ωa随机分为10份,选取其中9份进行NM-SMOTE平衡化用于训练RFC;剩余一份用于验证RFC的预测准确率σm(下标m代表Ωa中有m个岩性样本特征,下同)。将交叉验证过程中准确率最高的RFC模型记为Rm。重复这一过程,直到十份样本都完成了一次验证。将10次验证的准确率取均值,作为在m个特征下训练得到的RFC的平均准确率
(2) 根据特征重要性,剔除重要性最低的一种特征,记特征个数m=m-1,执行步骤(1)。
(3) 重复步骤(2),直到m=1。
(4) 取最高的平均准确率
最后,用测试样本集Ωb测试最优RFC模型的准确率,若满足要求(如不低于80%)则可用于岩性预测;否则调整RFC参数或更换训练样本集,重新训练RFC。针对不平衡样本集的随机森林岩性预测流程如图 3所示。
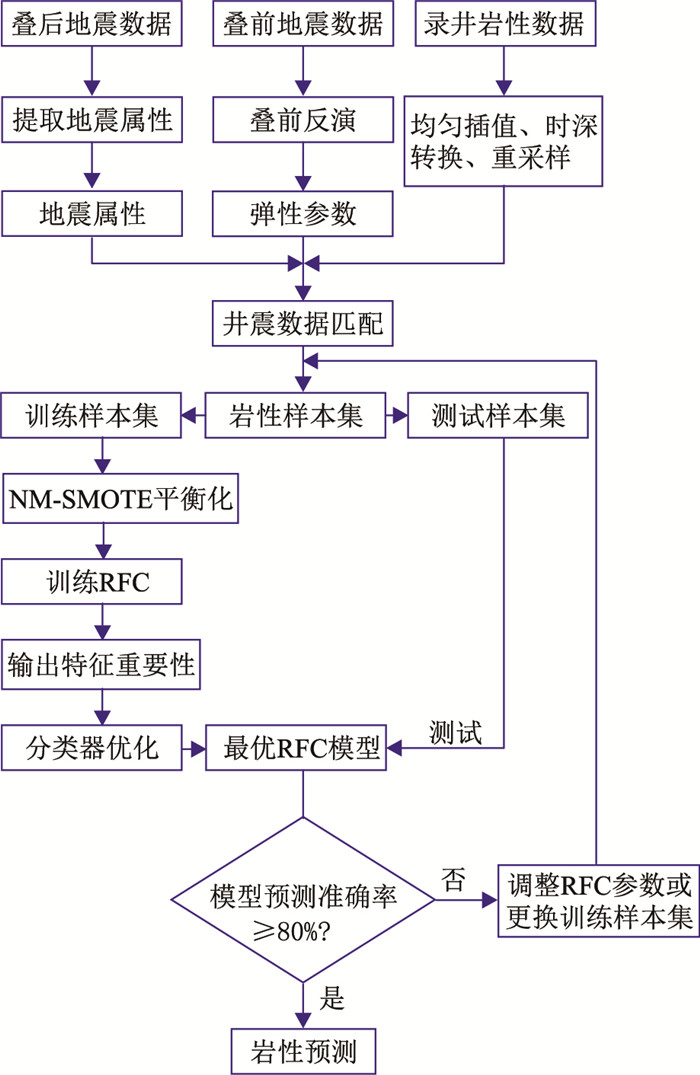
|
图 3 不平衡样本集随机森林岩性预测方法流程 |
在分类问题中,准确率是一种用于衡量分类器预测性能的常用指标,即
| $ \sigma(y, \hat{y})=\frac{1}{n} \sum\limits_{i=1}^{n} T\left(\hat{y}_{i}=y_{i}\right) $ | (3) |
式中:n表示样本数量;yi和ŷi分别表示第i个样本的真实值和预测值;T(x)为指示函数,若满足条件x,则T(x)=1,否则T(x)=0。但对不平衡样本集来说,如果有90个标签为“0”的样本、10个标签为“1”的样本,而分类器将100个样本都预测为“0”,尽管无法预测出任何一个标签为“1”的样本,分类器仍然有90%的准确率,这显然不能正确反映分类器的预测性能。针对这一问题,本文使用平衡准确率(Balanced Accuracy)[19]代替普通的准确率作为衡量分类器预测性能的指标,即
| $ \sigma_{b}(y, \hat{y}, \omega)=\frac{1}{\sum\limits_{i=1}^{n} \hat{\omega}_{i}} \sum\limits_{i=1}^{n} T\left(\hat{y}_{i}=y_{i}\right) \hat{\omega}_{i} $ | (4) |
其中
| $ \hat{\omega}_{i}=\frac{\omega_{i}}{\sum\limits_{j=1}^{n} T\left(y_{j}=y_{i}\right) \omega_{j}} $ | (5) |
式中:i和j都表示样本编号;ωi表示第i个样本对应的类别所占的样本比例。简单来说,平衡准确率计算分类器对每一类样本预测准确率的均值,不会受到样本类别数量不平衡的影响,更加适用于衡量分类器对不平衡样本集的预测效果。本文算法程序使用Imbalanced-learn、Scikit-learn、NumPy和Pandas等工具包在Python3.6上编程搭建。
2 实际资料应用选取济阳坳陷渤南地区某工区的三维叠前、叠后地震数据以及工区内14口井的录井数据资料,应用本文方法预测岩性。
研究区发育湖相沉积,具有地层薄、岩性垂向变化快、岩性复杂等特点。录井数据揭示区内主要有泥岩、灰岩、白云岩、砂岩、页岩和石膏岩等六类岩性,目标岩性为砂岩和页岩。岩石物理特征非常复杂(图 4),在弹性参数交会图上各种岩性参数重叠在一起,因此无法应用常规地震反演方法预测岩性。
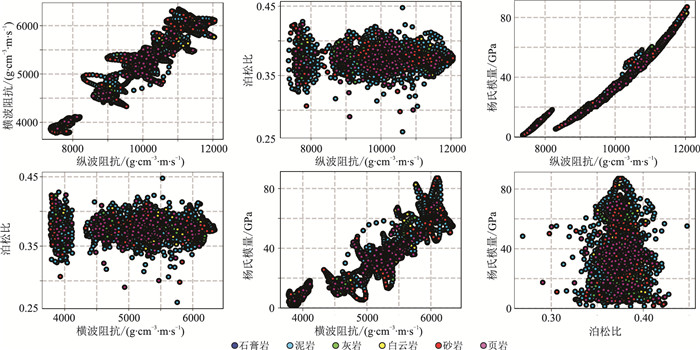
|
图 4 岩石弹性参数交会分析 |
充分发挥机器学习算法在高维度特征空间中划分岩性的优势,综合地震属性分析和地震反演两种岩性预测方法,从三维叠后地震数据中提取与地层岩性相关的振幅、均方根振幅、振幅加速度、弧长、能量半衰时、品质因子、平均频率、频率变化率、瞬时振幅、瞬时频率和瞬时带宽等共11种地震属性[20],并应用基于Zoeppritz方程的纵横波模量反演方法[21]得到纵波阻抗、横波阻抗、杨氏模量和泊松比,与地震属性一起组成15种岩性样本特征。根据本文的井震数据匹配方法,将工区内14口井的录井岩性数据作为岩性样本标签,与井旁道的15种岩性样本特征匹配,然后形成岩性样本集。
随机选取一口井的岩性样本作为测试样本集,其余井的岩性样本作为训练样本集,重复这一过程,直到每一口井都完成了一次测试,得到14组训练样本集和测试样本集。14组训练样本集的平均岩性样本数量为2686个,分布如图 5a所示,其中,泥岩样本为2089个,占比高达78%,石膏岩、灰岩、白云岩、砂岩、页岩样本分别为41、113、52、162、229个。每一组训练样本集都属于不平衡样本集,样本不平衡比例最高达到50∶1。将泥岩视为多数类样本,其余岩性视为少数类样本,通过NM-SMOTE算法对每一组训练样本集进行平衡化,平衡化后所有训练样本集中各类岩性样本的平均数量如图 5b所示。

|
图 5 原训练样本集(a)和NM-SMOTE平衡化后训练样本集(b)岩性样本分布 |
对每一组训练样本集设置RFC决策树个数t=300,随机特征选取个数

|
图 6 岩性样本特征重要性 |
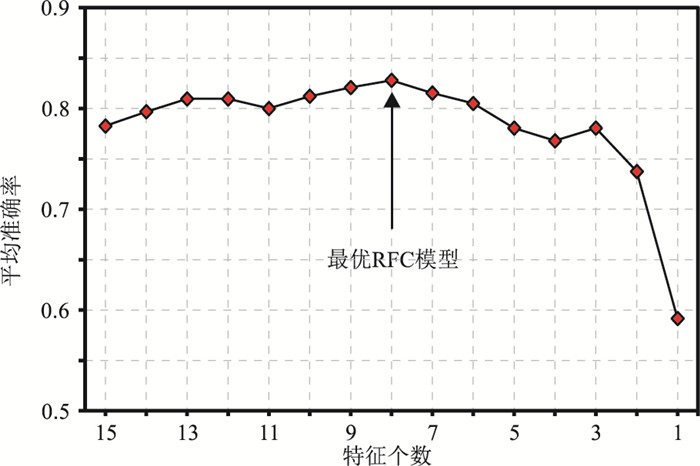
由于岩性样本特征较多,一些冗余的特征会使RFC的预测准确率降低,因此使用本文提出的RFC优化方法优选岩性样本特征组合,得到最优的RFC模型。图 7为岩性样本特征优选与RFC优化过程,当选择重要性排名前八位的岩性样本特征(即横波阻抗、纵波阻抗、杨氏模量、频率变化率、瞬时带宽、平均频率、瞬时频率和振幅加速度)对RFC进行十折交叉验证时,RFC的平均准确率最高。若选取的特征过少,则由于有效特征信息的丢失,RFC的预测准确率将会下降。
|
图 7 岩性样本特征优选与RFC优化 |
以优选的岩性样本特征作为输入,使用RFC预测研究区的岩性。将NM-SMOTE算法与两种常用的样本集不平衡问题解决方法,即惩罚系数法[22](在训练过程中提高少数类分类错误的成本)和随机欠采样(Random Under-sampling,RUS)-SMOTE[23]算法作对比,分析单井和三维空间岩性预测效果。
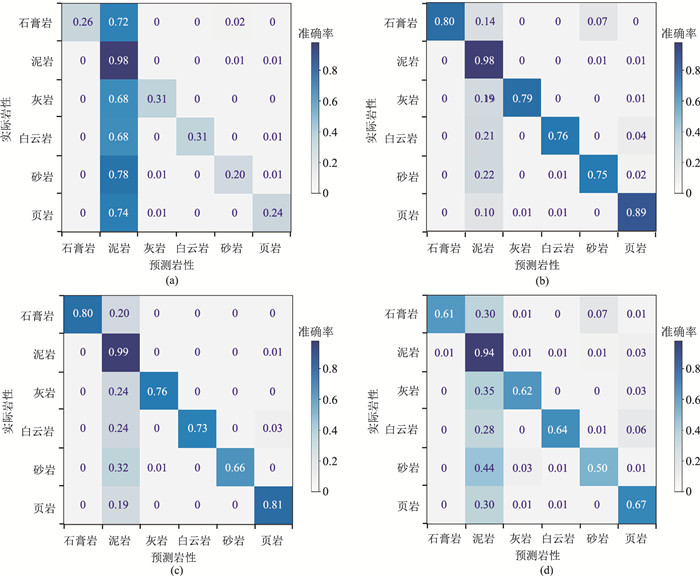
3.1 单井岩性预测效果计算14口井数据分别作为测试样本集时预测岩性与实际岩性的混淆矩阵,取平均值得到最终结果,如图 8所示,矩阵中的数字表示预测岩性数量占实际岩性数量的比例,对角线元素即为每类岩性的预测准确率。图 8a为用未经平衡化的样本集训练RFC得到的预测结果,由于训练样本集中泥岩样本过多,大量少数类岩性被误分为泥岩,RFC对页岩和砂岩这两种目标岩性的预测准确率分别为24%和20%,六类岩性平均预测准确率仅为38%。样本集经NM-SMOTE平衡化后,RFC对少数类岩性的误分类得到改善,页岩和砂岩的预测准确率分别提升至89%和75%,六类岩性平均预测准确率提升至83%(图 8b)。在训练RFC时用惩罚系数提高少数类岩性的误分代价,也可以提高RFC对少数类岩性的预测准确率,效果与NM-SMOTE算法相当,六类岩性平均预测准确率为79%(图 8c)。RUS-SMOTE算法在欠采样过程中采用随机减少多数类样本的策略,虽然能够使少数类样本与多数类样本的数量达到平衡,但与NM算法相比,RUS算法不能保证欠采样后,在特征空间中能很好地区分多数类样本与少数类样本。因此,与NM-SMOTE算法相比,应用RUS-SMOTE算法平衡化训练样本集后,RFC对少数类岩性的预测准确率较低,页岩和砂岩的预测准确率分别为67%和50%,同时RFC对泥岩的预测准确率也降低了4%,六类岩性的平均预测准确率为66%(图 8d)。
|
图 8 不同方法预测单井岩性效果 (a)RFC+不平衡样本集;(b)RFC+NM-SMOTE算法;(c)RFC+惩罚系数法;(d)RFC+RUS-SMOTE算法 |
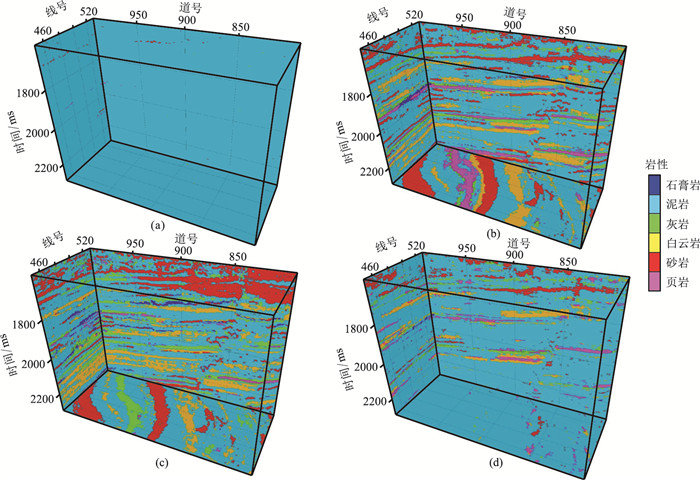
图 9为研究区的三维地震数据体,可见右侧发育有一条正断层。使用未经平衡化的样本集训练RFC会使岩性预测结果向泥岩严重偏倚,无法反映页岩、砂岩等少数类岩性的分布情况(图 10a)。在使用NM-SMOTE算法(图 10b)、惩罚系数法(图 10c)和RUS-SMOTE算法(图 10d)解决样本集不平衡问题后,RFC对少数类岩性的预测准确率得到提升,预测结果展现出多种岩性的空间分布情况,三种方法均能改善岩性预测效果。从细节来看,与惩罚系数法和RUS-SMOTE算法相比,NM-SMOTE算法对应的岩性预测结果与实际地震资料吻合程度更高,地层连续性更好,断层构造更清晰,反映的岩性信息也更丰富。

|
图 9 研究区三维地震数据体 |
|
图 10 不同方法预测三维岩性效果 (a)RFC+不平衡样本集;(b)RFC+NM-SMOTE算法;(c)RFC+惩罚系数法;(d)RFC+RUS-SMOTE算法 |
随机森林算法可以建立多种地震属性、岩石弹性参数与岩性之间的非线性关系,是在岩石物理特征复杂区域预测岩性的有效手段。然而,随机森林算法受训练样本的影响较大,在目标岩性样本远少于非目标岩性样本的不平衡样本集上训练时,岩性预测结果将向非目标岩性严重偏倚,无法准确预测目标岩性。
本文提出的针对不平衡样本集的随机森林岩性预测方法,通过应用NM-SMOTE平衡化算法解除了不平衡样本集对随机森林岩性预测的限制,拓宽了随机森林岩性预测方法的适用范围。实际数据测试结果证明,即使在样本集中目标岩性样本远少于非目标岩性样本,应用该方法也可准确预测目标岩性,并且效果优于解决样本集不平衡问题常用的惩罚系数法和RUS-SMOTE算法,获得的岩性数据体与地震资料吻合程度更高。
NM-SMOTE算法作为一种样本集平衡化方法,也可配合除随机森林外的其他机器学习分类算法预测岩性。该方法也存在缺陷,即对于多分类问题,目前只能在特征空间中减小多数类样本与少数类样本的重叠区域,而没有考虑不同类别的少数类样本间也存在重叠的情况。如何应用机器学习算法高效且准确地预测岩性,还需要进一步更深入地研究。
| [1] |
李玉存, 李君, 孙明, 等. 地震解释技术在高北斜坡带中深层岩性圈闭评价中的应用[J]. 石油地球物理勘探, 2017, 52(增刊1): 207-213. LI Yucun, LI Jun, SUN Ming, et al. Seismic interpretation techniques for middle and deep lithological trap evaluation in Gaobei Slope[J]. Oil Geophysical Prospecting, 2017, 52(S1): 207-213. |
| [2] |
付光明, 严加永, 张昆, 等. 岩性识别技术现状与进展[J]. 地球物理学进展, 2017, 32(1): 26-40. FU Guangming, YAN Jiayong, ZHANG Kun, et al. Current status and progress of lithology identification technology[J]. Progress in Geophysics, 2017, 32(1): 26-40. |
| [3] |
赵谦, 周江羽, 张莉, 等. 利用地震波形-振幅响应技术预测海相碎屑岩岩性组合——以北康盆地为例[J]. 石油地球物理勘探, 2017, 52(6): 1280-1289. ZHAO Qian, ZHOU Jiangyu, ZHANG Li, et al. Prediction of marine clastic rocks assemblage with seismic waveform and amplitude responses: an example in Beikang Basin, South China Sea[J]. Oil Geophysical Prospecting, 2017, 52(6): 1280-1289. |
| [4] |
黄凤祥, 夏振宇, 马秀玲, 等. 基于测井和地震技术变质岩潜山岩性识别与预测[J]. 断块油气田, 2016, 23(6): 721-725. HUANG Fengxiang, XIA Zhenyu, MA Xiuling, et al. Identification and prediction of metamorphic buried hill lithology based on logging and seismic technology[J]. Fault-Block Oil<Gas Field, 2016, 23(6): 721-725. |
| [5] |
孙明, 廖军, 陈伟超, 等. 南堡凹陷东部扇三角洲砂岩地震预测技术及应用[J]. 石油地球物理勘探, 2017, 52(增刊1): 128-133. SUN Ming, LIAO Jun, CHEN Weichao, et al. Seismic fan-delta sand prediction in the eastern Nanpu Depression[J]. Oil Geophysical Prospecting, 2017, 52(S1): 128-133. |
| [6] |
黄饶, 刘志斌. 叠前同时反演在砂岩油藏预测中的应用[J]. 地球物理学进展, 2013, 28(1): 380-386. HUANG Rao, LIU Zhibin. Application of prestack simultaneous inversion in sandstone oil reservoir prediction[J]. Progress in Geophysics, 2013, 28(1): 380-386. |
| [7] |
洪忠, 张猛刚, 苏明军. 应用地震波形分类技术识别岩相的适用性和局限性[J]. 物探与化探, 2013, 37(5): 904-910. HONG Zhong, ZHANG Menggang, SU Mingjun. The applicability and limitations of the seismic waveform classification technology to the identification of litho-logical facies[J]. Geophysical & Geochemical Exploration, 2013, 37(5): 904-910. |
| [8] |
田玉昆, 周辉, 袁三一. 基于马尔科夫随机场的岩性识别方法[J]. 地球物理学报, 2013, 56(4): 1360-1368. TIAN Yukun, ZHOU Hui, YUAN Sanyi. Lithologic discrimination method based on Markov random field[J]. Chinese Journal of Geophysics, 2013, 56(4): 1360-1368. |
| [9] |
李国福. 多参数储层预测及流体识别方法研究[D]. 四川成都: 成都理工大学, 2011. LI Guofu. Multi-parameter Reservoir Prediction and Fluid Identification Method Research[D]. Chengdu University of Technology, Chengdu, Sichuan, 2011. |
| [10] |
李国和, 郑阳, 李莹, 等. 基于深度信念网络的多采样点岩性识别[J]. 地球物理学进展, 2018, 33(4): 1660-1665. LI Guohe, ZHENG Yang, LI Ying, et al. Lithology recognition of multi-sampling points based on deep belief network[J]. Progress in Geophysics, 2018, 33(4): 1660-1665. |
| [11] |
张国印, 王志章, 林承焰, 等. 基于小波变换和卷积神经网络的地震储层预测方法及应用[J]. 中国石油大学学报(自然科学版), 2020, 44(4): 83-93. ZHANG Guoyin, WANG Zhizhang, LIN Chengyan, et al. Seismic reservoir prediction method based on wavelet transform and convolutional neural network and its application[J]. Journal of China University of Petroleum (Edition of Natural Science), 2020, 44(4): 83-93. DOI:10.3969/j.issn.1673-5005.2020.04.010 |
| [12] |
杨璐, 宋建国. 基于随机森林的地震储层分类方法研究[C]. 2017年中国地球科学联合学术年会, 2017.
|
| [13] |
于化龙. 类别不平衡学习: 理论与算法[M]. 北京: 清华大学出版社, 2017. YU Hualong. Class Imbalanced Learning: Theories and Algorithms[M]. Beijing: Tsinghua University Press, 2017. |
| [14] |
Zhang J, Mani I. KNN approach to unbalanced data distributions: A case study involving information extraction[C]. Proceedings of the ICML'2003 Workshop on Learning from Imbalanced Datasets, 2003.
|
| [15] |
Chawla N V, Bowyer K W, Hall L O, et al. SMOTE: Synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research, 2002, 16: 321-357. DOI:10.1613/jair.953 |
| [16] |
Breiman L. Random forests[J]. Machine Learning, 2001, 45(1): 5-32. DOI:10.1023/A:1010933404324 |
| [17] |
Efron B, Tibshirani R J. An Introduction to the Bootstrap[M]. Boca Raton: CRC Press, 1994.
|
| [18] |
Kohavi R. A study of cross-validation and bootstrap for accuracy estimation and model selection[C]. International Joint Conference on Artificial Intel-ligence, 1995.
|
| [19] |
Mosley L. A Balanced Approach to the Multi-class Imbalance Problem[D]. Iowa State University, Ames, 2013.
|
| [20] |
Barnes A E. Handbook of Poststack Seismic Attri-butes[M]. Tulsa: Society of Exploration Geophysicists, 2016.
|
| [21] |
冉然, 宋建国. 基于Zoeppritz方程的纵横波模量反演[J]. 物探与化探, 2017, 41(4): 707-714. RAN Ran, SONG Jianguo. Compressional and shear modulus inversion based on Zoeppritz equation[J]. Geophysical & Geochemical Exploration, 2017, 41(4): 707-714. |
| [22] |
Chen C, Liaw A, Breiman L. Using Random Forest to Learn Imbalanced Data[R]. University of California, Berkeley, 2004.
|
| [23] |
Batista G E, Prati R C, Monard M C. A study of the behavior of several methods for balancing machine learning training data[J]. ACM SIGKDD Explorations Newsletter, 2004, 6(1): 20-29. DOI:10.1145/1007730.1007735 |



 宋建国, 山东省青岛市长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
宋建国, 山东省青岛市长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: 