② 中国石油大庆油田公司勘探事业部, 黑龙江大庆 163453
② Research Institute of Exploration and Development, Daqing Oilfield Co Ltd, PetroChina, Daqing, Heilongjiang 163453, China
近年来,尽管单一的三维重、磁、电反演,尤其是三维大地电磁(MT)反演技术正渐趋成熟,但由于单一方法的局限性、观测数据有限且难免存在观测误差等原因,使反演的多解性问题较严重,增加了地质解释的难度。不同地球物理方法对地下介质不同物性参数的敏感度不同,综合利用多种地球物理方法,可从不同角度对同一地质体进行研究。综合多种地球物理方法进行反演与解释,减小多解性,已成为当前地球物理反演研究的热点问题[1-2]。地震资料通常对中、浅层具有较高分辨率,但在某些情况下,单一地震方法所得深层构造成像并不清晰,重、磁、电勘探可作为其补充。其中大地电磁方法由于具有不受高阻层屏蔽、横向分辨能力较强且探测深度大等优点,在油气勘探领域成为地震方法的重要辅助。同时,利用已知的地震、地质、测井等资料进行重、磁、电法数据约束反演,是提高重、磁、电勘探分辨率的重要途径。
不同物性参数的耦合是联合反演的关键,这些物性参数耦合约束主要分为岩石物理关系(经验性的或统计性的)约束和结构相似性约束两大类。结构相似耦合是从几何关系上进行约束,一般约束性相对较弱。Gallardo等[3]在进行电—震联合反演时利用交叉梯度算子识别结构边界的相似性,目前交叉梯度算子已成为应用最广泛的结构相似度量方式之一,在多种联合反演中得到应用。
基于岩石物理关系的联合反演的物性参数耦合性强,反演结果精度高。许多学者已针对构建岩石物理关系这一问题展开研究。在传统的基于经验关系的岩石物理耦合方法中,先定义模型之间的关系函数,并将该函数应用于整个区域,该类方法要求先验的岩石物理关系具有较高可靠性。Colombo等[4]建立了密度、电阻率与速度的经验关系,并通过重、电、震数据联合反演圈定了隐伏盐丘;De Stefano等[5]利用Gardner公式[6]建立了地层密度与地震纵波速度的关系式,开展重力与地震旅行时数据联合反演,并通过理论模型测试表明联合反演能提高成像精度。
Zhdanov等[7]研究了一种广义的耦合方式,即基于Gramian约束的多种地球物理数据联合反演,该耦合方式不需先定义模型之间具体的关系函数。近年来,人们将模糊C均值聚类(FCM)思想引入联合反演,通过聚类思想建立不同岩石物性之间的关系,该类方法可解决传统的统计方法难以将多个岩石物理关系应用于特定区域的问题。Sun等[8-9]提出基于引导FCM技术的联合反演,并将其与岩性分类相结合,提高了反演过程的稳定性及反演结果的可靠性;Carter-Mcauslan等[10]在重—震联合反演目标函数中引入FCM聚类,利用聚类约束实现速度与密度模型的岩性耦合。
陈晓等[11]提出基于宽范围岩石物性约束的大地电磁与地震联合反演,该类方法可降低由于先验岩石物理关系不够精确带来的影响。胡祖志等[12]利用已知的测井、地震剖面等先验信息进行约束建模,并基于井—震约束的MT和重力数据实现了人工鱼群联合反演。相鹏等[13]提出一种变密度—速度关系的重力与地震同步联合反演方法。
基于岩石物理关系的联合反演的前提是可靠的岩石物理关系,而可靠的岩石物理关系一般通过实测岩心、测井曲线等资料获得,实际应用中并不一定能获得足够的上述资料。再者,目前建立的岩石物理关系是一种点对点的映射,这与实际的空间对空间的岩石物性关系是不相符的。
地质统计学中的变差函数能定量表征地质模型空间特征,反映物性值纵、横向变化规律。若尚未知晓地下地质体精确的物性统计特征,则可间接从地震信息、试井解释、地质推理与解释等获取变差函数。
本文在Yang等[14]研究的基础上,提出一种基于聚类和多元地质统计学的电—震联合建模约束反演方法:首先根据地震反演得到的速度模型、无约束MT反演得到的电阻率模型和已知钻井信息建立初始电阻率模型;再利用多元地质统计学的交叉—变差函数建立速度与电阻率之间的岩石物理关系;同时利用机器学习中的引导FCM算法进行基于岩石物理关系的多重约束反演,实现电—震联合建模;将描述地质模型特征表征为定量化数据,并与地球物理数据相结合,得到既能拟合地球物理数据,又符合地质模型特征的最优解。将本文方法应用于大杨树盆地南部坳陷实际数据,取得了令人满意的处理效果及最终综合解释成果。
1 电—震联合建模约束反演方法 1.1 技术流程各种反演方法都存在多解性,对反演结果直接进行地质解释会产生较大误差。解决该问题的常用方法是综合利用各种已知信息进行反演和解释,以提高可靠性。本文提出采取基于机器学习和多元地质统计学的联合建模约束反演方法,分四个部分:
(1) 对由叠前深度偏移(PSDM)数据反演得到速度模型降维,得到大地电磁尺度的速度模型,并对其进行聚类分析;
(2) 利用根据已知电阻率测井数据和无约束MT反演得到的电阻率模型(无测井数据时)统计的平均电阻率值对聚类后的速度模型赋值,得到新的MT反演初始模型,更新模型的协方差模型,引入地震结构约束[15];
(3) 以测井数据和MT反演结果建立反映空间统计岩石物理关系的交叉—变差函数(垂向交叉—变差函数由测井数据求得,由反演结果求得垂向与主方向和次方向交叉—变差函数的比例关系,进而确定先验交叉—变差函数[16]);
(4) 将交叉—变差函数整合到传统的目标函数中,并利用模糊约束反演(FCI)[17]进行基于岩石物理关系的多重约束反演[14]。
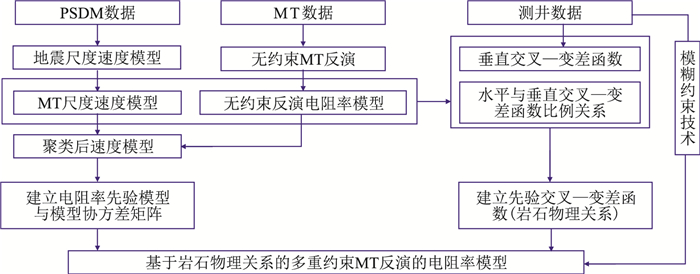
上述具体技术流程如图 1,易见基于岩石物理关系的多重约束MT反演是其中关键。
|
图 1 本文电—震联合建模约束反演技术流程 |
Kelbert等[18]提出了基于协方差矩阵的MT反演目标函数
| $ \begin{aligned} \phi(\boldsymbol{m})=&[\boldsymbol{d}-f(\boldsymbol{m})]^{\mathrm{T}} \boldsymbol{C}_{d}^{-1}[\boldsymbol{d}-f(\boldsymbol{m})]+\\ & \beta\left(\boldsymbol{m}-\boldsymbol{m}_{0}\right)^{\mathrm{T}} \boldsymbol{C}_{m}^{-1}\left(\boldsymbol{m}-\boldsymbol{m}_{0}\right) \end{aligned} $ | (1) |
式中:m是模型参数;d是实测MT数据;Cd是数据误差的协方差;f(m)是正演的MT数据;m0是初始模型;β是拉格朗日算子(正则化参数);Cm是模型协方差,也称为平滑算子,表征反演期间模型元素之间的平滑度。从理论上讲,Cm的每个元素都可针对m中的所有成对元素进行独立配置,从而可对相邻单元之间的平滑度进行相当大的微调。为了降低反演的多解性,拟采用综合不同地球物理数据的联合反演方法。对于基于岩石物理关系的联合反演而言,构建合理的岩石物理关系是关键。本文将多元地质统计学中的交叉—变差函数整合到MT反演的目标函数中,以表征速度与电阻率之间关系。
1.2.1 交叉—变差函数求取技术上已述及,地质统计学中变差函数可定量表征地质模型空间特征,反映物性值纵、横向变化规律。同时,变差函数也是地质统计学中最基本和最重要的模拟工具,用于描述数据值的空间互相关性,即数据点在空间上相距越远,相关性越小。其数值可表示为区域化变量Z(x)在x和x+h两点之差的方差的一半,此处h表示滞后距,或称距离、间隔、步长。变差函数与数据点位置无关,只依赖于h。
此处电阻率ρ被h分割为相隔h的点xi与xi+h上的N(h)对电阻率{ρ(xi),ρ(xi+h)} (i=1,2,…,N(h)),可根据下式计算其实验变差函数
| $ \gamma(h)=\frac{1}{2 N(h)} \sum\limits_{i=1}^{N(h)}\left[\rho\left(x_{i}\right)-\rho\left(x_{i}+h\right)\right]^{2} $ | (2) |
式中:i为样本序号;N(h)为数据对{ρ(xi),ρ(xi+h)}的个数,记为点对数。
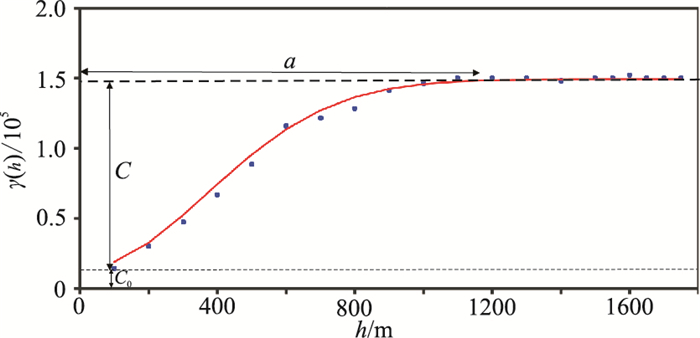
以h为横坐标、γ(h)为纵坐标作出图 2所示的变差图。
|
图 2 变差函数示意图 |
γ(h)可用四个参数来描述[19],即变差函数类型(如高斯模型、球状模型、指数模型)、变程a(表示超过该距离后,数据点之间就不再有明显相关性,也称作影响距离)、块金值C0(表示相距很近两点的样品变化)和基台值C0+C(反映变量的变化幅度)。
每对区域化变量Z1(x)和Z2(x)间的相关范围与方向差异问题定义为交叉—变差函数。针对实际情形,同一地质体可通过不同物性参数表征,如速度v和电阻率ρ,其交叉—变差函数可表示
| $ \begin{aligned} \gamma_{\rho v}(h)=& \frac{1}{2 N(h)} \sum\limits_{i=1}^{N(h)}\left[\rho\left(x_{i}\right)-\rho\left(x_{i}+h\right)\right] \times \\ &\left[v\left(x_{i}\right)-v\left(x_{i}+h\right)\right] \end{aligned} $ | (3) |
将多元地质统计学中的交叉—变差函数整合到式(1),以表征速度与电阻率之间的关系。交叉—变差函数项为
| $ \phi_{\gamma}=\left\|\boldsymbol{W}_{\gamma}\left[\boldsymbol{\gamma}_{\rho v}(\boldsymbol{m})-\boldsymbol{\gamma}_{\rho v}^{\mathrm{obs}}\right]\right\|^{2} $ | (4) |
式中:γρv(m)为从反演模型估计的交叉—变差函数;γρvobs为从先验岩石物理信息得到的先验—交叉变差函数;对角矩阵Wγ表示先验岩石物理关系中的不确定性,其对角线元素为交叉—变差函数失配的标准差的倒数。多重约束MT反演的最终目标函数为
| $ \begin{aligned} \phi(\boldsymbol{m})=&[\boldsymbol{d}-f(\boldsymbol{m})]^{\mathrm{T}} \boldsymbol{C}_{d}^{-1}[\boldsymbol{d}-f(\boldsymbol{m})]+\\ & \beta\left(\boldsymbol{m}-\boldsymbol{m}_{0}\right)^{\mathrm{T}} \boldsymbol{C}_{m}^{-1}\left(\boldsymbol{m}-\boldsymbol{m}_{0}\right)+\\ & \alpha\left[\boldsymbol{\gamma}_{\rho v}(\boldsymbol{m})-\boldsymbol{\gamma}_{\rho v}^{\mathrm{obs}}\right]^{\mathrm{T}} \boldsymbol{C}_{\gamma}^{-1}\left[\boldsymbol{\gamma}_{\rho v}\left(\boldsymbol{m}-\boldsymbol{\gamma}_{\rho v}^{\mathrm{obs}}\right)\right] \end{aligned} $ | (5) |
式中:Cγ-1=WγTWγ;参数α控制期望反演所得交叉—变差函数与先验交叉—变差函数的接近程度。
基于岩石物理关系的约束技术使得MT反演结果不仅可拟合观测MT数据,同时满足先验的电阻率—速度关系。
1.2.3 模糊约束技术许多学者已将FCM聚类技术集成到确定性反演框架中,以进一步约束地球物理反演[8-10, 17, 20-21]。
为使反演得到的物性值聚类为已知的岩石物性值,Sun等[8-9]提出引导FCM技术
| $ \phi^{c}=\sum\limits_{k=1}^{M} \sum\limits_{i=1}^{c} \mu_{k i}^{q}\left\|m_{k}-u_{i}\right\|_{2}^{2}+\sum\limits_{i=1}^{c}\left\|u_{i}-v_{i}\right\|_{2}^{2} $ | (6) |
式中:M是待聚类数据的数量;c是聚类中心的数量;mk是第k个数据;μki是隶属度值,用于度量第k个数据属于第i个聚类的程度;q是模糊化参数;ui是通过FCM算法自动更新的第i个聚类中心;vi是根据岩石样本测量确定的先验物性值。
该策略的一个优势是不会损害FCM算法的良好收敛性,同时还能根据先验的岩石物理信息将搜索聚类中心引导到所需位置。
对式(6)分别对聚类中心ui和隶属度μki求微分,并使其等于零,得到更新后的对应值
| $ u_{i}=\frac{\sum\limits_{k=1}^{M} \mu_{k i}^{q} m_{k}+v_{i}}{\sum\limits_{k=1}^{M} \mu_{k i}^{q}+1} $ | (7) |
| $ \mu_{k i}=\frac{\left\|m_{k}-u_{i}\right\|^{\frac{-2}{q-1}}}{\sum\limits_{i=1}^{c}\left\|m_{k}-u_{i}\right\|^{\frac{-2}{q-1}}} $ | (8) |
本文所使用FCI技术的基本思想是在反演的每一次迭代过程中利用引导FCM技术引入已知的电阻率信息来约束模型参数。
FCI技术的额外输入是聚类中心的数量和聚类中心的值(比如每种岩性的电阻率平均值)。
在基于岩石物理关系的多重约束反演过程中,第j+1次迭代中获得模型mj+1之后,分别计算第i个聚类中心uij+1及其对应的隶属度值μikj+1。此外,使用聚类中心和FCM的最大隶属度将模型mj+1分为c个聚类,以计算第j+1次迭代的模型参数(修改后模型)
| $ m_{k}^{j+1}=\sum\limits_{i=1}^{c} u_{i}^{j+1} \mu_{i k}^{j+1} $ | (9) |
通过这种方式实施反演,一起迭代、优化了三个参数,即模型m、聚类中心u和隶属度μ。
基于引导FCM分析技术的FCI技术使反演过程中实现反演与地质分类的互相改进,得到的电阻率模型不仅可拟合观测到的MT数据,同时更接近真实电阻率值,且更利于地质解释。
2 应用效果分析为了验证本文方法的实际应用效果,选取大杨树盆地南部坳陷实测数据进行实验。
大杨树盆地主要目的层由火山岩、火山碎屑岩和沉积岩组成。由于该区火山岩覆盖程度较高,使之对于地震波具有低通效应且对反射能量屏蔽、吸收衰减严重,导致九峰山组地震资料品质差,无法开展有效的沉积岩预测和构造解释[22-24]。通常从MT数据可获取深层结构,但其分辨率不及地震数据。因此,为了获得更可靠的地下结构,实施了电—震联合建模约束反演。
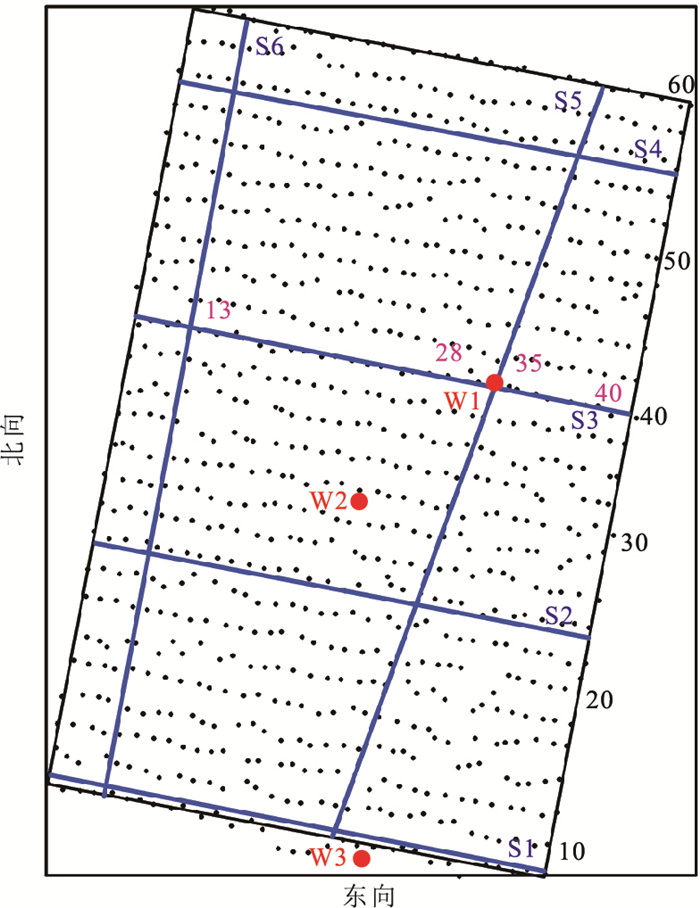
研究区是一北东向倾斜的面积为13km×10km的长方形区域(图 3),测网密度为0.50km×0.25km,布设26条测线,共计858个测点,每个测点MT数据频点数不少于38。MT40线与地震S3线一致并穿过钻孔,故此次选取40线为例进行分析。
|
图 3 研究区MT测点、地震测线及钻井位置 黑点/黑字分别表示MT测点位置/线号,粉字表示测点号;蓝线/蓝字分别表示地震测线/线号;红点/红字分别表示井位/井名 |
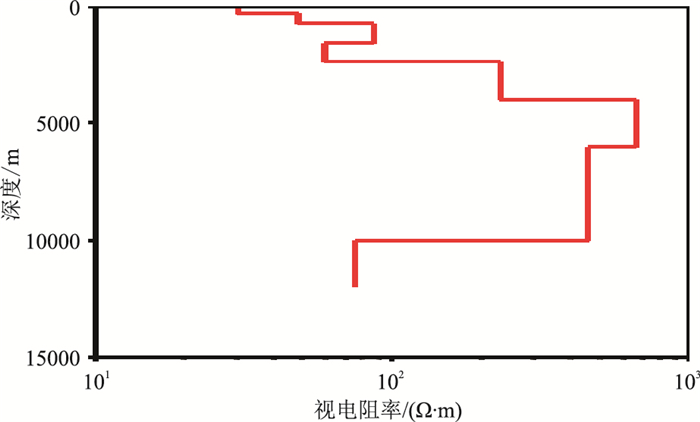
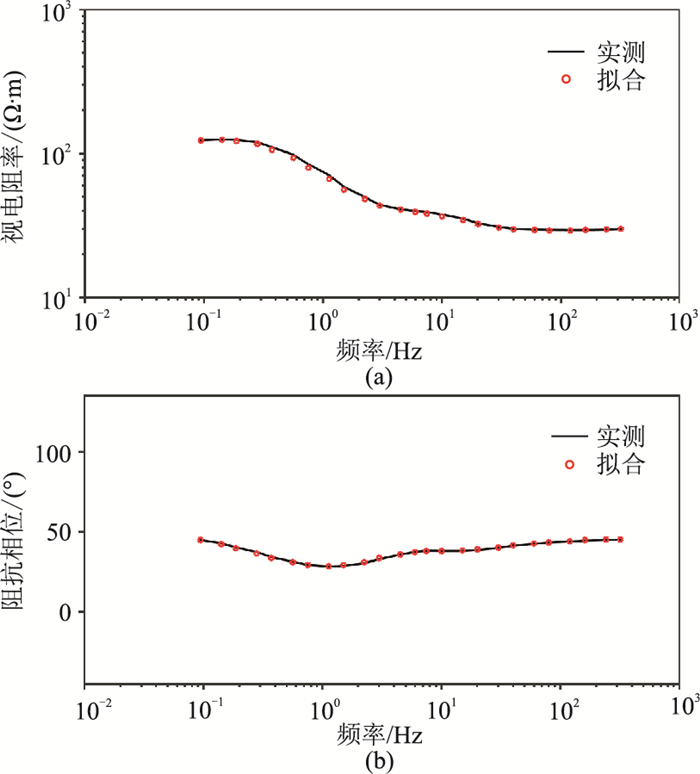
首先对40线做1D MT blocky反演,然后针对其中MT13测点的反演结果(图 4)与实测视电阻率及阻抗相位数据进行正演拟合(图 5),效果很好。
|
图 4 MT13测点1D MT blocky反演结果 |
|
图 5 MT13测点1D MT blocky反演结果的正演拟合图 (a)视电阻率;(b)阻抗相位 |
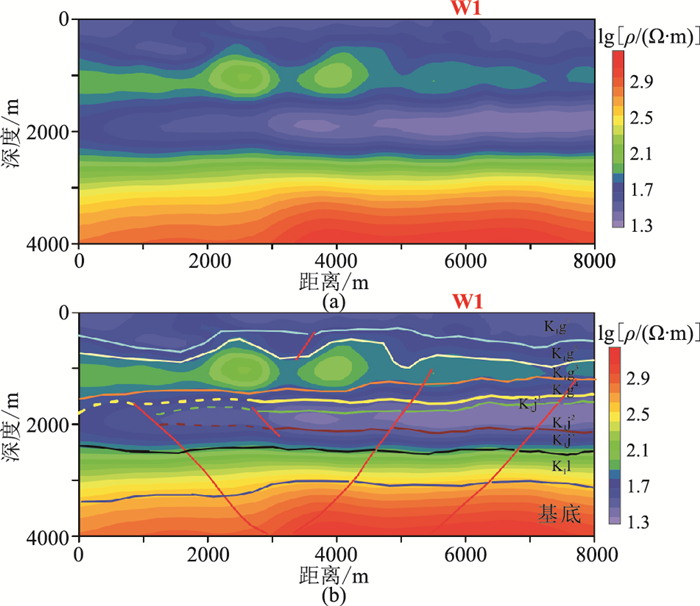
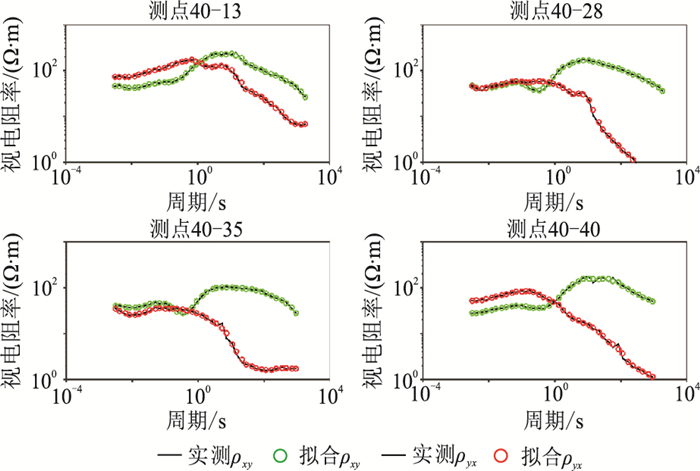
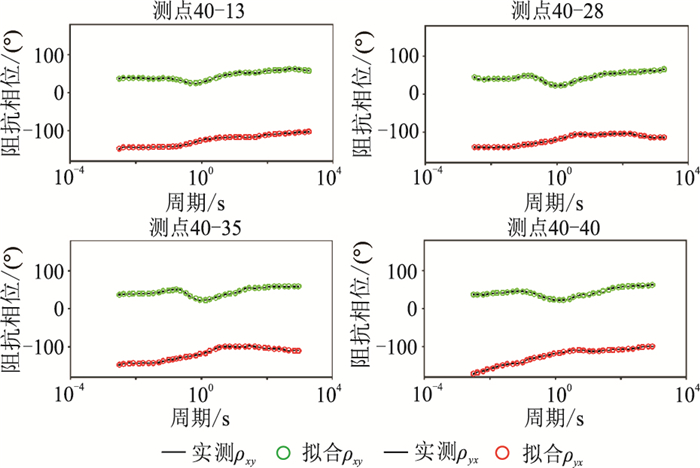
以1D反演结果作为初始模型,进行了无地震数据约束的2D MT反演,获得的40线电阻率剖面如图 6a所示;根据MT反演的电阻率数值的大小与高低变化进行地层解释,并依托S3地震数据进行断裂识别和描述(图 6b)。可见该方法反演的视电阻率(图 7)及阻抗相位(图 8)数据的正演响应很好地拟合了对应的实测数据。
|
图 6 MT40线无约束MT反演电阻率剖面(a)及其解释剖面(b) |
|
图 7 MT40线实测与无约束MT反演拟合视电阻率对比 测点位置如图 3 |
|
图 8 MT40线实测与无约束MT反演拟合阻抗相位对比 测点位置如图 3 |
由图 6可知,甘河组(K1g)电阻率值相对较高,这主要是由于该层大面积发育玄武岩等火山岩;九峰山组(K1j)是低阻,因为该层主要发育砂泥岩;龙江组(K1l)为电阻率较高,主要发育碎屑岩和酸性熔岩;基底为最高阻。反演的电阻率模型与已知的信息有较好一致性。通过钻井标定可看出,该电性异常剖面对目标层九峰山组顶、底界面有所反映,但对九峰山组内细节刻画欠清晰。
2.2 电—震联合建模约束反演为了更精细地描述目的层九峰山组地层细节,在无地震约束MT反演结果的基础上进行电—震联合建模约束反演。在应用聚类方法之前,应预知聚类中心的数量和聚类中心值。经综合整理分析工区测井数据、岩心露头及1D MT blocky反演结果,得到如表 1所示的每个地层的电阻率及速度。据此确定聚类中心数为7,速度、电阻率的聚类中心值分别为[4215, 4325, 4405, 4645, 4830, 5000, 6000](m/s)、[25, 50, 62, 93, 182, 345, 1260](Ω·m),以此作为聚类先验信息,优化反演结果。
|
|
表 1 各地层的速度及电阻率统计平均值 |
先验电阻率模型的构建是MT反演的重要部分。本文从地震数据体提取与地电结构相关的关键地震层构建先验模型的地电框架,作为MT反演的输入。以40线为例,构建先验电阻率模型的步骤如下:
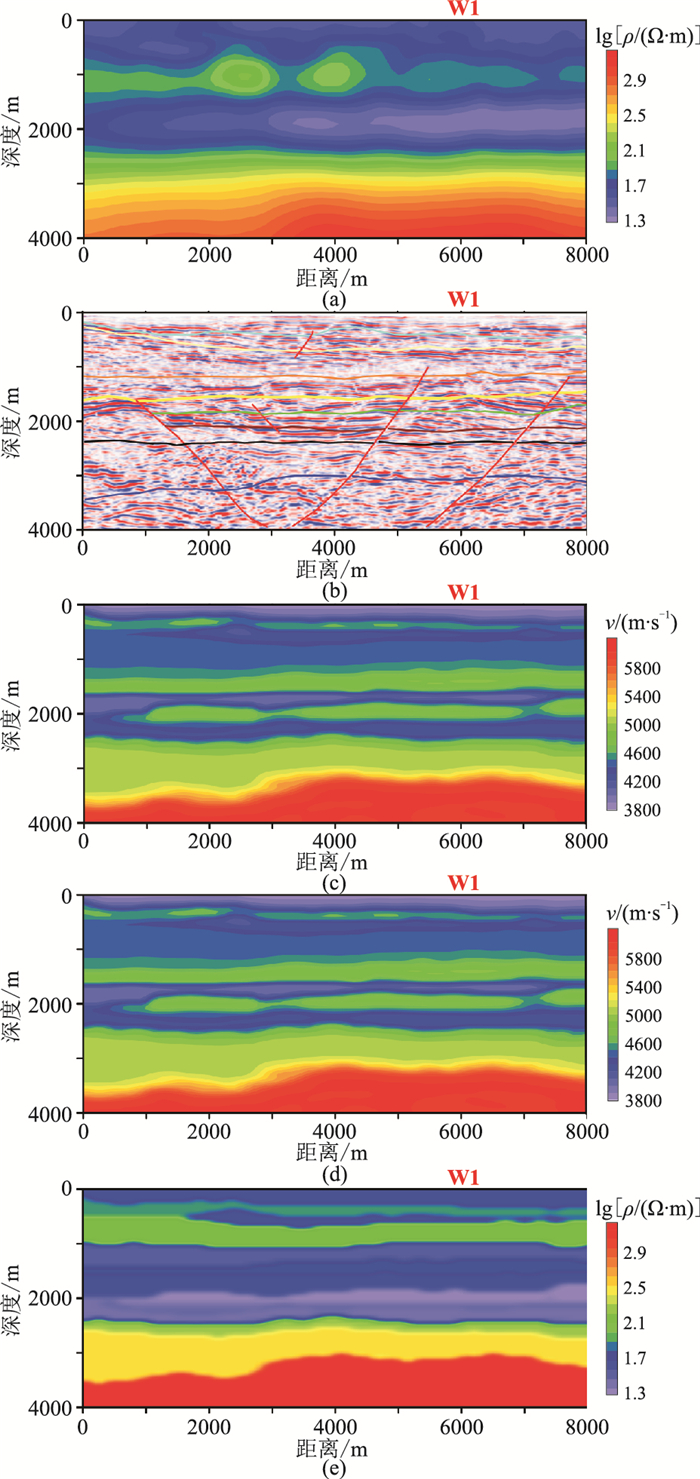
(1) 利用测井信息进行标定,综合PSDM数据与无约束MT反演得到的电阻率模型(图 9a)进行综合解释,得到关键层位解释结果(图 9b);
|
图 9 基于聚类分析的先验电阻率模型构建流程示意 (a)无约束MT反演的电阻率模型;(b)PSDM图像及综合解释得到关键层位;(c)MT尺度的速度模型;(d)聚类后速度模型;(e)生成的先验电阻率模型 |
(2) 基于层位解释结果进行地质统计学反演,得到速度模型(图 9c);
(3) 对速度模型进行聚类分析(图 9d);
(4) 利用无约束MT反演得到的电阻率模型的平均电阻率值对聚类后的速度模型赋值,得到新一轮MT反演初始模型(图 9e)。
所得的先验电阻率模型不仅反映了相应的地震构造形态,同时保持合理的电阻率分布。
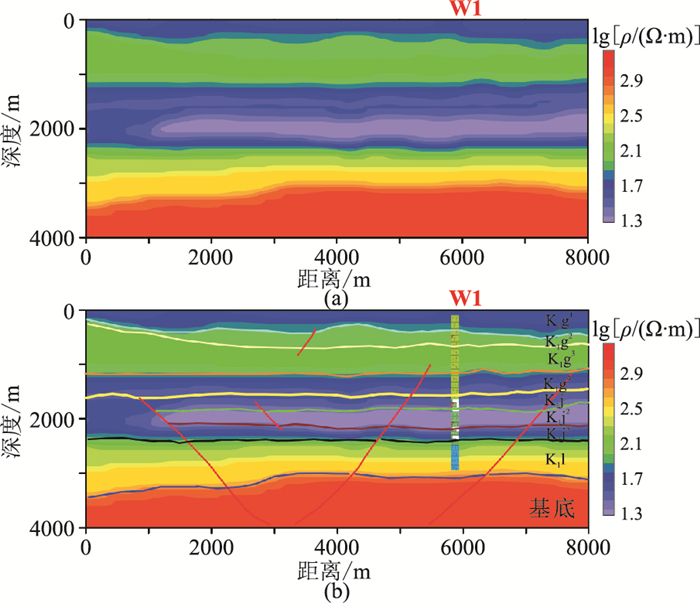
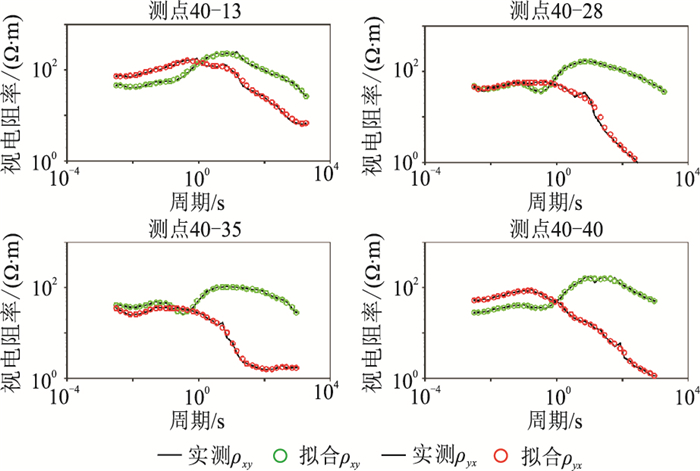
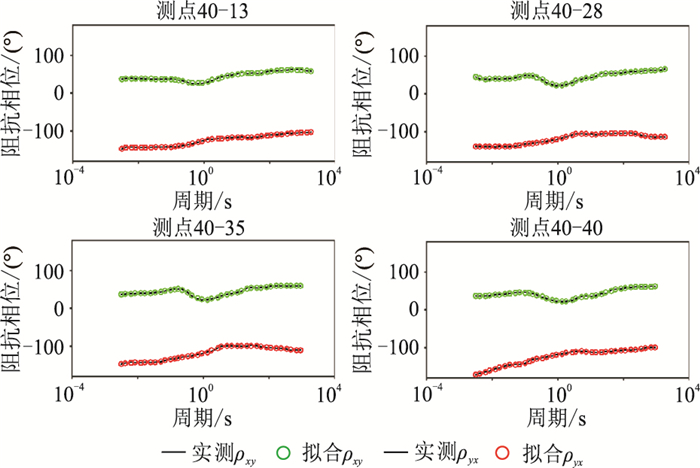
2.2.2 基于岩石物理关系的多重约束MT反演利用测井数据与40线速度和电阻率剖面建立交叉—变差函数,进行基于岩石物理关系多重约束反演,得到电阻率数据(图 10a),然后对其进行定量解释(图 10b)。图 11和图 12分别表明基于岩石物理关系的多重约束MT反演的视电阻率及阻抗相位数据的正演响应很好地拟合了相应实测数据。
|
图 10 本文反演策略所得40线电阻率剖面(a)及其解释剖面(b) |
|
图 11 MT40线实测与约束MT反演拟合视电阻率对比 所选测点位置如图 3所示 |
|
图 12 MT40线实测与约束MT反演拟合阻抗相位对比图 测点位置如图 3 |
本文反演策略与无约束反演结果(图 6a)的对比表明:①本文反演方法所得电阻率剖面成层性更好,且与主要地震构造形态一致,特别是对目的层九峰山组的划分更精细、清晰;②先验电阻率数据表明甘河组(普遍呈电阻率较高值)广泛分布火山岩,多重约束反演结果与该物性特征一致;③龙江组下部电阻率值应大于其上部电阻率值,与实际情况相吻合。
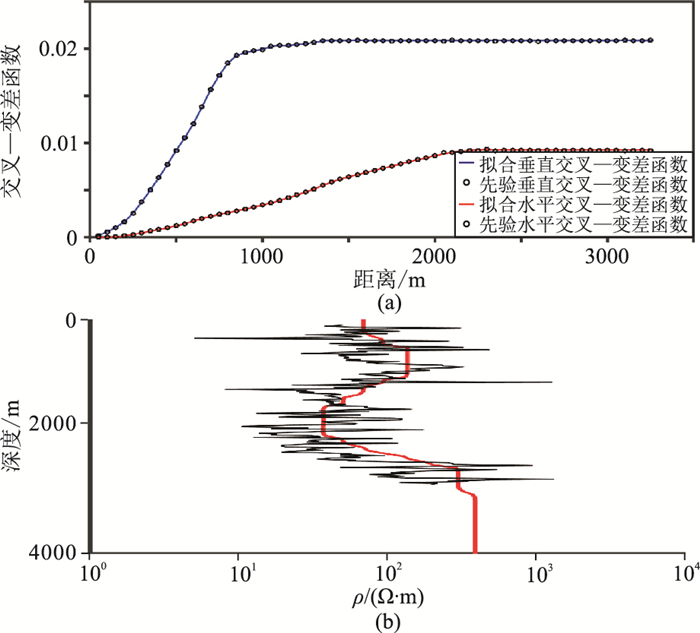
图 13显示电—震联合建模约束反演所得交叉—变差函数与先验交叉—变差函数相一致(图 13a)。图 13b显示了电—震联合建模约束反演结果与电阻率测井数据趋势一致。证实了反演结果的可靠性。
|
图 13 约束反演结果与先验信息对比 (a)交叉—变差函数;(b)W1测井曲线 |
单一地球物理勘探方法不可避免地具有片面性和局限性。为了提高对目标地质体的识别能力,利用聚类和多元地质统计学方法进行MT与地震数据联合建模反演,实现从无约束MT反演方法到基于岩石物理关系多重约束反演的流程。由于通过构建先验电阻率模型而引入地震结构约束、以交叉—变差函数引入先验电阻率与速度关系约束、用FCI技术引入先验电阻率信息并结合地质分类,所以多重约束反演得到的电阻率模型更符合先验信息且更利于地质解释。实际数据的应用结果证实了将多种地球物理方法整合到地球物理勘探中的必要性。
| [1] |
彭国民, 刘展. 电磁和地震联合反演研究现状及发展趋势[J]. 石油地球物理勘探, 2020, 55(2): 465-474. PENG Guomin, LIU Zhan. An overview of joint electromagnetic-seismic inversion and its future development[J]. Oil Geophysical Prospecting, 2020, 55(2): 465-474. |
| [2] |
刘洁, 张建中. 重震联合反演框架及应用新进展[J]. 地球物理学进展, 2020, 35(2): 743-752. LIU Jie, ZHANG Jianzhong. New development of gravity-seismic joint inversion framework and application[J]. Progress in Geophysics, 2020, 35(2): 743-752. |
| [3] |
Gallardo L A, Meju M A. Characterization of heterogeneous near-surface materials by joint 2D inversion of DC resistivity and seismic data[J]. Geophysical Research Letters, 2003, 30(13): 1658. |
| [4] |
Colombo D, De Stefano M. Geophysical modeling via simultaneous joint inversion of seismic, gravity, and electromagnetic data: Application to prestack depth imaging[J]. The Leading Edge, 2007, 26(3): 326-331. DOI:10.1190/1.2715057 |
| [5] |
De Stefano M, Andreasi F G, Re S, et al. Multiple-domain, simultaneous joint inversion of geophysical data with application to subsalt imaging[J]. Geophysics, 2011, 76(3): R69-R80. DOI:10.1190/1.3554652 |
| [6] |
Gardner G, Gardner L W, Gregory A R. Formation velocity and density-the diagnostic basics for stratigraphic traps[J]. Geophysics, 1974, 39(6): 770-780. DOI:10.1190/1.1440465 |
| [7] |
Zhdanov M S, Gribenko A, Wilson G. Generalized joint inversion of multimodal geophysical data using Gramian constraints[J]. Geophysical Research Letters, 2012, 39(9): L09301. |
| [8] |
Sun J, Li Y. Multidomain petrophysically constrained inversion and geology differentiation using guided fuzzy c-means clustering[J]. Geophysics, 2015, 80(4): D1-D18. |
| [9] |
Sun J, Li Y. Joint inversion of multiple geophysical data using guided fuzzy c-means clustering[J]. Geophysics, 2016, 81(3): D37-D57. DOI:10.1190/geo2015-0457.1 |
| [10] |
Carter-Mcauslan A, Lelièvre P G, Farquharson C G. A study of fuzzy c-means coupling for joint inversion, using seismic tomography and gravity data test scenarios[J]. Geophysics, 2014, 79(1): W1-W15. |
| [11] |
陈晓, 于鹏, 邓居智, 等. 基于宽范围岩石物性约束的大地电磁和地震联合反演[J]. 地球物理学报, 2016, 59(12): 4690-4700. CHEN Xiao, YU Peng, DENG Juzhi, et al. Joint inversion of MT and seismic data based on wide-range petrophysical constraints[J]. Chinese Journal of Geophysics, 2016, 59(12): 4690-4700. DOI:10.6038/cjg20161228 |
| [12] |
胡祖志, 石艳玲, 刘云祥, 等. 电磁与重力数据非线性约束联合反演[J]. 石油地球物理勘探, 2020, 55(1): 226-232. HU Zuzhi, SHI Yanling, LIU Yunxiang, et al. Nonlinear constrained joint inversion of MT and gravity data[J]. Oil Geophysical Prospecting, 2020, 55(1): 226-232. |
| [13] |
相鹏, 王金铎, 谭绍泉, 等. 一种变密度-速度关系的重力与地震同步联合反演方法[J]. 石油地球物理勘探, 2020, 55(3): 686-693. XIANG Peng, WANG Jinduo, TAN Shaoquan, et al. Simultaneous and joint inversion of gravity and seismic data based on variable density-velocity relation[J]. Oil Geophysical Prospecting, 2020, 55(3): 686-693. |
| [14] |
Yang B, Liu Z. Research on adaptive petrophysical modeling based on machine learning and multivariate geostatistics[C]. Extended Abstracts of 81st EAGE Conference & Exhibition, 2019, Tu_R16_03.
|
| [15] |
Cuong V A L, Harris B D, Pethick A M, et al. Semiautomatic and automatic cooperative inversion of seismic and magnetotelluric data[J]. Survey in Geophy-sics, 2016, 37(5): 845-896. DOI:10.1007/s10712-016-9377-z |
| [16] |
Hermans T, Vandenbohede A, Lebbe L, et al. Imaging artificial salt water infiltration using electrical resistivity tomography constrained by geostatistical data[J]. Journal of Hydrology, 2012, 438-439: 168-180. DOI:10.1016/j.jhydrol.2012.03.021 |
| [17] |
Yang B, Xu K, Liu Z, et al. Fuzzy constrained inversion of magnetotelluric data using guided fuzzy c-means clustering[J]. Surveys in Geophysics, 2021, 42(2): 399-425. DOI:10.1007/s10712-020-09628-y |
| [18] |
Kelbert A, Meqbel N, Egbert G D, et al. ModEM: A modular system for inversion of electromagnetic geophysical data[J]. Computers & Geosciences, 2014, 66(?): 40-53. |
| [19] |
孙洪泉. 地质统计学及其应用[M]. 北京: 中国矿业大学出版社, 1990.
|
| [20] |
Paasche H, Tronicke J. Cooperative inversion of 2D geophysical data sets: A zonal approach based on fuzzy c-means cluster analysis[J]. Geophysics, 2007, 72(3): A35-A39. DOI:10.1190/1.2670341 |
| [21] |
Singh A, Sharma S P, Akcaİ, et al. Fuzzy constrained Lp-norm inversion of direct current resistivity data[J]. Geophysics, 2018, 83(1): E11-E24. DOI:10.1190/geo2017-0040.1 |
| [22] |
金成志. 大杨树盆地含油气远景综合评价[D]. 北京: 中国石油大学(北京), 2007. JIN Chengzhi. Comprehensive Evaluation of the Oil and Gas Exploration Prospect in Dayangshu Basin[D]. China University of Petroleum (Beijing), Beijing, 2007. |
| [23] |
郭伟, 姚长利, 王亚民, 等. 重磁综合约束反演在大杨树盆地油气勘探中的应用[J]. 石油地球物理勘探, 2014, 49(增刊1): 233-242. GUO Wei, YAO Changli, WANG Yamin, et al. Comprehensive constrained inversion of gravity and magnetic in reservoir exploration in Dayangshu Basin[J]. Oil Geophysical Prospecting, 2014, 49(S1): 233-242. |
| [24] |
胡祖志, 刘云祥, 孟玉宇, 等. 三维MT数据处理解释技术及应用[J]. 石油地球物理勘探, 2018, 53(增刊1): 324-329. HU Zuzhi, LIU Yunxiang, MENG Yuyu, et al. 3D MT data processing and interpretation techniques[J]. Oil Geophysical Prospecting, 2018, 53(S1): 324-329. |



 刘展, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
刘展, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: 