② 地球内部多尺度成像湖北省重点实验室, 湖北武汉 430074;
③ 地质过程与矿产资源国家重点实验室, 湖北武汉 43007;
④ 河北地质大学勘查技术与工程学院, 河北石家庄 050031
② Hubei Subsurface Multi-scale Imaging Key Laboratory, Wuhan, Hubei 430074, China;
③ State Key Laboratory of Geological Processes and Mineral Resources, Wuhan, Hubei 430074, China;
④ College of Exploration Technology and Engineering, Hebei GEO University, Shijiazhuang, Hebei 050031, China
在地球物理学方法体系中,磁法发展最早,至今仍被广泛应用于地质调查、资源勘探、军事与国防建设、工程勘察与环境监测等诸多领域[1-3]。地磁场测量的平台、方式以及物理量多种多样,目前磁法勘探普遍采用标量磁力仪,基于航空、地面与船载等移动平台测量地磁场总强度的空间分布[4]。随着地磁场测量精度和测点定位精度的大幅提高,以及计算机与计算技术的快速发展,对深部目标及小型磁性体的探测需求日益增长。以往在磁力异常的校正计算、数据预处理、正演、反演及定量解释中的许多假设条件和近似条件逐渐变得不再合理,在传统算法中被忽略的系列因素也逐步纳入考虑范围,例如自退磁效应[5]、磁化率各向异性[6]、剩余磁化强度[7]、总磁场强度异常的非线性效应[8-17]等。
总磁场强度异常(ΔT)的非线性效应,指的是实际测量得到的磁异常ΔT为地磁场总场(T)的模量|T|与主磁场(T0)的模量|T0|之差(即ΔT=|T|-|T0|),与磁场矢量异常(Ta)以及岩石圈磁源的磁矩不满足线性关系。在实际数据预处理、正反演和定量解释时,通常将Ta在主磁场或正常地磁场T0方向上的投影分量ΔTPro近似为ΔT[10],这就意味着ΔT与其他磁分量异常一样,与场源的磁矩呈简单的线性关系,与主磁场T0无耦合关系,并且在场源外部空间满足拉普拉斯方程从而具备调和性质,因而可以简化实测ΔT数据的预处理、正反演及定量解释过程[8-9]。该近似的前提是|T0|»|Ta|,例如:当|T0|=30000nT、|Ta|=500nT时,ΔT近似为ΔTPro的误差仅为4nT;当|T0|=70000nT、|Ta|=10000nT时,ΔT近似为ΔTPro的误差可达714nT[11];随着磁异常模量Ta=|Ta|的增大,误差按照近似指数关系迅速增大[8-9]。总之,当Ta幅值较大时,这种近似处理会产生较大的误差,进而对实测ΔT的处理(例如空间延拓曲化平、分量与其他参量的转换、化极、磁源重力异常、导数计算等)、正反演及定量解释产生较大的影响。
针对该问题,Zhen等[12]和甄慧翔等[13-14]在波数域提出了空间域基于ΔT精确计算ΔTPro的最优化方法,Sun等[15]和孙石达等[16]提出基于三维成像反演的非线性等效源方法。这两种方法均需要求解大型方程组,不仅所需内存较大且计算效率较低,限制了其在实际生产与研究中的广泛应用。针对此问题,本文提出一种高效率的迭代方法,即采用ΔT近似为ΔTPro的理论误差公式进行迭代计算,并通过模型试验和实际数据应用验证了该方法的准确性、稳定性与计算效率,旨在推动高精度实测ΔT数据的实用化进程。
1 方法原理与算法流程首先介绍由ΔT迭代计算ΔTPro的方法原理,然后给出算法流程,最后从理论上分析该迭代算法计算精度与计算效率的影响因素。
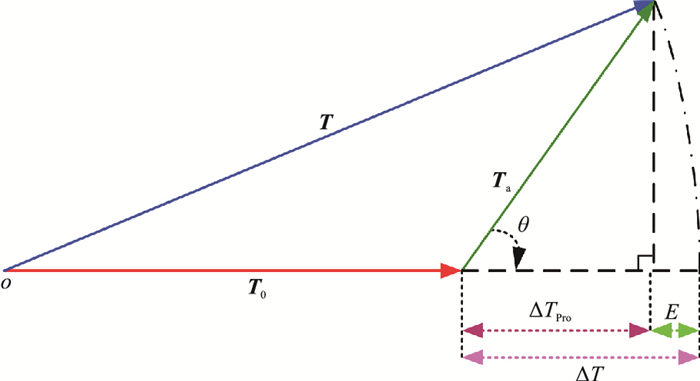
图 1所示为总磁场强度异常ΔT、磁异常模量Ta与磁场矢量异常Ta在主磁场T0方向投影ΔTPro之间的关系示意图。若忽略外源变化场及其在地球内部感应生成的二次磁场,地磁场T可视为主磁场T0与磁场矢量异常Ta之矢量和
| $ \boldsymbol{T}=\boldsymbol{T}_{0}+\boldsymbol{T}_{\mathrm{a}} $ | (1) |
|
图 1 总磁场强度异常(ΔT)、磁异常模量(Ta)与磁场矢量异常Ta在主磁场T0方向投影ΔTPro之间的关系示意图 |
如引言所述,实测总磁场强度异常ΔT往往表示为总磁场强度|T|与主磁场强度|T0|(即T0)之差
| $ \Delta T=|\bf{T}|-\left|\boldsymbol{T}_{0}\right| $ | (2) |
而在实际数据预处理、正反演及定量解释时,为了简化计算,通常将ΔTPro近似为ΔT(图 1),即
| $ \Delta T_{\text {Pro }}=\left|\boldsymbol{T}_{\mathrm{a}}\right| \cos \theta $ | (3) |
显然,将ΔTPro近似表示为ΔT存在误差
| $ E=\Delta T-\Delta T_{\mathrm{Pro}} $ | (4) |
| $ E=\frac{T_{\mathrm{a}}^{2}-(\Delta T)^{2}}{2 T_{0}} $ | (5) |
由前文所述的假设条件Ta≥ΔT,可得E≥0、ΔT≥ΔTPro[8]。
联合式(4)与式(5)可得
| $ \Delta T_{\mathrm{Pro}}=\Delta T-\frac{T_{\mathrm{a}}^{2}-(\Delta T)^{2}}{2 T_{0}} $ | (6) |
式(6)即为基于ΔT精确计算投影分量ΔTPro的方法基础。若假设研究区主磁场T0的大小和方向不变,根据投影分量ΔTPro可在波数域快速转换计算磁场矢量异常Ta的模Ta,又因ΔT为实测数据,则根据式(6)可以构建方程组,进而采用最优化方法求解ΔTPro。这是甄慧翔等[12-14]提出的方法思路,该方法需求解大型方程组,因而计算效率较低。
本文基于式(6),提出采用迭代算法求解ΔTPro,即
| $ \Delta T_{\mathrm{Pro}}^{(i+1)}=\Delta T-\frac{\left[T_{\mathrm{a}}^{(i)}\right]^{2}-\left[\Delta T^{(i)}\right]^{2}}{2 T_{0}} $ | (7) |
式中:i为非负整数,表示迭代次数;主磁场强度T0在研究区内为常数。ΔT(i)的计算公式为
| $ \Delta T^{(i)}=\left|\boldsymbol{T}_{0}+\boldsymbol{T}_{\mathrm{a}}^{(i)}\right|-\left|\boldsymbol{T}_{0}\right| $ | (8) |
Ta(i)的三个分量Ha, x(i)、Ha, y(i)与Za(i)可以在波数域基于ΔTPro快速计算获得[4, 10-11]
| $ \left\{ {\begin{array}{*{20}{l}} {H_{{\rm{a}},x}^{(i)} = {{\rm{F}}^{ - 1}}\left[ {\frac{{u{\rm{j}}}}{{{q_{{\mathit{\boldsymbol{t}}_0}}}}}{\rm{F}}\left( {\Delta T_{{\rm{Pro}}}^{(i)}} \right)} \right]}\\ {H_{{\rm{a}},y}^{(i)} = {{\rm{F}}^{ - 1}}\left[ {\frac{{v{\rm{j}}}}{{{q_{{\mathit{\boldsymbol{t}}_0}}}}}{\rm{F}}\left( {\Delta T_{{\rm{Pro}}}^{(i)}} \right)} \right]}\\ {Z_{\rm{a}}^{(i)} = {{\rm{F}}^{ - 1}}\left[ {\frac{{\sqrt {{u^2} + {v^2}} {\rm{j}}}}{{{q_{{\mathit{\boldsymbol{t}}_0}}}}}{\rm{F}}\left( {\Delta T_{{\rm{Pro}}}^{(i)}} \right)} \right]} \end{array}} \right. $ | (9) |
| $ {{q_{{\mathit{\boldsymbol{t}}_0}}} = \left( {{L_0}u + {M_0}v} \right){\rm{j}} + {N_0}\sqrt {{u^2} + {v^2}} } $ | (10) |
式中:F与F-1分别表示二维傅里叶正变换与反变换;j为虚数单位;L0、M0与N0分别为主磁场单位矢量t0与x、y、z轴之间的方向余弦;u、v分别表示x、y方向的波数。因此,根据式(9)可得
| $ T_{\mathrm{a}}^{(i)}=\sqrt{\left[H_{\mathrm{a}, x}^{(i)}\right]^{2}+\left[H_{\mathrm{a}, y}^{(i)}\right]^{2}+\left[Z_{\mathrm{a}}^{(i)}\right]^{2}} $ | (11) |
对于ΔTPro的初始值ΔTPro(0)可设定等于实测总磁场强度异常ΔT。本文设定式(7)的迭代停止条件为拟合误差ε满足
| $ \varepsilon=\max \left(\left|\Delta T-\Delta T^{(i)}\right|\right) \leqslant \varepsilon_{0} $ | (12) |
式中ε0为给定的阈值。迭代结束后,将最后一次迭代所得的投影分量ΔTPro(i)作为最终计算结果。根据上述迭代方法的相关原理,结合波数域磁场分量转换计算的精度影响因素(如噪声、点距与边界效应等),设计了算法流程,如图 2所示。

|
图 2 本文迭代算法流程图 图中虚线表示迭代更新过程 |
(1) 对实测数据ΔT进行数据预处理,依次进行奇异值剔除、数据网格化、扩边、初步去噪;
(2) 给定ε0;
(3) 令ΔTPro(i)等于实测数据ΔT;
(4) 根据实测数据ΔT、主磁场T0、ΔTPro(0)以及式(8)~式(11),采用式(7)进行迭代,并且根据式(12)计算拟合误差ε;
(5) 若迭代拟合误差ε≤ε0,则停止迭代,并将迭代所得的投影分量ΔTPro(i)作为最终计算结果输出,若需要也可以输出Ha, x(i)、Ha, y(i)与Za(i)三个分量异常及磁场矢量异常的模量Ta(i),如果必要,亦可同时计算并输出化极磁异常、磁源重力异常、导数异常、空间延拓异常、梯度张量异常、正则化磁源强度等其他参量。
由上述方法原理与算法流程可以看出,与Sun等[15]和孙石达等[16]采用的基于三维成像反演的非线性等效源方法不同,本文方法与文献[12-14]所提出的方法在原理上是一致的,差异仅在于所采用的计算方法不同:本文采用了迭代算法,后者采用的是基于最优化方法求解线性方程组。甄慧翔[13]明确指出:基于式(7)计算ΔTPro的精度影响因素仅在于采用傅里叶变换计算磁场分量异常的过程,而与场源相关的剩余磁化效应、自退磁效应、磁性结构复杂性等均无关系;对于实测ΔT数据所含误差的影响,由式(9)可知,分量转换的波数域转换因子并非如空间延拓和导数计算那样对噪声具有明显的压制或放大作用,而是略微受主磁场方向的影响,甄慧翔[13]所做的模型试验、以及Coleman等[18]基于等效源的相关研究也证明了此点。此外,从上述迭代计算过程还可以看出,计算速度主要决定于迭代总次数以及每次迭代所需的1次傅里叶正变换和3次傅里叶反变换。因此,本文所提方法的计算精度与计算效率在根源上主要取决于式(9)所示的傅里叶正、反变换。
2 模型试验为了检验本文方法的可靠性与稳定性,本节基于理论磁性结构模型、通过正演计算模拟观测数据与理论计算结果,对模拟的观测数据采用本文方法进行计算,并对计算结果与理论结果进行对比和分析。
2.1 理论模型鉴于本文方法与甄慧翔[13]所用方法的原理相似,为了避免重复性工作,不再进行数据噪声与背景场、剩余磁化效应、自退磁效应、磁性结构复杂性等模型试验研究,相关内容可参照文献[12-14]。本文重点研究三个方面的内容:一是分析迭代是否能够收敛,若能够收敛,进一步分析其计算精度;二是分析计算精度与迭代收敛速度的影响因素;三是分析计算效率。
本文针对性地设计了四组模型试验,均采用简单的磁偶极源,场源参数、主磁场参数与观测数据参数见表 1,所有试验均在直角坐标系中进行,x轴指向北、y轴指向东、z轴指向地下,观测面均为z=0的水平面,且仅考虑感应磁化问题,磁偶极源磁场的计算公式参见文献[19]中的式(32)~式(34)。第1组模型试验用于测试方法的有效性,即迭代是否收敛并分析计算精度;第2组和第3组模型试验分别改变磁偶极源的磁矩及主磁场的强度、倾角和偏角,分析磁场矢量异常的模量大小、主磁场强度和方向对收敛性和计算精度的影响;第4组模型试验的正演观测数据采用不同的点距与线距,主要测试分析计算效率随数据总量的变化规律。
|
|
表 1 理论磁性模型和磁场观测参数表 |
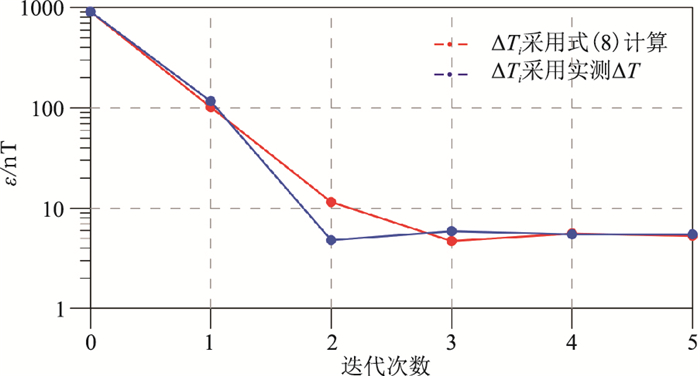
第1组模型试验结果见图 3。由图可见,拟合差ε随迭代次数增加呈先快速衰减、然后趋于稳定的特征,迭代2次时最大拟合误差即可达到约10nT,可见本文迭代方法具有快速与稳定的收敛特征。此外,图 3中ε趋于常值,说明迭代终止条件采用式(12)定义的阈值ε0不再合适,而应采用相邻两次迭代的拟合误差之差δ=|εi+1-εi|更合理。若ε0设置太小,则可能致使迭代结果永远达不到误差要求,因此在实际数据处理时可以采用δ作为迭代终止条件,也可以通过设定最大迭代次数停止迭代计算过程。
|
图 3 第1组模型试验拟合误差ε随迭代次数的变化曲线 |
Zhen等[12]和甄慧翔等[13-14]利用式(7)进行迭代时,ΔT(i)采用了实测ΔT。从图 3可见,ΔT(i)采用式(8)计算结果与采用实测ΔT两种策略对迭代收敛性的影响没有显著差异。但是笔者认为,式(5)所示误差E与ΔT、T0、Ta之间是耦合的,应采用式(8)计算,若采用实测ΔT数据代替可能会存在迭代过程振荡的风险,尽管在此例中并未出现这种现象。
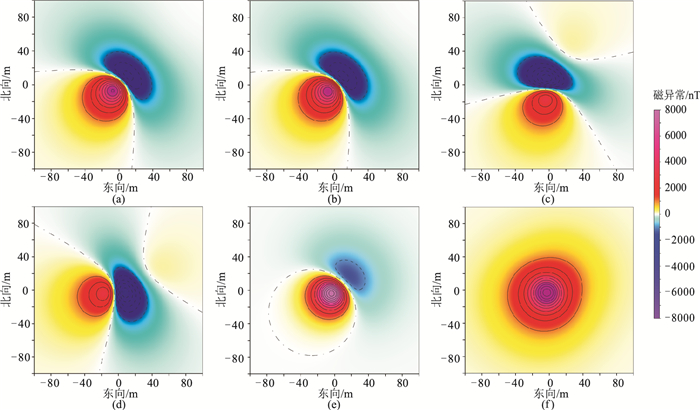
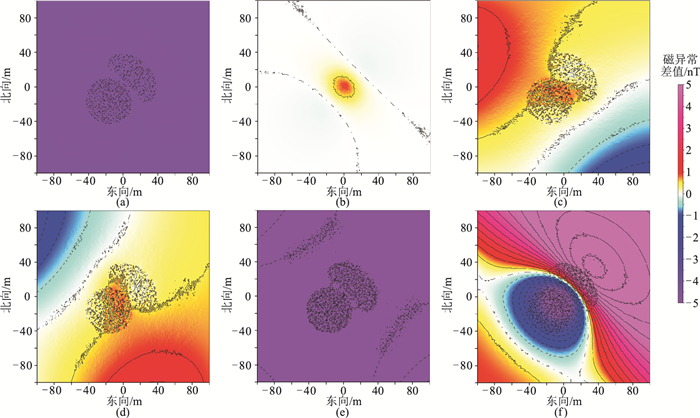
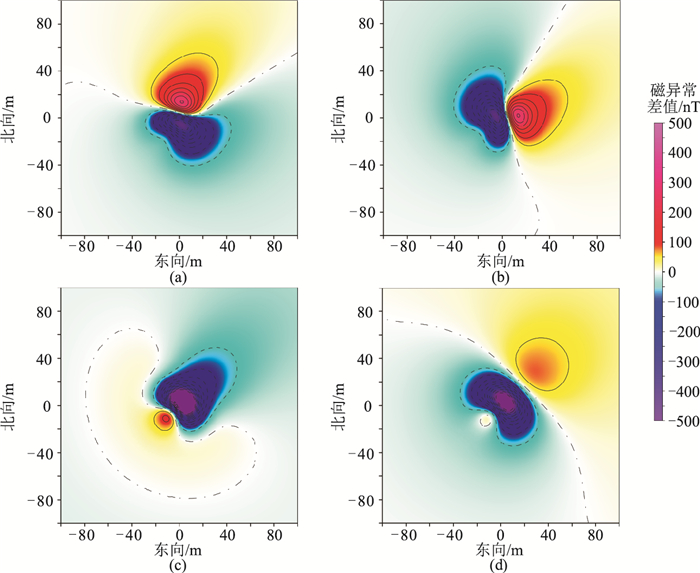
图 4为第1组模型的理论磁异常分布,图 5为理论值与本文方法计算结果的差值,其统计参数见表 2。可见转换处理的计算误差整体较低,其中磁场矢量异常的模量Ta计算误差相对较大,但也仅约±7nT,相比其最大幅值10614nT,该误差完全可以忽略,因此本文算法的计算精度较高。若直接将ΔT近似为ΔTPro,采用式(9)与式(11)分别计算三分量异常和模量异常,其计算误差见图 6和表 2,其中Za分量的最大误差达到了958.9nT,可见传统方法在高磁环境下具有较大的转换计算误差。
|
图 4 第1组模型的理论磁异常图
(a)ΔT;(b)ΔTPro;(c)Ha, x;(d)Ha, y;(e)Za;(f)Ta 等值线间隔为1000nT;黑色虚线、点划线与实线分别表示负值、零值与正值。图 5、图 6、图 9~图 11、图 14、图 15同 |
|
图 5 第1组模型的理论值与本文方法计算结果的差值
(a)ΔT;(b)ΔTPro;(c)Ha, x;(d)Ha, y;(e)Za;(f)Ta 等值线间隔为0.5nT |
|
|
表 2 第1组模型试验的理论值、计算值及误差统计表 |
|
图 6 第1组模型的理论值与传统方法计算值的差值
(a)Ha, x;(b)Ha, y;(c) Za;(d)Ta 等值线间隔为50nT |
图 3中另一个明显特征是当迭代达到一定次数(此例为3次)后,拟合误差ε趋于稳定(此例约趋于5nT),其原因可以从如下两个方面进行分析。
(1) 有限项傅里叶级数展开本身的Gibbs现象可能会产生边界效应。离散傅里叶变换的前提是信号在计算区域内是周期性的,显然此例所示磁力异常数据在研究区域内不具备完全的周期性,因为磁力异常在边界不能完全相等,因而去除常值之后在边界处存在不连续点。如此采用周期函数拟合非周期信号,必然在边界区域产生振荡,其压制方法是扩大数据范围[20-25]。一方面在计算完成之后可通过截取目标区域结果避免边界振荡;另一方面可通过合理扩边,使得边界处的数值趋于相等,从而压制边界效应。事实上,在此组模型试验中,已经先将数据向南北和东西方向各扩边了50m,边界处的数值已经均接近于零值,所以边界效应并不明显。但是,拟合误差随着迭代次数增加依然不能趋于零值,这说明除了边界效应之外还存在其他原因。
(2) 观察表 2可以发现,计算误差实际上存在常值成分,这源于有限项傅里叶级数展开的常值项,舒晴等[26]称之为波数域奇点,认为这是转换误差产生的根源,可通过减小点距、扩大计算范围有效提高转换处理的精度,其中扩大计算范围的改善效果非常显著。
甄慧翔等[14]所做的叠加背景场模型试验也已证明,背景场的存在使基于快速傅里叶变换的分量转换计算产生较大的误差,其本质原因即在于上述的边界效应和波数域奇点问题。因此,在实际应用中,建议尽量采用较大的计算区域并事先适当消除区域均值或者趋势场,当然这是在一般的情况下,即关注的目标是局部异常。另外,波数域奇点问题可以采用偏移抽样理论[27-30]进行压制,这是今后待改进之所在,本文不再过多论及。
2.2.2 迭代收敛速度与计算精度的影响因素由式(5)可知,采用ΔT近似ΔTPro所产生的误差主要源于Ta和T0,因此设计表 1所示的第2组与第3组模型试验,分别调查二者对转换计算精度和迭代收敛速度的影响。
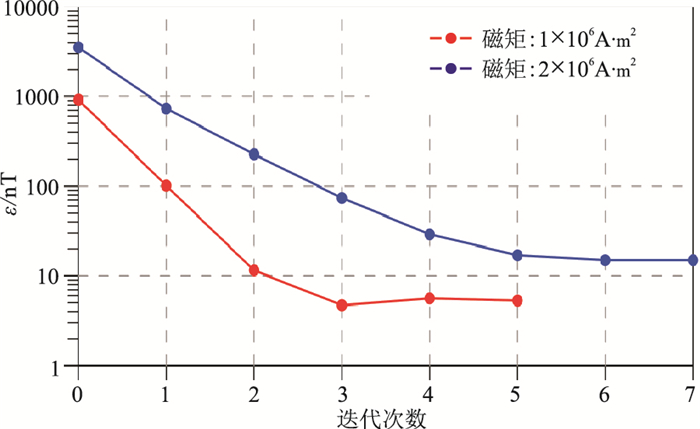
由于影响Ta大小的主要因素包括磁偶极源的磁矩大小及场源埋深,而埋深变化会影响磁异常在测区的分布形态,因此第2组模型试验仅考虑磁矩大小的影响。两个模型对应的拟合误差ε随迭代次数的变化曲线见图 7。可以看出,场源磁矩越大,迭代收敛速度越慢、计算精度越低。若取δ=1nT,则两个模型达到该阈值所需的最小迭代次数分别为4与7。分析其原因在于:磁场矢量异常的模量越大,式(7)的逼近误差也越大,因此迭代收敛变慢;并且在扩边相同的情况下,研究区域边界处的数值越高,波数域奇点的影响也就更加严重,因而计算精度越低。
|
图 7 第2组模型试验拟合误差ε随迭代次数的变化曲线 |
图 8为第3组模型的拟合误差ε随迭代次数的变化曲线。需要说明的是,此组模型的主磁场强度和方向以及磁偶极源的磁化方向均是变化的,但是通过改变磁偶极源体积保持了磁偶极源的磁矩不变,即1×106A·m2。由图 8可见,主磁场的强度T0和方向(I与D)对迭代收敛速度的影响均较小(图中三条曲线在第1次迭代后近于平行),差异仅在于计算精度,即当磁化倾角与主磁场倾角为90°时,无论主磁场强度为多大,其计算误差均较大且均趋于相同的拟合误差ε;而当磁倾角与主磁倾角接近0°时,则具有较高的计算精度。分析其原因在于:主磁场强度T0对式(7)的逼近误差的影响较小,因而主磁场强度T0对于迭代收敛性的影响程度较低;对于计算精度,当磁倾角与主磁场倾角为90°时,在扩边相同的情况下,研究区域内ΔT的均值越高,波数域奇点的影响也就越严重。

|
图 8 第3组模型试验拟合误差ε随迭代次数的变化曲线 |
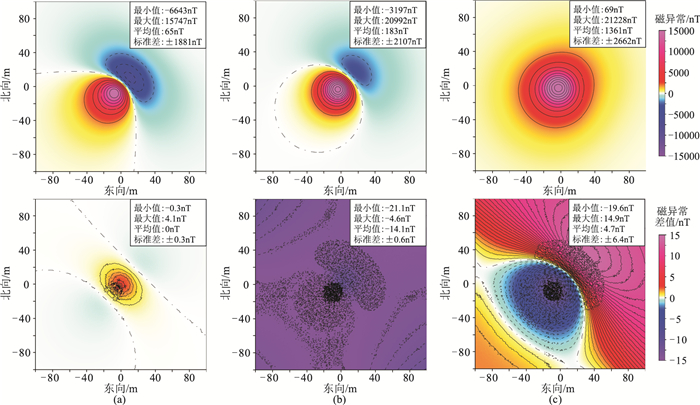
第2组与第3组模型试验转换计算结果及其与理论值的差值分别见图 9和图 10。由图可见,第2组模型的ΔTPro、Za、Ta计算值与理论值之差值均小于21.1nT,第3组模型试验ΔTPro的计算值与理论值之差均小于4.2nT,此误差相比于理论值可以忽略不计。这说明只要给定一个合理的阈值δ,迭代均能收敛且能够达到较高的计算精度。另外,转换计算ΔTPro的误差均低于其他分量的转换误差,原因在于ΔTPro与ΔT的分布形态和均值一致性更高,因而波数域奇点的影响也更弱。
|
图 9 第2组模型试验的模型理论值(上)及其与计算值之差值(下)
(a)ΔTPro;(b)Za;(c)Ta; 上图和下图的等值线间隔分别为2000nT和0.5nT |
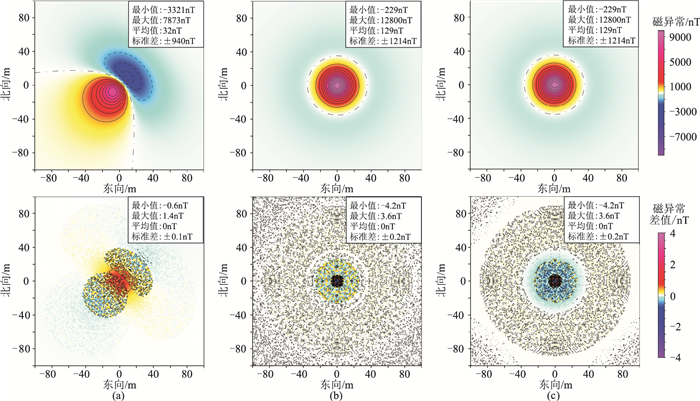
|
图 10 第3组模型试验ΔTPro的理论值(上)及其与计算值之差(下) 主磁场的强度(T0)、倾角(I)与偏角(D)分别为:50000 nT、45°与45° (a);50000 nT、90°与0° (b);20000 nT、90°与0° (c);上图和下图的等值线间隔分别为1000nT与0.5nT |
第4组模型的差异仅在于点距与线距的变化,旨在测试计算效率及其随数据总量的变化特征。
对于Zhen等[12]和甄慧翔等[13-14]提出的计算方法,由于目标函数的导数方程难以得到,因而采用差分代替微分计算每个测点处的导数,故计算量较大,不适用于较大数据量的情况。例如,对于101×101网格数据的计算,每次计算大约需要30min,对于201×201网格数据则需要8h。研究显示,计算耗时随着数据量增长呈二次幂增长[13],即当x与y方向的数据量均增大1倍时,每次迭代的耗时将增加至原来的16倍。
对于本文所提方法,第4组模型3套数据的数据量分别为801×801、401×401和201×201,在笔记本电脑(Inter(R) Xeon(R) CPU E3-1505M v6 @3.00 GHz的处理器、内存8GB、64位操作系统)上每次迭代分别耗时约4.0、0.9、0.2s,若设阈值δ=1nT,则3个模型的计算耗时分别为21.2、4.1、0.9s。这说明本文算法具有较高的计算效率。
由前文理论分析可知,本文算法的计算效率主要取决于快速傅里叶正、反变换,每次迭代需要进行1次傅里叶正变换和3次傅里叶反变换,而二维快速傅里叶变换的时间复杂度为O[M×Nlg(M×N)][31](M和N分别表示x与y方向的数据量),因此本文所提算法的时间复杂度为O[4×imax×M×Nlg(M×N)],其中imax为迭代总次数。
3 实际应用上节展示了本文算法的可靠性、稳定性及计算效率,并分析了计算精度和迭代收敛速度随磁场矢量异常的模量大小、主磁场大小和方向的变化关系,以及计算时间随测点数量的变化关系。Zhen等[12]、甄慧翔等[13-14]、Sun等[15]和Yang等[17]已经验证了在实际情况中考虑ΔT近似为ΔTPro误差的必要性。因此,此节仅讨论本文算法在实际应用中需要注意的问题,及其与传统方法计算结果之间的差异。
研究区位于河北省东部的麻城铁矿区,该铁矿为大型隐伏条带状铁建造(Banded Iron Formation, BIF)矿体[32]。图 11a为研究区部分地面实测总磁场强度异常分布,测点点距和线距均为25m,数据点数为181(北向)×129(东向)。由图可见,总磁异常幅值范围为-2806~11402nT。当地的主磁场强度为54000nT,倾角和偏角分别为57.9°和-7.1°[16]。根据文献[8-9],采用投影分量ΔT近似ΔTPro的最大误差Emax=Ta2/(2T0),可以估算出研究区该最大误差约为1204nT。如此大的计算误差将对后续的定量解释产生比较严重的影响,因此必须考虑投影分量ΔTPro与实测ΔT之间的差异。

|
图 11 研究区域实测总磁场强度异常(ΔT)及扩边结果
(a)实测数据;(b)四周均扩边500m;(c)四周均扩边1000m 等值线间距为1000 nT;红色、蓝色与黑色边框分别表示未扩边及四周均扩边500m、1000m后的区域边界 |
为了压制快速傅里叶变换的边界效应,并解决位场数据波数域转换处理的奇点问题,需要对实测ΔT进行背景场去除及扩边处理。从图 11a可以看出,研究区域主要具有两个明显的磁力异常:中北部的正值异常范围较小,且在其北侧具有明显的负值异常旁瓣;中南部的正值异常幅值较高、范围较大,没有明显的负值异常旁瓣。由于这两个磁异常相距较近,推测其场源磁化方向相同,因此猜测测区北部大面积的负值异常可能部分是南部大面积正值异常的旁瓣或延伸。由于该测区范围较小、背景场并不明显,直接地去除背景场极有可能使得目标磁力异常发生畸变,因此不进行背景场去除而仅进行扩边处理。根据测区南部大面积正值异常的空间分布特征,沿南北向和东西向均进行扩边,选择两种扩边方案:500m和1000m。扩边后的总数据量分别为221×169、261×209,扩边处理之后的结果如图 11b和图 11c所示,参数统计见表 3。另外,在研究区的西北边界还存在一个幅值略高的正值异常,该异常并不完整,其转换计算误差较大,所以本文不予关注。
|
|
表 3 实测ΔT磁异常数据扩边结果统计表 |
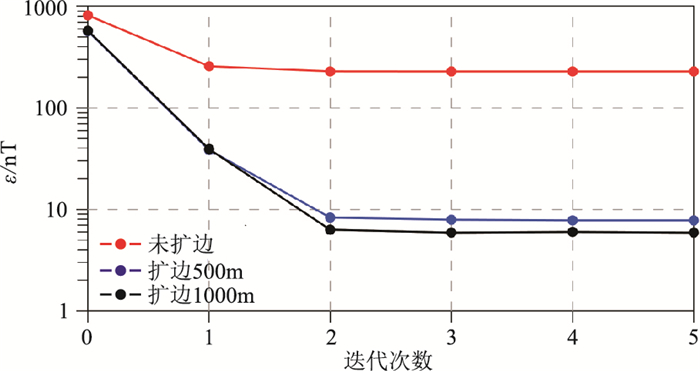
采用本文算法,对图 11所示3套数据分别进行计算。拟合误差ε随迭代次数的变化曲线见图 12,可见扩边范围越大,最终迭代收敛时的拟合差越小,但拟合差降低趋势越来越不明显。说明在实际数据处理时,适当的扩边是必要的,过度扩边会极大地增加计算量。从图 12还看出,本文方法迭代收敛速度较快、计算稳定且计算精度较高。
|
图 12 在不同扩边大小情况下拟合误差ε随迭代次数的变化曲线 |
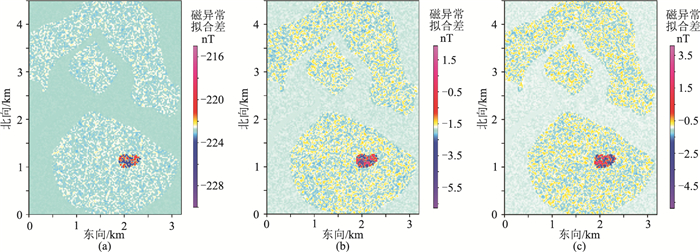
图 13为采用本文方法、5次迭代后的ΔT拟合差分布,其参数统计见表 4。可见,在未扩边时,ΔT拟合差幅值较大;而扩边之后,ΔT拟合差的平均值快速降低至几个nT量级;扩边与不扩边情况下ΔT拟合差的幅值变化范围与标准差几乎一致,说明通过扩边可以有效改善磁力异常波数域转换计算的奇点问题。
|
图 13 研究区采用本文方法计算的ΔT拟合差 (a)未扩边;(b)四周均扩边500m;(c)四周均扩边1000m |
|
|
表 4 本文方法计算的ΔT拟合差统计参数表 |
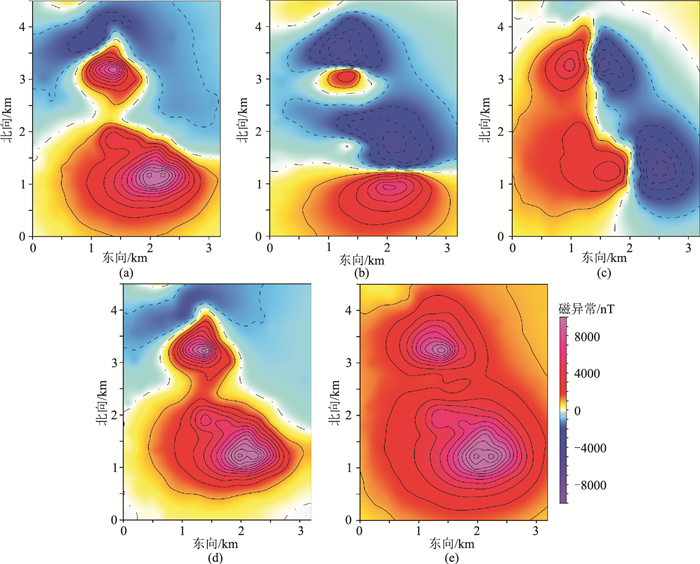
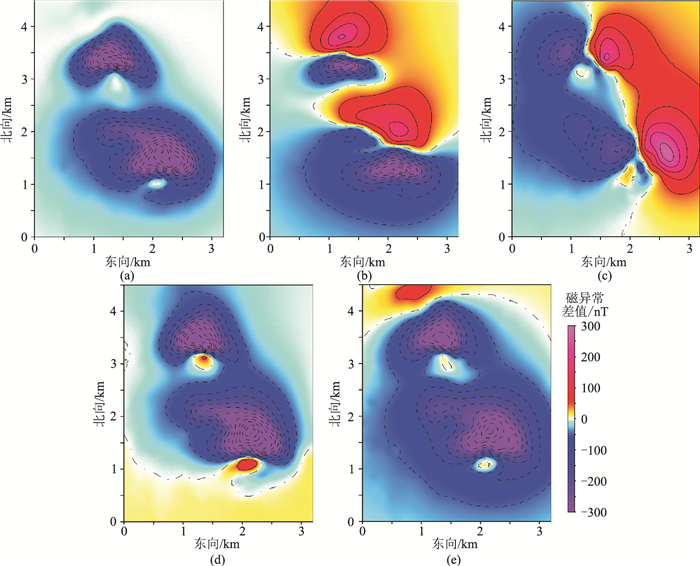
图 14是基于扩边1000m、迭代5次计算得到的Ha, x、Ha, y、Za、Ta分布。由图可知,前文关于研究区存在两个较大的ΔT磁力异常及其场源的推断是合理的。图 15是采用本文方法与直接采用传统波数域方法计算结果(ΔTPro、Ha, x、Ha, y、Za、Ta)的差值,其数据统计结果见表 5。可见两种方法的计算结果差值最高可达600nT,且该差异与磁异常在空间分布上关系密切。若忽略ΔT近似为ΔTPro的误差,直接进行分量与模量转换,会产生较大的误差,该误差对于磁异常的定性解释影响较小,但对于定量解释的影响较大,这再次说明在高磁环境中考虑ΔT近似为投影分量ΔTPro的误差是非常必要的。此外,由图 15a可以发现,ΔTPro均小于ΔT,这与前文理论分析结论一致,即ΔT≥ΔTPro,这也从另一个侧面证明了本文方法的可靠性。
|
图 14 研究区数据采用本文方法的计算结果
(a)ΔTPro;(b)Ha, x;(c)Ha, y;(d)Za;(e)Ta 等值线间距为1000nT |
|
图 15 研究区采用本文方法与传统波数域转换方法计算结果的差值
(a)ΔTPro;(b)Ha, x;(c)Ha, y;(d)Za;(e)Ta 等值线间距为50nT |
|
|
表 5 本文方法与传统方法计算结果及其差值统计 |
在高磁环境中,将ΔT近似为ΔTPro的误差较大,若忽略该误差,对实测ΔT的数据预处理、正演、反演及定量解释会产生较大的影响。虽然已有学者提出了基于ΔT精确计算ΔTPro的方法,但是计算量大、计算效率低,限制了实际应用。为此,本文提出了一种高效率的迭代计算方法,通过理论分析、模型试验与实际应用,得到如下结论。
(1) 本文方法具有较快的迭代收敛速度、较高的计算稳定性、计算精度及计算效率,一般仅需2~3次迭代即可将ΔT拟合差的幅值控制在几个nT之内。
(2) 在每次迭代计算ΔT近似为ΔTPro的误差时,采用式(8)或采用实测ΔT数据计算ΔT(i),迭代的收敛性没有显著差异。但是本文作者认为式(5)所示误差E与ΔT、T0、Ta之间是耦合的,应采用式(8)计算;若采用实测ΔT数据代替可能会致使迭代过程存在振荡的风险。
(3) 采用相邻两次迭代的拟合误差之差δ作为迭代终止条件比采用拟合误差更合理。
(4) 本文方法的迭代收敛速度主要受控于磁场矢量异常的模量大小Ta,而受主磁场强度的影响较弱。
(5) 本文方法的计算效率主要取决于快速傅里叶正、反变换,每次迭代需要进行1次正变换和3次反变换,因此本文所提算法的时间复杂度为O[4×imax×M×Nlg(M×N)]。
(6) 本文方法的计算误差主要来源于快速傅里叶正、反变换的计算精度,其根源在于边界效应与磁力异常波数域转换计算的奇点问题,背景场、模量Ta与主磁场方向或磁化方向对计算精度的影响均表现于此,对研究区进行适当扩边可以有效降低计算误差。
(7) 背景场对波数域转换存在较大影响,但是“粗暴”地去除背景场极有可能导致目标磁力异常发生畸变,因此在实际应用时应该事先仔细分析ΔT的分布特征,根据研究目标选择是否剔除背景场。另外,适当的扩边本身也可以压制背景场效应。
(8) 若忽略ΔT近似为ΔTPro的误差而直接进行分量与模量转换,会产生较大的误差,该差异对于磁异常定性解释影响较小,但对于定量解释的影响较大。因此,在高磁环境中,考虑ΔT近似为投影分量ΔTPro的误差是非常必要的。
笔者已经将本文算法编写为计算机软件,读者可与本文作者联系免费获取该软件程序。
本文所用实际地面磁测数据来源于中国冶金地质总局矿产资源研究院,在此表示衷心的感谢!
| [1] |
管志宁, 郝天珧, 姚长利. 21世纪重力与磁法勘探的展望[J]. 地球物理学进展, 2002, 17(2): 237-244. GUAN Zhining, HAO Tianyao, YAO Changli. Prospect of gravity and magnetic exploration in the 21st century[J]. Progress in Geophysics, 2002, 17(2): 237-244. DOI:10.3969/j.issn.1004-2903.2002.02.008 |
| [2] |
付丽华, 曾诚, 杨文采, 等. 用于地壳弧形构造信息提取的四阶谱矩分析[J]. 石油地球物理勘探, 2020, 55(4): 923-930. FU Lihua, ZENG Cheng, YANG Wencai, et al. Fourth-order spectral moment analysis for extracting the information of crustal arc structures[J]. Oil Geophysical Prospecting, 2020, 55(4): 923-930. |
| [3] |
熊盛青, 丁燕云, 李占奎. 西藏羌塘盆地的重磁场特征及地质意义[J]. 石油地球物理勘探, 2013, 48(6): 999-1008. XIONG Shengqing, DING Yanyun, LI Zhankui. Gravity and magnetic field characteristics and their geological significance in the Qiangtang Basin, China[J]. Oil Geophysical Prospecting, 2013, 48(6): 999-1008. |
| [4] |
管志宁. 地磁场与磁力勘探[M]. 北京: 地质出版社, 2005. GUAN Zhining. Geomagnetic Field and Magnetic Exploration[M]. Beijing: Geological Publishing House, 2005. |
| [5] |
Guo W, Dentith M, Bird R T, et al. Systematic error analysis of demagnetization and implications for magnetic interpretation[J]. Geophysics, 2001, 66(2): 562-570. DOI:10.1190/1.1444947 |
| [6] |
Biedermann A R, McEnroe S A. Effects of magnetic anisotropy on total magnetic field anomalies[J]. Journal of Geophysical Research: Solid Earth, 2017, 122(11): 8628-8644. DOI:10.1002/2017JB014647 |
| [7] |
Clark D A. Methods for determining remanent and total magnetizations of magnetic sources: A review[J]. Exploration Geophysics, 2014, 45(4): 271-304. DOI:10.1071/EG14013 |
| [8] |
袁晓雨, 姚长利, 郑元满, 等. 强磁性体ΔT异常计算的误差分析研究[J]. 地球物理学报, 2015, 58(12): 4756-4765. YUAN Xiaoyu, YAO Changli, ZHENG Yuanman, et al. Error analysis of calculation of total field ano-maly due to highly magnetic bodies[J]. Chinese Journal of Geophysics, 2015, 58(12): 4756-4765. DOI:10.6038/cjg20151235 |
| [9] |
袁晓雨. 强磁异常ΔT的计算误差及高精度处理转换分析研究[D]. 北京: 中国地质大学(北京), 2016. YUAN Xiaoyu. Research on Calculation Error and High-Precision Processing Conversion Analysis of Strong Magnetic Anomaly ΔT[D]. China University of Geosciences (Beijing), Beijing, 2016. |
| [10] |
Blakely R J. Potential Theory in Gravity and Magne-tic Applications[M]. Cambridge: Cambridge University Press, 1995.
|
| [11] |
Hinze W J, von Frese R R B, Saad A H. Gravity and Magnetic Exploration: Principles, Practices, and Applications[M]. Cambridge: Cambridge University Press, 2013.
|
| [12] |
Zhen H X, Li Y Y, Yang Y S. Transformation from total-field magnetic anomaly to the projection of the anomalous vector onto the normal geomagnetic field based on an optimization method[J]. Geophysics, 2019, 84(5): J43-J55. DOI:10.1190/geo2018-0671.1 |
| [13] |
甄慧翔. 基于优化算法的总场异常ΔT精确计算磁异常分量Tap方法[D]. 湖北武汉: 中国地质大学(武汉), 2019. ZHEN Huixiang. Method for Accurately Calculating the Magnetic Anomaly Component Tap from ΔT Based on Optimization Algorithm[D]. China University of Geosciences (Wuhan), Wuhan, Hubei, 2019. |
| [14] |
甄慧翔, 杨宇山, 李媛媛, 等. 基于L-BFGS反演算法的ΔT精确计算磁异常分量Tap方法[J]. 物探与化探, 2019, 43(3): 598-607. ZHEN Huixiang, YANG Yushan, LI Yuanyuan, et al. Method for accurately calculating magnetic ano-maly component using ΔT based on L-BFGS inversion algorithm[J]. Geophysical and Geochemical Exploration, 2019, 43(3): 598-607. |
| [15] |
Sun S, Chen C, Liu Y. Constrained 3D inversion of magnetic data with structural orientation and borehole lithology: a case study in the Macheng iron deposit, Hebei, China[J]. Geophysics, 2019, 84(2): B121-B133. DOI:10.1190/geo2018-0257.1 |
| [16] |
孙石达, 杜劲松, 陈超, 等. 基于等效源的总强度磁异常非线性处理方法[J]. 地球物理学报, 2020, 63(1): 351-361. SUN Shida, DU Jinsong, CHEN Chao, et al. Nonlinear equivalent source method for transformation and inversion of total-field magnetic anomaly[J]. Chinese Journal of Geophysics, 2020, 63(1): 351-361. |
| [17] |
Yang J, Liu S, Hu X. Inversion of high-amplitude magnetic total field anomaly: an application to the Mengku iron-ore deposit, northwest China[J]. Scientific Reports, 2020. DOI:10.1038/s41598-020-68494-1 |
| [18] |
Coleman C, Li Y. Quantifying the error level in computed magnetic amplitude data for 3D magnetization inversion[J]. Geophysics, 2018, 83(5): J75-J84. DOI:10.1190/geo2017-0413.1 |
| [19] |
Du J, Chen C, Lesur V, et al. Magnetic potential, vector and gradient tensor fields of a tesseroid in a geo-centric spherical coordinate system[J]. Geophysical Journal International, 2015, 201(3): 1977-2007. DOI:10.1093/gji/ggv123 |
| [20] |
Tsay L J. The use of Fourier series method in upward continuation with new improvements[J]. Geophysical Prospecting, 1975, 23(1): 28-41. DOI:10.1111/j.1365-2478.1975.tb00678.x |
| [21] |
段本春, 徐世浙. 磁(重力)异常局部场与区域场分离处理中的扩边方法研究[J]. 物探化探计算技术, 1997, 19(4): 298-304. DUAN Benchun, XU Shizhe. A study of the scheme of extending edge in the processing of separating local field from regional field for magnetic/gravity anomaly[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1997, 19(4): 298-304. |
| [22] |
王万银, 邱之云, 刘金兰, 等. 位场数据处理中的最小曲率扩边和补空方法研究[J]. 地球物理学进展, 2009, 24(4): 1327-1338. WANG Wanyin, QIU Zhiyun, LIU Jinlan, et al. The research to the extending edge and interpolation based on the minimum curvature method in potential field data processing[J]. Progress in Geophysics, 2009, 24(4): 1327-1338. DOI:10.3969/j.issn.1004-2903.2009.04.022 |
| [23] |
蒋涛, 李建成, 党亚民, 等. 基于矩谐分析的区域重力场建模[J]. 中国科学: 地球科学, 2014, 44(1): 82-89. JIANG Tao, LI Jiancheng, DANG Yamin, et al. Regional gravity field modeling based on rectangular harmonic analysis[J]. Science China: Earth Sciences, 2014, 44(1): 82-89. |
| [24] |
戴世坤, 陈轻蕊, 李昆, 等. 重力异常场空间-波数混合域三维数值模拟[J]. 地球物理学报, 2020, 63(5): 2107-2119. DAI Shikun, CHEN Qingrui, LI Kun, et al. Three-dimensional numerical simulation of the gravity ano-maly field in the space-wave number mixed domain[J]. Chinese Journal of Geophysics, 2020, 63(5): 2107-2119. |
| [25] |
周印明, 戴世坤, 李昆, 等. 基于样条插值的FFT及其在重磁场正演中的应用[J]. 石油地球物理勘探, 2020, 55(4): 915-922, 930. ZHOU Yinming, DAI Shikun, LI Kun, et al. Cubic-spline-interpolation-based FFT and its application in forward modeling of gravity and magnetic fields[J]. Oil Geophysical Prospecting, 2020, 55(4): 915-922, 930. |
| [26] |
舒晴, 张文志, 周坚鑫, 等. 重力梯度张量分量转换处理误差研究[J]. 物探与化探, 2016, 40(1): 111-116. SHU Qing, ZHANG Wenzhi, ZHOU Jianxin, et al. Error study on gravity gradient tensor components transformation[J]. Geophysical & Geochemical Exploration, 2016, 40(1): 111-116. |
| [27] |
Chai Y. Shift sampling theory of Fourier transform computation[J]. Science in China (Series E): Technological Sciences, 1997, 40(1): 21-27. DOI:10.1007/BF02916587 |
| [28] |
Chai Y. A-E equation of potential field transformations in wavenumber domain and its application[J]. Applied Geophysics, 2009, 6(3): 205-216. DOI:10.1007/s11770-009-0032-z |
| [29] |
柴玉璞, 贾继军. 偏移抽样理论在磁异常化极中的应用[J]. 石油地球物理勘探, 1998, 33(4): 486-495. CHAI Yupu, JIA Jijun. Application of shift sampling theory to magnetic anomaly reduction-to-the-pole[J]. Oil Geophysical Prospecting, 1998, 33(4): 486-495. DOI:10.3321/j.issn:1000-7210.1998.04.007 |
| [30] |
柴玉璞, 万海珍. 移样离散傅里叶变换在重磁勘探中的应用[J]. 石油地球物理勘探, 2020, 55(6): 1358-1363. CHAI Yupu, WAN Haizhen. Shift sampling DFT(SFT) theory and its application in gravity and magnetic prospecting[J]. Oil Geophysical Prospecting, 2020, 55(6): 1358-1363. |
| [31] |
Fertner A. Computationally efficient methods for analysis and synthesis of real signal using FFT and IFFT[J]. IEEE Transaction on Signal Processing, 1999, 47(4): 1061-1064. DOI:10.1109/78.752603 |
| [32] |
Wu H, Niu X, Zhang L, et al. Geology and geochemistry of the Macheng Algoma-type banded iron-formation, North China Craton: Constraints on mi-neralization events and genesis of high-grade iron ores[J]. Journal of Asian Earth Sciences, 2015, 113: 1179-1196. DOI:10.1016/j.jseaes.2015.05.024 |



 杜劲松, 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉), 430074。Email:
杜劲松, 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉), 430074。Email: 