② 中南大学地球科学与信息物理学院湖南长沙 41008;
③ 计算与随机数学教育部重点实验室(湖南师范大学数学与统计学院), 湖南长沙 410081;
④ 核资源与环境国家重点实验室(东华理工大学), 江西南昌 330013
② School of Geosciences and Info-Physics, Central South University, Changsha, Hunan 410083, China;
③ Key Laboratory of Computing and Stochastic Mathe-matics(School of Mathematics and Statistics, Hunan Normal University), Changsha, Hunan 410081, China;
④ State Key Laboratory of Nuclear Resources and Environment(East China University of Technology), Nanchang, Jiangxi 330013, China
随着深部资源勘探的不断深入,要求可探测深度越来越大[1]。可控源音频大地电磁测深法(CSAMT,Controlled Source Audio Electromagne-tic Method)[2]以勘探深度大、抗干扰能力强、工作效率高等特点成为研究热点,是中深部资源勘探的重要手段之一。该方法在隐伏矿体勘察、复杂地区页岩气勘探、地热资源调查及海洋油气勘探等领域都取得了良好效果[3-4],成为发展快且前景可期的地球物理勘探方法之一。
CSAMT电磁场正演的主流方法主要有边界单元法、有限差分法、积分方程法和有限单元法四种,其中有限单元法以其理论系统化、适应性强、计算精度高、弱解可微等优点得到了更多的重视和应用。Coggon[5]于1971年提出了大地电磁问题的有限元模拟方法,自此有限元计算在电磁领域得到了极大的发展。CSAMT有限元数值模拟中,边值问题包括控制方程和边界条件两个方面。对于控制方程,由于场源存在奇异性,场源的处理方式是关键,常用的方法有二次场法和总场法,其中二次场法是主流。二次场法将场分解为背景场和异常场,背景场利用均匀半空间或层状模型解析解可直接计算,二次场则通过有限元法求取[6-12]。总场法直接从总场着手,采用近似法模拟奇异性场源特征(例如伪delta函数法),然后通过有限元求解场值[13-22]。在CSAMT三维有限元正演模拟中,无论采用总场法还是二次场法,场值的求解精度都是正演模拟是否成功的标志,因此开展不同场源方案下场值求解精度的研究十分必要。
一般来说,对于边界条件的处理基本上采用传统截断边界方法[6-22],即在一个相对较大的区域内,将无穷边界问题近似为有限区域,这往往会造成有限元计算区域太大、节点数太多、存储量过大和计算耗时过长等问题。较合理的边界处理策略应该是将计算区域限制在较小的目标区域内,以减少单元数和节点数,实现节约计算资源及提高计算速度的目的。有限元-无限元耦合法是针对常规截断边界引起的大尺度模型问题提出的[23],具有离散区域小、求解速度快和计算精度高等优点。其核心思路是用“无限单元”取代传统截断边界,通过坐标映射将“无限单元”沿某一方向无限扩展,实现电磁场在无限单元中快速衰减为零,最后通过有限元-无限元耦合求解方程组,从而实现CSAMT的三维正演计算。
在地球物理领域,无限元思想主要应用于地震、测井和直流电领域。Blome等[24]应用Astley无限元处理直流电法边界问题,缩小了计算范围,减少了节点数, 且避免了采用Dirichlet或混合边界条件,但是其采用的无限元形函数较复杂,且由于引入了Astley无限元中特有的额外权重因子,使整体系数矩阵失去了对称性。Nath等[25-26]将无限元分别应用于重磁法的数值计算。在电磁法领域,公劲喆[27]将无限元应用到直流电阻率法的三维正演模拟。汤井田等[28]将基于有限元-无限元的三维直流电成功应用于泥河铁矿勘探实例;张林成等[10]、汤井田等[22]采用无限元代替截断边界条件,成功地将有限元-无限元耦合法应用于CSAMT法,实现了小区域内CSAMT数据的三维快速高精度正演,但其采用的是基于电场二次场的方案。
针对以上研究现状,本文从基于总场方案的边值问题出发,首先采用等效场源法,假设场源周围很小区域内电磁场的分布是均匀的,用区域内网格节点上电磁场的近场值表示场源,并将节点场值作为第一类边界条件带入场方程,实现场源的近似模拟;然后,用“无限单元”代替传统截断边界条件,采用Garlerkin有限元法和Pardiso并行直接求解器实现了三维CSAMT快速正演计算;最后,通过均匀半空间模型解析解验证方法的正确性,并开展了场源等效模拟最佳范围的研究。
1 边值问题 1.1 基本方程对于角频率为ω、时间因子为e-iω的水平电偶极子,在各向同性导电介质中产生的电场E满足双旋度方程[29]
| $ \nabla \times \nabla \times \boldsymbol{E}-\mathrm{i} \omega \mu_{0}\left(\sigma-\mathrm{i}{\omega {\varepsilon}_{0}}\right) \boldsymbol{E}=\mathrm{i} \omega \mu_{0} \boldsymbol{J}_{\mathrm{s}} $ | (1) |
式中:σ为电阻率;Js为电偶极子电流密度矢量;μ0表示真空磁导率,取空气和地下介质的磁导率均等于μ0;ε0是真空介电常数。
1.2 场源的计算由于水平电偶极源存在奇异性,如何精确加载场源成为基于电场总场数值模拟的关键问题。本文采用等效场源法,将其周围很小的区域看成均匀的,用此区域内离散网格节点上电磁场的近场值表示近似等效场源,并将源附近节点上的场值第一类边界条件代入方程。最后通过有限元—无限元耦合求解方程组,从而实现三维正演计算。
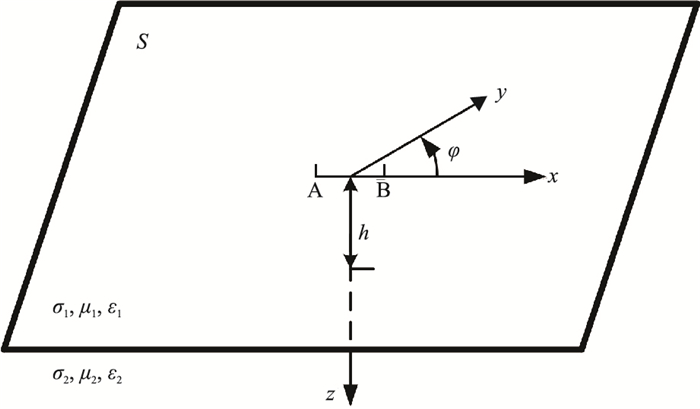
设在无穷大的空间中,存在一无限大分界平面S,把无穷空间分为上下两部分,如图 1所示。在分界面S上h高度处有一水平电偶极子AB,其偶极距为dL。建立直角坐标系和柱坐标系,选取共同原点,位于偶极子中心,偶极距与x轴正方向一致,z轴垂直向下。设上半空间和下半空间介质的电导率分别为σ1和σ2,导磁率为μ1和μ2,介电常数为ε1和ε2。在勘探地球物理中,通常下半空间代表大地,上半空间代表地面之上的空间。设偶极源中的电流为正弦交变电流I=I0e-iωt,其中I0为电流振幅。
|
图 1 均匀半空间参数及坐标示意图 |
在柱坐标系中,上、下半空间中任意一点的电场分量为
| $ \left\{ {\begin{array}{*{20}{l}} {{E_{1r}} = {\rm{i}}\omega {\mu _1}{\mathop{\rm PE}\nolimits} \cos \varphi \left[ {\int_0^\infty {\frac{m}{{{m_1} + {m_2}}}} {{\rm{e}}^{{m_1}z}}{J_0}(mr){\rm{d}}m - \int_0^\infty {\frac{{{m^3}}}{{{m_1}k_2^2 + {m_2}k_1^2}}} {J_0}(mr){{\rm{e}}^{{m_1}z}}{\rm{d}}m + } \right.}\\ {\;\;\;\;\;\;\;\;\;\;\;\left. {\frac{1}{r}\int_0^\infty {\frac{{{m^2}}}{{{m_1}k_2^2 + {m_2}k_1^2}}} {J_1}(mr){{\rm{e}}^{{m_1}z}}{\rm{d}}m} \right]}\\ {{E_{1\varphi }} = - {\rm{i}}\omega {\mu _1}{\mathop{\rm PEsin}\nolimits} \varphi \left[ {\int_0^\infty {\frac{m}{{{m_1} + {m_2}}}} {{\rm{e}}^{{m_1}z}}{J_0}(mr){\rm{d}}m - \frac{1}{r}\int_0^\infty {\frac{{{m^2}}}{{{m_1}k_2^2 + {m_2}k_1^2}}} {J_1}(mr){{\rm{e}}^{{m_1}z}}{\rm{d}}m} \right]}\\ {{E_{1z}} = - {\rm{i}}\omega {\mu _1}{\mathop{\rm PE}\nolimits} \cos \varphi \left[ {\int_0^\infty {\frac{{{m_2}{m^2}}}{{{m_1}k_2^2 + {m_2}k_1^2}}} {{\rm{e}}^{{m_1}z}}{J_1}(mr){\rm{d}}m} \right]} \end{array}} \right. $ | (2) |
| $ \left\{\begin{aligned} E_{2 r}=& \mathrm{i}{\omega \mu_{2}} \mathrm{PE} \cos \varphi\left[\int_{0}^{\infty} \frac{m}{m_{1}+m_{2}} \mathrm{e}^{-m_{2} z} J_{0}(m r) \mathrm{d} m-\int_{0}^{\infty} \frac{m^{3}}{m_{1} k_{2}^{2}+m_{2} k_{1}^{2}} J_{0}(m r) \mathrm{e}^{-m_{2} z} \mathrm{~d} m+\right.\\ &\left.\frac{1}{r} \int_{0}^{\infty} \frac{m^{2}}{m_{1} k_{2}^{2}+m_{2} k_{1}^{2}} J_{1}(m r) \mathrm{e}^{-m_{2} z} \mathrm{~d} m\right] \\ E_{2 \varphi}=&-\mathrm{i}\omega \mu_{2} \operatorname{PEsin} \varphi\left[\int_{0}^{\infty} \frac{m}{m_{1}+m_{2}} \mathrm{e}^{-m_{2} z} J_{0}(m r) \mathrm{d} m-\frac{1}{r} \int_{0}^{\infty} \frac{m^{2}}{m_{1} k_{2}^{2}+m_{2} k_{1}^{2}} \mathrm{e}^{-m_{2} z} J_{1}(m r) \mathrm{d} m\right] \\ E_{2 z}=& \mathrm{i}\omega \mu_{2} \operatorname{PE} \cos \varphi\left[\int_{0}^{\infty} \frac{m_{1} m^{2}}{m_{1} k_{2}^{2}+m_{2} k_{1}^{2}} \mathrm{e}^{-m_{2} z} J_{1}(m r) \mathrm{d} m\right] \end{aligned}\right. $ | (3) |
式中:下标“1”和“2”分别代表上半空间和下半空间;m表示空间频率,具有距离倒数的量纲;
根据电法理论,在电性分界面上,电场的法向分量是不连续的,而节点有限元要求电磁场法在法向上是连续的。因此,求解得到的有限元解往往不准确,需要对解进行校正。
在有源区,节点有限元的电场解不满足
| $ \nabla \cdot(\varepsilon \boldsymbol{E})=-\nabla \cdot\left[\boldsymbol{J}_{\mathrm{S}} /(\mathrm{i} \omega)\right] $ |
在无源区域不满足
| $ \nabla \cdot(\varepsilon \boldsymbol{E})=0 $ |
因此,需在式(1)中加入散度校正条件[25]
| $ \nabla \times \nabla \times \boldsymbol{E}+k^{2} \boldsymbol{E}+\nabla \cdot \boldsymbol{E}=\mathrm{i} \omega \mu_{0} \boldsymbol{J}_{\mathrm{S}} $ | (4) |
基于加权余值有限元法[30]将场源作为第一类边界条件,建立式(4)的残差公式
| $ \boldsymbol{r}=\nabla \times \nabla \times \boldsymbol{E}+k^{2} \boldsymbol{E}+\nabla \cdot \boldsymbol{E} $ | (5) |
取任意测试函数V,在区域Ω上令
| $ \iiint_{\varOmega} \boldsymbol{r} \cdot \boldsymbol{V} \mathrm{d} \varOmega=0 $ |
有
| $ \begin{array}{c} \int_{\Omega} \nabla \times \nabla \times \boldsymbol{E} \cdot \boldsymbol{V} \mathrm{d} \varOmega+\int_{\varOmega} k^{2} \boldsymbol{E} \cdot \boldsymbol{V} \mathrm{d} \varOmega+ \\ \int_{\varOmega} \nabla \cdot \boldsymbol{E} \cdot \boldsymbol{V} \mathrm{d} \varOmega=0 \end{array} $ | (6) |
设T为区域Ω的外边界面。用无限元处理无穷边界问题,在无限单元内电磁场衰减为零,即
| $ \boldsymbol{E}=0 $ |
利用第一矢量Green定理[31]可将式(6)简化为
| $ \begin{array}{c} \int_{\Omega}(\nabla \times \boldsymbol{V}) \cdot(\nabla \times \boldsymbol{E}) \mathrm{d} \varOmega+\int_{\varOmega} k^{2} \boldsymbol{E} \cdot \boldsymbol{V} \mathrm{d} \varOmega+ \\ \int_{\varOmega} \nabla \cdot \boldsymbol{E} \cdot \boldsymbol{V} \mathrm{d} \varOmega=0 \end{array} $ | (7) |
利用有限元对内部计算区域进行离散。假设内部计算区域内有n个节点,对于第j个测试函数Vj有
| $ \begin{array}{c} \int_{\varOmega}\left(\nabla \times \boldsymbol{V}_{j}\right) \cdot(\nabla \times \boldsymbol{E}) \mathrm{d} \varOmega+\int_{\varOmega} k^{2} \boldsymbol{E} \cdot \boldsymbol{V}_{j} \mathrm{~d} \varOmega+ \\ \int_{\varOmega} \nabla \cdot \boldsymbol{E} \cdot \boldsymbol{V}_{j} \mathrm{~d} \varOmega=0 \end{array} $ | (8) |
有限元—无限元耦合算法即将整个求解区域分为有限元区域和无限元区域,用无限元区域代替传统的外边界,在这两个区域分别采取有限元分析和无限元分析,通过总体刚度矩阵组装将两者结合,从而进行数值求解。
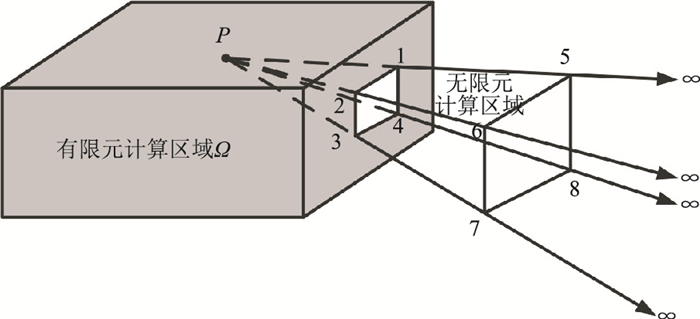
图 2为有限元和无限元计算区域划分示意图。图中灰黑色区域为有限元区域,即目标区域,包含场源、目标体及测点等;白色区域为无限元区域,即从有限元区域边界至无穷远,是边界计算区域。无限元分析就是在该区域的某一方向上采用无限元映射和形函数,将整体坐标映射到局部坐标上,其原理与有限元分析相同。
|
图 2 有限元和无限元计算区域划分示意图 图中P为坐标原点,节点1~8为无限元基本要素,节点1~4为有限元边界上某单元上的节点,P点到节点5~8的距离分别为P点到节点1~4距离的两倍,图 4同 |
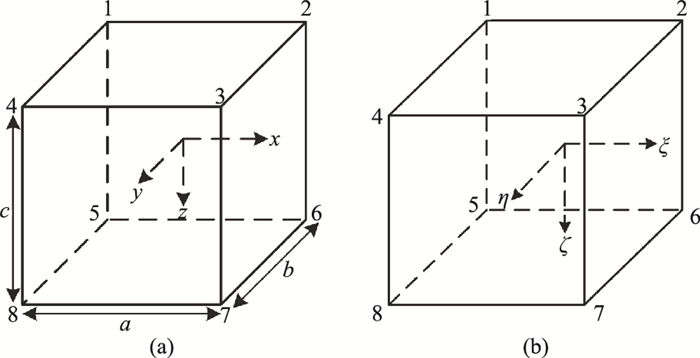
有限元单元分析时,采用矩形六面体进行区域离散,单元节点编号及坐标如图 3所示。
|
图 3 有限元映射示意图 (a)子单元;(b)母单元 |
图 3中,子、母单元坐标对应关系为
| $ \left\{\begin{array}{l} x=x_{0}+\frac{a}{2} \xi \\ y=y_{0}+\frac{b}{2} \eta \\ z=z_{0}+\frac{c}{2} \zeta \end{array}\right. $ | (9) |
矩形六面体形函数表达式为
| $ N_{q}^{\mathrm{e}}=\frac{1}{8}\left(1+\xi_{q} \xi\right)\left(1+\eta_{q} \eta\right)\left(1+\zeta_{q} \zeta\right) $ | (10) |
式中(ξq,ηq,ζq)(q=1,2,…,8)表示子单元节点q在母单元中的坐标。
2.2 无限元分析无限元单元分析时,采用三维八节点Astley型无限元。图 4是三维无限元映射示意图。无限元分析就是通过无限元映射将无穷坐标映射到图 4b中的局部坐标上。图 4b中无限单元最外围的四个节点9~12代表无穷远,其场值为零。

|
图 4 无限元映射示意图 (a)子单元;(b)母单元 |
图 4b中ξ方向表示无限元映射方向,在ζ-η平面内,无限单元与有限单元采用相同的映射形式和形函数。无限元坐标映射为
| $ \left\{\begin{array}{l} y=\sum\limits_{i=1}^{4} L_{i} y_{i} \\ z=\sum\limits_{i=1}^{4} L_{i} z_{i} \end{array}\right. $ | (11) |
式中
再结合ξ方向的坐标映射关系式,可得到8个结点无限单元坐标映射函数
| $ \left\{\begin{array}{l} x=\sum\limits_{i=1}^{8} N_{i} x_{i} \\ y=\sum\limits_{i=1}^{8} N_{i} y_{i} \\ z=\sum\limits_{i=1}^{8} N_{i} z_{i} \end{array}\right. $ | (12) |
式中
无限元形函数M的表达式为
| $ \left\{\begin{array}{l} M_{i}=L_{i} \times \frac{1-\xi}{2} \times \frac{-(1-\xi)}{2} \xi \\ M_{i+4}=L_{i} \times \frac{1-\xi}{2} \times\left(1-\xi^{2}\right) \end{array}\right. $ | (13) |
上式即Astley映射无限单元理论[30]中采用的形函数中的系数(1-ξ)/2与二阶Lagrange插值多项式的乘积。
有限元与无限元单元分析基本一致,都为八节点单元,因此在数值模拟中,可将无限元和有限元完美结合起来,保证刚度矩阵的对称性,从而使得求解更简单、更方便。
3 方程组求解三维CSAMT有限元-无限元耦合正演模拟最终形成大型、稀疏、对称的复系数线性方程组
| $ \boldsymbol{A} \boldsymbol{x}=\boldsymbol{b} $ | (14) |
式中:矩阵A为混合有限元-无限元总体刚度矩阵,为3×Nx×Ny×Nz阶方阵,其中Nx、Ny、Nz分别为x、y、z三个方向上的节点数,矩阵A中每行最多有81个非零元素;x为各节点待求解的电场值;b为右端项。对于大型稀疏线性方程组,本文采用性能良好、高度并行化的开源求解器Pardiso, Pardiso直接求解,采用LU分解,这种方法特别适合于多源CSAMT的情况。
4 精度验证为验证本文基于等效场源的CSAMT三维无限元数值模拟程序的正确性,对本文方法计算结果与均匀半空间地表水平电偶极子产生的电磁场解析解进行对比、分析。以下数值计算平台均为Intel(R) Xeon(R) CPU 3.10G,256GB RAM,16CPUs。
4.1 模型计算假设一个均匀半空间模型:地下介质电阻率为100Ω·m,空气中电阻率为1×109Ω·m,水平电偶极子沿x轴布设,长度为1m,供电电流为1A,水平电偶极子中心点位于坐标原点,计算频率为256Hz。对模拟区域进行网格剖分,x方向区域为-5000~5000m,网格距为100m, 共计101个网格节点,左右对称;y方向剖分方案与x方向一致;z方向(空气中z坐标为负)区域为-2000~2000m,网格距不等,场源附近较小,共35个网格节点,地面以上部分剖分为9层。
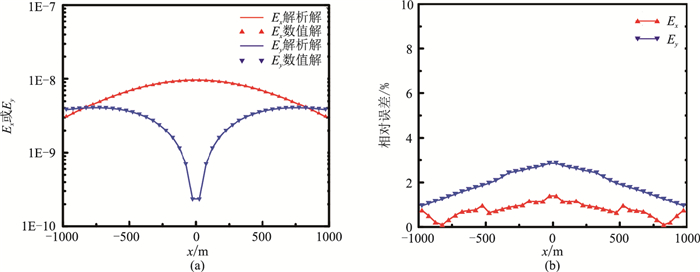
图 5为均匀半空间模型下基于等效场源的CSAMT三维有限元-无限元正演模拟数值解与解析解对比。场源加载范围为1.5倍趋肤深度, 所示结果为z=0、y=1500m、x为-1000~1000m剖面,频率为256Hz时,电场Ex和Ey振幅数值解与解析解及相对误差。
|
图 5 均匀半空间模型基于等效场源的CSAMT三维有限元—无限元正演模拟数值解和解析解(a)及相对误差(b) |
从图 5a可以看出,基于等效场源的CSAMT三维无限元数值计算的电场Ex和Ey数值解与解析解场值大小非常相近,且曲线变化形态一致。图 5b中,Ex数值解相对解析解最大误差为1.5%,平均相对误差小于0.8%;Ey数值解相对解析解误差较Ex稍大,但均小于2.8%,平均相对误差约为1.5%。因此,基于等效场源的CSAMT三维无限元数值模拟程序的计算结果是正确可靠的,其计算精度较高。
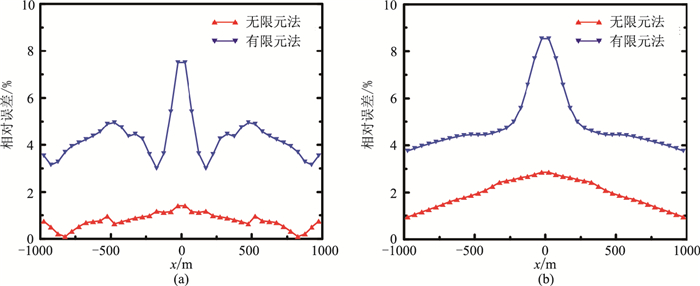
4.2 相同区域无限元法与传统有限元法结果对比针对上述均匀半空间模型,对相同区域进行相同的网格剖分,利用传统有限法进行模型正演,并对比分析本文方法与传统有限元法的计算结果。图 6为无限元法与传统有限元法电场分量Ex和Ey振幅数值解与解析解的相对误差。
|
图 6 无限元法与传统有限元法Ex(a)和Ey(b)数值解相对误差 |
由图 6可见,在相同的小区域内,即x为-1000~1000m范围内,传统有限元法计算所得电场分量Ex和Ey的平均相对误差约为5%,远大于无限元法(小于3%),即无限元单元法在较小的计算区域内的计算结果精度高于传统有限元法。因此,本文基于等效场源的CSAMT三维无限元法相对传统大区域有限元法,能在保证精度的前提下,缩小计算区域,提高计算速度。
4.3 无限元法与传统大区域有限元法计算效率对比关于无限元法与传统大区域有限元法计算效率对比,文献[10]有详细分析,此处不再赘述。从表 1可以看出,相对于基于总场法的传统大区域有限元法,本文提出的基于等效场源的CSAMT三维无限元计算性能更高,明显具有离散区域小、计算节点少、求解速度快等优势。
|
|
表 1 基于总场法的传统大区域有限元法与小区域无限元法计算数据对比[10] |
针对4.1节均匀半空间模型,分析不同频率下的计算结果的精度。图 7是频率分别为64、256、1024Hz时利用本文方法计算的z=0、y=1500m剖面的Ey值及Ey数值解相对误差。可以看出,在相同剖分方案下,1024、256、64Hz下的电场分量Ex和Ey的数值解平均相对误差都小于2%,精度较高。还可以看出,随着计算频率的降低,本文方法计算的Ex和Ey数值解的计算相对误差逐渐减小,这是由于频率降低,趋肤深度增大,均匀半空间模型剖分网格相对加密。因此在进行正演时,为提高精度,可根据频率的不同,进行不同的网格剖分。

|
图 7 不同频率下Ex(a)和Ey(b)数值解相对误差 |
等效场源法是将场源周围很小的区域看成均匀的,用此区域内网格节点上电磁场的近场值表示源,将源附近节点上的场值第一类边界条件带入方程。对于水平电偶极源,由于电磁场在近区、过渡区和远区的衰减规律不一样,利用节点电场值代替场源时,一方面仅限于近区,另一方面该区域中的网格应足够多,使得场值能充分模拟场源的特征。因此,如何精确确定源的加载范围是关键。本节以参照CSAMT的近区范围,通过数值模拟,分析场源不同加载范围的结果。
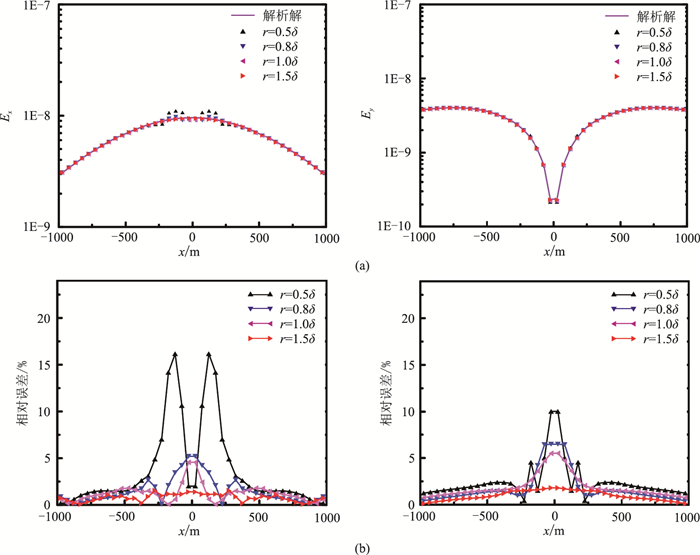
图 8所示是场源不同加载范围对比试验结果。采用均匀半空间模型,电阻率为100Ω·m,水平电偶极子沿x轴布设,其中心位于坐标原点,长度为1m,供电电流为1A,计算频率为256Hz。网格剖分与4.1节模型剖分方案一致。计算可知,256Hz对应的趋肤深度δ约为160m,分别对比观测点到原点的距离r=0.5δ、0.8δ、1.0δ、1.5δ时Ex和Ey本文方法计算结果与解析解的振幅及误差(图 8)。
|
图 8 场源不同加载范围时Ex(左)和Ey(右)数值解和解析解(a)及相对误差(b) |
根据CSAMT近区、过渡区和远区的划分原则可知,当加载范围r=0.5δ时,场源完全处于近区范围内。从图 8可以看出,当场源加载范围r=0.5δ时,测站位于-320~320m范围内,Ex和Ey数值解相对解析解出现明显的跳变,最大相对误差分别达到15%和10%,且其场源性质特征不明确,不能满足计算精度的要求;当加载范围r=0.8δ、测站位于-320~320m范围内时,Ex和Ey数值解相对解析解也出现一定的跳变,但相对于r=0.5δ计算结果,Ex和Ey数值解的最大相对误差分别降至5%和7%,且其场源性质表现为一定程度的连续变化的特征;当场源加载范围r=1.0δ时,场源加载范围已基本包含了近区范围,Ex和Ey的数值解与解析解非常接近,不存在跳变,在测线中垂线附近,其相对误差曲线规律性更强,误差更小。除紧靠中垂线的几个测点外,其他测点的数值模拟结果相对于r=0.5δ和r=0.8δ两种情形的计算结果更优。因此,当加载范围为r=1.5δ时,Ex和Ey数值解精度更高,特别是测线中垂线附近测点的相对误差得到了很好的控制。因此,利用等效场源进行CSAMT三维数值模拟时,对于场源的加载范围最好不小于1.5倍趋肤深度。
6 结论本文从CSAMT正演模拟三维边值问题出发,采用等效场源法处理场源的奇异性,并利用无限元代替传统截断边界条件,通过有限元-无限元耦合法,利用散度校正和直接法求解方程组的策略,实现了小区域的三维CSAMT快速高精度正演模拟。
与均匀半空间模型解析解的对比、分析可见,基于等效场源的CSAMT三维无限元数值模拟程序数值解与解析解平均相对误差均小于1%,精度较高,验证了基于等效场源法的三维CSAMT无限元方法的正确性;通过相同区域无限元法与传统有限元法结果对比、无限元法与传统大区域有限元法计算效率对比以及多频点计算结果的对比,可以看出,本文提出的基于等效场源的三维无限元法具有离散区域小、求解速度快、计算精度高等优点。
针对等效场源法中精确加载场源的问题,数值模拟结果表明,基于等效场源的CSAMT三维无限元数值模拟结果,场源等效模拟最佳范围应不小于1.5倍趋肤深度,其计算结果即能满足精度要求。
| [1] |
REN Z, Chen C, Pan K, et al. Gravity anomalies of arbitrary 3D polyhedral bodies with horizontal and vertical mass contrasts[J]. Surveys in Geophysics, 2017, 38(2): 1-24. DOI:10.1007/s10712-016-9395-x |
| [2] |
Goldstein M A, Strangway D W. Audio-frequency magnetotellurics with a grounded electric dipole source[J]. Geophysics, 1975, 40(4): 669-683. DOI:10.1190/1.1440558 |
| [3] |
何继善. 可控源音频大地电磁法[M]. 湖南长沙: 中南工业大学出版社, 1990: 74-90.
|
| [4] |
汤井田, 何继善. 可控源音频大地电磁法及其应用[M]. 湖南长沙: 中南大学出版社, 2005: 1-8.
|
| [5] |
Coggon J H. Electromagnetic and electrical modeling by the finite element method[J]. Geophysics, 1971, 36(1): 132-155. DOI:10.1190/1.1440151 |
| [6] |
Silva N V D, Morgan J V, Macgregor L, et al. A finite element multifrontal method for 3D CSEM mode-ling in the frequency domain[J]. Geophysics, 2012, 77(2): E101-E115. DOI:10.1190/geo2010-0398.1 |
| [7] |
REN Z Y, Kalscheuer T, Greenhalgh S, et al. A goal-oriented adaptive finite-element approach for plane wave 3-D electromagnetic modelling[J]. Geophysical Journal International, 2012, 194(2): 700-718. |
| [8] |
REN Z Y, Kalscheuer T, Greenhalgh S, et al. A finite-element-based domain decomposition approach for plane wave 3D electromagnetic modeling[J]. Geophysics, 2014, 79(6): 255-268. DOI:10.1190/geo2013-0376.1 |
| [9] |
Castillo R O, de la Puente J, Puzyrev V, et al. Edge-based electric field formulation in 3D CSEM simulations: a parallel approach[C]·Computing and Communication (IEMCON), International Conference and Workshop on IEEE, 2015.
|
| [10] |
张林成, 汤井田, 任政勇, 等. 基于二次场的可控源电磁法三维有限元-无限元数值模拟[J]. 地球物理学报, 2017, 60(9): 3655-3666. ZHANG Lincheng, TANG Jingtian, REN Zhengyong, et al. Forward modeling of 3D CSEM with the coupled finite-infinite element method based on the se-cond field[J]. Chinese Journal of Geophysics, 2017, 60(9): 3655-3666. |
| [11] |
殷长春, 惠哲剑, 张博, 等. 起伏海底地形时间域海洋电磁三维自适应正演模拟[J]. 地球物理学报, 2019, 62(5): 1942-1953. YIN Changchun, HUI Zhejian, ZHANG Bo, et al. 3D adaptive forward modeling for time-domain marine CSEM over topographic seafloor[J]. Chinese Journal of Geophysics, 2019, 62(5): 1942-1953. |
| [12] |
邱长凯, 殷长春, 刘云鹤, 等. 三维时间域航空电磁有理Krylov正演研究[J]. 地球物理学报, 2020, 63(2): 715-725. QIU Changkai, YIN Changchun, LIU Yunhe, et al. 3D time-domain airborne electromagnetic forward modeling using the rational Krylov method[J]. Chinese Journal of Geophysics, 2020, 63(2): 715-725. |
| [13] |
Unsworth M J. Electromagnetic induction by a finite electric dipole source over a 2-D earth[J]. Geophy-sics, 1993, 58(2): 198-214. |
| [14] |
Mitsuhata Y. 2-D electromagnetic modeling by finite-element method with a dipole source and topography[J]. Geophysics, 2000, 65(2): 465-475. DOI:10.1190/1.1444740 |
| [15] |
闫述. 基于三维有限元数值模拟的电和电磁探测研究[D]. 陕西西安: 西安交通大学, 2003. YAN Shu. Studies on the Electromagnetic Prospecting Based on Three-Dimensional Finite Element Method[D]. Xi'an Jiaotong University, Xi'an, Shaanxi, 2003. |
| [16] |
张继峰. 基于电场双旋度方程的三维可控源电磁法有限单元法数值模拟[D]. 湖南长沙: 中南大学, 2008. ZHANG Jifeng. Three Dimensional Controlled Source Electromagnetic Numerical Simulation Based on Electric Field Double Curl Equation Using Finite Element Method[D]. Central South University, Changsha, Hunan, 2008. |
| [17] |
汤文武, 柳建新, 叶益信, 等. 基于节点有限元与矢量有限元的可控源电磁三维正演对比[J]. 石油地球物理勘探, 2018, 53(3): 192-199. TANG Wenwu, LIU Jianxin, YE Yixin, et al. Three-dimensional forward modeling of controlled source electromagnetic based on nodal and vector finite elements[J]. Oil Geophysical Prospecting, 2018, 53(3): 192-199. |
| [18] |
赵宁, 黄明卫, 申亚行, 等. 高阶自适应有限元三维直流电阻率正演方法及其在沁水盆地煤气层压裂监测中的应用[J]. 石油地球物理勘探, 2021, 56(1): 209-216. ZHAO Ning, HUANG Mingwei, SHEN Yaxing, et al. High-order adaptive finite element 3D DC resisti-vity forward modeling method and its application in gas reservoir fracturing monitoring in Qinshui Basin[J]. Oil Geophysical Prospecting, 2021, 56(1): 209-216. |
| [19] |
周印明, 王金海, 胡晓颖, 等. 基于矢量位和标量位的广域电磁法三维有限元数值模拟[J]. 石油地球物理勘探, 2021, 56(1): 181-189. ZHOU Yinming, WANG Jinhai, HU Xiaoying, et al. WFEM 3D finite element numerical simulation based on vector potential and scalar potential[J]. Oil Geophysical Prospecting, 2021, 56(1): 181-189. |
| [20] |
朱成, 李桐林, 杨海斌, 等. 带地形频率域可控源电磁法三维反演研究[J]. 石油地球物理勘探, 2016, 51(5): 1031-1039. ZHU Cheng, LI Tonglin, YANG Haibin, et al. Three dimensional finite element numerical simulation of wide-area electromagnetic method based on vector and scalar potentials[J]. Oil Geophysical Prospecting, 2016, 51(5): 1031-1039. |
| [21] |
粟琪, 戴世坤, 赵东东. 可控源电磁法2.5维自适应有限元各向异性正反演[J]. 石油地球物理勘探, 2018, 53(2): 418-429. SU Qi, DAI Shikun, ZHAO Dongdong. Forward and backward modeling of 2.5-dimensional adaptive finite element anisotropy by CSAMT[J]. Oil Geophysical Prospecting, 2018, 53(2): 418-429. |
| [22] |
汤井田, 张林成, 公劲喆, 等. 三维频率域可控源电磁法有限元-无限元结合数值模拟[J]. 中南大学学报(自然科学版), 2014, 45(4): 1251-1260. TANG Jingtian, ZHANG Lincheng, GONG Jinzhe, et al. 3D frequency domain controlled source electromagnetic numerical modeling with coupled finite-infinite element method[J]. Journal of Central South University(Science and Technology), 2014, 45(4): 1251-1260. |
| [23] |
Astley R J, Macaulay G J, Coyette J P. Mapped wave envelope elements for acoustical radiation and scatte-ring[J]. Journal of Sound and Vibration, 1994, 170(1): 97-118. DOI:10.1006/jsvi.1994.1048 |
| [24] |
Blome M, Maurer H R, Schmidt K. Advances in three-dimensional geoelectric forward solver techniques[J]. Geophysical Journal International, 2009, 176(3): 740-752. DOI:10.1111/j.1365-246X.2008.04006.x |
| [25] |
Nath G H, Tromp J. A spectral-infinite-element solution of Poisson's equation: an application to self gravity[J]. arXiv.org, 2017, 6. |
| [26] |
Nath G H, Leah L, Jeroen T. Spectral infinite element simulations of earthquake induced gravity perturbations[J]. Geophysical Journal International, 2019, 217(1): 451-468. DOI:10.1093/gji/ggz028 |
| [27] |
公劲喆. 有限元-无限元耦合法在三维直流电和电磁数值模拟中的应用[D]. 湖南长沙: 中南大学, 2010. GONG Jinzhe. Application of Finite-Infinite Element Coupling Method on 3D Electric and Electromagnetic Numerical Modeling[D]. Central South University, Changsha, Hunan, 2010. |
| [28] |
汤井田, 原源, 周聪. 有限元-无限元耦合法在复杂金属矿体电阻率/极化率正演模拟中的应用——以庐枞盆地泥河铁矿床为例[J]. 地球物理学进展, 2013, 28(3): 1234-1242. TANG Jingtian, YUAN Yuan, ZHOU Cong. Application of finite-infinite element couple method in forward modeling of complex metal ore body: examples of Luzong, Nihe iron deposit[J]. Progress in Geophysics, 2013, 28(3): 1234-1242. |
| [29] |
Nabighian M N. Electromagnetic Methods in Applied Geophysics[M]. SEG Press, 1988.
|
| [30] |
Jin J M. The Finite Element Method in Electromagnetics[M]. John Wiley & Sons, 2014.
|
| [31] |
张秋光. 场论[M]. 北京: 地质出版社, 1983.
|



 胡宏伶, 湖南省长沙市麓山路36号湖南师范大学数学与统计学院, 410081。Email:
胡宏伶, 湖南省长沙市麓山路36号湖南师范大学数学与统计学院, 410081。Email: 